计量经济学计算题解法汇总
计量经济学大题例题

计量经济学大题例题计量经济学大题例题的正文如下:计量经济学大题是考研数学三中一个重要的部分,其中涉及到大量的计算和分析。
下面,我们将通过几个例题来讲解计量经济学大题的解题方法。
例题 1:某公司预计未来两年会有 20% 的增长率,当前股价为10 元。
该公司预计未来三年会有 15% 的增长率,此时股价为 8 元。
假设市场对公司未来的增长前景持乐观态度,请问能否通过公司未来的增长率来判断公司的投资价值?解答:我们可以使用现值公式来解决这道题。
设该公司的未来两年和未来三年的现金流分别为 C1、C2 和 C3,则它们的现值分别为: C1=10×(1+20%)=12.10 元C2=8×(1+15%)=9.39 元C3=10×(1+15%)×(1+20%)=12.31 元因此,现值为 12.10 元的现金流比现值为 9.39 元的现金流更具有投资价值。
例题 2:假设某公司预计未来三年会有 20%、25% 和 30% 的增长率,此时市场对公司未来的增长前景持乐观态度,请问能否通过公司未来的增长率来判断公司的投资价值?解答:与上一个问题类似,我们可以使用现值公式来解决这道题。
设该公司的未来两年和未来三年的现金流分别为 C1、C2 和 C3,则它们的现值分别为:C1=10×(1+20%)=12.10 元C2=8×(1+25%)=9.75 元C3=10×(1+30%)=12.00 元因此,现值为 12.10 元的现金流比现值为 9.75 元的现金流更具有投资价值。
以上两道题是计量经济学大题中比较典型的例题,希望大家能够熟练掌握它们的解题方法。
同时,我们也可以通过不断练习来提高自己的解题能力,从而在考试中取得优异的成绩。
拓展:除了上述例题之外,计量经济学大题还有很多其他类型的例题,例如面板数据模型、自回归移动平均模型等。
下面,我们举一个例子来说明面板数据模型的解题方法。
计量经济学计算题与答案解析

1、根据某城市1978——1998年人均储蓄(y)与人均收入(x)的数据资料建立了如下回归模型x y6843.1521.2187ˆ+-= se=(340.0103)(0.0622)6066.733,2934.0,425.1065..,9748.02====F DW E S R试求解以下问题:(1)取时间段1978——1985和1991——1998,分别建立两个模型。
模型1:x y3971.04415.145ˆ+-= 模型2:x y 9525.1365.4602ˆ+-= t=(-8.7302)(25.4269) t=(-5.0660)(18.4094) ∑==202.1372,9908.0212eR ∑==5811189,9826.0222e R计算F 统计量,即∑∑===9370.4334202.137258111892122eeF ,对给定的05.0=α,查F 分布表,得临界值28.4)6,6(05.0=F 。
请你继续完成上述工作,并回答所做的是一项什么工作,其结论是什么?(2)根据表1所给资料,对给定的显著性水平05.0=α,查2χ分布表,得临界值81.7)3(05.0=χ,其中p=3为自由度。
请你继续完成上述工作,并回答所做的是一项什么工作,其结论是什么? 表1F-statistic 6.033649 Probability 0.007410 Obs*R-squared10.14976 Probability0.017335Test Equation:Dependent Variable: RESID^2 Method: Least SquaresDate: 06/04/06 Time: 17:02 Sample(adjusted): 1981 1998Included observations: 18 after adjusting endpoints Variable Coefficie ntStd. Error t-Statistic Prob. C244797.2 373821.3 0.654851 0.5232 RESID^2(-1)1.226048 0.3304793.7099080.0023RESID^2(-2) -1.405351 0.379187 -3.706222 0.0023 R-squared 0.563876 Mean dependent var 971801.3 Adjusted R-squared 0.470421 S.D. dependent var 1129283. S.E. of regression 821804.5 Akaike info criterion 30.26952 Sum squared resid 9.46E+12 Schwarz criterion 30.46738 Log likelihood -268.4257 F-statistic6.033649 Durbin-Watson stat 2.124575 Prob(F-statistic) 0.0074101、(1)解:该检验为Goldfeld-Quandt 检验。
天津财经大学《计量经济学》(多元例题综合答案).

ˆ 2
2 x y x 2 1 x1 y x1x2
xi X i X
∑X1i=47.5 ∑x1i2=31.83 ∑yix1i=15.28 ∑yi2=7.37 ,
yi Yi Y
∑X2i=19.5 ∑x2i2=7.27
n=10
( 1)对我国 1991~2000 年的消费模型Yi 0 1 X 1i 2 X 2i u i 进行估计
结果表明,当前一期人均居民消费额(X ) 保持不变时,人均国内生产总值( X )每 增加 1 千元,人均居民消费额(Y)平均 增加 0.339 千元;当人均国内生产总值(X ) 保持不变时,前一期人均居民消费额( X ) 每增加 1 千元,人均居民消费额(Y)平均 增加 0.302 千元。
2
1
1
2
ˆ 不是由 0 这样的 检验结果表明,在 95%置信概率下, 1 1 总体产生的,1 显著地不为 0,即变量X 1 对被解释变量的影 响是显著的;也就是说,在 95%的置信概率下,人均国内生 产总值对人 2 0 ˆ 0.302 0 2 2 t 5.298 ˆ 0.057 SE ( 2 ) t0.025 , 7 2.365 t t0.025 , 7
≈0.026
t ,n k 1 t 0.025 ,7 2.365
2
P3.946 E (Y
P 4.007 2.365 * 0.026 E (Y 0) 4.007 2.365 * 0.026 1 0.05
计量经济学习题集及详解答案

第一章绪论一、填空题:1.计量经济学是以揭示经济活动中客观存在的为内容的分支学科,挪威经济学家弗里希,将计量经济学定义为、、三者的结合。
2.数理经济模型揭示经济活动中各个因素之间的关系,用性的数学方程加以描述,计量经济模型揭示经济活动中各因素之间的关系,用性的数学方程加以描述。
3.经济数学模型是用描述经济活动。
4.计量经济学根据研究对象和内容侧重面不同,可以分为计量经济学和计量经济学。
5.计量经济学模型包括和两大类。
6.建模过程中理论模型的设计主要包括三部分工作,即、、。
7.确定理论模型中所包含的变量,主要指确定。
8.可以作为解释变量的几类变量有变量、变量、变量和变量。
9.选择模型数学形式的主要依据是。
10.研究经济问题时,一般要处理三种类型的数据:数据、数据和数据。
11.样本数据的质量包括四个方面、、、。
12.模型参数的估计包括、和软件的应用等内容。
13.计量经济学模型用于预测前必须通过的检验分别是检验、检验、检验和检验。
14.计量经济模型的计量经济检验通常包括随机误差项的检验、检验、解释变量的检验。
15.计量经济学模型的应用可以概括为四个方面,即、、、。
16.结构分析所采用的主要方法是、和。
二、单选题:1.计量经济学是一门()学科。
A.数学B.经济C.统计D.测量2.狭义计量经济模型是指()。
A.投入产出模型B.数学规划模型C.包含随机方程的经济数学模型D.模糊数学模型3.计量经济模型分为单方程模型和()。
A.随机方程模型B.行为方程模型C.联立方程模型D.非随机方程模型4.经济计量分析的工作程序()A.设定模型,检验模型,估计模型,改进模型B.设定模型,估计参数,检验模型,应用模型C.估计模型,应用模型,检验模型,改进模型D.搜集资料,设定模型,估计参数,应用模型5.同一统计指标按时间顺序记录的数据列称为()A.横截面数据B.时间序列数据C.修匀数据D.平行数据6.样本数据的质量问题,可以概括为完整性、准确性、可比性和()。
计量经济学计算题汇总

计量经济学计算题汇总————————————————————————————————作者:————————————————————————————————日期:计量经济学计算题总结1、表中所列数据是关于某种商品的市场供给量Y和价格水平X的观察值:①用OLS法拟合回归直线;②计算拟合优度R2;③确定β1是否与零有区别。
2、求下列模型的参数估计量,3、设某商品需求函数的估计结果为(n=18):解:(1)45、模型式下括号中的数字为相应回归系数估计量的标准误。
又由t分布表和F分布表得知:t0.025(5)=2.57,t0.025(6)=2.45;F0.05(3,6)=4.76,F0.05(4,5)=5.19,试根据上述资料,对所给出的两个模型进行检验,并选择出一个合适的模型。
解:(1)总离差平方和的自由度为n-1,所以样本容量为35。
(2)(3)7.某商品的需求函数为其中,Y 为需求量,X1为消费者收入,X2为该商品价格。
(1)解释参数的经济意义。
(2)若价格上涨10%将导致需求如何变化?(3)在价格上涨10%情况下,收入增加多少才能保持需求不变。
(4)解释模型中各个统计量的含义。
220.6114384126783/(1)10.587/(1)ESS R TSS RSS n k R TSS n ===--=-=-ESS/k解:(1)由样本方程的形式可知,X1的参数为此商品的收入弹性,表示X2的参数为此商品的价格弹性。
(2)由弹性的定义知,如果其它条件不变,价格上涨10%,那么对此商品的需求量将下降1.8%。
8、 现有X 和Y 的样本观察值如下表: X 2 5 10 4 10 Y 4 7 4 5 9假设Y 对X 的回归模型为:试用适当的方法估计此回归模型。
9、10112、某地区家庭消费C,除依赖于收入Y之外,还同下列因素有关:(1)民族:汉,少数民族(2)家庭月收入:500元以下,500—1000元,1000元以上(3)家庭的文化程度:高中以下,高中,大专以上试设定该地区消费函数的回归模型。
计量经济学 课后练习题答案解析
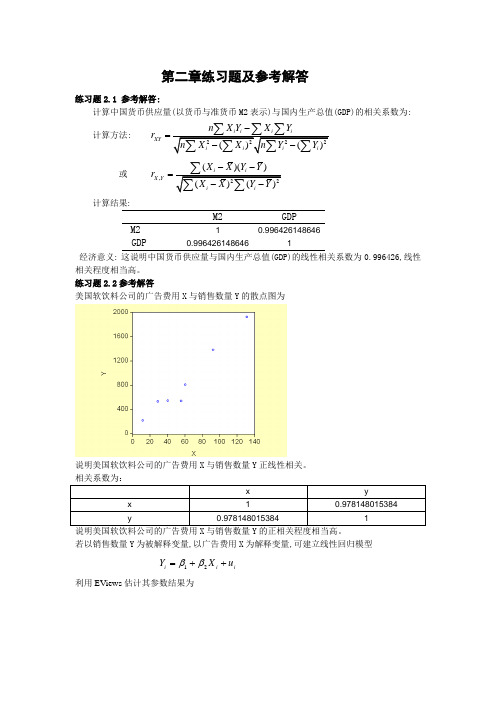
第二章练习题及参考解答练习题2.1 参考解答:计算中国货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相关系数为:计算方法: XY n X Y X Y r -=或,()()X Y X X Y Y r --=计算结果:M2GDPM2 10.996426148646GDP0.9964261486461经济意义: 这说明中国货币供应量与国内生产总值(GDP)的线性相关系数为0.996426,线性相关程度相当高。
练习题2.2参考解答美国软饮料公司的广告费用X 与销售数量Y 的散点图为说明美国软饮料公司的广告费用X 与销售数量Y 正线性相关。
相关系数为:说明美国软饮料公司的广告费用X 与销售数量Y 的正相关程度相当高。
若以销售数量Y 为被解释变量,以广告费用X 为解释变量,可建立线性回归模型 i i i u X Y ++=21ββ 利用EViews 估计其参数结果为经t 检验表明, 广告费用X 对美国软饮料公司的销售数量Y 确有显著影响。
回归结果表明,广告费用X 每增加1百万美元, 平均说来软饮料公司的销售数量将增加14.40359(百万箱)。
练习题2.3参考解答:1、 建立深圳地方预算内财政收入对GDP 的回归模型,建立EViews 文件,利用地方预算内财政收入(Y )和GDP 的数据表,作散点图可看出地方预算内财政收入(Y )和GDP 的关系近似直线关系,可建立线性回归模型: t t t u GDP Y ++=21ββ 利用EViews 估计其参数结果为即 ˆ20.46110.0850t tY GDP =+ (9.8674) (0.0033)t=(2.0736) (26.1038) R 2=0.9771 F=681.4064经检验说明,深圳市的GDP 对地方财政收入确有显著影响。
20.9771R =,说明GDP 解释了地方财政收入变动的近98%,模型拟合程度较好。
模型说明当GDP 每增长1亿元时,平均说来地方财政收入将增长0.0850亿元。
(完整word版)计量经济学题库(超完整版)及答案.详解(word文档良心出品)

计量经济学题库计算与分析题(每小题10分)1X:年均汇率(日元/美元) Y:汽车出口数量(万辆)问题:(1)画出X 与Y 关系的散点图。
(2)计算X 与Y 的相关系数。
其中X 129.3=,Y 554.2=,2X X 4432.1∑(-)=,2Y Y 68113.6∑(-)=,()()X X Y Y ∑--=16195.4 (3)采用直线回归方程拟和出的模型为 ˆ81.72 3.65YX =+ t 值 1.2427 7.2797 R 2=0.8688 F=52.99解释参数的经济意义。
2.已知一模型的最小二乘的回归结果如下:i iˆY =101.4-4.78X 标准差 (45.2) (1.53) n=30 R 2=0.31 其中,Y :政府债券价格(百美元),X :利率(%)。
回答以下问题:(1)系数的符号是否正确,并说明理由;(2)为什么左边是iˆY 而不是i Y ; (3)在此模型中是否漏了误差项i u ;(4)该模型参数的经济意义是什么。
3.估计消费函数模型i i i C =Y u αβ++得i i ˆC =150.81Y + t 值 (13.1)(18.7) n=19 R 2=0.81其中,C :消费(元) Y :收入(元)已知0.025(19) 2.0930t =,0.05(19) 1.729t =,0.025(17) 2.1098t =,0.05(17) 1.7396t =。
问:(1)利用t 值检验参数β的显著性(α=0.05);(2)确定参数β的标准差;(3)判断一下该模型的拟合情况。
4.已知估计回归模型得i i ˆY =81.7230 3.6541X + 且2X X 4432.1∑(-)=,2Y Y 68113.6∑(-)=, 求判定系数和相关系数。
5.有如下表数据(1拟合什么样的模型比较合适? (2)根据以上数据,分别拟合了以下两个模型:模型一:16.3219.14P U=-+ 模型二:8.64 2.87P U =- 分别求两个模型的样本决定系数。
计量经济学题库(超完整版)及标准答案

2.已知一模型的最小二乘的回归结果如下:i iˆY =101.4-4.78X 标准差 (45.2) (1.53) n=30 R 2=0.31其中,Y :政府债券价格(百美元),X :利率(%)。
回答以下问题:(1)系数的符号是否正确,并说明理由;(2)为什么左边是iˆY 而不是i Y ; (3)在此模型中是否漏了误差项i u ;(4)该模型参数的经济意义是什么。
13.假设某国的货币供给量Y 与国民收入X 的历史如系下表。
某国的货币供给量X 与国民收入Y 的历史数据年份 X Y 年份 X Y 年份 X Y 1985 2.0 5.0 1989 3.3 7.2 1993 4.8 9.7 1986 2.5 5.5 1990 4.0 7.7 1994 5.0 10.0 1987 3.2 6 1991 4.2 8.4 1995 5.2 11.2 19883.6719924.6919965.812.4根据以上数据估计货币供给量Y 对国民收入X 的回归方程,利用Eivews 软件输出结果为:Dependent Variable: Y Variable Coefficient Std. Error t-Statistic Prob. X 1.968085 0.135252 14.55127 0.0000 C 0.353191 0.5629090.6274400.5444 R-squared0.954902 Mean dependent var 8.258333 Adjusted R-squared 0.950392 S.D. dependent var 2.292858 S.E. of regression 0.510684 F-statistic 211.7394 Sum squared resid2.607979Prob(F-statistic)0.000000问:(1)写出回归模型的方程形式,并说明回归系数的显著性(0.05α=)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计量经济学:部分计算题解法汇总
1、求判别系数——R^2
已知估计回归模型得
i i ˆY =81.7230 3.6541X + 且2X X 4432.1∑
(-)=,2
Y Y 68113.6∑(-)=,
2、置信区间
、
有10户家庭的收入(X ,元)和消费(Y ,百元)数据如下表:
10户家庭的收入(X )与消费(Y )的资料
X 20 30 33 40 15 13 26
) 38
35 43 Y 7 9 8 11 5 4 | 8
10 9
10
若建立的消费Y 对收入X 的回归直线的Eviews 输出结果如下:
Dependent Variable: Y %
Adjusted R-squared —
F-statistic (1(2)在95%的置信度下检验参数的显著性。
(0.025(10) 2.2281t =,0.05(10) 1.8125t =,0.025(8) 2.3060t =,0.05(8) 1.8595t =)
(3)在90%的置信度下,预测当X =45(百元)时,消费(Y )的置信区间。
(其中29.3x =,2()992.1x x -=∑)
~
答:(1)回归模型的R 2=,表明在消费Y 的总变差中,由回归直线解释的部分占到90%以
上,回归直线的代表性及解释能力较好。
(2分)
家庭收入对消费有显著影响。
(2分)对于截距项,
检验。
(2分)
(3)Y f =+×45=(2分)
90%置信区间为(,+),即(,)。
(2分)
注意:a 水平下的t 统计量的的重要性水平,由于是双边检验,应当减半
3、求SSE 、SST 、R^2等
已知相关系数r =,估计标准误差ˆ8σ=,样本容量n=62。
~
求:(1)剩余变差;(2)决定系数;(3)总变差。
(2)2
2
2
0.60.36R r ===(2分)
4、联系相关系数与方差(标准差),注意是n-1
在相关和回归分析中,已知下列资料:
222X Y i 1610n=20r=0.9(Y -Y)=2000σσ∑=,=,,,。
(1)计算Y 对X 的回归直线的斜率系数。
(2)计算回归变差和剩余变差。
(3)
:
(2)R 2=r 2==,
总变差:TSS =RSS/(1-R 2)=2000/=(2分)
有个疑问
注意:用Eviews 或者是SAS 给出的结果中可以不用查表求t 值,因为用概率求解是同样的结果。
~
推导出一个1ˆβ
求解的公式:
两边ln 1ˆ
β表示弹性,如果一边则表示绝对量(相对量)的变化引起相对量(绝对量)的变
化。
特例::
5、异方差的修正
设消费函数为01i i i y b b x u =++,其中
i y 为消费支出,i x 为个人可支配收入,
i u 为随机误差项,并且22()0,()i i i E u Var u x σ==(其中2σ为常数)。
试回答
以下问题:
(1)选用适当的变换修正异方差,要求写出变换过程;(2)写出修正异方差后的参数估计量的表达式。
…
解:(一)原模型:01i i i y b b x u =++ (1)等号两边同除以i x ,
则:(2)变为
**10i i i y b b x v =++ (2分)
(二)对
**10i i i y b b x v =++进行普通最小二乘估计
(进一步带入计算也可)
6、类似的ML 检验:
$
检验下列模型是否存在异方差性,列出检验步骤,给出结论。
0112233t t t t t y b b x b x b x u =++++
样本共40个,本题假设去掉c=12个样本,假设异方差由1i x 引起,数值小的一组残差平方和为10.46617RSS E =-,数值大的一组平方和为20.3617RSS E =-。
0.05(10,10) 2.98F =
解:(1)01:; :;t t H u H u 为同方差性为异方差性(2分) (2)120.46617
1.290.3617
RSS E F RSS E -=
==-(3分) (3)0.05(10,10) 2.98F =(2分)
(4)0.05(10,10)F F ≤,接受原假设,认为随机误差项为同方差性。
(3分)
>。
