第三章扭转(习题解答)
(仅供参考)第3章扭转作业参考解答
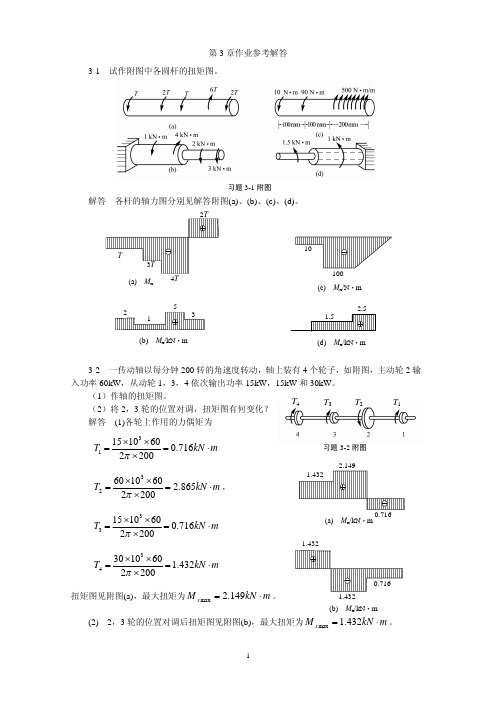
第3章作业参考解答3-1 试作附图中各圆杆的扭矩图。
习题3-1附图解答 各杆的轴力图分别见解答附图(a)、(b)、(c)、(d)。
3-2 一传动轴以每分钟200转的角速度转动,轴上装有4个轮子,如附图,主动轮2输入功率60kW ,从动轮1,3,4依次输出功率15kW ,15kW 和30kW 。
(1)作轴的扭矩图。
(2)将2,3轮的位置对调,扭矩图有何变化? 解答 (1)各轮上作用的力偶矩为m kN T ×=´´´=716.0200260101531pm kN T ×=´´´=865.2200260106032p ,m kN T ×=´´´=716.0200260101533pm kN T ×=´´´=432.1200260103034p扭矩图见附图(a),最大扭矩为m kN M x ×=149.2max 。
(2) 2,3轮的位置对调后扭矩图见附图(b),最大扭矩为m kN M x ×=432.1max 。
(a) M x(c) M x /N ·m(b)M x /kN ·m(d) M x /kN ·m习题3-2附图T 1T 2 T 3 T 4 (a)M x /kN ·m1.432(b) M x /kN ·m3-3 一直径d =60mm 的圆杆,其两端受T =2kN·m 的外力偶矩作用而发生扭转,如附图示。
设轴的切变模量G =80GPa 。
试求横截面上1,2,3点处的切应力和最大切应变,并在此三点处画出切应力的方向。
解答 1,2,3点处的切应力分别为MPaMPa W T p 4.313/22.4716/06.014.320000.031332===´===t t t t 切应力方向见附图(1)。
材料力学第三章答案

材料力学第三章答案材料力学第三章答案【篇一:材料力学习题册答案-第3章扭转】是非判断题二、选择题0 b 2t?d316?1?? ? b wp??d316?1?? ?2c wp??d316?1?? ? d w3p??d316?1?? ?46.对于受扭的圆轴,关于如下结论:①最大剪应力只出现在横截面上;②在横截面上和包含杆件的纵向截面上均无正应力;③圆轴内最大拉应力的值和最大剪应力的值相等。
现有四种答案,正确的是( a )a ②③对b①③对c①②对d 全对7.扭转切应力公式?mnp?i?适用于(d)杆件。
pa 任意杆件;b 任意实心杆件;c 任意材料的圆截面;d 线弹性材料的圆截面。
9.若将受扭实心圆轴的直径增加一倍,则其刚度是原来的( d a 2倍; b 4倍; c 8倍; d 16倍。
三、计算题1.试用截面法求出图示圆轴各段内的扭矩t,并作扭矩图2.图示圆轴上作用有四个外力偶矩me1 =1kn/m, me2 =0.6kn/m,)me3= me4 =0.2kn/m, ⑴试画出该轴的扭矩图;⑵若me1与me2的作用位置互换,扭矩图有何变化?(1)(2)解:me1与me2的作用位置互换后,最大扭矩变小。
3.如图所示的空心圆轴,外径d=100㎜,内径d=80㎜,m=6kn/m,m=4kn/m.请绘出轴的扭矩图,并求出最大剪应力解:扭矩图如上,则轴面极惯性矩id4?d4)(1004?804)(10?3)4p=?(32??32?5.8?10?6m4㎜,l=500tr4?103?50?103ip5.8?104.图示圆形截面轴的抗扭刚度为g ip,每段长1m,试画出其扭矩图并计算出圆轴两端的相对扭转角。
ab+ad=cdab=t1l?90?gipgipad=bc=t2l100gipgipcd=t3l40gipgip?90?100?4050?gipgip【篇二:《材料力学》第3章扭转习题解】[习题3-1] 一传动轴作匀速转动,转速n?200r/min,轴上装有五个轮子,主动轮ii输入的功率为60kw,从动轮,i,iii,iv,v依次输出18kw,12kw,22kw和8kw。
第3章 扭 转(答案)
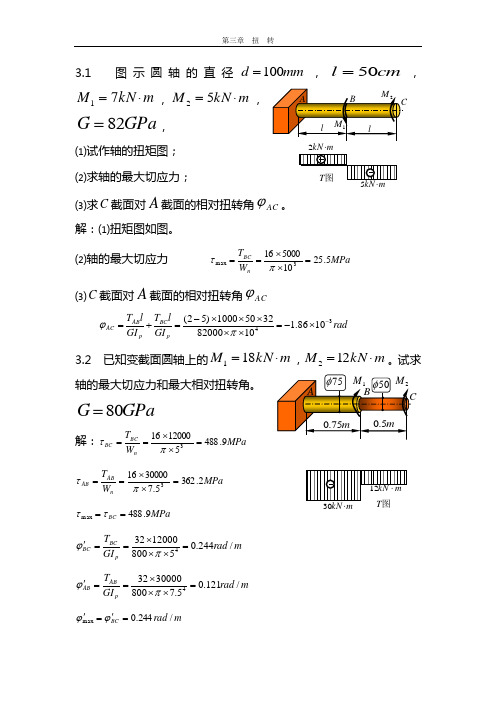
3.1 图示圆轴的直径mm d 100=,cm l 50=,m kN M ⋅=71,m kN M ⋅=52,GPaG 82=,⑴试作轴的扭矩图; ⑵求轴的最大切应力; ⑶求C 截面对A 截面的相对扭转角AC ϕ。
解:⑴扭矩图如图。
⑵轴的最大切应力 MPa W T n BC 5.25105000163max =⨯⨯==πτ ⑶C 截面对A 截面的相对扭转角AC ϕrad GI l T GI l T p BC p AB AC 341086.1108200032501000)52(-⨯-=⨯⨯⨯⨯⨯-=+=πϕ 3.2 已知变截面圆轴上的m kN M ⋅=181,m kN M ⋅=122。
试求轴的最大切应力和最大相对扭转角。
GPaG 80=解:MPa W T n BC BC 9.488512000163=⨯⨯==πτ MPa W T n AB AB 2.3625.730000163=⨯⨯==πτ MPa BC 9.488max ==ττm rad GI T p BC BC/244.0580012000324=⨯⨯⨯=='πϕ m rad GI T p AB AB /121.05.780030000324=⨯⨯⨯=='πϕ m rad BC /244.0max='='ϕϕmkN ⋅2mkN ⋅303.3 图示钢圆轴(GPaG 80=)所受扭矩分别为m kN M ⋅=801,m kN M ⋅=1202,及m kN M ⋅=403。
已知:cm L 301= ,cm L 702=,材料的许用切应力MPa 50][=τ,许用单位长度扭转角m /25.0][='ϕ解:按强度条件][maxmax ττ≤=nW T 计算 mm T d 20110508000016][16363=⨯⨯⨯=≥πτπ 按强度条件][maxmaxϕϕ'≤='pGI T 计算 mm G T d 8.21925.010801808000032][324924max =⨯⨯⨯⨯⨯='≥πϕπ 故,轴的直径取mm d 220≥3.4 实心轴和空心轴通过牙嵌离合器连在一起,已知轴的转速min /100r n =,传递功率kW P 35.7=,MPa 20][=τ。
扭转习题

第三章 扭转习题一、单项选择题1、横截面都为圆的两个杆,直径分别为d 和D ,并且d=。
两杆横截面上扭矩相等两杆横截面上的最大切应力之比maxDmaxdττ为A 、2倍,B 、4倍,C 、8倍,D 、16倍。
二、1、扭转变形时,公式pTlGI τ=中的 表示单位长度的扭转角,公式中的T 表示横截面上的 ;G 表示杆材料的 弹性模量;I P 表示杆横截面对形心的 ;GI P 表示杆的抗扭 。
2、截面为圆的杆扭转变形时,所受外力偶的作用面与杆的轴线 .3、实心圆轴扭转时,横截面上的切应力分布是否均匀,横截面上离圆心愈远的点处切应力 ,圆心处的切应力为 ,圆周上切应力4、两根实心圆轴的直径d 和长度L 都相同,而材料不同,在相同扭矩作用下,它们横截面上的最大切应力是否相同 ,单位长度的扭转角是否相同 。
5、剪切虎克定律的表达式 G τγ=,式中的G 表示材料的 模量,式中的γ称为 。
6、根据切应力互等定理,单元体两互相垂直截面上在其相交处的切应力成对存在, 且 相等,而 现反。
三、 1、如图所示圆轴,一端固定。
圆轴横截面的直径D=100mm ,所受的外力偶矩M 1=6kN•m,M 2=4kN•m。
试求圆轴横截面上的最大扭矩和最大切应力。
答:圆轴横截面上的最大扭矩为 kN•m;圆轴横截面上的最大切应力为 Mpa 。
2、如图所示阶梯形圆轴,一端固定。
圆轴横截面的直径分别为外力偶矩M C =1200 N•m,M B =1800 N•m。
试求BC 段横截面上的扭矩和该阶梯轴的最 大切应力。
答:BC 段横截面上的扭矩为 N•m;该阶梯轴的最大切应力为 Mpa 。
3、如图所示圆轴,一端固定。
圆轴横截面的直径d=100mm ,所受的外力偶矩M 1=7000 N•mM 2=5000 N•m。
试求圆轴横截面上的最大扭矩和最大切应力。
答:最大扭矩为 N •m 。
最大切应力为 Mpa 。
4、某传动轴为实心圆轴,轴内的最大扭矩=1.5kN m T g,许用切应力[]=50MPa τ,试确定该轴的横截面直径。
材料力学_陈振中_习题第三章扭转
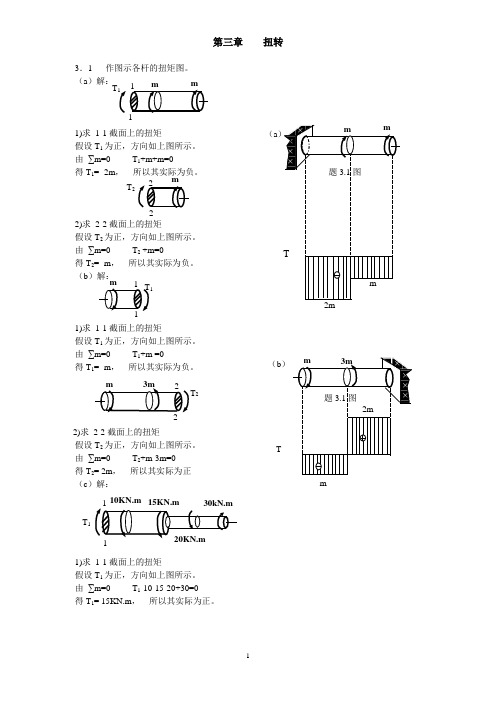
第三章 扭转3.1 作图示各杆的扭矩图。
(a )解:1)求 1-1截面上的扭矩假设T 1为正,方向如上图所示。
由 ∑m=0 T 1+m+m=0得T 1= -2m , 所以其实际为负。
2)求 2-2截面上的扭矩假设T 2为正,方向如上图所示。
由 ∑m=0 T 2 +m=0得T 2= -m , 所以其实际为负。
(b )解:1)求 1-1截面上的扭矩假设T 1为正,方向如上图所示。
由 ∑m=0 T 1+m =0得T 1= -m , 所以其实际为负。
2)求 2-2截面上的扭矩假设T 2为正,方向如上图所示。
由 ∑m=0 T 2+m-3m=0 得T 2= 2m , 所以其实际为正 (c )解:1)求 1-1截面上的扭矩假设T 1为正,方向如上图所示。
由 ∑m=0 T 1-10-15-20+30=0得T 1= 15KN.m , 所以其实际为正。
T 1T 2(a2(b )mTT 12)求 2-2截面上的扭矩假设T 2为正,方向如上图所示。
由 ∑m=0 T 2-15-20+30=0得T 2= 5KN.m , 所以其实际为正。
3)求 3-3截面上的扭矩 假设T 3为正,方向如上图所示。
由 ∑m=0 T 3-20+30=0得T 3= -10KN.m , 所以其实际为负。
4)求 4-4截面上的扭矩假设T 4为正,方向如上图所示。
由 ∑m=0 T 4 +30=0得T 4= -30KN.m , 所以其实际为负。
3.2 T 为圆杆横截面上的扭矩,试画出截面上与T 对应的剪应力分布图。
解:3.5 D=50mm 直径的圆轴,受到扭矩T=2.15KN .m 的作用。
试求在距离轴心10mm 处的剪应力,并求轴横截面上的最大剪应力。
T 230kN.m T 3T 4(题3.2图(a ) (b )解:求距离轴心10mm 处的剪应力, 由 I P =πD 4/32=π×0.054/32=6.13×10-7 m 4 W t = I P /R=6.13×10-7/0.025=2.454×10-5 m 3τρ=Tρ/ I P =2.15×103×10×10-3/(6.13 ×10-7 ) =35MPa求轴横截面上的最大剪应力τmax =T/ W t =2.15×103/(2.454 ×10-5 ) =87.6MPa3.8 阶梯形圆轴直径分别为d 1=40mm ,d 2=70mm ,轴上装有三个皮带轮,如图所示。
材料力学复习题第三章 扭 转

第三章 扭 转一、判断题1.圆杆受扭时,杆内各点均处于纯剪切状态。
( ) 2.非圆截面杆不能应用圆杆扭转切应力公式,是因为非圆截面杆扭转时“平面假设”不能成立。
( ) 3.当剪应力超过材料的剪切比例极限时,剪应力互等定律亦成立。
( ) 4.一点处两个相交面上的剪应力大小相等,方向指向(或背离)该两个面的交线。
( ) 5.直径和长度相同,材料不同的两根轴,受相同的扭转力偶矩作用,它们的最大剪应力和最大扭转角都相同。
6. 杆件受扭时,横截面上最大切应力发生在距截面形心最远处。
( )7. 薄壁圆管和空心圆管的扭转切应力公式完全一样。
( )8. 圆杆扭转变形实质上是剪切变形。
( )9. 横截面的角点处的切应力必为零。
( ) 1.√ 2.√ 3.√ 4.× 5.× 6.×(非圆截面) 7.× 8.√ 9.× 二、单项选择题1. 图示圆轴曲面C 左、右两侧的扭矩MC+和M C-的( )。
A .大小相等,正负号相同;B .大小不等,正负号相同; C .大小不等,正负号不同;D .大小相等,正负号不同。
2. 直径为D 的实心圆轴,两端受扭转力矩作用。
轴内最大剪应力τ,若轴的直径改为D/2,则轴内的最大剪应力变为( )。
A .2τ; B .τ; C . 8τ; D .16τ。
3. 阶梯圆轴的最大切应力发生在( )。
A .扭矩最大的截面;B .直径最小的截面;C .单位长度扭转角最大的截面;D .不能确定。
4.空心圆轴的外径为D ,内径为d,α=d/D 。
其抗扭截面系数为( )。
A .()απ-=1163D W P ;B 。
()23116απ-=D W P ;C 。
()33116απ-=D W PD .()43116απ-=D WP5.扭转的切应力公式ρτρPPI M =适用于( )杆件。
A .任意截面; B .任意实心截面;C .任意材料的圆截面; D .线弹性材料的圆面。
【精品】材料力学复习题第三章 扭 转.docx

第三章扭转一、判断题1.圆杆受扭时,杆内各点均处于纯剪切状态。
()2.非圆截面杆不能应用圆杆扭转切应力公式,是因为非圆截面杆扭转时“平面假设”不能成立。
()3.当剪应力超过材料的剪切比例极限时,剪应力互等定律亦成立。
()4.一点处两个相交面上的剪应力大小相等,方向指向(或背离)该两个而的交线。
()5.有径和长度柑同,材料不同的两根轴,受相同的扭转力偶矩作用,它们的最大剪应力和最大扭转角都相同。
6.杆件受扭时,横截面上最大切应力发生在距截面形心最远处。
7.薄星圆管和空心圆管的扭转切应力公式完全一样。
()&圆杆扭转变形实质上是剪切变形。
()9.横截面的角点处的切应力必为零。
()1.V2. V3. V4. X5. X6. X (非圆截面)7. X8. V9. X二、讥项选择题1.图示圆轴曲面C左、右两侧的扭矩血和的()。
—A.大小相等,止负号相同;B.大小不等,止负号相同;Q ({))cC.大小不等,正负号不同;D.大小相等,止负号不同。
》2.点径为D的实心圆轴,两端受扭转力矩作用。
轴内最大剪应力工,若轴的直径改为D/2,则轴内的绘大剪应力变为()o A. 2 T ;B. T; C. 8 T; D. 16 T O3.阶梯圆轴的最大切应力发生在()。
A.抓矩最大的截面:B.直径最小的截面;C.单位长度扭转角最大的截面;D.不能确定。
4.空心圆轴的外径为D,内径为d, a=d/Do其抗扭截面系数为()。
3 3 3宀)A.昭=晋(1 —a);B。
叫=晋(1 —c?);c。
必=^L(l-a3)D. W p5.扭转的切应力公式T=^p适用于()杆件。
° XA.任意截面;B.任意实心截面;C.任意材料的圆截面;D.线弹•性材料的圆面。
6.单位长度扭转角0与()无关。
A.杆的长度;B.扭矩;C.材料性质;D.截而的儿何性质。
7.切应力互等定理与剪切胡克定律的止确适用范围是()。
A.都只在比例极限范围内成立;B.超过比例极限时都成立;C. 切应力互等定理在比例极限范围内成立,剪切胡克定律不受比例极限限制;D. 剪切胡克立律在比例极限范围内成立,切应力互等定理不受比例极限限制。
3扭转 答案

第三章 圆轴的扭转一、填空题:1、扭矩,T2、G τγ=3、弹性范围内的等直圆杆4、。
5、2G d lϕ 二、选择题:B三、作图题1.分别画出图示三种截面上剪应力沿半径各点的分布规律。
:(a )圆截面 (b )空心圆截面 (c )薄壁圆截面2.将下列杆件的扭矩图画出。
m 122kN m1kN m T T =-⋅=⋅ ~四、计算题:1.一钻探机的功率为10kW ,转速n=180r/min 。
钻杆钻入土层的深度L=40m 。
如土壤对m,并作钻杆的扭矩图。
530.5N m =⋅ 530.5N m 13.26N m/m 40me M m l ⋅===⋅2、实心圆轴的直径d =100mm ,长l =1m ,其两端所受外力偶矩14kN m M =⋅作用,试求:图示截面上A ,B ,C 三点处剪应力的数值及方向。
M A AC B C OM25 B 100A C O B T τA τB τC解:6331410N mm 71.30MPa 100mm 16A B P T W ττπ⨯⋅====⨯ 136.65MPa 2C A ττ==;3、图示等直圆杆,已知外力偶矩M A =·m, M B =·m, M C =·m,许用剪应力[τ]=70MPa,许可单位长度扭转角[’]=1°/m,切变模量G =80GPa 。
试确定该轴的直径d 。
M B B1.0m A dM A0.5m C M C 解: 2.99kN m AB A T M =-=-⋅4.21kN m BC C T M ==⋅max 4.21kN m BC T T ==⋅对于BC 段按强度条件设计直径max max max 3p[]π16T T d W ττ==≤ 6max 331616 4.2110N mm 67mm π[]π70MPaT d τ⨯⨯⋅≥===⨯ 按刚度条件设计直径max max max 4p 180180[]πππ32T T d GI G ϕϕ''=⨯=⨯≤ max 4321801ππ[]T D G ϕ⇒≥⨯⨯'74mm ==0.3/m。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-1ab 作图求各杆的扭矩图 解:(1)轴的扭矩图分成二段,整个轴上无均布荷载扭矩图为间断水平线。
左段:m kN ⋅=6左T (背正)右段: m kN ⋅-=-=4106右T (指负背正),或m kN ⋅-=4右T (指负) (2)画扭矩图如图题3-1(a)所示。
从左至右,扭矩图的突变与外力偶矩转向一至,突变之值为外力偶的大小(从前往后看)m10kN 4kN mT (b )(a 题3-1(a )(b)T 图(kN m )4+题3-1(b )2m2m解:(1)轴的扭矩图分成二段,轴上的右段有均布荷载,该段扭矩图向下倾斜线段。
左段无均布荷载,扭矩图为水平线段。
左段:m kN ⋅=⨯=422AB T 右段: 0422=⋅=⨯=C B T T mkN(2)画扭矩图如图题3-1(b)所示。
扭矩图集中力偶处发生突变,而有均布力偶段扭矩图呈线性。
显而易见,A 端有大小为m kN ⋅4,力偶矩矢向左的外力偶。
3-2图示钢质圆轴,m kN m m l mm D ⋅===15,2.1,100。
试求:(1)n-n 截面上A 、B 、C 三点的剪应力数值及其方向(保留n-n 截面左段);(2)最大剪应力m ax τ;(3)两端截面的相对扭转角。
解:(1)圆轴受力偶作用面与轴线垂直的一对外力偶作用,发生扭转变形。
由于扭矩在整个轴内无变化,可不画扭矩图。
(2)扭转圆轴上各点的剪应力应在各自的横截面内,垂直于所在的“半径”,与扭矩的转向一致,如图3-2(c)所示。
由求扭转剪应力的公式知:MPa Pa D D T I T P B A 43.7621.0321.014.31015232434=⨯⨯⨯=⋅=⋅==πρττ MPa Pa D D T I T P C 21.3841.0321.014.31014432434=⨯⨯⨯=⋅=⋅=πρτ(2)最大剪应力m ax τ,圆轴发生扭转时,边缘各点的剪应力最大。
MPa B A 43.76max ===τττ(3)由公式求两端截面的相对扭转角。
31.1)(1029.21.03210802.110152493=⨯=⨯⨯⨯⨯⨯=⋅=-rad GI l T Pπϕ题3-2(c )+m A 52m A 53-T 图(b )题3-33-3图示钢制传动轴,A 为主动轮,B 、C 为从动轮,两从动轮转矩之比32=C Bm m ,轴径mm D 100=。
试按强度条件确定主动轮的容许转矩[]A m 。
解:(1)圆轴所受力偶的作用面与轴线垂直,轴发生扭转变形。
扭矩图如图所示,危险面是AC 各横截面,危险点是AC 段表面各点。
A m T 53max = (2)由强度条件确定主动轮的容许转矩[]A m[]mkN m N m m D m W T A A At⋅=⋅⨯⨯⨯⨯≤→⨯=≤⨯⨯⨯===63.194810601.0510601.05163165363633max max πτππτ []m kN m A ⋅=63.193-4某薄壁圆筒,其平均半径mm R 30=,壁厚mm t 2=,长度mm l 300=,当m kN T ⋅=2.1时,测得圆筒两端面间扭转角76.0=ϕ,试计算横截面上的剪应力和圆筒材料的剪变模量G 。
题3-41.2kN解:由薄壁圆筒剪应力公式计算横截面上的平均剪应力:MPa Pa t R T 106002.003.021200222=⨯⨯==ππτ,各点剪应力垂直于该点与圆心的连线,与扭矩转向一致。
(2)求圆筒材料的剪变模量G由剪切胡克定律可知:γτγτ=→=G G ……………………(a ) 由变形协调条件知:ll ϕργϕργ⋅=→⋅=⋅……………………(b )将(b )式代入(a )得:MPa Pa l R G 803.018076.003.0101066=⨯⨯⨯⨯=⋅⋅==πϕτγτ注意:若采用空心圆轴计算:3412412003110109.5586210(1())3262Pa MPa ρτπ--⨯⨯==⨯⨯⨯-12412424412000.31803212000.3101800.7679.958580.766210(1())62(1())326262G Pa GPaG πππ-⨯⨯⨯⨯=⨯→=⨯=⨯⨯⨯⨯-⨯⨯-3-5 某空心钢轴,内外直径之比8.0=α,传递功率kW P 60=,转速250=n 转/分,单位长度允许扭转角[]m /8.0=θ,试按强度条件与刚度条件选择内外径d 、D 。
解:(1)计算外力偶矩:m N ⋅=⨯==22922506095509550nP m A 圆轴受力偶作用面与轴线垂直的一对外力偶作用,发生扭转变形。
由于扭矩在整个轴内无变化,可不画扭矩图。
(2)按强度条件确定轴的外径D 1:()[]ταπτ≤-==431maxmax max 116D T W T t[]()()mm m m T D 69069.08.01106022921611634634max 1==-⨯⨯⨯⨯=-≥→πατπ(3)按刚度条件确定轴的外径D 2:()[][]()()mm m m G T D D GT GI T P 77077.08.018.010802292180321180321801321804492442max 2442maxmax max==-⨯⨯⨯⨯⨯⨯=-⨯≥→≤⨯-=⨯=παθπθπαππθ故,mm D D D 77),m ax (21==3-8图示钢制圆轴,受力和尺寸如图(a)所示。
试校核轴的强度和刚度。
T 图(kN m 题3-80.8(b)解:(1)圆轴所受力偶的作用面与轴线垂直,轴发生扭转变形。
扭矩图如图所示,AC 、AB 各横截面均是危险面,危险点是圆轴表面各点。
1)强度校核: AB :[]MPa MPa W T n ABt AB AB 6075.4704.0166003,max,=<=⨯==τπτAC :[]MPa MPa Pa W T n AC t AD AC 6088.1107.0168003,max,=<=⨯==τπτ 强度足够。
3)刚度校核:必须分段计算AB 、AC 两段。
AB :[]m m GI T P AB AB/1/71.118004.032108060018049=>=⨯⨯⨯⨯=⨯=θπππθAC :[]m m GI T AC P AC AC/1/243.018007.032108080018049,=≤=⨯⨯⨯⨯=⨯=θπππθ轴的刚度不够。
3-11一矩形截面杆,承受力偶m kN m ⋅=3.(1)计算最大剪应力m ax τ。
(2)若改用横截面面积相等的圆截面杆,试比较两者的最大剪应力m ax τ。
3kN m(a)题3-11解:(1)求矩形截面的τmax最大剪应力τmax 发生在横截面两长边的中点。
因h/b =90/60=1.5,查表可得:346.0=β, 故,3306.0346.0⨯==b W tβ解:(1)超静定梁的受力如图(b)所示,所对的扭矩图如图(c)所示。
(2)列杆的静力平衡方程,则2)变形协调关系:MPa Pa W T t 14.4106.0346.010333max =⨯⨯==τ (2)求圆形截面的τmax与矩形面积相同的圆截面的直径dm d d 0829.0060.0090.044060.0090.02=⨯⨯=→=⨯ππ,则圆形截面的MPa Pa W T 79.260829.01610333max=⨯⨯==πτ3-12图示两端固定的阶梯形圆轴,受一力偶m 作用,122d d =。
试求固定端力偶矩m A 与m A ,并作扭矩图将B A m m 32=代入静力平衡方程B A m m m -=:3332,3332B m m m m m m m B B B ==→-=(a )(b)m ABm133m 3233T 图(kN m )(c )(d )T 图题3-12BA B A m m m m m m -=→=--0()B B BA B A P B P A BC AB AC AC m m m m d m d m d G am d G a m GI am GI a m 320216022*********A A4242424121=→=-→=-+→=⋅-+⋅→=⋅-+⋅=+==ππϕϕϕϕ。
