(完整版)3固体物理-晶格振动1
合集下载
固体物理学:第3章 晶格振动

2 2
21 2
cos
qa
1 2
光学支
2 o
1
m
2 1 m
1
2 1
2 2
21
2
cos
qa
2
声学支
2A
1
m
2 1 m
12 22 21 2 cos qa
1 2
三、色散关系
UESTC
ω
当 q=0
ωO
ωA = 0 ωo = 21 2
m
ωA
当
q=
a
a
o
q
a
A
21
m
o
2 2
m
四、格波数
q 2 m
Na
2
Na
m 0 , 1, 2
q
o
波矢q 的取值是分立的,相邻q的“距离”N2a
五、格波数
UESTC
此前研究的晶格原子集体的波动运动就是格波。
晶体中所有原子以相同的频率和振幅在 平衡位置附近作简谐振动,原子的运动状 态在晶体中以波的形式传播,这种简谐波 称为格波。
五、格波数
UESTC
3.1 一维单原子链的振动
一. 物理模型 二. 运动方程 三. 色散关系 四. 波恩-卡曼周期性边界条件 五. 格波数 六. 小结
UESTC
一、物理模型
UESTC
一维简单晶格的振动
平衡位置 振动时偏离 平衡位置
un :第n个原子偏离平衡位置的位移 m :原子质量
一、物理模型
UESTC
V (r) V (0) dV (r) r 1 d 2V (r) r2
UESTC
❖ 对于一维原子链,简约区中波数q的取值总
《固体物理基础》晶格振动与晶体的热学性质

一、三维简单格子
二、三维复式格子
三、第一布里渊区
四、周期性边界条件
◇一个原胞内有P
个不同原子,则
有3P个不同的振
动模式,其中3支 声学波。
◇具有N个原胞的 晶体中共有3PN个
振动模式,其中
3N个声学波, 3N(P-1)个光学波。
四、周期性边界条件 总结
§ 3.4 声子
声子:晶格振动中格波的能量量子
二、一维单原子链的振动
格波
二、一维单原子链的振动
色散关系
二、一维单原子链的振动
色散关系
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
第一布里渊区
二、一维单原子链的振动
周期性边界条件
玻恩—卡曼边界条件
二、一维单原子链的振动
周期性边界条件
即q有N个独立的取值—晶格中的原胞数第一布
◇非弹性X射线散射、非弹性中子散射、可见光 的非弹性散射。
§ 3.4 声子
§ 3.4 声子
90K下钠晶体沿三个方向的色散关系
§ 3.5 晶格热容
一、晶格振动的平均能量
热力学中,固体定容热容:
根据经典理论,每一个自由度的平均能量是kBT, kBT/2为平均动能,kBT/2为平均势能,若固体有
N个原子,总平均能量: 取N=1摩尔原子数,摩尔热容是:
二、一维单原子链的振动
一维单原子链的振动
二、一维单原子链的振动
简谐近似下的运动方程
二、一维单Hale Waihona Puke 子链的振动简谐近似下的运动方程
在简谐近似下,原子的相互作用像一个弹 簧振子。一维原子链是一个耦合谐振子,各原 子的振动相互关联传播,形成格波。
固体物理05-晶格振动

周期性边界条件(Born-Karman边界条件)
包含N个原子的环状链。当系统移动N个原子后,振动情况完全复原。
i t naq u ( q ) Ae 格波解: n
周期性边界条件要求: e
iNaq
1
或
2 qn Na
n 为整数
周期性边界条件(Born-Karman边界条件)
b1 b 2 b 3 * N1 N 2 N 3 N
每个q 点有3n支模式,总共有3nN支模,正好是nN个 原子的全部自由度,即已包含所以得振动模式。
Pb的格波谱
无光学模 Why?
Cu的格波谱
光学支 金刚石的振动谱
声学支
作
业
1.分别画出 M=m, 1.5m, 2m 的一维双原子链的色散关系图。
上述方程有 解的条件是:
m 2 2 2 cos aq
2 cos aq M 2
2
0
最后解得方程:
2
( M m) Mm
( M m ) 2 4 Mm sin 2 aq
β(M m) 4 Mm 2 sin aq 1 1 2 Mm ( M m)
u ( x, q ) Ae i t qx
连续介质波中的x表示为空间中的任意一点,而晶格中的格波只 能取na格点的位置。在格波中将aq改变2π的整数倍,原子的实 际振动没有任何不同。可以将q的取值范围限制在:
a
q
a
第一布里渊区
q 取第一布里渊区外的值,不能提供新的波解。
对于格波白色和黑色的这两种波动解是等价的(只在离散 的晶格上有振动),但对连续介质波来说,这两个波是不 一样的。
固体物理:第三章 晶格振动总结-

长声学支格波可以看成连续波,晶体可以看成连续介质。
1.黄昆方程
离子晶体的长光学波
W
b11W
b12 E
P b21W b22E
(1) ---黄昆方程 ( 2)
(1)式代表振动方程,右边第一项
b11W
为准弹性恢复力,
第二项表示电场 E 附加了恢复力。
(2)式代表极化方程,b21W 表示离子位移引起的极化,第
..
m xn xn xn1 xn xn1
• 除了原子链两端的两个原子外, 其它任一个原子的运动都与相 邻的两个原子的运动相关. 即除了原子链两端的两个原子外, 其 它原子的运动方程构成了个联立方程组. 但原子链两端的两个 原子只有一个相邻原子, 其运动方程仅与一个相邻原子的运动 相关, 运动方程与其它原子的运动方程迥然不同. 与其它原子的 运动方程不同的这两个方程, 给整个联立方程组的求解带来了 很大的困难.
高次项均忽略掉的近似为简谐近似(忽略掉作用力中非线性项
的近似)。
f nk
d2u dr 2
r0
xnk
nk xnk
nk
d2u dr 2
r0
在简谐近似下,格波可以分解成许多简谐平面波的线性叠加。
模型 运动方程
试探解
色散关系
波矢q范围 B--K条件
波矢q取值
一维无限长原子链,m,a,
n-2 n-1 n n+1 n+2
• (2) 与实验结果吻合得较好.
• 对于原子的自由运动, 边界上的原子与其它原子一样, 无时无刻 不在运动. 对于有N个原子构成的的原子链, 硬性假定的边界条 件是不符合事实的. 其实不论什么边界条件都与事实不符. 但为 了求解近似解, 必须选取一个边界条件. 晶格振动谱的实验测定 是对晶格振动理论的最有力验证). 玻恩卡门条件是晶格振动理 论的前提条件. 实验测得的振动谱与理论相符的事实说明, 玻恩卡门周期性边界条件是目前较好的一个边界条件.
3晶格振动_1

N N l 2 2
a为原子间距,N为原胞数。 对一维单原子链组成的布拉维晶格: l 的取值只能取从-N/2到N/2包括0在内的N 个整数值。 q也只能取N个不同的值。 在一维单原子链情况下,每个q值对应一个ω, 一组 (ω,q)对应一个格波,故共有N个格波。这N个格波的频 率ω与波矢q的关系由一条色散曲线所概括,所以这N个格 波构成一支格波。一维单原子链只有一支格波。 结论2:q 的取值数目恰好等于晶体中原胞的数目。
单原子链的色散曲线
色散关系 —— q空间的周期: 2π/a
频率极大值
频率极小值
只有频率在 0 2 / m 之间的格波才能在晶体中传播, 其它频率的格波被强烈衰减 —— 低通滤波器。
2. 相速度和群速度
由于有色散关系,格波可用相速度和群速度来描述: 相速度:
vp
此时频率与波矢为线性关系。相速度与群速度相等,为 与波矢无关的常数。 由于q取小值属于长波振动模(λ=2π/q),故上述线性关 系为长波近似时的结果。
由于长波近似下,格波的波长远大于原子间距,晶格就象一 个连续介质。 在连续介质中传播的波为弹性波,其波速为声速,它是与波 矢无关的常数。 故单原子链中传播的长波近似下的格波叫声学波。 格波的色散关系与连续介质中弹性波的一致
两种波长的格波描述一维不连续原子的同一种运动
§3.1.3 晶格振动的色散关系
1. 色散关系的特点 一是偶函数:ω(q) =ω(-q), 二是周期函数:
2 4 2 1 sin ( : ) qa m 2
2 (q) (q s) a
这表明,当二个波矢相差为倒格矢的整数倍时,它 们对应的频率是一样的。 色散关系的上述二个性质对更为复杂的晶格振动也是适 用的。 它们实际上与晶格振动系统的对称性有关,前者涉及时 间反演对称性,后者与晶格的周期结构有关。 由于色散关系的周期性,可以把它约化到第一(或简约) 布里渊区中来表示。
固体物理 第三章 晶格振动
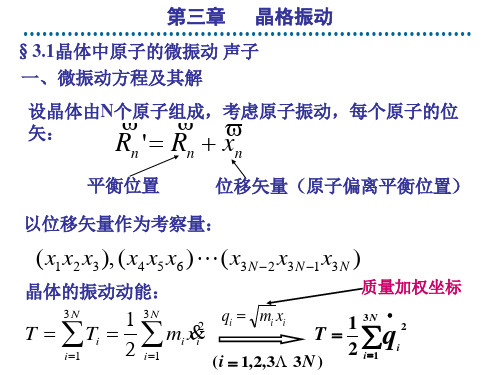
1 2 T = ∑q 2 i =1 i
3N •
3.1晶体中原子的微振动 3.1晶体中原子的微振动 声子 晶体振动势能U (qi ) 按 qi 的幂将势能在平衡位置附近展开为泰勒级数 ∂U 1 ∂ 2U U = U0 + ∑ ( ) 0 qi + ∑ ( ) 0 qi q j + 高阶项 ∂q i 2 ij ∂qi ∂q j i 其中 U 0 = 0 平衡位置处的势能为零势能点
xn = x N + n
又 : xn = Ae
i ( kna − ωt )
又 − π < k ≤ π s = − N + 1,− N + 2⋯⋯ N 共有N个取值 : a a 2 2 2
=1 e ⇒ 2π ⋅ s, = N+ 2π ,− π + 2 2π ,..., π 有N种均匀分布的分立取值 种均匀分布的分立取值 a L a L a 2π L 间隔∆k = ,密度 ,第一布里渊区倒格点数N。 L 2π
, ( l =1, 2, ⋯ 3N )
Ql = Ql0 sin(ωl t + α 1 )
1 ε l = (Q l + ωl2Ql2 ) 2
• 2
能量量子化
1 εl = (nl + )hυl 2
3.2 一维布拉菲格子的晶格振动 一、简谐近似
du 1 d 2u u( x) ≈ u( x0 ) + ∆x + (∆x)2 2 dx r0 2 dx x
3.1晶体中原子的微振动 声子 3.1晶体中原子的微振动 晶格振动模式
质量加权坐标下: 质量加权坐标下:
•• 3N
↔
独立的谐振子
↔
声子
第二章3固体物理

之间的体积是图中的球壳的体积。
g() 2
态密度的表达式:
g
V
2 2
2 s3
态密度公式的修正
0
在弹性介质中模或态的密度
上面的讨论已把单个的模与每一个q值联系起来,但对于三维的情形不十分确切。因为对 每一个q值,波可以是纵波也可以是横波,实际上与同一个q值相联系,存在三个不同的 模式,一种纵的,两种横的。对于纵波和横波,因为它们具有不同的速度,色散关系是 不同的。如假设它们存在一共同的速度,态密度关系式修正为:
V 4 q2dq
2 3
在三维空间中传播的波的q允许值(图中
所表示的仅是在qxqy平面中的截面)。阴 影部分的圆形壳层是用来计算模数的。
利用色散关系,得到g()d
2
g
d
V
2
3
4
q 2 dq
V
2
3
4
s
d s
这个方程给出了在恒定频率和+d的表面之间的 g ()
点的数目。在q空间中给出的这些表面是球面,它们
• 而对于声学支,0,q0,不管温度多么低,都不能忽略 低频对比热的贡献。因只对声学支,可用线性关系,即
q vsq
(6)
且三个方向都相同
• 利用关系式(6),将(4)式的求和改成积分后,
CV T s
vs q d q
e vsq/kBT 1 2 3
(7)
积分范围限在第一布里渊区
• 事实上,在很低的温度下, vsq kBT 部分对(7)式中积分 的贡献小到可以忽略,积分可视为在整个q空间中进行。采用 球坐标
3N
U E i
i1
3N 1 i1 2
i
e
i
固体物理学:声子--晶格振动

a
a
—— 第一布里渊区
—— 只需研究清楚第一布里渊区的晶格振动问题 —— 其它区域不能提供新的物理内容
29
在满足周期性边界条件下,凡是
波矢相差一个倒易点阵矢量
G
的简正
模式是同一个简正模式,这样我们就
可把格波的波矢k限制在第一布里渊
区平之移中一,个第G 后一用布第里一渊布区里以渊外区的中k总的可k以来
7
第s个原子所受到的力等于所有原子作用力 的总和
Fs
c(p us
us
)
p
p
运动方程:
m us
ቤተ መጻሕፍቲ ባይዱ
c(p us
p
u
)
s
(s 1.2.3.......N )
p
当s取不同值时,上述方程为一方程组, 代表各个原子的位移和运动。
8
原子在平衡位置附近的小振动可看作是 耦合的简谐振子的运动。这种耦合谐振子可 以通过正则变换化成一组独立的无相互耦合 的简谐振动的线性叠加。经过这样变换的每 一个独立的谐振子代表简正模式。点阵振动 的简正模式是指有一定频率、一定波矢的平 面波,第s个原子的位移按简正模式解可写成:
5
1. 简谐近似
这一章我们要考虑原子在平衡位置附近的振
动。这种考虑是建立在简谐近似的基础之上的, 所谓简谐近似即认为振动是小振动,振幅很小, 这种振动的位移与力之间是满足线性关系的。
F=-cx
从能量的角度来看,认为原子间有了相对位
移后,两原子间的相互作用势也有了变化将势能 展开成级数:
u
u0
( u x
模式,是代表同一个格波。
27
如上图. 5a
k 2
5a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
nN n 1N 1 0N 0
周期性边界条件既保证了 原子数的有限,又消除了 边界的影响,简化了方程 的求解
一维单原子链
在周期性边界条件下,不同原子运动方程满足通式
m
d 2n
dt2
n1 n1 2n
方程具有形式解 n Aeitnaq
其中
A为原子振动的振幅;ω=2πf为圆频率;q=2π/λ为波矢;
sin aq aq a q
22
m
波速 v a 为常数
qm
相邻两个原子的振动相位差 n 1q nq q 0
因此近似于连续介质弹性波(声波,无色散) 解释:当波长 a 时,原子链可以近似看作连续的;
一维单原子链色散关系
一维单原子链
一维单原子链色散关系 2 sin aq
形式解代回微分方程,可得到
m2 2 cosaq 1
2 4 sin2 aq 2 sin aq
m2
m2
一维单原子链
形式解 n
代回微分方程
Ae i t naq
m
d 2n
dt2
n1 n1 2n
d 2n
dt2
2 Aeitnaq
2n
n1 Aeitn1aq Aeitnaqeiaq eiaqn
一维单原子链
只考虑最近邻原子间的相互作用,分析第n个原子受力
受到第n+1个原子的作用力大小为 β(μn+1- μn),方向向右
受到第n-1个原子的作用力大小为 β(μn- μn-1),方向向左
第n个原子受合力为β(μn+1+μn-1 -2μn)
根据牛顿第二定律,可得到第n个原子运动方程
m
n1 Aeitn1aq Aeitnaqeiaq eiaqn
m2n eiaq eiaq 2 n
m2 2 cosaq 1
2 4 sin2 aq 2
m2
sin aq
m2
色散关系
一维单原子链
一维单原子链振动解 n Aeitnaq
描述的是所有原子同时做振幅为A,波矢为q,频率为ω的 振动;原子的集体运动形成了在晶体格子中传播的波,称 为格波;
固体物理学
晶格振动1
晶格振动
晶格振动的物理图像 (1)假定晶体中的原子位置用布拉维格子的格矢Rn标记, 但将Rn理解为原子的平衡位置; (2)原子在平衡位置附近做微小的振动,其瞬间位置对平 衡位置的偏离远小于离子间距。 考虑最简单的理想固体:一维单原子链
一维单原子链
一维单原子链 (1)所有原子相同,质量为m; (2)相邻原子平衡位置间距相等,为a; (3)原子间的相互作用相同 ,形式为U(r),r为原子间距;
nN
AeitnN aq
An
Ae i t naq e iNaq
eiNaq n
eiNaq 1 Naq 2m q 2 m
Na
又由 q 可得到 N m N
a
a
2
2
因此,一维单原子链中允许的波矢q数目为N,正好是系统自 由度的数目;
一维单原子链
一维单原子链色散关系 2 sin aq (1)长波极限 q 0, m 2
d 2n
dt2
n1 n1 2n
一维单原子链
第n个原子运动方程
m
d 2n
dt2
n1 n1 2n
对于原子链中的每个原子,都有一个运动方程
m
d 21
dt2
2
0
21
m
d 22
dt2
3
1
22
m
d 2N
dt2
N 1 N 1 2N
波恩-卡曼(Born-Karman) 周期性边界条件
(2)短波极限
m2
q , 2 2a
a
q
t
na
2a
Ae i
t
n 2
波矢q’和波矢q描述的是相同 的格波运动,因此只需要研 究波矢限制在一个周期(第 一布里渊区)内的情况即可
n
Ae i t naq
Aei
t
na
5 2a
Ae i
t 5n 2
Aei
t
5n 2
2n
Ae i
t
n 2
n
不同波长(波矢)格波的等价性
矢q描述的是相同的格波运动;
a
如右图
红色格波波矢
q
2
2
4a
2a
绿色格波波矢
q q 2
a
q
2
2
4a 5
5
2a
2 sin aq 2 sin a 2
m 2 m 2 2a m
2 sin aq 2 sin a 5 2
m2
m 2 2a m
n
Ae i t naq
Aei
某一时刻的格波运动如右图 所示 (1)图中向上的箭头表示原 子沿x轴向右振动,向下的箭 头表示原子沿x轴向左振动, 箭头的长度表示原子离开平 衡位置的位移大小; (2)相邻两个原子之间的相 位差为(n+1)aq-naq=aq某一 时刻
格波
不同波长(波矢)格波的等价性
当波矢相差为倒格矢整数倍即 q q 2 m时,波矢q’和波
U
α
δ
U
α
1 2
d 2U dr2
ra
δ2
一维单原子链
考虑原子间的相互作用
U α δ U α
1 2d 2U dr2 Nhomakorabeara
δ2
原子受力
令
d 2U dr2
f r dU dU
dr d
为恢复力常数 ra
d 2U dr2
ra
则有 f ,正好与胡克定律形式相同;
因此,我们所做的近似相当于把相邻原子之间的相互作用
使用一个劲度系数为β的弹簧代替;
这一近似称为“简谐近似”;
一维单原子链
一维单原子链 (1)原子质量为m;平衡位置间距为a;相互作用为U(r) ; (2)原子偏离平衡位置距离为μ; 由于热运动,第n个原子偏离平衡位置距离为μn; 第n和n+1个原子的距离由平衡时的a变为a+ μn+1- μn;
一维单原子链
考虑原子在平衡位置附近振动,偏离平衡位置的位移δ<<a
将U(r)=U(a+ δ)在a附近进行泰勒展开
U
α
δ
U
α
dU dr
ra
δ
1 2
d 2U dr2
ra
δ2
第一项U(r)为常数;
第二项中
dU dr
ra
f
r ra
0
说明:平衡位置处的原子受力为零;
保留二阶项,更高阶项忽略;
一维单原子链
一维单原子链色散关系 2 (1)格波波速(相速度)v
sin aq
m2
q
(2)由于 0 sin aq 1可得到
2
02
m (截止频率)
(3)ω具有周期性,周期T=2π/a,研究一个周期内性质即
可,一般取第一布里渊区 q
a
a
一维单原子链
(4)考虑周期性边界条件 nN n 代入 n Aeitnaq 可得到
周期性边界条件既保证了 原子数的有限,又消除了 边界的影响,简化了方程 的求解
一维单原子链
在周期性边界条件下,不同原子运动方程满足通式
m
d 2n
dt2
n1 n1 2n
方程具有形式解 n Aeitnaq
其中
A为原子振动的振幅;ω=2πf为圆频率;q=2π/λ为波矢;
sin aq aq a q
22
m
波速 v a 为常数
qm
相邻两个原子的振动相位差 n 1q nq q 0
因此近似于连续介质弹性波(声波,无色散) 解释:当波长 a 时,原子链可以近似看作连续的;
一维单原子链色散关系
一维单原子链
一维单原子链色散关系 2 sin aq
形式解代回微分方程,可得到
m2 2 cosaq 1
2 4 sin2 aq 2 sin aq
m2
m2
一维单原子链
形式解 n
代回微分方程
Ae i t naq
m
d 2n
dt2
n1 n1 2n
d 2n
dt2
2 Aeitnaq
2n
n1 Aeitn1aq Aeitnaqeiaq eiaqn
一维单原子链
只考虑最近邻原子间的相互作用,分析第n个原子受力
受到第n+1个原子的作用力大小为 β(μn+1- μn),方向向右
受到第n-1个原子的作用力大小为 β(μn- μn-1),方向向左
第n个原子受合力为β(μn+1+μn-1 -2μn)
根据牛顿第二定律,可得到第n个原子运动方程
m
n1 Aeitn1aq Aeitnaqeiaq eiaqn
m2n eiaq eiaq 2 n
m2 2 cosaq 1
2 4 sin2 aq 2
m2
sin aq
m2
色散关系
一维单原子链
一维单原子链振动解 n Aeitnaq
描述的是所有原子同时做振幅为A,波矢为q,频率为ω的 振动;原子的集体运动形成了在晶体格子中传播的波,称 为格波;
固体物理学
晶格振动1
晶格振动
晶格振动的物理图像 (1)假定晶体中的原子位置用布拉维格子的格矢Rn标记, 但将Rn理解为原子的平衡位置; (2)原子在平衡位置附近做微小的振动,其瞬间位置对平 衡位置的偏离远小于离子间距。 考虑最简单的理想固体:一维单原子链
一维单原子链
一维单原子链 (1)所有原子相同,质量为m; (2)相邻原子平衡位置间距相等,为a; (3)原子间的相互作用相同 ,形式为U(r),r为原子间距;
nN
AeitnN aq
An
Ae i t naq e iNaq
eiNaq n
eiNaq 1 Naq 2m q 2 m
Na
又由 q 可得到 N m N
a
a
2
2
因此,一维单原子链中允许的波矢q数目为N,正好是系统自 由度的数目;
一维单原子链
一维单原子链色散关系 2 sin aq (1)长波极限 q 0, m 2
d 2n
dt2
n1 n1 2n
一维单原子链
第n个原子运动方程
m
d 2n
dt2
n1 n1 2n
对于原子链中的每个原子,都有一个运动方程
m
d 21
dt2
2
0
21
m
d 22
dt2
3
1
22
m
d 2N
dt2
N 1 N 1 2N
波恩-卡曼(Born-Karman) 周期性边界条件
(2)短波极限
m2
q , 2 2a
a
q
t
na
2a
Ae i
t
n 2
波矢q’和波矢q描述的是相同 的格波运动,因此只需要研 究波矢限制在一个周期(第 一布里渊区)内的情况即可
n
Ae i t naq
Aei
t
na
5 2a
Ae i
t 5n 2
Aei
t
5n 2
2n
Ae i
t
n 2
n
不同波长(波矢)格波的等价性
矢q描述的是相同的格波运动;
a
如右图
红色格波波矢
q
2
2
4a
2a
绿色格波波矢
q q 2
a
q
2
2
4a 5
5
2a
2 sin aq 2 sin a 2
m 2 m 2 2a m
2 sin aq 2 sin a 5 2
m2
m 2 2a m
n
Ae i t naq
Aei
某一时刻的格波运动如右图 所示 (1)图中向上的箭头表示原 子沿x轴向右振动,向下的箭 头表示原子沿x轴向左振动, 箭头的长度表示原子离开平 衡位置的位移大小; (2)相邻两个原子之间的相 位差为(n+1)aq-naq=aq某一 时刻
格波
不同波长(波矢)格波的等价性
当波矢相差为倒格矢整数倍即 q q 2 m时,波矢q’和波
U
α
δ
U
α
1 2
d 2U dr2
ra
δ2
一维单原子链
考虑原子间的相互作用
U α δ U α
1 2d 2U dr2 Nhomakorabeara
δ2
原子受力
令
d 2U dr2
f r dU dU
dr d
为恢复力常数 ra
d 2U dr2
ra
则有 f ,正好与胡克定律形式相同;
因此,我们所做的近似相当于把相邻原子之间的相互作用
使用一个劲度系数为β的弹簧代替;
这一近似称为“简谐近似”;
一维单原子链
一维单原子链 (1)原子质量为m;平衡位置间距为a;相互作用为U(r) ; (2)原子偏离平衡位置距离为μ; 由于热运动,第n个原子偏离平衡位置距离为μn; 第n和n+1个原子的距离由平衡时的a变为a+ μn+1- μn;
一维单原子链
考虑原子在平衡位置附近振动,偏离平衡位置的位移δ<<a
将U(r)=U(a+ δ)在a附近进行泰勒展开
U
α
δ
U
α
dU dr
ra
δ
1 2
d 2U dr2
ra
δ2
第一项U(r)为常数;
第二项中
dU dr
ra
f
r ra
0
说明:平衡位置处的原子受力为零;
保留二阶项,更高阶项忽略;
一维单原子链
一维单原子链色散关系 2 (1)格波波速(相速度)v
sin aq
m2
q
(2)由于 0 sin aq 1可得到
2
02
m (截止频率)
(3)ω具有周期性,周期T=2π/a,研究一个周期内性质即
可,一般取第一布里渊区 q
a
a
一维单原子链
(4)考虑周期性边界条件 nN n 代入 n Aeitnaq 可得到
