《电路理论基础》(第三版 陈希有)习题答案第十章
电路理论教程答案陈希有
电路理论教程答案陈希有【篇一：《电路理论基础》(第三版陈希有)习题答案第一章】电路电流的参考方向是从a指向b。
当时间t2s时电流从a流向b,与参考方向相同，电流为正值；当t2s时电流从b流向a，与参考方向相反，电流为负值。
所以电流i的数学表达式为2a t?2s? i??-3at?2s ?答案1.2解：当t?0时u(0)?(5?9e0)v??4v0其真实极性与参考方向相反，即b为高电位端，a为低电位端；当t??时u(?)?(5?9e??)v?5v0其真实极性与参考方向相同，即a为高电位端，b为低电位端。
答案1.3解：(a)元件a电压和电流为关联参考方向。
元件a消耗的功率为pa?uaia则ua?pa10w??5v ia2a真实方向与参考方向相同。
(b) 元件b电压和电流为关联参考方向。
元件b消耗的功率为pb?ubib则ib?pb?10w1a ub10v真实方向与参考方向相反。
(c) 元件c电压和电流为非关联参考方向。
元件c发出的功率为pc?ucic则uc?pc?10w10v ic1a真实方向与参考方向相反。
答案1.4解：对节点列kcl方程节点③: i4?2a?3a?0，得i4?2a?3a=5a节点④: ?i3?i4?8a?0，得i3??i4?8a?3a节点①: ?i2?i3?1a?0，得i2?i3?1a?4a节点⑤: ?i1?i2?3a?8a?0，得i1?i2?3a?8a??1a若只求i2，可做闭合面如图(b)所示，对其列kcl方程，得 i28a-3a+1a-2a0解得i2?8a?3a?1a?2a?4a答案1.5解：如下图所示(1)由kcl方程得节点①：i1??2a?1a??3a节点②：i4?i1?1a??2a节点③：i3?i4?1a??1a节点④：i2??1a?i3?0若已知电流减少一个，不能求出全部未知电流。
(2)由kvl方程得回路l1：u14?u12?u23?u34?19v回路l2：u15?u14?u45?19v-7v=12v回路l3：u52?u51?u12??12v+5v=-7v回路l4：u53?u54?u43?7v?8v??1v若已知支路电压减少一个，不能求出全部未知电压。
电路理论基础(陈希有)习题解答10-14
uC (0 ) uC (0 ) 24V iL (0 ) iL (0 ) 2A
由 KVL 得开关电压：
6
6 3
Ri
u(0 ) uC (0 ) 8 iL (0 ) (24 8 2)V 8V
(b)
答案 10.3 解： t 0 时电容处于开路， i 0 ，受控源源电压 4i 0 ，所以 等 效 电 阻
由换路定律得：
t0
4 4
时 电 感 处 于 短 路 ， 故
Ri
(b)
8
3 i L (0 ) 9A 3A ，由换路定律得： 63 iL (0 ) iL (0 ) 3A
求等效电阻的电路如图(b)所示。 ，
等效电阻
Ri (4 // 4) // 8 1.6
时间常数
求稳态值的电路如图(b)所示。 i ( ) 2 2 10V 3 3 4 Ri iL ( ) 4 2 2
(b) (c)
(b)
Ri (
时间常数
6 3 3 1.5 )k 3k 6 3 3 1.5
3 6 3
答案 10.13
解：当 t 0 ， r 列 KVL 方程得：
-1-
答案 10.1
解： t
0 时，电容处于开路，故 uC (0 ) 10mA 2k 20V
t 0 时，求等效电阻的电路如图(b)所示。
i 6 3 4i
iL (t ) iL (0 )e t / 3e 2t A (t 0)
电感电压
由换路定律得：
u1 (t ) L
由换路定律得
L / Ri 0.5s
由三要素公式得： 解 得 A 答案 10.9 解：当 t 原始值
电路理论基础课后答案(哈工大陈希有)第9章
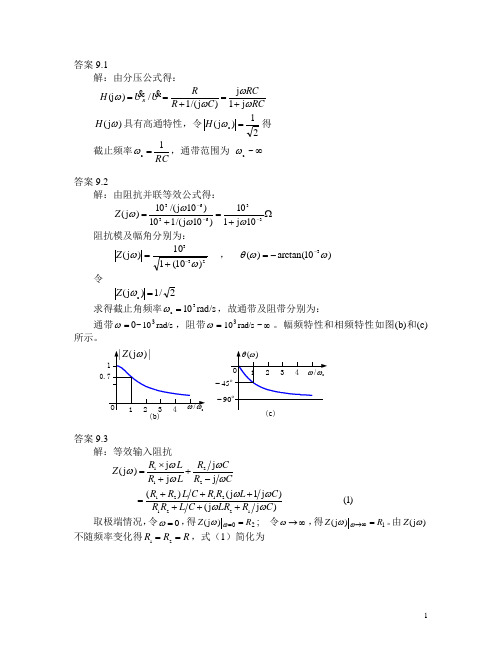
答案9.1解：由分压公式得：U U H R/)(j =ωRCRC C R R ωωωj 1j )j /(1+=+= )j (ωH 具有高通特性，令21)j (c =ωH 得截止频率RC1c =ω，通带范围为∞~c ω答案9.2解：由阻抗并联等效公式得：Ω+=+=---33636310j 110)10j /(110)10j /(10)j (ωωωωZ 阻抗模及幅角分别为：233)10(110)j (ωω-+=Z ， )10arctan()(3ωωθ--= 令2/1)j (c =ωZ求得截止角频率rad/s 103c =ω，故通带及阻带分别为：通带=ω0~rad/s 103，阻带=ωrad/s 103~∞。
幅频特性和相频特性如图(b)和(c)所示。
(b)--答案9.3解：等效输入阻抗)1()j j ()j 1j ()(j j j j )j (122121212211C R LR C L R R C L R R C L R R CR CR L R L R Z ωωωωωωωωω++++++=-++⨯=取极端情况，令0=ω，得20)j (R Z ==ωω; 令∞→ω，得1)j (R Z =∞→ωω。
由)j (ωZ 不随频率变化得R R R ==21，式（1）简化为)j 1j ()j 1j (2)j 1j ()j 1j (2)j (22C L RC L R C L R CL RC L R C L R C L R C L R Z ωωωωωωωωω+++++=+++++= 由)j (ωZ 为实数得：CL R R C L R R C L =+=2,2 故当C L R R ==21时端口电流与端口电压的波形相似，此时C L Z =)j (ω。
答案9.4解： RC 并联的等效阻抗RCRC R C R Z RC ωωωj 1j /1j /+=+=RC RCZ L Z U U H +==ωωj /)j (12 RL LC RC L R R /j 11)j 1(j 2ωωωω+-=++= 幅频特性222)/()1(1)j (R L LC H ωωω+-=当0→ω时，1)j (=ωH ；当∞→ω时，0)j (=ωH所以它具有低通特性。
《电路理论基础》(第三版陈希有)习题答案第十章
i答案10.1解：t ：：： 0时，电容处于开路，故u C (0 _) = 10mA 2k 「- 20V 由换路定律得：u C (0 .) +(0”20V换路后一瞬间，两电阻为串联，总电压为 u C (0 )。
所以再由节点①的KCL 方程得:i C (0 ) =10mA -i 1(0 .)二(10-5)mA =5mA答案10.2解：t ：：：0时电容处于开路，电感处于短路，3门电阻与61电阻相并联，所以45V6i(0J3A ，L(0Ji(0」= 2A(5+8 + 6 3)0 6+36+3u C (0J =8 i(0J = 24V 由换路定律得：U C (0 ) 7C (0J =24V ，匚(0.) “L (0_)=2A由KVL 得开关电压：u(0 ) --U c (0 ) 8 匚(0 .)=(-24 8 2)V 8V答案10.3解：t ：：： 0时电容处于开路，i =0 ,受控源源电压4i =0 ,所以U C (0 J =U C (0」=U 1(0」61.5V = 0.6V(9 6尸等效电阻i i (0 )=%(0 .) (2 2)k 」=5mA(b)所示。
R 段「4i (6 3)i容i时间常数二 R C 二 0 ・1st 0后电路为零输入响应，故电容电压为：u C (t)二 u C (0 ,)e~ =0.6e A0°V6“电阻电压为：“⑴工―6门 i 6门 ^C-dUc ^0.72e 10t V (t 0)dt答案10.43解：t ：：：0时电感处于短路，故L(0J= 39A=3A ，由换路定律得:6 + 3i L (0^i L (0J=3A求等效电阻的电路如图(b)所示。
等效电阻R 「6 •色卫=8」，时间常数.二L/R =0.5s6+3t 0后电路为零输入响应，故电感电流为i L (t) =i L (0 .)e^^ =3e 2t A (t _o ) 电感电压._2tu ,(t)二 L 匕二-24e V (t .0)dt31电阻电流为U 36C 汽L +U 1小2八i 3 2e A33「3「31电阻消耗的能量为：W3°= f 30i ；dt = f12/dt =12[-0.25ed=3W答案10.5解：由换路定律得i L (0.) “L (0」=0，达到稳态时电感处于短路，故LG) =20/4=5A求等效电阻的电路如图(b)所示。
电路理论基础课后习题答案 陈希有主编 第十到十四章
答案10.1解：0<t时，电容处于开路，故V 20k 2m A 10)0(=Ω⨯=-C u由换路定律得：V 20)0()0(==-+C C u u换路后一瞬间，两电阻为串联，总电压为)0(+C u 。
所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得：m A5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解：0<t时电容处于开路，电感处于短路，Ω3电阻与Ω6电阻相并联，所以A3)363685(V45)0(=Ω+⨯++=-i，A 2)0(366)0(=⨯+=--i i LV 24)0(8)0(=⨯=--i u C由换路定律得：V24)0()0(==-+C C u u ，A 2)0()0(==-+L L i i由KVL 得开关电压：V8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u答案10.3解：0<t 时电容处于开路，0=i ，受控源源电压04=i ，所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C>t 时，求等效电阻的电路如图(b)所示。
等效电阻Ω=++-==5)36(4i ii i i u R 时间常数s 1.0i ==C R τ0>t 后电路为零输入响应，故电容电压为：V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为：V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4 解：<t 时电感处于短路，故A 3A 9363)0(=⨯+=-L i ，由换路定律得： A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。
(b)等效电阻Ω=+⨯+=836366i R ，时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应，故电感电流为 A e 3e )0()(2/t t L L i t i --+==τ)0(≥t电感电压V e 24d d )(21t Lti Lt u --==)0(>t Ω3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为：W3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解：由换路定律得0)0()0(==-+L L i i ，达到稳态时电感处于短路，故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。
电路理论基础(陈希有)课后题答案
答案11.1解： (1)2020001e 1e 1e e )()(-ssdt s stdt t t s F stst stst =-=+-==∞-∞-∞-∞----⎰⎰ε (2)20)(20)(00)(1e)(1e 1e e )(e )(-ααααεααα+=+-=+++-==∞+-∞+-∞-∞-----⎰⎰s s dts s t dt t t s F ts t s st st t答案11.2解：)/1(//1)(1τττ+=+-=s s A s A s A s F 由拉氏变换的微分、线性和积分性质得：)/1(/)()()/(]/)([)()]0()([)(22111112ττ+++=++=++-=-s s A c bs as s F s c b as s s F c s bF f s sF a s F答案11.3解：设25)}({)(11+==s t f s F L ,52)}({)(22+==s t f L s F 则)5)(2(10)()(21++=s s s F s F)(1t f 与)(2t f 的卷积为)e e (310]e 31[e 10e e 10e 2e 5)(*)(520350350)(5221t t t tt ttt d d t f t f --------=⨯==⨯=⎰⎰ξξξξξξ对上式取拉氏变换得：)5)(2(10)5121(310)}(*)({21++=+-+=s s s s t f t f L 由此验证)()()}(*)({2121s F s F t f t f =L 。
答案11.4解：(a)6512)(2+++=s s s s F 3221+++=s A s A3|31221-=++=-=s s s A ， 3|31221-=++=-=s s s A 所以t t s s t f 321e 5e 3}3523{)(---+-=+++-=L(b))2)(1(795)(23+++++=s s s s s s F 212)2)(1(3221+++++=+++++=s A s A s s s s s 2|2311=++=-=s s s A 1|1321-=++=-=s s s A 所以t t t t s s s L t f 21e e 2)(2)(}21122{)(----++'=+-++++=δδ (c)623)(2++=s s s F 22)5()1(5)5/3(++⨯=s 查表得)5sin(e 53)(t t f t-=答案11.5解：(a) 由运算电路(略)求得端口等效运算阻抗为：11262241)3/(142)]3/(14[21)(22i ++++=++++=s s ss s s s s s Z ， 112611430)(22++++=s s s s s Z i (b) 画出运算电路如图11.5(c)所示U )(2s __在端口加电流，列写节点电压方程如下⎩⎨⎧-==++-=-+)2()]()([3)(3)()]5.0/(11[)()1()()()()1(2122s U s U s U s U s s U s I s U s U s由式（２）解得)(144)(2s U s ss U ⨯+=代入式（１）得)()()1221(s I s U s ss =+-+所以1212)(2i +++=s s s s Y答案11.6解：运算电路如图11.6(b)所示。
电路理论基础(哈尔滨工业大学陈希有第3版)13共44页文档
5 3
6 ② 1
两个子图
③
①
4
3
2
6
②
(a)
③①
4
③
6
②
(b)
有向图：图中的所有支路都指定了方向，则称为有向图；反之为无向图
回 路： 从图中某一节点出发，经过若干支路和节点(均只许经过一次)又 回到出发节点所形成的闭合路径称为回路。 割 集： 连通图的割集是一组支路集合，并且满足：
(1)如果移去包含在此集合中的全部支路(保留支路的两个端点)，则 此图变成两个分离的部分。
单树支割集
4
5
3
4
5
3
c1
1
2
6
c2 1
2
6
1
(a)
(b)
(c)
基本割集：每取一个树支作一个单树支图割基本集割，集称为基本割集。
基本割集的方向规定为所含树支的方向。
基本割集的性质 图中3个基本割集 KCL方程是（独立）：
c1
i1i5i6 0
c 2 i2i4i5i60
1 3 . 1 网 络 的 图 树
基本要求：掌握网络的图、子图、连通图、割集和树等概念。
1 网络的图
图( graph) :由“点” 和“线”组成。 • “点”也称为节点或顶点(vertex)，“线”也称为支路或
边(edge)。 • 图通常用符号G来表示。
图 (a) 电路只含二端元件，对应的图如图 (b)所示。
用点表示王宫，用线表示王宫间的 道路，便抽象成图。问题变成该图 是否为平面图？
4 四色定理
四色问题：只须4种不同颜色，就能使平面地图上任何两个相 邻的国家的颜色不同。
图论问题：用点表示国家，用边表示国家直接相邻。证明只 须4种颜色就可使所有相邻顶点具有不同颜色。
《电路理论基础》(第三版陈希有)习题答案
答案2.1解：本题练习分流、分压公式。
设电压、电流参考方向如图所示。
(a) 由分流公式得：23A 2A 23I R Ω⨯==Ω+解得75R =Ω(b) 由分压公式得：3V 2V 23R U R ⨯==Ω+解得47R =Ω答案2.2解：电路等效如图(b)所示。
20k Ω1U +-20k Ω(b)+_U图中等效电阻(13)520(13)k //5k k k 1359R +⨯=+ΩΩ=Ω=Ω++由分流公式得：220mA 2mA 20k RI R =⨯=+Ω电压220k 40V U I =Ω⨯=再对图(a)使用分压公式得：13==30V 1+3U U ⨯答案2.3解：设2R 与5k Ω的并联等效电阻为2325k 5k R R R ⨯Ω=+Ω(1)由已知条件得如下联立方程：32113130.05(2) 40k (3)eqR U UR R R R R ⎧==⎪+⎨⎪=+=Ω⎩由方程(2)、(3)解得138k R =Ω 32k R =Ω再将3R 代入(1)式得210k 3R =Ω答案2.4解：由并联电路分流公式，得1820mA 8mA (128)I Ω=⨯=+Ω2620mA 12mA (46)I Ω=⨯=+Ω由节点①的KCL 得128mA 12mA 4mA I I I =-=-=-答案2.5解：首先将电路化简成图(b)。
图 题2.5120Ω(a)(b)图中1(140100)240R =+Ω=Ω2(200160)120270360(200160)120R ⎡⎤+⨯=+Ω=Ω⎢⎥++⎣⎦ 由并联电路分流公式得211210A 6A R I R R =⨯=+及21104A I I =-=再由图(a)得321201A 360120I I =⨯=+由KVL 得，3131200100400V U U U I I =-=-=-答案2.6xRx(a-1)图2.6解：（a ）设R 和r 为1级，则图题2.6(a)为2级再加x R 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
答案10.1解：0<t 时，电容处于开路，故V 20k 2m A 10)0(=Ω⨯=-C u由换路定律得：V 20)0()0(==-+C C u u换路后一瞬间，两电阻为串联，总电压为)0(+C u 。
所以m A 5k )22()0()0(1=Ω+=++C u i再由节点①的KCL 方程得：m A 5m A )510()0(m A 10)0(1=-=-=++i i C答案10.2解：0<t 时电容处于开路，电感处于短路，Ω3电阻与Ω6电阻相并联，所以A 3)363685(V45)0(=Ω+⨯++=-i ，A 2)0(366)0(=⨯+=--i i L V 24)0(8)0(=⨯=--i u C 由换路定律得：V 24)0()0(==-+C C u u ，A 2)0()0(==-+L L i i 由KVL 得开关电压：V 8V )2824()0(8)0()0(-=⨯+-=⨯+-=+++L C i u u答案10.3解：0<t 时电容处于开路，0=i ，受控源源电压04=i ，所以V 6.0V 5.1)69(6)0()0()0(1=⨯Ω+Ω===--+u u u C C0>t 时，求等效电阻的电路如图(b)所示。
等效电阻Ω=++-==5)36(4i ii i i u R时间常数s 1.0i ==C R τ0>t 后电路为零输入响应，故电容电压为：V e 6.0e )0()(10/t t C C u t u --+==τΩ6电阻电压为：V e 72.0)d d (66)(101t Ctu Ci t u -=-⨯Ω-=⨯Ω-=)0(>t答案10.4解：0<t 时电感处于短路，故A 3A 9363)0(=⨯+=-L i ，由换路定律得： A 3)0()0(==-+L L i i求等效电阻的电路如图(b)所示。
(b)等效电阻Ω=+⨯+=836366i R ，时间常数s 5.0/i ==R L τ 0>t 后电路为零输入响应，故电感电流为 A e 3e )0()(2/t t L L i t i --+==τ)0(≥t电感电压V e 24d d )(21t L tiL t u --==)0(>tΩ3电阻电流为A e 23632133t L u i u i --=Ω+⨯Ω=Ω=Ω3电阻消耗的能量为：W 3]e 25.0[1212304040233=-==Ω=∞-∞-∞Ω⎰⎰t t dt e dt i W答案10.5解：由换路定律得0)0()0(==-+L L i i ，达到稳态时电感处于短路，故A 54/20)(==∞L i求等效电阻的电路如图(b)所示。
(b)等效电阻Ω==6.18//)4//4(i R时间常数s )16/1(/i ==R L τ0>t 后电路为零状态响应，故电感电流为：A )e 1(5)e 1)(()(16/t t L L i t i ---=-∞=τ)0(≥tA e 8e 1651.08/)d d (8)(1616t tL L t i L u t i --=⨯⨯⨯=Ω=Ω=)0(>t答案10.6解：0<t 时电路为零状态，由换路定律得：0)0()0(==-+C C u u0>t 时为简化计算，先将ab 左边电路化为戴维南电路形式。
当ab 端开路时，由02=+i i ，得0=i 所以开路电压V )100cos(210S OC t u u == 当ab 端短路时，Ω⨯==+=3332SSC u i i i i 故等效电阻Ω==1SCOCi i u R ， 0>t 时等效电路如图(b)所示。
(b)电路时间常数为s C R 01.0i ==τ。
用相量法计算强制分量p C u ：V 4525010j 1j )j /(11)j /(1p ︒-∠=︒∠⨯--=⨯+=OCC U C C U ωω V )45100cos(10)(p ︒-=t t u CV 25)45cos(10)0(p =︒-=+C u 由三要素公式得：]e 25)45100cos(10[e )]0()0([)()(100/p p t t C C C C t u u t u t u --++-︒-=-+=τV答案10.7解：0<t 时电容处于开路，由换路定律得：V 6V 9366)0()0(=⨯+==-+C C u u ，∞→t 电容又处于开路，V 12)V 18(366)(-=-⨯+=∞C u等效电阻Ω=Ω+⨯+=10)36368(i R时间常数s 2.0i ==C R τ 由三要素公式得：V )e 1812(e )]()0([)()(5/t t C C C C u u u t u --++-=∞-+∞=τ)0(≥t)e 1812()e 90(16.0d d 8)(55t t C Cu t u C t u --+-+-⨯=+⨯Ω= 所以]e 6.312[)(5t t u -+-= V )0(>t答案10.8解：当0<t 时，列写节点方程求原始值20123)0()2015161(1-=++-u ， 解得 V 76.5)0(1=-u 由换路定律得=+)0(L i A 04.2A )6/76.53(6)0(A 3)0(A 3)0(11=-=Ω-=-=---u i i L 换路后的电路如图(b)所示。
(b)列写节点方程得：2012)0()0()20151(1-=+++L i u 解得V 76.5)0(1=+u ，A 888.020)0(V 12)0(1=Ω+=++u i稳态时，电感处于短路，所以A 6.020V 12)(=Ω=∞i等效电阻Ω=+⨯=4205205i R时间常数s 5.0/i ==R L τ 由三要素公式得：)e 288.06.0(e )]()0([)()(2/t t i i i t i --++=∞-+∞=τ A答案10.9解：当0<t 时，电容处于开路，列写节点电压方程求原始值⎪⎩⎪⎨⎧=⨯-+++-=⨯--++----883)0()834121()0(210821)0(21)0()312121(2121n n n n u u u u 解得V 8.4)0(1=-n u ，由换路定律得：V 8.4)0()0()0(1===--+n C C u u u∞→t 电容又处于开路，再列写节点电压方程如下：⎪⎩⎪⎨⎧=∞++∞⨯-=⨯-∞⨯-∞++0)()4121()(210821)(21)()312121(2121n n n n u u u u 解得：V 4)()(1=∞=∞n C u u求等效电阻的电路如图(b)所示。
(b)Ω=+=1)]42//(3//[2i R时间常数s 1i ==C R τ 由三要素公式得：)e 8.04(e )]()0([)()(/t t C C C C u u u t u --++=∞-+∞=τ V答案10.10解：由换路定律得：A 52V10)0()0(=Ω==-+L L i i求稳态值的电路如图(b)所示。
10(b)A 65)2//342(V 10233)(233)(=Ω++⨯+=∞⨯+=∞i i L 求等效电阻的电路如图(c)所示。
等效电阻Ω=Ω++++=4]423)42(32[i R时间常数s 5.04/2/i ===R L τ 由三要素公式得：A )e 51(65e )]()0([)()(2/t t L L L L i i i t i --++=∞-+∞=τ答案10.11解：当0<t 时，电容处于开路，由换路定律得：3V V 9633)0()0()0(1-=⨯+-=-==--+u u u C C ∞→t 电容又处于开路V 3V 9633V 95.133)()()(12=⨯+-⨯+=∞-∞=∞u u u C 求等效电阻的电路如图(b)所示。
(b)等效电阻Ω=Ω+⨯++⨯=k 3k )5.135.133636(i R时间常数s 106F 102103363--⨯=⨯⨯Ω⨯=τ 由三要素公式得V )e 63(e )]()0([)()(610/3t t C C C C u u u t u --+-=∞-+∞=τ (1)设1t t =时，0=C u 。
由式(1)得：0e6313610=--t ， 解得：s 1016.42ln 106331--⨯=⨯=t答案10.12解：初始值4mA mA 5144)0()0(=⨯+==-+L L i i 稳态值mA 5.25444)(=⨯+=∞L i 等效电阻Ω=++=k 8314i R时间常数s 101088.043i -=⨯==R L τ 由三要素公式得：mA ]5.15.2[)(410t L e t i -+= 0(≥t )由KVL 得：V )e 1(5.7)(k 3d d )(4103tL L L t i ti L u u t u --=⨯Ω+=+=)0(>t答案10.13解：当0<t ，10r =Ω时，电容处于开路，对回路l 列KVL 方程得：20)0()51010()0(5)0()0(10=++=++----i i ri i解得A 8.0)0(=-i由换路定律得V 4)0(5)0()0(=⨯Ω==--+i u u C C当∞→t 时，5r =Ω，电容又处于开路，再对回路l 列KVL 方程得：20)()5510()(5)()(10=∞++=∞+∞+∞i i ri i解得A 1)(=∞iV 5)(5)(=∞⨯Ω=∞i u C当ab 端短路时 ，电路如图(b)所示。
201i i SC =0=i ，0ri =，A 210V201SC =Ω==i i 等效电阻Ω==∞=5.2A2V5)(SC i i u R C 时间常数i 1R C s τ== 由三要素公式得V )e 5(e )]()0([)()(/t t C C C C u u u t u --+-=∞-+∞=τ)0(≥t答案10.14解：由题接电容时的零状态响应，可得+=0t 和∞→t 时的计算电路，分别如图(b)和(c)所示。
u (c)(b)Su -+u -+u由于电感对直流稳态相当于短路，零状态电感在换路瞬间相当于开路，故接电感在+=0t 和∞→t 时的计算电路分别与接电容时∞→t 和+=0t 时的情况相同。
所以接L 时，初始值(0)10V u +=， 稳态值()5V u ∞=。
由接电容时的响应得时间常数C i 0.5R C τ==，所以 Ω==50i CR Cτ接电感后，i R 不变，故时间常数s 1.0i==R LL τ 将上述初始值、稳态值和时间常数代入三要素公式得10()[55]()V t u t e t ε-=+答案10.15解： 由于S i 为指数函数，故须列写关于i 的微分方程来计算i 的强制分量。