实验6 二阶电路响应的仿真
7.二阶电路响应的仿真实验

长江大学电工电子实验中心龙从玉
10
长江大学电工电子实验中心龙从玉 9
五.实验报告 实验报告
1.根据观测结果,在方格纸上描绘二阶电路过阻 根据观测结果, 根据观测结果 尼、临界阻尼和欠阻尼的响应波形 2.测算欠阻尼振荡曲线上的衰减常数和振荡频率。 测算欠阻尼振荡曲线上的衰减常数和振荡频率。 测算欠阻尼振荡曲线上的衰减常数和振荡频率 3.归纳、总结电路元件参数的改变对响应变化趋 归纳、 归纳 势的影响。 势的影响。
长江大学电工电子实验中心龙从玉
R2
r=4
图用瞬态分析方法观察 用瞬态分析方法观察RLC并联电路的零状态响应。 并联电路的零状态响应。 用瞬态分析方法观察 并联电路的零状态响应 在进行瞬态分析时,直流电源保持常数, 在进行瞬态分析时,直流电源保持常数,交流信号源 随着时间而改变,电容和电感都是能量储存模式元件。 随着时间而改变,电容和电感都是能量储存模式元件。 1 1.创建如图 创建如图13-7所示的仿真实验电路。 所示的仿真实验电路。 创建如图 所示的仿真实验电路 + 2.选择菜单栏 选择菜单栏Analysis(分 ( 选择菜单栏 1K 10mH 0.1µ 中的Transient(瞬态 析)中的 ( 1A 分析)。根据对话框的要求, )。根据对话框的要求 分析)。根据对话框的要求, 设置参数。 设置参数。
电路元件参数 R0 k
2
图-3 电路响应理论值 理论值 ωO r/s
105
电路响应uC测量值 C uf Td s U1m v U2m v α ωd r/s
R k
L mH 10 10 10 10 10
α
ωd r/s
0.01
0.1 0.001 长江大学电工电子实验中心龙从玉
二阶电路的仿真与实验

10
实验内容:
观察并纪录RLC串联电路,、的零输入响应、零
状态响应 。实验线路原理图如图11-8所示。
CH1 观察us波形
仿真: 选取f =5kHz 左右, C=2200PF, 5600PF, 0.01uF , L=10mH, R=10K
L
CH2
us
周期方波 发生器
+
R
C
+ uc -
观察uc波形
Td t2 t1
2 d Td
-U2m
t1
t2 t
由于: u c Ae t sin( t ) -U1m 而峰值时 sin( t ) 1
U 1m e (t2 t1 ) 得 U 2m
t1 t 2 U Ae U Ae 故: , 1m 2m
阻尼时us (t). uc (t) 波形。如图10-4所示。 方法:打开开关,按“暂停”按钮。
6
仿真示例
减小R到64%左右,调节示波器参数,观察临
界阻尼时us (t). uc (t) 波形。如图10-5所示。 方法:打开开关,按“暂停”按钮。
7
仿真示例
减小R到16%左右,调节示波器参数,观察欠
2、计算 及
d
,以仿真示例中欠阻尼为例
2 2 3.14 d T d 215.4 10 6 2.9110 4 raU1m=4.45V, U2m=0.98V;
1 U1m ln Td U 2 m 1 4.45 ln 6 215.4 10 0.98 7024
R 1600 8000 2 L 2 0.1
1 1 O LC 0.1 0.0110 6 3.16 10 4 rad / s
仿真实验二二阶电路响应
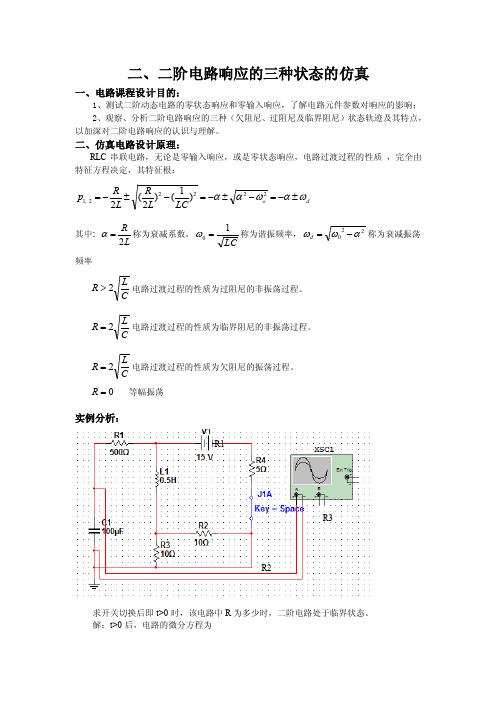
二、二阶电路响应的三种状态的仿真一、电路课程设计目的:1、测试二阶动态电路的零状态响应和零输入响应,了解电路元件参数对响应的影响;2、观察、分析二阶电路响应的三种(欠阻尼、过阻尼及临界阻尼)状态轨迹及其特点,以加深对二阶电路响应的认识与理解。
二、仿真电路设计原理:RLC 串联电路,无论是零输入响应,或是零状态响应,电路过渡过程的性质 ,完全由特征方程决定,其特征根:d o LCL R L R p ωαωαα±-=-±-=-±-=22222,1)1()2(2 其中: L R 2=α称为衰减系数,LC10=ω称为谐振频率,220αωω-=d 称为衰减振荡频率 CL R 2>电路过渡过程的性质为过阻尼的非振荡过程。
CL R 2=电路过渡过程的性质为临界阻尼的非振荡过程。
C L R 2=电路过渡过程的性质为欠阻尼的振荡过程。
0=R 等幅振荡实例分析:求开关切换后即t>0时,该电路中R 为多少时,二阶电路处于临界状态。
解:t>0后,电路的微分方程为R1R2R3Ai i V u u u dtdu C R dt u d LC c c c c c 5)0()0(25)0()0(0'22=-=+=-=+=++ Ate e e te A e A e A C t i Ve t e t A A u A A p p p C L R LC L R L R Cp R LCp t t t t t t t t c )5.5006975.35405.3535(10)()()5.354020()(5.35402542.141,42.14121)(2p 0142.14142.14142.141422142.14142.141212121'2''2,1'2-----------=-+--=+=+=∴==-===Ω==∴-±-==++δδδδδ,为两个相等的实根。
二阶电路响应实验报告

二阶电路响应实验报告二阶电路响应实验报告引言:二阶电路是电路理论中的重要内容之一,它由两个储能元件(电感和电容)和一个耗能元件(电阻)组成。
在实际应用中,二阶电路广泛用于滤波器、振荡器等电子设备中。
本次实验旨在通过对二阶电路的响应特性进行实验研究,深入理解二阶电路的工作原理和特性。
实验目的:1. 了解二阶电路的基本结构和工作原理;2. 掌握二阶电路的频率响应特性;3. 通过实验数据分析,验证理论模型的准确性。
实验器材和仪器:1. 信号发生器;2. 双踪示波器;3. 电压表;4. 电流表;5. 二阶电路实验箱。
实验步骤:1. 搭建二阶低通滤波器电路,并连接信号发生器和示波器;2. 调节信号发生器的频率,记录输入信号和输出信号的幅值;3. 改变输入信号频率,重复步骤2,记录数据;4. 换用高通滤波器电路,重复步骤2和3。
实验结果与分析:在实验中,我们记录了不同频率下输入信号和输出信号的幅值,并绘制了频率响应曲线。
通过观察和分析实验数据,我们得出以下结论:1. 低通滤波器的频率响应特性:在低频段,输出信号的幅值随频率的增加而增加,但增长速率逐渐减慢;在高频段,输出信号的幅值随频率的增加而迅速下降。
这表明低通滤波器对低频信号有较好的传递性能,但对高频信号有较强的衰减能力。
2. 高通滤波器的频率响应特性:与低通滤波器相反,高通滤波器在低频段对信号的传递能力较差,输出信号的幅值较小;而在高频段,输出信号的幅值随频率的增加而增加,但增长速率逐渐减慢。
这说明高通滤波器对高频信号有较好的传递性能,但对低频信号有较强的衰减能力。
3. 实验数据与理论模型的比较:将实验数据与理论模型进行比较,发现它们之间存在一定的偏差。
这可能是由于实验中存在的误差,例如电路元件的参数与理论值之间的差异,以及仪器的测量误差等。
然而,总体上实验数据与理论模型仍然具有较好的一致性,验证了理论模型的准确性。
结论:通过本次实验,我们深入了解了二阶电路的工作原理和频率响应特性。
二阶电路响应的仿真实验报告

二阶电路响应的仿真实验报告一、实验目的本次实验旨在通过仿真实验的方式,探究二阶电路响应的特性,并且了解其在不同频率下的响应情况。
二、实验原理1. 二阶电路的基本概念二阶电路是指带有两个存储元件(电容或电感)的电路,其具有更加复杂的响应特性。
其中,常见的二阶电路包括二阶低通滤波器、二阶高通滤波器以及二阶带通滤波器等。
2. 二阶低通滤波器的特性在二阶低通滤波器中,当输入信号频率很低时,输出信号基本上不会受到影响;而当输入信号频率逐渐升高时,输出信号将会逐渐减小。
当输入信号频率等于截止频率时,输出信号将会下降3dB;而当输入信号频率继续升高时,输出信号将会更加明显地下降。
3. 仿真实验步骤(1)构建一个RC电路,并且设置初始条件和参数值;(2)绘制RC电路的幅度-频率响应曲线;(3)绘制RC电路的相位-频率响应曲线;(4)分析幅度-频率响应曲线和相位-频率响应曲线的特点。
三、实验步骤1. 构建RC电路在Multisim软件中,选择“模拟”选项卡,然后选择“Passive”选项卡,接着选择“R”和“C”元件,并且将它们连接起来。
最终得到的电路图如下所示:2. 设置初始条件和参数值在Multisim软件中,点击“仿真设置”按钮,在弹出的对话框中,将仿真类型设置为“AC Analysis”,并且设置频率范围为1Hz~10MHz。
接着,设置电容C1的值为0.01μF,电阻R1的值为10kΩ。
3. 绘制RC电路的幅度-频率响应曲线在Multisim软件中,点击“仪表”选项卡,并且选择“AC Analysis”仪表。
接着,在弹出的对话框中,将X轴设置为“Frequency”,将Y轴设置为“Magnitude(dB)”,并且勾选上“Decibel Scale”。
最终得到的幅度-频率响应曲线如下图所示:4. 绘制RC电路的相位-频率响应曲线在Multisim软件中,点击“仪表”选项卡,并且选择“AC Analysis”仪表。
二阶电路响应的研究实验报告

二阶电路响应的研究实验报告摘要:本实验通过对二阶电路的响应进行研究,以深入了解二阶电路的工作原理和性质。
实验中通过利用示波器观察RC电路和RLC电路的频率响应曲线、计算共振频率和带宽等参数。
数据结果表明,当电路达到共振频率时,电路在谐振时的电压幅度最大,而带宽与电路的阻抗相关。
本次实验结论将有助于加深学生对于二阶电路的认识和理解,进一步提高本专业同学对于微电子学科的综合素质。
关键词:二阶电路;共振频率;带宽;频率响应曲线Introduction:二阶电路是指电路中包含了两个存储元件的线性电路。
存储元件可以是电容、电感或共同组成的电容电感(LC)元件,具有强烈的共振特性。
二阶电路在电子工程学科中具有重要意义,可以广泛应用于无线电、通信和信号处理等各种领域。
深入了解二阶电路的工作原理和性质是非常重要的。
本实验旨在通过研究二阶电路的响应,通过实验数据结果对二阶电路进行深入的分析,包括共振频率、带宽等参数。
实验结果将有助于加深学生对于二阶电路的认识和理解。
Experimental content:在实验中,我们分别通过示波器对RC电路和RLC电路进行了测量,计算了两个电路的共振频率和带宽。
在RC电路中,我们通过更改电阻和电容的数值,观察了频率响应曲线的变化。
在RLC电路中,我们将电路带入谐振状态并观测该状态下的电压幅度。
详细实验步骤如下:1. RC电路的实验:步骤1.1:所需器材:函数发生器、示波器、电阻器、电容器。
步骤1.2:根据电路图连cct,将电路接上函数发生器和示波器,以观察RC电路的响应曲线,并进行录像记录。
步骤1.3:逐渐调整函数发生器的频率,观测并记录RC电路的响应曲线,包括电压和相位。
记录下不同电容值对响应曲线的影响。
步骤1.4:通过观察响应曲线,计算出RC电路的共振频率和带宽。
步骤2.4:通过观察响应曲线,将RLC电路带入谐振状态,并记录下谐振状态下电压幅度的大小。
Results and analysis:实验结果表明,在RC电路中,随着电容值的不断增大,电路的共振频率也随之而增大。
二阶电路的暂态响应实验报告

二阶电路的暂态响应实验报告在这个二阶电路的暂态响应实验中,我们就像一群探险家,准备在电流的海洋里畅游。
想象一下,电路就像一艘船,电流是船上的水手,而电压就像那把指挥棒,时不时地给水手们下达指令。
我们要观察这艘船在不同情况下的表现,哦,真是让人期待呀!准备好实验器材,电阻、电感、电容,一个都不能少。
就像做一道美味的菜,材料齐全,才能发挥大厨的绝活儿。
实验开始前,心里总是有点紧张,就像在紧张的比赛前一样。
我们把电路连接好,心里暗自期盼。
然后,啪!一声开关的声音,电流就像火箭一样发射出去,哇,那一瞬间的感觉,简直让人兴奋得想跳起来。
电压一瞬间就冲上去了,电流也跟着嗖嗖嗖地跑了起来,真是如鱼得水,潇洒自如。
电容在这时候就像个小懒虫,慢慢吸收电能,给我们上演了一出“缓缓而行”的戏。
哦,电感也不甘示弱,它一开始抵抗电流的变化,就像在说:“嘿,等一下,我还没准备好呢!”这个过程,真的是一波三折,剧情跌宕起伏。
随着时间的推移,电容慢慢充满了电,电流的变化也开始减缓,整个电路像一场盛大的舞会,大家都渐渐放松了下来。
你看,电流的波形图就像是一幅画,刚开始激荡,后面却越来越平稳,真是美妙的画卷啊。
这个时候,大家都在窃窃私语:“你看,电路的暂态响应真有意思,就像人在成长,慢慢适应环境。
”说得没错,这种变化的过程,简直让人想起了人生的起伏,谁没有过风风雨雨呢?当电路进入稳态时,电流和电压都趋于平稳,仿佛一切都安静下来了,真是像小溪流水一样,轻轻柔柔。
我们在这过程中,不仅仅是在看数据,更是在观察一段故事的发展。
就像一部电视剧,高兴迭起,最后总会有个大团圆。
每一个波形的变化,都在诉说着电路的情感,就像人们在生活中经历的喜怒哀乐,真是感人至深。
总结这次实验,收获颇丰,心里那个乐啊,简直像捡到宝一样!不仅了解了二阶电路的暂态响应,还感受到了电流与电压之间的默契配合。
这种配合,真是相得益彰,像是绝配的情侣,缺一不可。
我们这次实验,不仅是一次技术上的挑战,更是一次心灵上的洗礼。
(完整版)实验二阶电路的响应PPT文档

d0 22 ,S 1 jd ,S 2 jd
零输入响应
零状态响应
电容电压 电感电流 电感电压
uc(t) d oV0e-tcosdt() uc(t)[1 d oe-tcodst ()k(t)
iL(t)Vd0Le-t sind(t)
iL(t)kdLe-t sind(t)(t)
uL(t) d oVoe-tcosdt()
实验:二阶电路的响应
实验目的 实验原理 实验仪器 实验步骤 实验报告 实验现象 实验结果分析 实验相关知识 实验标准报告
实验目的
1. 观察二阶网络在过阻尼、临界阻尼和欠阻尼三种情况下 响应波形。
2. 研究二阶网络参数与响应的关系。 3. 进一步掌握示波器的使用。
实验原理
1. 凡是可用二阶微分方程描述的电路称为二阶电路。
实验报告
1. 画出过阻尼、临界阻尼、欠阻尼的电容电压和电流波形。 2. 从欠阻尼振荡的波形,计算以下两个参数。 3.
d 2 fd 2 / Td
1/ Td
ln
u1m u2m
实验现象
实验结果分析
1.
当 0 , (R2
L )时,响应为过阻尼响应。
C
2.
当 0,(R 2
L )时,响应为临界阻尼响应。
( 进2一)步当掌电握示感波电器的流使时用,。S1,iL S(2t为)两个相(s等1的V -s负02实)L根(,es1t -es2t)
iL(t)[(s1-1 s2)L(es1t -es2t)k](t)
电感电压
vL(t)s1V 0s2(s1es1t s2es2t)
vL(t)[s11 -s2(s1es1t -s2es2t)k](t)
R
L
C
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验六 二阶电路响应的仿真
一、实验目的
(1) 研究二阶动态电路响应的特点。
(2) 学习二阶电路衰减系数、振荡频率的测量方法,了解电路参数对它们的影响; (3) 观察、分析二阶电路响应的三种变化曲线及其特点,加深对二阶电路响应的认识与
理解。
二、原理说明
(1) 二阶电路
在一个动态网络中,若同时有两个性质独立的储能元件L 和C 存在, 则这个可以用二阶微分方程描述的动态电路称为二
阶电路。
对于一个二阶电路,典型的RLC 串联电路(图6-1所示),无论是零输入响应还是零状态响应,电路过渡过程的性质都完全由特征方程
012=++RCp LCp (6.1)
的特征根
LC L R L R p 1222
2
,1-
⎪⎭
⎫
⎝⎛±-= (6.2) 来决定。
该特征根是二阶常系数齐次微分方程,所以该电路被称为二阶电路。
一般分三种情况来分析:
1) C
L
R 2
> P 1,2是两个不相等的负实根。
电路过渡过程的性质是过阻尼的非振荡过程。
响应是单调的。
波形如图6-2所示。
图6-2 过阻尼状态变化曲线图 图6-3 临界阻尼状态变化曲线
2) C
L R 2
= 图4-3-7 二阶电路
图6-1
P 1,2是两个相等的负实根。
电路过渡过程的性质是临界阻尼过程。
响应处于振荡与非振荡的临界点上。
其本质属于非周期暂态过程。
波形如图6-3所示
3) C
L R 2
< P 1,2是一对共扼复根。
零输入响应中的电压、电流具有衰减振荡的特点,称为欠阻尼状态。
此时,相应的数学表达式为
())t (ωke t)ωK t ω(K e t u d δt d d δt c ϕ+=+=--cos sin cos 21 (6.3)
式中: 2202
21δωω-=⎪⎭
⎫
⎝⎛-=
L R LC d , L R 2=δ, LC
10=ω
δ是衰减系数,通常是一个正实数,ωd 是衰减振荡角频率,δ越大衰减越快,ωd 越高振
荡周期越小。
若电路中电阻为零,就成为等幅振荡,即
001
d R LC ωω=== (6.4)
u C (t)的欠阻尼过渡过程如图6-4。
u L (t) 的欠阻尼过渡过程与u C (t)相似。
(当R→0时,u C (t)就变得与u L (t)完全一样而且是等幅振荡了)。
图6-4 欠阻尼状态变化曲线 图6-5串联电路接至方波激励的衰减振荡的波形
(2) 欠阻尼状态下的衰减系数δ和振荡角频率ωd 。
可以通过示波器观测电容电压的波形求得。
R 、L 、C 串联电路接至方波激励时, 呈现衰减振荡暂态过程的波形如图4-3-11所示。
由图可见,相邻两个最大值的间距为振荡周期m ,由此计算振荡频率为
n
T
m T d = (6.5)
式中 m -- 振荡周期T d 所占格数; n -- 方波周期 T 所占格数。
振荡角频率为
d d d T f π
πω22== (6.6)
衰减系数
2
1ln 1
h h T d =
δ (6.7)
T d也可在示波器上直接读出,即m
=。
k 为T/DIV 扫描速率开关所在档的读数,
T d⨯
k
即表示每格所占的时间。
三、实验设备:电脑
四、实验内容及步骤
仿真实验
(1)用Multisim仿真工具绘出图6-1 所示电路,绘图时不能漏掉信号源,否则无法进
行仿真。
为防止仿真数据的离散性,绘图时尽量选用虚拟元件。
图6-1
(2)把电阻R设为100Ω,C为0.2μF,L为100mH,电容和电感的初始条件参数均设为0
(即默认值),方波信号源参数设定为:
重复频率=50Hz
占空比=50%
电压幅度=2V
用瞬态分析法选定节点1、2和3,即对u(t)、u L(t)、u C(t)的零状态响应和零输入
响应进行仿真分析。
执行方法如下:
执行Simulate/Analysis/Transient Analysis命令。
在弹出的Analysis Parameters 对话框中把Start time(起始时间)设为0,End time(结束时间)设为0.02(即20ms),其余按默认值。
然后点击Simulate按钮即可给出仿真曲线。
曲线的前半部分是零状态响应,后半部分是零输入响应。
分析仿真曲线属于什么状态(欠阻尼、临界阻尼还是过阻尼),并与计算值比较。
如果是欠阻尼振荡形,请测量振荡角频率ωd、衰减系数δ,与理论计算值比较并填入表6-1(过阻尼和临界阻尼不用)。
(3)把R的阻值改为500Ω、1.4 kΩ、2.5kΩ,重复 2)的内容。
R(Ω)阻尼状态属性ωdδ波形
五、实验报告要求(请在下面的空白页中完成,上面已有的表格除外)
(1)根据实验观测结果,与理论计算结果作比较,分析误差原因。
