微专题——立体几何中的应用题
高中数学立体几何应用题练习及参考答案2023

高中数学立体几何应用题练习及参考答案2023立体几何作为数学中的一个重要分支,涉及到几何图形的三维立体空间的研究。
在高中数学学习中,学生要学习和掌握各种各样的立体几何知识和运用技巧。
本文将为大家提供高中数学立体几何应用题练习及参考答案,帮助大家更好地掌握这一领域的知识。
第一部分:平面与立体几何1.如图,已知平面内三角形ABC,E、F分别是AB、AC上的点,BE=CF,G是AE的中点,连接GF,证明:∠BGC为直角。
```[图片描述:一个三角形ABC,E、F分别是AB、AC上的点。
BE=CF,G是AE的中点,连接GF。
]证明:(1)作BE的中垂线交AC于点D,作CF的中垂线交AB于点H,连接DG,GH。
(2)因为BE=CF,BD=HC,所以三角形BDE和CFH是全等的,即∠BDE=∠CFH,∠BED=∠CHF。
(3)因为G是AE的中点,所以AG=GE,而∠AGE=∠FCE,所以△AGE和△FCE是全等的。
(4)因为DG是三角形ABC中的中线,所以DG=BG,又∠DBG=∠C,所以△DGB和△CHF是全等的。
(5)因此,∠DGB=∠CHF,又∠DGC=∠HGC,所以∠BGC=90°。
```2. 如图,正方体ABCDEFGH的边长为1,P为立方体内一点,且有AP=√3/3,BP=CP=DF,连PE,证明PE⊥(ABCD)。
```[图片描述:正方体ABCDEFGH,P为内部一点,AP=√3/3,BP=CP=DF,PE与ABCD垂直相交。
]证明:(1)设PE所在直线交(ABCD)于点O,连接PA、PB、PC、PD。
(2)因为BP=CP=DF,所以BPFC是菱形。
(3)又因为AF=FB=BE=EC=CD=DE=1,所以AFPE和FBPE和BEPC和CEPD和DEPA都是全等的。
即∠APE=∠DPF,∠APB=∠DPB,∠BPC=∠DPC,∠CPD=∠APD,∠DPE=∠BPE。
(4)结合BPFC是菱形,可得∠BFP=∠CFP=∠PFC,所以∠BPC=2∠PFC,∠FDC=∠FCD,所以△FDC和△FCD是全等的,即∠FDC=∠DFC。
专题19 解决立体几何中的计算问题-2021年高考数学二轮复习核心考点微专题(苏教版)(原卷版)

1.如图,直三棱柱ABCA1B1C1中,AB=1,BC=2,AC=5,AA1=3,M为线段B1B上的一动点,则当AM +MC1最小时,△AMC1的面积为________.2.如图,在直三棱柱ABCA1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点.当AD+DC1最小时,三棱锥D-ABC1的体积为________.(1) 若D为线段AC的中点,求证:AC⊥平面PDO;(2) 求三棱锥P-ABC体积的最大值;(3) 若BC=2,点E在线段PB上,求CE+OE的最小值.4.如图,在棱长为4的正方体ABCDA 1B 1C 1D 1中,E ,F 分别为棱AA 1,D 1 C 1上的动点,点G 为正方形B 1BCC 1的中心,则空间四边形AEFG 在该正方体各个面上的正投影所构成的图形中,面积的最大值为________.【考向分析】有关立体几何体的计算,是历年高考中命题的重点和难点,几乎每年都考,考查题目巧妙、灵活、新颖.近几年高考立体几何体计算除了通常的题型外,还有几何体的组合问题、翻折问题、以生活实际为背景的问题、融入数学文化的问题等渐成为亮点,集中考查距离、表面积、体积等计算问题.这类问题题目新颖,能够考查空间想象能力与思维能力(一)立体几何中关于面积计算的问题变式1 已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径,若平面SCA ⊥平面SCB ,SA =AC ,SB =BC ,三棱锥S -ABC 的体积为9,则球O 的表面积为________.变式2 正三棱锥S -ABC 中,BC =2,SB =3,D ,E 分别是棱SA ,SB 上的点,Q 为边AB 的中点,SQ ⊥平面CDE ,则△CDE 的面积为________.(二)立体几何中关于体积计算的问题例2. 已知棱长为3的正方体ABCD -A 1B 1C 1 D 1中,P ,M 分别为线段BD 1,B 1C 1上的点,若BP PD 1=12,则三棱锥M-PBC的体积为________.变式1如图,在边长为4的菱形ABCD中,∠DAB=60°,点E,F分别在边CD,CB上,点E与点C,D 不重合,EF⊥AC,EF∩AC=O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABFED.(1) 求证:BD⊥平面POA;(2) 当PB取得最小值时,求四棱锥P-BDEF的体积.变式2如图,在圆柱O1,O2内有一个球O,该球与圆柱的上、下面及母线均相切,记圆柱O1,O2的体积为V1,球O的体积为V2,则V1V2的值是________.(三)以实际生活为背景的立体几何问题例3.将一个半径为5 cm的水晶球放在如图所示的工艺支架上,支架是由三根细金属杆P A,PB,PC组成,它们两两成60°角,则水晶球的球心到支架顶点P的距离是________cm.变式1如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△F AB分别是以BC,CA,AB为底边的等腰三角形,沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△F AB,使得D、E、F重合,得到三棱锥,当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为________.变式2《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有________斛.(保留两位有效数字)3.在三棱锥S-ABC中,底面ABC是边长为3的等边三角形,SA⊥SC,SB⊥SC,SA=SB=2, 则该三棱锥的体积为________.4.如图,在平面四边形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,现将四边形ABCD 沿BD折起,使平面ABD⊥平面BDC,E,F分别为棱AC,AD的中点.(1) 求证:DC⊥平面ABC;(2) 设CD=a,求三棱锥A-BFE的体积.1.已知正四棱锥的底面边长是6,高为7,则这个正四棱锥的侧面积是________.2.如图,在长方体ABCD -A 1B 1C 1D 1中,AB =AD =3 cm ,AA 1=2 cm ,则三棱锥A -B 1D 1D 的体积为______ cm 3.3.已知一个圆锥的底面积为2π,侧面积为4π,则该圆锥的体积为________.4.如图,已知正三棱柱ABCA 1B 1C 1的底面边长为2 cm ,高为5 cm ,一质点自点A 出发,沿着三棱柱的侧面绕行两周到点A 1点的最短路线的长为________cm.5. 若正四面体的棱长为a ,则其外接球的表面积为多少?6. 若一个正四面体的表面积为S 1,其内切球的表面积为S 2,则S 1S 2=________. 7. 如图,在矩形ABCD 中,AD =2,AB =4,E ,F 分别为边AB ,AD 的中点,现将△ADE 沿DE 折起,得四棱锥ABCDE .(1) 求证:EF //平面ABC ;(2)若平面ADE ⊥平面BCDE ,求四面体FDCE 的体积.8. 如图,在三棱柱A 1B 1C 1-ABC 中,D ,E ,F 分别是AB, AC ,AA 1的中点,设三棱锥F -ADE 的体积为V 1,三棱柱A 1B 1C 1-ABC 的体积为V 2,则V 1∶V 2=________.9. 一个长方体的三条棱长分别为3,8,9,若在该长方体上面钻一个圆柱形的孔后其表面积没有变化,则圆孔的半径为________.10.一块边长为10 cm的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形作侧面,以它们的公共顶点P为顶点,加工成一个如图所示的正四棱锥形容器,当x=6 cm时,该容器的容积为________cm3.11.(1) 给出两块面积相同的正三角形纸片(如图1,图2),要求用其中一块剪拼成一个正三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等.请设计一种剪拼方法,分别用虚线标示在图1、图2中,并作简要说明.(2) 试比较你剪拼的正三棱锥与正三棱柱的体积的大小.(3) 如果给出的是一块任意三角形的纸片(如图3),要求剪拼成一个直三棱柱模型,使它的全面积与给出的三角形的面积相等,请设计一种剪拼方法,用虚线标示在图3中,并作简要说明.12.如图,已知正方体ABCD -A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围________.。
2025届立体几何微专题外接球问题
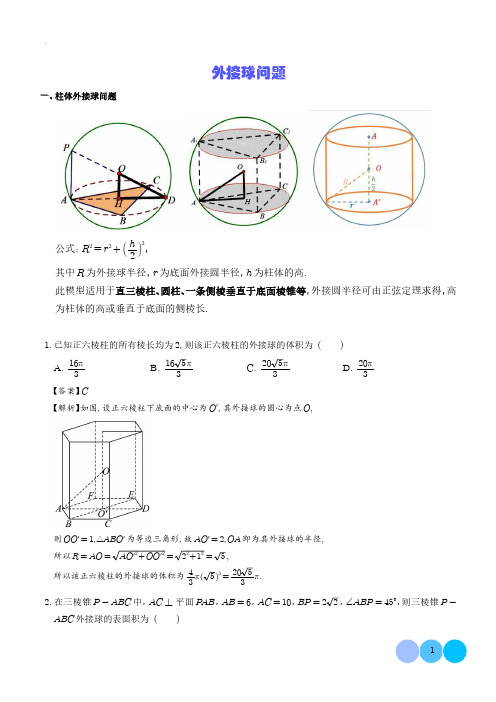
外接球问题一、柱体外接球问题公式:R 2=r 2+h 22,其中R 为外接球半径,r 为底面外接圆半径,h 为柱体的高.此模型适用于直三棱柱、圆柱、一条侧棱垂直于底面棱锥等,外接圆半径可由正弦定理求得,高为柱体的高或垂直于底面的侧棱长.1.已知正六棱柱的所有棱长均为2,则该正六棱柱的外接球的体积为()A.16π3B.165π3C.205π3D.20π3【答案】C【解析】如图,设正六棱柱下底面的中心为O ,其外接球的圆心为点O ,则OO =1,△ABO 为等边三角形,故AO =2,OA 即为其外接球的半径,所以R =AO =AO 2+OO 2=22+12=5,所以该正六棱柱的外接球的体积为43π5 3=2053π.2.在三棱锥P -ABC 中,AC ⊥平面P AB ,AB =6,AC =10,BP =22,∠ABP =45°,则三棱锥P -ABC 外接球的表面积为()A.144πB.128πC.140πD.148π【答案】C【解析】在△ABP中由余弦定理AP2=AB2+BP2-2AB⋅BP cos∠ABP=62+222-2×6×22×22=20,所以AP=25,设△ABP外接圆的半径为,则2r=APsin∠ABP=2522=210,所以r=10,又AC⊥平面P AB,AC=10,设三棱锥P-ABC外接球的半径为,则R2=r2+AC22=102+52=35,所以三棱锥P-ABC外接球的表面积S=4πR2=140π.3.直三棱柱ABC-A B C 的各个顶点都在球O的球面上,且AB=AC=1,BC= 2.若球O的表面积为3π,则这个三棱柱的体积是.【答案】1 2【解析】∵AB=AC=1,BC=2,∴AB⊥AC,∴直三棱柱ABC-A B C 外接球的球心O即为侧面BCC B 的中心,设球O半径为r,则4πr2=3π,∴r=32,即OC=r=3 2,∴直三棱柱ABC-A B C 的高h=2r2-12BC2=1,∴直三棱柱ABC-A B C 的体积V=S△ABC⋅h=12×1×1×1=124.圆柱的底面半径为1,侧面积为10π,则该圆柱外接球的表面积为.【答案】29π【解析】设圆柱的高为h,其外接球的半径为R,由圆柱的底面半径为1,侧面积为10π,得2πh=10π,解得h=5,由圆柱和球的对称性可知,球心位于圆柱上下底面中心连线的中点处,因此R=1+522=292,所以球的表面积为S=4πR2=29π.5.如图,该“四角反棱柱”是由两个相互平行且全等的正方形经过旋转、连接而成,其侧面均为等边三角形,已知该“四角反棱柱”的棱长为4,则其外接球的表面积为.【答案】32+82π【解析】如图,由题意可知旋转角度为π2,设上、下正方形的中心分别为O1,O2,连接O1O2,则O1O2的中点O即为外接球的球心,其中点B为所在棱的中点,OA即为该几何体的外接球的半径,O1A=22,O2B=2,AB=23,过点B作BC⊥O1A于点C,则AC=O1A-O2B=22-2,BC=AB2-AC2=8 2.易得四边形CBO1O2为矩形,即O1O2=BC=82,OO1=12O1O2=22,则OA=OO12+O1A2=8+22,即R=8+22,S=4πR2=32+82π,即该“四角反棱柱”的外接球的表面积为32+82π.二、长方体外接球问题公式:R=a2+b2+c22此模型适用于长方体、三条棱两两垂直的三棱锥、四棱锥等模型,其中a、b、c为长方体的长宽高,或者锥体的三条互相垂直的棱长.此类型外接球问题,可拓展出对棱相等模型:若三棱锥三组对棱分别对应相等,则三棱锥可看作为长方体的一部分,则其外接球公式为:R=λ2+μ2+ϕ28,其中λ、μ、ϕ为三组对棱的长.6.已知长方体的一条棱长为2,体积为16,则其外接球表面积的最小值为()A.5πB.12πC.20πD.80π【答案】C【解析】设长方体的长、宽、高分别为a,b,2,所以长方体的体积为V=2ab=16,解得:ab=8,设长方体的外接球的半径为R,所以2R=a2+b2+4,即4R2=a2+b2+4≥2ab+4=20,即R≥5,当且仅当a=b=22时取等,所以R min=5,所以其外接球表面积的最小值为S=4πR2=20π.7.已知三棱锥S-ABC的四个顶点都在球O的球面上,且SA=BC=2,SB=AC=7,SC=AB=5,则球O的体积是().A.83π B.3223π C.423π D.823π【答案】D【解析】将三棱锥放入长方体中,设长方体的长宽高分别为a,b,c,如图所示:则a2+b2=5a2+c2=7b2+c2=4,故a2+b2+c2=8,球O的半径R=12a2+b2+c2=2,故体积为43πR3=82π3.故选:D.将三棱锥放入长方体中,设长方体的长宽高分别为a,b,c,可得则a2+b2=5 a2+c2=7 b2+c2=4,得到球半径,计算体积得到答案.三、锥体外接球模型公式:R2=r2+h-R2此模型适用于圆锥、正棱锥等,其中R为外接球半径,r为底面圆的半径,h为锥体的高,特别的,正四面体的外接球半径公式为:R=64a.8.已知正三棱锥P-ABC的四个顶点都在半径为R的球面上,且AB=2,若三棱锥P-ABC的体积为32R,则该球的表面积为()A.32π27B.16π9C.64π27D.64π9【答案】D【解析】由题意得,△ABC为等边三角形,取△ABC的中心O1,设球心为O ,易得P ,O ,O 1共线,设三棱锥的高为h ,S △ABC =12×22×32=3,则V P -ABC =13⋅S △ABC ⋅h =32R ,则h =32R ,又OA =OP =R ,由正弦定理得,O 1A =12⋅2sin π3=233,在△OAO 1中,O 1O 2+O 1A 2=OA 2,即32R -R2+2332=R 2,解得R =43,则球的表面积为4πR 2=64π9.9.已知正四棱锥P -ABCD 的各顶点都在同一球面上,且该球的体积为36π,若正四棱锥P -ABCD 的高与底面正方形的边长相等,则该正四棱锥的底面边长为()A.16B.8C.4D.2【答案】C【解析】如图所示,设P 在底面的投影为G ,易知正四棱锥P -ABCD 的外接球球心在PG 上,不妨设球半径r ,OG =h ,AB =2a ,该球的体积为36π,即43πr 3=36π⇒r =3=OA =OP ,又正四棱锥P -ABCD 的高与底面正方形的边长相等,则AG =2a ,PG =2a ,AG 2+OG 2=r 2=PG -OG 2即2a -h2=92a 2+h 2=9⇒h =12a =4.四、垂面模型(两平面互相垂直)公式:R 2=r 21+r 22-l 24,其中R 为外接圆半径,r 1、r 2分别为两个垂直平面的外接圆半径,l 为公共边长.10.在体积为12的三棱锥A -BCD 中,AC ⊥AD ,BC ⊥BD ,平面ACD ⊥平面BCD ,∠ACD =π3,∠BCD =π4,若点A ,B ,C ,D 都在球O 的表面上,则球O 的表面积为()A.12πB.16πC.32πD.48π【答案】D 【解析】如图,取CD 的中点O ,连接AO ,BO ,因为AC ⊥AD ,BC ⊥BD ,所以OA =OB =OC =OD ,因此点O 就是球心,又∠BCD =π4,故△BCD 是等腰直角三角形,所以OB ⊥CD .因为平面ACD ⊥平面BCD ,平面ACD ∩平面BCD =CD ,所以OB ⊥平面ACD .设球O 半径为R ,则OB =R ,AC =R ,又∠ACD =π3,则AD =3R ,所以三棱锥A -BCD 的体积V =13S △ACD ⋅OB =13×12×AC ⋅AD ⋅OB =36R 3=12,所以R =23,所以球O 的表面积为4πR 2=48π.11.在三棱锥P -ABC 中,AB =BC =10,∠ABC =120°,D 为AC 的中点,PD ⊥平面ABC ,且PD =15,则三棱锥P -ABC 外接球的表面积为.【答案】500π【解析】在△ABC 中,AB =BC =10,∠ABC =120°,由余弦定理得AC 2=AB 2+BC 2-2AB ⋅BC ⋅cos ∠ABC =300,所以AC =103,设△ABC 的外接圆O 1的半径为r ,则由正弦定理得2r =AC sin ∠ABC =103sin120°,解得r =10结合图形分析:因为D 为AC 的中点,PD ⊥平面ABC ,且PD =15,在Rt △ABD 中,AD =12AC =53,BD =AB 2-AD 2=5,又O 1B =r =10,则圆心O 1到D 点的距离为O 1D =5,另设三棱锥P -ABC 的外接球球心O 到平面ABC 的距离为OO 1=d ,设外接球的半径为R ,则Rt △O 1OB 中,O 1B 2+OO 21=OB 2,即102+d 2=R 2,直角梯形O 1OPD 中,O 1D 2+PD -OO 1 2=OP 2,即52+15-d 2=R 2,解得d =5,R 2=125,所以S =4πR 2=500π..五、两面相交模型公式:R 2=m 2+n 2-2mn cos θsin 2θ+l 24,其中m 、n 为外心到公共边的距离,l 为公共边长,θ为二面角大小,若仅有一个面为钝角三角形,则取其补角.12.如图,在三棱锥P -ABC ,△P AC 是以AC 为斜边的等腰直角三角形,且CB =22,AB =AC =6,二面角P -AC -B 的大小为120°,则三棱锥P -ABC 的外接球表面积为.【答案】10π【解析】先分别作BC ,AC 中点E ,F ,连接AE ,PF ;再过点F 在平面ABC 内作AC 垂线,与AE 相交于点G ,AB 相交于点H ;分别过点F ,G 作平面P AC ,平面ABC 垂线,相交于点O ,连接AO ,如图所示,由题可知,二面角P -AC -B 的平面角为∠HFP =120°,点F ,G 分别为△P AC ,△ABC 的外心,故O 为该三棱锥外接球球心,AO 为外接球半径,可得,OF ⊥PF ,OG ⊥FH ,OG ⊥AG ,所以∠OFG =30°在△ABC 中,sin ∠CAE =CE AC=12BCAC=26=33所以tan ∠CAE =22,sin ∠BAC =sin2∠CAE =223,所以FG =AF tan ∠CAE =62×22=32,由正弦定理可知BCsin ∠BAC=2AG ⇒AG =32因为∠OFG =30°,OG ⊥FH 所以OG =FG tan30°=12因为OG ⊥AG所以有OA 2=AG 2+OG 2=52所以外接表面积为4πOA 2=10π13.如图,三棱锥P -ABC 的四个顶点都在球O 的球面上,P A ⊥PC ,△ABC 是边长为6的正三角形,二面角P -AC -B 的大小为120°,则球O 的体积为.【答案】52133π/5213π3【解析】取AC 的中点D ,连接BD ,设E 为△ABC 的外心,则点E 在BD 上且BE =2ED ,因为P A ⊥PC ,则D 为Rt △APC 的外心,根据球的几何性质,则OE ⊥平面ABC ,OD ⊥平面P AC ,因为二面角P -AC -B 的大小为120°,平面OAC ⊥平面P AC ,则二面角O -AC -B 的大小为30°,所以∠ODE =30°,因为△ABC 是边长为6的正三角形,则BD =6sin60°=33,所以ED =BD3=3,在Rt △OED 中,OD =EDcos30°=2,在Rt △ADO 中,因为AD =3,则OA =AD 2+OD 2=13,所以球O 的半径R =13,表面积为V 球=43πR 3=43π×1313=52133π.14.三棱锥A -BCD 中,BC =CD =2,BC ⊥CD ,△ABD 是正三角形,AC =14,则三棱锥A -BCD 的体积为;此三棱锥外接球的表面积为.【答案】63;56π3【解析】设BD的中点为P,连接CP,AP因为△ABD是正三角形,所以AB=AD,又因为BC=CD=2,所以有CP⊥BD,AP⊥BD,而CP∩AP=P,CP,AP⊂平面ACP,因此有BD⊥平面ACP,因为BC=CD=2,BC⊥CD,所以BD=BC2+CD2=4+4=22,CP=12BD=2因为△ABD是正三角形,BD的中点为P,所以AP=(22)2-12×222=6,而AC=14,根据余弦定理可知:cos∠APC=6+2-142×6×2=-32⇒∠APC=5π6因为BD的中点为P,所以三棱锥A-BCD的体积为:1 3S△ACP⋅BD=13×12×6×2×12×22=63因为BC=CD=2,BC⊥CD,BD的中点为P,所以P是△BCD的外心,设O1为△ABD的外心,过P作平面BCD的垂线,过O1作平面ABD的垂线,两个垂线的交点为球心O,在正△ABD中,O1P=13AP=63,O1A=23AP=263由上可知:∠APC=5π6,于是∠OPO1=5π6-π2=π3,于是有OO1=tan π3⋅O1P=3×63=2,在直角三角形OO1A中,OA=O1O2+O1A2=2+249=423因此此三棱锥外接球的表面积为4π⋅4232=56π3.六、台体的外接球模型公式:利用R2=r21+h-x2=r22+x2建立方程求解,其中h为台体高,r1、r2为底面圆(或外接圆)半径.15.已知某圆台的母线长为22,母线与轴所在直线的夹角是45°,且上、下底面的面积之比为1:4,则该圆台外接球的表面积为()A.40πB.64πC.80πD.128π【答案】C【解析】根据题意,将圆台补全为圆锥,记圆锥顶点为E,取圆锥的轴截面EAB,记该轴截面与圆台的交点为ABCD,记圆台上底面圆心为M,下底面圆心为N,根据圆台的对称性可知,其圆台的对称性可知,其外接球球心O在中轴线EN上,连接OC,OB如图所示:因为上、下底面的面积之比为1:4,则上底面半径与下底面半径之比为1:2,即BN=2MC,则有EB=2EC=2BC,EN=2MN,又由∠AEN=45°,则∠AEB=90°,而BC=22,则有MC=2,BN= 4,EN=4,则有NM=2,记圆台外接球半径为R,ON=h,在直角△OCM和直角△OBN中由勾股定理知:OM2+CM2=OC2,ON2+BN2=OB2,则有(h+2)2+4= h2+16,解可得h=2,故圆台外接球的半径R2=OB2=4+16=20,则该圆台外接球的表面积S=4πR2= 80π.16.已知正四棱台的顶点都在同一球面上,其上、下底面边长分别为2,22,高为3,则该球的表面积为()A.40πB.20πC.16πD.205π3【答案】B【解析】法一:正四棱台的对角面的外接圆为其外接球O 的大圆(如下图),对角面为等腰梯形AA C C ,其上下底边长分别为2,4,高为3,由正四棱台的对称性可知,球O 的球心O 在梯形上下底的中点连线O 1O 2所在直线上,设OO 1=d ,则OO 2=3-d ,球O 半径为OC =R =OC ,由Rt △OO 1C ,Rt △OO 2C 可得R 2=|3-d |2+22=d 2+12,解得d =2,R =5,所以所求的球O 的表面积为4πR 2=20π,法二:下底的外接圆不大于球的大圆,故球半径R ≥2(下底对角线长的一半),表面积4πR 2≥16π,排除D ;对角面等腰梯形AA C C 的对角线长32,故球半径R >322,表面积4πR 2>18π,排除C ;若4πR 2=40π,则R =10,易求球心到A C 的距离为d 1=3,球心到AC 的距离为d 2=6,无法满足d 1+d 2 =h =3,或d 1-d 2 =h =3,排除A .。
高三数学习题集:立体几何的应用

高三数学习题集:立体几何的应用立体几何是数学中一个重要的分支,也是高中数学中的一部分内容。
它通过研究空间中的图形与体的形状、位置关系等,帮助我们理解和应用几何概念,并在实际生活中找到问题的解决方案。
本文将为高三学生提供一些立体几何应用的习题,帮助他们巩固相关知识,提升解题能力。
1. 计算体积:已知一个长方体的底面积为20平方厘米,高为10厘米,求长方体的体积是多少?2. 计算表面积:一个正方体的边长为5厘米,求该正方体的总表面积。
3. 体积的应用:甲、乙两个柱体的底面半径都为4厘米,高分别为10厘米和15厘米,求两个柱体的体积之比。
4. 直方体的应用:甲的纸盒长20厘米、宽15厘米、高10厘米,乙的纸盒长28厘米、宽18厘米、高16厘米,请比较两个纸盒的体积。
5. 圆柱的应用:一个圆柱的底面半径为6厘米,高为9厘米,求其体积和侧面积。
6. 圆台的应用:一个圆台的底面半径为8厘米,上底面半径为6厘米,高为10厘米,求其体积和全面积。
7. 球的应用:一个球的表面积为200平方厘米,求其半径和体积。
8. 锥的应用:一个锥的高为12厘米,底面半径为5厘米,在底面上削去一个半径为3厘米的小圆锥,求大锥的体积。
通过解答以上习题,我们可以提升对立体几何的应用能力,加深对体积、表面积等概念的理解。
这些题目既可以巩固基础知识的掌握,又能锻炼思维能力和解题技巧。
总结:立体几何的应用领域广泛,包含了对不同几何体的体积、表面积的计算,以及一些实际问题的解决等。
通过解答相关习题,我们可以提升对立体几何知识的理解和应用能力,为日后的学习和实际生活中遇到的问题提供更好的解决方案。
在高三数学学业中,合理地运用立体几何知识,学生可以更加灵活地思考问题,提升解决数学问题的能力。
高考大题专练四:立体几何的综合运用

专练40高考大题专练(四)立体几何的综合运用1.[2021·全国新高考Ⅰ卷]如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)证明:OA⊥CD;(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E-BC -D的大小为45°,求三棱锥A-BCD的体积.2.[2020·新高考Ⅰ卷]如图,四棱锥P ABCD的底面为正方形,PD⊥底面ABCD.设平面P AD与平面PBC的交线为l.(1)证明:l⊥平面PDC;(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.3.[2022·全国乙卷(理),18]如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC的中点.(1)证明:平面BED⊥平面ACD;(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.4.[2020·全国卷Ⅰ]如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE=AD.△ABC是底面的内接正三角形,P为DO上一点,PO=66DO.(1)证明:P A⊥平面PBC;(2)求二面角B-PC-E的余弦值.5.[2020·全国卷Ⅱ]如图,已知三棱柱ABC-A1B1C1的底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点,过B1C1和P的平面交AB于E,交AC于F.(1)证明:AA1∥MN,且平面A1AMN⊥平面EB1C1F;(2)设O为△A1B1C1的中心.若AO∥平面EB1C1F,且AO=AB,求直线B1E与平面A1AMN 所成角的正弦值.6.[2021·全国乙卷]如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM.(1)求BC;(2)求二面角A-PM-B的正弦值.7.[2021·全国甲卷]已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.(1)证明:BF⊥DE;(2)当B1D为何值时,面BB1C1C与面DFE所成的二面角的正弦值最小?8.[2022·新高考Ⅰ卷,19]如图,直三棱柱ABC-A1B1C1的体积为4,△A1BC的面积为22.(1)求A到平面A1BC的距离;(2)设D到A1C的中点,AA1=AB,平面A1BC⊥平面ABB1A1,求二面角A-BD-C的正弦值.。
2023年高考数学微专题练习专练46高考大题专练四立体几何的综合运用含解析理

专练46 高考大题专练(四) 立体几何的综合运用1.[2022·全国甲卷(理),18]在四棱锥P-ABCD中,PD⊥底面ABCD,CD∥AB,AD=DC =CB=1,AB=2,DP= 3.(1)证明:BD⊥PA;(2)求PD与平面PAB所成的角的正弦值.2.[2022·全国乙卷(理),18]如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E为AC的中点.(1)证明:平面BED⊥平面ACD;(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.3.[2022·安徽省安庆市高三二模]如图,四边形ABCD是梯形,AB∥CD,AD⊥AB,AB =BC=2CD,△PBC是等腰三角形,PB=PC,且平面PBC⊥平面ABCD.(1)求证:BC⊥PA;(2)如果直线PD与平面ABCD所成角的大小为45°,求平面PAD与平面PBC所成锐二面角的余弦值.4.[2022·安徽省蚌埠市高三质检]《九章算术》记录形似“楔体”的所谓“羡除”,就是三个侧面都是梯形或平行四边形(其中最多只有一个平行四边形)、两个不平行对面是三角形的五面体.如图,羡除ABCDEF 中,ABCD 是正方形,且△EAD ,△FBC 均为正三角形,棱EF 平行于平面ABCD ,EF =2AB .(1)求证:AE ⊥CF ;(2)求二面角E AC F 的大小.5.[2022·安徽省皖北协作区联考]如图,在多面体ABCDEF 中,四边形ABEF 为正方形,AB ⊥BC ,BE ∥CD ,∠BCD =π3,AB =2,BC =CD =1,CM →=13CA →.(1)线段AD 上是否存在一点P ,使得AF ∥面BMP ?若存在,确定点P 的位置,若不存在,请说明理由;(2)求直线DM 与平面DEF 所成角的正弦值.专练46 高考大题专练(四) 立体几何的综合运用1.解析:(1)证明:∵CD ∥AB ,AD =CB =1,DC ≠AB , ∴四边形ABCD 是等腰梯形.如图,过点C 作CE ⊥AB 于点E ,过点D 作DF ⊥AB 于点F , 则AF =BE =12(AB -CD )=12,CD =EF .又AD =1,∴DF =AD 2-AF 2=32. 又BF =EF +BE =32,∴BD =BF 2+DF 2= 3.又AD =1,AB =2,∴AD 2+BD 2=AB 2,∴AD ⊥BD . ∵PD ⊥平面ABCD ,BD ⊂平面ABCD ,∴PD ⊥BD . 又AD ∩PD =D , ∴BD ⊥平面PAD .∵PA ⊂平面PAD ,∴BD ⊥PA .(2)如图,以D 为原点,DA ,DB ,DP 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,则D (0,0,0),A (1,0,0),B (0,3,0),P (0,0,3),∴PD →=(0,0,-3),PA →=(1,0,-3),PB →=(0,3,-3). 设平面PAB 的法向量为n =(x ,y ,z ). 由⎩⎪⎨⎪⎧PA →·n =0,PB →·n =0,得⎩⎨⎧x -3z =0,3y -3z =0.令z =1,得x =3,y =1,则n =(3,1,1). 设直线PD 与平面PAB 所成的角为θ,则sin θ=|cos 〈n ,PD →〉|=|n ·PD →||n |·||PD→=35×3=55.∴PD 与平面PAB 所成的角的正弦值为55.2.解析:(1)证明:∵AD =CD ,∠ADB =∠BDC ,BD =BD , ∴△ABD ≌△CBD ,∴AB =CB .∵E 为AC 的中点,∴DE ⊥AC ,BE ⊥AC . ∵DE ∩BE =E ,DE ,BE ⊂平面BED , ∴AC ⊥平面BED .∵AC ⊂平面ACD ,∴平面BED ⊥平面ACD .(2)如图,连接EF .由(1)知AC ⊥平面BED . 又∵EF ⊂平面BED , ∴EF ⊥AC . ∴S △AFC =12AC ·EF .当EF ⊥BD 时,EF 的长最小,此时△AFC 的面积最小. 由(1)知AB =CB =2. 又∵∠ACB =60°,∴△ABC 是边长为2的正三角形,∴BE = 3. ∵AD ⊥CD ,∴DE =1, ∴DE 2+BE 2=BD 2,∴DE ⊥BE .以点E 为坐标原点,直线EA ,EB ,ED 分别为x 轴、y 轴、z 轴建立空间直角坐标系,则E (0,0,0),A (1,0,0),B (0,3,0),C (-1,0,0),D (0,0,1),∴AB →=(-1,3,0),AD →=(-1,0,1),DB →=(0,3,-1),ED →=(0,0,1),EC →=(-1,0,0).设DF →=λDB →(0≤λ≤1),则EF →=ED →+DF →=ED →+λDB →=(0,0,1)+λ(0,3,-1)=(0,3λ,1-λ). ∵EF ⊥DB ,∴EF →·DB →=(0,3λ,1-λ)·(0,3,-1)=4λ-1=0,∴λ=14,∴EF →=(0,34,34),∴CF →=EF →-EC →=(0,34,34)-(-1,0,0)=(1,34,34). 设平面ABD 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·AB →=0,n ·AD →=0,即⎩⎨⎧-x +3y =0,-x +z =0.取y =1,则x =3,z =3,∴n =(3,1,3).设当△AFC 的面积最小时,CF 与平面ABD 所成的角为θ,则sin θ=|cos 〈n ,CF →〉|=|n ·CF →||n ||CF →|=⎪⎪⎪⎪⎪⎪3×1+1×34+3×343+1+3×1+316+916=437.故当△AFC 的面积最小时,CF 与平面ABD 所成的角的正弦值为437.3.解析:(1)证明:如图,取AB 的中点E ,连接CE .因为AB =2CD ,AB ∥CD ,AD ⊥AB , 所以四边形AECD 是矩形,所以CE ⊥AB . 在Rt△BEC 中,cos∠CBE =BE BC =12AB BC =12,所以∠CBE =60°.连接AC ,则△ABC 是等边三角形. 取BC 的中点O ,连接AO ,则AO ⊥BC .连接PO , 因为PB =PC ,所以PO ⊥BC , 因为PO ∩AO =O ,所以BC ⊥平面PAO,所以BC ⊥PA .(2)因为平面PBC ⊥平面ABCD ,PO ⊥BC ,平面PBC ⊥平面ABCD =BC ,PO ⊂平面PBC , 所以PO ⊥平面ABCD .连接DO ,则∠PDO 就是直线PD 与平面ABCD 所成的角, 所以∠PDO =45°,所以PO =OD .在△OCD 中,OC =CD ,∠DCO =120°, 所以OD 2=OC 2+CD 2-2OC ·CD ·(-12)=3OC 2,所以PO =OD =3OC .如图,以O 为坐标原点,OA →、OB →、OP →分别为x 轴、y 轴和z 轴的正方向,建立空间直角坐标系,令AB =BC =2CD =2a ,则A (3a ,0,0),B (0,a ,0),C (0,-a ,0),P (0,0,3a ). 由CD →=12BA →,可得D (32a ,-32a ,0).所以DA →=(32a ,32a ,0),AP →=(-3a ,0,3a ).设平面PAD 的一个法向量为m =(x 0,y 0,z 0), 由⎩⎪⎨⎪⎧m ·DA →=0,m ·AP →=0,得⎩⎪⎨⎪⎧32a ·x 0+32a ·y 0=0,-3a ·x 0+3a ·z 0=0.可取x 0=z 0=3,y 0=-1,则m =(3,-1,3).因为平面PBC 的一个法向量为OA →,所以cos 〈OA →,m 〉=OA →·m |OA →||m |=3a 21a =217,所以平面PAD 与平面PBC 所成锐二面角的余弦值为217. 4.解析:(1)延长AB 到M 点,使BM =AB ,连接CM ,FM , ∵EF ∥平面ABCD ,平面AMF ∩平面ABCD =AM ,∴EF ∥AM ,∵AM =2AB =EF ,∴四边形AMFE 是平行四边形, ∴AE ∥MF .在△FCM 中,令FC =2,则FM =2,CM =2, ∴FC 2+FM 2=CM 2,∴∠CFM =90°,即MF ⊥CF . ∴AE ⊥CF .(2)分别取AD ,BC ,EF 的中点G ,H ,Q ,连接EG ,GH ,HF ,AC ,BD ,设AC ∩BD =O ,连接OQ ,∵△EAD 为正三角形,G 是AD 中点, ∴AD ⊥EG ,∵AD ⊥AB ,GH ∥AB ,∴AG ⊥GH ,∴AD ⊥平面EFHG ,平面EFHG ⊥平面ABCD , ∵OQ ⊥GH ,平面EFHG ∩平面ABCD =GH , ∴OQ ⊥平面ABCD , ∴OQ ⊥AC ,OQ ⊥BD .分别以OA →,OB →,OQ →为x ,y ,z 轴的正方向,建立空间直角坐标系O -xyz ,令OA =1,则OB =1,OQ =1,A (1,0,0),C (-1,0,0),E (1,-1,1),F (-1,1,1), AC →=(-2,0,0),AE →=(0,-1,1),CF →=(0,1,1), AF →=(-2,1,1),设平面EAC 的法向量m =(x ,y ,z ), 则⎩⎪⎨⎪⎧m ·AC →=0m ·AE →=0,⎩⎪⎨⎪⎧-2x =0-y +z =0,令y =1,则m =(0,1,1), 设平面FAC 的法向量m =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·AC →=0n ·AF →=0,⎩⎪⎨⎪⎧-2x =0-2x +y +z =0,令y =1,则n =(0,1,-1),m ·n =0×0+1×1-1×1=0,∴〈m ,n 〉=90°,即二面角E AC F 的平面角为90°.5.解析:(1)存在P 为AD 上靠近D 点的三等分点,使得AF ∥面BMP ; 理由:过点M 作MP ∥CD ,交AD 于P ,因为CM →=13CA →,即有CM =13CA ,故DP =13DA ,即P 为AD 上靠近D 点的三等分点,而BE ∥CD ,AF ∥BE ,故AF ∥MP ,又MP ⊂面BMP ,AF ⊄面BMP ,所以AF ∥面BMP .(2)取CD 的中点为G ,连接BG ,BD ,因为∠BCD =π3,BC =CD =1,故△BCD 为正三角形,则BG ⊥CD ,故以B 为坐标原点,分别以BG ,BE ,BA 为x ,y ,z 轴,建立空间直角坐标系, 则D (32,12,0),E (0,2,0),F (0,2,2),A (0,0,2), C (32,-12,0), 则EF →=(0,0,2),DE →=(-32,32,0),又∵CM →=13CA →=13(-32,12,2),可求得M (33,-13,23), 设平面DEF 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·EF →=0n ·DE →=0,即⎩⎪⎨⎪⎧z =0-32x +32y =0, 不妨取y =1,则n =(3,1,0), 记直线DM 与平面DEF 所成角为θ, 又∵DM →=(-36,-56,23),∴sin θ=|cos 〈DM →,n 〉|=⎪⎪⎪⎪⎪⎪-12-562×(-36)2+(56)2+(23)2=21111,即直线DM 与平面DEF 所成角的正弦值为21111.。
微专题4:+立体几何中的探索问题+2022-2023学年高一下学期数学人教A版(2019)必修第二册

解:AD 上存在一点 P,AP=λPD,使得 CP
∥平面 ABEF,此时λ=3. 2
理由如下: 当λ=32时,AP=32PD,可知AADP=35,如图,过点 P 作 MP∥FD 交 AF 于点 M,连接 EM,PC,则有MFDP=AADP=35, 又 BE=1,可得 FD=5,故 MP=3, 又 EC=3,MP∥FD∥EC,故有 MP 綊 EC, 故四边形 MPCE 为平行四边形,所以 CP∥ME,
变式:如图,直三棱柱 ABC A1B1C1中,D,E分别是棱BC , AB的中点,点F在棱 CC1 上,已知AB=AC,AA1 3 , BC=CF=2.
(1)求证: C1E//平面ADF; (2)在棱 BB1 上是否存在点M,使平面 CAM 平面ADF ,若存在,试求出BM的值; 若不存在,请说明理由.
又BM=1,BC=2,CD=1,FC=2, Rt△CBM≌Rt△FCD
故 CM DF
DF . AD=D DF,AD
易证CM ,又
,
平面ADF,
故CM 平面ADF .
CAM
又 平面 CAM ,故平面
平面ADF.
翻折中的位置关系探索问题
例 3:如图,四边形 ABCD 中,AB⊥AD,AD∥BC,AD=6, BC=4,E,F 分别在 BC,AD 上,EF∥AB.现将四边形 ABCD 沿 EF 折起,使平面 ABEF⊥平面 EFDC.
证明如下:因为AB=AC, AD 平面ABC,故 AD BC.
在直三棱柱 ABC
中, A1B1C1
BB1
平面
ABC
高中数学立体几何的应用试题

高中数学立体几何的应用试题题目一:计算一个给定棱长的正方体的体积和表面积。
解析:一个正方体的体积可以通过将其棱长的立方来计算。
设正方体的棱长为a,则体积V = a³。
另一方面,正方体的表面积可以通过将每个面的面积相加来计算。
正方体有六个面,每个面的面积等于a²,所以表面积S = 6a²。
题目二:已知一个圆锥的底面半径和高,计算其体积和侧面积。
解析:一个圆锥的体积可以通过将其底面积乘以高再除以3来计算。
设圆锥的底面半径为r,高为h,则体积V = πr²h/3。
另一方面,圆锥的侧面积可以通过计算圆的周长乘以斜高来得到。
侧面积S = πrl,其中l为圆锥的斜高,可以通过勾股定理计算得到,l= √(r²+h²)。
题目三:给定一个正方体和一个球体,已知它们的体积相等,求球体的半径与正方体的边长的比值。
解析:设正方体的边长为a,球体的半径为r。
由已知条件可得,正方体的体积与球体的体积相等,即a³ = (4/3)πr³。
解方程可得球体的半径与正方体的边长的比值为r/a = (∛(3/4π))。
题目四:已知一个圆锥的底面半径和高,计算其表面积。
解析:一个圆锥的表面积由底面积、底面到尖顶的直线和侧面积三部分组成。
圆锥的底面积为πr²。
底面到尖顶的直线可以通过勾股定理计算得到,记为l = √(r²+h²)。
由于侧面是一个锥形,所以其侧面积可以通过计算圆的周长乘以斜高得到,记为Sl = πrl,其中l为底面到尖顶的直线。
综上所述,圆锥的表面积为S = πr² + πrl。
题目五:已知一个球体的体积,求其半径。
解析:设球体的体积为V,半径为r。
球体的体积可以通过将π乘以半径的立方来计算,即V = (4/3)πr³。
将公式重整为r³ =(3V)/(4π)。
解出r的立方根即可得到球体的半径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
微专题——立体几何中应用题 1.(2006江苏)(本小题满分14分)
请您设计一个帐篷。
它下部的形状是高为1m 的正六棱柱,上部的形状是侧棱长为3m 的正六棱锥(如右图
所示)。
试问当帐篷的顶点O 到底面中心1o 的距离为多少时,帐篷的体积最大?
2.(2011江苏)请你设计一个包装盒,如图所示,ABCD 是边长为60cm 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD 四个点重合于图中的点P ,正好形成一个正四棱柱形状的包装盒,E 、F 在AB 上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm
(1)若广告商要求包装盒侧面积S (cm 2)最大,试问x 应取何值?
(2)若广告商要求包装盒容积V (cm 3)最大,试问x 应取何值?并求出此时包装盒的高与底面边长的比值。
P
3.(2016江苏)
O 1 O x x E F A B
D C
4.某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按
照设计要求容器的容积为80
3
π
立方米,且2
l r
≥.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平
方米建造费用为3千元,半球形部分每平方米建造费用为c(3
c>)千元.设该容器的建造费用为y千元.
(1)写出y关于r的函数表达式,并求该函数的定义域;
(2)求该容器的建造费用最小时的r.
5.要制作一个由同底圆锥和圆柱组成的储油罐(如图),设计要求:圆锥和圆柱的总高度和圆柱底面半径相等,都为r米.市场上,圆柱侧面用料单价为每平方米a元,圆锥侧面用料单价分别是圆柱侧面用料单价和圆柱底面用料单价的4倍和2倍.设圆锥母线和底面所成角为θ(弧度),总费用为y(元).
(1)写出θ的取值范围;
(2)将y表示成θ的函数关系式;
(3)当θ为何值时,总费用y最小?
6。
