txw微专题——立体几何1学生版
全国通用高中数学第一章立体几何初步1.1空间几何体1.1.1构成空间几何体的基本元素练习新人教B版
（全国通用版）2018-2019高中数学第一章立体几何初步1.1 空间几何体1.1.1 构成空间几何体的基本元素练习新人教B版必修2编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（全国通用版）2018-2019高中数学第一章立体几何初步 1.1 空间几何体 1.1.1 构成空间几何体的基本元素练习新人教B版必修2）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（全国通用版）2018-2019高中数学第一章立体几何初步1.1 空间几何体1.1.1 构成空间几何体的基本元素练习新人教B版必修2的全部内容。
1。
1.1 构成空间几何体的基本元素1下列叙述中,一定是平面的是(）A。
一条直线平行移动形成的面B.三角形经过延展得到的面C.组成圆锥的面D.正方形围绕一条边旋转形成的面解析：直线平行移动可以形成平面或曲面,只有在方向不变的情况下才能得到平面.答案：B2下列说法中,正确的是(）A。
直线平移只能形成平面B.直线绕定直线旋转一定形成柱面C。
固定射线的端点让其绕着一个圆弧转动可以形成锥面D。
曲线平移一定形成曲面解析：A中，将直线平移时,可以形成柱面,故A错；B中,直线绕定直线旋转可以形成锥面，也可以形成柱面，故B错;C正确;D中,将一条平面内的曲线平移时，这个平面就可以看作是这条曲线平移所形成的平面，故D错。
因此选C。
答案：C3下面空间图形的画法中，错误的是（）解析：被遮住的地方应该画成虚线或不画，故选项D中的图形画法有误.答案:D4如图，在正方体ABCD-A1B1C1D1中,M，N，P,Q分别是线段C1D1，A1D1，BD1，BC的中点,给出下面四个命题：①MN∥平面APC;②B1Q∥平面ADD1A1;③A,P,M三点共线;④平面MNQ∥平面ABCD。
高中数学第一章立体几何初步1.7简单几何体的面积和体积1.7.1简单几何体的侧面积高一数学
12/13/2021
同理可得 SB＝40 cm， ∴AB＝SB－SA＝20(cm)， ∴S 表面积＝S 侧＋S 上＋S 下＝π(r1＋r2)AB＋πr21＋πr22 ＝π(10＋20)×20＋π×102＋π×202＝1 100π(cm2)． 故圆台的表面积为 1 100π cm2.
等腰梯形的高
12/13/2021
1．判断下列命题．(正确的打“√”，错误的打“×”) (1)把柱、锥、台的侧面无论沿哪一条侧棱或母线剪开，所得 到的展开图形状都相同，面积都相等．( √ ) (2)无论是哪种几何体，它们的侧面展开图都是极为规则的平 面图形．( × ) (3)空间几何体的侧面积即是表面积．( × ) (4)圆台的侧面展开图是一个扇环．( √ )
12/13/2021
④正棱锥被平行于底面的平面所截，截面和底面之间的部分叫 做正棱台． (4)要区分四棱柱、直四棱柱、正四棱柱、长方体、正方体等 几何体的区别与联系． 四 棱柱侧棱―垂―直→底面直 四 棱柱底―面―为→矩形长 方 体底面―为―正→方形 正 四棱柱 各―棱―相→等正方体． (5)正棱柱、正棱锥、正棱台的侧面展开图分别是由全等的矩 形、等腰三角形、等腰梯形组成，
∴AM1＝2 89，即绳子的最短长度为 2 89.
12/13/2021
︵ (2)过点 S 作 SQ⊥AM1，交BB1于点 P，交 AM1 于点 Q，则 PQ 的长度即为所求．
在
Rt△ ASM1
中，SQ＝SA·SM1＝16×10＝80 89.
AM1
2 89 89
∴当绳子最短时，上底圆周上的点到绳子的最短距离为80 89 89
12/13/2021
最新新课标人教版高考数学立体几何1空间几何体知识点及题型精选总结------(有答案)--37
立体几何初步本章知识结构与体系立体几何体知识点：（1）空间几何体（2）点、直线、面的位置关系（3）空间直角坐标系（1）空间几何体的知识点：（2）点、直线、面的位置关系：（3）空间直角坐标系:一、空间几何体知识点梳理：一、常见空间几何体定义：1 ．棱柱：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱，(1) 侧棱垂直于底面的棱柱称为直棱柱，直棱柱的侧棱即为棱柱的高．(2) 底面为正多边形的直棱柱称为正棱柱，两底面中心的连线即为棱柱的高．2 ．棱锥：有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱锥．(1) 如果一个棱锥的底面是正多边形，且顶点与底面中心的连线垂直于底面，这样的棱锥称为正棱锥．正棱锥具有性质：①正棱锥的顶点和底面中心的连线即为高线；②正棱锥的侧面是全等的等腰三角形，这些等腰三角形底边上的高都相等，叫做这个正棱锥的斜高．(2) 底边长和侧棱长都相等的三棱锥叫做正四面体．(3) 依次连结不共面的四点构成的四边形叫做空间四边形．3 ．棱台：用一个平行于棱锥底面的平面去截棱锥，底面与截面之间的部分，叫做棱台．4 ．圆柱：以矩形的一边所在的直线为旋转轴，其余三边旋转形成的曲面所围成的几何体叫做圆柱．5 ．圆锥：以直角三角形的一条直角边所在的直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫做圆锥．6 ．圆台：用一个平行于圆锥底面的平面去截圆锥，底面与截面之间的部分叫做圆台．7 ．球：以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的几何体叫做球．二、空间几何体的三视图和直观图空间几何体的三视图是用平行投影得到，这种投影下，与投影面平行的平面图形留下的影子，与平面图形的形状和大小是全等和相等的，三视图包括正视图、侧视图、俯视图．注：1、球的三视图都是圆，长方体的三视图都是矩形．2、圆柱的正视图、侧视图都是全等矩形，俯视图是圆．3、圆锥的正视图、侧视图都是全等的等腰三角形，俯视图是圆及圆心．4、圆台的正视图、侧视图都是全等的等腰体性，俯视图是两个同心圆。
立体几何全章(多面体棱柱等67个 人教课标版25精品公开PPT课件
A1
B1
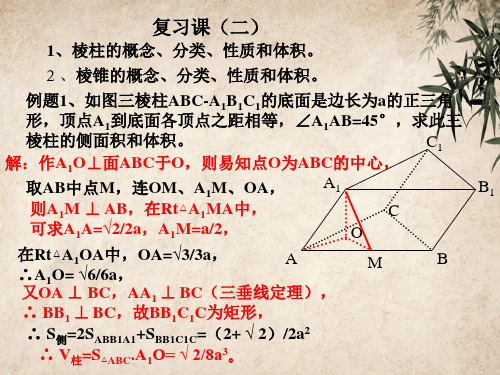
则A1M ⊥ AB，在Rt△A1MA中，
C
可求A1A=√2/2a，A1M=a/2，
O
在Rt△A1OA中，OA=√3/3a，
A
∴又AO1AO=⊥√6B/C6a，，AA1 ⊥ BC（三垂线定理），
M
B
∴ BB1 ⊥ BC，故BB1C1C为矩形，
∴ S侧=2SABB1A1+SBB1C1C=（2+ √ 2）/2a2
A1
C1 B1
（2）易知∠ DOB是异面直线 AB1与
BCDA中B1，=5D，B∴=4√C3o，s ∠OBD=O5，B=1/25为所求A。 D
C
（3）设A到面BDC1之距为h，由BC=8，
B
B1C=10;DC=4， DB=4√3 ∴ CC1=6，DC1= 2√13，
A
C
= 1/3S△BEC.AP=1/6hl2。
D
注：求体积时常进行拆分或组合。
B
例题3、（苏州P135例1）如图正三棱柱ABC-A1B1C1的底面是
边长为8，B1C=10，D为AC的中点。（1）求证：AB1//平面
C1BD；（2）求异面直线AB1与BC1所成角的余弦值；（3）
求直线AB1到平面C1BD的距离。 分析：（1）连OD，证OD//AB1即可。
连AC1，由VA-BDC1=VC1-ADB
∴ 1/3.1/2. 4√3 .（2√13）.h=1/3.1/2. 4√3. 4.6
∴ h= (12√13)/13为所求。
例题4:(苏州P138 3)多面体ABCDE中,AB ⊥面ACD,DE ⊥面 ACD,AC=AD=CD=DE=2,AB=1,F为CE中点.
复习课（二）
1、棱柱的概念、分类、性质和体积。
txw微专题——向量在立体几何中的应用学生版
向量在立体几何中的应用专题训练一、选择题1．向量a ＝(－2，－3,1)，b ＝(2,0,4)，c ＝(－4，－6,2)，下列结论正确的是( )A ．a ∥b ，a ∥cB ．a ∥b ，a ⊥cC ．a ∥c ，a ⊥bD ．以上都不对2．[2018·珠海模拟]已知A (1，－1,3)，B (0,2,0)，C (－1,0,1)，若点D 在z 轴上，且AD →⊥BC →，则|AD →|等于( )A. 2B. 3C. 5D.63．[2018·东营质检]已知A (1,0,0)，B (0，－1,1)，OA →＋λOB →与OB →的夹角为120°，则λ的值为( )A ．±66 B.66 C ．－66D ．±6 4．如图所示，在平行六面体ABCD －A 1B 1C 1D 1中，M 为A 1C 1与B 1D 1的交点．若AB →＝a ，AD →＝b ，AA 1→＝c ，则下列向量中与BM →相等的向量是( )A ．－12a ＋12b ＋cB.12a ＋12b ＋c C ．－12a －12b ＋cD.12a －12b ＋c 5．[2018·广西模拟]A ，B ，C ，D 是空间不共面的四点，且满足AB →·AC →＝0，AC →·AD →＝0，AB →·AD →＝0，M 为BC 中点，则△AMD 是( )A ．钝角三角形B ．锐角三角形C ．直角三角形D ．不确定6．已知两平面的法向量分别为m ＝(0,1,0)，n ＝(0,1,1)，则两平面所成的二面角为( )A ．45°B ．135°C ．45°或135°D ．90°7．[2018·金华模拟]在空间直角坐标系Oxyz 中，平面OAB 的一个法向量为n ＝(2，－2,1)，已知点P (－1,3,2)，则点P 到平面OAB 的距离d 等于( )A ．4B ．2C ．3D ．18．[2018·邯郸模拟]如图所示，已知正方体ABCD －A 1B 1C 1D 1，E ，F 分别是 正方形A 1B 1C 1D 1和ADD 1A 1的中心，则EF 和CD 所成的角是( )A ．60°B ．45°C ．30°D ．135°9．在三棱锥P －ABC 中，P A ⊥平面ABC ，∠BAC ＝90°，D ，E ，F 分别是棱AB ，BC ，CP 的中点，AB ＝AC ＝1，P A ＝2，则直线P A 与平面DEF 所成角的正弦值为( )A.15B.255C.55D.2510．在正方体ABCD －A 1B 1C 1D 1中，点E 为BB 1的中点，则平面A 1ED 与平面ABCD 所成的锐二面角的余弦值为( )A.12B.23C.33D.2211．一个四面体的顶点在空间直角坐标系Oxyz 中的坐标分别是(0,0,0)，(0,1,1)，(1,0,1)，(1,1,0)，则该四面体的体积为( )A.13B.64C ．1D ．23 12．已知正四棱锥S －ABCD 的侧棱长与底面边长都相等，E 是SB 的中点，则AE ，SD 所成角的余弦值为( )A.13B.23C.33D.23 二、填空题13．在空间直角坐标系中，以点A (4,1,9)，B (10，－1,6)，C (x,4,3)为顶点的△ABC 是以BC 为斜边的等腰直角三角形，则实数x 的值为________．14.如图，在正方形ABCD 中，EF ∥AB ，若沿EF 将正方形折成一个二面角后，AE ∶ED ∶AD ＝1∶1∶2， 则AF 与CE 所成角的余弦值为________．15.正三棱柱(底面是正三角形的直棱柱)ABC －A 1B 1C 1的底面边长为2，侧棱长为22，则AC 1与侧面ABB 1A 1 所成的角为________．16．[2018·沈阳检测]已知正四棱柱ABCD －A 1B 1C 1D 1，AB ＝1，AA 1＝2，点E 为CC 1的中点，则点D 1到平面BDE 的距离为 .三、解答题17．如图，直三棱柱ABC －A 1B 1C 1底面△ABC 中，CA ＝CB ＝1，∠BCA ＝90°，棱AA 1＝2，M ，N 分别是A 1B 1，A 1A 的中点．(1)求BN →的模；(2)求cos 〈BA 1→，CB 1→〉的值； (3)求证：A 1B ⊥C 1M .18．[2017·福建模拟]如图，在几何体ABCDE 中，四边形ABCD 是矩形，15题图14题图AB ⊥平面BEC ，BE ⊥EC ，AB ＝BE ＝EC ＝2，G ，F 分别是线段BE ，DC 的中点．(1)求证：GF ∥平面ADE ；(2)求平面AEF 与平面BEC 所成锐二面角的余弦值．19．[2018·西宁模拟]如图，正方形AMDE 的边长为2，B ，C 分别为AM ，MD 的中点．在五棱锥P －ABCDE 中，F 为棱PE 的中点，平面ABF 与棱PD ，PC 分别交于点G ，H .(1)求证：AB ∥FG ；(2)若P A ⊥底面ABCDE ，且P A ＝AE ，求直线BC 与平面ABF 所成角的大小，并求线段PH 的长．20．[2017·北京高考]如图，在四棱锥P －ABCD 中，底面ABCD 为正方形，平面P AD ⊥平面ABCD ，点M 在线段PB 上，PD ∥平面MAC ，P A ＝PD ＝6，AB ＝4.(1)求证：M 为PB 的中点； (2)求二面角B －PD －A 的大小；(3)求直线MC 与平面BDP 所成角的正弦值．21.如图甲，设正方形ABCD 的边长为3，点E 、F 分别在AB 、CD 上，且满足2AE EB =，2CF FD =．如图乙，将直角梯形AEFD 沿EF 折到11A EFD 的位置，使得点1A 在平面BEFC 上的射影G 恰好在BC 上． (1)证明：1A E平面1CD F ；(2)求平面BEFC 与平面11A EFD 所成二面角的余弦值．22．【2017届四川成都市高三一诊】如图1，在正方形ABCD 中，点,E F 分别是,AB BC 的中点，BD 与EF 交于点,H G 为BD 中点，点R 在线段BH 上，且()0BRRHλλ=>.现将BEF CFD AED ∆∆∆,,分别沿,,DE DF EF 折起，使点,A C 重合于点B （该点记为P ），如图2所示. （1）若2λ=，求证：GR ⊥平面PEF ；（2）是否存在正实数λ，使得直线FR 与平面DEF 所成角的 正弦值为22？若存在，求出λ的值；若不存在，请说明理由.A BD E F1A 1D CGEF图甲图乙。
(完整版)立体几何基础题题库(600道附详细答案)
立体几何基础题题库（有详细答案）1、二面角βα--l 是直二面角，βα∈∈B A ，，设直线AB 与βα、所成的角分别为∠1和∠2，则 （A ）∠1+∠2=900 （B ）∠1+∠2≥900 （C ）∠1+∠2≤900 （D ）∠1+∠2＜900 解析：C1和∠2分别为直线AB 与平面,αβ所成的角。
根据最小角定理：斜线和平面所成的角，是这条斜线和平面内经过斜足的直线所成的一切角中最小的角2ABO ∴∠>∠1902190ABO ∠+∠=∴∠+∠≤oo Q2. 下列各图是正方体或正四面体，P ，Q ，R ，S 分别是所在棱的中点，这四个点中不共面．．．的一个图是PPQQRSSPPPQQRR RSSSPP PQQQ R RSSS PP Q QR RRS S（A ） （B ） （C ） （D ） D解析： A 项：PS P 底面对应的中线，中线平行QS ，PQRS 是个梯形B 项：如图C 项：是个平行四边形D 项：是异面直线。
3. 有三个平面α，β，γ，下列命题中正确的是（A ）若α，β，γ两两相交，则有三条交线 （B ）若α⊥β，α⊥γ，则β∥γ （C ）若α⊥γ，β∩α=a ，β∩γ=b ，则a ⊥b （D ）若α∥β，β∩γ=∅，则α∩γ=∅ D解析：A 项：如正方体的一个角，三个平面相交，只有一条交线。
B 项：如正方体的一个角，三个平面互相垂直，却两两相交。
C 项：如图4. 如图所示，在正方体ABCD －A 1B 1C 1D 1的侧面AB 1内有一动点P 到直线AB 与直线B 1C 1的距离相等，则动点P 所在曲线的形状为P1BPA 1B PA 1OBPA 1OABCDP A C 1D 1C解析：11B C ⊥平面AB 111,B C PB ∴⊥，如图：PCD C'D'BB'AA'P 点到定点B 的距离与到定直线AB 的距离相等，建立坐标系画图时可以以点B 1B 的中点为原点建立坐标系。
高中数学第1章立体几何初步阶段综合提升第1课立体几何初步课件北师大版必修2
37
∵AO＝R，SO＝ 3R，
2 ∴ 2Ra＝ 3R3－R h，∴h＝ 3R－ 26a.
∴S 表＝2a2＋4ah＝2a2＋4a
3R－ 26a.
整理得 S 表＝(2－2
6)a－
63－R12＋
30
截面问题
【例 4】 如图，已知正三棱锥 S-ABC，过 B 和侧棱 SA，SC 的中点 E， F 作一截面，若这个截面与侧面 SAC 垂直，求此三棱锥的侧面积与底面积 之比．
[思路探究] 构建截面，利用几何知识巧妙判断各棱之间的关系．
31
[解] 取 AC 的中点 M，连接 SM，设 SM∩EF ＝D.
6
1．以三视图为载体的几何体的表面积问题，关键是分析三视图 确定几何体中各元素之间的位置关系及数量．
2．多面体的表面积是各个面的面积之和，组合体的表面积问题 要注意衔接部分的处理．
3．旋转体的表面积问题注意其侧面展开图的应用．
7
[跟进训练] 1．一个几何体的三视图如图所示，其中左视图与俯视图均为半 径是 2 的圆，则这个几何体的体积是________．
连接 EG，GH， ∵H 为 BC 的中点， ∴GH 綊21AB.
17
休息时间到啦
同学们，下课休息十分钟。现在是休息时间，你们休息一 下眼睛，
看看远处，要保护好眼睛哦~站起来动一动，久坐对身体不 好哦~
返 首 页
18
又 EF 綊12AB，
∴EF 綊 GH，
∴四边形 EFHG 为平行四边形， ∴EG∥FH，∵EG 平面 EDB，FH 平面 EDB， ∴FH∥平面 EDB.
高中数学 第一章 立体几何初步 1.1.6 棱柱、棱锥、棱台和球的表面积学案(含解析)新人教B版必修
2018版高中数学第一章立体几何初步1.1.6 棱柱、棱锥、棱台和球的表面积学案（含解析）新人教B版必修2编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018版高中数学第一章立体几何初步1.1.6 棱柱、棱锥、棱台和球的表面积学案（含解析）新人教B版必修2）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018版高中数学第一章立体几何初步1.1.6 棱柱、棱锥、棱台和球的表面积学案（含解析）新人教B版必修2的全部内容。
1。
1.6 棱柱、棱锥、棱台和球的表面积1.理解棱柱、棱锥、棱台和球的表面积的概念，了解它们的侧面展开图.(重点）2.掌握直棱柱、正棱锥、正棱台的表面积公式，并会求它们的表面积.（重点)3.了解球的表面积公式,会运用公式求球的表面积。
(重点)4。
组合体的表面积计算。
（难点)［基础·初探］教材整理1 棱柱、棱锥、棱台的表面积阅读教材P25~P26“倒数第5行"以上内容，完成下列问题.棱柱、棱锥、棱台是由多个平面图形围成的多面体，它们的表面积就是各个面的面积和.判断(正确的打“√”，错误的打“×"）（1）多面体的表面积等于各个面的面积之和。
( ）（2)棱台的侧面展开图是由若干个等腰梯形组成的。
( )(3)沿不同的棱将多面体展开,得到的展开图相同，表面积相等.（）【解析】(1)正确。
多面体的表面积等于侧面积与底面积之和。
（2）错误.棱台的侧面展开图是由若干个梯形组成的，不一定是等腰梯形.(3)错误。
由于剪开的棱不同，同一个几何体的表面展开图可能不是全等形.但是，不论怎么剪,同一个多面体表面展开图的面积是一样的.【答案】(1）√(2）×(3)×教材整理2 圆柱、圆锥、圆台和球的表面积阅读教材P26“倒数第3行”~P27“例1”以上内容，完成下列问题。
全国通用高中数学第一章立体几何初步1.1空间几何体1.1.3圆柱、圆锥、圆台和球练习新人教B版必修
（全国通用版）2018-2019高中数学第一章立体几何初步1.1 空间几何体1.1.3 圆柱、圆锥、圆台和球练习新人教B版必修2编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（全国通用版）2018-2019高中数学第一章立体几何初步 1.1 空间几何体 1.1.3 圆柱、圆锥、圆台和球练习新人教B 版必修2）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（全国通用版）2018-2019高中数学第一章立体几何初步1.1 空间几何体1.1.3 圆柱、圆锥、圆台和球练习新人教B版必修2的全部内容。
1。
1.3 圆柱、圆锥、圆台和球1关于下列几何体,说法正确的是(）A。
图①是圆柱 B.图②和图③是圆锥C。
图④和图⑤是圆台 D.图⑤是圆台解析:因为图①与图④中几何体两个底面不互相平行,所以它们不是圆柱和圆台.因为图②与图③中几何体的过旋转轴的截面（轴截面）不是等腰三角形,所以它们不是圆锥.图⑤是圆台。
答案:D2下列判断正确的是(）A。
平行于圆锥某一母线的截面是等腰三角形B。
平行于圆台某一母线的截面是等腰梯形C。
过圆锥顶点的截面是等腰三角形D.过圆台上底面中心的截面是等腰梯形解析：根据圆锥与圆台的定义和图形进行判断即可.答案：C3若一条直线被一个半径为13的球截得的线段长为24,则球心到这条直线的距离为（）A。
13 B.12 C.5 D.24解析：如图，d==5。
答案：C4上、下底面面积分别为36π和49π，母线长为5的圆台,则其两底面之间的距离为（)A.4B.3C。
2 D.2解析:圆台的母线长l、高h和上、下两底面圆的半径r,R满足关系式l2=h2+（R-r）2，求得h=2，即两底面之间的距离为2.答案：D5已知某地球仪上北纬30°纬线圈的长度为12π cm，则该地球仪的半径是()A.4 cmB.6 cmC。
“高中数学必修一课件-立体几何”
圆锥的体积公式证明
1
演绎和证明
2
通过逻辑推理和几何证明，演绎出圆
锥体积公式。
3
圆锥体积公式
介绍圆锥的体积公式。
实际应用
讲解圆锥体积公式在实际生活和其他 领域中的应用。
球体表面积公式推导
1
推导过程
2
通过几何推导和数学推理，演示球体
表面积公式的推导过程。
3
球体表面积公式
介绍球体表面积的计算公式。
应用领域
讨论球体表面积公式在实际应用中的 重要性。
柏拉图立体和其性质
柏拉图立体类型 四面体
六面体
八面体 十二面体 二十面体
性质和特点
具有四个面、六个边和四个顶点，每个面都是 一个三角形。
由六个正方形面组成，具有八个顶点和十二条 边。
具有八个面，每个面都是一个正等边三角形。
讨论三棱柱和三棱锥的表面积和体积计算方法。
曲面体的计算
圆柱的表面积和体积
讲解圆柱的计算方法和性质。
锥体的表面积和体积
讲解锥体的计算方法和性质。
球体的表面积和体积
讲解球体的计算方法和性质。
立体几何中的相似与全等
1
相似性
解释相似性的定义和判定方法，以及
全等性
2
相似性在立体几何中的应用。
阐述全等性的定义和判定方法，以及
具有十二个面，每个面都是一个正五边形。
由二十个等边三角形构成，具有十二个顶点和 三十个边。
立体几何在数学和其他领域中的重要性
数学领域
探索立体几何在数学领域中的 重要性和应用范围。
工程与建筑
研究立体几何在工程和建筑领 域的关键作用和创新。
全国通用高中数学第一章立体几何初步1.1空间几何体1.1.2棱柱、棱锥和棱台的结构特征练习新人教B
（全国通用版）2018-2019高中数学第一章立体几何初步1.1 空间几何体1.1.2 棱柱、棱锥和棱台的结构特征练习新人教B版必修2编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（全国通用版）2018-2019高中数学第一章立体几何初步 1.1 空间几何体 1.1.2 棱柱、棱锥和棱台的结构特征练习新人教B版必修2）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（全国通用版）2018-2019高中数学第一章立体几何初步1.1 空间几何体1.1.2 棱柱、棱锥和棱台的结构特征练习新人教B版必修2的全部内容。
1.1.2 棱柱、棱锥和棱台的结构特征1过正棱台两底面中心的截面一定是(）A.直角梯形B。
等腰梯形C.一般梯形或等腰梯形D。
矩形答案：C2如图是一个简单多面体的表面展开图(沿图中虚线折叠即可还原），则这个多面体的顶点数为（）A。
6 B。
7C。
8 D.9解析：还原几何体，如图.由图观察知，该几何体有7个顶点.答案：B3一个正四面体的各条棱长都是a,则这个正四面体的高是（)A。
a B。
a C.a D。
解析：因为正四面体底面外接圆半径为a,所以正四面体的高为h=a。
答案:B4有四种说法:①底面是矩形的平行六面体是长方体；②棱长相等的直四棱柱是正方体；③有两条侧棱垂直于底面一边的平行六面体是直平行六面体;④对角线相等的平行六面体是直平行六面体.以上说法中，正确的个数是(）A。
1 B。
2 C。
3 D.4解析：①不正确，除底面是矩形外还应满足侧棱与底面垂直才是长方体;②不正确,当底面是菱形时就不是正方体;③不正确，两条侧棱垂直于底面一边不一定垂直于底面,故不一定是直平行六面体;④正确,因为对角线相等的平行四边形是矩形，由此可以推测此时的平行六面体是直平行六面体，故选A。
(新课改省份专用)202x版高考数学一轮复习 第七章 立体几何 第一节 空间几何体及表面积与体积讲义
第一节空间几何体及表面积与体积突破点一空间几何体[基本知识]1．简单旋转体的结构特征(1)圆柱可以由矩形绕其任一边旋转得到；(2)圆锥可以由直角三角形绕其直角边旋转得到；(3)圆台可以由直角梯形绕直角腰或等腰梯形绕上下底中点连线旋转得到，也可由平行于圆锥底面的平面截圆锥得到；(4)球可以由半圆或圆绕直径旋转得到．[提醒] (1)球是以半圆面为旋转对象的，而不是半圆．(2)要注意球面上两点的直线距离、球面距离以及在相应的小圆上的弧长三者之间的区别与联系．2．简单多面体的结构特征(1)棱柱的侧棱都平行且相等，上下底面是全等的多边形；(2)棱锥的底面是任意多边形，侧面是有一个公共点的三角形；(3)棱台可由平行于棱锥底面的平面截棱锥得到，其上下底面是相似多边形．[提醒] (1)棱柱的所有侧面都是平行四边形，但侧面都是平行四边形的几何体却不一定是棱柱．(2)棱台的所有侧面都是梯形，但侧面都是梯形的几何体却不一定是棱台．(3)注意棱台的所有侧棱相交于一点．3．直观图(1)画法：常用斜二测画法．(2)规则：①原图形中x轴、y轴、z轴两两垂直，直观图中，x′轴、y′轴的夹角为45°(或135°)，z′轴与x′轴和y′轴所在平面垂直．②原图形中平行于坐标轴的线段，直观图中仍平行于坐标轴．平行于x轴和z轴的线段在直观图中保持原长度不变，平行于y轴的线段长度在直观图中变为原来的一半．[基本能力]一、判断题(对的打“√”，错的打“×”)(1)有两个面平行，其余各面都是平行四边形的几何体是棱柱．( )(2)有一个面是多边形，其余各面都是三角形的几何体是棱锥．( )(3)夹在两个平行的平面之间，其余的面都是梯形，这样的几何体一定是棱台．( )答案：(1)×(2)×(3)×二、填空题1．在如图所示的几何体中，是棱柱的为________．(填写所有正确的序号)答案：③⑤2．下列命题中正确的是________．①由五个平面围成的多面体只能是四棱锥；②棱锥的高线可能在几何体之外；③仅有一组相对的面平行的六面体一定是棱台；④有一个面是多边形，其余各面是三角形的几何体是棱锥．答案：②3．一个棱柱至少有________个面；面数最少的一个棱锥有________个顶点；顶点最少的一个棱台有________条侧棱．答案：5 4 34.用斜二测画法画出的某平面图形的直观图如图，边AB平行于y轴，BC，AD平行于x轴．已知四边形ABCD的面积为2 2 cm2，则原平面图形的面积为________ cm2.解析：依题意可知∠BAD＝45°，则原平面图形为直角梯形，上下底面的长与BC，AD 相等，高为梯形ABCD的高的22倍，所以原平面图形的面积为8 cm2.答案：8[典例感悟]1．给出下列几个命题：①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线；②底面为正多边形，且有相邻两个侧面与底面垂直的棱柱是正棱柱；③棱台的上、下底面可以不相似，但侧棱长一定相等．其中正确命题的个数是( )A．0 B．1C．2 D．3解析：选B ①错误，只有这两点的连线平行于轴时才是母线；②正确；③错误，棱台的上、下底面是相似且对应边平行的多边形，各侧棱延长线交于一点，但是侧棱长不一定相等．故正确命题的个数是1.2．给出下列命题：①棱柱的侧棱都相等，侧面都是全等的平行四边形；②若三棱锥的三条侧棱两两垂直，则其三个侧面也两两垂直；③在四棱柱中，若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱；④存在每个面都是直角三角形的四面体．其中正确命题的序号是________．解析：①不正确，根据棱柱的定义，棱柱的各个侧面都是平行四边形，但不一定全等；②正确，若三棱锥的三条侧棱两两垂直，则三个侧面构成的三个平面的二面角都是直二面角；③正确，因为两个过相对侧棱的截面的交线平行于侧棱，又垂直于底面；④正确，如图，正方体ABCDA1B1C1D1中的三棱锥C1ABC，四个面都是直角三角形．答案：②③④[方法技巧] 辨别空间几何体的2种方法定义法紧扣定义，由已知构建几何模型，在条件不变的情况下，变换模型中的线面关系或增加线、面等基本要素，根据定义进行判定反例法通过反例对结构特征进行辨析，要说明一个结论是错误的，只需举出一个反例即可[针对训练]1．用任意一个平面截一个几何体，各个截面都是圆面，则这个几何体一定是( ) A．圆柱B．圆锥C．球体D．圆柱、圆锥、球体的组合体解析：选C 截面是任意的且都是圆面，则该几何体为球体．2．下列命题正确的是( )A．两个面平行，其余各面都是梯形的多面体是棱台B．两个面平行且相似，其余各面都是梯形的多面体是棱台C．直角梯形以一条直角腰所在的直线为旋转轴，其余三边旋转形成的面所围成的旋转体是圆台D．用平面截圆柱得到的截面只能是圆和矩形解析：选C 如图所示，可排除A、B选项．对于D选项，只有截面与圆柱的母线平行或垂直时，截得的截面为矩形或圆，否则截面为椭圆或椭圆的一部分．故选C.突破点二 空间几何体的表面积与体积[基本知识]空间几何体的表面积与体积公式 名称几何体表面积 体积 柱体(棱柱和圆柱)S 表面积＝S 侧＋2S 底 V ＝Sh 锥体(棱锥和圆锥) S 表面积＝S 侧＋S 底V ＝13Sh 台体(棱台和圆台) S 表面积＝S 侧＋S 上＋S下V ＝13(S 上＋S 下＋S 上S 下)h 球S ＝4πR 2 V ＝43πR 3 [提醒] 解决与几何体的面积有关问题时，务必要注意是求全面积还是求侧面积．[基本能力]一、判断题(对的打“√”，错的打“×”)(1)多面体的表面积等于各个面的面积之和．( )(2)锥体的体积等于底面积与高之积．( )(3)球的体积之比等于半径比的平方．( )(4)简单组合体的体积等于组成它的简单几何体体积的和或差．( )答案：(1)√ (2)× (3)× (4)√二、填空题1.如图，将一个长方体用过相邻三条棱的中点的平面截出一个棱锥，则该棱锥的体积与剩下的几何体体积的比为________．答案：1∶472．以长为a ，宽为b 的矩形的一边所在的直线为轴旋转一周所得圆柱的侧面积为________．答案：2πab3．已知圆锥的表面积等于12π cm 2，其侧面展开图是一个半圆，则底面圆的半径为________ cm.答案：2[全析考法]考法一 空间几何体的表面积[例1] 在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2.将梯形ABCD 绕AD 所在直线旋转一周而形成的曲面所围成的几何体的表面积为( )A ．4πB ．(4＋2)πC ．6πD ．(5＋2)π(2)(2019·合肥质检)已知圆锥的高为3，底面半径为4，若一球的表面积与此圆锥侧面积相等，则该球的半径为( )A ．5 B.5 C ．9 D ．3[解析] (1)∵在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ， BC ＝2AD ＝2AB ＝2，∴将梯形ABCD 绕AD 所在直线旋转一周而形成的曲面所围成的几何体是一个底面半径为AB ＝1，高为BC ＝2的圆柱减去一个底面半径为AB ＝1，高为BC －AD ＝2－1＝1的圆锥的组合体，∴几何体的表面积S ＝π×12＋2π×1×2＋12×2π×1×12＋12＝(5＋2)π.(2)∵圆锥的底面半径r ＝4，高h ＝3，∴圆锥的母线l ＝5，∴圆锥的侧面积S ＝πrl ＝20π，设球的半径为R ，则4πR 2＝20π，∴R ＝5，故选B.[答案] (1)D (2)B[方法技巧]求空间几何体表面积的常见类型及思路求不规则 几何体的 表面积 通常将所给几何体分割成基本的柱体、锥体、台体，先求出这些基本的柱体、锥体、台体的表面积，再通过求和或作差，求出所给几何体的表面积考法二 空间几何体的体积[例2] (1)如图所示，已知三棱柱ABC A 1B 1C 1的所有棱长均为1，且AA 1⊥底面ABC ，则三棱锥B 1ABC 1的体积为( )A.312B.34C.612D.64(2)如图，在多面体ABCDEF 中，已知四边形ABCD 是边长为1的正方形，且△ADE ，△BCF 均为正三角形，EF ∥AB ，EF ＝2，则该多面体的体积为________．[解析] (1)三棱锥B 1ABC 1的体积等于三棱锥A B 1BC 1的体积，三棱锥A B 1BC 1的高为32，底面积为12，故其体积为13×12×32＝312. (2)如图，分别过点A ，B 作EF 的垂线，垂足分别为G ，H ，连接DG ，CH ，BF ，易求得EG ＝HF ＝12，AG ＝GD ＝BH ＝HC ＝32，则△BHC 中BC 边的高h ＝22.∴S △AGD ＝S △BHC ＝12×22×1＝24，∴V 多面体＝V E ADG ＋V F BHC ＋V AGD BHC ＝2V E ADG ＋V AGD BHC ＝13×24×12×2＋24×1＝23.[答案] (1)A (2)23[方法技巧] 求空间几何体的体积的常用方法公式法 对于规则几何体的体积问题，可以直接利用公式进行求解 割补法 把不规则的图形分割成规则的图形，然后进行体积计算；或者把不规则的几何体补成规则的几何体，不熟悉的几何体补成熟悉的几何体，便于计算其体积 等体一个几何体无论怎样转化，其体积总是不变的．如果一个几何体的底面面积和高[集训冲关]1.[考法一]圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面的半径为( )A ．7B ．6C ．5D ．3解析：选A 设上底面半径为r ，则下底面半径为3r ，截得圆台的大圆锥母线为l ，则l －3l＝13，l ＝92，由π×3r ×92－π×r ×32＝84π，解得r ＝7. 2.[考法二]如图，已知正方体ABCD A 1B 1C 1D 1的棱长为1，则四棱锥A 1BB 1D 1D 的体积为________．解析：∵正方体ABCD A 1B 1C 1D 1的棱长为1， ∴矩形BB 1D 1D 的长和宽分别为1,2.∵四棱锥A 1BB 1D 1D 的高是正方形A 1B 1C 1D 1对角线长的一半，即为22， ∴V 四棱锥A 1BB 1D 1D ＝13Sh ＝13×(1×2)×22＝13.答案：133.[考法一、二]如图，正四棱锥P ABCD 的底面边长为2 3 cm ，侧面积为83cm 2，则它的体积为________ cm 3.解析：记正四棱锥P ABCD 的底面中心为点O ，棱AB 的中点为H ，连接PO ，HO ，PH ，则PO ⊥平面ABCD ，因为正四棱锥的侧面积为8 3 cm 2，所以83＝4×12×23×PH ，解得PH ＝2，在Rt △PHO 中，HO＝3，所以PO ＝1，所以V P ABCD ＝13·S 正方形ABCD ·PO ＝4 cm 3.答案：4突破点三 与球有关的切、接问题与球有关的组合体问题常涉及内切和外接.解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图.如球内切于正方体时，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体时，正方体的各个顶点均在球面上，正方体的体对角线长等于球的直径.球与其他旋转体组合时，通常作它们的轴截面解题；球与多面体组合时，通常过多面体的一条侧棱和球心及“切点”或“接点”作截面图进行解题.[全析考法]考法一 与球有关的外接问题[例1] (1)(2019·福州模拟)已知圆锥的高为3，底面半径为3，若该圆锥的顶点与底面的圆周都在同一个球面上，则这个球的体积等于( )A.83πB.323π C ．16πD ．32π(2)(2018·成都模拟)在三棱锥P ABC 中，已知PA ⊥底面ABC ，∠BAC ＝60°，PA ＝2，AB ＝AC ＝3，若该三棱锥的顶点都在同一个球面上，则该球的表面积为( )A.4π3B.82π3C ．8πD ．12π[解析] (1)设该圆锥的外接球的半径为R ，依题意得，R 2＝(3－R )2＋(3)2，解得R ＝2，所以所求球的体积V ＝43πR 3＝43π×23＝323π.(2)易知△ABC 是等边三角形．如图，作OM ⊥平面ABC ，其中M 为△ABC 的中心，且点O 满足OM ＝12PA ＝1，则点O 为三棱锥P ABC外接球的球心．于是，该外接球的半径R ＝OA ＝AM 2＋OM 2＝⎝ ⎛⎭⎪⎫32×3×232＋12＝ 2.故该球的表面积S ＝4πR 2＝8π.[答案] (1)B (2)C[方法技巧]处理球的外接问题的策略(1)把一个多面体的几个顶点放在球面上即为球的外接问题．解决这类问题的关键是抓住外接的特点，即球心到多面体的顶点的距离等于球的半径．(2)三条侧棱互相垂直的三棱锥的外接球：①如果三棱锥的三条侧棱互相垂直并且相等，那么可以补形为一个正方体，正方体的外接球的球心就是三棱锥的外接球的球心；②如果三棱锥的三条侧棱互相垂直但不相等，那么可以补形为一个长方体，长方体的外接球的球心就是三棱锥的外接球的球心．考法二与球有关的内切问题[例2] (1)如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切．记圆柱O 1O 2的体积为V 1，球O 的体积为V 2，则V 1V 2的值是________．(2)已知正三棱锥的高为1，底面边长为23，内有一个球与四个面都相切，则棱锥的内切球的半径为________．[解析] (1)设圆柱内切球的半径为R ，则由题设可得圆柱O 1O 2的底面圆的半径为R ，高为2R ，故V 1V 2＝πR 2·2R 43πR3＝32. (2)如图，过点P 作PD ⊥平面ABC 于点D ，连接AD 并延长交BC 于点E ，连接PE ，∵△ABC 是正三角形，∴AE 是BC 边上的高和中线，D 为△ABC 的中心． ∵AB ＝23，∴S △ABC ＝33，DE ＝1，PE ＝ 2.∴S 表＝3×12×23×2＋33＝36＋3 3.∵PD ＝1，∴三棱锥的体积V ＝13×33×1＝ 3.设球的半径为r ，以球心O 为顶点，三棱锥的四个面为底面把正三棱锥分割为四个小棱锥，则r ＝3336＋33＝2－1.[答案] (1)32 (2)2－1[方法技巧]处理与球有关内切问题的策略解答此类问题时首先要找准切点，通过作截面来解决．如果内切的是多面体，则作截面时主要抓住多面体过球心的对角面来作．[集训冲关]1.[考法一]已知直三棱柱ABC A 1B 1C 1的6个顶点都在球O 的球面上，若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，则球O 的半径为( )A.3172B ．210C.132 D ．310解析：选C 如图，由球心作平面ABC 的垂线，则垂足为BC 的中点M .又AM ＝12BC ＝1232＋42＝52，OM ＝12AA 1＝6，所以球O 的半径R ＝OA ＝ ⎝ ⎛⎭⎪⎫522＋62＝132. 2.[考法二]已知一个圆锥底面半径为1，母线长为3，则该圆锥内切球的表面积为( )A ．πB.3π2 C ．2π D ．3π解析：选C 依题意，作出圆锥与球的轴截面，如图所示，设球的半径为r ，易知轴截面三角形边AB 上的高为22，因此22－r 3＝r 1，解得r ＝22，所以圆锥内切球的表面积为4π×⎝ ⎛⎭⎪⎫222＝2π，故选C. 3.[考法二]已知三棱锥P ABC 中，△ABC 为等边三角形，PA ＝PB ＝PC ＝3，PA ⊥PB ，则三棱锥P ABC 的外接球的体积为( )A.272π B.2732π C ．273π D ．27π解析：选B ∵三棱锥P ABC 中，△ABC 为等边三角形，PA ＝PB ＝PC＝3，∴△PAB ≌△PBC ≌△PAC .∵PA ⊥PB ，∴PA ⊥PC ，PC ⊥PB .以PA ，PB ，PC 为过同一顶点的三条棱作正方体(如图所示)，则正方体的外接球同时也是三棱锥P ABC 的外接球．∵正方体的体对角线长为32＋32＋32＝33，∴其外接球半径R ＝332.因此三棱锥P ABC 的外接球的体积V ＝4π3×⎝ ⎛⎭⎪⎫3323＝2732π.如有侵权请联系告知删除，感谢你们的配合！如有侵权请联系告知删除，感谢你们的配合！。
专题4 立体几何(学生版)
专题4 立体几何【玩转高考】1．（2020年北京卷）如图，在正方体1111ABCD A B C D -中，E 为1BB 的中点．（Ⅰ）求证：1//BC 平面1AD E ；（Ⅱ）求直线1AA 与平面1AD E 所成角的正弦值．2．（2020年山东卷）如图，四棱锥P -ABCD 的底面为正方形，PD ⊥底面ABCD ．设平面PAD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知PD =AD =1，Q 为l 上的点，求PB 与平面QCD 所成角的正弦值的最大值．3．（2020年天津卷）如图，在三棱柱111ABC A B C -中，1CC ⊥平面,,2ABC AC BC AC BC ⊥==，13CC =，点,D E 分别在棱1AA 和棱1CC 上，且12,AD CE M ==为棱11A B 的中点．（Ⅰ）求证：11C M B D ⊥；（Ⅱ）求二面角1B B E D --的正弦值；（Ⅲ）求直线AB 与平面1DB E 所成角的正弦值．4．（2020年海南卷）如图，四棱锥P -ABCD 的底面为正方形，PD ⊥底面ABCD ．设平面PAD 与平面PBC 的交线为l ．（1）证明：l ⊥平面PDC ；（2）已知PD =AD =1，Q 为l 上的点，QB ，求PB 与平面QCD 所成角的正弦值．5．（2020年浙江卷）如图，三棱台ABC—DEF中，平面ACFD⊥平面ABC，∠ACB=∠ACD=45°，DC =2BC．（I）证明：EF⊥DB；（II）求DF与面DBC所成角的正弦值．【玩转模拟】（1）求证：SC 平面ADE；（2）求点B到平面AEC的距离，（1）求证：平面PAB ⊥平面PAC ；（2）,E F 分别是棱,PB BC 的中点，G 为棱PC 上的点，求三棱锥A EFG -的体积.（1）求证：平面PBD ⊥平面PBC ；（1）求证：//AC 平面PDB ；（2）求二面角P AB C 的余弦值；（3）线段PC 上是否存在点E 使得PC ⊥平面ABE ，如果存在，求CE CP的值；如果不存在，请说明理由.（Ⅰ）证明：无论点F在PC上如何移动，都有平面AEF⊥平面PAD；--的余弦值.（Ⅱ）求点F恰为PC的中点时，二面角C AF E()1试判断PB与平面MEF的位置关系，并给出证明；()2求二面角M EF D--的余弦值.。
2021年立体几何第一问学生版
1．如图所示，在正方体ABCD—A1B1C1D1中，E、F分别是棱BC、C1D1的中点．求证：EF∥平面BDD1B1．2．如图所示，P是▱ABCD所在平面外一点，E、F分别在P A、BD上，且PE∶EA＝BF∶FD．求证：EF∥平面PBC．．3．三棱柱ABC－A1B1C1，D是BC上一点，且A1B∥平面AC1D，D1是B1C1的中点．求证：平面A1BD1∥平面AC1D．4．如图所示，在正方体ABCD—A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，问：当点Q在什么位置时，平面D1BQ∥平面P AO?．．5．ABCD是平行四边形，点P是平面ABCD外一点，M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH，求证：AP∥GH．6．如图所示，已知正方体ABCD－A1B1C1D1中，面对角线AB1、BC1上分别有两点E、F，且B1E＝C1F．求证：EF∥平面ABCD．7．如图所示，在正方体ABCD—A1B1C1D1中，E、F分别是棱B1C1、B1B的中点．求证：CF⊥平面EAB．8．如图所示，在四棱锥P—ABCD中，底面ABCD是矩形，侧棱P A垂直于底面，E、F分别是AB，PC的中点，P A＝AD．求证：(1)CD⊥PD；(2)EF⊥平面PCD．9．如图，在直三棱柱ABC—A1B1C1中，E、F分别是A1B、A1C的中点，点D在B1C1上，A1D⊥B1C．求证：(1)EF∥平面AB(2)平面A1FD⊥平面BB1C1C．10．如图所示，在直三棱柱ABC－A1B1C1中，AC⊥BC，AC＝BC＝CC1，M，N分别是A1B，B1C1的中点．(1)求证：MN⊥平面A1BC；(2)求直线BC1和平面A1BC所成的角的大小．11．如图，在三棱锥P－ABC中，P A⊥平面ABC，平面P AB⊥平面PBC．求证：BC⊥AB．12．如图所示，在正方体ABCD－A1B1C1D1中，P为DD1的中点，O为ABCD的中心，求证B1O⊥平面P AC．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
立体几何专题训练
一、选择题
1.[2018·云南玉溪模拟]将长方体截去一个四棱锥后得到的几何体如图所示，则该几何体的侧视图为( )
2.[2018·南昌模拟]如图，在正四棱柱ABCD －A 1B 1C 1D 1中，点P 是平面A 1B 1C 1D 1
内一点，则三棱锥P －BCD 的正视图与侧视图的面积之比为( )
A ．1∶1
B ．2∶1
C.2∶3
D ．3∶2
3．[2016·浙江高考]已知互相垂直的平面α，β交于直线l .若直线m ，n 满足m ∥α，n ⊥β，则( )
A ．m ∥l
B ．m ∥n
C ．n ⊥l
D ．m ⊥n
4．如图在底面为正方形，侧棱垂直于底面的四棱柱ABCD －A 1B 1C 1D 1中，
AA 1＝2AB ＝2，则异面直线A 1B 与AD 1所成角的余弦值为( ) A.15 B.25 C.35 D.45 5．[2018·赤峰模拟]如图，在正方体ABCD －A 1B 1C 1D 1中，
M ，N 分别是BC 1，CD 1的中点，则下列说法错误的是( )
A ．MN 与CC 1垂直
B ．MN 与A
C 垂直
C ．MN 与B
D 平行
D ．MN 与A 1B 1平行
6.某几何体的三视图如图所示，则该几何体的体积为( )
A.16
B.12
C.23
D.13
7．[2018·济南模拟]已知如图，六棱锥P－ABCDEF的底面是正六边形，
P A⊥平面ABCDEF，则下列结论不正确的是()
A．CD∥平面P AF
B．DF⊥平面P AF
C．CF∥平面P AB
D．CF⊥平面P AD
8．正三棱柱的底面边长为3，侧棱长为2，且三棱柱的顶点都在同一个球面上，则该球的表面积为()
A.4πB．8π
C．12π D．16π
9.[2017·北京高考]某三棱锥的三视图如图所示，则该三棱锥的体积为()
A．60
B．30
C．20
D．10
10.[2018·遵义模拟]一个几何体的三视图如图所示，其中俯视图是菱形，
则该几何体的侧面积为()
A.3＋ 6
B.3＋ 5
C.2＋ 6
D.2＋ 5
11．设α，β，γ为三个不同的平面，m，n是两条不同的直线，在命题“α∩β＝m，n⊂γ，且________，则m ∥n”中的横线处填入下列三组条件中的一组，使该命题为真命题．
可以填入的条件有()
①α∥γ，n⊂β；②m∥γ，n∥β；③n∥β，m⊂γ.
A．①②B．②③C．①③D．①②③
12．[2018·河北唐山模拟]如图，在正方形ABCD中，E，F分别是BC，CD的中点，G是EF的中点，现在沿AE，AF及EF把这个正方形折成一个空间图形，使B，C，D三点重合，重合后的点记为H，那么，在这个空间图形中必有()
A．AG⊥平面EFH
B．AH⊥平面EFH
C．HF⊥平面AEF
D．HG⊥平面AEF
二、填空题
13.如右图，正方形OABC的边长为1 cm，它是水平放置的一个平面图形的直观图，
则原图形的周长为________．
14．如图所示，ABCD－A1B1C1D1是长方体，O是B1D1的中点，直线A1C交平面AB1D1于点M，则下列结论错误的是________．(填序号)
①A，M，O三点共线；
②A，M，O，A1四点共面；
③A，O，C，M四点共面；
④B，B1，O，M四点共面．
15．[2017·江苏高考]如图，在圆柱O1O2内有一个球O，该球与圆柱的上、
下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，
则V1
V2的值是________．
16．如图，P A⊥⊙O所在平面，AB是⊙O的直径，C是⊙O上一点，
AE⊥PC，AF⊥PB，给出下列结论：①AE⊥BC；②EF⊥PB；
③AF⊥BC；④AE⊥平面PBC，其中真命题的序号是________．
三、解答题
17．[2018·邯郸一中模拟]已知三棱柱ABC－A1B1C1的侧棱长和底面边长均为2，A1在底面ABC内的射影O 为底面△ABC的中心，如图所示．
(1)连接BC1，求异面直线AA1与BC1所成角的大小；
(2)连接A1C，A1B，求三棱锥C1－BCA1的体积．
18．[2018·延安模拟] 已知四棱锥S－ABCD中，底面ABCD是边长为2的菱形，∠BAD＝60°，SA＝SD＝5，
SB＝7，点E是棱AD的中点，点F在棱SC上，且SF
SC＝λ，SA∥平面BEF.
(1)求实数λ的值；
(2)求三棱锥F－EBC的体积．
19．[2016·山东高考]在如图所示的几何体中，D 是AC 的中点，EF ∥DB .
(1)已知AB ＝BC ，AE ＝EC ，求证：AC ⊥FB ；
(2)已知G ，H 分别是EC 和FB 的中点，求证：GH ∥平面ABC .
20．如图，在三棱柱ABC －A 1B 1C 1中，侧棱AA 1⊥底面ABC ，AB ⊥BC ，D 为AC 的中点，AA 1＝AB ＝2.
(1)求证：AB 1∥平面BC 1D ；
(2)设BC ＝3，求四棱锥B －DAA 1C 1的体积．
21．[2018·江西九江模拟]如图，在几何体ABCDEF 中，四边形ABCD 是菱形，BE ⊥平面ABCD ，DF ∥BE ，且DF ＝2BE ＝2，EF ＝3.
(1)证明：平面ACF ⊥平面BEFD .
(2)若cos ∠BAD ＝15，求几何体ABCDEF 的体积．
22．[2017·全国卷Ⅲ]如图，四面体ABCD 中，△ABC 是正三角形，AD ＝CD .
(1)证明：AC ⊥BD ；
(2)已知△ACD 是直角三角形，AB ＝BD ，若E 为棱BD 上与D 不重合的点，且AE ⊥EC ，求四面体ABCE 与四面体ACDE 的体积比．。