矩形翻折问题集锦及答案解析
初中数学-矩形翻折问题小专题

矩形翻折问题小专题【知识方法总结】1.联系实际,内容丰富,具有开放性,有利于考查学生的动手能力,空间观念和几何变换的思想。
2.图形的折叠就是对称变换,即翻折。
3.其解法看似灵活,抓住翻折前后的图形是全等图形这一关键,“边相等,角相等,折线为角平分线”再利用勾股定理或比例关系或线段的相等关系列方程,即可求解。
4.注意点:(1)折叠就是轴对称(2)其中蕴含着全等图形;即边和角的相等关系。
【经典例题】例1.已知,一张矩形纸片ABCD的边长分别为9cm和3cm,把顶点A和C叠合在一起,得折痕EF (如图).(1)猜想四边形AECF是什么四边形,并证明你的猜想;(2)求折痕EF的长.【解答】解:(1)菱形,理由如下:∵四边形ABCD为矩形,∴AB∥CD,∠AFE=∠CEF.∵矩形ABCD沿EF折叠,点A和C重合,∴∠CEF=∠AEF,AE=CE∴∠AFE=∠AEF,∴AE=AF.∴AF=CE,又∵AF∥CE,∴AECF为平行四边形,∵AE=EC,即四边形AECF的四边相等.∴四边形AECF为菱形.例2.已知:长方形纸片ABCD中,AB=10cm,AD<AB.(1)当AD=6.5cm时,如图①,将长方形纸片ABCD折叠,使点D落在AB边上,记作点D′,折痕为AE,如图②.此时,图②中线段D′B长是cm.(2)若AD=xcm,先将长方形纸片ABCD按问题(1)的方法折叠,再将三角形AED′沿D′E向右翻折,使点A落在射线D′B上,记作点A′.若翻折后的图形中,线段BD′=2BA′,请根据题意重新画出图形(草图),并求出x的值.【解答】解:(1)由题意知AD′=AD=6.5cm,∴D′B=AB﹣AD′=10﹣6.5=3.5(cm),故答案为:3.5;(2)如图所示,由题意知,AD=AD′=A′D′=xcm,∵AB=10cm,∴BD′=10﹣x,A′B=2x﹣10,由BD′=2BA′得10﹣x=2(2x﹣10),解得:x=6.例3.如图,在矩形纸片ABCD中,BC=a,将矩形纸片翻折,使点C恰好落在对角线交点O处,折痕为BE,点E在边CD上,则CE的长为()a;A. 12a;B. 25a;C. √33a.D. √32【答案】C例4.(1)如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,折痕的一端G 点在边BC上,BG=10.①当折痕的另一端点F在AB边上时,如图①,求△EFG的面积;②当折痕的另一端点F在AD边上时,如图②,证明四边形BGEF为菱形,并求出折痕GF的长.(2)在矩形纸片ABCD中,AB=5,AD=13.如图③所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ.当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,求点A′在BC边上可移动的最大距离.【解答】例5.折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在线段AE上的点H处,折痕为=.DG,点G在BC边上,若AB=AD+2,EH=1,则ADAB【答案】3+4√313例6.在学习完特殊的平行四边形之后,某学习小组针对矩形中的折叠问题进行了研究.问题背景:在矩形ABCD中,点E、F分别是BC、AD 上的动点,且BE=DF,连接EF,将矩形ABCD沿EF折叠,点C落在点C′处,点D落在点D′处,射线EC′与射线DA相交于点M.猜想与证明:(1)如图1,当EC′与线段AD交于点M时,判断△MEF的形状并证明你的结论;操作与画图:(2)当点M与点A重合时,请在图2中作出此时的折痕EF和折叠后的图形(要求:尺规作图,不写作法,保留作图痕迹,标注相应的字母);操作与探究:(3)如图3,当点M在线段DA延长线上时,线段C′D'分别与AD,AB交于P,N两点时,C′E与AB交于点Q,连接MN 并延长MN交EF于点O.求证:MO⊥EF 且MO平分EF;【解答】解:(1)△MEF是等腰三角形.理由:∵四边形ABCD是矩形,∴AD∥BC,∴∠MFE=∠CEF,由折叠可得,∠MEF=∠CEF,∴∠MFE=∠MEF,∴ME=MF,∴△MEF是等腰三角形.(2)折痕EF和折叠后的图形如图2所示:7.如图1,矩形纸片ABCD的边长AB=4cm,AD=2cm.同学小明现将该矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图2),观察图形对比前后变化,回答下列问题:(1)GF FD(直接填写=、>、<);(2)判断△CEF的形状,并说明理由;(3)运用所学知识,请计算着色部分多边形BCHFE的面积.【解答】解:(1)由翻折的性质,可得GD=FD;故答案为:=;(2)△CEF是等腰三角形.∵矩形ABCD,∴AB∥CD,∴∠AEF=∠CFE,由翻折的性质,∠AEF=∠FEC,∴∠CFE=∠FEC,∴CF=CE,故△CEF为等腰三角形;8.如图,已知矩形纸片ABCD,AB=4,BC=10,M是BC的中点,点P沿折线BA﹣AD运动,以MP为折痕将矩形纸片向右翻折,使点B落在矩形的边上,则折痕MP的长.√5或2√5或4【答案】529.如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE,(1)求证:四边形AFCE为菱形;(2)设AE=a,ED=b,DC=c.请写出一个a、b、c三者之间的数量关系式.【解答】(1)由矩形ABCD与折叠的性质,易证得△CEF是等腰三角形,即CE=CF,即可证得AF=CF=CE=AE,即可得四边形AFCE为菱形;(2)由折叠的性质,可得CE=AE=a,在Rt△DCE中,利用勾股定理即可求得:a、b、c三者之间的数量关系式为:a2=b2+c2.(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠AEF=∠EFC,由折叠的性质,可得:∠AEF=∠CEF,AE=CE,AF=CF,∴∠EFC=∠CEF,∴CF=CE,∴AF=CF=CE=AE,∴四边形AFCE为菱形;(2)a、b、c三者之间的数量关系式为:a2=b2+c2.理由:由折叠的性质,得:CE=AE,∵四边形ABCD是矩形,∴∠D=90°,∵AE=a,ED=b,DC=c,∴CE=AE=a,在Rt△DCE中,CE2=CD2+DE2,∴a、b、c三者之间的数量关系式为:a2=b2+c2.10.如图,把正方形纸片ABCD沿对边中点所在直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE,若AB=4,则FM的长为()A. 4B. 2√3C. 2√2D. 2【答案】B11.在一张长方形ABCD纸张中,AB=25cm,AD=20cm,现将这张纸片按下列图示方法折叠,请解决下列问题(1)如图1,折痕为DE,点A的对应点F在CD上,则折痕DE的长为cm;(2)如图2,H、G分别为BC、AD的中点,点A的对应点F在HG上,折痕为DE,求重叠部分(△DEF)的面积;(3)如图3,在图2中,把长方形ABCD沿着HG剪开,变成两张长方形纸片,将这两张纸按图形位置任意叠合后,发现重叠部分都是菱形,显然,这些菱形中周长最短是40cm.是否存在叠后周长最大的菱形?若存在,请求出叠合后周长最大的菱形的周长和面积;若不存在,请说明理由.【解答】12.如图,在矩形ABCD中,AB=4,AD=10,点E在AD边上,已知B、E两点关于直线l对称,直线l 分别交AD、BC边于点M、N,连接BM、NE.(1)求证:四边形BMEN是菱形;(2)若DE=2,求NC的长.【解答】(1)证明:∵B、E两点关于直线l对称,∴BM=ME,BN=NE,∠BMN=∠EMN,在矩形ABCD中,AD∥BC,∴∠EMN=∠MNB,∴∠BMN=∠MNB,∴BM=BN,∴BM=ME=BN=NE,∴四边形BMEN是菱形;(2)解:设菱形边长为x,则AM=8−x,在Rt△ABM中,42+(8−x)2=x2,解得:x=5,∴NC=5.【答案】(1)略;(2)5.。
矩形的折叠问题(专题)

→ Bx
D
,故OE= 。
练习8 如图,在直角三角形ABC中, C ∠C=90º ,沿着B点的一条直线BE折 叠这个三角形,使C点与AB边上的 一点D重合。当∠A满足什么条件时, 点D恰好是AB的中点?写出一个你 B 认为适当的条件,并利用此条件证 明D为AB中点。 条件:∠A=30º
E D A
证明:由轴对称可得,△BCE≌△BDE,∴ BC=BD , 在△ABC中,∵ ∠C=90º,∠A=30º, ∴ BC= ∴ BD =
答案:矩形的长为10,宽为8。
D F E A
C
B
4、求线段与面积间的变化关系
例5 已知一三角形纸片ABC,面积为25,BC的长为 10,B和C都为锐角,M为AB上的一动点(M与A、B 不重合),过点M作MN∥BC,交AC于点N,设MN=x. (1)用x表示△AMN的面积SΔ AMN。 (2)Δ AMN沿MN折叠,设点A关于Δ AMN对称的点为A¹ , Δ A¹ MN与四边形BCMN重叠部分的面积为y.①试求出 y与x的函数关系式,并写出自变量X的取值范围; ②当x为何值时,重叠部分的面积y最大,最大为多 少?
矩形的折叠问题
(复习课)
练习1 如图,有一块直角三角形纸片,两 直角边AC=6,BC=8,现将直角边AC沿 直线AD折叠,使它落在斜边AB上,且与AE 重合,求CD
A E C B D
如图,折叠矩形的一边AD,点D 落在BC边上点F处,已知AB=8, BC=10,求EC的长 D A
E B F C
练习2 如图,在梯形ABCD中, DCAB,将梯形对折,使点D、 C分别落在AB上的D¹ 、C¹ 处, 折痕为EF。若CD=3,EF=4, 则AD¹ +BC¹ = 。
矩形的翻折及答案

矩形的翻折矩形的翻折一直是中考的重点,关于矩形的翻折通常有以下几种情况一、沿对角线翻折二、将一个顶点折到一边上三、将一条对角线的顶点折叠重合四、将一边折到对角线上1. 矩形ABCD中,AB=8,BC=4,将矩形沿对角线AC折叠,点D落在E处,求重叠部分△AFC 的面积解:由折叠,可证显然S△AEF≌S△CBF,∴AF=FC。
可设AF=FC=x,则BF=8-x,在Rt△CBF中,BC=4,得x2=(8-x)2+42,解得x=5,即AF=5.S△AFC=12•5•4=10.2.折叠矩形,使点D落在点F处,已知AB=8,BC=10,求EC的长由翻折可知△AFE≌△CBF,得EF=DE,AF=AD.因为而在Rt△ABF中,AB=8,AF=AD=10,∴BF=6,∴FC=10-6=4.设EC为x,则DE=EF=8-x,在△ECF中,由8-x()2=x2+42,解得x=3,即EC=33..矩形ABCD中,AB=6,BC=8将矩形折叠,使点B与点D重合,求折痕EF的长度解:连结BD、FD.由翻折可知BD⊥EF,且BO=DO,OF=OE,BF=DF.设BF=DF=x,则FC=8-x,由勾股定理得x2=(8-x)2+62,解得x=254.可得OF=154,EF=2•OF=152.4.矩形ABCD 中,AB=4,AD=3,折叠纸片使AD 与对角线BD 重合,折痕为DE ,求AE 长 解:由翻折AD=DF=6,设EF=AE=x ,则BE=8-x,在Rt △ABD 中,可求BD=10,所以BF=10-6=4,在Rt △BEF 中,x 2+42=8-x ()2,解得x=3,即AE=35.如图,ABCD 是矩形纸片,翻折∠B 、∠D ,使BC 、AD 恰好落在AC 上.设F 、H 分别是B 、D 落在AC 上的点,E 、G 分别是折痕CE 与AB 、AG 与CD 的交点.(1)试说明四边形AECG 的形状,并说明理由;(2)若矩形的一边AB=4,BC=3,求△AEC 的面积;(1)证明:在矩形ABCD 中,∵AD ∥BC ,∴∠DAC=∠BCA .由题意,得∠GAH=12∠DAC ,∠ECF=12∠BCA . ∴∠GAH=∠ECF ,∴AG ∥CE .又∵AE ∥CG ,∴四边形AECG 是平行四边形.(2)解法1:在Rt △ABC 中,∵AB=4,BC=3,∴AC=5.∵CF=CB=3,∴AF=2.在Rt △AEF 中,设EF=x ,则AE=4-x .根据勾股定理,得AE 2=AF 2+EF 2,即(4-x )2=22+x 2.解得x=32,即线段EF 长为32. ∴S △AEC=12×AC ×EF=12×5×32=1546.(2012•南平)如图,正方形纸片ABCD 的边长为3,点E 、F 分别在边BC 、CD 上,将AB 、AD 分别和AE 、AF 折叠,点B 、D 恰好都将在点G 处,已知BE=1,求EF 的长解:∵正方形纸片ABCD 的边长为3,∴∠C=90°,BC=CD=3,根据折叠的性质得:EG=BE=1,GF=DF ,设DF=x ,F B则EF=EG+GF=1+x,FC=DC﹣DF=3﹣x,EC=BC﹣BE=3﹣1=2,在Rt△EFC中,EF2=EC2+FC2,即(x+1)2=22+(3﹣x)2,解得:x=1.5,∴DF=1.5,即 EF=1+1.5=2.5.7.(2011•重庆)如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE 对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的是 .解:①正确.因为AB=AD=AF,AG=AG,∠B=∠AFG=90°,∴△ABG≌△AFG;②正确.因为:EF=DE=CD=2,设BG=FG=x,则CG=6﹣x.在直角△ECG中,根据勾股定理,得(6﹣x)2+42=(x+2)2,解得x=3.所以BG=3=6﹣3=GC;③正确.因为CG=BG=GF,所以△FGC是等腰三角形,∠GFC=∠GCF.又∠AGB=∠AGF,∠AGB+∠AGF=180°﹣∠FGC=∠GFC+∠GCF,∴∠AGB=∠AGF=∠GFC=∠GCF,∴AG∥CF;④错误.过C作C H⊥GE于H,∵EF=2,FG=3, ∴EG=5,∴35GFEG=,∴S△EGC= =×3×4=6,∴356GF S GFCEG==∴S△FGC=≠3.答案①②③8.(2014河南省)如图,矩形ABCD中,AD=5,AB=7.点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D/落在∠ABC的角平分线上时,DE的长为 .答案:53或52解析:过D/作FH⊥AB交AB于F,交CD于H;如图1,由翻折,△EDA≌△ED/A,∴ED=ED/,AD=AD/=5, 设AF=x,则BF=7-x,在Rt△BD/F中,∵D/B是∠ABC的平分线,∴∠ABD/=450, 则D/F=BF=7-x,在Rt△AD/F中,AD/2=AF2+D/F2,即52=(7-x)2+x2,解得x=4或x=3,即D/F=BF=3或4.当x=4时,如图1,设DE=y,在Rt△D/HE中,EH=4-y,ED/=y,HD/=2,即(4-y)2+22=y2,解得y=52,即DE=52当x=3时,如图2,设DE=y,在Rt△D/HE中,EH=3-y,ED/=y,HD/=1,即(3-y)2+12=y2,解得y=53,即DE=53图1FA图2DA。
八年级数学翻折变换(折叠问题)参考答案与试题解析

八年级数学翻折变换(折叠问题)参考答案与试题解析work Information Technology Company.2020YEAR八年级数学翻折变换(折叠问题)参考答案与试题解析一.选择题(共12小题)1.如图,矩形纸片ABCD,长AD=9m,宽AB=3cm,将其折叠,使点D与点B重合,那么折叠后DE的长为()A.7cm B.6cm C.5.5cm D.5cm【分析】由矩形的性质和折叠的性质以及勾股定理得出方程,解方程即可.【解答】解:由折叠的性质得:BE=DE,设DE长为xcm,则AE=(9﹣x)cm,BE=xcm,∵四边形ABCD是矩形,∴∠A=90°,根据勾股定理得:AE2+AB2=BE2,即(9﹣x)2+32=x2,解得:x=5,即DE长为5cm,故选:D.【点评】本题考查了矩形的性质、翻折变换、勾股定理等知识;熟练掌握矩形和翻折变换的性质,运用勾股定理进行计算是解决问题的关键.2.如图,在等边三角形ABC中,点D、E分别是边AC、BC上两点.将△ABC沿DE翻折,点C正好落在线段AB上的点F处,使得AF:BF=2:3.若BE=16,则点F到BC边的距离是()A.8B.12C.D.【分析】作EM⊥AB于M,由等边三角形的性质和直角三角形的性质求出BM=BE=8,ME=BM=8,由折叠的性质得出FE=CE,设FE=CE=x,则AB=BC=16+x,得出BF=(16+x),求出FM=BF﹣BM=(16+x)﹣8=+x,在Rt△EFM中,由勾股定理得出方程,解方程求出BF=21.作FN⊥BC于N,则∠BFN=30°,由直角三角形的性质得出BN=BF=,得出FN=BN=即可.【解答】解:作EM⊥AB于M,如图所示:∵△ABC是等边三角形,∴BC=AB,∠B=60°,∵EM⊥AB,∴∠BEM=30°,∴BM=BE=8,ME=BM=8,由折叠的性质得:FE=CE,设FE=CE=x,则AB=BC=16+x,∵AF:BF=2:3,∴BF=(16+x),∴FM=BF﹣BM=(16+x)﹣8=+x,在Rt△EFM中,由勾股定理得:(8)2+(+x)2=x2,解得:x=19,或x=﹣16(舍去),∴BF=(16+19)=21,作FN⊥BC于N,则∠BFN=30°,∴BN=BF=,∴FN=BN=,即点F到BC边的距离是,故选:D.【点评】本题考查了翻折变换的性质、等边三角形的性质、直角三角形的性质、勾股定理等知识;熟练掌握翻折变换和等边三角形的性质,由勾股定理得出方程是解题的关键.3.如图,在等腰Rt△ABC中∠C=90°,AC=BC=2.点D和点E分别是BC边和AB 边上两点,连接DE.将△BDE沿DE折叠,得到△B′DE,点B恰好落在AC的中点处设DE与BB交于点F,则EF=()A.B.C.D.【分析】根据等腰直角三角形的性质得到AB=AC=4,∠A=∠B=45°,过B′作B′H⊥AB与H,得到AH=B′H=AB′,求得AH=B′H=1,根据勾股定理得到BB′===,由折叠的性质得到BF=BB′=,DE ⊥BB′,根据相似三角形即可得到结论.【解答】解:∵在等腰Rt△ABC中∠C=90°,AC=BC=2,∴AB=AC=4,∠A=∠B=45°,过B′作B′H⊥AB与H,∴△AHB′是等腰直角三角形,∴AH=B′H=AB′,∵AB′=AC=,∴AH=B′H=1,∴BH=3,∴BB′===,∵将△BDE沿DE折叠,得到△B′DE,∴BF=BB′=,DE⊥BB′,∴∠BHB′=∠BFE=90°,∵∠EBF=∠B′BH,∴△BFE∽△BHB′,∴=,∴=,∴EF=,故答案为:.故选:C.【点评】本题考查了翻折变换(折叠问题),等腰直角三角形的判定和性质,勾股定理,相似三角形的判定和性质,正确的作出辅助线是解题的关键.4.如图,在△ABC中,AB=AC=2,∠BAC=30°,将△ABC沿AC翻折得到△ACD,延长AD交BC的延长线于点E,则△ABE的面积为()A.B.C.3D.【分析】由折叠的性质可知∠CAD=30°=∠CAB,AD=AB=2.由等腰三角形的性质得出∠BCA=∠ACD=∠ADC=75°.求出∠ECD=30°.由三角形的外角性质得出∠E=75°﹣30°=45°,过点C作CH⊥AE于H,过B作BM⊥AE于M,由直角三角形的性质得出CH=AC=1,AH=CH=.得出HD=AD﹣AH=2﹣.求出EH =CH=1.得出DE=EH﹣HD=﹣1,AE=AD+DE=1+,由直角三角形的性质得出AM=AB=1,BM=AM=.由三角形面积公式即可得出答案.【解答】解:由折叠的性质可知:∠CAD=30°=∠CAB,AD=AB=2.∴∠BCA=∠ACD=∠ADC=75°.∴∠ECD=180°﹣2×75°=30°.∴∠E=75°﹣30°=45°.过点C作CH⊥AE于H,过B作BM⊥AE于M,如图所示:在Rt△ACH中,CH=AC=1,AH=CH=.∴HD=AD﹣AH=2﹣.在Rt△CHE中,∵∠E=45°,∴△CEH是等腰直角三角形,∴EH=CH=1.∴DE=EH﹣HD=1﹣(2﹣)=﹣1,∴AE=AD+DE=1+,∵BM⊥AE,∠BAE=∠BAC+∠CAD=60°,∴∠ABM=30°,∴AM=AB=1,BM=AM=.∴△ABE的面积=AE×BM=×(1+)×=;故选:B.【点评】本题考查了翻折变换的性质、等腰三角形的性质、含30°角的直角三角形的性质、等腰直角三角形的判定与性质、三角形面积等知识;熟练掌握翻折变换和等腰三角形的性质是解题的关键.5.如图,点F是长方形ABCD中BC边上一点将△ABF沿AF折叠为△AEF,点E落在边CD上,若AB=5,BC=4,则BF的长为()A.B.C.D.【分析】根据矩形的性质得到CD=AB=5,AD=BC=4,∠B=∠D=∠C=90°,根据折叠的性质得到AE=AB=5,EF=BF,根据勾股定理得到DE===3,求得CE=2,设BF=EF=x,则CF=4﹣x,根据勾股定理列方程即可得到结论.【解答】解:∵四边形ABCD是矩形,∴CD=AB=5,AD=BC=4,∠B=∠D=∠C=90°,∵将△ABF沿AF折叠为△AEF,∴AE=AB=5,EF=BF,∴DE===3,∴CE=2,设BF=EF=x,则CF=4﹣x,∵EF2=CF2+CE2,∴x2=(4﹣x)2+22,解得:x=,故选:B.【点评】本题考查了翻折变换(折叠问题),矩形的矩形,勾股定理,熟练掌握折叠的性质是解题的关键.6.如图,在矩形纸片ABCD中,CB=12,CD=5,折叠纸片使AD与对角线BD重合,与点A重合的点为N,折痕为DM,则△MNB的面积为()A.B.C.D.26【分析】由勾股定理得出BD==13,由折叠的性质可得ND=AD=12,∠MND=∠A=90°,NM=AM,得出∠EA′B=90°,BN=BD﹣ND=1,设AM=NM =x,则BM=AB﹣AM=5﹣x,在Rt△BMN中,由勾股定理得出方程,解方程得出NM =AM=,即可得出答案.【解答】解:∵四边形ABCD是矩形,∴∠A=90°,AD=BC=12,AB=CD=5,∴BD===13,由折叠的性质可得:ND=AD=12,∠MND=∠A=90°,NM=AM,∴∠EA′B=90°,BN=BD﹣ND=13﹣12=1,设AM=NM=x,则BM=AB﹣AM=5﹣x,在Rt△BMN中,NM2+BN2=BM2,∴x2+12=(5﹣x)2,解得:x=,∴NM=AM=,∴△MNB的面积=BN×NM=×1×=;故选:A.【点评】此题考查了折叠的性质、勾股定理以及矩形的性质.熟练掌握折叠的性质和矩形的性质,由勾股定理得出方程是解题的关键.7.如图,在△ABC中∠ACB=90°、∠CAB=30°,△ABD是等边三角形、将四边形ACBD折叠,使点D与点C重合,HK为折痕,则sin∠ACH的是()A.B.C.D.【分析】在Rt△ABC中,设BC=a,则AB=2BC=2a,AD=AB=2a.设AH=x,则HC=HD=AD﹣AH=2a﹣x.在Rt△ABC中,由勾股定理得AC2=3a2,在Rt△ACH 中,由勾股定理得AH2+AC2=HC2,即x2+3a2=(2a﹣x)2.解得x=a,即AH=a.求得HC的值后,利用sin∠ACH=AH:HC求值.【解答】解:∵△ABD是等边三角形,∴∠BAD=60°,AB=AD,∵∠CAB=30°,∴∠CAH=90°.在Rt△ABC中,∠CAB=30°,设BC=a,则AB=2BC=2a.∴AD=AB=2a.设AH=x,则HC=HD=AD﹣AH=2a﹣x,在Rt△ABC中,AC2=(2a)2﹣a2=3a2,在Rt△ACH中,AH2+AC2=HC2,即x2+3a2=(2a﹣x)2,解得x=a,即AH=a.∴HC=2a﹣x=2a﹣a=a.∴sin∠ACH==,故选:C.【点评】本题考查了折叠的性质,锐角三角函数值,勾股定理的应用,熟练掌握折叠的性质和解直角三角形是解题的关键.8.如图,在矩形ABCD中,AB=1,在BC上取一点E,连接AE、ED,将△ABE沿AE翻折,使点B落在B'处,线段EB'交AD于点F,将△ECD沿DE翻折,使点C的对应点C'落在线段EB'上,若点C'恰好为EB'的中点,则线段EF的长为()A.B.C.D.【分析】由折叠的性质可得AB=AB'=CD=C'D=1,∠B=∠B'=90°=∠C=∠DC'E,BE=B'E,CE=C'E,由中点性质可得B'E=2C'E,可得BC=AD=3EC,由勾股定理可求可求CE的长,由“AAS”可证△AB'F≌△DC'F,可得C'F=B'F=,即可求解.【解答】解:∵四边形ABCD是矩形,∴AB=CD=1,AD=BC,∠B=∠C=90°由折叠的性质可得:AB=AB'=CD=C'D=1,∠B=∠B'=90°=∠C=∠DC'E,BE=B'E,CE=C'E,∵点C'恰好为EB'的中点,∴B'E=2C'E,∴BE=2CE,∴BC=AD=3EC,∵AE2=AB2+BE2,DE2=DC2+CE2,AD2=AE2+DE2,∴1+4CE2+1+CE2=9CE2,解得:CE=,∴B'E=BE=,BC=AD=,C'E=,∴B'C'=,在△AB'F和△DC'F中,∴△AB'F≌△DC'F(AAS),∴C'F=B'F=,∴EF=C'E+C'F=,故选:D.【点评】本题考查了翻折变换,矩形的性质,全等三角形的性质,勾股定理,求出CE 的长是本题的关键.9.如图,▱ABCD中,AB=6,∠B=75°,将△ABC沿AC边折叠得到△AB′C,B′C交AD于E,∠B′AE=45°,则点A到BC的距离为()A.2B.3C.D.【分析】过B′作B′H⊥AD于H,根据等腰直角三角形的性质得到AH=B′H=AB′,根据折叠的性质得到AB′=AB=6,∠AB′E=∠B=75°,求得∠AEB′=60°,解直角三角形得到HE=B′H=,B′E=2,根据平行线的性质得到∠DAC=∠ACB,推出AE=CE,根据全等三角形的性质得到DE=B′E=2,求得AD=AE+DE=3+3,过A作AG⊥BC于G,根据直角三角形的性质即可得到结论.【解答】解:过B′作B′H⊥AD于H,∵∠B′AE=45°,∴△AB′H是等腰直角三角形,∴AH=B′H=AB′,∵将△ABC沿AC边折叠得到△AB′C,∴AB′=AB=6,∠AB′E=∠B=75°,∴∠AEB′=60°,∴AH=B′H=×6=3,∴HE=B′H=,B′E=2,∵▱ABCD中,AD∥BC,∴∠DAC=∠ACB,∵∠ACB=∠ACB′,∴∠EAC=∠ACE,∴AE=CE,∵∠AB′E=∠B=∠D,∠AEB′=∠CED,∴△AB′E≌△CDE(AAS),∴DE=B′E=2,∴AD=AE+DE=3+3,∵∠AEB′=∠EAC+∠ACE=60°,∴∠ACE=∠CAE=30°,∴∠BAC=75°,∴AC=AD=BC,∠ACB=30°,过A作AG⊥BC于G,∴AG=AC=,故选:C.【点评】本题考查了翻折变换(折叠问题),全等三角形的判定和性质,解直角三角形,正确的作出辅助线是解题的关键.10.如图1,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB 的中点,连结CE并延长交AD于F,如图2,现将四边形ACBD折叠,使D与C重合,HK为折痕,则sin∠ACH的值为()A.B.C.D.【分析】在Rt△ABC中,设BC=a,则AB=2BC=2a,AD=AB=2a.设AH=x,则HC=HD=AD﹣AH=2a﹣x.在Rt△ABC中,由勾股定理得AC2=3a2,在Rt△ACH 中,由勾股定理得AH2+AC2=HC2,即x2+3a2=(2a﹣x)2.解得x=a,即AH=a.求得HC的值后,利用sin∠ACH=AH:HC求值.【解答】解:∵∠BAD=60°,∠CAB=30°,∴∠CAH=90°.在Rt△ABC中,∠CAB=30°,设BC=a,∴AB=2BC=2a.∴AD=AB=2a.设AH=x,则HC=HD=AD﹣AH=2a﹣x,在Rt△ABC中,AC2=(2a)2﹣a2=3a2,在Rt△ACH中,AH2+AC2=HC2,即x2+3a2=(2a﹣x)2,解得x=a,即AH=a.∴HC=2a﹣x=2a﹣a=a.∴sin∠ACH==,故选:B.【点评】本题考查了折叠的性质,锐角三角函数值,勾股定理的应用,注意:折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.11.如图,在△ABC中,D是AC边上的中点,连结BD,把△BDC沿BD翻折,得到△BDC',DC′与AB交于点E,连结AC',若AD=AC′=2,BD=3,则点D到BC′的距离为()A.B.C.D.【分析】连接CC',交BD于点M,过点D作DH⊥BC'于点H,由翻折知,△BDC≌△BDC',BD垂直平分CC',证△ADC'为等边三角形,利用解直角三角形求出DM=1,C'M=DM=,BM=2,在Rt△BMC'中,利用勾股定理求出BC'的长,在△BDC'中利用面积法求出DH的长.【解答】解:如图,连接CC',交BD于点M,过点D作DH⊥BC'于点H,∵AD=AC′=2,D是AC边上的中点,∴DC=AD=2,由翻折知,△BDC≌△BDC',BD垂直平分CC',∴DC=DC'=2,BC=BC',CM=C'M,∴AD=AC′=DC'=2,∴△ADC'为等边三角形,∴∠ADC'=∠AC'D=∠C'AC=60°,∵DC=DC',∴∠DCC'=∠DC'C=×60°=30°,在Rt△C'DM中,∠DC'C=30°,DC'=2,∴DM=1,C'M=DM=,∴BM=BD﹣DM=3﹣1=2,在Rt△BMC'中,BC'===,∵S△BDC'=BC'•DH=BD•CM,∴DH=3×,∴DH=,故选:B.【点评】本题考查了轴对称的性质,解直角三角形,勾股定理等,解题关键是会通过面积法求线段的长度.12.如图,在△ABC中,∠ABC=45°,AB=3,AD⊥BC于点D,BE⊥AC于点E,AE=1.连接DE,将△AED沿直线AE翻折至△ABC所在的平面内,得△AEF,连接DF.过点D作DG⊥DE交BE于点G.则四边形DFEG的周长为()A.8B.4C.2+4D.3+2【分析】先证△BDG≌△ADE,得出AE=BG=1,再证△DGE与△EDF是等腰直角三角形,在直角△AEB中利用勾股定理求出BE的长,进一步求出GE的长,可通过解直角三角形分别求出GD,DE,EF,DF的长,即可求出四边形DFEG的周长.【解答】解:∵∠ABC=45°,AD⊥BC于点D,∴∠BAD=90°﹣∠ABC=45°,∴△ABD是等腰直角三角形,∴AD=BD,∵BE⊥AC,∴∠GBD+∠C=90°,∵∠EAD+∠C=90°,∴∠GBD=∠EAD,∵∠ADB=∠EDG=90°,∴∠ADB﹣∠ADG=∠EDG﹣∠ADG,即∠BDG=∠ADE,∴△BDG≌△ADE(ASA),∴BG=AE=1,DG=DE,∵∠EDG=90°,∴△EDG为等腰直角三角形,∴∠AED=∠AEB+∠DEG=90°+45°=135°,∵△AED沿直线AE翻折得△AEF,∴△AED≌△AEF,∴∠AED=∠AEF=135°,ED=EF,∴∠DEF=360°﹣∠AED﹣∠AEF=90°,∴△DEF为等腰直角三角形,∴EF=DE=DG,在Rt△AEB中,BE===2,∴GE=BE﹣BG=2﹣1,在Rt△DGE中,DG=GE=2﹣,∴EF=DE=2﹣,在Rt△DEF中,DF=DE=2﹣1,∴四边形DFEG的周长为:GD+EF+GE+DF=2(2﹣)+2(2﹣1)=3+2,故选:D.【点评】本题考查了等腰直角三角形的判定与性质,全等三角形的判定与性质,勾股定理,解直角三角形等,解题关键是能够灵活运用等腰直角三角形的判定与性质.二.填空题(共7小题)13.如图,把三角形纸片折叠,使点B、点C都与点A重合,折痕分别为DE、FG,得到∠AGE=30°,若AE=EG=2厘米,则△ABC的边BC的长为(6+4)厘米.【分析】根据折叠的性质和含30°的直角三角形的性质解答即可.【解答】解:∵把三角形纸片折叠,使点B、点C都与点A重合,折痕分别为DE,FG,∴BE=AE,AG=GC,∵∠AGE=30°,AE=EG=2厘米,∴AG=6厘米,∴BE=AE=2厘米,GC=AG=6厘米,∴BC=BE+EG+GC=(6+4)厘米,故答案为:(6+4),【点评】此题考查翻折问题,关键是根据折叠的性质和含30°的直角三角形的性质解答.14.如图,在Rt△ABC中,∠ACB=90°,BC=6,CD是斜边AB上的中线,将△BCD沿直线CD翻折至△ECD的位置,连接AE.若DE∥AC,计算AE的长度等于.【分析】根据题意、解直角三角形、菱形的性质、翻折变化可以求得AE的长.【解答】解:由题意可得,DE=DB=CD=AB,∴∠DEC=∠DCE=∠DCB,∵DE∥AC,∠DCE=∠DCB,∠ACB=90°,∴∠DEC=∠ACE,∴∠DCE=∠ACE=∠DCB=30°,∴∠ACD=60°,∠CAD=60°,∴△ACD是等边三角形,∴AC=CD,∴AC=DE,∵AC∥DE,AC=CD,∴四边形ACDE是菱形,∵在Rt△ABC中,∠ACB=90°,BC=6,∠B=30°,∴AC=,∴AE=.【点评】本题考查翻折变化、平行线的性质、直角三角形斜边上的中线,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.15.已知Rt△ABC中,∠ACB=90°,AC=8,BC=4,D为斜边AB上的中点,E是直角边AC上的一点,连接DE,将△ADE沿DE折叠至△A′DE,A′E交BD于点F,若△DEF的面积是△ADE面积的一半,则CE=2.【分析】根据等高的两个三角形的面积比等于边长比可得AD=2DF,A'F=EF,通过勾股定理可得AB的长度,可可求AD,DF,BF的长度,可得BF=DF,可证BEDA'是平行四边形,可得BE=A'D=2,根据勾股定理可得CE的长度【解答】解:如图连接BE∵∠ACB=90°,AC=8,BC=4∴AB=4∵D是AB中点∴BD=AD=2∵折叠∴AD=A'D=2,S△ADE=S△A'DE∵S△DEF=S△ADE∴AD=2DF,S△DEF=S△A'DE∴DF=,A'F=EF∴BF=DF=,且A'F=EF∴四边形BEDA'是平行四边形∴A'D=BE=∴根据勾股定理得:CE=2故答案为2【点评】本题考查了折叠问题,直角三角形斜边上的中线等于斜边的一半,关键是用面积法解决问题.16.如图,在△ABC中,AB=AC=5,tan A=,BC=,点D是AB边上一点,连接CD,将△BCD沿着CD翻折得△B1CD,DB1⊥AC且交于点E,则DE=.【分析】作BF⊥AC于F,证明△B1EC≌△CFB(AAS),得出B1E=CF=1,设DE=3a,则AD=5a,得出BD=B1D=3a+1,得出方程,解方程即可.【解答】解:作BF⊥AC于F,如图所示:则∠AFB=∠CFB=90°,在Rt△ABF中,tan A==,AB=5,∴AF=4,BF=3,sin A==,∴CF=AC﹣AF=1,由折叠的性质得:B1C=BC=,∠CB1E=∠ABC,B1D=BD,∵AB=AC,∴∠ABC=∠BCF,∴∠CB1E=∠BCF,∵DB1⊥AC,∴∠B1EC=90°=∠CFB,在△B1EC和△CBF中,,∴△B1EC≌△CFB(AAS),∴B1E=CF=1,设DE=3a,则AD=5a,∴BD=B1D=3a+1,∵AD+BD=AB,∴3a+1+5a=5,∴a=,∴DE=;故答案为:【点评】本题考查了翻折的性质、等腰三角形的性质、全等三角形的判定与性质、解直角三角形以及方程的解题思想,熟练掌握翻折变换的性质,证明三角形全等是解题的关键.17.如图,在Rt△ABC中,∠ABC=90°,把△ABC沿斜边AC折叠,使点B落在B’,点D,点E分别为BC和AB′上的点,连接DE交AC于点F,把四边形ABDE沿DE 折叠,使点B与点C重合,点A落在A′,连接AA′交B′C于点H,交DE于点G.若AB=3,BC=4,则GE的长为.【分析】设HC=HA=x,在Rt△CA′H中,可得x2=32+(4﹣x)2,解得x=,由△CA′H∽△AGE,可得=,由此即可解决问题.【解答】解:由题意四边形ABCA′是矩形,BD=CD=2,AG=GA′=2,∵BC∥AA′,∴∠BCA=∠CAA′,∵∠ACB=∠ACB′,∴∠HCA=∠HAC,∴HC=HA,设HC=HA=x,在Rt△CA′H中,x2=32+(4﹣x)2,∴x=,∴A′H=4﹣=,由△CA′H∽△AGE,可得:=,∴=,∴EG=.【点评】本题考查翻折变换,解直角三角形,勾股定理,相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.18.如图,在平行四边形ABCD中,∠B=30°,且BC=CA,将△ABC沿AC翻折至△AB′C,AB′交CD于点E,连接B′D.若AB=3,则B′D的长度为6.【分析】作CM⊥AB于M,由折叠的性质得:B'C=BC=AC,∠AB'C=∠B=∠CAB'=30°,AB'=AB=CD,由平行四边形的性质得出AD=CB,AB=CD,∠ADC=∠B=30°,求出AD=AC,AM=BM=AB=,∠BAC=∠B=30°,由等腰三角形的性质得出∠ACD=∠ADC=30°,由直角三角形的性质得出CM=,证出AD=BC=2CM=3,再由勾股定理即可得出结果.【解答】解:作CM⊥AB于M,如图所示:由折叠的性质得:B'C=BC=AC,∠AB'C=∠B=∠CAB'=30°,AB'=AB=CD,∵四边形ABCD是平行四边形,∴AD=CB,AB=CD,∠ADC=∠B=30°,∠BAD=∠BCD=180°﹣∠B=150°,∴∠B'AD=150°﹣30°﹣30°=90°,∵BC=AC,∴AM=BM=AB=,∠BAC=∠B=30°,∴CM=,∴AD=BC=2CM=3,在Rt△AB'D中,由勾股定理得:B'D===6;故答案为:6.【点评】本题考查了翻折变换的性质、平行四边形的性质、等腰三角形的性质以及勾股定理等知识;熟练掌握翻折变换的性质和平行四边形的性质,求出∠B'AD=90°是解题关键.19.如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,使点D恰好落在BC 边上的F点处.已知折痕AE=10,且CE:CF=4:3,那么该矩形的周长为96.【分析】由CE:CF=4:3,可以假设CE=4k,CF=3k推出EF=DE=5k,AB=CD=9k,利用相似三角形的性质求出BF,再在Rt△ADE中,利用勾股定理构建方程即可解决问题.【解答】解:∵四边形ABCD是矩形,∴AB=CD,AD=BC,∠B=∠C=∠D=90°,∵CE:CF=4:3,∴可以假设CE=4k,CF=3k∴EF=DE=5k,AB=CD=9k,∵∠AFE=∠D=90°,∴∠AFB+∠EFC=90°,∠EFC+∠FEC=90°,∴∠AFB=∠CEF,∴△ABF∽△FCE,∴∴∴BF=12k∴AD=BC=15k,在Rt△AED中,∵AE2=AD2+DE2,∴1000=225k2+25k2,∴k=2或﹣2(舍弃),∴矩形的周长=48k=96,故答案为:96【点评】本题考查翻折变换,矩形的性质,相似三角形的判定和性质等知识,解题的关键是学会利用参数构建方程解决问题.。
矩形的翻折问题

是.Leabharlann 12 或2712..如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰 好落在AC上.设F、H分别是B、D落在AC上的点,E、G分别 是折痕CE与AB、AG与CD的交点. (1)试说明四边形AECG的形状,并说明理由; (2)若矩形的边AD=3cm,AB=4cm,求△AGC的面积; (3)当四边形AECG是菱形时,求∠AGC的度数。
答案3
10.(09内江)如图12所示,将△ABC沿着DE翻折,若∠1+
∠2 =800,则∠B= 答案400
11.(09德州) 将三角形纸片(△ABC)按如图14所示的方式折叠,使
点B落在边AC上,记为点B/,折痕为EF.已知AB = AC=3,BC=4,
若以点B/,F,C为顶点的三角形与△ABC相似,那么BF的长度
若∠A=75°,则∠1+∠2=
(A)
A.150° B.210° C.105° D.75°
8.(2008·郴州)如图1所示,D是AB边上的中点,将△ABC沿
过D的直线折叠,使点A落在BC上的F处,若DE为折痕,∠B
=500,则∠BDF =
( 800 )
9.(09河北) 如图8,等边△ABC的边长为1 cm,D、E分别是AB、AC 上的点,将△ADE沿直线DE折叠,点A落在点A/处,且点A/在 △ABC外部,则阴影部分图形的周长为 cm.
3
6.(2012上海)如图,在Rt△ABC中,∠C=900,∠A=300,BC=1, 点D在AC上,将△ADB沿直线BD翻折后,将点A落在点E处,如
果AD⊥ED,那么线段DE的长为
.
7.(2012•梅州)如图,在折纸活动中,小明制作了一张△ABC纸片,
点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,
矩形的翻折及答案

矩形的翻折矩形的翻折一直是中考的重点,关于矩形的翻折通常有以下几种情况一、沿对角线翻折二、将一个顶点折到一边上三、将一条对角线的顶点折叠重合四、将一边折到对角线上1. 矩形ABCD中,AB=8,BC=4,将矩形沿对角线AC折叠,点D落在E处,求重叠部分△AFC 的面积解:由折叠,可证显然S△AEF≌S△CBF,∴AF=FC。
可设AF=FC=x,则BF=8-x,在Rt△CBF中,BC=4,得x2=(8-x)2+42,解得x=5,即AF=5.S△AFC=12•5•4=10.2.折叠矩形,使点D落在点F处,已知AB=8,BC=10,求EC的长由翻折可知△AFE≌△CBF,得EF=DE,AF=AD.因为而在Rt△ABF中,AB=8,AF=AD=10,∴BF=6,∴FC=10-6=4.设EC为x,则DE=EF=8-x,在△ECF中,由8-x()2=x2+42,解得x=3,即EC=33..矩形ABCD中,AB=6,BC=8将矩形折叠,使点B与点D重合,求折痕EF的长度解:连结BD、FD.由翻折可知BD⊥EF,且BO=DO,OF=OE,BF=DF.设BF=DF=x,则FC=8-x,由勾股定理得x2=(8-x)2+62,解得x=254.可得OF=154,EF=2•OF=152.4.矩形ABCD 中,AB=4,AD=3,折叠纸片使AD 与对角线BD 重合,折痕为DE ,求AE 长 解:由翻折AD=DF=6,设EF=AE=x ,则BE=8-x,在Rt △ABD 中,可求BD=10,所以BF=10-6=4,在Rt △BEF 中,x 2+42=8-x ()2,解得x=3,即AE=35.如图,ABCD 是矩形纸片,翻折∠B 、∠D ,使BC 、AD 恰好落在AC 上.设F 、H 分别是B 、D 落在AC 上的点,E 、G 分别是折痕CE 与AB 、AG 与CD 的交点.(1)试说明四边形AECG 的形状,并说明理由;(2)若矩形的一边AB=4,BC=3,求△AEC 的面积;(1)证明:在矩形ABCD 中,∵AD ∥BC ,∴∠DAC=∠BCA .由题意,得∠GAH=12∠DAC ,∠ECF=12∠BCA . ∴∠GAH=∠ECF ,∴AG ∥CE .又∵AE ∥CG ,∴四边形AECG 是平行四边形.(2)解法1:在Rt △ABC 中,∵AB=4,BC=3,∴AC=5.∵CF=CB=3,∴AF=2.在Rt △AEF 中,设EF=x ,则AE=4-x .根据勾股定理,得AE 2=AF 2+EF 2,即(4-x )2=22+x 2.解得x=32,即线段EF 长为32. ∴S △AEC=12×AC ×EF=12×5×32=1546.(2012•南平)如图,正方形纸片ABCD 的边长为3,点E 、F 分别在边BC 、CD 上,将AB 、AD 分别和AE 、AF 折叠,点B 、D 恰好都将在点G 处,已知BE=1,求EF 的长解:∵正方形纸片ABCD 的边长为3,∴∠C=90°,BC=CD=3,根据折叠的性质得:EG=BE=1,GF=DF ,设DF=x ,F B则EF=EG+GF=1+x,FC=DC﹣DF=3﹣x,EC=BC﹣BE=3﹣1=2,在Rt△EFC中,EF2=EC2+FC2,即(x+1)2=22+(3﹣x)2,解得:x=1.5,∴DF=1.5,即 EF=1+1.5=2.5.7.(2011•重庆)如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE 对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的是 .解:①正确.因为AB=AD=AF,AG=AG,∠B=∠AFG=90°,∴△ABG≌△AFG;②正确.因为:EF=DE=CD=2,设BG=FG=x,则CG=6﹣x.在直角△ECG中,根据勾股定理,得(6﹣x)2+42=(x+2)2,解得x=3.所以BG=3=6﹣3=GC;③正确.因为CG=BG=GF,所以△FGC是等腰三角形,∠GFC=∠GCF.又∠AGB=∠AGF,∠AGB+∠AGF=180°﹣∠FGC=∠GFC+∠GCF,∴∠AGB=∠AGF=∠GFC=∠GCF,∴AG∥CF;④错误.过C作C H⊥GE于H,∵EF=2,FG=3, ∴EG=5,∴35GFEG=,∴S△EGC= =×3×4=6,∴356GF S GFCEG==∴S△FGC=≠3.答案①②③8.(2014河南省)如图,矩形ABCD中,AD=5,AB=7.点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D/落在∠ABC的角平分线上时,DE的长为 .答案:53或52解析:过D/作FH⊥AB交AB于F,交CD于H;如图1,由翻折,△EDA≌△ED/A,∴ED=ED/,AD=AD/=5, 设AF=x,则BF=7-x,在Rt△BD/F中,∵D/B是∠ABC的平分线,∴∠ABD/=450, 则D/F=BF=7-x,在Rt△AD/F中,AD/2=AF2+D/F2,即52=(7-x)2+x2,解得x=4或x=3,即D/F=BF=3或4.当x=4时,如图1,设DE=y,在Rt△D/HE中,EH=4-y,ED/=y,HD/=2,即(4-y)2+22=y2,解得y=52,即DE=52当x=3时,如图2,设DE=y,在Rt△D/HE中,EH=3-y,ED/=y,HD/=1,即(3-y)2+12=y2,解得y=53,即DE=53图1FA图2DA。
矩形翻折问题

矩形翻折问题二、方法剖析与提炼例1.如图,折叠矩形的一边AD,使点D 落在BC 边上的点F 处.已知AB=8cm,BC= 10cm.则折痕AE 的长是____________cm.【解答】55【解析】△AEF 由△AED 翻折而成,得AF=AD=10cm ,在Rt △ABF 中,利用勾股定理可得BF=6cm, CF=4cm.设DE=EF=x,EC=8-x, 在Rt △ECF 中, 2224)8(x x =+-,解得DE=5cm. 再在Rt △ADE 中,利用勾股定理得AE=55cm.【解法】这是一个矩形翻折的边长问题,由翻折得到对应线段相等,设元利用勾股定理构造一元二次方程可解线段长度。
【解释】此题涵盖了三角形全等,勾股定理,一元二次方程求边长等知识,意在培养学生翻折找对应边。
例2:将一矩形纸片OABC 放在平面直角坐标系中,O (0,0),A (8,0),C (0,4)。
动点Q 从点C 出发以每秒1个单位长的速度沿CB 向终点B 运动,动点P 从点A 出发以相等的速度沿AO 向终点O 运动。
当其中一点到达终点时,另一点也停止运动.设点P 的运动时间为t (秒)。
如图,将矩形OABC 沿PQ 翻折,当A 与C 重合时,求另一落点M 的坐标及折痕PQ【解答】62,532,516-=⎪⎭⎫⎝⎛x y M【解析】过M 点作MN ⊥y 轴,垂足为N ,由翻折得Rt ∠A=Rt ∠MCP,所以△OPC ≈△NMC,由例1可知△OPC 是3,4,5的直角三角形,利用相似比分别求得FMN=516,CN=512,所以62,532,516-=⎪⎭⎫⎝⎛x y M 【解法】这是与一个矩形翻折有关的动点问题。
利用Rt ∠A 翻折到y 轴,构造K 字相似三角形。
利用对应边成比例,可求得CN,MN 的长度,继而求得M 的坐标及折痕PQ 的解析式。
【解释】此题是将矩形翻折到一个固定状态,利用特殊位置求对应的量,而下面变式题则变为一个不确定的状态。
矩形翻折问题集锦及答案解析
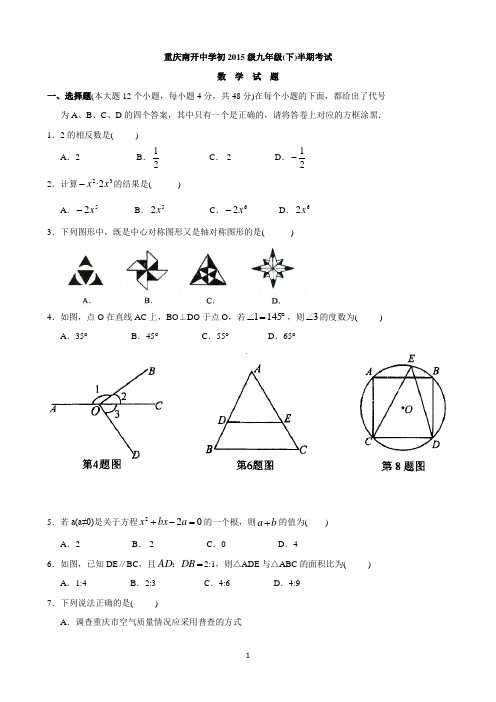
重庆南开中学初2015级九年级(下)半期考试数 学 试 题一、选择题(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号 为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将答卷上对应的方框涂黑. 1.2的相反数是( ) A .2 B .21 C .-2 D .21- 2.计算322·x x -的结果是( )A .52x - B .52x C .62x - D .62x 3.下列图形中,既是中心对称图形又是轴对称图形的是( )4.如图,点O 在直线AC 上,BO ⊥DO 于点O ,若︒=∠1451,则3∠的度数为( ) A .35° B .45° C .55° D .65°5.若a(a≠0)是关于方程022=-+a bx x 的一个根,则b a +的值为( ) A .2 B .-2 C .0 D .46.如图,已知DE ∥BC ,且=DB AD :2:1,则△ADE 与△ABC 的面积比为( ) A .1:4 B .2:3 C .4:6 D .4:9 7.下列说法正确的是( )A .调查重庆市空气质量情况应采用普查的方式B .若A 、B 两组数据的平均数相同,A 组数据的方差2A S =0.03,B 组数据的方差2B S =0.2,则8组数据比A 组数据稳定C .南开中学明年开运动会一定会下雨D .为了解初三年级24个班课间活动的使用情况。
李老师采用普查的方式 8.如图,O 是正方ABCD 的外接圆,点E 是弧AB 上任意一点,则DEC ∠的度数为( )A .40°B .45°C .48°D .50° 9.关于x 的方程11=+x a的解是负数,则口的取值范围是( ) A .a<l B .a<1且a≠0 C .a≤1 D .a≤l 且a≠010.2015年4月l8日周杰伦“摩天轮2”演唱会在重庆奥体中心如期举行.小王开车从家出发前去观看,预计1个小时能到达,可当天路上较为拥堵,行驶了半个小时,刚好行驶了一半路程,道路被“堵死”,堵了几分钟突然发现旁边刚好有一个轻轨站,于是小王将车停在轻轨站的车库,然后坐轻轨前往,结果按预计时间到达.下面能反映小王距离奥体中心的距离y (千米)与时间x (小时)的函数关系的大致图象是( )11.将一些形状相同的小棒按如图所示的方式摆放。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆南开中学初2015级九年级(下)半期考试数 学 试 题一、选择题(本大题12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号 为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将答卷上对应的方框涂黑. 1.2的相反数是( ) A .2 B .21 C .-2 D .21- 2.计算322·x x -的结果是( )A .52x - B .52x C .62x - D .62x 3.下列图形中,既是中心对称图形又是轴对称图形的是( )4.如图,点O 在直线AC 上,BO ⊥DO 于点O ,若︒=∠1451,则3∠的度数为( ) A .35° B .45° C .55° D .65°5.若a(a≠0)是关于方程022=-+a bx x 的一个根,则b a +的值为( ) A .2 B .-2 C .0 D .46.如图,已知DE ∥BC ,且=DB AD :2:1,则△ADE 与△ABC 的面积比为( ) A .1:4 B .2:3 C .4:6 D .4:9 7.下列说法正确的是( )A .调查重庆市空气质量情况应采用普查的方式B .若A 、B 两组数据的平均数相同,A 组数据的方差2A S =0.03,B 组数据的方差2B S =0.2,则8组数据比A 组数据稳定C .南开中学明年开运动会一定会下雨D .为了解初三年级24个班课间活动的使用情况。
李老师采用普查的方式 8.如图,O 是正方ABCD 的外接圆,点E 是弧AB 上任意一点,则DEC ∠的度数为( )A .40°B .45°C .48°D .50° 9.关于x 的方程11=+x a的解是负数,则口的取值范围是( ) A .a<l B .a<1且a≠0 C .a≤1 D .a≤l 且a≠010.2015年4月l8日周杰伦“摩天轮2”演唱会在重庆奥体中心如期举行.小王开车从家出发前去观看,预计1个小时能到达,可当天路上较为拥堵,行驶了半个小时,刚好行驶了一半路程,道路被“堵死”,堵了几分钟突然发现旁边刚好有一个轻轨站,于是小王将车停在轻轨站的车库,然后坐轻轨前往,结果按预计时间到达.下面能反映小王距离奥体中心的距离y (千米)与时间x (小时)的函数关系的大致图象是( )11.将一些形状相同的小棒按如图所示的方式摆放。
图①中有3根小棒,图②中有9根小棒,图③中有18根小棒。
照此规律,图⑧中小棒的根数为( )12.如图,一次函数b x y +=的图象与x 轴交于点A ,与y 轴交于点B ,与反比例函数xy 2=交于点C(2,m ),则点B 到OC 的距离是( )A .2B .5C .52D .552二、填空题(本大题6个小题,每小题4分,共24分)请将每小题的答案直接填在答卷中对 应的横线上.13.计算()=--+++-302015812131π . 14.方程组⎩⎨⎧=++=421y x x y 的解为 .15.我校初三年级许多同学经过刻苦锻炼,在4月9、10日的中考体考中取得了优良的成绩.年级上随机抽取了6名同学的体育成绩如下表所示:则这6名同学的平均分是 .16.如图,在ABC Rt ∆中,︒=∠90C ,︒=∠30A ,AB=4,以AC 为直径作半圆交AB 于点D ,则图中阴影部分的面积为 .17.从1-,0,1,3,4这五个数中任选一个数,记为a ,则使二次函数()1222-+--=a ax x a y 的顶点在第四象限且双曲线xay 27-=在第一、三象限的概率是 . 18.如图,矩形ABCD 中,AB=6,BC=8,将△ACD 沿对角线AC 翻折得△ACE 。
AE 交BC 于点F ,将△CEF 绕点C 逆时针旋转a 角(0°<a<180°)得''F CE ∆,点E 、F 的对应点分别为'E 、'F ,旋转过程中直线'CF 、''F E 分别交直线AE 于点N M 、,当NM F '∆是等腰三角形且'MF MN =时,则MN = .程或推理步骤,请将解答过程书写在答卷中对应的位置上.19.如图,AC 与BD 相交于点O ,AO=DO ,21∠=∠,求证:DCB ABC ∆≅∆.20.暑假期间,一些同学将要到A ,B ,C ,D 四个地方参加夏令营活动,现从这些同学中随机调查了一部分同学.根据调查结果,绘制成了如下两幅统计图:(1)扇形A 的圆心角的度数为 °,若此次夏令营一共有320名学生参加,则前往C 地的学生约有 人,并将条形统计图补充完整;(2)若某姐弟两人中只能有一人参加夏令营,姐弟俩决定用一个游戏来确定参加者:在4张形状、大小完全相同的卡片上分别写上1-,1,2,3四个整数,先让姐姐随机地抽取一张,再由弟弟从余下的三张卡片中随机地抽取一张.若抽取的两张卡片上的数字之和小于3则姐姐参加,否则弟弟参加.用列表法或树状图分析这种方法对姐弟俩是否公平?过程或推理步骤,请将解答过程书写在答卷中对应的位置上. 21.化简下列各式.(1)()()()()y x y y x x y y x 222222--+-+-;(2)222⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-++-a b a ab b a bab b.22.重庆市是著名的山城,许多美丽的建筑建在山上.如图,刘老师为了测量小山项一建筑物DE 的高度,和潘老师一起携带测量装备前往测量.刘老师在山脚下的A 处测得建筑物顶端D 的仰角为53°,山坡AE 的坡度i=1:5,潘老师在B 处测得建筑物顶端D 的仰角为45°,若此时刘老师与潘老师的距离AB=200m ,求建筑物DE 的高度.(5453sin ≈︒,5353cos ≈︒,3453tan ≈︒,结果精确到0.1m )23.每年的3月15日是 “国际消费者权益日”,许多商家都会利用这个契机进行打折促销活动.甲卖家的A 商品成本为500元,在标价800元的基础上打9折销售.(1)现在甲卖家欲继续降价吸引买主,问最多降价多少元,才能使利润率不低于10%?(2)据媒体爆料,有一些卖家先提高商品价格后再降价促销,存在欺诈行为.乙卖家也销售A 商品,成本、标价与甲卖家一致,以前每周可售出50件,为扩大销量,尽快减少库存,他决定打折促销.但他先将标价提高m 3%,再大幅降价m 26元,使得A 商品在3月15日那一天卖出的数量就比原来一周卖出的数量增加了m 512%,这样一天的利润达到了20000元,求m .24.阅读材料:如图,在平面直角坐标系中,O 为坐标原点,对于任意两点A (1x ,1y ),()22y x B ,,由勾股定理可得:()()2212212y y x x AB -+-=,我们把()()221221y y x x -+- 叫做A 、B 两点之间的距离,记作()()221221y y x x AB -+-=.例题:在平面直角坐标系中,O 为坐标原点,设点P(x ,0). ①A(0,2),B (3,-2),则AB= .;PA = .; 解:由定义有()()[]5223022=--+-=AB ;()()4203222+=-+-=x x PA .②()412+-x 表示的几何意义是 .;()92122+-++x x 表示的几何意义是 ..解:因为()()()22220141-+-=+-x x ,所以()412+-x 表示的几何意义是点()0,x P 到点()21,的距离;同理可得,()92122+-++x x 表示的几何意义是点()0,x P 分别到点(0,1)和点(2,3)的距离和.根据以上阅读材料,解决下列问题:(1)如图,已知直线82+-=x y 与反比例函数xy 6=(x >0)的图像交于()()2211y x B y x A ,、,两点,则点A 、B 的坐标分别为A( , ),B( , ),AB= .(2)在(1)的条件下,设点()0,x P ,则()()22222121y x x y x x +-++-表示的几何意义是 ;试求()()22222121y x x y x x +-++-的最小值,以及取得最小值时点P的坐标.五、解答题 25.如图1,ABCD 中,AE ⊥BC 于E ,AE=AD ,EG ⊥AB 于G ,延长GE 、DC 交于点F ,连接AF .(1)若BE=2EC ,AB =13,求AD 的长; (2)求证:EG=BG+FC ;(3)如图2,若AF=25,EF=2,点M 是线段AG 上的一个动点,连接ME ,将GME ∆沿ME 翻折得ME G '∆,连接'DG ,试求当'DG 取得最小值时GM 的长.26.已知抛物线c bx x y ++-=23与x 轴交于点A (1,0)、B(3,0),与y 轴交于点C ,抛物线的顶点为D .(1)求b 、c 的值及顶点D 的坐标;(2)如图1,点E 是线段BC 上的一点,且BC=3BE ,点F(0,m )是y 轴正半轴上一点,连接BF 、EF ,EF 与线段OB 交于点G ,OF:OG=2:3,求△FEB 的面积;(3)如图2,P 为线段BC 上一动点,连接DP ,将△DBP 绕点D 顺时针旋转60°得''P DB ∆’(点B 的对 应点是点'B ,点P 的对应点是点'P ),'DP 交y 轴于点M ,N 为'MP 的中点,连接'PP 、NO ,延长NO 交BC 于点Q ,连接'QP ,若Q PP '∆的面积是BOC ∆面积的91,求线段BP 的长.如图,有一张矩形纸片ABCD ,已知AB=2,BC=4,若点E 是AD 上的一个动点(与点A 不重合),且0<AE ≤2,沿BE 将△ABE 翻折后,点A 落到点P 处,连接PC .有下列说法: ①△ABE 与△PBE 关于直线BE 对称; ②线段PC 的长有可能小于2; ③四边形ABPE 有可能为正方形; ④当△PCD 是等腰三角形时,PC=2或 5 . 其中说法正确的序号是.① ③如图,矩形ABCD 中,AB=4,AD=8,点E 、F 分别在线段BC 、CD 上,将△CEF 沿EF 翻折,点C 的落点为M (1)如图1,当 CE=5,M 点落在线段AD 上时,求MD 的长 (2)如图2,若点F 是CD 如图所示,矩形纸片ABCD 中,AB=6cm ,BC=8 cm ,现将其沿EF 对折,使得 点C 与点A 重合,则AF 长为【 】A.25cm 8 B. 25cm 4 C. 25cm 2D. 8cm 【答案】B 。
