矩形翻折问题
初中数学-矩形翻折问题小专题

矩形翻折问题小专题【知识方法总结】1.联系实际,内容丰富,具有开放性,有利于考查学生的动手能力,空间观念和几何变换的思想。
2.图形的折叠就是对称变换,即翻折。
3.其解法看似灵活,抓住翻折前后的图形是全等图形这一关键,“边相等,角相等,折线为角平分线”再利用勾股定理或比例关系或线段的相等关系列方程,即可求解。
4.注意点:(1)折叠就是轴对称(2)其中蕴含着全等图形;即边和角的相等关系。
【经典例题】例1.已知,一张矩形纸片ABCD的边长分别为9cm和3cm,把顶点A和C叠合在一起,得折痕EF (如图).(1)猜想四边形AECF是什么四边形,并证明你的猜想;(2)求折痕EF的长.【解答】解:(1)菱形,理由如下:∵四边形ABCD为矩形,∴AB∥CD,∠AFE=∠CEF.∵矩形ABCD沿EF折叠,点A和C重合,∴∠CEF=∠AEF,AE=CE∴∠AFE=∠AEF,∴AE=AF.∴AF=CE,又∵AF∥CE,∴AECF为平行四边形,∵AE=EC,即四边形AECF的四边相等.∴四边形AECF为菱形.例2.已知:长方形纸片ABCD中,AB=10cm,AD<AB.(1)当AD=6.5cm时,如图①,将长方形纸片ABCD折叠,使点D落在AB边上,记作点D′,折痕为AE,如图②.此时,图②中线段D′B长是cm.(2)若AD=xcm,先将长方形纸片ABCD按问题(1)的方法折叠,再将三角形AED′沿D′E向右翻折,使点A落在射线D′B上,记作点A′.若翻折后的图形中,线段BD′=2BA′,请根据题意重新画出图形(草图),并求出x的值.【解答】解:(1)由题意知AD′=AD=6.5cm,∴D′B=AB﹣AD′=10﹣6.5=3.5(cm),故答案为:3.5;(2)如图所示,由题意知,AD=AD′=A′D′=xcm,∵AB=10cm,∴BD′=10﹣x,A′B=2x﹣10,由BD′=2BA′得10﹣x=2(2x﹣10),解得:x=6.例3.如图,在矩形纸片ABCD中,BC=a,将矩形纸片翻折,使点C恰好落在对角线交点O处,折痕为BE,点E在边CD上,则CE的长为()a;A. 12a;B. 25a;C. √33a.D. √32【答案】C例4.(1)如图,矩形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD的E点上,折痕的一端G 点在边BC上,BG=10.①当折痕的另一端点F在AB边上时,如图①,求△EFG的面积;②当折痕的另一端点F在AD边上时,如图②,证明四边形BGEF为菱形,并求出折痕GF的长.(2)在矩形纸片ABCD中,AB=5,AD=13.如图③所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ.当点A′在BC边上移动时,折痕的端点P,Q也随之移动.若限定点P,Q分别在AB,AD边上移动,求点A′在BC边上可移动的最大距离.【解答】例5.折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在线段AE上的点H处,折痕为=.DG,点G在BC边上,若AB=AD+2,EH=1,则ADAB【答案】3+4√313例6.在学习完特殊的平行四边形之后,某学习小组针对矩形中的折叠问题进行了研究.问题背景:在矩形ABCD中,点E、F分别是BC、AD 上的动点,且BE=DF,连接EF,将矩形ABCD沿EF折叠,点C落在点C′处,点D落在点D′处,射线EC′与射线DA相交于点M.猜想与证明:(1)如图1,当EC′与线段AD交于点M时,判断△MEF的形状并证明你的结论;操作与画图:(2)当点M与点A重合时,请在图2中作出此时的折痕EF和折叠后的图形(要求:尺规作图,不写作法,保留作图痕迹,标注相应的字母);操作与探究:(3)如图3,当点M在线段DA延长线上时,线段C′D'分别与AD,AB交于P,N两点时,C′E与AB交于点Q,连接MN 并延长MN交EF于点O.求证:MO⊥EF 且MO平分EF;【解答】解:(1)△MEF是等腰三角形.理由:∵四边形ABCD是矩形,∴AD∥BC,∴∠MFE=∠CEF,由折叠可得,∠MEF=∠CEF,∴∠MFE=∠MEF,∴ME=MF,∴△MEF是等腰三角形.(2)折痕EF和折叠后的图形如图2所示:7.如图1,矩形纸片ABCD的边长AB=4cm,AD=2cm.同学小明现将该矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图2),观察图形对比前后变化,回答下列问题:(1)GF FD(直接填写=、>、<);(2)判断△CEF的形状,并说明理由;(3)运用所学知识,请计算着色部分多边形BCHFE的面积.【解答】解:(1)由翻折的性质,可得GD=FD;故答案为:=;(2)△CEF是等腰三角形.∵矩形ABCD,∴AB∥CD,∴∠AEF=∠CFE,由翻折的性质,∠AEF=∠FEC,∴∠CFE=∠FEC,∴CF=CE,故△CEF为等腰三角形;8.如图,已知矩形纸片ABCD,AB=4,BC=10,M是BC的中点,点P沿折线BA﹣AD运动,以MP为折痕将矩形纸片向右翻折,使点B落在矩形的边上,则折痕MP的长.√5或2√5或4【答案】529.如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE,(1)求证:四边形AFCE为菱形;(2)设AE=a,ED=b,DC=c.请写出一个a、b、c三者之间的数量关系式.【解答】(1)由矩形ABCD与折叠的性质,易证得△CEF是等腰三角形,即CE=CF,即可证得AF=CF=CE=AE,即可得四边形AFCE为菱形;(2)由折叠的性质,可得CE=AE=a,在Rt△DCE中,利用勾股定理即可求得:a、b、c三者之间的数量关系式为:a2=b2+c2.(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠AEF=∠EFC,由折叠的性质,可得:∠AEF=∠CEF,AE=CE,AF=CF,∴∠EFC=∠CEF,∴CF=CE,∴AF=CF=CE=AE,∴四边形AFCE为菱形;(2)a、b、c三者之间的数量关系式为:a2=b2+c2.理由:由折叠的性质,得:CE=AE,∵四边形ABCD是矩形,∴∠D=90°,∵AE=a,ED=b,DC=c,∴CE=AE=a,在Rt△DCE中,CE2=CD2+DE2,∴a、b、c三者之间的数量关系式为:a2=b2+c2.10.如图,把正方形纸片ABCD沿对边中点所在直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE,若AB=4,则FM的长为()A. 4B. 2√3C. 2√2D. 2【答案】B11.在一张长方形ABCD纸张中,AB=25cm,AD=20cm,现将这张纸片按下列图示方法折叠,请解决下列问题(1)如图1,折痕为DE,点A的对应点F在CD上,则折痕DE的长为cm;(2)如图2,H、G分别为BC、AD的中点,点A的对应点F在HG上,折痕为DE,求重叠部分(△DEF)的面积;(3)如图3,在图2中,把长方形ABCD沿着HG剪开,变成两张长方形纸片,将这两张纸按图形位置任意叠合后,发现重叠部分都是菱形,显然,这些菱形中周长最短是40cm.是否存在叠后周长最大的菱形?若存在,请求出叠合后周长最大的菱形的周长和面积;若不存在,请说明理由.【解答】12.如图,在矩形ABCD中,AB=4,AD=10,点E在AD边上,已知B、E两点关于直线l对称,直线l 分别交AD、BC边于点M、N,连接BM、NE.(1)求证:四边形BMEN是菱形;(2)若DE=2,求NC的长.【解答】(1)证明:∵B、E两点关于直线l对称,∴BM=ME,BN=NE,∠BMN=∠EMN,在矩形ABCD中,AD∥BC,∴∠EMN=∠MNB,∴∠BMN=∠MNB,∴BM=BN,∴BM=ME=BN=NE,∴四边形BMEN是菱形;(2)解:设菱形边长为x,则AM=8−x,在Rt△ABM中,42+(8−x)2=x2,解得:x=5,∴NC=5.【答案】(1)略;(2)5.。
初中数学中折叠问题
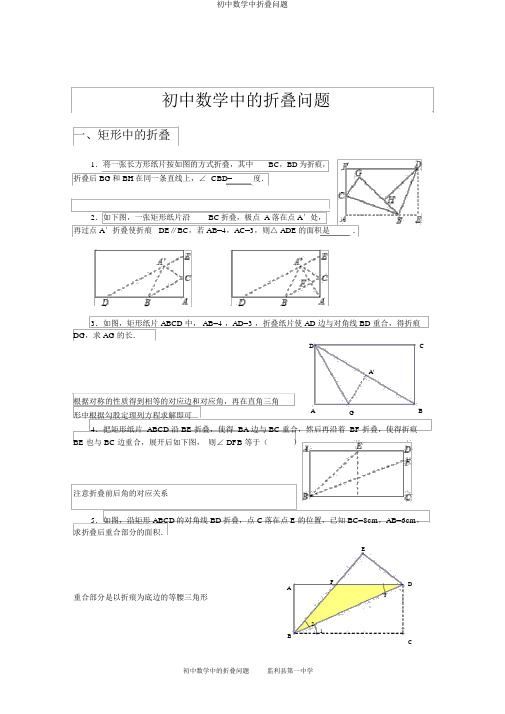
初中数学中的折叠问题一、矩形中的折叠1.将一张长方形纸片按如图的方式折叠,其中BC,BD为折痕,折叠后 BG和 BH在同一条直线上,∠ CBD=度.2.如下图,一张矩形纸片沿BC折叠,极点 A 落在点 A′处,再过点 A′折叠使折痕DE∥BC,若 AB=4,AC=3,则△ ADE的面积是.3.如图,矩形纸片 ABCD 中, AB=4 ,AD=3 ,折叠纸片使 AD 边与对角线 BD 重合,得折痕DG,求 AG 的长.D CA'根据对称的性质得到相等的对应边和对应角,再在直角三角形中根据勾股定理列方程求解即可 A G B 4.把矩形纸片 ABCD 沿 BE 折叠,使得 BA 边与 BC 重合,然后再沿着 BF 折叠,使得折痕BE 也与 BC 边重合,展开后如下图,则∠ DFB 等于()注意折叠前后角的对应关系5.如图,沿矩形 ABCD的对角线 BD折叠,点 C落在点 E 的位置,已知 BC=8cm,AB=6cm,求折叠后重合部分的面积.EF DA3重合部分是以折痕为底边的等腰三角形21BC6.将一张矩形纸条ABCD按如下图折叠,若折叠角∠的形状三角形.对折前后图形的位置变化,但形状、大小不变,注意一般情况下要画出对折前后的图形,便于寻找对折前后图形之间的关系,注意以折痕为底边的等腰△ GEF FEC=64°,则∠ 1=度;△ EFGD‘C‘A1G F D5432B E C7.如图,将矩形纸片ABCD 按如下的次序进行折叠:对折,展平,得折痕EF(如图①);延 CG 折叠,使点 B 落在 EF 上的点 B ′处,(如图②);展平,得折痕 GC(如图③);沿 GH 折叠,使点 C 落在 DH 上的点 C′处,(如图④);沿 GC′折叠(如图⑤);展平,得折痕 GC′,GH(如图⑥).(1)求图②中∠ BCB ′的大小;(2)图⑥中的△ GCC′是正三角形吗?请说明原因.理清在每一个折叠过程中的变与不变8.如图,正方形纸片ABCD的边长为 8,将其沿 EF折叠,则图中①②③④四个三角形的周长之和为折叠前后对应边相等9.如图,将边长为 4 的正方形 ABCD沿着折痕 EF 折叠,使点 B落在边 AD的中点 G处,求四边形 BCFE的面积注意折叠过程中的变与不变,图形的形状和大小不变,对应边与对应角相等10.如图,将一个边长为 1 的正方形纸片ABCD 折叠,使点 B 落在边 AD 上不与A、D重合.MN 为折痕,折叠后 B ’C’与 DN 交于 P.(1)连结 BB ’,那么 BB ’与 MN 的长度相等吗?为什么?(2)设 BM=y, AB ’=x,求 y 与 x 的函数关系式;(3)猜想当 B 点落在什么位置上时,折叠起来的梯形MNC ’B’面积最小?并考证你的猜想.二、纸片中的折叠11.如图,有一条直的宽纸带,按图折叠,则∠α的度数等于()CD30° BF E a21A题考察的是平行线的性质,同位角相等,及对称的性质,折叠的角与其对应角相等,和平角为 180度的性质,注意△ EAB 是以折痕 AB 为底的等腰三角形12.如图,将一宽为2cm 的纸条,沿 BC,使∠ CAB=45 °,则后重合部分的面积为在折叠问题中,一般要注意折叠前后图形之间的联系,将图形补充完整,对于矩形(纸片)折叠,折叠后会形成“平行线 +角平分线”的基本结构,即重叠部分是一个以折痕为底边的等腰三角形ABC13.将宽 2cm的长方形纸条成如下图的形状,那么折痕PQ的长是注意掌握折叠前后图形的对应关系.在矩形(纸片)折叠问题中,会出现“平行线 +角平分线”的基本结构图形,即有以折痕为底边的等腰三角形 APQ14.如图 a 是长方形纸带,∠ DEF=20°,将纸带沿EF 折叠成图 b,再沿 BF 折叠成图 c,则图 c 中的∠ CFE 的度数是()AE D A E E DACFB FC B G B G FC 图c图 a 图 bD本题考察图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变.由题意知∠ DEF= ∠EFB=20°图 b∠GFC=140°,图 c 中的∠ CFE=∠GFC-∠ EFG 15.将一张长为70 cm 的长方形纸片ABCD ,沿对称轴 EF 折叠成如图的形状,若折叠后,AB 与 CD 间的距离为 60cm,则原纸片的宽AB 是()DCFG60cmEA FDBE C B A16.一根 30cm、宽 3cm 的长方形纸条,将其按照图示的过程折叠(阴影部分表示纸条的反面),为了雅观,希望折叠达成后纸条两头高出点P 的长度相等,则最初折叠时,求MA 的长三、三角形中的折叠17.如图,把 Rt△ABC(∠ C=90°),使 A, B两点重合,得到折痕 ED,再沿 BE折叠, C点恰巧与 D点重合,则 CE:AE=18.在△ ABC中,已知 AB=2a,∠ A=30°, CD是 AB边的中线,若将△ ABC沿 CD对折起来,1折叠后两个小△ ACD与△ BCD重叠部分的面积恰巧等于折叠前△ABC的面积的4.(1)中间线 CD等于 a 时,重叠部分的面积等于;(2)有如下结论(不在“ CD等于 a”的限制条件下):① AC边的长能够等于a;②折叠前的3 2△ABC的面积能够等于 2 a ;③折叠后,以A、B为端点的线段AB与中线CD平行且相等.其中,结论正确(把你认为正确结论的代号都填上,若认为都不正确填“无”).C CB'12A E 3 D BAD BB'注意“角平分线 +等腰三角形”的基本构图,折叠前后图形之间的对照,找出相等的对应角和对应边19.在△ ABC 中,已知∠ A=80°,∠ C=30°,现把△ CDE 沿 DE 进行不同的折叠得△DE,对折叠后产生的夹角进行探究:(1)如图( 1)把△ CDE 沿 DE 折叠在四边形 ADEB 内,则求∠ 1+∠2 的和;(2)如图( 2)把△ CDE 沿 DE 折叠覆盖∠ A ,则求∠ 1+∠2 的和;(3)如图( 3)把△ CDE 沿 DE 斜向上折叠,探究∠ 1、∠ 2、∠ C 的关系.(1)根据折叠前后的图象全等可知,∠ 1=180° -2∠CDE,∠2=180°-2∠CED,再根据三角形内角和定理比 A 可求出答案;(2)连结 DG,将∠ ADG+ ∠AGD 作为一个整体,根据D 1C'三角形内角和定理来求;(3)将∠ 2 看作 180° -2∠CED,∠ 1 看作 2∠C2CDE-180°,再根据三角形内角和定理来求. E 图 (1)C'C' AA12D1G D2 C′B由于等腰三角形是轴对称图形,所以在折叠三角形时经常会出现等腰三角形20.察看与发现:将三角形纸片ABC(AB >AC )沿过点 A 的直线折叠,使得 AC 落在 AB 边上,折痕为 AD ,展开纸片(如图①);在第一次折叠的基础上第二次折叠该三角形纸片,使点 A 和点 D 重合,折痕为EF,展平纸片后得到△ AEF (如图②).小明认为△ AEF 是等腰三角形,你同意吗?请说明原因.实践与运用:(1)将矩形纸片 ABCD 沿过点 B 的直线折叠,使点 A 落在 BC 边上的点 F 处,折痕为 BE(如图③);再沿过点E 的直线折叠,使点D 落在BE 上的点D’处,折痕为EG(如图④);再展平纸片(如图⑤).求图⑤中∠α的大小.由于角平分线所在的直线是角的对称轴,所以在三角形中的折叠往常都与角平分线相关。
2023年中考数学【选择题】讲练必考重点03 几何变换之翻折问题

【选择题】必考重点03 几何变换之翻折问题几何变换中的折叠问题,是江苏各地中考中常考的题型,难度多为一般或者较难。
几何的翻折问题,本质上考查的是轴对称的性质,常和矩形相结合。
在解题时,首先要明确折叠前后的图形全等,折叠前后的对应边、对应角相等,对称轴垂直平分对应点之间的连线,在结合矩形、菱形、三角形等的性质,运用勾股定理,列出方程,求出相应的线段长度。
【2022·江苏连云港·中考母题】如图,将矩形ABCD 沿着GE 、EC 、GF 翻折,使得点A 、B 、D 恰好都落在点O 处,且点G 、O 、C 在同一条直线上,同时点E 、O 、F 在另一条直线上.小炜同学得出以下结论:①GF ∥EC ;②AB ;③GE DF ;④OC ;⑤△COF ∽△CEG .其中正确的是( )A .①②③B .①③④C .①④⑤D .②③④【考点分析】本题主要考查了折叠问题,解题时,我们常常设要求的线段长为x ,然后根据折叠和轴对称的性质用含x 的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案. 【思路分析】由折叠的性质知∠FGE =90°,∠GEC =90°,点G 为AD 的中点,点E 为AB 的中点,设AD =BC =2a ,AB =CD =2b ,在Rt △CDG 中,由勾股定理求得b ,然后利用勾股定理再求得DF =FO =【2021·江苏苏州·中考母题】如图,在平行四边形ABCD 中,将ABC 沿着AC 所在的直线翻折得到AB C ',B C '交AD 于点E ,连接B D ',若60B ∠=︒,45ACB ∠=︒,AC =B D '的长是( )A.1BC D 【考点分析】本题考查翻折变换、等腰三角形的性质、勾股定理、平行四边形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.【思路分析】利用平行四边形的性质、翻折不变性可得△AEC 为等腰直角三角形,根据已知条件可得CE 得长,进而得出ED 的长,再根据勾股定理可得出B D ';1.(2022·江苏苏州·二模)如图把一张矩形纸片ABCD 沿对角线AC 翻折,点B 的对应点为B ′,AB ′与DC 相交于点E ,则下列结论一定正确的是( )A .BC =12ACB .AE =CEC .AD =DE D .∠DAE =∠CAB2.(2022·江苏南京·二模)如图,矩形ABCO ,点A 、C 在坐标轴上,点B 的坐标为()2,4-.将△ABC 沿AC 翻折,得到△ADC ,则点D 的坐标是( )A.612,55⎛⎫⎪⎝⎭B.65,52⎛⎫⎪⎝⎭C.312,25⎛⎫⎪⎝⎭D.35,22⎛⎫⎪⎝⎭3.(2022·江苏泰州·一模)如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平后再次折叠,使点A落在EF上的点A′处,得到折痕BM,BM与EF相交于点N.若直线BA′交直线CD于点O,BC=11,EN=2,则FO的长为()A B C D4.(2022·江苏宿迁·三模)已知长方形纸条ABCD,点E、G在AD边上,点F、H在BC边上.将纸条分别沿着EF、GH折叠,如图,当DC恰好落在EA'上时,1∠与2∠的数量关系是()A.12135∠+∠=︒B.2115∠-∠=︒C.1290∠+∠=︒D.22190∠-∠=︒5.(2022·江苏苏州·二模)如图①,②,③,④,两次折叠等腰三角形纸片ABC,先使AB与AC重合,折痕为AD,展平纸片:再使点A与点C重合,折痕为EF,展平纸片,AD、EF交于点G.若5cmAB AC==,6cmBC,则DG的长为()A.3cm4B.7cm8C.1cm D.7cm66.(2022·江苏·苏州中学二模)如图,菱形ABCD中,点E在AD上,将△ABE沿着BE翻折,点A恰好落在CD上的点F处.若∠A=65°,则∠DFE的度数为()A.85︒B.82.5︒C.65︒D.50︒7.(2022·江苏扬州·二模)如图,在矩形ABCD中,2AB=,BC=E是BC的中点,将ABE△沿直线AE翻折,点B落在点F处,连结CF,则tan ECF∠的值为()A B C.23D8.(2022·江苏苏州·模拟)如图,在矩形ABCD中,点E在DC上,将矩形沿AE折叠,使点D落在BC 边上的点F处,若3AB=,5BC=,则tan FEC∠的值为().A.12B.35C.34D.459.(2022·江苏苏州·一模)如图,在平面直角坐标系中,O为坐标原点,平行四边形ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限,将△AOD沿y轴翻折,使点A落在x轴上的点E处、点B恰好为OE的中点.DE与BC交于点F.若y=kx(k≠0)图象经过点C.且S△BEF=1,则k的值为()A.18B.20C.24D.2810.(2022·江苏·江阴市第一初级中学一模)如图,把三角形纸片ABC沿DE折叠,当点A落在四边形BCDE外部时,则∠A与∠1、∠2之间的数量关系是()A.2∠A=∠1-∠2B.3∠A=2(∠1-∠2)C.3∠A=2∠1-∠2D.∠A=∠1-∠211.(2022·江苏·无锡市天一实验学校二模)已知:如图,在Rt△ABC中,∠A=90°,AB=8,tan∠ABC=32,点N是边AC的中点,点M是射线BC上的一动点(不与B,C重合),连接MN,将△CMN沿MN 翻折得△EMN,连接BE,CE,当线段BE的长取最大值时,sin∠NCE的值为()A B C D12.(2022·江苏省南菁高级中学实验学校九年级)如图,在ABC 中,点D 是线段AB 上的一点,过点D 作DE ∥AC 交BC 于点E ,将BDE 沿DE 翻折,得到B DE ',若点C 恰好在线段B D '上,若90BCD ∠=︒,DC :3CB '=:2,AB =CE 的长度为( )A.B C .D 13.(2022·江苏·九年级专题练习)如图,在△ABC 中,90ACB ∠=,点D 是AB 的中点,将△ACD 沿CD 对折得△A ′CD .连接BA ',连接AA ′交CD 于点E ,若14cm AB =,4cm BA '=,则CE 的长为( )A .4cmB .5cmC .6cmD .7cm14.(2022·江苏·宜兴市树人中学九年级)如图,在△ABC 中,点D 是线段AB 上的一点,过点D 作DE ∥AC 交BC 于点E ,将△BDE 沿翻折,得到△B 'DE ,若点C 恰好在线段B 'D 上,若∠BCD =90°,DC :CB '=3:2,AB =CE 的长度为( )A.B .4C .D .615.(2022·江苏·九年级专题练习)如图①,AB =5,射线AM ∥BN ,点C 在射线BN 上,将△ABC 沿AC 所在直线翻折,点B 的对应点D 落在射线BN 上,点P ,Q 分别在射线AM 、BN 上,PQ ∥AB .设AP =x ,QD =y .若y 关于x 的函数图象(如图②)经过点E (9,2),则cos B 的值等于( )A.25B.12C.35D.71016.(2022·江苏·苏州市吴江区铜罗中学九年级期中)如图,在△ABC中,D是AC边上的中点,连接BD,把△BDC沿BD翻折,得到△BDC′,DC'与AB交于点E,连接AC′,若AD=AC′=2,BD=3,则点D到BC的距离为()A B C D17.(2022·江苏南通·九年级)如图,AB为⊙O的一条弦,C为⊙O上一点,OC∥AB.将劣弧AB沿弦AB 翻折,交翻折后的弧AB交AC于点D.若D为翻折后弧AB的中点,则∠ABC=()A.110°B.112.5°C.115°D.117.5°18.(2022·江苏南京·九年级专题练习)如图,在矩形纸片ABCD中,点E、F分别在矩形的边AB、AD 上,将矩形纸片沿CE、CF折叠,点B落在H处,点D落在G处,点C、H、G恰好在同一直线上,若AB=6,AD=4,BE=2,则DF的长是()A .2B .74C D .319.(2022·江苏·宿迁青华中学九年级期末)如图,四边形ABCD 内接于O ,AB AD =,3BC =.劣弧BC 沿弦BC 翻折,刚好经过圆心O .当对角线BD 最大时,则弦AB 的长为( )A B .C .32D .【选择题】必考重点03 几何变换之翻折问题几何变换中的折叠问题,是江苏各地中考中常考的题型,难度多为一般或者较难。
矩形的翻折问题

是.Leabharlann 12 或2712..如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰 好落在AC上.设F、H分别是B、D落在AC上的点,E、G分别 是折痕CE与AB、AG与CD的交点. (1)试说明四边形AECG的形状,并说明理由; (2)若矩形的边AD=3cm,AB=4cm,求△AGC的面积; (3)当四边形AECG是菱形时,求∠AGC的度数。
答案3
10.(09内江)如图12所示,将△ABC沿着DE翻折,若∠1+
∠2 =800,则∠B= 答案400
11.(09德州) 将三角形纸片(△ABC)按如图14所示的方式折叠,使
点B落在边AC上,记为点B/,折痕为EF.已知AB = AC=3,BC=4,
若以点B/,F,C为顶点的三角形与△ABC相似,那么BF的长度
若∠A=75°,则∠1+∠2=
(A)
A.150° B.210° C.105° D.75°
8.(2008·郴州)如图1所示,D是AB边上的中点,将△ABC沿
过D的直线折叠,使点A落在BC上的F处,若DE为折痕,∠B
=500,则∠BDF =
( 800 )
9.(09河北) 如图8,等边△ABC的边长为1 cm,D、E分别是AB、AC 上的点,将△ADE沿直线DE折叠,点A落在点A/处,且点A/在 △ABC外部,则阴影部分图形的周长为 cm.
3
6.(2012上海)如图,在Rt△ABC中,∠C=900,∠A=300,BC=1, 点D在AC上,将△ADB沿直线BD翻折后,将点A落在点E处,如
果AD⊥ED,那么线段DE的长为
.
7.(2012•梅州)如图,在折纸活动中,小明制作了一张△ABC纸片,
点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,
高中教案:高考数学难点突破八立体几何中的翻折问题

高考数学难点突破八----立体几何中的翻折问题一、知识储备翻折问题就是把平面图形经过折叠变成一个空间图形,实际上,折叠问题就是轴对称的问题,折痕就是对称轴,重合的即是全等图形,解决折叠问题时,要把运动着的空间图形不断地与原平面图形进行对照,看清楚其中哪些量在变化,哪些量没有变化,从而寻找出解决问题的方法,达到空间问题与平面问题相互转化的目的。
核心是抓牢折痕就是翻折前与翻折后平面图形的公共底边,折痕与公共底边上两高所在平面垂直。
二、应用举例例1.如图,在矩形ABCD 中,M 在线段AB 上,且1AM AD ==,3AB =,将ADM ∆沿DM 翻折.在翻折过程中,记二面角A BC D --的平面角为θ,则tan θ的最大值为(C )ABCD例2.在矩形ABCD 中,4,3AB AD ==,E 为边AD 上的一点,1DE =,现将ABE ∆沿直线BE 折成A BE '∆,使得点A '在平面 BCDE 上的射影在四边形BCDE 内(不含边界),设二面角 A BE C '--的大小为θ,直线,A B A C ''与平面BCDE 所成的角分 别为αβ,,则( D ) A.βαθ<< B.βθα<< C.αθβ<< D.αβθ<<例3.如图,矩形ABCD 中心为, O BC AB >,现将DAC 沿着对角线AC 翻折成EAC ,记BOE a ∠=,二面角B AC E --的平面角为β,直线DE 和BC 所成角为γ,则( D )A. ,2a ββγ>>B. ,2a ββγ><C. ,2a ββγ<>D. ,2a ββγ<<例4.如图,在ABC △中,1AB =,22BC =,4B π=,将ABC △绕边AB 翻转至ABP △,使面ABP ⊥面ABC ,D 是BC 中点,设Q 是线段PA 上的动点,则当PC 与DQ 所成角取得最小值时,线段AQ 的长度为( B ) A .52B .255C .355D .253例5.已知在矩形ABCD 中,2AD AB =,沿直线BD 将ABD ∆ 折成'A BD ∆,使得点'A 在平面BCD 上的射影在BCD ∆内(不含边界),设二面角'A BD C --的大小为θ,直线','A D A C 与平面BCD 所成的角分别为,αβ,则( )A. αθβ<<B. βθα<<C. βαθ<<D. αβθ<< 【答案】DQ DPCBA【解析】分析:由题意画出图形,由两种特殊位置得到点A′在平面BCD上的射影的情况,由线段的长度关系可得三个角的正弦的大小,则答案可求.详解:如图,∵四边形ABCD为矩形,∴BA′⊥A′D,当A′点在底面上的射影O落在BC上时,有平面A′BC⊥底面BCD,又DC⊥BC,可得DC⊥平面A′BC,则DC⊥BA′,∴BA′⊥平面A′DC,在Rt△BA′C中,设BA′=1,则,∴A′C=1,说明O为当A′点在底面上的射影E落在BD上时,可知A′E⊥BD,设BA′=1,则A D'=,要使点A′在平面BCD上的射影F在△BCD内(不含边界),则点A′的射影F落在线段OE上(不含端点).可知∠A′EF为二面角A′﹣BD﹣C的平面角θ,直线A′D与平面BCD所成的角为∠A′DF=α,直线A′C与平面BCD所成的角为∠A′CF=β,<,而A′C的最小值为1,可求得DF>CF,∴A′C<A′D,且A′E=13∴sin∠A′DF<sin∠A′CF<sin∠A′EO,则α<β<θ.故答案为:D点睛:本题主要考查二面角的平面角和直线与平面所成的角,考查正弦函数的单调性,意在考查学生对这些基础知识的掌握能力和空间想象能力分析推理能力.例6、(嘉兴市2020年1月期终)已知矩形ABCD ,4AB =,2BC =,E 、F 分别为AB 、CD 的中点,沿直线DE 将ADE △翻折成PDE △,在点P 从A 至F 的运动过程中,CP 的中点G 的轨迹长度为 .22π分析:设 AC ,FC 的中点为 M , N ,CP 的中点G 的轨迹是以 MN 为直径的半圆.例7、(宁波市2020年1月期终)已知平面四边形ABCD 中,90A C ∠=∠=︒,BC CD =,AB AD >,现将ABD △沿对角线BD 翻折得到三棱锥A BCD '-,在此过程中,二面角A BC D '--、A CDB '--的大小分别为α,β,直线A B '与平面BCD 所成角为γ,直线A D '与平面BCD 所成角为δ,则( )A .γδβ<<B .γαβ<<C .αδβ<<D .γαδ<<例8、(柯桥一中2020年1月期终)已知在矩形ABCD 中,2AB =,4AD =,E ,F 分别在边AD ,BC 上,且1AE =,3BF =,如图所示, 沿EF 将四边形AEFB 翻折成A EFB '',则在翻折过程中,二面角B CD E '--的大小为θ,则tan θ的最大值为( C ) A.5B.5C.4例9、(名校合作体2020年3月)已知C 为ABD Rt ∆斜边BD 上一点,且ACD ∆为等边三角形,现将ABC ∆沿AC 翻折至C B A '∆,若在三棱锥ACD B -'中,直线B C '和直线B A '与平面ACD 所成角分别为βα,,则( )A. βα<<0B.βαβ2≤<C.βαβ32≤≤例10、(2020年1月嘉兴期终)已知矩形ABCD ,4AB =,2BC =,E 、F 分别为AB 、CD 的中点,沿直线DE 将ADE △翻折成PDE △,在点P 从A 至F 的运动过程中,CP 的中点G 的轨迹长度为 .分析:取DE 中点O ,连CO PO ,,则点G 的轨迹是以CO 的中点为圆心,2221=PO 为半径的半圆,轨迹长为22ππ=r例11、(2020年4月温州模拟)如图,在ABC ∆中,点M 是边BC 的中点,将ABN ∆沿着AM 翻折成M B A '∆,且点B '不在平面AMC 内,点P 是线段C B '上一点,若二面角B AM P '--与二面角C AM P --的平面角相等,则直线AP 经过C B A '∆的( A ) A. 重心 B. 垂心 C. 内心 D.外心G PFD B A例12、(2020年嘉兴一模)将边长为1的正方形ABCD 沿对角线BD 翻折,使得二面角A BD C --的平面角的大小为π3,若点E ,F 分别是线段AC 和BD 上的动点,则BE CF 的取值范围为 ( )A .[1,0]-B .1[1,]4-C .1[,0]2-D . 11[,]24-例13、(2020年5月暨阳联考)如图:ABC ∆中,︒=∠⊥90,ACB BC AB ,D 为AC 的中点,ABD ∆沿BD 边翻折过程中,直线AB 与BC 直线所成的最大角,最小角分别记为11βα,,直线AD 与直线BC 所成的最大角,最小角分别记为22βα,,则有( D )A. ββαα≤<121,B. 2121ββαα><,C. 2121ββαα≤≥,D.2121ββαα>≥,分析一:翻折到180时,,AB BC 所成角最小,可知130β=,,AD BC 所成角最小,20β=,翻折0时,,AB BC 所成角最大,可知190α=,翻折过程中,可知AD 的投影可与BC 垂直,所以,AD BC 所成最大角290α=,所以 1190,30αβ︒︒==,2290,0αβ︒︒==分析二:对角线向量定理例14、(2020年4月台州二模)如下图①,在直角梯形ABCD 中,90=∠=∠=∠DAB CDB ABC , 30=∠BCD ,4=BC ,点E 在线段CD 上运动,如下图②,沿BE 将BEC ∆折至C BE '∆,使得平面⊥'C BE 平面ABED ,则C A '的最小值为 .⇒例15、(2020年嘉兴市基础知识测试)如图,矩形ABCD 中,2,1==BC AB ,点E 为AD 中点,将ABE ∆沿BE 折起,在翻折过程中,记二面角B DC A --的平面角大小为α,则当α最大时,=αtan ( ) A. 22 B. 32 C. 31 D.21例16、(2020学年温州中学高二上期中)等边三角形ABC 边长为4,N M ,为AC AB ,的中点,沿MN 将AMN ∆折起,当直线AB 与平面BCMN 所成的角最大时,线段AB 的长度为( )A.6B. 22C. 10D.32例17、(2020学年杭外高二上期中)如图,在菱形ABCD 中,︒=∠60BAD ,线段AD ,BD 的中点分别为E ,F ,现将ABD ∆沿对角线BD 翻折,则异面直线BE 与CF 所成的角的取值范围是( )A.),(36ππ B.⎥⎦⎤26ππ,( C. ⎥⎦⎤ ⎝⎛2,3ππ, D.⎪⎭⎫⎝⎛323ππ,例18、(2020学年杭四中高二上期中)如图,矩形ABCD 中,AD AB 2=,E 为边AB 的中点,将ADE ∆沿直线DE 翻折成DE A 1∆,若M 为线段C A 1的中点,则在ADE ∆翻折过程中,下面四个选项中正确的是 (填写所有的正确选项).(1)BM 是定值;(2)点M 在某个球面上运动;(3)存在某个位置,使C A DE 1⊥;(4)存在某个位置,使//MB 平面DE A 1.例19、(2020学年杭师大附中高二上期中)如图,在矩形ABCD 中,6=AB ,4=BC ,E 为DC 边的中点,沿AE 将ADE ∆折起至E D A '∆,设二面角B AE D --'为α,直线D A '与平面ABCE 所成角为β,若︒︒<<9060α,则在翻折过程中( )A. 存在某个位置,使得βα<B. 存在某个位置,使得︒<+90βαB. ︒>45β D.︒︒<<4530β例20、(2020学年台州市高二上期终)如图,在ABC ∆,1=AC ,3=BC ,2π=C ,点D 是边AB (端点除外)上的一动点,若将ACD ∆沿直线CD 翻折,能使点A 在平面BCD内的射影A '落在BCD ∆的内部(不包括边界)且37='C A ,设t AD =,则t 的取值范围是 .例21、(2020学年杭州七县市高二上期末)如图,正方形ABCD 的边长为4,点F E ,分别是BC AB ,的中点,将DAE ∆,EBF ∆,FCD ∆分别沿DE ,EF ,FD 折起,使得A ,B ,C 三点重合于点A ',若点G 及四面体DEF A -'的四个顶点都在同一个球面上,则以DEF ∆为底面的三棱锥DEF G -的高h 的最大值是( ) 326+ B. 346+ C.3462- D.3262-例22、(2020学年慈溪市高二上期终)如图,三棱锥BCD A -的底面BCD 在平面α内,所有棱均相等,E 是棱AC 的中点,若三棱锥BCD A -绕棱CD 旋转,设直线BE 与平面α所成角为θ,则θcos 的取值范围为( )A.⎥⎦⎤⎢⎣⎡163,B. ⎥⎦⎤⎢⎣⎡1,65 C.⎥⎦⎤⎢⎣⎡6110, D.⎥⎦⎤⎢⎣⎡6330,例23、(2021年2月“日知”新高考命题研究联盟高三期终)如图所示,正方形ABCD ,ADEF ,AFGH 平铺在水平面上,先将矩形EDHG 沿AD 折起,使二面角BAD E --'为︒30,再将正方形H G F A ''沿F A '折起,使二面角D F A H -'-'为︒30,则平面H G F A '''与平面ABCD 所成的锐二面角的正切值是( ) A.42 B.37 C.43 D.26例24、(2021年2月丽水中学合作校高三联考卷)如图,在ABC ∆中,MC BM 21=,1==AC AB ,32=BM ,点D 在线段BM 上运动,沿AD 将ADB ∆折到B AD '∆,使得二面角C AD B --'的度数为︒60,若点B '在平面ABC 内的射影为O ,则OC 的最小值为 .例25、(2021年4月杭州二模第10题)如图,在长方体ABCD 中,215=AB ,1=AD ,点E 在线段AB (端点除外)上,现将ADE ∆沿DE 折起为DE A '∆,设α=∠ADE ,二面角C DE A --'的大小为β,若2πβα=+,则四棱锥BCDE A -'体积的最大值为( )A.41 B.32 C. 121-15 D. 81-5例26、(2020学年之江教育联盟高二下开学考)如图,已知椭圆的长轴端点为21,A A ,短轴端点为21,B B ,焦点为21,F F ,长半轴为2,短半轴为3,将左边半个椭圆沿短轴进行翻折,则在翻折过程中,以下说法错误的是( )A. 12F B 与短轴21B B 所成角为6π B. 12F B 与直线22F A 所成角的取值范围为⎥⎦⎤⎢⎣⎡23ππ,C. 12F A 与平面212B B A 所成角的最大值为6πD. 存在某个位置,使得12F B 与21F B 垂直例27、(2021年5月义务高三适应性考试第10题)如图,在等边三角形ABC 中,点ED 、分别是线段AC AB ,上异于端点的动点,且CE BD =,现将三角形ADE 沿直线DE 折起,使平面⊥ADE 平面BCED ,D 从B 滑动到A 的过程中(D 与A B ,均不重合),则下列选项中错误的是( )A. ADB ∠的大小不会发生变化B. 二面角C BD A --的平面角的大小不会发生变化C.BD 与平面ABC 所成的角变大D.AB 与DE 所成的角先变小后变大例28、(2020年4月嘉兴二模第9题)如图,矩形ABCD 中,已知2=AB ,4=BC ,E 为AD 的中点,将ABE ∆沿着BE 向上翻折至BE A '∆,记锐二面角C BE A --'的平面角为α,B A '与平面BCDE 所成的角为β,则下列结论不可能成立的是( )A. βαsin 2sin =B.βαcos cos 2=C.βα2<D. 4πβα>-例29、(2020学年温州十校联盟高二下期终)如图,在等腰三角形ABC 中,2=BC ,︒=∠90C ,D ,E 分别是线段AB ,AC 上异于端点的动点,且BC DE //,先将ADE ∆沿直线DE 折起至DE A ',使平面⊥'DE A 平面BCED ,当D 从B 滑动到A 的过程中,下列选项错误的是( )A. DE A '∠的大小不会发生变化B. 二面角C BD A --'的平面角的大小不会发生变化C. 三棱锥EBC A -'的体积先变大在变小D. B A '与DE 所成的角先变大再变小例30、(2020学年浙南名校联盟高二下期终第17题)如图,在矩形ABCD 中,a AB =,a BC 2=,点E 为AD 的中点,将ABE ∆沿BE 翻折到BE A '∆的位置,在翻折过程中,A '不在平面BCDE 内时,记二面角B DC A --'的平面角为α,则当α最大时,αcos 的值为 .。
《勾股定理》模型(二)——矩形翻折模型

《勾股定理》模型(二)——矩形翻折模型模型讲解一、折在外【结论1】如图,将矩形ABCD沿EF折叠,使点B和点D重合,则(1)∠1=∠2=∠3(2)DE=DF=BE,(3)FC=FH【证明】如图,将矩形ABCD沿EF折叠,点B与点D重合,∴∠1=∠2,DE=BE, FC=FH∵四边形ABCD是矩形,∴AB∥CD,∴∠2=∠3,∴∠1=∠2=∠3 ,∴DE=DF,∴DE=DF=BE【结论2】如图,矩形ABCD,将△ACD沿对角线AC折叠,D点对应点为F 则(1)△AFE≌△CBE(2)AE=CE(3)∠EAC=∠ECA【证明】如图,△ACF由△ACD沿AC折叠而得,∴∠F=∠D=90º,AF=AD,∵四边形ABCD是矩形,∴∠B=∠F=∠D=90º,CB=AD=AF,AB∥CD,在△AFE和△CBE中,∠F=∠B=90º,AF=CB,∠FEA=∠BEC,∴△AFE≌△CBE∴AE=CE ,∴∠EAC=∠ECA二、折在里【结论3】如图,矩形ABCD,将△AFD沿AF折叠,使点D的落点(E)在对角线AC上,则CE=AC -AD,CF=CD-EF【证明】∵△AFD沿AF折叠得△AFE,∴△AFD≌△AFE∴AE=AD,EF=DF,∴CE=AC-AD=AC-AE,CF=CD-DF=CD-EF【结论4】如图,将矩形ABCD对折,折痕EF,再将△ADH沿AH折叠,使点G落在EF上,则(1)AG=2AE(2)∠1=∠2=∠3=30°【证明】∵△ADH 沿AH 折叠得△AGH ,E 是AD 的中点,∴AG =AD =2AE ,∠1=∠2,在Rt △AEG 中,AG =2AE ,∴Rt △AEG 是含30º角的直角三角形∴∠3=∠1=∠2=30º.典例1☆☆☆☆☆如图所示,沿着AE 折叠长方形,使点D 落在边BC 上的点F 处,已知AB=8cm ,BC=10cm ,则 EC 的长为() A.3 cmB. 4 cmC.5 cm D.6 cm【答案】A【解析】根据折叠的性质得△ADE ≌△AFE ,∴AF=AD=10 cm,EF=DE,∴BF =22AB AF =6(cm ). ∴CF =BC -BF =10-6=4(cm).设EC =x cm ,则 EF =(8-x )cm.在Rt △EFC 中,CF ²+CE2=EF2,即42+x2=(8-x )2解得 x =3.∴EC 的长为 3 cm.故选 A.典例2 ☆☆☆☆☆如图所示,在矩形纸片ABCD 中,AB= 6 cm ,BC=8 cm ,现将其沿 EF 对折,使得点C 与点A 重合,则 AF 的长为( ).典例秒杀A.825cmB.425cmC.225cmD.8 cm【答案】B【解析】设 AF =x cm ,则 DF =(8-x )cm.在矩形纸片ABCD 中,AB=6cm ,BC=8 cm ,将其沿EF 折叠后,点C 与点A 重合,DF=D ´F.在 Rt △AD ´F 中,AF2=AD ´2+D ´F2,即 2²=6²+(8-x )2,解得 x =425,∴AF =425cm,故选B典例3 ☆☆☆☆☆如图,将矩形纸片 ABCD 沿直线 EF 折叠,使点 C 落在 AD 边的中点 C ´处,点 B 落在点B ´处,其中 AB=9,BC=6,则 FC ´的长为()A.310B.4C.4.5D.5【答案】D【解析】由题意,设 FC =FC ´=x ,则 FD =9-x.∵BC =6,四边形 ABCD 为矩形,点 C ´为AD 的中点,∴AD=BC=6,C ´D=3.在 Rt △FC ´D 中,FC ´2=FD2+C ´D2,即x2=(9-x )2+32,解得 x=5.故 FC ´的长为 5.故选 D.1.(★★★☆☆)如图,已知矩形 ABCD 沿着直线 BD 折叠,使点C 落在C ´处,BC ´交AD 于点E ,AD=8,AB=4,则 DE 的长为( ). 小试牛刀A.3B.4C.5D.62.(★★★☆☆)如图,将矩形ABCD沿EF折叠,使点D与点B重合.已知AB=3,AD=9,则折痕EF 的长为().A.3B.10C.5D.4直击中考1.如图,将长方形ABCD沿EF 折叠,使顶点C恰好落在AB 边的中点C´上.若AB=6,BC=9,则BF 的长为()A.4B.32C.4.5D.52.如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE 折叠,点C恰好落在AD边上的点F处,则CE的长为_________.矩形的折叠,注意折叠前后的边角对应关系,计算时联想到利用勾股定理对新形成的直角三角形进行求解。
矩形的五种折叠方法

矩形的五种折叠方法折叠问题的实质是轴对称问题,折叠原理实际上是图形的全等问题,对应角相等,对应线段相等。
对应点的连线被折痕垂直平分。
矩形在日常生活中随处可见,矩形的性质又具有平行四边形的所有性质,并且具有对角线互相平分且相等的特有性质,它不仅是中心对称图形,而且还是轴对称图形.所以矩形的折叠问题是中考热点问题,并且折叠的方法不同,问题不同,给参加中考的考生带来各种各样的困境,为了让参加中考的孩子们轻松应考,先把矩形的折叠问题进行总结一下.一.沿对角线折叠例1.在平面直角坐标系中,矩形OABC的两边OA、OC分别落在x轴,y轴上,且OA=4,0C=3。
如图,将△OAB沿对角线OB翻折得到△OBN,ON与AB交于点M。
(1)判断△OBM是什么三角形,并说明理由,并求出△OBM的面积(2)求MN的长.【分析】由矩形性质可知,AB=OC=3,BC=OA=4,∠COA=∠OAB=90°OA∥BC 所以∠AOB=∠MBO根据折叠原理得∠AOB=∠MOB,所以∠MBO=∠MOB,∴MB=MO所以△OBM是等腰三角形,二.折一角,使直角顶点到对边例2.如图,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A 在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC =4.在OC 边上取一点D ,将纸片沿AD 翻折,使点O 落在BC 边上的点E 处.则点D 的坐标是 .【分析】折叠原理知,AE=AO=5,AB=OC=4,OD=ED 由勾股先求得BE=3,∴CE=2,然后设OD=x ,则CD=4-x在Rt △DCE 中由勾股定理即可求得OD 的长,然后就得到点D 的坐标。
练习:如图,折叠矩形的一边AD ,点D 落在BC 边上点F 处,已知AB=8,BC=10,则EC 的长是 。
(这道题目先求BF 的长,再求CF 的长,然后再勾股定理)练习2.如图,矩形纸片ABCD ,若把△ABE 沿折痕BE 上折叠,使A 点恰好落在CD 上,此时,AE:ED=5:3,BE=55,求矩形的长和宽。
八年级下册数学矩形翻折专题
矩形翻折专题
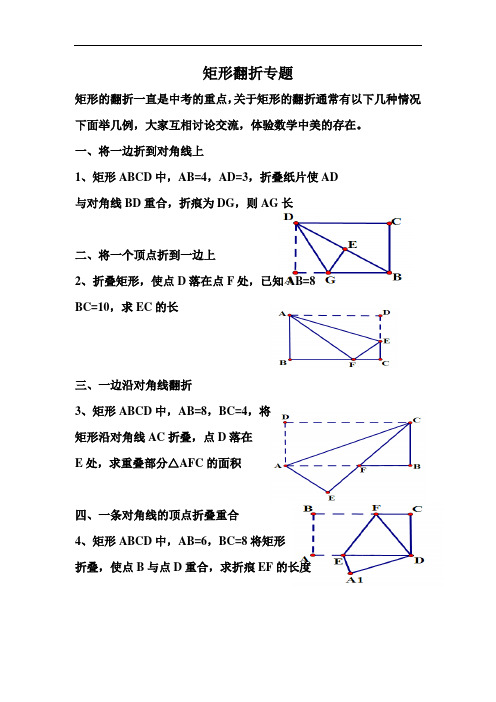
矩形的翻折一直是中考的重点,关于矩形的翻折通常有以下几种情况下面举几例,大家互相讨论交流,体验数学中美的存在。
一、将一边折到对角线上
1、矩形ABCD中,AB=4,AD=3,折叠纸片使AD
与对角线BD重合,折痕为DG,则AG长
二、将一个顶点折到一边上
2、折叠矩形,使点D落在点F处,已知AB=8
BC=10,求EC的长
三、一边沿对角线翻折
3、矩形ABCD中,AB=8,BC=4,将
矩形沿对角线AC折叠,点D落在
E处,求重叠部分△AFC的面积
四、一条对角线的顶点折叠重合
4、矩形ABCD中,AB=6,BC=8将矩形
折叠,使点B与点D重合,求折痕EF的长度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E
B
F
A
关于矩形中翻折问题 一、预习交流:
1、已知:如图在Rt △ABC 中,AC=6,CB=8,则AB= 若CD 长为x ,则BD= (用含x 的代数式表示),如果AC 所在的直角边沿AD 折叠,使AC 落在斜边上,且点C 与点E 重合, ≌ ;求CD 的长
1题
二、互助探究(矩形中的折叠问题) 1.动手折矩形(按要求) 2.动手画一画 3.动脑比一比
若AD=4,AB=8求AE 的长?(写过程)
C'
F
E
D
C
B
A
三、巩固练习 1.如图,在矩形ABCD 中,将AD 边沿AE 折叠,使点D 落在BC 边上的点F 处 (1) 若AB=3,AD=5,求线段CE 的长 四、拓展提高
矩形OABC ,OA=4,OC=3,
将△OAB 沿对角线OB 翻折得到△OBN ,ON 与BC 交于点M ,求线段MN 的长
N
B
五.课堂小结:谈谈你的收获
六.课堂检测 1、已知:如图,将矩形纸片ABCD 折叠,使点D 与点B 重合,点C 落在点C ’处,折痕为EF ,若∠ABE=20°,则 ∠FED= ,∠EFC ’= ,∠C ’FB=
2、把一张矩形纸片ABCD 沿BD 对折,使C 点落在E 处,BE 与AD 相交于O ,若AB=4,BC=8,求OE 的长。
3、如图,将矩形ABCD 纸片沿EF 折叠,使点D 与BC 边的D ’重合,若BC=8,BD ’=5,CD=6,求线段CF 长。
