机械振动理论基础及其应用作业
机械振动理论基础及其应用

旋转机械振动与故障诊断研究综述1.前言工业生产离不开回转机械,随着装置规模不断扩大,越来越多的高速回转机械应用于工业生产,诸如高速离心压缩机、汽轮机发电机组。
动态失稳造成的重大恶性事故屡见不鲜。
急剧上升的振动可在几十秒之内造成机组解体,甚至祸及厂房,造成巨大的经济损失和人员伤亡。
此外,机械振动可能降低设备机械性能,加速机械零部件的磨损,发出的噪声损害操作者的健康。
但是振动也能合理运用,如工业上常用的振动筛、振动破碎等都是振动的有效利用。
工程技术人员必须认真对待机械振动问题,当机组产生有害的振动时,及时分析原因,坚持用合理的振动测试标准,采取科学的防治措施。
2.旋转机械振动标准●旋转机械分类:Ⅰ类:为固定的小机器或固定在整机上的小电机,功率小于15KW。
Ⅱ类:为没有专用基础的中型机器,功率为15~75KW。
刚性安装在专用基础上功率小于300KW的机器。
Ⅲ类:为刚性或重型基础上的大型旋转机械,如透平发电机组。
Ⅳ类:为轻型结构基础上的大型旋转机械,如透平发电机组。
●机械振动评价等级:好:振动在良好限值以下,认为振动状态良好。
满意:振动在良好限值和报警值之间,认为机组振动状态是可接受的(合格),可长期运行。
不满意:振动在报警限值和停机限值之间,机组可短期运行,但必须加强监测并采取措施。
不允许:振动超过停机限值,应立即停机。
3.振动产生的原因旋转机械振动的产生主要有以下四个方面原因,转子不平衡,共振,转子不对中和机械故障。
4.旋转机械振动故障诊断4.1转子不平衡振动的故障特征当发生不平衡振动时,其故障特征主要表现在如下方面:1 )不平衡故障主要引起转子或轴承径向振动,在转子径向测点上得到的频谱图, 转速频率成分具有突出的峰值。
2 )单纯的不平衡振动,转速频率的高次谐波幅值很低,因此在时域上的波形是一个正弦波。
3 )转子振幅对转速变化很敏感,转速下降,振幅将明显下降。
4 )转子的轴心轨迹基本上为一个圆或椭圆,这意味着置于转轴同一截面上相互垂直的两个探头,其信号相位差接近90°。
振动控制理论及其在工程中的应用

振动控制理论及其在工程中的应用一、引言振动是指由于突然的力量或者频繁的震动导致的物体固有运动。
在实际工程中,振动问题是不可避免的,因此如何有效控制振动成为研究和实践工程的关键问题之一。
振动控制理论作为一门分支学科,已成为日益成熟和重要的领域,它的优化成果和空间变形研究对实际工程问题的解决,具有重要的支撑和指导价值。
二、振动控制理论的概念及其理论基础1、概念振动控制是指以控制理论和控制方法尽量抑制或减小系统振动或使系统保持平衡的控制制度。
2、理论基础振动控制理论本质上是一个多学科的领域,其研究对象包括力学、结构动力学、材料科学、信号处理、数学和控制学等,它综合了这些学科的方法和手段。
因此,振动控制理论的理论基础涵盖了多个学科理论的相关基础,包括控制论、信号处理、机械振动、结构动力学和材料科学中的材料设计理论等。
三、常见的振动控制方法及其应用1、有源振动控制有源振动控制采用控制器来实现力或位移等控制方式,其最大优点是能够通过系统控制实现精确的抑制和减振。
该方法由于其对环境噪声来源有较强的抑制力,因此在某些飞机、汽车、电子设备和地铁等运输工具的控制系统中被广泛应用。
2、无源振动控制无源振动控制是采用材料或结构的特殊设计,通过双层材料或结构的选择、合理的材料叠层方式、结构变形和局部加强等来实现抑制和减振控制。
该方法的优点是控制代价小,控制方式简单,因此在一些无源振动控制设备中得到广泛应用。
3、混合振动控制混合振动控制是将有源振动控制和无源振动控制相结合,以充分利用有源振动控制和无源振动控制的优点,来实现系统的抑制和减振。
该方法应用在飞机、汽车和高铁等控制系统中,具有较好的效果。
四、振动控制的应用示例振动控制的应用以自然灾害和工程领域应用较为广泛。
自然灾害领域,地震的不可预报性和突发性,使地震响应控制成为重要技术。
在工程领域中,如大型建筑、桥梁、塔等建筑结构和机械系统振动等,均需要利用振动控制技术来维护其安全稳定运行。
机械振动的理论与应用

机械振动的理论与应用机械振动是指机械系统在受到外部激励或系统内部某种力的作用下,发生自由或强迫振动的现象。
它是在机械制造、运动控制、结构分析、信号处理、机械故障诊断和振动控制等领域得到广泛应用的重要基础理论。
本文将探讨机械振动的理论与应用,并举例说明其在实际中的应用。
一、机械振动的基本理论机械振动的基本理论包括振动信号的特征、振动系统的描述与分析方法和振动控制的原理等方面。
其中,振动信号的特征指振动信号中包含的振动频率、振幅和相位等特性;振动系统的描述与分析方法主要涉及到质点运动学、动力学和能量守恒原理等;振动控制的原理则是指控制理论中的反馈控制、前馈控制和模糊控制等。
在实际应用中,机械振动的分析和控制都要基于振动系统的模型。
根据振动系统的特点,通常可以将其分为单自由度振动系统和多自由度振动系统两类。
其中,单自由度振动系统是指系统中只有一个自由度方向运动的情况;而多自由度振动系统则是指系统中包含多个自由度运动的情况。
二、机械振动在实际中的应用1.机械制造在机械制造中,机械振动可用于检测机构的不平衡状况、机轴的转子平衡状况、齿轮齿形误差以及机床等制造设备的精度等方面。
例如,通过检测振动信号的频率和振幅来诊断机器设备的运转状态,进而预测其故障情况和损坏的时间,以便及时进行维修和更换。
2.运动控制在运动控制中,机械振动可用于控制机器设备的姿态、位置、速度和加速度等参数。
例如,在航空航天领域中,机械振动可用于控制飞行器的姿态和方向稳定,从而保证其飞行安全和稳定性。
3.结构分析在结构分析中,机械振动可用于评估结构物的稳定性和安全性。
例如,在建筑结构领域中,机械振动可用于评估建筑物的抗震性能,从而为其设计提供依据。
4.信号处理在信号处理中,机械振动可用于处理振动信号的频谱、功率谱、自相关函数和互相关函数等特征参数。
例如,在音乐合成领域中,机械振动可用于模拟和合成各种音效和乐器的声音。
5.机械故障诊断在机械故障诊断中,机械振动可用于检测机器设备的磨损、松动、故障和损坏。
机械振动理论及工程应用

机械振动学学习报告摘要:简述了机械振动学的发展历程,振动利用中的若干新工艺理论与技术,振动机械及其相关技术的应用与发展,介绍了振动在人类生活工作中起到了非常重要的作用。
通过对具体实例——单电机振动给料机的计算分析,得出机械振动对机器工作性能的影响。
并介绍了单自由度、多自由度的线性振动系统振动的基本理论和隔振的基本原理。
关键词:机械振动;振动给料机;线性振动系统Abstract:This paper describes the development course of study of mechanical vibration and the utilization of some new technology theory and technology. The vibration has played a very important role in human life and work. By analyzing the practical example-single motor , vibrating feeder calculation and analysis of mechanical vibration machine has influence on the performance. And introduced the single-degree-of-freedom, multi-freedom system vibration of the linear vibration of the basic theory and the basic principle of vibration isolation.Keywords:Mechanical vibration; Vibrates the feeding machine; Linear vibration system第一章绪论1.1振动振动学的发展振动振动学科是20世纪后半期逐渐形成和发展起来的一门新学科。
振动理论基础

例16-1
质量m=0.5kg的物块,沿光滑斜面无初速滑下,如图所示。 当物块下落高度h=0.1m时撞于无质量的弹簧上并不再分 离。弹簧刚度k=0.8kN/m,倾角β=300,求系统振动的固 有频率和振幅,并写出物块的运动方程。
解:物块在平衡位置时,弹簧静变形
以此位置为原点O,建立图示 坐标。物块受力如图,其运动 微分方程为
1、激振力直接作用下的受迫振动 ★ 振动微分方程 图为受迫振动系统的简化模型。 激振力 其中,H为最大激振力,ω为激振 力的圆频率。 以平衡位置为坐标原点,则 :
令 整理化简后,得单自由度系统受迫振动微分方程的标准形式
★ 微分方程的解
方程的通解由两部分构成:对应的齐次方程的通解和该方程 的一个特解。 上式右端第一项为衰减振动,经过短暂时间,即趋于衰减, 称瞬态响应。最后得到持续的等幅振动,称稳态响应,即系 统的受迫振动 由式可知,受迫振动的频率等于激振力的频率。 将上式代入微分方程式,化简后得到受迫振动的振幅和位相差
距 2l 处有一阻尼器,其阻尼系数为c,A 端有一刚度为k 的弹簧,
并作用一简谐激振力
。刚杆在水平位置平衡,试列
出系统的振动微分方程,并求系统的固有频率ωn,以及当激振 力频率ω 等于ωn 时质点的振幅。
解:取摆角θ为广义坐标,系统平衡位置为坐标原点。 受力如图示。由刚体转动微分方程得
整理后得
令
当
解:取摆角 为广义坐标,设其微振动规律为
圆柱体中心O1的速度 由运动学知,当圆柱体作纯滚动时, 角速度 系统动能
整理后得 系统的势能为重力势能,取圆柱在最低处时的圆心位置C 为 势能零点,则系统势能
圆柱体作微振动
由
3m 4
(R
r
第二章机械振动理论基础

工程中常见的振动问题 A 机械中的振动问题 B 结构中的振动问题 C 机械加工过程中的振动问题
振动诊断,就是对正在运行的机械设备或 给非工作状态的系统某种激励,测其振动响 应,对由测量响应得到的各种数据进行分析处 理,然后将结果与事先制订的某一标准进行比 较。进而判断系统内部结构的破坏、裂纹、开 焊、磨损、松脱及老化等各种影响系统正常运 行的故障。依此采取相应的对策来消除故障, 保证系统安全运行。
第三节 单自由度系统的自由振动
自由振动:就是指系统在初始干扰的作用后,仅靠弹性恢
复力来维持的振动形式。其中,系统中不存在阻尼的叫无阻 尼自由振动,而有阻尼的则称之为有阻尼的自由振动。 一.单自由度系统的无阻尼自由振动 1.直线振动 单自由度系统的无阻尼自由振动的力学模型可用弹簧-质 量系统来描述。
个周期内,摩擦力作功为FA,而在一个整周期内作 功总和为 We=4FA 将其代入式 We ,即可求得干摩擦阻尼的等 Ce 效阻尼系数为 A2
4F Ce A
②流体阻尼的等效粘性阻尼 当物体以较高的 速度在粘性较小的流体(包括空气、液体)中运动 时,物体所受的阻力与速度的平方成正比,即有
Wr Fr xdt Ce A2 2 cos2 (t )dt Ce A2
0 0
T
T
由We=Wr可得,等效粘性阻尼系数为
We Ce A2
① 干摩擦阻尼的等效粘性阻尼 干摩擦力F 一般 可近似认为是一个常力。它在整个强迫振动过程中 大小不变,但方向始终与运动方向相反。即在每1/4
x(t ) xi cos(2 fi t i )
i 1
至少有一组fm /fn为无理数
准周期振动时历曲线及频谱图 a-时历曲线 b-频谱图
机械振动理论基础及其应用(张)

机车传动轴振动分析与仿真优化Vibration Analysis of Commercial VehicleDriveline摘要:机车传动轴的振动及噪声直接影响了整车传动的平稳性与乘坐的舒适性,甚至影响到整车的可靠性。
作为商用车制造厂,必须对传动轴的振动情况进行研究并对传动轴系进行合理的布置与设计,从根本上控制产生振动与噪声的因素。
为了尽快解决某车型传动系振动带来的汽车传动轴中间支承横梁开裂的问题,本文应用了国内外的一些研究成果,从理论和试验两方面分析了某重型机车传动系振动的原因和机理,提出解决措施,并对传动系进行了优化设计。
同时,本文还从系统论的观点出发,对传动系振动问题寻求最优解决方案。
关键词:传动轴系振动分析仿真优化Abstract:The NVH of commercial-vehicle driveline directly affects easiness andsafety of the whole vehicle.In order to reduce the vibration and noise,it isnecessary for the vehicle manufacture to research the NVH of driveline and tocarry out rational layout and design to the driveline which is the fundamentalways of all.In this paper,some research results of the domestic and foreign havebeen applied to analyze the vibration of driveline theoretically andexperimentally.Furthermore,the vehicle chassis intermediate mounting crossmember abruption problem due to the vibration of driveline has been resolvedby optimizing the driveline layout.Based on system theory,this thesis givesout the optimal solution to the driveline vibration. Keywords: Vehicle Drive line;Vibration Analysis;Optimization第一章引言1.1课题背景和实际意义机车是一个复杂的多自由度“质量—刚度—阻尼”振动系统,是由多个具有固有振动特性的子系统组成,如车身的垂直振动、纵向角振动和侧倾振动、发动机曲轴的扭转振动、传动系统的振动等。
机械振动基础习题
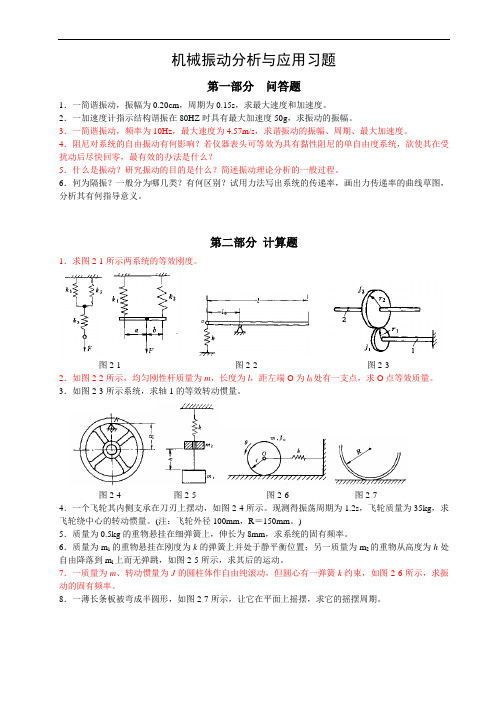
机械振动分析与应用习题第一部分问答题1.一简谐振动,振幅为0.20cm,周期为0.15s,求最大速度和加速度。
2.一加速度计指示结构谐振在80HZ时具有最大加速度50g,求振动的振幅。
3.一简谐振动,频率为10Hz,最大速度为4.57m/s,求谐振动的振幅、周期、最大加速度。
4.阻尼对系统的自由振动有何影响?若仪器表头可等效为具有黏性阻尼的单自由度系统,欲使其在受扰动后尽快回零,最有效的办法是什么?5.什么是振动?研究振动的目的是什么?简述振动理论分析的一般过程。
6.何为隔振?一般分为哪几类?有何区别?试用力法写出系统的传递率,画出力传递率的曲线草图,分析其有何指导意义。
第二部分计算题1.求图2-1所示两系统的等效刚度。
图2-1 图2-2 图2-32.如图2-2所示,均匀刚性杆质量为m,长度为l,距左端O为l0处有一支点,求O点等效质量。
3.如图2-3所示系统,求轴1的等效转动惯量。
图2-4 图2-5 图2-6 图2-74.一个飞轮其内侧支承在刀刃上摆动,如图2-4所示。
现测得振荡周期为1.2s,飞轮质量为35kg,求飞轮绕中心的转动惯量。
(注:飞轮外径100mm,R=150mm。
)5.质量为0.5kg的重物悬挂在细弹簧上,伸长为8mm,求系统的固有频率。
6.质量为m1的重物悬挂在刚度为k的弹簧上并处于静平衡位置;另一质量为m2的重物从高度为h处自由降落到m l上而无弹跳,如图2-5所示,求其后的运动。
7.一质量为m、转动惯量为J的圆柱体作自由纯滚动,但圆心有一弹簧k约束,如图2-6所示,求振动的固有频率。
8.一薄长条板被弯成半圆形,如图2-7所示,让它在平面上摇摆,求它的摇摆周期。
图2-8 图2-99.长度为L 、重量为W 的均匀杆对称地支承在两根细绳上,如图2-8所示。
试建立杆相对于铅垂轴线o-o 的微角度振动方程并确定它的周期。
10.求图2-9所示系统的等效刚度和固有频率。
11.用能量法求图2-10所示均质圆柱体振荡的固有频率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关键词:旋转机械;故障诊断;振动;小波包;信息熵
The Summary of Vibration and Fault Diagnosis for Rotating Machinery Abstract The standards of rotating machinery vibration and reasons were reviewed in summary. Based on the rotating machineries are widespread used in many fields, more and more attentions are drawn by fault diagnosis technology for rotating machinery. Summarize the method of fuzzy diagnosis for fault diagnosis of rotating machinery, the method of wavelet packet analysis used in the signal processing, the information entropy theory and the restrictions of vibration. Keywords: Rotating machinery;fault diagnosis;vibration;wavelet packet; information entropy
4
机械振动理论基础及其应用
旋转机械振动与故障诊断研究综述
承温度升高,以至损坏轴承。 4)支座软弱是描述旋转机械 4 个支脚不在同一平面上的状态术语。旋转机械用螺 栓紧固在这 4 点时, 如果各轴承相互不对中, 必然造成剧烈振动, 甚至会损坏整个设备。 因此, 防止的方法是, 旋转机械安装时, 应该先用适当力矩对称拧紧几个紧固点。 然后, 每次松开一个紧固点, 并用千分表测量该点垂直变形量。 如果垂直变形量大于 0.05mm, 应在此支脚下加垫片,其厚度等于所测的变形量。进行下―个紧固点前,要检查每个点 并再次紧固。重复以上过程,直到松开时每个点垂直变形量小于 0.05mm 为止。 5)旋转机械底座和地基的问题有可能是振动过大的直接原因。如果不消除这类振 动,地脚螺栓可能拉断,地基可能龟裂,转轴不对中,振动将逐渐加大甚至“飞车” 。 因此,旋转机械地脚螺栓必须强度足够,混凝土基础结实无空洞,旋转机械运行中要经 常检査地脚螺栓是否松动、断裂,支脚垫铁是否滑出,发现松动、滑出,必须及时停机 拧紧复位;旋转机械的附属连接设施支承是否牢靠,如,锅炉引风机出口烟道支承是否 脱焊等。
4.旋转机械振动故障诊断
故障是指机器的功能失效, 即其动态性能劣化, 不符合技术要求。 如机械运行失稳, 产生异常振动和噪声, 工作转速、 输出功率发生变化, 介质的温度、 压力、 流量异常等。 机械发生故障的原因不同导致反映出的信息也不一样, 根据这些特有的信息可以对故障 进行诊断。由于旋转机械的结构及零部件设计加工、安装调试、维护检修等方面的原因 和运行操作方面的失误,使得机械在运行过程中会引起振动,其振动类型可分为径向振 动、轴向振动和扭转振动三类,其中过大的径向振动往往是造成机械损坏的主要原因, 也是状态监测的主要参数和进行故障诊断的主要依据。目前,旋转机械应用振动信号进 行故障诊断的方法不仅简单可行,而且经过不断地实践、研究,积累的经验和技术相对 比较成熟。
3.4 机械故障
如质量低劣的联轴器、轴承、润滑不良以及支座不坚固,都是产生不同频率和幅值 的激振力的起因。 1)质量低劣的联轴器主要表现在铸造质量差、连接螺孔偏斜、毛刺,橡皮垫圏很 快损坏,使联轴器由螺孔橡皮垫圈软连接变为金属硬连接,产生振动、磨损。 2)对于径向轴承的更换,用户一般是简单地拿掉磨损轴承,换上新轴承,这样很 容易发生轴承 “跑” 外圈而产生振动。 且高负荷将使轴承迅速损坏, 因此, 换新轴承时, 应对轴承接触是否合适作图色检査,如果接触面积很小,则需处理轴承座。 3)轴向波动是造成旋转机械,包括联轴器、轴承在内的另一振动问题的起因。一 般旋转机械的轴向推力必须靠它的止推轴承来约束。但是,如果旋转机械设备的轴向对 中不良,且转子允许与其轴向止点相接触,则可能会产生剧烈的轴向振动,且伴随着轴
4.2 旋转机械振动模糊诊断 4.2.1 振动模糊诊断基本原理
振动反映了系统状态及变化规律的主要信息, 统计资料表明: 机械设备的故障有 67 % 左右是由于振动引起的,并且能从振动和振动辐射出的噪声反映出来。回转机械的振动 信息尤其明显,且振动诊断具有快速、简便、准确和在线诊断等一系列优点,所以振动 诊断法是旋转机械状态识别和故障诊断的最有效、最常用的方法。 但是,由于机械系统本身的复杂性以及所摄取的振动信号强烈的模糊性,使故障之 间没有清晰的界限, 这时利用传统的振动频谱分析, 对一个故障可能有多个征兆来表现, 一个征兆也可能有多个故障原因的复杂现象,往往难定两者的对应关系进行指导维修。 振动模糊法,将模糊数学与振动诊断相结合,利用模糊综合评判技术,较好地处理了回 转机械故障的不确定性问题。
6
机械振动理论基础及其应用 表 4.2.2.1 幅值频率对表
旋转机械振动与故障诊断研究综述
幅值 频率
F1
0-0.5X
F2
0.5X
F3
0.5-1X
F4
1X
F5
2X
F6
3-5X
F7
3,5,7X
F8
>5X
F9
F10
F11
其中 X 为基频 本系统隶属函数用升半哥西分布,确定如下
0 uF1 2 2 K ( Fi - a) / 1 K ( Fi a)
3.2 共振
它存在于所有机械系统中。系统中的共振频率取决于其自由度数量;共振频率则由
3
机械振动理论基础及其应用
旋转机械振动与故障诊断研究综述
力学量中的质量、刚度和衰减系数决定。旋转机械最佳支承结构共振频率应远离任何激 振频率。 与旋转机械转速相应的共振频率应尽可能避开。对于新装置,可以向旋转机械制造 厂咨询所需地基刚度以达到此目的。对于共振频率与转速相同的现有装置,用户有两种 选择:或者最大限度地减少激振力,或者改变共振频率使其不接近转速。后者可以通过 改变系统刚度和增加系统质量来实现。处理共振问题时,最好改变共振频率,否则振动 问题可能再次发生。 请注意,尽管转速下的共振一般由不平衡引起,它也常常由不对中或机械和电气故 障而引起。转速下谐波下的共振频率也易造成故障。它们也可能由于不对中或机械和电 气故障而诱发。但是,与相同频率下的问题相比这些共振造成的问题并不常见。
旋转机械振动与 故障诊断研究综述
作 者 姓 名 : 班 学 级 : 号 :
东北大学 2012 年 5 月
机械振动理论基础及其应用
摘要
旋转机械振动与故障诊断研究综述
摘 要
对旋转机械振动标准以及产生的原因进行了综述, 基于旋转机械在各行业的广泛应 用,旋转机械的故障诊断技术也倍受重视。综述了旋转机械故障诊断的模糊诊断法,信 号的处理方法中的小波包分析法,信息熵理论以及振动的防治。
3.3 不对中
它可能在转速和两倍转速下造成径向和轴向的激振力。 但是绝不能因为没有上述现 象中的一种或两种而断定不存在对中问题。 各种手册和教科书中已介绍了大量的实用的 对中技术,这些技术对于旋转机械及其所驱动的设备均可适用。同时,还应该特别注意 考虑旋转机械及其所驱动的设备的热膨胀;对用螺栓联结的靠背轮联轴器,二联轴节之 间一定要留有间隙, 根据旋转机械设备的安装使用说明书和安装图, 一般为 1.5〜3mm。
4.2.2 旋转机械振动模糊诊断法的实现
隶属函数的确定 回转机械的能量在频谱图中主要集中于倍频和工倍的分数倍频带内, 故可将频谱图 中的各部分能量分布的变化作为衡量机器振动状态的基础, 通过模糊识别技术观察状态 变化的相关性来反映机械故障的特征。为了体现故障的特征,对于小于 0.5 倍频部分选 最大的幅值为 F1 ;0.5 倍频部分的幅值为 F2 ;…… F9 为滚动轴承内圈的固有频率处的幅 值; F10 为外圈的固有频率的幅值; F11 为钢球固有频率的幅值,如表 4.2.2.1 所示。
2.旋转机械振动标准
旋转机械分类: Ⅰ类:为固定的小机器或固定在整机上的小电机,功率小于 15KW。 Ⅱ类:为没有专用基础的中型机器,功率为 15~75KW。刚性安装在专用基础上功率 小于 300KW 的机器。 Ⅲ类:为刚性或重型基础上的大型旋转机械,如透平发电机组。 Ⅳ类:为轻型结构基础上的大型旋转机械,如透平发电机组。 机械振动评价等级: 好:振动在良好限值以下,认为振动状态良好。 满意:振动在良好限值和报警值之间,认为机组振动状态是可接受的(合格) ,可长 期运行。 不满意:振动在报警限值和停机限值之间,机组可短期运行,但必须加强监测并采 取措施。 不允许:振动超过停机限值,应立即停机。
1
机械振动理论基础及其应用
旋转机械振动与故障诊断研究综述
1.前言
工业生产离不开回转机械,随着装置规模不断扩大,越来越多的高速回转机械应用 于工业生产,诸如高速离心压缩机、汽轮机发电机组。动态失稳造成的重大恶性事故屡 见不鲜。 急剧上升的振动可在几十秒之内造成机组解体,甚至祸及厂房, 造成巨大的经济 损失和人员伤亡。此外,机械振动可能降低设备机械性能,加速机械零部件的磨损,发 出的噪声损害操作者的健康。但是振动也能合理运用,如工业上常用的振动筛、振动破 碎等都是振动的有效利用。工程技术人员必须认真对待机械振动问题,当机组产生有害 的振动时,及时分析原因,坚持用合理的振动测试标准,采取科学的防治措施。
4.1 转子不平衡振动的故障特征
当发生不平衡振动时,其故障特征主要表现在如下方面: 1 )不平衡故障主要引起转子或轴承径向振动,在转子径向测点上得到的频谱图 ,
5
机械振动理论基础及其应用
旋转机械振动与故障诊断研究综述
