高等代数与解析几何第九章答案
第九章习题答案高数下

作 业 9—1一.填空:1.已知D 是长方形域:,10;≤≤≤≤y b x a 且⎰⎰=Dd x yf 1)(σ,则⋅=b adx x f )(2 .解:⎰⎰=Dd x yf σ)(⎰⎰⋅=baydy dx x f 1)(21⎰⋅badx x f )( 故⎰⋅=badx x f )( 22.若D 是由1=+y x 和两个坐标轴围成的三角形域,且⎰⎰⎰⋅=Ddx x dxdy x f 1)()(ϕ,那么.=)(x ϕ)()1(x f x -解:⎰⎰=Ddxdy x f )(⎰⎰-⋅=xdy x f xdx 1010)(⎰⋅-10)()1(dx x f x ⎰⋅=1)(dx x ϕ二、单项选择题:1. 设1D 是正方形域,2D 是1D 的内切圆,3D 是1D 的外接圆,1D 的中心在(-1,1)处,记1I =⎰⎰---12222D xy x y dxdy e;2I =⎰⎰---22222D xy x y dxdy e;3I =⎰⎰---32222D xy x y dxdy e.则1I ,2I ,3I 大小顺序为( B )。
A .1I ≤2I ≤3I B.2I ≤1I ≤3I C. 3I ≤2I ≤1I D. 3I ≤1I ≤2I解:因为三个被积函数一样,均为正值,213D D D ⊃⊃,故2I ≤1I ≤3I 2. 设D 是第二象限的一个有界闭区域,且10<<y ,记1I =⎰⎰Dd yx σ3;2I =⎰⎰Dd x y σ32;3I =⎰⎰Dd x y σ321.1I ,2I ,3I 的大小顺序是( )。
A .1I ≤2I ≤3I B.2I ≤1I ≤3I C. 3I ≤1I ≤2I D. 3I ≤2I ≤1I 解:因10<<y ,故212y y y <<,而03<x ,从而323321x y yx x y <<,选(C )。
三.利用二重积分定义证明: 1.σσ=⎰⎰Dd (其中σ为D 的面积)解:ini iiDf d σηξσλ∑⎰⎰=→∆=⋅10),(lim 1i ni σλ∑=→∆⋅=11limσσσλλ==∆=→=→∑01lim limini故 σσ=⎰⎰Dd (其中λ是各iσ∆的最大直径)2.k d y x kf D=⎰⎰σ),(⎰⎰Dd y x f σ),( (其中k 为常数)解:=⎰⎰Dd y x kf σ),( ini iif σηξλ∑=→∆1),(lim i ni i i f k σηξλ∑=→∆=1),(limi ni i i f k σηξλ∑=→∆=1),(lim ⎰⎰=Dd y x f k σ),( (k 为常数)四.利用二重积分的性质估计下列积分的值: 1.}10,10|),{(,)(⎰⎰≤≤≤≤=+=Dy x y x d y x xy I 其中Dσ解: 10,10≤≤≤≤y x∴2)(0≤+≤y x xy∴⎰⎰⎰⎰≤≤+≤DDd d y x xy 22)(0σσ2.}4|),{(,)49(22⎰⎰≤+=++=Dy x d y x I 22yx其中Dσ 解: 中在D ,422ππσ=⋅=,()22222249499yx y x y x ++≤++≤++2549922≤++≤y x∴ σσσ25)49(922≤++≤⎰⎰⎰⎰DDd y x d即 ππ10036≤≤I五.根据二重积分的性质比较下列积分的大小: 1.⎰⎰⎰⎰++DDd y x d y x σσ32)()(与其中积分区域D 是由圆周2)1()2(22=-+-y x 所围成。
2018高考数学文人教新课标大一轮复习配套文档:第九章
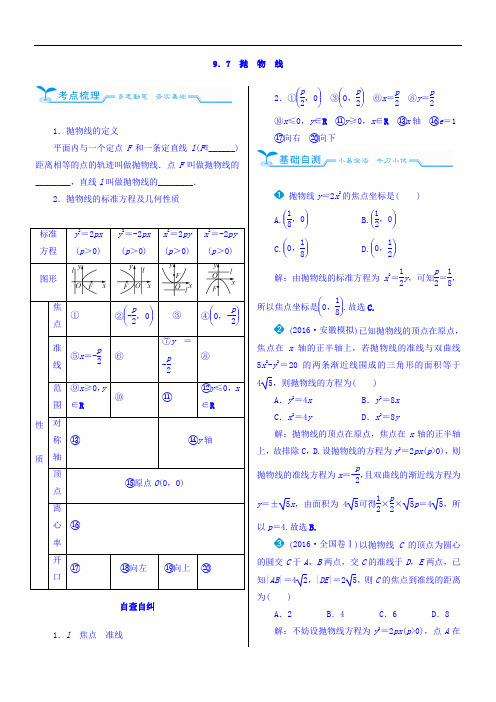
9.7 抛物线1.抛物线的定义平面内与一个定点F和一条定直线l(F∉______)距离相等的点的轨迹叫做抛物线.点F叫做抛物线的________,直线l叫做抛物线的________.2.抛物线的标准方程及几何性质自查自纠1.l焦点准线2.①⎝⎛⎭⎪⎫p2,0③⎝⎛⎭⎪⎫0,p2⑥x=p2⑧y=p2⑩x≤0,y∈R⑪y≥0,x∈R⑬x轴⑯e=1 ⑰向右⑳向下抛物线y=2x2的焦点坐标是( )A.⎝⎛⎭⎪⎫18,0 B.⎝⎛⎭⎪⎫12,0C.⎝⎛⎭⎪⎫0,18D.⎝⎛⎭⎪⎫0,12解:由抛物线的标准方程为x2=12y,可知p2=18,所以焦点坐标是⎝⎛⎭⎪⎫0,18.故选C.(2016·安徽模拟)已知抛物线的顶点在原点,焦点在x轴的正半轴上,若抛物线的准线与双曲线5x2-y2=20的两条渐近线围成的三角形的面积等于45,则抛物线的方程为( )A.y2=4x B.y2=8xC.x2=4y D.x2=8y解:抛物线的顶点在原点,焦点在x轴的正半轴上,故排除C,D.设抛物线的方程为y2=2px(p>0),则抛物线的准线方程为x=-p2,且双曲线的渐近线方程为y=±5x,由面积为45可得12×p2×5p=45,所以p=4.故选B.(2016·全国卷Ⅰ)以抛物线C的顶点为圆心的圆交C于A,B两点,交C的准线于D,E两点,已知|AB|=42,|DE|=25,则C的焦点到准线的距离为( )A.2 B.4 C.6 D.8解:不妨设抛物线方程为y2=2px(p>0),点A在(标轴上,又知抛物线上一点,0)到直线l1+6|=2.故选+(-3)2用数形结合的方法判断抛物线的开口B .yD .y 分别作准线的垂线,及抛物线的定义知的中点到准线的距离为又抛物线的准线为x =-12,所以线段.代入抛物线方程y 2=3,所以|AC |=6. 的中点,32,故抛物线方程为抛物线焦点弦的性质AB 为过抛物线y 2=的弦,点在抛物线准线上的射影分别为y 2).求证:x 2+p ; y 2=-p 2;为直径的圆与抛物线的准线相切;|=2p.由抛物线的定义知||AB +x 2+p .BN ∥x 轴, KFM ,∠BNF =∠KFM +∠KFN KFB ) 为AB 的中点,连接AB |,则∠ARB知R ⎝ ⎛-p 2,y 1+⎭⎪⎫x 2+p 2,y 2-y 12,⎭⎪⎫+p 2⎝ ⎛⎭⎪⎫x 2+p 2-14(+p 24-14(y 21+y 22.90°,所以F 在以|MR |=|FR |,AMF ,∠MFR =∠MFA +∠MFR =为垂足.为直径的圆必与直线的方程为y =y 1x 1=-p 2y 1=y 2,与点N 重合.因此,平行于抛物线的对称轴..抛物线的定义、标准方程和性质是解决有关抛物线问题的基础,应当熟练掌握.求抛物线的标准方程的常用方法是待定系数法或轨迹法.若抛物线的开口不确定,为避免多种情况分类求解的麻烦,可以设抛物线方程为>0,开口向右;若有两解时,则抛物线的标准方程有两个.对,有类似的讨论.抛物线的离心率e =1,体现了抛物线上的点到BF |-|AF ||+|BF |=12,由此得2016·贵州模拟)过抛物线y 2交抛物线于A ,的面积为____________解:由题意知,抛物线焦点的坐标为,与抛物线方程联立,设A ,B 的坐标分别为=4,y 1y 2=-442,则S △OAB =的焦点为F,+b )y +ab =0.(1)证明:由于F 在线段AB 上,故1+ab =0. 记AR 的斜率为k 1,FQ 的斜率为k 2,则k 1=a -b 1+a 2=a -b a 2-ab =1a =-aba=-b =k 2. 所以AR ∥FQ .(2)设l 与x 轴的交点为D (x 1,0),则S △ABF =12|b -a |·|FD |=12|b -a |⎪⎪⎪⎪⎪⎪x 1-12,S △PQF =|a -b |2. 由题设可得|b -a |⎪⎪⎪⎪⎪⎪x 1-12=|a -b |2,所以x 1=0(舍去)或x 1=1.设满足条件的AB 的中点为E (x ,y ). 当AB 与x 轴不垂直时, 由k AB =k DE 可得2a +b =yx -1(x ≠1). 而a +b2=y ,所以y 2=x -1(x ≠1).当AB 与x 轴垂直时,E 与D 重合. 所以,所求轨迹方程为y 2=x -1.。
高等数学第九章习题解答

习题9.11. 计算曲线积分22(),LI x y ds =+⎰其中L 是中心在(,0)R 、半径为R 的上半圆周.解 由于上半圆周的参数方程为(1cos )sin x R t y R t=+⎧⎨=⎩(0),t π≤≤ 所以 I 22()Lx y ds =+⎰22220[(1cos )sin ]R t R t π=++⎰32(1cos )Rt dt π=+⎰32[sin ]R t t π=+32.R π=2.计算半径为R , 中心角为2α的圆弧L 对于它的对称轴的转动惯量I (设线密度1ρ=).解 取坐标系,则2.LI y ds =⎰为计算方便, 利用L 的参数方程cos ,x R t =sin y R t =().t αα-≤≤故 2LI y ds =⎰22sin R ααθ-=⎰32sin R tdt αα-=⎰3sin 222R t t αα-⎡⎤=-⎢⎥⎣⎦ 3(2sin 2)2R αα=-3(sin cos ).R ααα=- 3. 计算Lyds ⎰, 其中积分弧段L 是由折线OAB 组成, 而(1,0),A (1,2).B解 在OA 上,0,y =,ds dx = 所以 0.OAyds =⎰在AB 上,1,x =,ds dy =所以AByds ⎰2ydy =⎰ 2.=从而OAByds ⎰yds yds =+⎰⎰02=+ 2.=4.LI xds =⎰,其中L 是圆221x y +=中(0,1)A到B 之间的一段劣弧;解 L AB =的参数方程为:cos ,sin x y θθ==()42ππθ-≤≤,于是24cos I ππθ-=⎰24cos (1d ππθθ-==⎰. 5.(1)Lx y ds ++⎰,其中L 是顶点为(0,0),(1,0)O A 及(0,1)B 所成三角形的边界;解 L 是分段光滑的闭曲线,如图9-2所示,根据积分的可加性,则有(1)Lx y ds ++⎰(1)OAx y ds =++⎰(1)ABx y ds +++⎰ (1)BOx y ds +++⎰,由于OA :0y =,01x ≤≤,于是ds dx ===,故 13(1)(01)2x y ds x dx ++=++=⎰⎰OA, 而:AB 1y x =-,01x ≤≤,于是ds ===. 故xyoABC1(1)[(1)ABx y ds x x ++=+-+=⎰⎰,同理可知:BO 0x =(01y ≤≤),0d s =,则103(1)[01]2BOx y ds y dy ++=++=⎰⎰. 综上所述33(1)322Lx y ds -+=+=+⎰ 6.2 Lx yzds ⎰,其中L 为折线段ABCD ,这里(0,0,0)A ,(0,0,2),B (1,0,2),C(1,2,3)D ;解 如图所示, 2222 LABBCCDx yzds x yzds x yzds x yzds =++⎰⎰⎰⎰.线段AB 的参数方程为 0,0,2(01)x y z t t ===≤≤ds =2dt =, 故12 000220x yzds t dt =⋅⋅⋅=⎰⎰.线段BC 的参数方程为,0,2(01)x t y z t ===≤≤,则 ,ds dt == 故122 0020BCx yzds t dt =⋅⋅⋅=⎰⎰,线段CD 的参数方程为1,2,2x y t z t ===+(01)t ≤≤,则ds =, 故11222 0 012(2) (2)CD x yzds t t t t dt =⋅⋅+=+=⎰⎰所以 2222 L AB BC CD x yzds x yzds x yzds x yzds =++=⎰⎰⎰⎰7. 设一段曲线ln (0)y x a x b =<≤≤上任一点处的线密度的大小等于该点横坐标的平方,求其质量.解 依题意曲线的线密度为2x ρ=,故所求质量为2LM x ds =⎰,其中:ln (0)L y x a x b =<≤≤.则L 的参数方程为ln x xy x =⎧⎨=⎩ (0)a x b <≤≤, 故ds ===,所以3221[(1)]3b aaM x ==+⎰3322221[(1)(1)]3b a =+-+. 习题9.21 设L 为xOy 面内一直线=y b (b 为常数),证明(,)0=⎰LQ x y dy 。
2019版高考数学大一轮复习人教B版全国通用文档:第九

§9.1 直线的方程1.平面直角坐标系中的基本公式 (1)两点的距离公式:已知平面直角坐标系中的两点A (x 1,y 1),B (x 2,y 2),则d (A ,B )=|AB |=(x 2-x 1)2+(y 2-y 1)2. (2)中点公式:已知平面直角坐标系中的两点A (x 1,y 1),B (x 2,y 2),点M (x ,y )是线段AB 的中点,则x =x 1+x 22,y =y 1+y 22.2.直线的倾斜角(1)定义:x 轴正向与直线向上的方向所成的角叫做这条直线的倾斜角,我们规定,与x 轴平行或重合的直线的倾斜角为零度角.(2)倾斜角的范围:[0°,180°). 3.直线的斜率(1)定义:通常,我们把直线y =kx +b 中的系数k 叫做这条直线的斜率,垂直于x 轴的直线,人们常说它的斜率不存在;(2)计算公式:若由A (x 1,y 1),B (x 2,y 2)确定的直线不垂直于x 轴,则k =y 2-y 1x 2-x 1 (x 1≠x 2).若直线的倾斜角为θ⎝⎛⎭⎫θ≠π2,则k =tan_θ. 4.直线方程的五种形式题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)根据直线的倾斜角的大小不能确定直线的位置.( √ ) (2)坐标平面内的任何一条直线均有倾斜角与斜率.( × ) (3)直线的倾斜角越大,其斜率就越大.( × ) (4)若直线的斜率为tan α,则其倾斜角为α.( × ) (5)斜率相等的两直线的倾斜角不一定相等.( × )(6)经过任意两个不同的点P 1(x 1,y 1),P 2(x 2,y 2)的直线都可以用方程(y -y 1)(x 2-x 1)=(x -x 1)(y 2-y 1)表示.( √ ) 题组二 教材改编2.若过点M (-2,m ),N (m,4)的直线的斜率等于1,则m 的值为( ) A .1 B .4 C .1或3 D .1或4答案 A解析 由题意得m -4-2-m=1,解得m =1.3.过点P (2,3)且在两坐标轴上截距相等的直线方程为________________. 答案 3x -2y =0或x +y -5=0解析 当截距为0时,直线方程为3x -2y =0; 当截距不为0时,设直线方程为x a +ya =1,则2a +3a =1,解得a =5.所以直线方程为x +y -5=0. 题组三 易错自纠4.(2018·石家庄模拟)直线x +(a 2+1)y +1=0的倾斜角的取值范围是( ) A.⎣⎡⎦⎤0,π4 B.⎣⎡⎭⎫3π4,π C.⎣⎡⎦⎤0,π4∪⎝⎛⎭⎫π2,π D.⎣⎡⎭⎫π4,π2∪⎣⎡⎭⎫3π4,π答案 B解析 由直线方程可得该直线的斜率为-1a 2+1,又-1≤-1a 2+1<0,所以倾斜角的取值范围是⎣⎡⎭⎫3π4,π.5.如果A ·C <0且B ·C <0,那么直线Ax +By +C =0不通过( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 答案 C解析 由已知得直线Ax +By +C =0在x 轴上的截距-C A >0,在y 轴上的截距-CB >0,故直线经过第一、二、四象限,不经过第三象限.6.过直线l :y =x 上的点P (2,2)作直线m ,若直线l ,m 与x 轴围成的三角形的面积为2,则直线m 的方程为____________. 答案 x -2y +2=0或x =2解析 ①若直线m 的斜率不存在,则直线m 的方程为x =2,直线m ,直线l 和x 轴围成的三角形的面积为2,符合题意;②若直线m 的斜率k =0,则直线m 与x 轴没有交点,不符合题意;③若直线m 的斜率k ≠0,设其方程为y -2=k (x -2),令y =0,得x =2-2k ,依题意有12×⎪⎪⎪⎪2-2k ×2=2,即⎪⎪⎪⎪1-1k =1,解得k =12,所以直线m 的方程为y -2=12(x -2),即x -2y +2=0. 综上可知,直线m 的方程为x -2y +2=0或x =2.题型一 直线的倾斜角与斜率典例 (1)直线2x cos α-y -3=0⎝⎛⎭⎫α∈⎣⎡⎦⎤π6,π3的倾斜角的取值范围是 ( ) A.⎣⎡⎦⎤π6,π3 B.⎣⎡⎦⎤π4,π3 C.⎣⎡⎦⎤π4,π2 D.⎣⎡⎦⎤π4,2π3答案 B解析 直线2x cos α-y -3=0的斜率k =2cos α, 因为α∈⎣⎡⎦⎤π6,π3,所以12≤cos α≤32, 因此k =2cos α∈[1, 3 ].设直线的倾斜角为θ,则有tan θ∈[1, 3 ]. 又θ∈[0,π),所以θ∈⎣⎡⎦⎤π4,π3, 即倾斜角的取值范围是⎣⎡⎦⎤π4,π3.(2)直线l 过点P (1,0),且与以A (2,1),B (0,3)为端点的线段有公共点,则直线l 斜率的取值范围为___________________. 答案 (-∞,-3]∪[1,+∞) 解析 如图,∵k AP =1-02-1=1,k BP =3-00-1=-3, ∴k ∈(-∞,- 3 ]∪[1,+∞).引申探究1.若将本例(2)中P (1,0)改为P (-1,0),其他条件不变,求直线l 斜率的取值范围. 解 ∵P (-1,0),A (2,1),B (0,3), ∴k AP =1-02-(-1)=13,k BP =3-00-(-1)= 3.如图可知,直线l 斜率的取值范围为⎣⎡⎦⎤13,3.2.若将本例(2)中的B 点坐标改为(2,-1),其他条件不变,求直线l 倾斜角的取值范围. 解 如图,直线P A 的倾斜角为45°, 直线PB 的倾斜角为135°,由图象知l 的倾斜角的范围为[0°,45°]∪[135°,180°).思维升华 直线倾斜角的范围是[0,π),根据斜率求倾斜角的范围时,要分⎣⎡⎭⎫0,π2与⎝⎛⎭⎫π2,π两种情况讨论.跟踪训练 已知过定点P (2,0)的直线l 与曲线y =2-x 2相交于A ,B 两点,O 为坐标原点,当△AOB 的面积取到最大值时,直线l 的倾斜角为( ) A .150° B .135° C .120° D .不存在 答案 A解析 由y =2-x 2,得x 2+y 2=2(y ≥0),它表示以原点O 为圆心,以2为半径的圆的一部分,其图象如图所示.显然直线l 的斜率存在,设过点P (2,0)的直线l 为y =k (x -2), 则圆心到此直线的距离d =|-2k |1+k 2, 弦长|AB |=22-⎝ ⎛⎭⎪⎫|-2k |1+k 22=22-2k 21+k 2, 所以S △AOB =12×|-2k |1+k 2×22-2k 21+k 2≤(2k )2+2-2k 22(1+k 2)=1, 当且仅当(2k )2=2-2k 2,即k 2=13时等号成立,由图可得k =-33⎝⎛⎭⎫k =33舍去, 故直线l 的倾斜角为150°. 题型二 求直线的方程典例 (1)求过点A (1,3),斜率是直线y =-4x 的斜率的13的直线方程;(2)求经过点A (-5,2),且在x 轴上的截距等于在y 轴上的截距的2倍的直线方程. 解 (1)设所求直线的斜率为k , 依题意k =-4×13=-43.又直线经过点A (1,3),因此所求直线方程为y -3=-43(x -1),即4x +3y -13=0.(2)当直线不过原点时,设所求直线方程为x 2a +y a =1,将(-5,2)代入所设方程,解得a =-12,所以直线方程为x +2y +1=0;当直线过原点时,设直线方程为y =kx ,则-5k =2,解得k =-25,所以直线方程为y =-25x ,即2x +5y =0.故所求直线方程为2x +5y =0或x +2y +1=0.思维升华 在求直线方程时,应先选择适当的直线方程的形式,并注意各种形式的适用条件.若采用截距式,应注意分类讨论,判断截距是否为零;若采用点斜式,应先考虑斜率不存在的情况.跟踪训练 根据所给条件求直线的方程: (1)直线过点(-4,0),倾斜角的正弦值为1010; (2)经过点P (4,1),且在两坐标轴上的截距相等; (3)直线过点(5,10),到原点的距离为5.解 (1)由题设知,该直线的斜率存在,故可采用点斜式. 设倾斜角为α,则sin α=1010(0<α<π), 从而cos α=±31010,则k =tan α=±13.故所求直线方程为y =±13(x +4).即x +3y +4=0或x -3y +4=0. (2)设直线l 在x ,y 轴上的截距均为a . 若a =0,即l 过(0,0)及(4,1)两点, ∴l 的方程为y =14x ,即x -4y =0.若a ≠0,则设l 的方程为x a +ya =1,∵l 过点(4,1),∴4a +1a =1,∴a =5,∴l 的方程为x +y -5=0.综上可知,直线l 的方程为x -4y =0或x +y -5=0. (3)当斜率不存在时,所求直线方程为x -5=0; 当斜率存在时,设其为k ,则所求直线方程为y -10=k (x -5), 即kx -y +(10-5k )=0. 由点到直线的距离公式,得|10-5k |k 2+1=5,解得k =34.故所求直线方程为3x -4y +25=0.综上可知,所求直线方程为x -5=0或3x -4y +25=0.题型三 直线方程的综合应用命题点1 与均值不等式相结合求最值问题典例 (2018·济南模拟)已知直线l 过点M (2,1),且与x 轴、y 轴的正半轴分别相交于A ,B 两点,O 为坐标原点,求当|MA →|·|MB →|取得最小值时直线l 的方程. 解 设A (a,0),B (0,b ),则a >0,b >0, 直线l 的方程为x a +y b =1,所以2a +1b=1.|MA →|·|MB →|=-MA →·MB →=-(a -2,-1)·(-2,b -1)=2(a -2)+b -1=2a +b -5 =(2a +b )⎝⎛⎭⎫2a +1b -5=2b a +2ab≥4, 当且仅当a =b =3时取等号,此时直线l 的方程为x +y -3=0. 命题点2 由直线方程解决参数问题典例 已知直线l 1:ax -2y =2a -4,l 2:2x +a 2y =2a 2+4,当0<a <2时,直线l 1,l 2与两坐标轴围成一个四边形,当四边形的面积最小时,求实数a 的值.解 由题意知直线l 1,l 2恒过定点P (2,2),直线l 1在y 轴上的截距为2-a ,直线l 2在x 轴上的截距为a 2+2,所以四边形的面积S =12×2×(2-a )+12×2×(a 2+2)=a 2-a +4=⎝⎛⎭⎫a -122+154, 当a =12时,四边形的面积最小.思维升华 与直线方程有关问题的常见类型及解题策略(1)求解与直线方程有关的最值问题.先设出直线方程,建立目标函数,再利用均值不等式求解最值.(2)求直线方程.弄清确定直线的两个条件,由直线方程的几种特殊形式直接写出方程. (3)求参数值或范围.注意点在直线上,则点的坐标适合直线的方程,再结合函数的单调性或均值不等式求解.跟踪训练 已知直线l 过点P (3,2),且与x 轴、y 轴的正半轴分别交于A ,B 两点,如图所示,求△ABO 的面积的最小值及此时直线l 的方程.解 方法一 设直线方程为x a +yb =1(a >0,b >0),把点P (3,2)代入得3a +2b=1≥26ab,得ab ≥24, 从而S △AOB =12ab ≥12,当且仅当3a =2b 时等号成立,这时k =-b a =-23,从而所求直线方程为2x +3y -12=0.方法二 由题意知,直线l 的斜率k 存在且k <0, 则直线l 的方程为y -2=k (x -3)(k <0), 且有A ⎝⎛⎭⎫3-2k ,0,B (0,2-3k ), ∴S △ABO =12(2-3k )⎝⎛⎭⎫3-2k =12⎣⎡⎦⎤12+(-9k )+4(-k )≥12⎣⎢⎡⎦⎥⎤12+2 (-9k )·4(-k )=12×(12+12)=12. 当且仅当-9k =4-k ,即k =-23时,等号成立.即△ABO 的面积的最小值为12. 故所求直线的方程为2x +3y -12=0.求与截距有关的直线方程典例 设直线l 的方程为(a +1)x +y +2-a =0(a ∈R ). (1)若l 在两坐标轴上的截距相等,求直线l 的方程; (2)若l 在两坐标轴上的截距互为相反数,求a . 错解展示:现场纠错解 (1)当直线过原点时,该直线在x 轴和y 轴上的截距为0,∴a =2,方程即为3x +y =0. 当直线不经过原点时,截距存在且均不为0, 直线方程可写为x a -2a +1+ya -2=1,∴a -2a +1=a -2,即a +1=1. ∴a =0,方程即为x +y +2=0.综上,直线l 的方程为3x +y =0或x +y +2=0. (2)由a -2a +1=-(a -2),得a -2=0或a +1=-1,∴a =2或a =-2.纠错心得 在求与截距有关的直线方程时,注意对直线的截距是否为零进行分类讨论,防止忽视截距为零的情形,导致产生漏解.1.直线3x -y +a =0(a 为常数)的倾斜角为( ) A .30° B .60° C .150° D .120°答案 B解析 化直线方程为y =3x +a , ∴k =tan α= 3.∵0°≤α<180°,∴α=60°.2.(2018·北京海淀区模拟)过点(2,1)且倾斜角比直线y =-x -1的倾斜角小π4的直线方程是( )A .x =2B .y =1C .x =1D .y =2 答案 A解析 ∵直线y =-x -1的斜率为-1,则倾斜角为3π4,依题意,所求直线的倾斜角为3π4-π4=π2,∴斜率不存在,∴过点(2,1)的直线方程为x =2.3.若直线l 与直线y =1,x =7分别交于点P ,Q ,且线段PQ 的中点坐标为(1,-1),则直线l 的斜率为( ) A.13 B .-13C .-32D.23答案 B解析 依题意,设点P (a,1),Q (7,b ),则有⎩⎪⎨⎪⎧a +7=2,b +1=-2,解得a =-5,b =-3,从而可知直线l 的斜率为-3-17+5=-13.4.(2017·深圳调研)在同一平面直角坐标系中,直线l 1:ax +y +b =0和直线l 2:bx +y +a =0有可能是( )答案 B解析 当a >0,b >0时,-a <0,-b <0.选项B 符合.5.如图中的直线l 1,l 2,l 3的斜率分别为k 1,k 2,k 3,则 ( )A .k 1<k 2<k 3B .k 3<k 1<k 2C .k 3<k 2<k 1D .k 1<k 3<k 2答案 D解析 直线l 1的倾斜角α1是钝角,故k 1<0,直线l 2与l 3的倾斜角α2与α3均为锐角且α2>α3,所以0<k 3<k 2,因此k 1<k 3<k 2,故选D.6.已知两点M (2,-3),N (-3,-2),直线l 过点P (1,1)且与线段MN 相交,则直线l 的斜率k 的取值范围是( )A .k ≥34或k ≤-4 B .-4≤k ≤34 C.34≤k ≤4 D .-34≤k ≤4 答案 A解析 如图所示,∵k PN =1-(-2)1-(-3)=34, k PM =1-(-3)1-2=-4, ∴要使直线l 与线段MN 相交,当l 的倾斜角小于90°时,k ≥k PN ;当l 的倾斜角大于90°时,k ≤k PM ,∴k ≥34或k ≤-4. 7.已知直线l :(a -2)x +(a +1)y +6=0,则直线l 恒过定点__________.答案 (2,-2)解析 直线l 的方程变形为a (x +y )-2x +y +6=0,由⎩⎪⎨⎪⎧x +y =0,-2x +y +6=0,解得x =2,y =-2, 所以直线l 恒过定点(2,-2).8.若直线l 的斜率为k ,倾斜角为α,而α∈⎣⎡⎭⎫π6,π4∪⎣⎡⎭⎫2π3,π,则k 的取值范围是_____.答案 [)-3,0∪⎣⎡⎭⎫33,1 解析 当π6≤α<π4时,33≤tan α<1,∴33≤k <1; 当2π3≤α<π时,-3≤tan α<0,∴-3≤k <0. ∴k ∈[-3,0)∪⎣⎡⎭⎫33,1. 9.已知三角形的三个顶点A (-5,0),B (3,-3),C (0,2),则BC 边上中线所在的直线方程为______.答案 x +13y +5=0解析 BC 的中点坐标为⎝⎛⎭⎫32,-12,∴BC 边上中线所在的直线方程为y -0-12-0=x +532+5,即x +13y +5=0.10.直线l 过点(-2,2)且与x 轴、y 轴分别交于点(a,0),(0,b ),若|a |=|b |,则直线l 的方程为_____.答案 x +y =0或x -y +4=0解析 若a =b =0,则直线l 过(0,0)与(-2,2)两点,直线l 的斜率k =-1,直线l 的方程为y =-x ,即x +y =0.若a ≠0,b ≠0,则直线l 的方程为x a +y b=1, 由题意知⎩⎪⎨⎪⎧ -2a +2b =1,|a |=|b |,解得⎩⎪⎨⎪⎧a =-4,b =4, 此时,直线l 的方程为x -y +4=0.11.已知直线l 与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线l 的方程:(1)过定点A (-3,4);(2)斜率为16. 解 (1)由题意知,直线l 存在斜率.设直线l 的方程为y =k (x +3)+4,它在x 轴、y 轴上的截距分别为-4k-3,3k +4, 由已知,得(3k +4)⎝⎛⎭⎫4k +3=±6, 解得k 1=-23或k 2=-83. 故直线l 的方程为2x +3y -6=0或8x +3y +12=0.(2)设直线l 在y 轴上的截距为b ,则直线l 的方程是y =16x +b ,则它在x 轴上的截距是-6b , 由已知,得|-6b ·b |=6,∴b =±1.∴直线l 的方程为x -6y +6=0或x -6y -6=0.12.如图,射线OA ,OB 分别与x 轴正半轴成45°和30°角,过点P (1,0)作直线AB 分别交OA ,OB 于A ,B 两点,当AB 的中点C 恰好落在直线y =12x 上时,求直线AB 的方程.解 由题意可得k OA =tan 45°=1,k OB =tan(180°-30°)=-33, 所以直线l OA :y =x ,l OB :y =-33x . 设A (m ,m ),B (-3n ,n ),所以AB 的中点C ⎝ ⎛⎭⎪⎫m -3n 2,m +n 2, 由点C 在直线y =12x 上,且A ,P ,B 三点共线得 ⎩⎪⎨⎪⎧ m +n 2=12·m -3n 2,m -0m -1=n -0-3n -1,解得m =3,所以A (3,3).又P (1,0),所以k AB =k AP =33-1=3+32, 所以l AB :y =3+32(x -1), 即直线AB 的方程为(3+3)x -2y -3-3=0.13.已知直线l 过点(1,0),且倾斜角为直线l 0:x -2y -2=0的倾斜角的2倍,则直线l 的方程为( )A .4x -3y -3=0B .3x -4y -3=0C .3x -4y -4=0D .4x -3y -4=0答案 D解析 由题意可设直线l 0,l 的倾斜角分别为α,2α,因为直线l 0:x -2y -2=0的斜率为12,则tan α=12, 所以直线l 的斜率k =tan 2α=2tan α1-tan 2α=2×121-⎝⎛⎭⎫122=43,所以由点斜式可得直线l 的方程为y -0=43(x -1),即4x -3y -4=0. 14.设点A (-1,0),B (1,0),直线2x +y -b =0与线段AB 相交,则b 的取值范围是________. 答案 [-2,2]解析 b 为直线y =-2x +b 在y 轴上的截距,如图,当直线y =-2x +b 过点A (-1,0)和点B (1,0)时,b 分别取得最小值-2和最大值2. ∴b 的取值范围是[-2,2].15.(2017·豫南九校联考)若θ是直线l 的倾斜角,且sin θ+cos θ=55,则l 的斜率为( ) A .-12 B .-12或-2C.12或2 D .-2答案 D解析 ∵sin θ+cos θ=55,① ∴(sin θ+cos θ)2=1+sin 2θ=15, ∴2sin θcos θ=-45,∴(sin θ-cos θ)2=95, 易知sin θ>0,cos θ<0,∴sin θ-cos θ=355,② 由①②解得⎩⎨⎧ sin θ=255,cos θ=-55,∴tan θ=-2,即l 的斜率为-2,故选D.16.(2017·福建四地六校联考)已知函数f (x )=a sin x -b cos x (a ≠0,b ≠0),若f ⎝⎛⎭⎫π4-x =f ⎝⎛⎭⎫π4+x ,则直线ax -by +c =0的倾斜角为( )A.π4B.π3C.2π3D.3π4 答案 D解析 由f ⎝⎛⎭⎫π4-x =f ⎝⎛⎭⎫π4+x 知,函数f (x )的图象关于x =π4对称,所以f (0)=f ⎝⎛⎭⎫π2,所以a =-b ,则直线ax -by +c =0的斜率为k =a b=-1,又直线倾斜角的取值范围为[0,π),所以该直线的倾斜角为3π4,故选D.。
高考复习·数学(文)试题:第九章解析几何Word版含答案
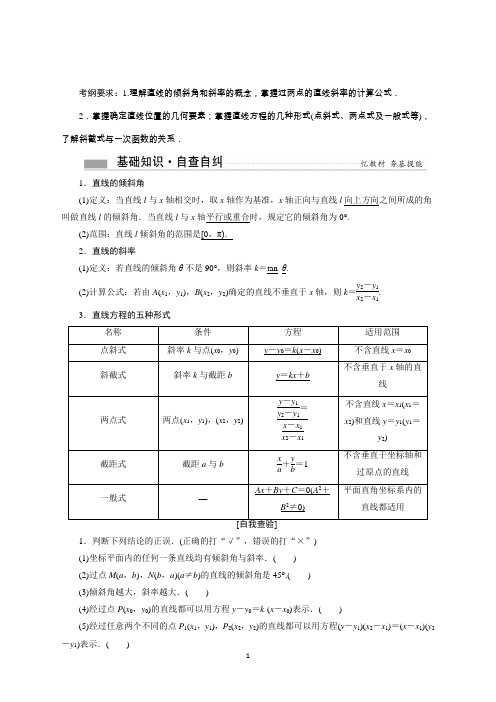
考纲要求:1.理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式. 2.掌握确定直线位置的几何要素;掌握直线方程的几种形式(点斜式、两点式及一般式等),了解斜截式与一次函数的关系.1.直线的倾斜角(1)定义:当直线l 与x 轴相交时,取x 轴作为基准,x 轴正向与直线l 向上方向之间所成的角叫做直线l 的倾斜角.当直线l 与x 轴平行或重合时,规定它的倾斜角为0°.(2)范围:直线l 倾斜角的范围是[0,π). 2.直线的斜率(1)定义:若直线的倾斜角θ不是90°,则斜率k =tan_θ.(2)计算公式:若由A (x 1,y 1),B (x 2,y 2)确定的直线不垂直于x 轴,则k =y 2-y 1x 2-x 1.3.直线方程的五种形式1.判断下列结论的正误.(正确的打“√”,错误的打“×”) (1)坐标平面内的任何一条直线均有倾斜角与斜率.( ) (2)过点M (a ,b ),N (b ,a )(a ≠b )的直线的倾斜角是45°.( ) (3)倾斜角越大,斜率越大.( )(4)经过点P (x 0,y 0)的直线都可以用方程y -y 0=k ·(x -x 0)表示.( )(5)经过任意两个不同的点P 1(x 1,y 1),P 2(x 2,y 2)的直线都可以用方程(y -y 1)(x 2-x 1)=(x -x 1)(y 2-y 1)表示.( )(6)直线的截距即是直线与坐标轴的交点到原点的距离.( )(7)若直线在x 轴,y 轴上的截距分别为m ,n ,则方程可记为x m +yn =1.( )答案:(1)× (2)× (3)× (4)× (5)√ (6)× (7)×2.若过两点A (-m,6),B (1,3m )的直线的斜率为12,则m =________. 答案:-23.直线3x -y +a =0的倾斜角为________. 答案:60°4.已知三角形的三个顶点A (-5,0),B (3,-3),C (0,2),则BC 边上中线所在的直线方程为____________.答案:x +13y +5=05.直线l 经过点P (-2,5),且斜率为-34,则直线l 的方程为________.答案:3x +4y -14=0[典题1] (1)直线2x cos α-y -3=0α∈π6,π3的倾斜角的取值范围是( )A.⎣⎡⎦⎤π6,π3B.⎣⎡⎦⎤π4,π3C.⎣⎡⎦⎤π4,π2D.⎣⎡⎦⎤π4,2π3 (2)直线l 过点P (1,0),且与以A (2,1),B (0,3)为端点的线段有公共点,则直线l 斜率的取值范围为________.[听前试做] (1)直线2x cos α-y -3=0的斜率k =2cos α,因为α∈⎣⎡⎦⎤π6,π3,所以12≤ cos α≤32,因此k =2·cos α∈[1, 3 ].设直线的倾斜角为θ,则有tan θ∈[1, 3 ].又θ∈[0,π),所以θ∈⎣⎡⎦⎤π4,π3,即倾斜角的取值范围是⎣⎡⎦⎤π4,π3. (2)如图,∵k AP =1-02-1=1,k BP =3-00-1=-3, ∴k ∈(-∞,- 3 ]∪[1,+∞).答案:(1)B (2)(-∞,- 3 ]∪[1,+∞)[探究1] 若将题(2)中P (1,0)改为P (-1,0),其他条件不变,求直线l 斜率的取值范围. 解:∵P (-1,0),A (2,1),B (0,3),∴k AP =1-02-(-1)=13,k BP =3-00-(-1)= 3.如图可知,直线l 斜率的取值范围为⎣⎡⎦⎤13,3.[探究2] 若将题(2)条件改为“经过P (0,-1)作直线l ,若直线l 与连接A (1,-2),B (2,1)的线段总有公共点”,求直线l 的倾斜角α的范围.解:法一:如图所示,k P A =-2-(-1)1-0=-1,k PB =1-(-1)2-0=1,由图可观察出:直线l 倾斜角α的范围是⎣⎡⎦⎤0,π4∪⎣⎡⎭⎫3π4,π.法二:由题意知,直线l 存在斜率.设直线l 的斜率为k , 则直线l 的方程为y +1=kx ,即kx -y -1=0. ∵A ,B 两点在直线的两侧或其中一点在直线l 上. ∴(k +2-1)(2k -1-1)≤0,即2(k +1)(k -1)≤0. ∴-1≤k ≤1.∴直线l 的倾斜角α的范围是⎣⎡⎦⎤0,π4∪⎣⎡⎭⎫3π4,π.直线倾斜角的范围是[0,π),而这个区间不是正切函数的单调区间,因此根据斜率求倾斜角的范围时,要分⎣⎡⎭⎫0,π2与⎝⎛⎭⎫π2,π两种情况讨论.由正切函数图象可以看出,当α∈⎣⎡⎭⎫0,π2时,斜率k ∈[0,+∞);当α=π2时,斜率不存在;当α∈⎝⎛⎭⎫π2,π时,斜率k ∈(-∞,0).[典题2] 根据所给条件求直线的方程: (1)直线过点(-4,0),倾斜角的正弦值为1010; (2)直线过点(-3,4),且在两坐标轴上的截距之和为12; (3)直线过点(5,10),且到原点的距离为5.[听前试做] (1)由题设知,该直线的斜率存在,故可采用点斜式. 设倾斜角为α,则sin α=1010(0<α<π), 从而cos α=±31010,则k =tan α=±13.故所求直线方程为y =±13(x +4).即x +3y +4=0或x -3y +4=0.(2)由题设知截距不为0,设直线方程为x a +y12-a =1,又直线过点(-3,4),从而-3a +412-a =1,解得a =-4或a =9.故所求直线方程为4x -y +16=0或x +3y -9=0. (3)当斜率不存在时,所求直线方程为x -5=0;当斜率存在时,设其为k ,则所求直线方程为y -10=k (x -5),即kx -y +(10-5k )=0. 由点线距离公式,得|10-5k |k 2+1=5,解得k =34.故所求直线方程为3x -4y +25=0.综上知,所求直线方程为x -5=0或3x -4y +25=0.求直线方程的注意点(1)用斜截式及点斜式时,直线的斜率必须存在;(2)两点式不能表示与坐标轴垂直的直线,截距式不能表示与坐标轴垂直或经过原点的直线,故在解题时,若采用截距式,注意分类讨论,判断截距是否为零.已知点A (3,4),求满足下列条件的直线方程: (1)经过点A 且在两坐标轴上截距相等;(2)经过点A 且与两坐标轴围成一个等腰直角三角形. 解:(1)设直线在x ,y 轴上的截距均为a . ①若a =0,即直线过点(0,0)及(3,4). ∴直线的方程为y =43x ,即4x -3y =0.②若a ≠0,设所求直线的方程为x a +ya =1,又点(3,4)在直线上, ∴3a +4a =1, ∴a =7.∴直线的方程为x +y -7=0.综合①②可知所求直线的方程为4x -3y =0或x +y -7=0. (2)由题意可知,所求直线的斜率为±1. 又过点(3,4),由点斜式得y -4=±(x -3). 所求直线的方程为x -y +1=0或x +y -7=0.[典题3] 已知直线l 过点P (3,2),且与x 轴、y 轴的正半轴分别交于A ,B 两点,如图所示,求△ABO 的面积的最小值及此时直线l 的方程.[听前试做] 依题意知,直线l 的斜率k 存在且k <0. 则直线l 的方程为y -2=k (x -3)(k <0),且有A ⎝⎛⎭⎫3-2k ,0,B (0,2-3k ), ∴S △ABO =12(2-3k )⎝⎛⎭⎫3-2k =12⎣⎢⎡⎦⎥⎤12+(-9k )+4(-k ) ≥12⎣⎢⎡⎦⎥⎤12+2(-9k )·4(-k )=12×(12+12)=12. 当且仅当-9k =4-k ,即k =-23时,等号成立.即△ABO 的面积的最小值为12. 此时直线l 的方程为2x +3y -12=0.(1)含有参数的直线方程可看作直线系方程,这时要能够整理成过定点的直线系,即能够看出“动中有定”.(2)求解与直线方程有关的最值问题,先求出斜率或设出直线方程,建立目标函数,再利用基本(均值)不等式求解最值.已知直线l :kx -y +1+2k =0(k ∈R ). (1)证明:直线l 过定点;(2)若直线不经过第四象限,求k 的取值范围;(3)若直线l 交x 轴负半轴于A ,交y 轴正半轴于B ,△AOB 的面积为S (O 为坐标原点),求S 的最小值并求此时直线l 的方程.解:(1)证明:直线l 的方程是k (x +2)+(1-y )=0,令⎩⎪⎨⎪⎧ x +2=0,1-y =0,解得⎩⎪⎨⎪⎧x =-2,y =1,∴无论k 取何值,直线总经过定点(-2,1).(2)由方程知,当k ≠0时直线在x 轴上的截距为-1+2kk,在y 轴上的截距为1+2k ,要使直线不经过第四象限,则必须有⎩⎨⎧-1+2k k ≤-2,1+2k ≥1,解之得k >0;当k =0时,直线为y =1,符合题意,故k ≥0.即k 的取值范围是[0,+∞).(3)由l 的方程,得A ⎝ ⎛⎭⎪⎫-1+2k k ,0,B (0,1+2k ).依题意得⎩⎨⎧-1+2k k <0,1+2k >0,解得k >0.∵S =12·|OA |·|OB |=12·⎪⎪⎪⎪⎪⎪1+2k k ·|1+2k | =12·(1+2k )2k =12⎝⎛⎭⎫4k +1k +4 ≥12×(2×2+4)=4, “=”成立的条件是k >0且4k =1k ,即k =12,∴S min =4,此时直线l 的方程为x -2y +4=0.—————————————[课堂归纳——感悟提升]——————————————[方法技巧]1.直线的斜率k 与倾斜角θ之间的关系2.求直线方程的方法(1)直接法:根据已知条件选择恰当的直线方程形式,直接求出直线方程.(2)待定系数法:先根据已知条件设出直线方程,再根据已知条件构造关于待定系数的方程(组),求出待定系数,从而求出直线方程.[易错防范]1.利用两点式计算斜率时易忽视x 1=x 2时斜率k 不存在的情况.2.用直线的点斜式求方程时,在斜率k 不明确的情况下,注意分k 存在与不存在讨论,否则会造成失误.3.直线的截距式中易忽视截距均不为0这一条件,当截距为0时可用点斜式.4.由一般式Ax +By +C =0确定斜率k 时易忽视判断B 是否为0的情况,当B =0时,k 不存在;当B ≠0时,k =-AB.[全盘巩固]一、选择题1.若方程(2m 2+m -3)x +(m 2-m )y -4m +1=0表示一条直线,则参数m 满足的条件是( ) A .m ≠-32 B .m ≠0C .m ≠0且m ≠1D .m ≠1解析:选D 由⎩⎪⎨⎪⎧2m 2+m -3=0,m 2-m =0,解得m =1,故m ≠1时方程表示一条直线.2.直线l :x sin 30°+y cos 150°+1=0的斜率是( ) A.33 B. 3 C .- 3 D .-33解析:选A 设直线l 的斜率为k ,则k =-sin 30°cos 150°=33.3.已知直线l :ax +y -2-a =0在x 轴和y 轴上的截距相等,则a 的值是( ) A .1 B .-1 C .-2或-1 D .-2或1 解析:选D 由题意可知a ≠0.当x =0时,y =a +2. 当y =0时,x =a +2a.∴a +2a=a +2,解得a =-2或a =1. 4.直线ax +by +c =0同时要经过第一、第二、第四象限,则a ,b ,c 应满足( ) A .ab >0,bc <0 B .ab >0,bc >0 C .ab <0,bc >0 D .ab <0,bc <0解析:选A 由于直线ax +by +c =0经过第一、二、四象限,所以直线存在斜率,将方程变形为y =-a b x -c b .易知-a b <0且-cb>0,故ab >0,bc <0.5.两直线x m -y n =a 与x n -ym=a (其中a 为不为零的常数)的图象可能是( )A B C D解析:选B 直线方程x m -y n =a 可化为y =n m x -na ,直线x n -y m =a 可化为y =mn x -ma ,由此可知两条直线的斜率同号.二、填空题6.若直线l 与直线y =1,x =7分别交于点P ,Q ,且线段PQ 的中点坐标为(1,-1),则直线l 的斜率为________.解析:设P (x P ,1),由题意及中点坐标公式得x P +7=2,解得x P =-5,即P (-5,1),所以k =-13. 答案:-137.过点M (-3,5)且在两坐标轴上的截距互为相反数的直线方程为________________. 解析:(1)当直线过原点时,直线方程为y =-53x ;(2)当直线不过原点时,设直线方程为x a +y-a =1,即x -y =a .代入点(-3,5),得a =-8. 即直线方程为x -y +8=0. 答案:y =-53x 或x -y +8=08.直线l :ax +(a +1)y +2=0的倾斜角大于45°,则a 的取值范围是________.解析:当a =-1时,直线l 的倾斜角为90°,符合要求;当a ≠-1时,直线l 的斜率为-a a +1,只要-a a +1>1或-a a +1<0即可,解得-1<a <-12或a <-1或a >0.综上可知,实数a 的取值范围是⎝⎛⎭⎫-∞,-12∪(0,+∞). 答案:⎝⎛⎭⎫-∞,-12∪(0,+∞) 三、解答题9.已知直线l 与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线l 的方程:(1)过定点A (-3,4); (2)斜率为16.解:(1)设直线l 的方程为y =k (x +3)+4,它在x 轴,y 轴上的截距分别是-4k -3,3k +4,由已知,得(3k +4)⎝⎛⎭⎫4k +3=±6, 解得k 1=-23或k 2=-83.故直线l 的方程为2x +3y -6=0或8x +3y +12=0.(2)设直线l 在y 轴上的截距为b ,则直线l 的方程是y =16x +b ,它在x 轴上的截距是-6b ,由已知,得|-6b ·b |=6,∴b =±1.∴直线l 的方程为x -6y +6=0或x -6y -6=0.10.如图,射线OA ,OB 分别与x 轴正半轴成45°和30°角,过点P (1,0)作直线AB 分别交OA ,OB 于A ,B 两点,当AB 的中点C 恰好落在直线y =12x 上时,求直线AB 的方程.解:由题意可得k OA =tan 45°=1, k OB =tan(180°-30°)=-33, 所以直线l OA :y =x ,l OB :y =-33x . 设A (m ,m ),B (-3n ,n ), 所以AB 的中点C ⎝⎛⎭⎪⎫m -3n 2,m +n 2,由点C 在直线y =12x 上,且A ,P ,B 三点共线得⎩⎨⎧m +n 2=12·m -3n2,m -0m -1=n -0-3n -1,解得m =3,所以A (3,3).又P (1,0),所以k AB =k AP =33-1=3+32,所以l AB :y =3+32(x -1),即直线AB 的方程为(3+3)x -2y -3-3=0.[冲击名校]1.在等腰三角形AOB 中,AO =AB ,点O (0,0),A (1,3),点B 在x 轴的正半轴上,则直线AB 的方程为( )A .y -1=3(x -3)B .y -1=-3(x -3)C .y -3=3(x -1)D .y -3=-3(x -1)解析:选D 因为AO =AB ,所以直线AB 的斜率与直线AO 的斜率互为相反数,所以k AB =-k OA =-3,所以直线AB 的点斜式方程为:y -3=-3(x -1).2.若直线ax +by =ab (a >0,b >0)过点(1,1),则该直线在x 轴,y 轴上的截距之和的最小值为( ) A .1 B .2 C .4 D .8解析:选C ∵直线ax +by =ab (a >0,b >0)过点(1,1), ∴a +b =ab ,即1a +1b =1,∴a +b =(a +b )⎝⎛⎭⎫1a +1b =2+b a +ab≥2+2b a ·ab=4, 当且仅当a =b =2时上式等号成立.∴直线在x 轴,y 轴上的截距之和的最小值为4.3.若ab >0,且A (a,0),B (0,b ),C (-2,-2)三点共线,则ab 的最小值为________. 解析:根据A (a,0),B (0,b )确定直线的方程为x a +yb =1,又C (-2,-2)在该直线上,故-2a +-2b =1,所以-2(a +b )=ab .又ab >0,故a <0,b <0.根据基本(均值)不等式ab =-2(a +b )≥4ab ,从而ab ≤0(舍去)或ab ≥4,故ab ≥16,当且仅当a =b =-4时取等号.即ab 的最小值为16.答案:164.已知直线PQ 的斜率为-3,将直线绕点P 顺时针旋转60°所得的直线的斜率为________.解析:直线PQ 的斜率为-3,则直线PQ 的倾斜角为120°,所求直线的倾斜角为60°,tan 60°= 3.答案: 35.已知A (3,0),B (0,4),直线AB 上一动点P (x ,y ),则xy 的最大值是________. 解析:直线AB 的方程为x 3+y4=1,设P (x ,y ),则x =3-34y ,∴xy =3y -34y 2=34(-y 2+4y )=34[-(y -2)2+4]≤3. 即当P 点坐标为⎝⎛⎭⎫32,2时,xy 取最大值3. 答案:36.设点A (-1,0),B (1,0),直线2x +y -b =0与线段AB 相交,则b 的取值范围是________. 解析:b 为直线y =-2x +b 在y 轴上的截距,如图,当直线y =-2x +b 过点A (-1,0)和点B (1,0)时,b 分别取得最小值和最大值. ∴b 的取值范围是[-2,2]. 答案:[-2,2]第二节 两直线的位置关系考纲要求:1.能根据两条直线的斜率判断这两条直线平行或垂直. 2.能用解方程组的方法求两条相交直线的交点坐标.3.掌握两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离.1.两条直线平行与垂直的判定 (1)两条直线平行①对于两条不重合的直线l 1,l 2,其斜率分别为k 1,k 2,则有l 1∥l 2⇔k 1=k 2; ②当不重合的两条直线l 1,l 2的斜率都不存在时,l 1与l 2的关系为平行. (2)两条直线垂直①如果两条直线l 1,l 2的斜率存在,设为k 1,k 2,则l 1⊥l 2⇔k 1k 2=-1;②如果l 1,l 2中有一条直线的斜率不存在,另一条直线的斜率为0时,l 1与l 2的关系为垂直. 2.两条直线的交点3.三种距离1.判断下列结论的正误.(正确的打“√”,错误的打“×”) (1)当直线l 1和l 2的斜率都存在时,一定有k 1=k 2⇒l 1∥l 2.( ) (2)如果两条直线l 1与l 2垂直,则它们的斜率之积一定等于-1.( )(3)已知直线l 1:A 1x +B 1y +C 1=0,l 2:A 2x +B 2y +C 2=0(A 1,B 1,C 1,A 2,B 2,C 2为常数),若直线l 1⊥l 2,则A 1A 2+B 1B 2=0.( )(4)l 1:y =k 1x +b 1,l 2:y =k 2x +b 2,当k 1≠k 2时,l 1与l 2相交.( )(5)过l 1:A 1x +B 1y +C 1=0,l 2:A 2x +B 2y +C 2=0的交点的直线方程为A 1x +B 1y +C 1+λ(A 2x +B 2y +C 2)=0(λ∈R ).( )(6)点P (x 0,y 0)到直线y =kx +b 的距离为|kx 0+b |1+k 2.( )(7)直线外一点与直线上一点的距离的最小值就是点到直线的距离.( ) 答案:(1)× (2)× (3)√ (4)√ (5)× (6)× (7)√ 2.已知直线l 过点P (1,2),直线l 1:2x +y -10=0. (1)若l ∥l 1,则直线l 的方程为________; (2)若l ⊥l 1,则直线l 的方程为________. 答案:(1)2x +y -4=0 (2)x -2y +3=03.经过两直线2x +y -8=0与x -2y +1=0的交点,且平行于直线4x -3y -7=0的直线方程为____________.答案:4x -3y -6=04.原点到直线x +2y -5=0的距离是________. 答案: 55.已知直线l 1的方程为3x +4y -7=0,直线l 2的方程为6x +8y +1=0,则直线l 1与l 2的距离为________.答案:32[典题1] (1)已知过点A (-2,m )和点B (m,4)的直线为l 1,直线2x +y -1=0为l 2,直线x +ny +1=0为l 3.若l 1∥l 2,l 2⊥l 3,则实数m +n 的值为________.(2)已知两条直线l 1:ax -by +4=0和l 2:(a -1)x +y +b =0,求满足下列条件的a ,b 的值. ①l 1⊥l 2,且l 1过点(-3,-1);②l 1∥l 2,且坐标原点到这两条直线的距离相等.[听前试做] (1)∵l 1∥l 2,∴k AB =4-m m +2=-2,解得m =-8.又∵l 2⊥l 3,∴⎝⎛⎭⎫-1n ×(-2)=-1. 解得n =-2,∴m +n =-10.(2)①由已知可得l 2的斜率存在,∴k 2=1-a . 若k 2=0,则1-a =0,a =1.∵l 1⊥l 2,直线l 1的斜率k 1必不存在,即b =0. 又∵l 1过点(-3,-1), ∴-3a +4=0,即a =43(矛盾),∴此种情况不存在,∴k 2≠0, 即k 1,k 2都存在. ∵k 2=1-a ,k 1=ab ,l 1⊥l 2,∴k 1k 2=-1,即ab (1-a )=-1.(*)又∵l 1过点(-3,-1), ∴-3a +b +4=0.(**)由(*)(**)联立,解得a =2,b =2. ②∵l 2的斜率存在,l 1∥l 2, ∴直线l 1的斜率存在,k 1=k 2,即ab=1-a .(ⅰ)又∵坐标原点到这两条直线的距离相等,且l 1∥l 2, ∴l 1,l 2在y 轴上的截距互为相反数,即4b =b .(ⅱ)联立(ⅰ)(ⅱ),解得⎩⎪⎨⎪⎧a =2,b =-2或⎩⎪⎨⎪⎧a =23,b =2.∴a =2,b =-2或a =23,b =2.答案:(1)-10(1)当直线方程中存在字母参数时,不仅要考虑到斜率存在的一般情况,也要考虑到斜率不存在的特殊情况.同时还要注意x 、y 的系数不能同时为零这一隐含条件.(2)在判断两直线平行、垂直时,也可直接利用直线方程的系数间的关系得出结论.[典题2] 经过两直线l 1:x -2y +4=0和l 2:x +y -2=0的交点P ,且与直线l 3:3x -4y +5=0垂直的直线l 的方程为________________.[听前试做] 法一:由方程组⎩⎪⎨⎪⎧ x -2y +4=0,x +y -2=0,得⎩⎪⎨⎪⎧x =0,y =2,即P (0,2).∵l ⊥l 3,∴直线l 的斜率k 1=-43,∴直线l 的方程为y -2=-43x ,即4x +3y -6=0.法二:∵直线l 过直线l 1和l 2的交点,∴可设直线l 的方程为x -2y +4+λ(x +y -2)=0, 即(1+λ)x +(λ-2)y +4-2λ=0. ∵l 与l 3垂直,∴3(1+λ)+(-4)(λ-2)=0,∴λ=11,∴直线l 的方程为12x +9y -18=0,即4x +3y -6=0.答案:4x +3y -6=0[探究] 若将本例中的“垂直”改为“平行”,如何求解?解:法一:由方程组⎩⎪⎨⎪⎧ x -2y +4=0,x +y -2=0,得⎩⎪⎨⎪⎧x =0,y =2,即P (0,2).∵l ∥l 3,∴直线l 的斜率k 1=34,∴直线l 的方程为y -2=34x ,即3x -4y +8=0.法二:∵直线l 过直线l 1和l 2的交点,∴可设直线l 的方程为x -2y +4+λ(x +y -2)=0, 即(1+λ)x +(λ-2)y +4-2λ=0. ∵l 与l 3平行,∴3(λ-2)-(-4)(1+λ)=0,且(-4)(4-2λ)≠5(λ-2),∴λ=27,∴直线l 的方程为3x -4y +8=0.(1)两直线交点的求法求两直线的交点坐标,就是解由两直线方程组成的方程组,以方程组的解为坐标的点即为交点. (2)常见的三大直线系方程①与直线Ax +By +C =0平行的直线系方程是 Ax +By +m =0(m ∈R 且m ≠C ).②与直线Ax +By +C =0垂直的直线系方程是 Bx -Ay +m =0(m ∈R ).③过直线l 1:A 1x +B 1y +C 1=0与l 2:A 2x +B 2y +C 2=0的交点的直线系方程为A 1x +B 1y +C 1+λ(A 2x +B 2y +C 2)=0(λ∈R ),但不包括l 2.[典题3] 已知点P (2,-1).(1)求过点P 且与原点的距离为2的直线l 的方程.(2)求过点P 且与原点的距离最大的直线l 的方程,最大距离是多少?(3)是否存在过点P 且与原点的距离为6的直线?若存在,求出方程;若不存在,请说明理由.[听前试做] (1)过点P 的直线l 与原点的距离为2,而点P 的坐标为(2,-1),显然,过P (2,-1)且垂直于x 轴的直线满足条件,此时l 的斜率不存在,其方程为x =2. 若斜率存在,设l 的方程为y +1=k (x -2), 即kx -y -2k -1=0.由已知得|-2k -1|k 2+1=2,解得k =34.此时l 的方程为3x -4y -10=0.综上,可得直线l 的方程为x =2或3x -4y -10=0.(2)作图可得过点P 与原点O 的距离最大的直线是过点P 且与PO 垂直的直线,如图.由l ⊥OP ,得k l k OP =-1,所以k l =-1k OP =2.由直线方程的点斜式得y +1=2(x -2), 即2x -y -5=0.所以直线2x -y -5=0是过点P 且与原点O 的距离最大的直线,最大距离为|-5|5= 5.(3)由(2)可知,过点P 不存在到原点的距离超过5的直线,因此不存在过点P 且到原点的距离为6的直线.利用距离公式应注意:(1)点P (x 0,y 0)到直线x =a 的距离d =|x 0-a |,到直线y =b 的距离d =|y 0-b |; (2)两平行线间的距离公式要把两直线方程中x ,y 的系数化为相等.1.已知两条平行直线l 1:mx +8y +n =0与l 2:2x +my -1=0间的距离为5,则直线l 1的方程为___________________.解析:∵l 1∥l 2,∴m 2=8m ≠n-1,∴⎩⎪⎨⎪⎧m =4,n ≠-2或⎩⎨⎧m =-4,n ≠2.①当m =4时,直线l 1的方程为4x +8y +n =0, 把l 2的方程写成4x +8y -2=0, ∴|n +2|16+64=5,解得n =-22或18.故所求直线l 1的方程为2x +4y -11=0或2x +4y +9=0. ②当m =-4时,直线l 1的方程为4x -8y -n =0, 把l 2的方程写成为4x -8y -2=0, ∴|-n +2|16+64=5,解得n =-18或22. 故所求直线l 1的方程为2x -4y +9=0或2x -4y -11=0. 答案:2x ±4y +9=0或2x ±4y -11=02.直线l 过点P (-1,2)且到点A (2,3)和点B (-4,5)的距离相等,则直线l 的方程为________. 解析:法一:当直线l 的斜率存在时,设直线l 的方程为y -2=k (x +1),即kx -y +k +2=0. 由题意知|2k -3+k +2|k 2+1=|-4k -5+k +2|k 2+1,即|3k -1|=|-3k -3|,∴k =-13.∴直线l 的方程为y -2=-13(x +1),即x +3y -5=0.当直线l 的斜率不存在时,直线l 的方程为x =-1,也符合题意.法二:当AB ∥l 时,有k =k AB =-13,直线l 的方程为y -2=-13(x +1),即x +3y -5=0.当l 过AB 中点时,AB 的中点为(-1,4). ∴直线l 的方程为x =-1.故所求直线l 的方程为x +3y -5=0或x =-1. 答案:x +3y -5=0或x =-1对称问题是高考常考内容之一,也是考查学生转化能力的一种常见题型,且主要有以下几个命题角度:角度一:点关于点的中心对称问题[典题4] 过点P (0,1)作直线l ,使它被直线l 1:2x +y -8=0和l 2:x -3y +10=0截得的线段被点P 平分,则直线l 的方程为________________.[听前试做] 设l 1与l 的交点为A (a,8-2a ),则由题意知,点A 关于点P 的对称点B (-a,2a -6)在l 2上,代入l 2的方程得-a -3(2a -6)+10=0,解得a =4,即点A (4,0)在直线l 上,所以直线l 的方程为x +4y -4=0.答案:x +4y -4=0角度二:点关于直线的对称问题[典题5] 已知直线l :2x -3y +1=0,点A (-1,-2),则点A 关于直线l 的对称点A ′的坐标为________.[听前试做] 设A ′(x ,y ),由已知得⎩⎨⎧y +2x +1×23=-1,2×x -12-3×y -22+1=0,解得⎩⎨⎧x =-3313,y =413,故A ′⎝⎛⎭⎫-3313,413. 答案:⎝⎛⎭⎫-3313,413 角度三:直线关于直线的对称问题[典题6] 已知直线l :2x -3y +1=0,求直线m :3x -2y -6=0关于直线l 的对称直线m ′的方程.[听前试做] 在直线m 上任取一点,如M (2,0),则M (2,0)关于直线l 的对称点M ′必在直线m ′上.设对称点M ′(a ,b ),则⎩⎨⎧2×⎝ ⎛⎭⎪⎫a +22-3×⎝ ⎛⎭⎪⎫b +02+1=0,b -0a -2×23=-1,解得⎩⎨⎧a =613,b =3013,∴M ′⎝⎛⎭⎫613,3013.设直线m 与直线l 的交点为N ,则由⎩⎪⎨⎪⎧2x -3y +1=0,3x -2y -6=0,得N (4,3). 又∵m ′经过点N (4,3),∴由两点式得直线m ′的方程为9x -46y +102=0. 角度四:对称问题的应用[典题7] 在等腰直角三角形ABC 中,AB =AC =4,点P 是边AB 上异于A ,B 的一点.光线从点P 出发,经BC ,CA 反射后又回到点P (如图).若光线QR 经过△ABC 的重心,则AP 等于________.[听前试做] 以AB 、AC 所在直线分别为x 轴、y 轴 建立如图所示平面直角坐标系,则A (0,0),B (4,0),C (0,4),得△ABC 的重心D ⎝⎛⎭⎫43,43, 设AP =x ,P (x,0),x ∈(0,4),由光的反射定理,知点P 关于直线BC 、AC 的对称点P 1(4,4-x )、P 2(-x,0),与△ABC 的重心D 43,43共线, 所以4343+x =43-(4-x )43-4,求得x =43,AP =43.答案:43(1)点P (x ,y )关于O (a ,b )的对称点P ′(x ′,y ′)满足⎩⎪⎨⎪⎧x ′=2a -x ,y ′=2b -y .(如角度一)(2)解决点关于直线对称问题要把握两点,点M 与点N 关于直线l 对称,则线段MN 的中点在直线l 上,直线l 与直线MN 垂直.(如角度二)(3)若直线l 1、l 2关于直线l 对称,则有如下性质:①若直线l 1与l 2相交,则交点在直线l 上;②若点B 在直线l 1上,则其关于直线l 的对称点B ′在直线l 2上.(如角度三)(4)解决中心对称问题的关键在于运用中点坐标公式,而解决轴对称问题,一般是转化为求对称点的问题,在求对称点时,关键是抓住两点:一是两对称点的连线与对称轴垂直;二是两对称点的中心在对称轴上,即抓住“垂直平分”,由“垂直”列出一个方程,由“平分”列出一个方程,联立求解.(如角度四)—————————————[课堂归纳——感悟提升]——————————————[方法技巧]1.两直线的位置关系要考虑平行、垂直和重合.对于斜率都存在且不重合的两条直线l 1,l 2,l 1∥l 2⇔k 1=k 2;l 1⊥l 2⇔k 1·k 2=-1.2.与已知直线垂直及平行的直线系的设法与直线Ax +By +C =0(A 2+B 2≠0)垂直和平行的直线方程可设为: (1)垂直:Bx -Ay +m =0; (2)平行:Ax +By +n =0.3.直线l 1:A 1x +B 1y +C 1=0(A 21+B 21≠0),l 2:A 2x +B 2y +C 2=0(A 22+B 22≠0),则:(1)l 1⊥l 2⇔A 1A 2+B 1B 2=0; (2)l 1∥l 2⇔A 1A 2=B 1B 2≠C 1C 2(A 2B 2C 2≠0);(3)l 1与l 2相交⇔A 1A 2≠B 1B 2(A 2B 2≠0);(4)l 1与l 2重合⇔A 1A 2=B 1B 2=C 1C 2(A 2B 2C 2≠0).4.对称问题一般是将线与线的对称转化为点与点的对称,利用坐标转移法.[易错防范]1.在判断两条直线的位置关系时,首先应分析直线的斜率是否存在.若两条直线都有斜率,可根据判定定理判断,若直线无斜率时,要单独考虑;2.运用两平行直线间的距离公式d =|C 1-C 2|A 2+B2的前提是将两方程中的x ,y 的系数化为对应相等.[全盘巩固]一、选择题1.当0<k <12时,直线l 1:kx -y =k -1与直线l 2:ky -x =2k 的交点在( )A .第一象限B .第二象限C .第三象限D .第四象限解析:选B 解方程组⎩⎪⎨⎪⎧kx -y =k -1,ky -x =2k ,得交点为⎝ ⎛⎭⎪⎫k k -1,2k -1k -1.因为0<k <12,所以kk -1<0,2k -1k -1>0.故交点在第二象限. 2.若直线l 1:ax +2y +6=0与直线l 2:x +(a -1)y +a 2-1=0垂直,则实数a =( ) A.23B .-1C .2D .-1或2 解析:选A ∵a ×1+(a -1)×2=0,∴a =23.3.若直线l 1:x -2y +m =0(m >0)与直线l 2:x +ny -3=0之间的距离是5,则m +n =( ) A .0 B .1 C .-1 D .2解析:选A ∵直线l 1:x -2y +m =0(m >0)与直线l 2:x +ny -3=0之间的距离为5,∴⎩⎨⎧n =-2,|m +3|5=5,∴n =-2,m =2(负值舍去).∴m +n =0.4.已知直线l 1:y =2x +3,直线l 2与l 1关于直线y =-x 对称,则直线l 2的斜率为( ) A.12 B .-12C .2D .-2 解析:选A 因为l 1,l 2关于直线y =-x 对称,所以l 2的方程为-x =-2y +3,即y = 12x +32,即直线l 2的斜率为12.5.已知A ,B 两点分别在两条互相垂直的直线2x -y =0和x +ay =0上,且AB 线段的中点为P ⎝⎛⎭⎫0,10a ,则线段AB 的长为( ) A .11 B .10 C .9 D .8解析:选B 依题意,a =2,P (0,5),设A (x,2x ),B (-2y ,y ),故⎩⎪⎨⎪⎧x -2y =0,2x +y =10,则A (4,8),B (-4,2),∴|AB |=(4+4)2+(8-2)2=10.二、填空题6.已知直线l 1:(3+m )x +4y =5-3m ,l 2:2x +(5+m )y =8, l 1∥l 2,则实数m 的值为________. 解析:由(3+m )(5+m )-4×2=0,得m =-1或m =-7, 当m =-1时,直线l 1与l 2重合,舍去; 当m =-7时,5-3m 4=132≠85+m ,两直线平行.答案:-77.若三条直线y =2x ,x +y =3,mx +2y +5=0相交于同一点,则m 的值为________.解析:由⎩⎪⎨⎪⎧ y =2x ,x +y =3,得⎩⎪⎨⎪⎧x =1,y =2.∴点(1,2)满足方程mx +2y +5=0, 即m ×1+2×2+5=0,∴m =-9. 答案:-98.已知l 1,l 2是分别经过A (1,1),B (0,-1)两点的两条平行直线,当l 1,l 2间的距离最大时,则直线l 1的方程是__________________________.解析:当直线AB 与l 1,l 2垂直时,l 1,l 2间的距离最大.因为A (1,1),B (0,-1),所以k AB =-1-10-1=2,所以两平行直线的斜率为k =-12,所以直线l 1的方程是y -1=-12(x -1),即x +2y -3=0.答案:x +2y -3=0 三、解答题9.正方形的中心为点C (-1,0),一条边所在的直线方程是x +3y -5=0,求其他三边所在直线的方程.解:点C 到直线x +3y -5=0的距离d =|-1-5|1+9=3105.设与x +3y -5=0平行的一边所在直线的方程是x +3y +m =0(m ≠-5), 则点C 到直线x +3y +m =0的距离 d =|-1+m |1+9=3105,解得m =-5(舍去)或m =7,所以与x +3y -5=0平行的边所在直线的方程是x +3y +7=0. 设与x +3y -5=0垂直的边所在直线的方程是3x -y +n =0, 则点C 到直线3x -y +n =0的距离 d =|-3+n |1+9=3105,解得n =-3或n =9,所以与x +3y -5=0垂直的两边所在直线的方程分别是3x -y -3=0和3x -y +9=0. 10.已知△ABC 的顶点A (5,1),AB 边上的中线CM 所在直线方程为2x -y -5=0,AC 边上的高BH 所在直线方程为x -2y -5=0,求直线BC 的方程.解:依题意知:k AC =-2,A (5,1), ∴l AC 为2x +y -11=0,联立l AC ,l CM 得⎩⎪⎨⎪⎧2x +y -11=0,2x -y -5=0,∴C (4,3).设B (x 0,y 0),AB 的中点M 为⎝⎛⎭⎪⎫x 0+52,y 0+12,代入2x -y -5=0,得2x 0-y 0-1=0,∴⎩⎪⎨⎪⎧2x 0-y 0-1=0,x 0-2y 0-5=0,∴B (-1,-3), ∴k BC =65,∴直线BC 的方程为y -3=65(x -4),即6x -5y -9=0.[冲击名校]1.若动点P 1(x 1,y 1),P 2(x 2,y 2)分别在直线l 1:x -y -5=0,l 2:x -y -15=0上移动,则P 1P 2的中点P 到原点的距离的最小值是( )A.522 B .5 2 C.1522D .15 2解析:选B由题意得P1P2的中点P的轨迹方程是x-y-10=0,则原点到直线x-y-10=0的距离为d=102=5 2.2.若直线l1:y=k(x-4)与直线l2关于点(2,1)对称,则直线l2恒过定点()A.(0,4) B.(0,2)C.(-2,4) D.(4,-2)解析:选B直线l1:y=k(x-4)恒过定点(4,0),其关于点(2,1)对称的点为(0,2).又由于直线l1:y=k(x-4)与直线l2关于点(2,1)对称,故直线l2恒过定点(0,2).3.设A,B是x轴上的两点,点P的横坐标为3,且|P A|=|PB|,若直线P A的方程为x-y+1=0,则直线PB的方程是()A.x+y-5=0 B.2x-y-1=0C.x-2y+4=0 D.x+y-7=0解析:选D由|P A|=|PB|知点P在AB的垂直平分线上.由点P的横坐标为3,且P A的方程为x-y+1=0,得P(3,4).直线P A,PB关于直线x=3对称,直线P A上的点(0,1)关于直线x=3的对称点(6,1)在直线PB上,∴直线PB的方程为x+y-7=0.4.若在平面直角坐标系内过点P(1,3),且与原点的距离为d的直线有两条,则d的取值范围为________.解析:因为原点到点P的距离为2,所以过点P的直线与原点的距离都不大于2,故d∈(0,2).答案:(0,2)5.如图,已知A(-2,0),B(2,0),C(0,2),E(-1,0),F(1,0),一束光线从F点出发射到BC上的D点,经BC反射后,再经AC反射,落到线段AE上(不含端点),则直线FD的斜率的取值范围为________.解析:从特殊位置考虑.如图,∵点A(-2,0)关于直线BC:x+y=2的对称点为A1(2,4),∴kA1F=4.又点E(-1,0)关于直线AC:y=x+2的对称点为E1(-2,1),点E1(-2,1)关于直线BC:x+y=2的对称点为E2(1,4),此时直线E2F的斜率不存在,∴k FD>kA1F,即k FD∈(4,+∞).答案:(4,+∞)6.设m∈R,过定点A的动直线x+my=0和过定点B的动直线mx-y-m+3=0交于点P(x,y),则|P A|·|PB|的最大值是________.解析:易求定点A(0,0),B(1,3).当P与A和B均不重合时,因为P为直线x+my=0与mx-y-m+3=0的交点,且易知两直线垂直,则P A⊥PB,所以|P A|2+|PB|2=|AB|2=10,所以|P A|·|PB|≤|P A|2+|PB|22=5(当且仅当|P A|=|PB|=5时,等号成立);当P与A或B重合时,|P A|·|PB|=0,故|P A|·|PB|的最大值是5.答案:5第三节圆的方程考纲要求:1.掌握确定圆的几何要素.2.掌握圆的标准方程与一般方程.1.圆的定义及方程2.(1)理论依据:点与圆心的距离与半径的大小关系.(2)三种情况圆的标准方程(x-a)2+(y-b)2=r2,点M(x0,y0),①(x0-a)2+(y0-b)2=r2⇔点在圆上;②(x0-a)2+(y0-b)2>r2⇔点在圆外;③(x0-a)2+(y0-b)2<r2⇔点在圆内.[自我查验] 1.判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)确定圆的几何要素是圆心与半径.()(2)已知点A (x 1,y 1),B (x 2,y 2),则以AB 为直径的圆的方程是(x -x 1)(x -x 2)+(y -y 1)(y -y 2)=0.( )(3)方程Ax 2+Bxy +Cy 2+Dx +Ey +F =0表示圆的充要条件是A =C ≠0,B =0,D 2+E 2-4F >0.( )(4)若点M (x 0,y 0)在圆x 2+y 2+Dx +Ey +F =0外,则x 20+y 20+Dx 0+Ey 0+F >0.( )(5)已知圆的方程为x 2+y 2-2y =0,过点A (1,2)作该圆的切线只有一条.( ) 答案:(1)√ (2)√ (3)× (4)√ (5)×2.方程x 2+y 2+ax +2ay +2a 2+a -1=0表示圆,则a 的取值范围是( ) A .(-∞,-2)∪⎝⎛⎭⎫23,+∞ B.⎝⎛⎭⎫-23,0 C .(-2,0) D.⎝⎛⎭⎫-2,23 解析:选D 由题意知a 2+4a 2-4(2a 2+a -1)>0,解得-2<a <23.3.将圆x 2+y 2-2x -4y +1=0平分的直线是( ) A .x +y -1=0 B .x +y +3=0 C .x -y +1=0 D .x -y +3=0解析:选C 要使直线平分圆,只要直线经过圆的圆心即可,圆心坐标为(1,2).A ,B ,C ,D 四个选项中,只有C 选项中的直线经过圆心.4.若点(1,1)在圆(x -a )2+(y +a )2=4的内部,则实数a 的取值范围是________. 解析:因为点(1,1)在圆(x -a )2+(y +a )2=4的内部,所以(1-a )2+(1+a )2<4. 即a 2<1,故-1<a <1. 答案:(-1,1)5.经过三点(2,-1)、(5,0)、(6,1)的圆的一般方程为________________. 解析:设所求方程为x 2+y 2+Dx +Ey +F =0,则⎩⎪⎨⎪⎧22+(-1)2+2D -E +F =0,52+02+5D +0+F =0,62+12+6D +E +F =0,解得⎩⎪⎨⎪⎧D =-4,E =-8,F =-5,故所求圆的一般方程为x 2+y 2-4x -8y -5=0. 答案:x 2+y 2-4x -8y -5=0[典题1] 根据下列条件,求圆的方程.(1)经过点A (5,2),B (3,-2),且圆心在直线2x -y -3=0上; (2)经过P (-2,4)、Q (3,-1)两点,并且在x 轴上截得的弦长等于6; (3)圆心在直线y =-4x 上,且与直线l :x +y -1=0相切于点P (3,-2). [听前试做] (1)法一:由题意知k AB =2,AB 的中点为(4,0),设圆心为C (a ,b ), ∵圆过A (5,2),B (3,-2)两点, ∴圆心一定在线段AB 的垂直平分线上.则⎩⎨⎧ba -4=-12,2a -b -3=0,解得⎩⎪⎨⎪⎧a =2,b =1,∴C (2,1),∴r =|CA |=(5-2)2+(2-1)2=10.∴所求圆的方程为(x -2)2+(y -1)2=10. 法二:设圆的方程为(x -a )2+(y -b )2=r 2, 则⎩⎪⎨⎪⎧2a -b -3=0,(5-a )2+(2-b )2=r 2,(3-a )2+(-2-b )2=r 2,解得⎩⎪⎨⎪⎧a =2,b =1,r =10,故圆的方程为(x -2)2+(y -1)2=10.法三:设圆的方程为x 2+y 2+Dx +Ey +F =0(D 2+E 2-4F >0), 则⎩⎪⎨⎪⎧25+4+5D +2E +F =0,9+4+3D -2E +F =0,2×⎝⎛⎭⎫-D 2+E 2-3=0,解得⎩⎪⎨⎪⎧D =-4,E =-2,F =-5,∴所求圆的方程为x 2+y 2-4x -2y -5=0.(2)设圆的方程为x 2+y 2+Dx +Ey +F =0,将P 、Q 两点的坐标分别代入得⎩⎪⎨⎪⎧ 2D -4E -F =20,3D -E +F =-10.①②又令y =0,得x 2+Dx +F =0.③ 设x 1,x 2是方程③的两根, 由|x 1-x 2|=6有D 2-4F =36,④ 由①、②、④解得D =-2,E =-4, F =-8,或D =-6,E =-8,F =0.故所求圆的方程为x 2+y 2-2x -4y -8=0,或x 2+y 2-6x -8y =0. (3)法一:如图,设圆心(x 0,-4x 0),依题意得4x 0-23-x 0=1,∴x 0=1,即圆心坐标为(1,-4),半径r =22,故圆的方程为(x -1)2+(y +4)2=8. 法二:设所求方程为(x -x 0)2+(y -y 0)2=r 2,根据已知条件得⎩⎪⎨⎪⎧y 0=-4x 0,(3-x 0)2+(-2-y 0)2=r 2,|x 0+y 0-1|2=r ,解得⎩⎪⎨⎪⎧x 0=1,y 0=-4,r =2 2.因此所求圆的方程为(x -1)2+(y +4)2=8.求圆的方程的方法(1)方程选择原则求圆的方程时,如果由已知条件易求得圆心坐标、半径或需要用圆心坐标列方程,常选用标准方程;如果已知条件与圆心坐标、半径无直接关系,常选用一般方程.(2)求圆的方程的方法和步骤确定圆的方程的主要方法是待定系数法,大致步骤如下: ①根据题意,选择标准方程或一般方程;②根据条件列出关于a ,b ,r 或D ,E ,F 的方程组; ③解出a ,b ,r 或D ,E ,F 代入标准方程或一般方程.(2015·江苏高考)在平面直角坐标系xOy 中,以点(1,0)为圆心且与直线mx -y -2m -1=0(m ∈R )相切的所有圆中,半径最大的圆的标准方程为________________.解析:直线mx -y -2m -1=0经过定点(2,-1).当圆与直线相切于点(2,-1)时,圆的半径最大,此时半径r 满足r 2=(1-2)2+(0+1)2=2. 答案:(x -1)2+y 2=2与圆有关的最值问题也是命题的热点内容,它着重考查数形结合与转化思想.归纳起来常见的命题角度有:角度一:斜率型最值问题[典题2] 已知实数x ,y 满足方程x 2+y 2-4x +1=0,则yx 的最大值为________,最小值为________.[听前试做] 原方程可化为(x -2)2+y 2=3,表示以(2,0)为圆心,3为半径的圆.yx 的几何意义是圆上一点与原点连线的斜率,所以设yx =k ,即y =kx .当直线y =kx 与圆相切时,斜率k 取最大值或最小值(如图),此时|2k -0|k 2+1=3,解得k =±3,所以yx的最大值为3,最小值为- 3.答案:3 - 3 角度二:截距型最值问题[典题3] 在典题2条件下,求y -x 的最大值.。
高数答案第9章

第9章(之1) (总第44次)*1. 微分方程7359)(2xy y y y =''''-''的阶数是 ( ) (A )3; (B )4; (C )6; (D )7. 答案(A )解 微分方程的阶数是未知函数导数的最高阶的阶数.*2. 下列函数中的C 、α、λ及k 都是任意常数,这些函数中是微分方程04=+''y y 的通解的函数是 ( ) (A )x C x C y 2sin )2912(2cos 3-+=; (B ))2sin 1(2cos x x C y λ+=; (C )x C k x kC y 2sin 12cos 22++=; (D ))2cos(α+=x C y . 答案 (D )解 二阶微分方程的通解中应该有两个独立的任意常数. (A )中的函数只有一个任意常数C ;(B )中的函数虽然有两个独立的任意常数,但经验算它不是方程的解;(C )中的函数从表面上看来也有两个任意常数C 及k ,但当令kC C =时,函数就变成了x C x C y 2sin 12cos 2++=,实质上只有一个任意常数;(D )中的函数确实有两个独立的任意常数,而且经验算它也确实是方程的解.*3.在曲线族 xxec e c y -+=21中,求出与直线x y =相切于坐标原点的曲线.解 根据题意条件可归结出条件1)0(,0)0(='=y y , 由xxe c e c y -+=21, xx ec e c y --='21,可得1,02121=-=+c c c c ,故21,2121-==c c ,这样就得到所求曲线为)(21x x e e y --=,即x y sinh =.*4.证明:函数y e x x =-2333212sin 是初值问题⎪⎪⎩⎪⎪⎨⎧===++==1d d ,00d d d d 0022x x x y y y x yx y 的解.证明 '=-+--y e x e x x x 3332321212sin cos ,''=----y e x e x x x 3332321212sin cos ,代入方程得 ''+'+=y y y 0, 此外,,1)0(0)0(='=y y 故y e x x =-2333212sin 是初始值问题的解.*5.验证y e e t Ce x t xx=+⎰20d (其中C 为任意常数)是方程'-=+y ye x x 2的通解.证明 '=+⋅+⎰y ee t e e Ce xt xx x x 220d =++ye x x 2, 即 2x x e y y +=-',说明函数确实给定方程的解.另一方面函数y ee t Ce xt x x=+⎰2d 含有一任意常数C ,所以它是方程的通解.**6.求以下列函数为通解的微分方程: (1)31+=Cx y ;解 将等式31+=Cx y 改写为13+=Cx y ,再在其两边同时对x 求导,得C y y ='23,代入上式,即可得到所求之微分方程为1332-='y y xy . (2)xC x C y 21+=. 解 因为给定通解的函数式中有两个独立的任意常数,所以所求方程一定是二阶方程,在方程等式两边同时对x 求两次导数,得221x C C y -=',322xC y =''. 从以上三个式子中消去任意常数1C 和2C ,即可得到所求之微分方程为02=-'+''y y x y x .**7.建立共焦抛物线族)(42C x C y +=(其中C 为任意常数)所满足的微分方程[这里的共焦抛物线族是以x 轴为对称轴,坐标原点为焦点的抛物线].解 在方程)(42C x C y +=两边对x 求导有C y y 42=',从这两式中消去常数所求方程为)2(y y x y y '+'=.**8.求微分方程,使它的积分曲线族中的每一条曲线)(x y y =上任一点处的法线都经过坐标原点.解 任取)(x y y =上的点 ),(y x ,曲线在该点处的切线斜率为 y '=dxdy . 所以过点),(y x 的法线斜率为y '-1, 法线方程为y Y -=y '-1)(x X -, 因为法线过原点,所以=-y 0y '-1)0(x -从而可得所求微分方程为0='+y y x .第9章(之2)(总第45次)教学容:§9.2 .1可分离变量的方程; §9.2 .2一阶线性方程**1.求下列微分方程的通解:(1)21)1(x y x y +-=';解: 分离变量21d 1d x x x y y +=-,两边积分⎰⎰+=-21d 1d x xx y y , 得C x y ln )1ln(21)1ln(2-+=--,即211xC y +-=. (2)222y x e yx y -='; 解:分离变量x xe y ye x y d d 222=,两边积分就得到了通解)d (21222x e xe e x x y ⎰-=c e xe x x +-=)21(2122.(3)042)12(=-+'+y y e y e x .解: 12d 42d +-=-x xe y e y y ,C x e y ln 21)12ln(21)2ln(21++-=-, 即 ()()e x C y-+=221.**2.试用两种不同的解法求微分方程xy y x y +--='1的通解.解法一 (可分离变量方程的分离变量法)这是一个一阶可分离变量方程,同时也是一个一阶线性非齐次方程,这时一般作为可分离变量方程求解较为容易. 分离变量,)1)(1(y x y --=',x x y y d )1(1d -=-,并积分 x x y yd )1(1d -=-⎰⎰ 得c x x y +-=--221)1ln(,所求通解为 x x ce y -+=2211.解法二 (线性方程的常数变易法)将原方程改写为x y x y -=-+'1)1(,这是一个一阶线性非齐次方程.对应的齐次方程为0)1(=-+'y x y ,其通解为○1x x e C y -=221.代入原非齐次方程得x e C x x -='-1221,解得○2C eC x x +=-221,○2代入○1即可得原方程的通解xx Cey -+=2211.*3.求解下列初值问题:(1)21x yy -=',6)21(πe y -=.解:Θy '=21xy -,∴21d d xx y y -= (0≠y ), 21d d xx y y -=⎰⎰,∴C x y +=arcsin ln , ∴ x Ce y arcsin =,Θπ6)21(e y -=,∴21arcsin 6Ce e =-π,∴1-=C , ∴ x e y arcsin -=.(2)22x e xy y -=+',1)0(=y ;解: Θ22x e xy y -=+', x x p 2)(=∴,2)(x e x q -=,=∴)(x y ⎰-xx ed 2⎥⎦⎤⎢⎣⎡+⎰⎰-C dx e e x x x d 222x e -=⎥⎦⎤⎢⎣⎡+⎰⎰-C dx e e x x x d 2222x x Ce xe --+=, Θ 1)0(=y , 101=⇒+=∴c c , 2)1(x e x y -+=∴.(3)xex y y cos cot =+',1)2(=πy ;解: Θ xex y y cos cot =+', ∴x x P cot )(=,xex Q cos )(=.∴ ⎥⎦⎤⎢⎣⎡⎰+⎰=⎰-x C y xx x x x d e e e d cot cos d cot )d e e (e sin ln cos sin ln ⎰+=-x C x x x)d sin e (csc cos ⎰+=x x C x x x C xcsc )e(cos -=,由1)2(=πy , 可确定 2=C ,所以x y x csc )e 2(cos -=.(4)0d )12(d 2=+-+x x xy y x ,01==x y .解: 方程变形为 2112xx y x y -=+',是一阶线性非齐次方程,其通解为⎥⎦⎤⎢⎣⎡⎰-+⎰=⎰-dx ex x c e y dx x dx x 222)11( ⎥⎦⎤⎢⎣⎡-+=⎰dx x x x c x 222)11(1⎥⎦⎤⎢⎣⎡-+=x x c x22211x xc 1212-+= 由 0)1(=y , 得 21=c , 所以特解为:x xy 121212-+=.**4.求微分方程 0d )ln (d ln =-+y y x x y y 的通解(提示将x 看作是y 的函数). 解:将x 看作是y 的函数,原方程可化为yx y y dy dx 1ln 1=+,这是一阶线性方程,将其中yy Q y y y P 1)( ,ln 1)(==代入一阶线性方程求解公式,得通解 1e 1)ln(ln )ln(ln ln 1ln 1⎥⎦⎤⎢⎣⎡+=⎥⎥⎦⎤⎢⎢⎣⎡⎰+⎰=⎰⎰--dy e y c dy ey c e x y y dy y y dy y y y y c dy y y c y ln 21ln ln ln 1+=⎥⎦⎤⎢⎣⎡+=⎰.**5.求满足关系式)(d )(22x y x u u uy x +=⎰的可导函数)(x y .解:这是一个积分方程,在方程等式两边同对x 求导,可得微分方程xy x x y x()d d =+2,即d d yxxy x -=-2,分离变量得d d y y x x -=2,积分得y Ce x =+222,在原方程两边以2=x 代入,可得初试条件22-==x y.据此可得14--=e C ,所以原方程的解为 24122+-=-x e y .**6.设降落伞自塔顶自由下落,已知阻力与速度成正比(比例系数为k ),求降落伞的下落速度与时间的函数关系. 解:根据牛顿运动第二定理有kv mg tvm -=d d .这是一个可分离变量方程,分离变量并积分得--=+1k mg kv tmC ln(). 由初始条件0)0(=v , 得)ln(1mg k C -=,即得 v mg k e kmt =-⎛⎝ ⎫⎭⎪-1.**7.求一曲线,已知曲线过点)1,0(,且其上任一点),(y x 的法线在x 轴上的截距为kx . 解:曲线在点(,)x y 处的法线斜率为y '-1,所以法线方程为Y y y X x -=-'-1().只要令0=Y ,就可以得到法线在x 轴上的截距为 y y x X '+= .据题意可得微分方程x yy kx +'=,即x k y y )1(-='.这是一个可分离变量方程,分离变量并积分得所求曲线C x k y =-+22)1(,由于曲线过点)1,0(,所以1=C ,所以所求曲线方程为 y k x 2211+-=().***8.求与抛物线族2Cx y =(C 是常数)中任一抛物线都正交的曲线(族)的方程. 解:在给定曲线2cx y =上任意一点),(y x 处切线斜率为cx y k 20='=,从上面两式中消去c 得x y y k 20='=,这样就得到了给定曲线族所满足的微分方程xyy 2='. 设所求曲线方程为 )(x y y =,在同一点),(y x 处切线斜率为y k '=,则根据正交要求有10-=k k ,这样就得到了所求曲线族应该满足的微分方程yx y 2-='. 这是一个可分离变量方程,分离变量xdx ydy -=2,积分得所求曲线族c x y +-=2221,即椭圆族c x y =+2221. ***9.作适当变换,求微分方程 1224+-='-x e y y的通解. 解 原方程可化为4122=++'y ye x y e ,在换元y e z =下方程可化为4122=++'x zz ,这是一个一阶线性方程,其通解为⎭⎬⎫⎩⎨⎧+=⎰+⎰+-⎰x eC ez x xx xd 412d 212d 2}44{1212x x C x +++=.***10.作适当变换,求微分方程 d d tan y x y x y y x =+⎛⎝ ⎫⎭⎪2122的通解.解:令ux y =2,代入方程整理得 xxu u d tan d =,积分得 Cx u =sin ,以 x y u 2= 代入上式,即得原方程的通解: Cx xy =2sin .第9章 (之3) (总第46次)教学容:§9.2 .3齐次型方程;9.2.4伯努利方程.**1.求下列微分方程的通解:(1) )ln ln 1(d d x y xyx y -+=; 解: Θ )ln ln 1(d d x y x y x y -+=, ∴ dx dy =x y (1+xyln ),这是一个一阶齐次型方程.令 xyu =,则 ux y =,即u x u y '+=',于是原方程可化为u u u x ln ='.这是一个可分离变量方程.分离变量x dx u u du =ln ,并积分⎰⎰=xdxu u du ln ,得c x u ln ln ln ln +=,即cx e u =. 以 xy u =代入,得所求的通解为cxxe y =.(2)()arctan xy y yxx '-=. 解:方程可化为xy xy y arctan1+=',这是一个一阶齐次型方程.令 x y u =,则 ux y =,即u x u y '+=',于是原方程可化为ux u x arctan 1d d =,这是一个可分离变量方程.分离变量后积分得 x u Ce u u 12+=arctan .以 xy u =代入上式得原方程的通解:x y Cey x yx 22+=arctan . **2.求解下列初值问题:(1)0d )2(d 22=+-y y x x xy 满足初始条件 1)2(=y 的特解. 解: Θ 0d )2(d 22=+-y y x x xy ,dy dx =x y y x +2, 令 yxu = , 则 u u dy du yu 12+=+, u u du 1+=y dy , ∴⎰+uu du 1=⎰y dy,c y u ln ln )1ln(212+=+∴, cy u =+∴12, 即 2221y c u =+ , 代回即得22y x +1=22y c , 1)2(=y Θ, ∴52=c , 因此 22y x +=54y .(2)⎩⎨⎧==-++=.0,0d )(d )(0x y y y x x y x解:原方程可表为11d d -+=-+=x y x yx y y x x y ,令 x y u =,u x u y '+=', 代入方程,有 11-+='+u uu x u ,即 121d d 2--+=u u u x u x , 分离变量x x u uu u d 1d 2112=-+-,积分得 C x u u ln ln )21ln(212-=-+- ⇒通解 C y xy x =-+222,令 0,0==y x ,得 0=C .所以初值问题的解为 0222=-+y xy x .***3.试证明:当1221b a b a ≠时,总能找到适当的常数h ,k ,使一阶微分方程)(222111c y b x a c y b x a f y ++++='在变换k y s -=,h x t -=之下,可化为一阶齐次型方程)(d d 2211sb t a s b t a f t s++=. 并求方程 0d )32(d )12(=++++y y x x y x 的解.证明:令⎩⎨⎧+=+++=++s b t a c y b x a sb t ac y b x a 2222211111 1221b a b a ≠Θ,∴可解得:⎪⎪⎩⎪⎪⎨⎧---=---=1221122112212112b a b a c b c b x t b a b a c a c a y s 因此可取:⎪⎪⎩⎪⎪⎨⎧--=--=1221122112212112b a b a c b c b h b a b a c a c a k解:0)32()12(=++++dy y x dx y x Θ,令⎩⎨⎧-=+=32x t y s ⎩⎨⎧==⇒x t ys d d d d[][]0)2(3)3(21)2(23=-++++-++∴ds s t dt s t ,()0)32(2=+++ds s t dt s t ,ts t sdt ds dtdst s t s 32210)32(21++-=⇒=+++⇒, 令dt dutu dt ds t s u +=⇒=, 23)1)(13(3221+++-=⇒++-=+∴u u u dt du t u u dt du t u , ⎰⎰-=⎥⎦⎤⎢⎣⎡+++∴-=+++⇒t dtdu u u t dt du u u u )13(23)1(21,)1)(13()23(, c t u u ln ln )13)(1ln(21+-=++即,c tst s t ct u u =++⇒=⋅++∴)13)(1()13)(1(,c x xy x y c x y x y x 243)3631)(321()3(22=+++⇒=-++-++-∴.**4.求下列微分方程的通解(1)0ln 2=+-'x y y y x ;解: 0ln '2=+-x y y xy Θ xxy x y y ln 1'12-=-∴-- 令x x t x dx dt y t ln 11=+⇒=-, ,ln )Q( ,1)(xx x x x P ==∴ln 1 d ln )(d 1d 1⎥⎦⎤⎢⎣⎡⋅+=⎥⎦⎤⎢⎣⎡⎰+⎰=∴⎰⎰-xdx x x C x x e x x C e x t x x x x1ln C )ln (C 11-+=-+=---x x x x x x x x , 111ln --+-=Cx x y .(2)0d d )2(=+-y x x xy y .解: Θ 0d d )2(=+-y x x xy y , x y d d +y x 1=212y x, y y '-21+211y x =x 2, 21y u =,x u d d +x 21x u 1=, ∴x x P 21)(=,xx Q 1)(.∴⎥⎦⎤⎢⎣⎡⎰+⎰=⎰-x e x C e x u x x x x d 1)(d 21d 2121-=x ⎥⎦⎤⎢⎣⎡+⎰x x x C d 121[]x C x +=-21, ∴ []x C xy +=-2121, ∴xC x y +=.(3)'=-y y xy x 3222()解一:令u y =2,原方程化为: d d u x u x u x =⎛⎝ ⎫⎭⎪⎛⎝ ⎫⎭⎪-21,解此方程得 u Ce u x =, 以u y =2代入上式,原方程通解为 y Ce y x22=.解二:原方程写成d d x y y x yx -=-2232, 令x z -=1,则方程化为:322d d yz y y z =+, 则通解 z eC y e y yy y y =+⎡⎣⎢⎢⎤⎦⎥⎥-⎰⎰⎰2322d d d ]ln 2[12y C y+= , 故原方程通解:1122x yC y =+[ln ]. **5.求下列伯努力方程满足初始条件的特解:yxy y 2-=',1)0(=y . 解:x y yy', xy y y 22'21-=-∴-=-Θ,令 x t dxdty t 42 2-=-⇒=, x x Q x P 4)( ,2)(-=-=∴, []12010211)0(1212 )]2[ d 4 d )4()(2022222222d 2d 2+=∴=⇒++⨯=∴=++=∴++=++=-=⎥⎦⎤⎢⎣⎡⎰-+⎰=∴----⎰⎰x y C Ce y Ce x y x Ce e xe C e xxe C e x e x C e x t xx x x x x x x x,Θ****6.作适当的变换求方程 12222212+⋅'=++x y y x y e x sin sin 的通解.解:原方程化为:12222212+=++x yxx y e x d sin d sin ,令z y =sin 2,得d d z x x x ze x x -+=++21122122,故 ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧++=⎰⎰+-+⎰+x exeC ez xx x x x x x d 1d 12212d 12222)1ln(2121222x x eCex x +++=++原方程的通解为 sin ln()221212221y Ce e x x x x =+++++.***7.已知)(2d )(1)(2202x y x y y x+='+⎰ξξξ,求y x ().解:两边关于x 求导得212yy y '-=-, 解得 y Ce x 21=+, 由yx ==00,求得C =-1,故原方程的解为:y e x21=-.***8.曲线过点(,)11,其上任一点与原点的距离平方等于该点横坐标与该点的曲线的法线在x 轴上的截距乘积的两倍,求曲线方程. 解:x y x x yy y 22211+=+'=(),(), 212yy xy x '-=- 令y z 2=,解得z y x C x ==-2()由y ()11=, 得 C =2, 曲线方程为: x y x 222+=.***9.根据托里斥利定律,液体从容器小孔中流出的速度为 gh A v 2α=,其中 g 为重力加速度,h 为液面与底部孔口之间的距离,A 为孔口面积,α为孔口收缩系数,实验确定其取值为 62.0=α.现有一直径为1m ,高为2m 的直立圆柱形容器,其中盛满的水从底部直径为1=d cm 的圆孔流出,要多长时间容器的水才会完全流尽?解:设在时刻t 时, 容器中液面高度)(t h ,则经过t ∆后液面高度为)(t t h ∆+, 于是有t t gh A t t h t h r ∆=∆+-)(2))()((2απ,即 22)()(rghA t t h t t h πα=∆-∆+-, 令0→∆t , 得⎪⎩⎪⎨⎧==-200)0(2d d 2h gh r At h πα解得 200222+=t g rAh πα, 代入0=h , 980=g , 50=r , 4π=A , 62.0=α, 得10304=t (秒).第9章 (之4)(总第47次)教学容:§9.3可降阶的高阶微分方程**1.解下列问题:(1).微分方程'+''=''y y xy 满足条件'==y y (),()2121的解是 ( ) (A )y x =-()12(B )y x =+-()122142(C )y x =-+121122() (D )y x =--()12542解:(C )(2).微分方程''-'=y yy 203满足条件'=-=y y (),()0101的解是 ( )(A )y x 3313=+(B )x y 331=- (C )y x 3313=-+(D )x y 331=-+ 解:(C )**2.求下列微分方程的通解. (1)0='+''y y x ;解: Θ 0='+''y y x 是一不显含因变量y 的二阶方程, 令 y p '= ⇒ y ''x p d d =∴0=+'p p x , ⇒p p d =xxd -,⇒⎰⎰-=x xp p d d ⇒ 1ln ln ln C x p +-= ⇒xC p 1=, ∴=xy d d x C 1, x x C y d d 1=, ⎰⎰=x x C y d d 1 ,21ln C x C y +=. (2)()1212+''+'=x y xy ; 解:''++'=+y x x y x 211122, '=++y x x C 1121(), y x C x C =+++121212ln()arctan.(3)()02='+''y y y ;解:∵()02='+''y y y , 令 y p '=, 则 yppy d d ='',代入方程有 0d d 2=+⋅⋅p ypp y , 0)d d (=+⋅⇒p ypy p , 因为求通解,所以 p 满足 0d d =+⋅p ypy . 由⎰⎰-=⇒-=y yp p y y p p d d d d , y C p C y p 11ln ln ln '=⇒+-=⇒, ⎰⎰'=⇒'=⇒'=⇒x C y y x C y y yC x y d d d d d d 111 212C x C y +=⇒. ∴ 通解:212C x C y +=. (4)()1222+''='y y yy解:令:'=''='y p y y pp (),,得()1222+⋅'=y p p p y , 即d d p p yy y =+212, 得 p C y =+121(),所以 d d yyC x 121+=,通解为:arctan y C x C =+12.第9章 (之5)(总第48次)教学容:§9 .4 .1二阶线性方程和解的存在性;§9 .4 .2二阶线性方程解的结构**1.若21,y y 是方程)()()(x R y x Q y x P y =+'+''的两个解,试证12y y - 必是其对应齐次方程0)()(=+'+''y x Q y x P y 的解.证明:因为21,y y 是方程)()()(x R y x Q y x P y =+'+''的解. 所以成立下式:)2()()()()1()()()(222111x R y x Q y x P y x R y x Q y x P y =+'+''=+'+''将 (1)、(2) 两式相减,得)3(0))(())(()(212121=-+'-'+''-''y y x Q y y x P y y(2) 式可写为0))(())(()(212121=-+'-+''-y y x Q y y x P y y ,所以 21y y - 是齐次方程 0)()(=+'+''y x Q y x P y 的解.***2.已知23211,1,1x y x y y +=+==是方程22222xy x y x y =+'-''的三个特解,问能否求出该方程得通解?若能则求出通解来.解:按(1)证明可知 21312,x y y x y y =-=- 分别是其对应齐次方程0222=+'-''y xy x y 的解,并且线性无关,所以221x C x C + 为齐次方程的通解. 所以原方程的通解可以表示为:1221++=x C x C y .*3.验证:22,t t e e -是微分方程''-'-=x tx t x 1402的两个线性无关特解,并求此方程的通解.证明:因为()()222241t t t e t e t e -'-"0421********=-⨯-+=t t t t e t te te t e ,()()2222"41t t t e t e t e ----'-=-+-⨯--=--241240222222e t e tte t e t t t t (), 故22,t t e e -是方程的解,且≠=-2222t t t e ee 常数.于是22,t t e e -是方程线性无关的解(构成基本解组),故方程的通解为2221t t e C e C x -+=,其中21,C C 为任意常数.*4.已知函数 x y e y x==21, 是方程 0)1(=-'+''-y y x y x 的两解,试求该方程满足初始条件 0)0(,1)0(='=y y 的特解.解:方程的通解为 x c e c y x21+=,将初始条件代入,有:,,0)0('1)0(21211=+=+===c c c e c y c y x解得21,c c 为: 1,121-==c c ,所以特解为:x e y x -=.**5.设x t 1()是非齐次线性方程''+'+=x t a t x t a t x t f t ()()()()()()()1211的解.x t 2()是方程''+'+=x t a t x t a t x t f t ()()()()()()()1222的解.试证明 x x t x t =+12()()是方程''+'+=+x t a t x t a t x t f t f t ()()()()()()()()12123的解.解:因为)(2),(1t x t x 分别为方程(1)和方程(2)的解,所以)1()()()()()()(112111'≡+'+''t f t x t a t x t a t x''+'+≡'x t a t x t a t x t f t 2122222()()()()()()()()()12'+'得:()()())()()()()()()()()()(2121221121t f t f t x t x t a t x t x t a t x t x +='++'++"+即 x x t x t =+12()() 是方程(3)的解.第9章 (之6)(总第49次)教学容:§9 .4 .3二阶线性常系数方程的解法**1.解下列问题:(1)方程08=+''y y 的通解为=y _______________.解:x c x c y 22sin 22cos 21+=.(2)方程025'6"=++y y y 的通解为=y _______________. 解:)4sin 4cos (213x c x c e y x+=-.(3)方程0158=+'-''y y y 的通解为=y _______________. 解:x xC C y 5231e e +=.(4)方程031525=+'+''y y y 的通解为=y _______________. 解:)(21515C x C e y x +=-.(3)方程06=+'+''py y y 的通解为)2sin 2cos (e 21x C x C y kx+=,则=p ___,=k _____. 解:11,3-.**2.求解下列初值问题:(1)0)1(,)1(,01684='==+'-''y e y y y y ;解:∵0)4(16822=-=+-λλλ, ∴421=,λ, 通解为:xe x c c y 421)(+=.将初始条件代入,有 4421)()1(e e c c y =+=,04)(4)(4)1('4424214242142=+=++=++=e e c e c c e c e x c c e c y x x得到:4521-==c c , 所以特解为:x e x y 4)45(-=.(2)3)2(,1)2(,0294='==+'+''ππy y y y y ; 解:02942=++λλ, i i5221042116164±-=±-=-±-=λ,通解为:)5sin 5cos (212x c x c ey x+=-.代入初始条件有: πππe c c ey =⇒=+=-221)0()2(,)5cos 55sin 5()5sin 5cos (2)2(212212x c x c e x c x c ey x x+-++-='--π,得:πe c -=1. 特解为:)5sin 5cos (2x x e y x+-=-π.(3)10)0(,6)0(,034='==+'+''y y y y y ;解: 0342=++λλ, 0)3)(1(=++λλ, 所以通解为 x xe c e c y 321--+=.代入初始条件有:6)0(21=+=c c y ,1033)0('21321=--=--=--c c e c e c y x x ,特解为:x xe ey 3814---=.**3.求解初值问题'++==⎧⎨⎪⎩⎪≥⎰y y y x y x x210100d ()解:将原方程对x 求导得 ''+'+=y y y 201()且有'=-=-y y ()()01201微分方程(1)的通解为:y e C x C x =+-()12,代入初始条件1)0(,1)0(-='=y y ,得1,021==C C , 故所求问题的解为:xe y -=.***4.设函数)(x ϕ二阶连续可微,且满足方程⎰-+=xu u u x x 0d )()(1)(ϕϕ,求函数ϕ()x .解:原方程关于x 求导得⎰⎰=-+='xxu u x x x x u u x 0d )()()(d )()(ϕϕϕϕϕ,0)0(='ϕ,再求导得: )()(x x ϕϕ='', 且由原方程还有:1)0(=ϕ,微分方程的通解为: xxeC e C x -+=21)(ϕ,代入条件0)0(,1)0(='=ϕϕ,得2121==C C , 故所求函数为:x e e x x x ch )(21)(=+=-ϕ.***5.长为100cm 的链条从桌面上由静止状态开始无摩擦地沿桌子边缘下滑.设运动开始时,链条已有20cm 垂于桌面下,试求链条全部从桌子边缘滑下需多少时间.解:设链条单位长度的质量为ρ,则链条的质量为ρ100.再设当时刻 t 时,链条的下端距桌面的距离为)(t x ,则根据牛顿第二定律有:gx dt x d ρρ=22100, 即 010022=-x gdtx d . 又据题意知:20)0(=x , 0)0(='x ,所以 )(t x 满足下列初值问题:⎪⎩⎪⎨⎧='==-0)0(20)0(010022x x x gdt x d , 解得方程的通解为:tg tgec ec x 102101-+=.又因为有初始条件: ()()⎩⎨⎧==⇒⎩⎨⎧==1010020021'c c x x 所以 tg t gee x 10101010-+=.又当链条全部从桌子边缘滑下时,100=x ,求解t ,得:tg tg e e 10101010100-+=,即: 510=t gch, 510arch gt =.***6.设弹簧的上端固定,下端挂一个质量为2千克的物体,使弹簧伸长2厘米达到平衡,现将物体稍下拉,然后放手使弹簧由静止开始运动,试求由此所产生的振动的周期. 解:取物体的平衡位置为坐标原点,x 轴竖直向下,设t 时刻物体m 位于x t ()处,由牛顿第二定律:22222d d ()xtg g x gx =-+=- , 其中g =980厘米/秒2其解为:x C g t C g t =+1222cossin , 振动周期为 T g ==≈222490028ππ..第9章 (之7)(总第50次)教学容:§9.4.3二阶线性常系数方程的解法; §9.4.4高阶线性常系数微分方程 **1.微分方程x x y y sin =+''的一个特解应具有形式 ( )(A )()sin Ax B x +(B )x Ax B x x Cx D x ()sin ()cos +++ (C )x Ax B x x ()(cos sin )++ (D )x Ax B C x D x ()(sin cos )++ 解:(B )**2.设A B C D ,,,是待定常数,则微分方程''+=+y y x x cos 的一个特解应具有形式 ( )(A )Ax B C x ++cos(B )Ax B C x D x +++cos sin(C )Ax B x C x D x +++(cos sin ) (D )Ax B Cx x ++cos 答:(C )**3.求下列非齐次方程的一个解 (1)122+=-'-''x y y y ;解:∵ 022=--λλ, ∴1,22,1-=λ, 0Θ不是特征根.设 01b x b y p +=, 代入原方程,得:1222011+=---x b x b b ,有:1,010-=b b ,特解为:x y -=.(2)xey y y -=+'+''2.解: ∵ 1- 是二重特征根, ∴ 设 02b e x y xp -=, 0202b e x b xe y xxp ---=',02002022b e x b xe b e x b e y x x x x p----+--='', 代入 xe y y y -=++'2'', 解得:210=b ,特解为:xe x y -=221.**4.求微分方程''-'+=y y y xe x32满足条件y y ()()000='=的特解. 解:特征方程0232=+-r r 的根为2,121==r r ,相应齐次方程的通解为x x h e C e C y 221+=,设特解为x p e B Ax x y )(+=,代入方程得: 1,21-=-=B A . 故方程的通解为xxx e x x eC e C y ⎪⎪⎭⎫ ⎝⎛+-+=22221,代入条件0)0()0(='=y y ,得1,121=-=C C ,因此所求特解为 x xe x x ey ⎪⎪⎭⎫ ⎝⎛++-=1222.**5. 求下列非齐次方程的通解:)(2x f y y ='+''x x f e x f x x f x cos )()3,)()2,14)()12==+=;解:特征方程:022=+λλ, 特征根: 2,021-==λλ,所以方程0'2=+''y y 的通解为 xh e c c y 221-+=.1)对于方程14'2+=+''x y y , 由于0是特征方程的单根,故设其特解为:x b x b y p )(10+=,代入方程有:14242100+=++x b x b b ,解得 21110-==b b , 所以特解为:x x y p 212-=. 所以方程的通解为:x x e c c y y y xp h 212221-++=+=-.2)对于方程xe y y 2'2=+''',由于2不是特征方程的根,故设其特解为:02b e y xp =, 代入方程有:810=b , xp e y 281=, 所以方程的通解为:x xp h e ec c y y y 222181++=+=-.3)对于方程:x y y cos '2=+''',由于i ±不是特征方程的根,故设其特解为: x b x b y p sin cos 10+=, 代入方程有:x b x b y p cos sin '10+-=, x b x b y p sin cos "10--=,x x b x b x b x b cos cos sin 2sin cos 1010=+---, 得:525120=-=b b , x x y p sin 52cos 51+-=,所以方程的通解为:x x e c c y y y xp h sin 52cos 51221+-+=+=-.**6.求微分方程''-'+=y y y e x x6925sin 的通解.解:特征方程r r 2690-+=的根为r 123,=,相应齐次方程的通解为xh e x C C y 321)(+=设特解为y e A x B x p x=+(cos sin ),代入方程得:A B ==43,故方程的通解为 y C C x e e x x x x =+++()(cos sin )12343***7.已知曲线y y x x =≥()()0过原点,位于x 轴上方,且曲线上任一点),(00y x M =处切线斜率数值上等于此曲线与x 轴,直线x x =0所围成的面积与该点横坐标的和,求此曲线方程.解:由已知y ()00=,且'=+'=⎰y y x x y xd ,()000,将此方程关于x 求导得''=+y y 1其通解为: y C e C exx=+--121 ,代入初始条件y y (),()0000='=,得 C C 1212==, 故所求曲线方程为:y e e x xx =+-=--1211()ch .***8.设一物体质量为m ,以初速v 0从一斜面滑下,若斜面与水平面成θ角,斜面摩擦系数为μμθ(tan )0<<,试求物体滑下的距离与时间的关系.解:设t 时刻物体滑过的距离为S ,由牛顿第二定律m Stmg mg d d sin cos 22=-θμθ 且 S S v (),()0000='=方程的通解为S gt C t C =-++12212(sin cos )θμθ 代入初始条件得C v C 1020==,,故物体滑下的距离与时间的关系为S gt v t =-+1220(sin cos )θμθ***9.设弹簧的上端固定,下端挂一质量为m 的物体,开始时用手托住重物,使弹簧既不伸长也不缩短,然后突然放手使物体开始运动,弹簧的弹性系数为k ,求物体的运动规律.解:取物体未发生运动时的位置为坐标原点,x 轴垂直向下,设t 时刻物体位于x t ()处,由牛顿第二定律: m xtkx mg d d 22+=, 且 0)0(0)0(='=x x ,. 方程的通解为: x C k m t C k m t m kg =++12cos sin , 代入初始条件得C mkg C 120=-=,,故物体的运动规律为x mg k k m t =-⎛⎝ ⎫⎭⎪1cos.***10. 求下列方程的通解: (1)02)4(=''+'''-y y y;解: 02234=+-λλλ, 0)12(22=+-λλλ, 0)1(22=-λλ,所以通解为 x e x c c x c c y )(4321+++=.(2)0365)4(=-''+y y y.解:036524=-+λλ, 0)9)(2)(2(2=++-λλλ,所以通解为 x c x c ec e c y xx 3sin 3cos 432221+++=-.****11* 试证明,当以 x t ln =为新的自变量时,变系数线性方程(其中a,b,c 为常数,这是欧拉方程))('"2x f cy bxy y ax =++可化为常系数线性方程)()(22t e f cy dt dya b dty d a =+-+并求下列方程通解:(1)022=-''y y x ; (2)x x y y x y x ln 22=+'-''. 证明:令 x t ln =, t e x =,dtdyx dx dt dt dy dx dy 1==,⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛+-=dt dy dt y d x dt dy dx d x dt dy x dx y d 222222111, 将y y ''',代入方程有:()()te f cy dt dy a b dt y d a cy dt dy b dt dy dt y d a cy y bx y ax =+-+=++⎪⎪⎭⎫ ⎝⎛-=+'+''22222, 得证.(1)令 x t ln =, te x =,原方程化为:0222=--y dt dydty d . 其通解为t t e c e c y -+=221.将x 代入,得:xc x c y 221+=. (2) 令 x t ln =, te x =,原方程化为:tte y dt dy dty d =+-2222, 上述方程的相应其次方程的通解为:()t c t c e y t h sin cos 21+=.令上述方程一个特解为:()10b t b e y t p +=,代入方程得:0,110==b b , 即:t e y t p =.原方程得通解为:()t t c t c e y t ++=sin cos 21,即:()()[]x x c x c x y ln ln sin ln cos 21++=.***12.一质量为m 的潜水艇在水面从静止状态开始下降,所受阻力与下降速度成正比(比例系数为k >0),浮力为常数B ,求潜水艇下降深度x 与时间t 之间的函数关系. 解: ma B F F =--阻重, a 为加速度, ma B kv mg =--, v 为下降速度,因为 22,dt x d dt dv a dt dx v ===, 所以 22dt xd m B dt dx k mg =--,即 m Bg dt dx m k dtx d -=+22 , 其特征方程为: 02=+λλmk , 解得特征根为 m k-==21,0λλ.所以对应的齐次方程的通解为:21c e c x t mkh +=-.由于0是特征方程的单根,故设其特解为:t b x 01=, 代入方程有:m B g b m k -=0, 得 kBmg b -=0. 所以微分方程的通解为:t kBmg c e c x t mk-++=-21, 因为初始位置为0,初始速度为0,所以有初始条件 ()()00,00'==x x ,代入微分方程有: ⎪⎩⎪⎨⎧=-+-=++000121k Bmg c mk c c 求得:222221,kgm Bm c k Bm g m c -=-=, 所以x 与t 的关系可表示为: t k B mg e k g m Bm x t m k-+⎪⎪⎭⎫ ⎝⎛--=-122.***13.证明:若有方程'=-f x f x ()()1,则必有''+=f x f x ()()0,并求解此方程. 证明:由于'=-f x f x ()()1,两边关于x 求导得''=-'-=---=-f x f x f x f x ()()[()]()111故得''+=f x f x ()()0(1)解方程(1)得通解为 f x C x C x ()cos sin =+12(2)'=-+f x C x C x ()sin cos 12 (3)'='=f f f f ()(),()()0110,将此代入(2),(3)得C C C C C C 1221211111cos sin sin cos +=-+=⎧⎨⎩ 解得:C C 21111=+sin cos所以原方程的解为: f x C x x ()cos sin cos sin =++⎛⎝⎫⎭⎪1111.第9章 (之8) (总第51次)教学容:§9.6 微分方程应用举例 (机动)第9章 (之9) (总第52次)教学容:§9.7 差分方程1. 已知t t e y 3=是二阶差分方程tt t e ay y =+-+11的一个特解,求a .解: )31(3e ea -=.2. 求下列差分方程的一般解: (1) 0721=+-t t y y ; 解:tt C y )27(-=(2) 431-=--t t y y ;解:23+=tt C y(3) 051021=-++t y y t t ; 解:)61(125)5(-+-=t C y tt (4) tt t y y 2124=-+; 解:144-+=t t t t C y (5) tt t t y y 21⋅=-+. 解:tt t C y 2)2(-+=3. 写出下列差分方程的一个特解形式: (1) t y y t t sin 1=-+; 解:t B t B Y t cos sin 21+=(2) t y y t t πcos 31-=++. 解:)sin cos (21t B t B t Y t ππ+=4. 设t y 为第t 期国民收入,t C 为第t 期消费,I 为每期投资(I 为常数).已知t y ,t C ,I 之间有关系 I C y t t +=,βα+=-1t t y C ,其中10<<α,0>β,试求t y ,t C . 解:t y 满足:βα+=--I y y t t 1,解得 αβα-++=1I C y tt , 从而 =-=I y C t t ααβα-++1I C t.5. 已知差分方程t t t cy y by a =++1)(,其中a ,b ,c 为正的常数.设初始条件0)0(0>=y y ,证明:(1) 对任意Λ,2,1=t ,有0>t y ;(2) 在变换tt y u 1=之下,原差分方程可化为有关t u 的线性差分方程,写出该线性差分方程并求其一般解;(3) 求方程t t t y y y =++1)21(的满足初始条件20=y 的解. 解:(1)归纳法证明. (2)令 t t y u 1=,即t t u y 1=,111++=t t u y , 则原方程化为线性差分方程 b au cu t t =-+1, 其一般解为 a c ≠时, ac bcaC u tt -+=)( ; a c =时, b C u t +=. (3)令 tt y u 1=,原方程化为 21=-+t t u u ,一般解为 2+=C u t , 所以原方程的一般解为 t t u y 1=21+=C ,代入 20=y ,得 23-=C , 所以 特解为 2=t y .。
2024年高考数学总复习第九章《平面解析几何》复习试卷及答案解析

2024年高考数学总复习第九章《平面解析几何》复习试卷及答案解析一、选择题1.已知椭圆C:16x2+4y2=1,则下列结论正确的是()A.长轴长为12B.焦距为34C.短轴长为14D.离心率为32答案D解析由椭圆方程16x2+4y2=1化为标准方程可得x2 1 16+y214=1,所以a=12,b=14,c=34,长轴2a=1,焦距2c=32,短轴2b=12,离心率e=ca=32.故选D.2.双曲线x23-y29=1的渐近线方程是()A.y=±3x B.y=±13xC.y=±3x D.y=±33x 答案C解析因为x23-y29=1,所以a=3,b=3,渐近线方程为y=±ba x,即为y=±3x,故选C.3.已知双曲线my2-x2=1(m∈R)与抛物线x2=8y有相同的焦点,则该双曲线的渐近线方程为()A.y=±3x B.y=±3xC.y=±13x D.y=±33x答案A解析∵抛物线x 2=8y 的焦点为(0,2),∴双曲线的一个焦点为(0,2),∴1m +1=4,∴m =13,∴双曲线的渐近线方程为y =±3x ,故选A.4.已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)和直线l :x 4+y3=1,若过C 的左焦点和下顶点的直线与l平行,则椭圆C 的离心率为()A.45B.35C.34D.15答案A解析直线l 的斜率为-34,过C 的左焦点和下顶点的直线与l 平行,所以b c =34,又b 2+c 2=a 2+c 2=a 2⇒2516c 2=a 2,所以e =c a =45,故选A.5.(2019·洛阳、许昌质检)若双曲线x 2-y 2b2=1(b >0)的一条渐近线与圆x 2+(y -2)2=1至多有一个交点,则双曲线离心率的取值范围是()A .(1,2]B .[2,+∞)C .(1,3]D .[3,+∞)答案A 解析双曲线x 2-y 2b2=1(b >0)的一条渐近线方程是bx -y =0,由题意圆x 2+(y -2)2=1的圆心(0,2)到bx -y =0的距离不小于1,即2b 2+1≥1,则b 2≤3,那么离心率e ∈(1,2],故选A.6.(2019·河北武邑中学调研)已知直线l :y =k (x +2)(k >0)与抛物线C :y 2=8x 相交于A ,B 两点,F 为C 的焦点,若|FA |=2|FB |,则k 等于()A.13B.23C.23D.223答案D解析=k (x +2),2=8x ,消去y 得k 2x 2+(4k 2-8)x +4k 2=0,Δ=(4k 2-8)2-16k 4>0,又k >0,解得0<k <1,设A (x 1,y 1),B (x 2,y 2),x 1+x 2=8k 2-4,①x 1x 2=4,②根据抛物线定义及|FA |=2|FB |得x 1+2=2(x 2+2),即x 1=2x 2+2,③且x 1>0,x 2>0,由②③解得x 1=4,x 2=1,代入①得k 2=89,∵0<k <1,∴k =223.故选D.7.(2019·唐山模拟)双曲线E :x 2a 2-y 2b 2=1(a >0,b >0)的渐近线方程为y =±7x ,则E 的离心率为()A .2 B.2147C .22D .23答案C解析由题意,双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线方程为y =±7x ,即ba=7,所以双曲线的离心率为e =ca=a 2+b 2a2=22,故选C.8.(2019·河北衡水中学模拟)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,过F 1作圆x 2+y 2=a 2的切线,交双曲线右支于点M ,若∠F 1MF 2=45°,则双曲线的渐近线方程为()A .y =±2xB .y =±3xC .y =±xD .y =±2x答案A解析如图,作OA ⊥F 1M 于点A ,F 2B ⊥F 1M 于点B .因为F 1M 与圆x 2+y 2=a 2相切,∠F 1MF 2=45°,所以|OA |=a ,|F 2B |=|BM |=2a ,|F 2M |=22a ,|F 1B |=2b .又点M 在双曲线上,所以|F 1M |-|F 2M |=2a +2b -22a =2a .整理,得b =2a .所以ba= 2.所以双曲线的渐近线方程为y =±2x .故选A.9.(2019·湖南五市十校联考)在直角坐标系xOy 中,抛物线C :y 2=4x 的焦点为F ,准线为l ,P 为C 上一点,PQ 垂直l 于点Q ,M ,N 分别为PQ ,PF 的中点,直线MN 与x 轴交于点R ,若∠NFR =60°,则|FR |等于()A .2 B.3C .23D .3答案A解析由抛物线C :y 2=4x ,得焦点F (1,0),准线方程为x =-1,因为M ,N 分别为PQ ,PF 的中点,所以MN ∥QF ,所以四边形QMRF 为平行四边形,|FR |=|QM |,又由PQ 垂直l 于点Q ,可知|PQ |=|PF |,因为∠NFR =60°,所以△PQF 为等边三角形,所以FM ⊥PQ ,所以|FR |=2,故选A.10.已知F 1,F 2分别是双曲线E :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,点M 在E 上,MF 1与x 轴垂直,sin ∠MF 2F 1=13,则E 的离心率为()A.2B.32C.3D .2答案A解析因为MF 1与x 轴垂直,所以|MF 1|=b 2a .又sin ∠MF 2F 1=13,所以|MF 1||MF 2|=13,即|MF 2|=3|MF 1|.由双曲线的定义,得2a =|MF 2|-|MF 1|=2|MF 1|=2b 2a ,所以b 2=a 2,所以c 2=b 2+a 2=2a 2,所以离心率e =ca= 2.11.(2019·湖南长沙长郡中学调研)已知点P (-1,0),设不垂直于x 轴的直线l 与抛物线y 2=2x交于不同的两点A ,B ,若x 轴是∠APB 的角平分线,则直线l 一定过点()B .(1,0)C .(2,0)D .(-2,0)答案B解析根据题意,直线的斜率存在且不等于零,设直线的方程为x =ty +m (t ≠0),与抛物线方程联立,消元得y 2-2ty -2m =0,设A (x 1,y 1),B (x 2,y 2),因为x 轴是∠APB 的角平分线,所以AP ,BP 的斜率互为相反数,所以y 1x 1+1+y 2x 2+1=0,所以2ty 1y 2+(m +1)(y 1+y 2)=0,结合根与系数之间的关系,整理得出2t (-2m )+2tm +2t =0,2t (m -1)=0,因为t ≠0,所以m =1,所以过定点(1,0),故选B.12.(2019·陕西四校联考)已知椭圆和双曲线有共同的焦点F 1,F 2,P 是它们的一个交点,且∠F 1PF 2=2π3,记椭圆和双曲线的离心率分别为e 1,e 2,则3e 21+1e 22等于()A .4B .23C .2D .3答案A解析如图所示,设椭圆的长半轴长为a 1,双曲线的实半轴长为a 2,则根据椭圆及双曲线的定义:|PF 1|+|PF 2|=2a 1,|PF 1|-|PF 2|=2a 2,∴|PF 1|=a 1+a 2,|PF 2|=a 1-a 2,设|F 1F 2|=2c ,∠F 1PF 2=2π3,则在△PF 1F 2中,由余弦定理得4c 2=(a 1+a 2)2+(a 1-a 2)2-2(a 1+a 2)(a 1-a 2)cos2π3,化简得3a 21+a 22=4c 2,该式可变成3e 21+1e 22=4.故选A.二、填空题13.已知双曲线C :x 2-y 2=1,则点(4,0)到C 的渐近线的距离为________.答案22解析双曲线C :x 2-y 2=1的渐近线方程为y =±x ,点(4,0)到C 的渐近线的距离为|±4|2=2 2.14.(2019·新乡模拟)设P 为曲线2x =4+y 2上一点,A (-5,0),B (5,0),若|PB |=2,则|PA |=________.答案4解析由2x =4+y 2,得4x 2=4+y 2(x >0),即x 2-y 24=1(x >0),故P 为双曲线x 2-y 24=1右支上一点,且A ,B 分别为该双曲线的左、右焦点,则|PA |-|PB |=2a =2,|PA |=2+2=4.15.已知抛物线y 2=4x ,圆F :(x -1)2+y 2=1,直线y =k (x -1)(k ≠0)自上而下顺次与上述两曲线交于点A ,B ,C ,D ,则|AB |·|CD |的值是________.答案1解析设A (x 1,y 1),D (x 2,y 2),则|AB |·|CD |=(|AF |-1)(|DF |-1)=(x 1+1-1)(x 2+1-1)=x 1x 2,由y =k (x -1)与y 2=4x 联立方程消y 得k 2x 2-(2k 2+4)x +k 2=0,x 1x 2=1,因此|AB |·|CD |=1.16.(2019·四省联考诊断)在平面上给定相异两点A ,B ,设P 点在同一平面上且满足|PA ||PB |=λ,当λ>0且λ≠1时,P 点的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故我们称这个圆为阿波罗尼斯圆,现有椭圆x 2a 2+y 2b 2=1(a >b >0),A ,B 为椭圆的长轴端点,C ,D为椭圆的短轴端点,动点P 满足|PA ||PB |=2,△PAB 的面积最大值为163,△PCD 面积的最小值为23,则椭圆的离心率为________.答案32解析依题意A (-a ,0),B (a ,0),设P (x ,y ),依题意得|PA |=2|PB |,(x +a )2+y 2=2(x -a )2+y 2,两边平方化简得-53a +y 2,r =4a3.所以△PAB 的最大面积为12·2a ·43a =163,解得a =2,△PCD 的最小面积为12·2b b ·a 3=23,解得b =1.故椭圆的离心率为e =1-14=32.三、解答题17.(2019·湖南长沙长郡中学调研)在平面直角坐标系xOy 中,已知圆M :(x -3)2+(y -b )2=r 2(r 为正数,b ∈R ).(1)若对任意给定的r ∈(0,+∞),直线l :y =-x +r +4总能把圆M 的周长分成3∶1的两部分,求圆M 的标准方程;(2)已知点A (0,3),B (1,0),且r =103,若线段AB 上存在一点P ,使得过点P 的某条直线与圆M 交于点S ,T (其中|PS |<|PT |),且|PS |=|ST |,求实数b 的取值范围.解(1)根据题意可得,圆心到直线的距离为22r 恒成立,即|3+b -r -4|2=22r ,整理得|b -1-r |=r ,去绝对值符号可得b -1-r =r 或b -1-r =-r ,根据恒成立,可得b =1,所以圆M 的标准方程为(x -3)2+(y -1)2=r 2.(2)根据题意,如果存在满足条件的点,对应的边界值为过圆心的弦,而从另一个角度,即为线段端点值满足条件即可,先考虑点A ,即为|AM |≤3r ,即(0-3)2+(b -3)2≤9×109,解得2≤b ≤4,再考虑点B ,即为|BM |≤3r ,即(1-3)2+b 2≤10,解得-6≤b ≤6,两者取并集,得到b 的取值范围是[-6,4].18.(2019·陕西四校联考)已知抛物线C :y 2=2px 过点A (1,1).(1)求抛物线C的方程;(2)若过点P(3,-1)的直线与抛物线C交于M,N两个不同的点(均与点A不重合).设直线AM,AN的斜率分别为k1,k2,求证:k1·k2为定值.(1)解由题意得2p=1,所以抛物线方程为y2=x.(2)证明设M(x1,y1),N(x2,y2),直线MN的方程为x=t(y+1)+3,代入抛物线方程得y2-ty-t-3=0.所以Δ=(t+2)2+8>0,y1+y2=t,y1y2=-t-3.所以k1·k2=y1-1x1-1·y2-1x2-1=y1-1y21-1·y2-1y22-1=1(y1+1)(y2+1)=1y1y2+y1+y2+1=1-t-3+t+1=-12,所以k1·k2是定值.。
高数下第九章的答案

,即 ;又 在直线 上,
联立方程 解得
从而点 到直线 的距离为 .
9.5空间曲面
P.31.习题9.5
1.指出下列方程在平面解析几何和在空间解析几何中分别表示什么图形.
(1) ;
(2) ;
(3) ;
(4) ;
(5) ;
(6) ;
解:(1) 在平面解析几何中表示平行于y轴的直线,在x轴上的截距为2; 在空间解析几何中表示平行于yoz面的平面,在x轴上的截距为2;
.
(3)已知非零向量a、b、c且满足 ,证明 .
(4)设向量 ,证明三向量a、b、c共面.
证明:(1)
(2)
相加得 .
(3)已知 ,右乘b得 ,即 ;同理 ;
所以 .
(4)因为 ;
所以设向量 ,证明三向量a、b、c共面.
南阳理工学院高等数学(下)课后答案选解
第九章向量代数与空间解析几何
9.1向量及其坐标表示
P.9习题9.1
2.已知一边长为a的正方体,现取正方体下底面的中心为原点,正方体的顶点在x轴、y轴上,求此正方体各顶点的坐标.
解:下底面的四个顶点分别是:
对应的上底面的四个顶点分别是:
3.求出点 到原点、各坐标轴及坐标面的距离.
;所求直线为 .
(5)过点 且与直线 垂直相交的直线方程为
;则 ;联立
解得
所以,过点 且与直线 垂直相交的直线方程为
.
2.用点向式方程及参数方程表示直线
解:设直线的方向向量为 ;在直线
上任取一点 ,则 解得
所以,点向式方程为 ;参数方程为
3.求直线 与平面 之间的夹角.
解:因为
