下册 小专题训练 与圆的基本性质有关的计算-2020秋九年级北师大版数学全一册作业课件
北师大版九年级数学下册练习:小专题(十四) 与圆的基本性质有关的计算-最新学习文档

第 1 页 小专题(十四) 与圆的基本性质有关的计算类型1 求角度1.(2019·北京)如图,点A ,B ,C ,D 在⊙O 上,CB ︵=CD ︵,∠CAD=30°,∠ACD =50°,则∠ADB=70°.2.如图,AB 是⊙O 的直径,CD 是⊙O 的弦,BA ,DC 的延长线交于点E ,AB =2CE ,∠E=25°,则∠BOD =75°.3.如图,A ,B 是⊙O 上的两个定点,P 是⊙O 上的动点(P 不与A ,B 重合),我们称∠APB 是⊙O 上关于点A ,B 的滑动角.已知∠APB 是⊙O 上关于点A ,B 的滑动角.(1)若AB 是⊙O 的直径,则∠APB 的度数是90°;(2)若⊙O 的半径是1,AB =2,则∠APB 的度数是45°或135°__.4.如图,AB 为⊙O 的直径,弦CD 与AB 相交于点E ,∠ACD=60°,∠ADC=50°,则∠CEB 的度数为100°.5.如图,在⊙O 中,∠OAB=22.5°,则∠C 的度数为112.5°__.6.(2019·南京)如图,四边形ABCD 是菱形,⊙O 经过点A ,C ,D ,与BC 相交于点E ,连接AC ,AE.若∠D=78°,则∠EAC=27°.类型2 求长度7.(2019·咸宁)如图,已知⊙O 的半径为5,弦AB ,CD 所对的圆心角分别是∠AOB,∠COD.若∠AOB 与∠COD 互补,弦CD =6,则弦AB 的长为(B)A .6B .8C .5 2D .5 38.如图,⊙O 的半径是3,点P 是弦AB 延长线上的一点,连接OP.若OP =4,∠APO=30°,则弦AB 的长是25.9.如图,⊙O 的半径OD⊥弦AB 于点C ,连接AO 并延长交⊙O 于点E ,连接EC.若AB =8,CD =2,则EC 的长为213__.10.如图,AB ,AC ,AD 为⊙O 的弦,∠BAC=60°,∠DAC=30°,AB =4,AD =6,则CD 的长为13.11.(2019·十堰)如图,△ABC 内接于⊙O,∠ACB=90°,∠ACB 的平分线交⊙O 于点D.若AC =6,BD =52,则BC 的长为8.。
北师大版九年级数学下册第三章《圆》专题测试含答案

《圆》专题训练含答案一.选择题(共9小题)1.已知⊙O中最长的弦长8cm,则⊙O的半径是()A.2cm B.4cm C.8cm D.16cm2.有下列说法:①直径是圆中最长的弦;②等弧所对的弦相等;③圆中90°的角所对的弦是直径;④相等的圆心角对的弧相等.其中正确的有()A.1个B.2个C.3个D.4个3.如图,已知AB、AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,若MN=,那么BC等于()A.5B.C.2D.4.如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=37°,那么∠BAD=()A.51°B.53°C.57°D.60°5.已知⊙O的半径等于3,圆心O到点P的距离为5,那么点P与⊙O的位置关系是()A.点P在⊙O内B.点P在⊙O外C.点P在⊙O上D.无法确定6.如图EF与⊙O相切于点D,A、B为⊙O上点,则下列说法中错误的()A.∠AOB是圆心角B.∠ADB是圆周角C.∠BDF是圆周角D.∠BOD是圆心角7.如图,P A、PB、分别切⊙O于A、B两点,∠P=40°,则∠C的度数为()A.40°B.140°C.70°D.80°8.如图,⊙O与正五边形ABCDE的边AB,DE分别相切于点B,D,则劣弧BD所对的圆心角∠BOD的大小为()A.108°B.118°C.144°D.120°9.如图,在Rt△ABC中,∠C=90°,AB=6,AD是∠BAC的平分线,经过A,D两点的圆的圆心O恰好落在AB上,⊙O分别与A、B、AC相交于点E、F.若圆半径为2.则阴影部分面积()A.B.C.D.二.填空题(共8小题)10.有下列说法:①半径是弦;②半圆是弧,但弧不一定是半圆;③面积相等的两个圆是等圆,其中正确的是(填序号)11.如图,某种齿轮有20个齿,每两齿之间的间隔相等,则相邻两齿间的圆心角α等于°.12.如图所示,⊙O的半径为5,AB为弦,半径OC⊥AB,垂足为D,如果CD=2,那么AB的长是.13.如图△ABC中,AC=BC=5,AB=6,以AB为直径的⊙O与AC交于点D,若E为的中点,则DE.14.如图,在⊙O中,半径OC=6,D是半径OC上一点,且OD=4.A,B是⊙O上的两个动点,∠ADB=90°,F是AB的中点,则OF的长的最大值等于.15.如图,⊙O是四边形ABCD的内切圆,连接OA、OB、OC、OD.若∠AOB=110°,则∠COD的度数是°.16.正n边形内接于半径为R的圆,这个n边形的面积为3R2,则n等于.17.已知扇形的圆心角为120°,它所对弧长为20πcm,则扇形的半径为.三.解答题(共8小题)18.如图,在△ABC中,点O为BC边上一点,⊙O经过A、B两点,与BC边交于点E,点F为BE下方半圆弧上一点,FE⊥AC,垂足为D,∠BEF=2∠F.(1)求证:AC为⊙O切线.(2)若AB=5,DF=4,求⊙O半径长.19.如图,A,B,C,D在⊙O上,AB∥CD经过圆心O的线段EF⊥AB于点F,与CD交于点E.(1)如图1,当⊙O半径为5,CD=4,若EF=BF,求弦AB的长;(2)如图2,当⊙O半径为,CD=2,若OB⊥OC,求弦AC的长.20.如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.(1)求证:∠ECD=∠EDC;(2)若OC=2,求DE长;(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.21.如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.(1)求证:AC是⊙O的切线;(2)若BF=4,DF=,求⊙O的半径.22.如图,不等边△ABC内接于⊙O,I是△ABC内心,AI交⊙O于D点,交BC于点E,连接BD,BI.(1)求证BD=ID;(2)连接OI,若AI⊥OI.且AB=4,BC=6,求AC的长.23.如图,已知AB、AC分别是⊙O的直径和弦,过点C的切线与AB的延长线交于点E,点D为EC的延长线上一点,DH⊥AB,垂足为点H,交AC于点F.(1)求证:△FCD是等腰三角形;(2)若点F为AC的中点,且∠E=30°,BE=2,求DF的长.24.如图,在△ABC中,AB=AC=8,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AC于点E,连接OD.(1)求证:OD∥AC;(2)若∠A=45°,求DE的长.25.在⊙O中,直径AB⊥弦CD于点F,点E是弧AD上一点,连BE交CD于点N,点P 在CD的延长线上,PN=PE.(1)求证:PE是⊙O的切线;(2)连接DE,若DE∥AB,OF=3,BF=2,求PN的长.圆专题参考答案与试题解析一.选择题(共9小题)1.已知⊙O中最长的弦长8cm,则⊙O的半径是()A.2cm B.4cm C.8cm D.16cm【解答】解:∵⊙O中最长的弦为8cm,即直径为8cm,∴⊙O的半径为4cm.故选:B.2.有下列说法:①直径是圆中最长的弦;②等弧所对的弦相等;③圆中90°的角所对的弦是直径;④相等的圆心角对的弧相等.其中正确的有()A.1个B.2个C.3个D.4个【解答】解:①正确;②在同圆或等圆中,能够重合的弧叫做等弧,等弧所对的弦相等;故②正确;③圆中,90°圆周角所对的弦是直径;故③错误;④在同圆或等圆中,相等的圆心角所对的弧相等;故④错误;因此正确的结论是①②;故选:B.3.如图,已知AB、AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,若MN=,那么BC等于()A.5B.C.2D.【解答】解:∵OM⊥AB,ON⊥AC,垂足分别为M、N,∴M、N分别是AB与AC的中点,∴MN是△ABC的中位线,∴BC=2MN=2,故选:C.4.如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=37°,那么∠BAD=()A.51°B.53°C.57°D.60°【解答】解:连接BD,如图所示.∵AB是⊙O的直径,∴∠ADB=90°.在△ABD中,∠ABD=∠ACD=37°,∠ADB=90°,∴∠BAD=180°﹣∠ABD﹣∠ADB=53°.故选:B.5.已知⊙O的半径等于3,圆心O到点P的距离为5,那么点P与⊙O的位置关系是()A.点P在⊙O内B.点P在⊙O外C.点P在⊙O上D.无法确定【解答】解:∵r=3,d=5,∴d>r,∴点P在⊙O外.故选:B.6.如图EF与⊙O相切于点D,A、B为⊙O上点,则下列说法中错误的()A.∠AOB是圆心角B.∠ADB是圆周角C.∠BDF是圆周角D.∠BOD是圆心角【解答】解:∵EF与⊙O相切于点D,∴点D有圆上,∴∠AOB和∠BOD是圆心角,∠ADB是圆周角,∵点F不在圆O上,∴∠BDF不是圆周角,故选:C.7.如图,P A、PB、分别切⊙O于A、B两点,∠P=40°,则∠C的度数为()A.40°B.140°C.70°D.80°【解答】解:∵P A是圆的切线.∴∠OAP=90°,同理∠OBP=90°,根据四边形内角和定理可得:∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=360°﹣90°﹣90°﹣40°=140°,∴∠ACB=∠AOB=70°.故选:C.8.如图,⊙O与正五边形ABCDE的边AB,DE分别相切于点B,D,则劣弧BD所对的圆心角∠BOD的大小为()A.108°B.118°C.144°D.120°【解答】解:∵五边形ABCDE是正五边形,∴∠E=∠A=180°﹣=108°.∵AB、DE与⊙O相切,∴∠OBA=∠ODE=90°,∴∠BOD=(5﹣2)×180°﹣90°﹣108°﹣108°﹣90°=144°,故选:C.9.如图,在Rt△ABC中,∠C=90°,AB=6,AD是∠BAC的平分线,经过A,D两点的圆的圆心O恰好落在AB上,⊙O分别与A、B、AC相交于点E、F.若圆半径为2.则阴影部分面积()A.B.C.D.【解答】解:连接OD,OF.∵AD是∠BAC的平分线,∴∠DAB=∠DAC,∵OD=OA,∴∠ODA=∠OAD,∴∠ODA=∠DAC,∴OD∥AC,∴∠ODB=∠C=90°,∴S△AFD=S△OF A,∴S阴=S扇形OF A,∵OD=OA=2,AB=6,∴OB=4,∴OB=2OD,∴∠B=30°,∴∠A=60°,∵OF=OA,∴△AOF是等边三角形,∴∠AOF=60°,∴S阴=S扇形OF A==.故选:C.二.填空题(共8小题)10.有下列说法:①半径是弦;②半圆是弧,但弧不一定是半圆;③面积相等的两个圆是等圆,其中正确的是②③(填序号)【解答】解:①半径是弦,错误,因为半径的一个端点为圆心;②半圆是弧,但弧不一定是半圆,正确;③面积相等的两个圆是等圆,正确,正确的结论有②③,故答案为:②③.11.如图,某种齿轮有20个齿,每两齿之间的间隔相等,则相邻两齿间的圆心角α等于18°.【解答】解:由题意这是正二十边形,中心角α==18°,故答案为18.12.如图所示,⊙O的半径为5,AB为弦,半径OC⊥AB,垂足为D,如果CD=2,那么AB的长是8.【解答】解:连接OA,∵半径OC⊥AB,∴AE=BD=AB,∵OC=5,CD=2,∴OE=3,在Rt△AOD中,AD===4,∴AB=2AD=8,故答案为8.13.如图△ABC中,AC=BC=5,AB=6,以AB为直径的⊙O与AC交于点D,若E为的中点,则DE.【解答】解:连接OC、OE、BD,OE与BD交于点F,如图所示:∵AC=BC=5,O为AB的中点,∴OA=OB=3,OC⊥AB,∴OC===4,∵AB为⊙O的直径,∴∠ADB=90°∴AD⊥BD,∴BD===,∴AD===,∵E为的中点,∴OE⊥BD,∴OE∥AD,∵OA=OB,∴OF为△ABD的中位线,∴DF=BF=BD=,OF=AD=,∴EF=OE﹣OF=3﹣=,∴DE===;故答案为:.14.如图,在⊙O中,半径OC=6,D是半径OC上一点,且OD=4.A,B是⊙O上的两个动点,∠ADB=90°,F是AB的中点,则OF的长的最大值等于2+.【解答】解:∵当点F与点D运动至共线时,OF长度最大,如图,∵F是AB的中点,∴OC⊥AB,设OF为x,则DF=x﹣4,∵△ABD是等腰直角三角形,∴DF=AB=BF=x﹣4,在Rt△BOC中,OB2=OF2+BF2,∵OB=OC=6,∴36=x2+(x﹣4)2,解得x=2+或2﹣(舍去)∴OF的长的最大值等于2+,故答案为2+.15.如图,⊙O是四边形ABCD的内切圆,连接OA、OB、OC、OD.若∠AOB=110°,则∠COD的度数是70°.【解答】解:如图所示:连接圆心与各切点,在Rt△DEO和Rt△DFO中,∴Rt△DEO≌Rt△DFO(HL),∴∠1=∠2,同理可得:Rt△AFO≌Rt△AMO,Rt△BMO≌Rt△BNO,Rt△CEO≌Rt△CNO,∴∠3=∠4,∠5=∠7,∠6=∠8,∴∠5+∠6=∠7+∠8=110°,∴2∠2+2∠3=360°﹣2×110°,∴∠2+∠3=∠DOC=70°.故答案为:70°.16.正n边形内接于半径为R的圆,这个n边形的面积为3R2,则n等于10.【解答】解:根据正n边形内接于半径为R的圆,则可将分割成n个全等的等腰三角形,其中等腰三角形的腰长为圆的半径R,顶角为,∵个n边形的面积为3R2,∴n××R×R×sin=3R2n sin=6解得n=10.故答案为10.17.已知扇形的圆心角为120°,它所对弧长为20πcm,则扇形的半径为30cm.【解答】解:根据题意得,r=30cm,故答案为30cm.三.解答题(共8小题)18.如图,在△ABC中,点O为BC边上一点,⊙O经过A、B两点,与BC边交于点E,点F为BE下方半圆弧上一点,FE⊥AC,垂足为D,∠BEF=2∠F.(1)求证:AC为⊙O切线.(2)若AB=5,DF=4,求⊙O半径长.【解答】(1)证明:连结OA,∴∠AOE=2∠F,∵∠BEF=2∠F,∴∠AOE=∠BEF,∴AO∥DF,∵DF⊥AC,∴OA⊥AC,∴AC为⊙O切线;(2)解:连接OF,∵∠BEF=2∠F,∴设∠AFE=α,则∠BEF=2α,∴∠BAF=∠BEF=2α,∵∠B=∠AFE=α,∴∠BAO=∠B=α,∴∠OAF=∠BAO=α,∵OA=OF,∴∠AFO=∠OAF=α,∴△ABO≌△AFO(AAS),∴AB=AF=5,∵DF=4,∴AD==3,∵BE是⊙O的直径,∴∠BAE=90°,∴∠BAE=∠FDA,∵∠B=∠AFD,∴△ABE∽△DF A,∴=,∴=,∴BE=,∴⊙O半径=.19.如图,A,B,C,D在⊙O上,AB∥CD经过圆心O的线段EF⊥AB于点F,与CD交于点E.(1)如图1,当⊙O半径为5,CD=4,若EF=BF,求弦AB的长;(2)如图2,当⊙O半径为,CD=2,若OB⊥OC,求弦AC的长.【解答】解:(1)如图1中,连接OB,OC.设BF=EF=x,OF=y.∴∠CEF∠CEF∵AB∥CD,EF⊥AB,∴EF⊥CD,∴AF=BF=x,DE=EC=2,根据勾股定理可得:,解得或(舍弃),∴BF=4,AB=2BF=8.(2)如图2中,作CH⊥AB于H.∵OB⊥OC,∴∠A=∠BOC=45°,∵AH⊥CH,∴△ACH是等腰直角三角形,∵AC=CH,∵AB∥CD,EF⊥AB,∴EF⊥CD,∠CEF=∠EFH=∠CHF=90°,∴四边形EFHC是矩形,∴CH=EF,在Rt△OEC中,∵EC=,OC=,OE===2,∵∠EOC+∠OCE=90°,∠EOC+∠FOB=90°,∴∠FOB=∠ECO,∵OB=OC,∴△OFB≌△CEO(AAS),∴OF=EC=,∴CH=EF=3,∴AC=EF=6.20.如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.(1)求证:∠ECD=∠EDC;(2)若OC=2,求DE长;(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.【解答】解:(1)如图1,连接OD,则OD⊥DE,∵∠∠ODA+∠EDC=90°,∵OA=OD,∴∠OAD=∠ODA,又∵OA⊥OB,∴∠OAD+∠OCA=90°,且∠OCA=∠ECD,∴∠ECD=∠EDC;(2)由(1)知,∠ECD=∠EDC,∴ED=EC,在Rt△ODE中,设ED=x,则OE=CE+OC=2+x,∵OD2+DE2=OE2,∴82+x2=(2+x)2,解得,x=15,∴DE的长为15;(3)如图2,连接OD',过点O作OH⊥AD'于点H,延长AO交⊙O于点M,过点D作DN⊥AM于点N,设弦AD在圆内扫过的面积为S,则S=S扇形OAD﹣S△OAD﹣S弓形ABD',由题意知,∠OAH=30°,∴在Rt△OAH中,∠AOH=60°,AH=OA=4,OH=OA=4,∴AD'=2AH=8,∠AOD'=120°,∴S弓形ABD'=S扇形OAD'﹣S△OAD'=﹣×8×4=﹣16,在Rt△ODN中,∠DON=2∠OAD=30°,∴DN=OD=4,∴S△OAD=OA•DN=×8×4=16,∵∠AOD=180°﹣∠DON=150°,∴S扇形OAD==,∴S=S扇形OAD﹣S△OAD﹣S弓形ABD'=﹣16﹣(﹣16)=+16﹣16,∴弦AD在圆内扫过的面积为+16﹣16.21.如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.(1)求证:AC是⊙O的切线;(2)若BF=4,DF=,求⊙O的半径.【解答】证明:(1)连接AO,∵OA=OD,∴∠OAD=∠ODA,∵AC=FC,∴∠CAF=∠CF A=∠OFD,∵D为BE的下半圆弧的中点,∴OD⊥BE,∴∠ODA+∠OFD=90°,∴∠CF A+∠DAO=90°,∴∠OAC=90°,且OA是半径,∴AC是⊙O的切线;(2)在Rt△ODF中,DF2=OD2+OF2,∴10=OD2+(4﹣OD)2,∴OD=1(不合题意舍去),OD=3,∴⊙O的半径为3.22.如图,不等边△ABC内接于⊙O,I是△ABC内心,AI交⊙O于D点,交BC于点E,连接BD,BI.(1)求证BD=ID;(2)连接OI,若AI⊥OI.且AB=4,BC=6,求AC的长.【解答】解:(1)证明:∵I是△ABC内心,∴∠BAD=∠CAD,∴=,∴∠DBC=∠DAB,∵∠ABI=∠CBI,∵∠DBI=∠DBC+∠CBI∠DIB=∠DAB+∠ABI∴∠DBI=∠DIB,∴BD=ID.(2)连接OD,∵=,根据垂径定理,得OD⊥BC于点H,CH=BH=BC=3,∵AI⊥OI.∴AI=DI,∴AI=BD,作IG⊥AB于点G,∴∠AGI=∠BED=90°,∠DBC=∠BAD,∴△AGI≌△BHD(AAS)∴AG=BH=3.过点I作IM⊥BC,IN⊥AC于点M、N,∵I是△ABC内心,∴AN=AG=3,BM=BG=4﹣3=1,CN=CM=6﹣1=5,∴AC=AN+CN=8.答:AC的长为8.23.如图,已知AB、AC分别是⊙O的直径和弦,过点C的切线与AB的延长线交于点E,点D为EC的延长线上一点,DH⊥AB,垂足为点H,交AC于点F.(1)求证:△FCD是等腰三角形;(2)若点F为AC的中点,且∠E=30°,BE=2,求DF的长.【解答】(1)证明:连结OC,如图1,∵DC为⊙O的切线,∴OC⊥DC,∴∠OCD=90°,即∠ACO+∠FCD=90°,∵DH⊥AB,∴∠DHA=90°,∴∠CAO+∠AFH=90°,∵OA=OC,∴∠ACO=∠AOC,∴∠FCD=∠AFH,而∠AFH=∠DFC,∴∠DFC=∠DCF,∴△FCD是等腰三角形;(2)解:连结OF,OC,如图2,在Rt△COE中,∠E=30°,BE=2,∴OE=2OC,即OB+2=2OC,而OB=OC,∴OC=2,∴⊙O的半径为2;∵∠EOC=90°﹣∠E=60°,∴∠ACO=∠AOC=30°,∴∠FCD=90°﹣∠ACO=60°,∴△FCD为等边三角形,∵F为AC的中点,∴OF⊥AC,∴AF=CF,在Rt△OCF中,OF=OC=1,∴CF=OF=,∴.24.如图,在△ABC中,AB=AC=8,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线交AC于点E,连接OD.(1)求证:OD∥AC;(2)若∠A=45°,求DE的长.【解答】(1)证明:∵AB=AC,∴∠B=∠C,∵OB=OD,∴∠B=∠ODB,∴∠C=∠ODB,∴OD∥AC;(2)解:过点O作OF⊥AC于点F,∵DE是⊙O的切线,∴DE⊥OD.∵OD∥AC,∴DE⊥AC.∴四边形OFED是矩形.∴OF=DE.在Rt△AOF中,∠A=45°,∴OF=OA=2,∴DE=2.25.在⊙O中,直径AB⊥弦CD于点F,点E是弧AD上一点,连BE交CD于点N,点P 在CD的延长线上,PN=PE.(1)求证:PE是⊙O的切线;(2)连接DE,若DE∥AB,OF=3,BF=2,求PN的长.【解答】(1)证明:连接OE,如图1所示:∵PN=PE,∴∠PEN=∠PNE=∠BNF,∵OE=OB,∴∠OEB=∠OBE.∵AB⊥CD,∴∠OBE+∠BNF=90°,∴∠OEB+∠PEN=90°,即∠OEP=90°,∴PE⊥OE,∴PE是⊙O的切线.(2)解:连接CE,如图2所示:∵DE∥AB,AB⊥CD,∴∠EDC=90°∴CE为⊙O的直径.∵AB⊥CD,∴CF=DF,∴DE=2OF=6.∵OF=3,BF=2,∴OC=OB=5,CE=10,∴CD===8,由(1)知PE⊥CE.设PD=x,则PC=x+8.在Rt△PDE和Rt△PCE中,由勾股定理,得:PD2+DE2=PE2=PC2﹣CE2,即x2+62=(x+8)2﹣102,解得:x=,∴PD=.∴PE===,∴PN=PE=.。
下册 3.1圆-2020秋九年级北师大版数学全一册作业课件

与任何人接触时,要常常问自己,我有什么对他有用?使他得益。如果我不能以个人的道德学问和修持的力量,来使人受益,就等于欠了一份 债。 要做的事情总找得出时间和机会;不愿意做的事情也总能找得出借口。 人而无信,不知其可也。——《论语·为政》 君子不器。——《论语·为政》 只要面对现实,你才能超越现实。
身体健康,学习进步! 在任何时候都要坚信:“方法会比困难多一点”。
北师大版2019-2020九年级数学下册圆综合练习题1(培优 含答案)
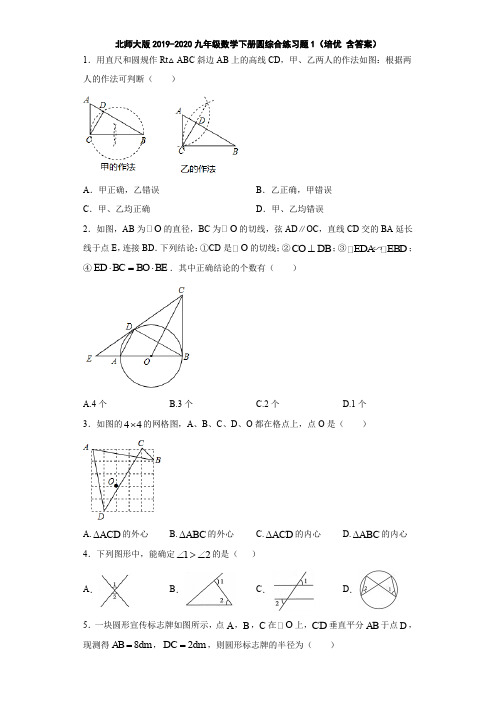
北师大版2019-2020九年级数学下册圆综合练习题1(培优 含答案)1.用直尺和圆规作Rt △ABC 斜边AB 上的高线CD ,甲、乙两人的作法如图:根据两人的作法可判断( )A .甲正确,乙错误B .乙正确,甲错误C .甲、乙均正确D .甲、乙均错误 2.如图,AB 为O 的直径,BC 为O 的切线,弦AD ∥OC ,直线CD 交的BA 延长线于点E ,连接BD .下列结论:①CD 是O 的切线;②CO DB ⊥;③EDA EBD ∽;④ED BC BO BE ⋅=⋅.其中正确结论的个数有( )A.4个B.3个C.2个D.1个3.如图的44⨯的网格图,A 、B 、C 、D 、O 都在格点上,点O 是( )A.ΔACD 的外心B.ΔABC 的外心C.ΔACD 的内心D.ΔABC 的内心 4.下列图形中,能确定12∠>∠的是( )A .B .C .D . 5.一块圆形宣传标志牌如图所示,点A ,B ,C 在O 上,CD 垂直平分AB 于点D ,现测得8dm AB =,2dm DC =,则圆形标志牌的半径为( )A.6dmB.5dmC.4dmD.3dm6.考虑下面六个命题(1)任意三点确定一个圆;(2)平分弦的直径垂直于弦,且平分这条弦所对的弧;(3)90°的圆周角所对的弦是直径;(4)同弧或等弧所对的圆周角相等;(5)相等的圆周角所对的弧相等.其中正确的命题有( )A .2个B .3个C .4个D .5个7.如图,AB AC 、都是圆O 的弦,OM AB ON AC ⊥⊥,,垂足分别为M N 、,如果MN =,那么BC =( )A .3BC .D .8.中心角为30°的圆内接正n 边形的n 等于( )A .10B .12C .14D .159.如图,在正方形ABCD 中,边长AD =2,分别以顶点A 、D 为圆心,线段AD 的长为半径画弧交于点E ,则图中阴影部分的面积是_____.10.已知P 是⊙O 内一点,OP=4cm ,过点P 的最长弦为10cm ,则过P 点最短弦长为 ________cm .11.直径相等的两个圆是等圆.(______)12.如图,AC 1=,BAC 60∠=,弧BC 所对的圆心角为60,且AC ⊥弦BC.若点P 在弧BC 上,点E 、F 分别在AB 、AC 上.则PE EF + FP +的最小值为______.13.已知在Rt△ABC中,∠C=90°,AC、BC的长分别是一元二次方程x2﹣14x+48=0的两根,则Rt△ABC内切圆的半径为________.14.圆心角相等,所对的弦也相等.(______)15.如图1 是台湾某品牌手工蛋卷的外包装盒,其截面图如图2 所示,盒子上方是一段圆弧(弧MN ).D,E 为手提带的固定点,DE 与弧MN 所在的圆相切,DE=2.手提带自然下垂时,最低点为C,且呈抛物线形,抛物线与弧MN 交于点F,G.若△CDE是等腰直角三角形,且点C,F 到盒子底部AB 的距离分别为1,94,则弧MN 所在的圆的半径为_____.16.如图,在O中,若AB MN于C,AB为直径,试填写一个你认为正确的结论:________.17.等边三角形ABC内接于⊙O,连接OA,OB,OC,延长AO分别交BC于点P,弧BC于点D,连接BD,CD.(1)判断四边形BDCO是哪一种特殊四边形,并说明理由;(2)若等边三角形ABC的边长,求⊙O的半径;(3)在劣弧BD上有一点Q,请求出弓形BQD的面积.18.如图,点I是△ABC的内心,AI的延长线交BC于点D,与△ABC的外接圆相交于点E ,连接BE .⑴ 求证:BE IE =;⑵ 若6AD =,2DE =,求AI 的长.19.如图,在O 中AB 是直径,点F 是O 上一点,点E 是AF 的中点,过点E 作O 的切线,与BA 、BF 的延长线分别交于点C 、D ,连接BE .(1)求证:BD CD ⊥.(2)已知O 的半径为2,当AC 为何值时,BF DF =,并说明理由.20.如图,点E 是△ABC 的内心,AE 的延长线和△ABC 的外接圆相交于点D . (1)当△ABC 的外接圆半径为1时,且∠BAC=60°,求弧BC 的长度.(2)连接BD ,求证:DE=DB .21.如图,在△ABC 中,∠90C =,点D 是AB 边上一点,以BD 为直径的⊙O 与边AC 相切于点E ,与边BC 交于点F ,过点E 作EH ⊥AB 于点H ,连接BE . (1)求证:EH EC =;(2)若4BC =,2sin 3A =,求AD 的长.22.如图,AB 为⊙O 的直径,C 为⊙O 上一点,AD ⊥CE 于点 D ,AC 平分∠DAB . (1) 求证:直线 CE 是⊙O 的切线;(2) 若 AB =10,CD =4,求 BC 的长.23.如图,D 、E 分别是⊙O 两条半径OA 、OB 的中点,AC=CB .(1)求证:CD=CE .(2)若∠AOB=120°,OA=x ,四边形ODCE 的面积为y ,求y 与x 的函数关系式.24.如图1,△AOB 的三个顶点A 、O 、B 分别落在抛物线F 1:21733y x x =+的图象上,点A 的横坐标为﹣4,点B 的纵坐标为﹣2.(点A 在点B 的左侧)(1)求点A 、B 的坐标; (2)将△AOB 绕点O 逆时针旋转90°得到△A 'OB ',抛物线F 2:24y ax bx =++经过A '、B '两点,已知点M 为抛物线F 2的对称轴上一定点,且点A '恰好在以OM 为直径的圆上,连接OM 、A 'M ,求△OA 'M 的面积;(3)如图2,延长OB '交抛物线F 2于点C ,连接A 'C ,在坐标轴上是否存在点D ,使得以A 、O 、D 为顶点的三角形与△OA 'C 相似.若存在,请求出点D 的坐标;若不存在,请说明理由.参考答案1.C【解析】【分析】甲的做法是根据直径所对的圆周角为直角得出;乙的做法根据线段的垂直平分线性质得出.此题考查了作图﹣基本作图,熟练掌握基本作图的方法是解本题的关键.【详解】解:观察可得甲、乙两人的作法均正确,故选:C .【点睛】此题考查了作图﹣基本作图,熟练掌握基本作图的方法是解本题的关键.2.A【解析】【分析】由切线的性质得CBO 90∠=,首先连接OD ,易证得()COD COB SAS ≅,然后由全等三角形的对应角相等,求得CDO 90∠=,即可证得直线CD 是O 的切线,根据全等三角形的性质得到CD CB =,根据线段垂直平分线的判定定理得到即CO DB ⊥,故②正确;根据余角的性质得到ADE BDO ∠∠=,等量代换得到EDA DBE ∠∠=,根据相似三角形的判定定理得到EDA EBD ~,故③正确;根据相似三角形的性质得到ED OD BE BC=,于是得到ED?BC BO?BE =,故④正确. 【详解】解:连结DO . AB 为O 的直径,BC 为O 的切线,CBO 90∠∴=,AD //OC ,DAO COB ∠∠∴=,ADO COD ∠∠=.又OA OD =,DAO ADO ∠∠∴=,COD COB ∠∠∴=.在COD 和COB 中,CO CO COD COB OD OB =⎧⎪∠=∠⎨⎪=⎩,()COD COB SAS ∴≅,CDO CBO 90∠∠∴==. 又点D 在O 上,CD ∴是O 的切线;故①正确,COD COB ≅,CD CB ∴=,OD OB =,CO ∴垂直平分DB ,即CO DB ⊥,故②正确; AB 为O 的直径,DC 为O 的切线,EDO ADB 90∠∠∴==,EDA ADO BDO ADO 90∠∠∠∠∴+=+=,ADE BDO ∠∠∴=,OD OB =,ODB OBD ∠∠∴=,EDA DBE ∠∠∴=,E E ∠∠=,EDA EBD ∴~,故③正确;EDO EBC 90∠∠==,E E ∠∠=,EOD ECB ∴~,ED OD BE BC∴=, OD OB =,ED ?BC BO ?BE ∴=,故④正确;故选:A .【点睛】本题主要考查了切线的判定、全等三角形的判定与性质以及相似三角形的判定与性质,注意掌握辅助线的作法,注意数形结合思想的应用是解答此题的关键.3.B【解析】【分析】连接OA、OB、OC、OD,设网格的边长为1,利用勾股定理分别求出OA、OB、OC、OD 的长,根据O点与三角形的顶点的距离即可得答案.【详解】连接OA、OB、OC、OD,设网格的边长为1,∴∵∴O为△ABC的外心,故选B.【点睛】本题考查勾股定理的应用,熟练掌握三角形的外心和内心的定义是解题关键.4.B【解析】【分析】根据对顶角相等对选项A进行判断;根据三角形外角性质对选项B进行判断;根据平行线的性质和对顶角相等对选项C 进行判断;根据圆周角定理对选项D 进行判断.【详解】解:A 、∵∠1与∠2是对顶角,∴∠1=∠2,故本选项不合题意;B 、∵∠1是∠2所在三角形的一个外角,∴∠1>∠2,故本选项正确;C 、若两条直线平行,则∠1=∠2,若所截两条直线不平行,则∠1与∠2无法进行判断,故本选项不合题意;D 、∵∠1、∠2是同弧所对的圆周角,∴∠1=∠2.故本选项不合题意.故选:B .【点睛】本题考查的是对顶角相等、平行线的性质、三角形外角的性质及直角三角形的性质,熟知以上知识是解答此题的关键.5.B【解析】【分析】连结OD ,OA ,设半径为r ,根据垂径定理得4,2AD OD r ==- ,在Rt ADO ∆中,由勾股定理建立方程,解之即可求得答案.【详解】连结OD ,OA ,如图,设半径为r ,∵8AB =,CD AB ⊥,∴4=AD ,点O 、D 、C 三点共线,∵2CD =,∴2OD r =-,在Rt ADO ∆中,∵222AO AD OD =+,,即2224(2)r r =+-,解得=5r ,故选:B.【点睛】本题考查勾股定理,关键是利用垂径定理解答.6.A【解析】【分析】根据圆中的定理进行分析.确定圆的定理:不在同一条直线上的三个点确定一个圆;垂径定理的推论:平分弦(非直径)的直径垂直于弦,且平分这条弦所对的弧;圆周角定理的推论:在同圆或等圆中,相等的圆周角所对的弧相等,同弧或等弧所对的圆周角相等;90°的圆周角所对的弦是直径.【详解】解:根据圆中的定理及其推论,知(1)当三点共线的时候不能确定一个圆,故错误;(2)当该弦是直径的时候,不一定能够垂直,故错误;(3)和(4)根据圆周角定理的推论,故正确;(5)必须在同圆或等圆中,故错误.故选:A .【点睛】此题考查了圆中的重要定理及其推论.注意:因为等弧的概念已经强调了在同圆或等圆中,所以当等弧做为条件时,不用强调在同圆或等圆中.7.C【解析】【分析】由OM ⊥AB ,ON ⊥AC ,根据垂径定理易得MN 是△ABC 的中位线,即可求得BC 的长.【详解】∵OM⊥AB,ON⊥AC,∴AN=CN,AM=BM,即MN是△ABC的中位线,∴MN=12 BC,∴,故选C.【点睛】此题考查了垂径定理、三角形的中位线的性质以及等边三角形的性质.此题难度不大,注意掌握数形结合思想的应用.8.B【解析】正n边形的n=360°÷30°=12,故选B.【点睛】本题考查了正多边形的中心角,解题的关键是要知道正多边形的中心角相等,一个周角为360度.9..【解析】【分析】连接AE、DE,可以阴影部分的面积是扇形ADE的面积与弓形DE的面积之和,由题目中的数据可以用代数式表示出阴影部分的面积,本题得以解决.【详解】如图所示,连接AE、DE,∵AE=DE=AD,∴△AED是等边三角形,∴∠ADE=60°,∴图中阴影部分的面积是:+(﹣×2×2×sin60°)=.故答案为:.【点睛】题考查扇形面积的计算、正方形的性质,解答本题的关键是明确题意,利用数形结合的思想解答,注意:圆心角是n°,半径为r的扇形的面积S=.10.6【解析】【分析】结合题意画出图形,过点P的最长弦就是直径,最短弦就是垂直于OP的弦,由最长的弦长求出半径的长;在圆中以半径、弦心距和弦长的一半为三边构成直角三角形,根据垂径定理和勾股定理即可求出最短的弦长.【详解】如图所示,OP⊥AB于P.∵过点P的最长弦就是直径,∴半径为10÷2=5cm,∵最短弦就是垂直于OP的弦,OA=5cm,OP=4cm,∴∴弦AB=2AP=2×3=6cm.即过P点最短弦长为6cm.故答案为:6.【点睛】本题考查勾股定理,垂径定理及推论,解题关键是构造以半径、弦心距和弦长的一半为三边的直角三角形.11.正确【解析】【分析】根据等圆的定义即可得答案.【详解】∵能够重合的圆叫做等圆,∴半径相等的圆是等圆,∴直径相等的圆是等圆,故答案为:正确【点睛】本题考查了圆的认识,熟练掌握圆的有关概念是解题关键.123【解析】【分析】连接AP,OP,OA.分别以AB、AC所在直线为对称轴,作出P关于AB的对称点为M,P 关于AC的对称点为N,连接MN,交AB于点E,交AC于点F,连接PE、PF,所以==,设AP rAM AP AN=,易求得:MN=,所以++可取得最++=++==,即当AP最小时,PE EF PFPE EF PF ME EF FN MN小值.【详解】连接AP,O,OA.分别以AB、AC所在直线为对称轴,作出P关于AB的对称点为M,P 关于AC的对称点为N,连接MN,交AB于点E,交AC于点F,连接PE、PF.∴==,AM AP ANMAB PAB ∠∠=,NAC PAC ∠∠=,BAC PAB PAC MAB NAC 60∠∠∠∠∠=+=+=,MAN 120∠∴=,M ∴、P 、N 在以A 为圆心,AP 为半径的圆上,设AP r =,易求得:MN =,PE ME =,PF FN =,PE EF PF ME EF FN MN ∴++=++==,∴当AP 最小时,PE EF PF ++可取得最小值AP OP OA +≥,AP OA OP ∴≥-,即点P 在OA 上时,AP 可取得最小值,在Rt ABC 中,AC 1=,BAC 60∠=,BC ∴=,BOC 60∠=,OB OC =, OBC ∴是等边三角形,OC BC ∴==OH AC ⊥交AC 的延长线于H .在Rt OCH 中,OC 3=OCH 30∠=,1OH OC 2∴==,3CH 2==,在Rt AOH 中,AO ===此时AP r ==,PE EF PF ∴++3,3.【点睛】本题考查圆的有关知识,涉及轴对称的性质,勾股定理,垂径定理,等边三角形的性质与判定等知识,综合程度较高,需要学生灵活运用知识.13.2【解析】【分析】先解一元二次方程可得AC和BC的长,根据勾股定理计算AB的长,再用直角三角形内切圆公式进行解答即可.【详解】∵AC、BC的长分别是一元二次方程x2﹣14x+48=0的两根可得(x−6)(x−8)=0,解得方程的两个根为x=6或8,∵∠C=90°∴由勾股定理可得10AB=∴Rt△ABC的内切圆的半径为68122+-=【点睛】本题主要考查解一元二次方程、勾股定理、直角三角形内切圆公式,熟悉公式定理是关键. 14.错【解析】【分析】利用圆心角定理:同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等,判断即可.【详解】根据圆心角定理:同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等,判断可知原命题为假命题,故答案为×.【点睛】此题考查圆心角定理,解题关键在于熟悉定理概念.15.21 8.【解析】【分析】以DE的垂直平分线为y轴,AB所在的直线为x轴建立平面直角坐标系,设抛物线的表达式为y=ax2+1,因为△CDE是等腰直角三角形,DE=2,得点E的坐标为(1,2),可得抛物线的表达式为y =x 2+1,把当y 94=代入抛物线表达式,求得MH 的长,再在Rt △FHM 中,用勾股定理建立方程,求得MN 所在的圆的半径.【详解】如图,以DE 的垂直平分线为y 轴,AB 所在的直线为x 轴建立平面直角坐标系,设MN 所在的圆的圆心为P ,半径为r ,过F 作y 轴的垂线交y 轴于H ,设抛物线的表达式为y =ax 2+1.∵△CDE 是等腰直角三角形,DE =2,∴点E 的坐标为(1,2),代入抛物线的表达式,得:2=a +1,a =1,∴抛物线的表达式为y =x 2+1,当y 94=时,即2914x =+,解得:x =,∴FH =.∵∠FHM =90°,DE 与MN 所在的圆相切,∴222924r r =++-(),解得:218r =,∴MN 所在的圆的半径为218. 故答案为:218.【点睛】本题考查了圆的切线的性质,待定系数法求抛物线的表达式,垂径定理.解题的关键是建立合适的平面直角坐标系得出抛物线的表达式.16.CM CN =(答案不唯一)【解析】【分析】根据垂径定理的要求即可解题.【详解】解:∵AB MN 于C ,AB 为直径,∴CM=CN (垂径定理).【点睛】本题考查了垂径定理的应用,属于简单题,熟悉垂径定理的内容是解题关键.17.(1)四边形BDCO 是菱形理由见解析;(2)6;(3)6π.【解析】【分析】(1)可先由四边形各角的大小求出各边之间的关系,然后即可判断四边形BDCO 为何种特殊四边形;(2)先由菱形性质求出BP 的长,再由等边三角形性质及求出∠POB 的角度,然后即可由三角形边角关系求出OB 的长,即⊙O 的半径;(3)弓形BQD 的面积可由求扇形OBD 与三角形OBD 之差间接求得.【详解】解:(1)四边形BDCO 是菱形,理由如下:∵AB =BC =AC ,∴∠AOB =∠BOC =∠COA =120°,∴∠BOD =180°﹣∠AOB =60°,∴∠COD =180°﹣∠AOC =60°;又∵OB =OD ,∴△OBD 为正三角形,∴OB =OD =BD同理可得OC =CD ,∴OB =OC =BO =CD 即四边形BDCO 是菱形;(2)由菱形性质可知,BP=12BC=12× ∵△ABC 为等边三角形,∠PBO =30°,OP =3,BO =6,∴⊙O 的半径OB 为6.(3)S 弓形BQD =S 扇形-S △BOD =2606360π⨯62 =6π. 【点睛】本题考查了正三角形与圆,正三角形的性质,菱形的性质与判定及面积求法,具有较强的综合性.18.(1)详见解析;(2)4AI =.【解析】【分析】(1)要证明BE IE =只需证出BIE EBI ∠=∠;(2)求出△EBD ∽△EAB ,可得4IE BE ==,进而可得到4AI =.【详解】⑴ 连接BI ,∵点I 是△ABC 的内心,∴ABI IBD ∠=∠,BAE EAC ∠=∠.∵EBC EAC ∠=∠,∴BIE BAI ABI ∠=∠+∠,EBI EBC IBD ∠=∠+∠.∴BIE EBI ∠=∠,BE EI =. ⑵ ∵EBC EAC BAE ∠=∠=∠,BED AEB ∠=∠,∴△EBD ∽△EAB .∴()222616BE ED EA =⋅=⨯+=,4IE BE ==.∴2644AI AD DE IE =+-=+-=.【点睛】本题考查了三角形的外接圆与外心、三角形的内切圆和内心和相似三角形的性质,熟练掌握这些知识点是本题解题的关键.19.(1)证明见解析;(2)当4AC =时,BF DF =.理由见解析.【解析】【分析】(1)连接OE ,由点E 是AF 的中点,过点E 作⊙O 的切线,可得OE ⊥CD ,BD ∥OE ,进而得出BD ⊥CD ;(2)当AC=4时,连接AF ,证明△AFB ∽△BCD ,所以12BF BA BD BC ==,即BF=DF. 【详解】(1)如图1,连接OE ,∵CD 与O 相切于点E ,∴OE CD ⊥,∴90CEO ∠=︒.∵点E 是AF 的中点,∴AE EF =,∴23∠∠=,∵OB OE =,∴21∠=∠,∴13∠=∠,∴OE BD ,∴90D CEO ∠=∠=︒,∴BD CD ⊥.(2)当4AC =时,BF DF =.理由如下:如图2,连接AF ,∵AB 是O 的直径,∴90AFB ∠=︒,由(1)知90D ∠=︒,∴D AFB ∠=∠,∴△AFB ∽△BCD , ∴BF BA BD BC=, 当4AC =时,∵O 的半径为2,∴4AB =,∴BC=AB+AC=8, ∴4182BF BA BD BC ===, ∴1BF DF =, ∴BF DF =.【点睛】本题考查圆的切线的性质,相似三角形的判定和性质,菱形的判定.解题的关键是掌握圆的切线的性质.20.(1)2π3;(2)详见解析. 【解析】【分析】(1)设△ABC 的外接圆的圆心为O ,连接OB 、OC ,由圆周角定理得出∠BOC=120°,再由弧长公式即可得出结果;(2)连接BE ,由三角形的内心得出∠1=∠2,∠3=∠4,再由三角形的外角性质和圆周角定理得出∠DEB=∠DBE ,即可得出结论.【详解】(1)解:设△ABC 的外接圆的圆心为O ,连接OB 、OC ,如图1所示:∵∠BAC=60°,∴∠BOC=120°,∴弧BC的长度=120π1180=2π3.(2)证明:连接BE,如图2所示:∵E是△ABC的内心,∴∠1=∠2,∠3=∠4,∵∠DEB=∠1+∠3,∠DBE=∠4+∠5∠5=∠2,∴∠DEB=∠DBE,∴DE=DB.【点睛】本题考查了三角形的外心与内心、圆周角定理、弧长公式、三角形的外角性质、等腰三角形的判定等知识;本题综合性强,根据圆周角定理得出角的数量关系是解题的关键.21.(1)见解析;(2)6 5【解析】【分析】(1)连接OE,根据切线的性质得到OE⊥AC,根据平行线的性质、角平分线的性质证明结论;(2)根据正弦的定义求出AB,根据相似三角形的性质求出半径,计算即可.【详解】证明:(1)连结OE∵AC为⊙O切线,∴OE⊥AC∵∠C=90°,∴OE∥BC ∴∠EBC=∠BEO∵OE=OB,∴∠EBO=∠BEO∴∠EBC=∠EBO∵EH⊥AB,∠C=90°,∴EH EC=(2)∵∠C=90°,∴2sin3BCAAB==,∴AB=6,设⊙O半径为r,∵OE∥BC,∴△AEO∽△ACB,∴OE AO BC AB=,∴646r r-=∴125r=,∴AD=AB-12626255 BD AB r=-=-⨯=.【点睛】本题考查的是切线的性质、解直角三角形、圆周角定理,掌握相关的判定定理和性质定理是解题的关键.22.(1)证明见解析;(2)BC=【解析】【分析】(1)如图,连接OC,由AC平分∠DAB得到∠DAC=∠CAB,然后利用等腰三角形的性质得到∠OCA=∠CAB,接着利用平行线的判定得到AD∥CO,而CD⊥AD,由此得到CD⊥AD,最后利用切线的判定定理即可证明CD为⊙O的切线;(2)证明△DAC∽△CAB,根据相似三角形对应边成比例进行求解即可. 【详解】(1)如图,连接OC∵AC平分∠DAB,∴∠DAC=∠CAB,∵OA=OC,∴∠OCA=∠CAB,∴∠OCA=∠DAC,∴AD∥CO,∵CD⊥AD,∴OC⊥CD,∵OC是⊙O直径且C在半径外端,∴CD为⊙O的切线;(2)∵AB是直径,∴∠ACB=90°,∵AD⊥CD,∴∠ADC=∠ACB=90°,∵∠DAC=∠CAB,∴△DAC∽△CAB,∴DC AC BC AB,∴BC•AC=DC•AB=4×10=40,∵BC2+AC2=100,∴(BC+AC)2=BC2+AC2+2BC•AC=180,(BC-AC)2= BC2+AC2-2BC•AC=20,∴AC ﹣BC ﹣,∴【点睛】本题考查了切线的判定、圆周角定理、相似三角形的判定与性质等,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.23.(1)证明见解析;(2)x 2. 【解析】【分析】(1)连接OC ,根据圆心角、弧、弦的关系定理得到∠COA=∠COB ,证明△COD ≌△COE ,根据全等三角形的性质证明;(2)连接AC ,根据全等三角形的判定定理得到△AOC 为等边三角形,根据正切的定义求出CD ,根据三角形的面积公式计算即可.【详解】(1)证明:连接OC ,∵AC=CB ,∴∠COA=∠COB ,∵D 、E 分别是⊙O 两条半径OA 、OB 的中点,∴OD=OE ,在△COD 和△COE 中,OD OE COD COE OC OC ⎧⎪∠∠⎨⎪⎩===,∴△COD ≌△COE (SAS )∴CD=CE ;(2)连接AC ,∵∠AOB=120°,∴∠AOC=60°,又OA=OC ,∴△AOC 为等边三角形,∵点D 是OA 的中点,∴CD ⊥OA ,OD=12OA=12x ,在Rt △COD 中,CD=OD•tan ∠COD=2,∴四边形ODCE 的面积为y=12×OD×CD×2. 【点睛】 本题考查的是圆心角、弧、弦的关系定理,全等三角形的判定和性质,等边三角形的性质,掌握圆心角、弧、弦的关系定理,全等三角形的判定定理和性质定理是同角的关键. 24.(1)点A 坐标为(﹣4,﹣4),点B 坐标为(﹣1,﹣2);(2)S △OA 'M =8;(3)点D 坐标为(4,0)、(8,0)、(0,4)或(0,8)时,以A 、O 、D 为顶点的三角形与△OA 'C 相似.【解析】【分析】(1)把x =﹣4代入解析式,求得点A 的坐标,把y=-2代入解析式,根据点B 与点A 的位置关系即可求得点B 的坐标;(2)如图1,过点B 作BE ⊥x 轴于点E ,过点B'作B'G ⊥x 轴于点G ,先求出点A'、B'的坐标,OA=OA'=F 2解析式为:21y x 3x 44=-+,对称轴为直线:x 6=,设M(6,m),表示出OM 2,A'M 2,进而根据OA'2+A'M 2=OM 2,得到)2+m 2+8m+20=36+m 2,求得m =﹣2,继而求得A'M =再根据S △OA'M =12OA'•A'M 通过计算即可得; (3)在坐标轴上存在点D ,使得以A 、O 、D 为顶点的三角形与△OA'C 相似,先求得直线OA 与x 轴夹角为45°,再分点D 在x 轴负半轴或y 轴负半轴时,∠AOD =45°,此时△AOD 不可能与△OA'C 相似,点D 在x 轴正半轴或y 轴正半轴时,∠AOD =∠OA'C =135°(如图2、图3),此时再分△AOD ∽△OA'C ,△DOA ∽△OA'C 两种情况分别讨论即可得.【详解】(1)当x =﹣4时,()()217y 44433=⨯-+⨯-=-, ∴点A 坐标为(﹣4,﹣4),当y =﹣2时,217x x 233+=-, 解得:x 1=﹣1,x 2=﹣6,∵点A 在点B 的左侧,∴点B 坐标为(﹣1,﹣2);(2)如图1,过点B 作BE ⊥x 轴于点E ,过点B'作B'G ⊥x 轴于点G ,∴∠BEO =∠OGB'=90°,OE =1,BE =2,∵将△AOB 绕点O 逆时针旋转90°得到△A'OB',∴OB =OB',∠BOB'=90°,∴∠BOE+∠B'OG =∠BOE+∠OBE =90°,∴∠B'OG =∠OBE ,在△B'OG 与△OBE 中B B B OG BEO OG OBE O BO ∠=∠⎧⎪∠=='∠'⎨'⎪⎩,∴△B'OG ≌△OBE(AAS),∴OG =BE =2,B'G =OE =1,∵点B'在第四象限,∴B'(2,﹣1),同理可求得:A'(4,﹣4),∴OA =OA'=∵抛物线F 2:y =ax 2+bx+4经过点A'、B',∴164444241a b a b ++=-⎧⎨++=-⎩, 解得:143a b ⎧=⎪⎨⎪=-⎩,∴抛物线F 2解析式为:21y x 3x 44=-+, ∴对称轴为直线:3x 6124-=-=⨯, ∵点M 在直线x =6上,设M(6,m),∴OM 2=62+m 2,A'M 2=(6﹣4)2+(m+4)2=m 2+8m+20,∵点A'在以OM 为直径的圆上,∴∠OA'M =90°,∴OA'2+A'M 2=OM 2,∴2+m 2+8m+20=36+m 2,解得:m =﹣2,∴A'M=∴S △OA'M =12OA'•A'M=182⨯=; (3)在坐标轴上存在点D ,使得以A 、O 、D 为顶点的三角形与△OA'C 相似,∵B'(2,﹣1),∴直线OB'解析式为y =﹣12x , 2121x 344y x y x ⎧=⎪⎪⎨⎪=-+⎪⎩, 解得:11x 2y 1=⎧⎨=-⎩(即为点B'),22x 8y 4=⎧⎨=-⎩, ∴C(8,﹣4),∵A'(4,﹣4),∴A'C ∥x 轴,A'C =4,∴∠OA'C =135°,∴∠A'OC <45°,∠A'CO <45°,∵A(﹣4,﹣4),即直线OA 与x 轴夹角为45°,∴当点D 在x 轴负半轴或y 轴负半轴时,∠AOD =45°,此时△AOD 不可能与△OA'C 相似, ∴点D 在x 轴正半轴或y 轴正半轴时,∠AOD =∠OA'C =135°(如图2、图3),①若△AOD ∽△OA'C , 则OD OA 1A C OA ''==, ∴OD =A'C =4,∴D(4,0)或(0,4);②若△DOA ∽△OA'C ,则DO OA OA A C ''===∴OD OA'=8,∴D(8,0)或(0,8),综上所述,点D 坐标为(4,0)、(8,0)、(0,4)或(0,8)时,以A 、O 、D 为顶点的三角形与△OA'C 相似.【点睛】本题考查的是二次函数与几何的综合题,涉及了待定系数法,全等三角形的判定与性质,相似三角形的判定与性质,圆周角定理等知识,综合性较强,有一定的难度,熟练掌握和灵活运用相关知识是解题的关键.注意数形结合思想与分类讨论思想的运用.。
北师大版九年级数学下册习题课件:小专题(十四) 与圆的基本性质有关的计算 (共11张PPT)

•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/8/312021/8/31Tuesday, August 31, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/8/312021/8/312021/8/318/31/2021 9:54:18 AM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/8/312021/8/312021/8/31Aug-2131-Aug-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/8/312021/8/312021/8/31Tuesday, August 31, 2021
• You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
北师大版2020九年级数学下册第三章圆单元综合基础达标训练题1(附答案详解)
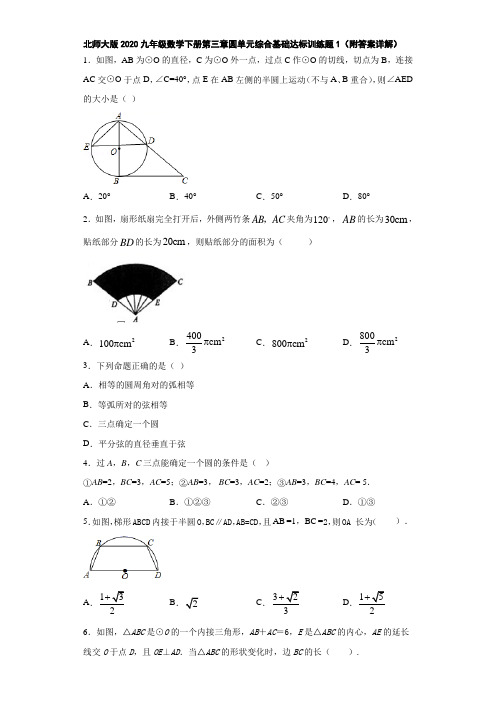
北师大版2020九年级数学下册第三章圆单元综合基础达标训练题1(附答案详解) 1.如图,AB 为⊙O 的直径,C 为⊙O 外一点,过点C 作⊙O 的切线,切点为B ,连接AC 交⊙O 于点D ,∠C=40°,点E 在AB 左侧的半圆上运动(不与A 、B 重合),则∠AED 的大小是( )A .20°B .40°C .50°D .80°2.如图,扇形纸扇完全打开后,外侧两竹条AB AC ,夹角为120,AB 的长为30cm ,贴纸部分BD 的长为20cm ,则贴纸部分的面积为( )A .2100cm πB .2400cm 3πC .2800cm πD .2800cm 3π 3.下列命题正确的是( )A .相等的圆周角对的弧相等B .等弧所对的弦相等C .三点确定一个圆D .平分弦的直径垂直于弦4.过A ,B ,C 三点能确定一个圆的条件是( )①AB =2,BC =3,AC =5;②AB =3, BC =3,AC =2;③AB =3,BC =4,AC = 5.A .①②B .①②③C .②③D .①③5.如图,梯形ABCD 内接于半圆O ,BC∥AD,AB=CD ,且AB =1,BC =2,则OA 长为( ).A .132B 2C .323+D .152+ 6.如图,△ABC 是⊙O 的一个内接三角形,AB +AC =6,E 是△ABC 的内心,AE 的延长线交O 于点D ,且OE ⊥AD .当△ABC 的形状变化时,边BC 的长( ).A .有最大值4B .等于3C .有最小值3D .等于47.Rt △ABC 中,∠C=90°,AC=2,BC=4,如果以点A 为圆心,AC 为半径作⊙A ,那么斜边中点D 与⊙A 的位置关系是( )A .点D 在⊙A 外B .点D 在⊙A 上C .点D 在⊙A 内 D .无法确定 8.如图,△ABC 内接于⊙O ,∠A 的度数为60°,∠ABC 、∠ACB 的角平分线分别交于AC 、AB 于点D 、E ,CE 、BD 相交于点F ,以下四个结论:①1cos 2BFE ∠=;②BC BD =;③=EF FD ;④2BF DF =;其中结论一定正确的序号数是( )A .①②B .①③C .③④D ②④ 9.如图,已知⊙O 中∠AOB 度数为100°,C 是圆周上的一点,则∠ACB 的度数为( )A .130°B .100°C .80°D .50°10.如图,在ABC △中,1086AB AC BC ,,===,经过点C 且与边AB 相切的动圆与CB CA ,分别相交于点E F ,,则线段EF 长度的最小值是( )A .2B .4.75C .4.8D .511.有下列说法:①等弧的长度相等;②直径是圆中最长的弦;③相等的圆心角对的弧相等;④圆中90°角所对的弦是直径;⑤同圆中等弦所对的圆周角相等.其中正确的有( )A.1个B.2个C.3个D.4个12.如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为()A.26πB.13πC.965πD.39105π13.如图,⊙O是△ABC的外接圆,AO⊥BC于点F,D为AC的中点,且CD的度数为70°则∠BAF=__________度14.如图所示,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为_______________.15.如图,P是⊙O外一点,A、B、C是⊙O上的三点,∠AOB=60°,PA、PB分别交ACB于M、N两点,则∠APB的范围是______.16.如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠ACO=_______°.17.如图,⊙O的半径为5,P为圆内一点,P点到圆心O的距离为4,则过P点的弦长的最小值是______.18.圆锥的底面周长为6πcm,高为4cm,则该圆锥的全面积是;侧面展开扇形的圆心角是.19.如图,AE,AD,BC分别切⊙O于点E、D和点F,若AD=8cm,则△ABC的周长为_______cm.20.如图,已知点C是AB的一点,圆周角∠ACB为125°,则圆心角∠AOB=_______度.21.如图,的半径为2,点,在上,,则阴影部分的面积为.22.如图,AB是⊙O的直径,O是圆心,BC与⊙O相切于点B,CD交⊙O于点D,且BC =8,CD=4,那么⊙O的半径是______。
北师大版2020九年级数学:圆的知识点总结及典型例题
【文库独家】圆的知识点总结(一)圆的有关性质[知识归纳]1. 圆的有关概念:圆、圆心、半径、圆的内部、圆的外部、同心圆、等圆;弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧、弓形、弓形的高;圆的内接三角形、三角形的外接圆、三角形的外心、圆内接多边形、多边形的外接圆;圆心角、圆周角、圆内接四边形的外角。
2. 圆的对称性圆是轴对称图形,经过圆心的每一条直线都是它的对称轴,圆有无数条对称轴;圆是以圆心为对称中心的中心对称图形;圆具有旋转不变性。
3. 圆的确定不在同一条直线上的三点确定一个圆。
4. 垂直于弦的直径垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧;推论1(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧。
垂径定理及推论1 可理解为一个圆和一条直线具备下面五个条件中的任意两个,就可推出另外三个:①过圆心;②垂直于弦;③平分弦(不是直径);④平分弦所对的优弧;⑤平分弦所对的劣弧。
推论2圆的两条平行弦所夹的弧相等。
5. 圆心角、弧、弦、弦心距之间的关系定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等;所对的弦的弦心距相等。
推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
此定理和推论可以理解成:在同圆或等圆中,满足下面四个条件中的任何一个就能推出另外三个:①两个圆心角相等;②两个圆心角所对的弧相等;③两个圆心角或两条弧所对的弦相等;④两条弦的弦心距相等。
圆心角的度数等于它所对的弧的度数。
6. 圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半;推论1同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧也相等;推论2半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径;推论3如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
北师版数学九年级下册课时练 第三章 圆 专项11 圆中常见的计算问题

北师版数学九年级下册第三章圆类型1有关角度的计算圆中角的计算,首先应该从弧入手,圆的弧与角是紧密相连的,然后再从特殊三角形入手.1.如图,AB是⊙O的直径,C,D分别为圆周上直径AB两侧的点,若∠ADC=3∠CAB.求∠CAB的度数.解:如图,连接BC.∵AB是⊙O的直径,∴∠ACB=90°,∴∠CAB+∠B=90°.∵∠ADC=∠B,∠ADC=3∠CAB,∴4∠CAB=90°,∴∠CAB=22.5°.2.如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.(1)求证:△ABD≌△CDB;(2)若∠DCB=37°,求∠EBD的度数.解:(1)证明:∵AB,CD是直径,∴∠ADB=∠CBD=90°.在Rt △ABD 和Rt △CDB 中,⎩⎨⎧AB =CD ,BD =DB ,∴Rt △ABD ≌Rt △CDB (HL). (2)∵BE 是切线,∴AB ⊥BE , ∴∠ABE =90°, ∴∠DBE +∠ABD =90°.∵∠C +∠BDO =90°,∠ODB =∠OBD , ∴∠EBD =∠C =37°. 类型2 有关线段的计算计算线段长的方法主要有:勾股定理,三角函数,相似三角形等,因此遇到求半径或弦长问题时,应该从构造三角形入手.3.如图,在⊙C 中,CA ⊥CB ,且CA =3,CB =4,求AD 的长. 解:∵AC ⊥BC ,∴∠ACB =90°, ∴AB =AC 2+BC 2=32+42=5.如图,过点C 作CE ⊥AB 于点E , 则由垂径定理,得AD =2AE . ∴cos A =AC AB =AE AC =35,∴AE =35AC =95,∴AD =2AE =185.4.如图,AB 是⊙O 的直径,C ,D 是⊙O 上两点,且AB =4,AC =CD =1,求BD 的长.解:如图,连接OC ,AD . ∵AB 是⊙O 的直径,AB =4, ∴∠ADB =90°,OA =2. ∵AC =CD =1,∴AC ︵=CD ︵,∴AD ⊥OC .设OE =x ,则CE =2-x .在Rt △ACE 中,AE 2+CE 2=AC 2,即AE 2=AC 2-CE 2;在Rt △AOE 中,AE 2+OE 2=OA 2,即AE 2=OA 2-OE 2,∴AC 2-CE 2=OA 2-OE 2,即12-(2-x )2=22-x 2,解得x =74.∵∠ADB =∠AEO ,点O 是AB 的中点, ∴OE 是△ABD 的中位线, ∴BD =2OE =72. 类型3 有关弧长的计算弧长的计算可以用公式,公式中的关键量是半径和圆心角,因此求弧长就是先要求出这两个量.角度1:直接应用公式求弧长5.如图,边长为2的正方形ABCD 的四个顶点分别在扇形OEF 的半径OE ,OF 和 EF ︵上,且点A 是线段OB 的中点,则EF ︵的长为( D )A.55πB.54πC.12πD.52π6.(2019·浙江湖州吴兴区期末)如图,探究:用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M ,P ,H 三点的圆弧与AH 交于点R ,则HR ︵的长为( D )A.π2B.24πC.34π D .52π 角度2:点旋转后的路径长问题7.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么点B 从开始至结束所走过的路径长度为( B )A.3π2B.4π3 C .4D .2+3π28.如图,Rt △ABC 的斜边AB 在直线l 上,AC =1,AB =2.将Rt △ABC 绕点B 在平面内按顺时针方向旋转,使边BC 落在直线l 上,得到△A 1BC 1,再将△A 1BC 1绕点C 1在平面内按顺时针方向旋转,使边A 1C 1落到直线l 上,得到△A 2B 1C 1,则点A 所经过的两条弧的长度和为__136π__.类型4 有关扇形面积的计算简单的扇形面积公式相关的量是半径和圆心角,因此求扇形面积首先从这两个量入手.复杂图形的面积方法比较灵活,如和(差)法、割补法、等积转化法等.近几年图形旋转扫过面积问题是个热点,通常也需要用到扇形面积求解. 方法1:直接计算法9.如图,AD 是半圆O 的直径,AD =12,B ,C 是半圆O 上两点.若AB ︵=BC ︵=CD ︵,则图中阴影部分的面积是(A)A.6π B.12π C.18π D.24π10.如图,在四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是__6π__.方法2:利用作差法求面积11.如图,一个半径为1的⊙O1经过一个半径为2的⊙O的圆心,则图中阴影部分的面积为(A)A.1 B.12 C. 2 D.2212.(2019·山东德州模拟)如图,在平面直角坐标系中,已知⊙D经过原点O,与x轴、y轴分别交于A,B两点,点B的坐标为(0,23),OC与⊙D相交于点C,∠OCA=30°,则图中阴影部分的面积为__2π-23__.方法3:利用等积转化法求面积13.如图,矩形ABCD的长和宽分别为2 cm和1 cm,以D为圆心,AD为半径作弧AE,再以AB的中点F为圆心,FB的长为半径作弧BE,则阴影部分的面积是(A)A.1 cm2B.2 cm2 C.3 cm2D.4 cm214.(2018·广东东莞中考)如图,在矩形ABCD中,BC=4,CD=2,以AD为直径的半圆O 与BC相切于点E,连接BD,则阴影部分的面积为__π__.(结果保留π)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 、有时费尽唇舌,争执一个不易化解的问题,还不如来一个简单的行动容易。这样的话,你就能化解敌人的攻势于无形。 5 、每个人都有美好的梦想,只有坚持,你的梦想才能实现。 18 、须交有道之人,莫结无义之友。饮清静之茶,莫贪花色之酒。开方便之门,闲是非之口。 1 、勇敢的人不是天生的,需要你经过很多的磨炼。但是在磨炼的过程中你能不能变得勇敢,那就取决于你的决心了。 11 、这个世界从不缺乏有才能的人,但缺少有精神的人。生活是没有路标的单程轮回,固守心的航向,需要非凡的勇气。以微笑驾驭人生之 舟情,友情还是爱情,平安就是福。且行且惜,且走且悟,人生之中唯有自强不息,勇敢向前,方可走 出一条阳光大道。
1 、成功就是凭着勇气和努力,不断地超越自己,做最好的自己。 14 、男人最大的武器是眼神,女人最大的武器是眼泪。 14 、不管你干什么,都会有两种结果: 一种是笑话,一种是神话。如果你半途而废,只能成为别人眼中的笑话;但如果你成功了,你就变成她 们眼中的神话。社会就是现实!要么不做,要么做好。 7 、准备种子,就收获果实;准备努力,就收获成功;准备今天,就收获明天。 3 、行动是通向成功的唯一途径。 1 、人应该活到老学到老,我们不应该取笑那些勤奋好学的老年人,相反,我们应该鼓励和支持他们的精神。 10 、争分夺秒巧复习,勤学苦练创佳绩、攀蟾折桂,舍我其谁。 3 、尊严来自实力,实力来自拼搏! 14 、自动自发地做事,同时为自己的所作所为承担责任,那么你终究会获得回报,取得最后的成功。 10 、以前喜欢一个人,可以任由招之即来,挥之即去。现在喜欢一个人,仍可以招之即来,但不再接受挥之即去。因为我现在知道,我很好 ,所以你爱我,也只有一次机会。
