高中化学晶体结构的有关计算答题技巧
高中化学知识点复习 晶体计算类型归纳

面(实际为椅式结构),碳原子为 sp3 杂化
(3)每个碳原子被 12 个六元环共用,每个共价键被 6 个六元环共用,一个六元
1
环实际拥有 个碳原子
2
(4)C 原子数与 C—C 键数之比为 1∶2,12g 金刚石中有 2 mol 共价键
(5)密度=8×12 g·mol-1 NA×a3
(a 为晶胞边长,NA 为阿伏加德罗常数)
NA×a3
离子晶体的配位数
离子晶体中与某离子距离最近的异性离子的数目叫该离子的配位数
(1)正、负离子半径比:AB 型离子晶体中,阴、阳离子的配位数相等,但正、
影响离子晶体配位数的因素
负离子半径比越大,离子的配位数越大。如:ZnS、NaCl、CsCl (2)正、负离子的电荷比。如:CaF2 晶体中,Ca2+和 F-的配位数不同
晶体
晶体结构
结构分析
干冰
(1)面心立方最密堆积:立方体的每个顶点有一个 CO2 分子,每个面上也有一
个 CO2 分子,每个晶胞中有 4 个 CO2 分子
(2)每个 CO2 分子周围等距且紧邻的 CO2 分子有 12 个
(3)密度=4×44 g·mol-1 NA×a3
(a 为晶胞边长,NA 为阿伏加德罗常数)
Cu Ag Au 12 4
2 a=4r
2
Mg Zn Ti 12
6或2
——
(2)金属晶胞中原子空间利用率计算: 空间利用率 V球
球数 4 r3
3
V晶胞
a3
①简单立方堆积:如图所示,原子的半径为 r,立方体的棱长为 2r,则 V 球=43πr3,V 晶胞=(2r)3=8r3,空间利
(4)在 NaCl 晶体中,每个 Na+周围与它最接近且距离相等的 Na+共有 12 个,
高中化学新教材同步选择性必修第二册第3章微专题6:晶体结构的分析与计算
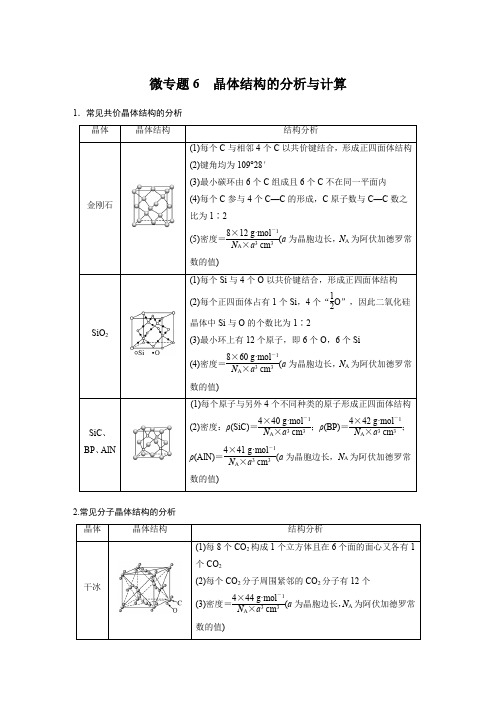
微专题6晶体结构的分析与计算1.常见共价晶体结构的分析晶体晶体结构结构分析金刚石(1)每个C与相邻4个C以共价键结合,形成正四面体结构(2)键角均为109°28′(3)最小碳环由6个C组成且6个C不在同一平面内(4)每个C参与4个C—C的形成,C原子数与C—C数之比为1∶2(5)密度=8×12 g·mol-1N A×a3 cm3(a为晶胞边长,N A为阿伏加德罗常数的值)SiO2(1)每个Si与4个O以共价键结合,形成正四面体结构(2)每个正四面体占有1个Si,4个“12O”,因此二氧化硅晶体中Si与O的个数比为1∶2(3)最小环上有12个原子,即6个O,6个Si(4)密度=8×60 g·mol-1N A×a3 cm3(a为晶胞边长,N A为阿伏加德罗常数的值)SiC、BP、AlN (1)每个原子与另外4个不同种类的原子形成正四面体结构(2)密度:ρ(SiC)=4×40 g·mol-1N A×a3 cm3;ρ(BP)=4×42 g·mol-1N A×a3 cm3;ρ(AlN)=4×41 g·mol-1N A×a3 cm3(a为晶胞边长,N A为阿伏加德罗常数的值)2.常见分子晶体结构的分析晶体晶体结构结构分析干冰(1)每8个CO2构成1个立方体且在6个面的面心又各有1个CO2(2)每个CO2分子周围紧邻的CO2分子有12个(3)密度=4×44 g·mol-1N A×a3 cm3(a为晶胞边长,N A为阿伏加德罗常数的值)白磷密度=4×124 g·mol-1N A×a 3 cm 3(a为晶胞边长,N A为阿伏加德罗常数的值)3.常见离子晶体结构的分析NaCl型CsCl型ZnS型CaF2型晶胞配位数684F-:8;Ca2+:4密度的计算(a为晶胞边长,N A为阿伏加德罗常数的值)4×58.5 g·mol-1N A×a3 cm3168.5 g·mol-1N A×a3 cm34×97 g·mol-1N A×a3 cm34×78 g·mol-1N A×a3 cm31.AB型化合物形成的晶体结构多种多样。
晶体结构的分析和计算

一、晶胞对组成晶胞的各质 点的占有率
立方晶胞
体心: 1 面心: 1/2 棱边: 1/4 顶点: 1/8
有关晶体的计算
1、当题给信息为晶体中最小重 复单元——晶胞(或平面结构)中 的微粒排列方式时,要运用空间想 象力,将晶胞在三维空间内重复延 伸,得到一个较完整的晶体结构, 形成求解思路。
例1:
因C60分子含30个双键,与极活泼的F2发生加成反应即可生成C60F60 (只 要指__出__“___C_6_0_含__3_0_个__双__键__”__即__可__,_但__答__“__因__C_6_0_含__有__双__键__”__不__行__)____.
(3)通过计算,确定C60分子所含单键数.C60分子所含单键数为___________. 可由欧拉定理计算键数(即棱边数):60+(12+20)-2=90 C60分子中单键为:90-30=60
例4:
金刚石晶体中 含有共价键形成的 C原子环,其中最
小的C环上有__6___
个C原子。
巩固练习一:
石墨晶体的层状结构,层内 为平面正六边形结构(如图), 试回答下列问题: (1)图中平均每个正六边形占
有C原子数为__2__个、占有的碳 碳键数为__3__个。
(2)层内7个六元环完全占有
的C原子数为1_4____个,碳原子
2、当题给信息为晶体中微粒 的排列方式时,可在晶体结构中 确定一个具有代表性的最小重复 单元——晶胞为研究对象,运用 点、线、面的量进行解答。
例2:
右图是石英晶 体平面示意图(它实 际上是立体的网状结 构),其中硅、氧原 子数之比为____.
1:2
例3:Байду номын сангаас
如图直线交点处 的圆圈为NaCl晶体中 Na+或Cl-所处位置, 晶体中,每个Na+周 围与它最接近的且距 离相等的Na+个数为: ____ 12
晶体结构知识汇总及解题方法技巧

晶体结构知识汇总及解题方法技巧一、晶胞中质点得占有率在一个晶胞结构中出现得多个原子,并不就是只为这一个晶胞所独立,而就是为多个晶胞共用,所以每一个晶胞只能按比例分摊。
分摊得根本原则:晶胞任意位置上得原子如果就是被n 个晶胞所共有,则每个晶胞只能分得这个原子得n 1。
立方晶胞,顶点上得粒子占 棱上得粒子占 面上得粒子占 体心得粒子占二、常见晶胞分析1. NaCl 型⑴每个晶胞占有 个Na+, 个Cl-,即 个NaCl 粒子⑵每个Na +周围有 个Cl -,每个Cl -周围有 个Na +,与一个Na +距离最近且相等得Cl-围成得空间构型为 。
每个Na +周围与其最近且距离相等得Na +有 个。
⑶0、585g NaCl 晶体(0、01mol)含有 个晶胞。
⑷若已知Na+与Cl-得最短距离为a cm,则NaCl 晶体得密度为 。
2. CsCl 型⑴在CsCl 晶体中,每个Cs+周围与之最接近得且距离相等得Cs+有 个,每个Cs+周围与之最接近得且距离相等得Cl-有 个。
⑵每个晶胞占有 个CsCl 粒子。
3. 干冰型在干冰晶体中,每个CO2分子周围与之最接近得且距离相等得CO2分子有 个。
每个晶胞中含有 个CO2分子。
4. 金刚石型金刚石得网状结构中,,每个碳原子与其她4个碳原子等距离紧邻,含有由共价键形成得碳原子环,其中最小得环上有6个碳原子,每个碳原子上得任意两个C—C键得夹角都就是109°28′,其中C原子个数:C—C个数= 。
5.石英晶体在二氧化硅晶体中,一个硅原子与4个氧原子形成4个共价键,1个氧原子与2个硅原子形成2个共价键,故Si原子与O原子数目之比为。
实际上,该晶体就是由硅原子与氧原子按1:2得比例组成得立体网状晶体,没有单个分子存在。
在晶体中最小得环为十二元环,每个环占有6个Si原子与6个O原子。
6.石墨晶体结构石墨晶体就是一种混合型晶体,层内存在共价键,层间以范德华力结合,兼具有原子晶体、分子晶体得特征与特性。
晶胞计算技巧

晶胞计算技巧一、引言晶体结构的计算是固体物理和化学研究中的重要环节之一。
为了研究晶体的性质和行为,研究者经常需要进行晶胞计算。
晶胞计算是指通过计算机模拟和计算,研究晶体的结构和性质。
在晶胞计算中,有一些技巧和方法可以帮助我们更好地进行计算和分析。
本文将介绍一些常用的晶胞计算技巧。
二、晶胞的生成与优化在晶体结构计算中,首先要生成晶胞。
晶胞的生成可以通过实验测量得到,也可以通过计算方法来得到。
一种常用的计算方法是通过密度泛函理论(DFT)来计算晶胞的结构。
在生成晶胞后,还需要对晶胞进行优化。
晶胞的优化可以通过分子动力学模拟来实现,通过调整晶格参数和原子位置,使得晶胞能量达到最低。
三、晶胞的对称性分析晶胞的对称性分析可以帮助我们更好地理解和描述晶体的结构。
在晶胞计算中,可以通过对晶胞的对称性进行分析,得到晶体的空间群和点群。
晶体的空间群和点群描述了晶体中原子的排列方式和对称性。
通过对晶胞的对称性分析,我们可以得到关于晶体结构的更多信息。
四、电子结构计算在晶胞计算中,电子结构计算是一个重要的步骤。
电子结构计算可以通过密度泛函理论(DFT)来实现。
通过DFT计算,可以得到晶体的能带结构、态密度和电子密度等信息。
这些信息可以帮助我们研究晶体的导电性、磁性和光学性质等。
五、声子计算声子计算是晶胞计算中的另一个重要内容。
声子计算可以用来研究晶体的振动性质。
在声子计算中,可以计算晶体的声子能谱、声子态密度和声子热容等。
这些信息对于研究晶体的热传导和热膨胀等性质非常重要。
六、缺陷和表面计算在晶体中,常常存在各种缺陷和表面。
研究晶体的缺陷和表面性质对于理解晶体的性质和行为非常重要。
在晶胞计算中,可以通过引入缺陷和表面来研究晶体的性质。
通过计算和模拟,可以研究缺陷的形成和扩散机制,以及表面的催化性能和吸附性能等。
七、后处理和可视化在晶胞计算中,后处理和可视化是一个重要的环节。
通过后处理和可视化,可以对计算得到的数据进行分析和展示。
高中化学:晶体的类型与性质 有关化学式和分子式的确定

二. 晶体微观结构推断:
例2.
例3:
例4.
例5,6.
例9:
Y
X
X
例10
1mol晶体的体积为:
1个立方体的体积为:
边长为: 对角线为:
例7.
(1) B的确定: NH3
C的确定: 分子中含B 81*40%/10.8 = 3 H 81*7.4%/1 = 6 另一元素为N 81*52.6%/14 = 3 分子式为:B3N3H6
(2) C6H6
B
N
N
B
B
N
H
H
H
H
H
H
方法一:计算晶胞中 铜原子个数=8*1/8 + 8*1/4 = 3
方法二:设Y = Ba,两 种微粒为一种位置(即 晶格的体心),则可以 计算一个晶格中铜原子 与体心原子的个数比为 8*1/8 : 1 = 1:1,选项中Y 和Cu之和为3,则Cu原子 个数也为3.
例6.
(1) 平均每个正六边形拥有2个锗原子, 3个氧原子.
(2) 化学式为: (GeCH2CH2COOH)2O3
Ge2C6H10O3
例7.
N
N
N
N
CH 三 C ----C 三 N
属于某一环的碳原 子数为: 1+ 4*1/2= 3; 氢原子数为1; 氮原子数为1. 因此, C : H : N = 3:1:1. 此聚合物的化学式 为:(C3HN)n
CH2 = CH ---CN
一. 有关化学式和分子式的确定
例一.
晶胞与晶格
1
2
3
4
5
6
7
8
9
10
11
【解题策略】晶体结构解题方法技巧

晶体结构解题方法技巧晶体结构类习题最常见的题型就是已知晶胞的结构而求晶体的化学式。
解答这类习题首先要明确一个概念:由晶胞构成的晶体,其化学式不是表示一个分子中含有多少个原子,而是表示每个晶胞中平均含有各类原子的个数,即各类原子的最简个数比。
解答这类习题,通常采用分摊法,在一个晶胞结构中出现的多个原子,这些原子并不是只为这个晶胞所独立占有,而是为多个晶胞所共有,那么,在一个晶胞结构中出现的每个原子,这个晶胞能分摊到多少比例呢。
这就是分摊法。
分摊法的根本目的就是算出一个晶胞单独占有的各类原子的个数。
分摊法的根本原则是:晶胞任意位置上的一个原子如果是被x个晶胞所共有,那么,每个晶胞对这个原子分得的份额就是1/x。
下面对立方晶胞进行详细分析。
下图1就表示一个立方晶胞。
在图中,原子可以位于它的顶点,也可以位于它的棱上,还可以在它的面上(不含棱),当然,它的体内也可以有原子;图2是这种晶胞进行堆积的情况,图3是图2的单图。
从这些图可以看出:(1)每个顶点被8个晶胞共有,所以晶胞对自己顶点上的每个原子只占1/8份额;(2)每条棱被4个晶胞共有,所以晶胞对自己棱上的每个原子只占1/4份额;(3)每个面被2个晶胞共有,所以晶胞对自己面上(不含棱)的每个原子只占1/2份额;(4)晶胞体内的原子不与其它晶胞分享;透过以某个顶点为中心的三维坐标系后可以清楚的看到:(5)每个顶点是被8个晶胞的6条棱共享,6条棱包括X轴上的二条、Y轴上的二条和Z轴上的二条;(6)每个顶点也被这6条棱构成的12个晶胞面共享,这12个面包括XY平面内的4个面、YZ平面内的4个面和ZX平面内的4个面;分摊法的本意不只是把原子分摊到晶胞,还可以把原子分摊到棱或面,例如:根据上面第(5)条,结论:棱对自己每个顶点占的份额是1/6;根据上面第(6)条,结论:面对自己每个顶点占的份额是1/12;同样,分摊法也不只是对原子进行分摊,还可以把棱分摊到面或把面分摊到棱,等等。
高中化学选修3:晶体结构与性质知识点总结
一.晶体常识
1 .晶体与非晶体比较
2 .获得晶体的三条途径
①熔融态物质凝固。
②气态物质冷却不经液态直接凝固(凝华)。
③溶质从溶液中析出。
3 .晶胞
晶胞是描述晶体结构的基本单元。
晶胞在晶体中的排列呈“无隙并置”。
4 .晶胞中微粒数的计算方法 —— 均摊 法
如某个粒子为n个晶胞所共有,则该粒子有1/n属于这个晶胞。
中学中常见的晶胞为立方晶胞
立方晶胞中微粒数的计算方法如下:
注意:在使用“均摊法”计算晶胞中粒子个数时要注意晶胞的形状
二.四种晶体的比较
晶体熔、沸点高低的比较方法
(1)不同类型晶体的熔、沸点高低一般规律:原子晶体>离子晶体>分子晶体。
金属晶体的熔、沸点差别很大,如钨、铂等熔、沸点很高,汞、铯等熔、沸点很低。
(2)原子晶体
由共价键形成的原子晶体中,原子半径小的键长短,键能大,晶体的熔、沸点高.如熔点:金刚石>碳化硅>硅
(3)离子晶体
一般地说,阴阳离子的电荷数越多,离子半径越小,则离子间的作用力就越强,相应的晶格能大,其晶体的熔、沸点就越高。
(4)分子晶体
①分子间作用力越大,物质的熔、沸点越高;具有氢键的分子晶体熔、沸点反常的高。
②组成和结构相似的分子晶体,相对分子质量越大,熔、沸点越高。
③组成和结构不相似的物质(相对分子质量接近),分子的极性越大,其熔、沸点越高。
④同分异构体,支链越多,熔、沸点越低。
(5)金属晶体
金属离子半径越小,离子电荷数越多,其金属键越强,金属熔、沸点就越高。
三.几种典型的晶体模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答题技巧|高中化学晶体结构的有关计算
中学课本中列举了NaCl、CsCl、金刚石、石墨、干冰、二氧化硅等典型晶体的结构示意图。
它们的结构都是立体的,如何从平面图想像出三维实物的结构形态,这是解决有关问题的关键。
首先可以利用直观结构模型,逐步建立起准确、清晰的立体形象,提高空间想像力。
其次还需掌握基本的解题技巧:在晶体结构中切割一个基本结构单元,弄清该单元中点、边、面为多少个基本结构单元所共有,则这一个点、一条边、一个面对一个基本结构单元的贡献只能是它的10/n(n为共有的基本结构单元数)。
中学阶段所需掌握的几种晶体类型及有关问题:
一、NaCl型(如图1)
1.在晶体中,每个Na+同时吸引6个Cl-,每个Cl-同时吸引着6个Na+,阴、阳离子数目之比是1∶1。
2.在晶体结构中,每个基本结构单元(小立方体)的8个顶点分别由4个Na+、4个Cl-相邻占据,每个小立方体含Na+:(1/8)×4=(1/2)个、含Cl-:(1/8)×4=(1/2)个。
每个晶胞由8个小立方体构成,故每个晶胞有NaCl微粒8×(1/2)=4个。
3.在晶体中,经过立方体的中心Na+的平面有三个,每个平面的四个顶点上的Na+都同晶体中与中心Na+最接近且距离相等。
所以,在晶体中,每个Na+周围与它最接近的距离相等的Na+的个数共有12个。
同理,每个Cl-周围与它最接近且距离相等的Cl-的个数也有12个。
二、CsCl型(如图2)
1.在晶体中,每个Cl-吸引8个Cs+,每个Cs+吸引8个Cl-,Cs+与Cl-的个数比为1∶1。
2.每个基本结构单元中(小立方体)含Cl-:(1/8)×8=1个,含Cs+1个。
12个。
拥有6×(1/12)=(1/2)个碳原子。
1.石墨晶体为层状结构。
每一层中碳原子排列成六边形,一个个六边形(六元环)排列成平面的网状结构,键角120°。
2.每一个碳原子都跟相邻的碳原子以共价键相结合。
因此,每个六元环拥有碳原子(1/3)×6=2个,每个环拥有C—C键(1/2)×6=3个。
3.mg石墨中,正六边形数目为(m/12)NA÷2=(mNA/24)。
