统计学计算题目解析
《统计学原理》计算题及答案
《统计学原理》计算题及答案第四章1、某生产车间30名工人日加工零件数（件）如下：30 26 42 41 36 44 40 37 37 25 45 29 43 31 36 36 49 34 47 33 43 38 42 32 34 38 46 43 39 35要求：（1）根据以上资料分成如下几组：25－30，30－35，35－40，40－45，45－50， 计算出各组的频数和频率，整理编制次数分布表。
（2）根据整理表计算工人生产该零件的平均日产量。
答 案：（1）40名工人日加工零件数次数分布表为：（6分）（2）平均日产量17.3830==∑=f x （件） （4分） 2、某班40名学生统计学考试成绩分别为：57 89 49 84 86 87 75 73 72 68 75 82 97 81 67 81 54 79 87 95 76 71 60 90 65 76 72 70 86 85 89 89 64 57 83 81 78 87 72 61学校规定：60分以下为不及格，60─70分为及格，70─80分为中， 80─90分为良，90─100分为优。
要求：（1）将该班学生分为不及格、及格、中、良、优五组,编制一张次数分配表。
（2）指出分组标志及类型；分组方法的类型；分析该班学生考试情况。
答 案：（1）40名学生成绩的统计分布表：（6分）2）分组标志为“成绩”，其类型是数量标志。
（1分）分组方法是变量分组中的组距分组，而且是开口式分组。
（1分）该班学生的考试成绩的分布呈两头小，中间大的“正态分布”形态。
（2分）3、 某厂三个车间一季度生产情况如下：根据以上资料计算：（1）一季度三个车间产量平均计划完成百分比。
（2）一季度三个车间平均单位产品成本。
答 案 产量平均计划完成百分比%81.10172073310.122005.13159.0198220315198==++++==∑∑x m m （5分） 平均单位成本75.1022031519822083151019815=++⨯+⨯+⨯==∑∑f xf （元/件） （5分）4、 某自行车公司下属20个企业，1999年甲种车的单位成本分组资料如下：试计算该公司1999年甲种自行车的平均单位成本。
统计学计算题目解析
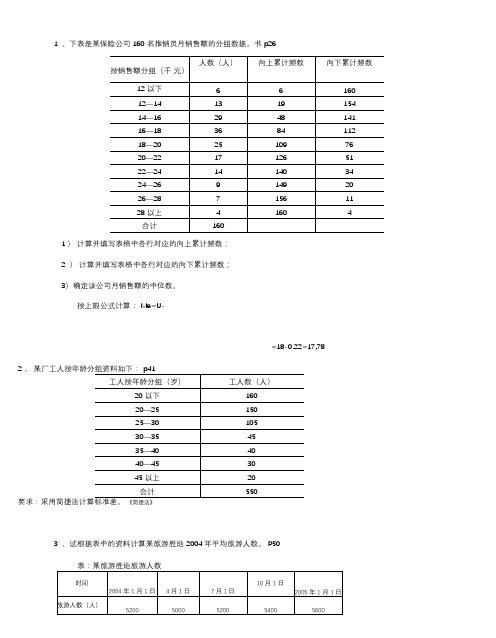
1、下表是某保险公司 160 名推销员月销售额的分组数据。
书 p261 ）计算并填写表格中各行对应的向上累计频数；2）计算并填写表格中各行对应的向下累计频数；3）确定该公司月销售额的中位数。
按上限公式计算： Me=U-=18-0.22=17,78 2 、某厂工人按年龄分组资料如下： p41要求：采用简捷法计算标准差。
《简捷法》3、试根据表中的资料计算某旅游胜地 2004 年平均旅游人数。
P50表：某旅游胜地旅游人数4 、某大学 2004 年在册学生人数资料如表 3-6 所示，试计算该大学 2004 年平均在册学生人数时间1月1日3月1日 7月1日 9月1日 12 月 31 日 在册学生人数（人）340835283250359035755 、已知某企业 2004 年非生产人员以及全部职工人数资料如下表所示，求该企业第四季度非生产人员占全部职工 人数的平均比重。
表： 某企业非生产人员占全部职工人数比重时间9 月末 10 月末 11 月末 12 月末 非生产人数（人） 200 206 206 218 全部职工人数（人） 1000105010701108非生产人员占全部职 工人数比重（ % ）20.0 19.62 19.25 19.686、根据表中资料填写相应的指标值。
表：某地区 1999~2004 年国内生产总值发展速度计算表7 、根据表中资料计算移动平均数，并填入相应的位置。
P618 、根据表中资料计算移动平均数，并填入相应的位置。
P621977 10001978 11601979 13871980 15861981 14871982 14151983 16179、某百货商场某年上半年的零售额、商品库存额如下：（单位：百万元）日期1月2月3月4月5月6月零售额42.30 43.64 40.71 40.93 42.11 44.54月初库存额20.82 21.35 23.98 22.47 23.16 23.76试计算该商城该年上半年商品平均流转次数（注：商品流通次数 = 商品销售额 / 库存额； 6 月末商品库存额为24.73 百万元）。
《统计学原理》常用公式汇总及计算题目分析
《统计学原理》常用公式汇总及计算题目分析第一部分常用公式第三章统计整理a）组距＝上限－下限b)组中值＝（上限+下限)÷2c）缺下限开口组组中值＝上限－1/2邻组组距d)缺上限开口组组中值＝下限+1/2邻组组距第四章综合指标i.相对指标1。
结构相对指标＝各组（或部分）总量/总体总量2。
比例相对指标＝总体中某一部分数值/总体中另一部分数值3。
比较相对指标＝甲单位某指标值/乙单位同类指标值4。
强度相对指标＝某种现象总量指标/另一个有联系而性质不同的现象总量指标5.计划完成程度相对指标＝实际数/计划数＝实际完成程度（%)/计划规定的完成程度（％）ii.平均指标1.简单算术平均数:2。
加权算术平均数或iii。
变异指标1.全距＝最大标志值－最小标志值2.标准差: 简单σ= ；加权σ=3。
标准差系数:第五章抽样估计1。
平均误差:重复抽样：不重复抽样:2。
抽样极限误差3。
重复抽样条件下：平均数抽样时必要的样本数目成数抽样时必要的样本数目4.不重复抽样条件下：平均数抽样时必要的样本数目第七章相关分析1.相关系数2。
配合回归方程ｙ＝ａ＋ｂｘ3.估计标准误:第八章指数分数一、综合指数的计算与分析（1）数量指标指数此公式的计算结果说明复杂现象总体数量指标综合变动的方向和程度。
（—）此差额说明由于数量指标的变动对价值量指标影响的绝对额。
（2）质量指标指数此公式的计算结果说明复杂现象总体质量指标综合变动的方向和程度.（—）此差额说明由于质量指标的变动对价值量指标影响的绝对额.加权算术平均数指数=加权调和平均数指数=(3)复杂现象总体总量指标变动的因素分析相对数变动分析：= ×绝对值变动分析：—= （—）×(—）第九章动态数列分析一、平均发展水平的计算方法:(1）由总量指标动态数列计算序时平均数①由时期数列计算②由时点数列计算在间断时点数列的条件下计算：a.若间断的间隔相等，则采用“首末折半法”计算。
统计学计算题答案(课后)
9.(1)工人日产量平均数： =64.85(件∕人)(2)通过观察得知，日产量的工人数最多为260人，对应的分组为60~70，则众数在60~70这一组中，则众数的取值范围在60~70之间。
利用下限公式计算众数： =65.22（件）(3)首先进行向上累计，计算出各组的累计频数：比较各组的累计频数和330.5，确定中位数在60~70这一组。
利用下限公式计算中位数：(4)分析：由于o e M M x <<，所以该数列的分布状态为左偏。
10.(1)全距R=最大的标志值—最小的标志值=95—55=40(2)∑∑=ff x x ii 平均日装配部件数=73.8（个）462412448.739568.7385248.7375128.736548.7355++++⨯-+⨯-+⨯-+⨯-+⨯-==7.232（件） (3)∑∑==-=ni ini ii ff x x1122)(σ方差46241244)8.7395(6)8.7385(24)8.7375(12)8.7365(4)8.7355(22222++++⨯-+⨯-+⨯-+⨯-+⨯-==98.56（个）(4)%46.138.7393.9%100==⨯=xV σσ标准差系数 13.267281101269084702550430⨯+⨯+⨯+⨯+⨯==∑∑ff x x ii 甲甲企业的平均日产量=81.16（件）1001811042903070850230⨯+⨯+⨯+⨯+⨯==∑∑ff x x ii 乙乙企业的平均日产量=83.2（件）26728)16.81110(126)16.8190(8416.8170256.1815046.1813022222⨯-+⨯-+⨯-+⨯-+⨯-=）（）（）（41.293==17.13（件）∑∑==-=ni ini i i ff x x 112)(乙乙的标准差σ10018).283110(42).28390(302.83708.283502.2833022222⨯-+⨯-+⨯-+⨯-+⨯-=）（）（）（76.345==18.59（件）.11%21%1006.1813.117%100=⨯=⨯=甲甲甲甲企业的标准差系数：x V σσ%3.322%100.2839.518%100=⨯=⨯=乙乙乙乙企业的标准差系数：x V σσ由计算结果表明：甲企业的标准差系数小于乙企业，因此甲企业工人的日产量资料更有代表性。
最新统计学原理计算分析题教学题目答案.11.11
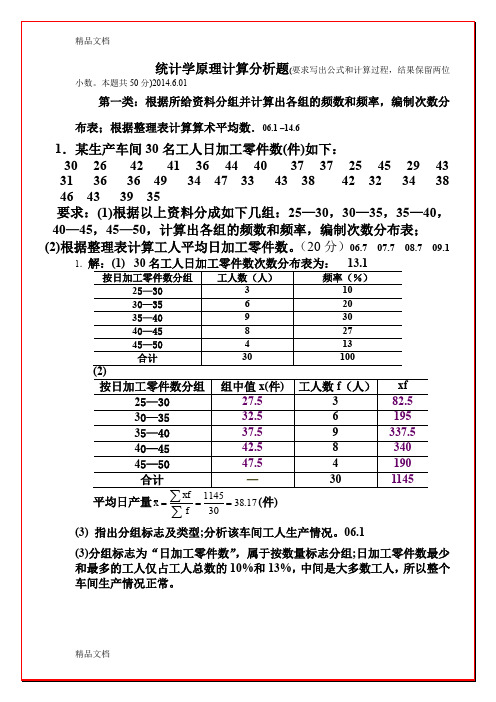
试分别计算该商品在两个市场上的平均价格。
(20分)09.7 11.7 12.72014.1合计50—3870 —4312乙班学生的标准差()()分＝乙29.924.865043122===-∑∑ffx x σ甲、乙两个生产小组， 甲组平均每个工人的日产量为36 件， 标准差为件； 乙组工人日产量资料如下:第三类：采用简单重复抽样的方法计算平均数（成数）的抽样平均误差；根据要3.某工厂有2000个工人,用简单重复方法抽出其100个工人作为样本出平均产量560件,标准差点32.45件.要求:(1)计算抽样平均平均误差;(2)以95.45％(z=2)的可靠性估计该厂工人的月平均产量及总产量区间.(20分)07.1解: (1)25.310045.32==nxσμ＝13.1（19. 某单位按简单随机重复抽样方式抽取40 名职工，对其业务情况进行考核,核成绩平均分数77分,标准差为1 0.54分.试以95. 45%的概率保证程度( Z= 2)断全体职工业务考试成绩的区间范围。
( 1 5分)11.7第四类：计算相关系数；建立直线回归方程并指出回归系数的含义；利用建立的方程预测因变量的估计值。
04.7 05.1 06.1 06.7 07.1 08.7 09.7 11.1 11.7 14.1 1．根据某地区历年人均收入(元)与商品销售额(万元)资料计算的有关数据如下：(x代表人均收入，y代表销售额)：计算：(1)建立以商品销售额为因变量的直线回归方程，并解释回归系数的含义；∑∑∑=72925 ∑计算销售额与销售利润之间的相关系数(2)配合销售利润对销售额的直线线回归方程.(15分: (1)计算相关系数要求 :( 1)建立销售利润倚可比产品成本降低率的直线回归方程，预测可比(2 )计算学习时间和学习成绩之间的相关系数，并解释相关的密切程度和方向。
(要求写出公式和计算过程，结果保留两位小20. 某企业机床使用年限和维修费用的资料计算出如下数据( x 代表使用年限，y 代表维=83 ∑xy=1300修费用) : n=6 ∑x =21 ∑y ==350 2x要求:建立机床维修费用对使用年限的直线回归方程，并解释回归系数的含义。
统计学组距均值例题
统计学组距均值例题一、统计学概述统计学是一门研究数据收集、整理、分析、解释和应用的科学。
在统计学中，组距均值是一种常用的描述性统计指标，用于衡量一组数据的集中趋势。
二、组距均值的计算方法组距均值（Mean Deviation）是指在组距分组的基础上，用每组的平均值减去总体均值，再求平方，最后求和并除以总频数得到的平均数。
其计算公式为：MD = ∑[(Xi - X_mean) / N]其中，MD表示组距均值，Xi表示每组的平均值，X_mean表示总体均值，N表示总频数。
三、例题解析题目：某企业对员工工资进行分组，共分为5组，组距为1000元，各组的频数分别为20、30、40、30、20。
试求组距均值。
解题步骤：1.计算每组的平均值：第一组平均值= （1500 + 1600）/ 20 = 1550元第二组平均值= （1700 + 1800）/ 30 = 1750元第三组平均值= （1900 + 2000）/ 40 = 1950元第四组平均值= （2100 + 2200）/ 30 = 2150元第五组平均值= （2300 + 2400）/ 20 = 2350元2.计算组距均值：MD = [(1550 - 1750) × 20 + (1750 - 1950) × 30 + (1950 - 2150) × 40 + (2150 - 2350) × 30 + (2350 - 2450) × 20] / (20 + 30 + 40 + 30 +20) = 270000 / 120四、解题步骤与技巧1.仔细阅读题目，了解题意，确定所需求解的统计指标。
2.根据题目给出的数据，进行适当的预处理，如计算每组的平均值。
3.利用公式计算组距均值，注意单位的转换和计算过程中的精度。
4.如有需要，可以进行误差分析，检验计算结果的可靠性。
五、总结与应用组距均值是一种常用的描述性统计指标，掌握其计算方法和应用场景对于分析和解释数据具有重要意义。
统计学原理计算题及参考答案
3．某地区历年粮食产量如下：1、某生产车间30名工人日加工零件数（件）如下： 30 26 42 41 36 44 40 37 37 25 45 29 43 31 36 36 49 34 47 33 43 38 42 32 34 38 46 43 39 35 要求：（1）根据以上资料分成如下几组：25—30，30—35，35—40，40—45，45—50，计算各组的频数和频率，编制次数分布表；（2） 根据整理表计算工人平均日产零件数。
（20分）解：（1）根据以上资料编制次数分布表如下：则工人平均劳动生产率为：17.38301145===∑∑fxf x（2）当产量为10000件时，预测单位成本为多少元？（15分）xbx a y n x b n y a x x n y x xy n b c 5.2808010703125.232105.26151441502520250512503210128353)(222-=+==+=⨯+=-=-=-=--=-⨯⨯-⨯=--=∑∑∑∑∑∑∑因为，5.2-=b ，所以产量每增加1000件时，即x 增加1单位时，单位成本的平均变动是：平均减少2.5元 （2）当产量为10000件时，即10=x 时，单位成本为55105.280=⨯-=c y 元>课程的测试,甲班平均成绩为81分,标准差为9.5分;乙班的成绩分组资料如下:计算乙班学生的平均成绩,并比较甲.乙两班哪个班的平均成绩更有代表性?解：乙班学生的平均成绩∑∑=f xf x ，所需的计算数据见下表：75554125===∑∑fxf x （比较甲.乙两班哪个班的平均成绩更有代表性，要用变异系数σν的大小比较。
）甲班%73.11815.9===xσνσ 从计算结果知道，甲班的变异系数σν小，所以甲班的平均成绩更有代表性。
%65.207549.1549.152405513200)(2======-=∑∑x ffx x σνσσ计算(1)产品产量总指数及由于产量增长而增加的总成本.(2)总成本指数及总成本增减绝对额. 解；（1）产品产量总指数为： %42.1112102342106351120605010060%10550%102100%12000==++=++⨯+⨯+⨯=∑∑qp qkp 由于产量增长而增加的总成本：∑∑=-=-242102340000qp q kp（2）总成本指数为：%62.10721022660501006046120011==++++=∑∑qp qp总成本增减绝对额：∑∑=-=-16210226011qp q p计算第二季度平均每月商品流转次数和第二季度商品流转次数. 解：商品流转次数c=商品销售额a/库存额bba c =商品销售额构成的是时期数列，所以67.23837163276240200==++==∑na a 库存额b 构成的是间隔相等的时点数列，所以33.533160327545552453224321==+++=+++=b b b b b 第二季度平均每月商品流转次数475.433.5367.238===ba c 第二季度商品流转次数3*4.475=13.425解：甲市场的平均价格为：04.123270033220027001507001080007350011009007001100137900120700105==++=++⨯+⨯+⨯==∑∑fxf x乙市场的平均价格为74.1172700317900700800120031790013795900120960001051260009590096000126000==++=++++==∑∑xM M x。
《统计学》计算题型与参考答案
《统计学》计算题型（第二章）1．某车间40名工人完成生产计划百分数（％）资料如下：90 65 100 102 100 104 112 120 124 98110 110 120 120 114 100 109 119 123 107110 99 132 135 107 107 109 102 102 101110 109 107 103 103 102 102 102 104 104要求：（1）编制分配数列；（4分）（2）指出分组标志及其类型；（4分）（3）对该车间工人的生产情况进行分析。
（2分）解答：（1）（2类型：数量标志（3）从分配数列可以看出，该计划未能完成计划的有4人，占10%，超额完成计划在10％以内的有22人，占55％，超额20％完成的有7人，占17.5％。
反映该车间，该计划完成较好。
（第三章）2．2005年9份甲、乙两农贸市场某农产品价格和成交量、成交额资料如下：解答：(1)x 甲＝∑∑m x m 1＝248.416.36.314.24.21246.34.2⨯+⨯+⨯++＝30/7=4.29(元)x 乙＝∑∑fxf ＝12418.426.344.2++⨯+⨯+⨯＝21.6/7=3.09(元)(2)原因分析：甲市场在价格最高的C 品种成交量最高，而乙市场是在最低的价格A 品种成交量最高，根据权数越大其对应的变量值对平均数的作用越大的原理，可知甲市场平均价格趋近于C ，而乙市场平均价格却趋近于A ，所以甲市场平均价格高于乙市场平均价格。
（第三章）3．甲、乙两企业产量资料如下表：工人人数比重（％）产量（件）甲企业 乙企业 100以下 2 4 100－110 8 5 110－120 30 28 120－130 35 31 130－140 20 25 140－150 3 4 150以上 2 3 合 计 100 100要求：（1）分别计算甲、乙两企业的平均产量？（5分）（2）计算有关指标比较两企业职工的平均产量的代表性。
统计学计算题例题及计算分析
μp=√σp2/n(1-n/N) =√0.16/100*(1-100/10000) =3.98%
△p=zμp=2*3.98%=7.96%
户数所占比重的下限=p-△p=20%-7.96%=12.04%
户数所占比重的上限=p+△p=20%+7.96%=27.96%
∴ μp=√σp2/n =√0.0736/100 =2.71%
△p=zμ
合格率下限=p-△p=92%-5.31%=86.69%
合格率上限=p+△p=92%+5.31%=97.31%
合格品数量下限=10000*86.69%=8669(只)
合格品数量上限=10000*97.31%=9731(只)
即在95%概率保证下,该新型灯泡合格率区间范围为86.69%～97.31%,合格品数量的区间范围为8669～9731只。
（1）这种新的电子元件平均寿命的区间范围；
（2）这种新的电子元件合格率的区间范围。
解：已知N=10000只n=100只x=1192小时σ=101.17小时p=88% z=1.96
(1)μx=√σ2/n(1-n/N) =√101.172/100*(1-100/10000) =10.07(小时)
△x=zμx=1.96*10.07=19.74(小时)
即全部农户中,户均月收入在6000元以上的户数所占比重的范围为12.04%～27.96%。
(3)户数下限=10000*12.04%=1204(户)
户数上限=10000*27.96%=2796(户)
即全部农户中,户均月收入在6000元以上的户数范围为1204～2796户。
3.2．某企业生产一种新的电子元件10000只,用简单随机不重复抽样方法抽取100只作耐用时间试验,试验得到的结果：平均寿命1192小时,标准差101.17小时,合格率88%；试在95%概率保证度下估计：
【统计学期末考试题库】经典必考计算分析题
计算分析题(要求写出公式和计算过程，结果保留两位小数)1、按照某市城市社会发展十年规划，该市人均绿化面积要在2010年的人均4平方米的基础上十年后翻一番。
试问：（1）若在2020年达到翻一番的目标，每年的平均发展速度是多少？（2）若在2018年就达到翻一番的目标，每年的平均增长速度是多少？（3）若2011年和2012年的平均发展速度都为110%，那么后8年应该以怎样的平均发展速度才能实现这一目标？（4）假定2017年的人均绿化面积为人均6.6平方米，以2010年为基期，那么其平均年增长量是多少?2、某地区市场销售额报告期为40万元，比上年增加了5万元，销售量与上年相比上升了3%，试计算：（1）市场销售量总指数；（2）市场销售价格指数；（3）由于销售量变动对销售额的影响。
3、某乡有5000农户，按随机原则重复抽取100户调查，得平均每户年纯收入12000元，标准差2000元。
要求：（1）以95%的概率（Z=1.96）估计全乡平均每户纯收入的区间。
（2）以同样概率估计全乡农户年纯收入总额的区间范围。
4、某企业工人的日产量情况如下表所示：试计算该企业工人平均日产量。
(10分)1、某乡2012-2013年三种鲜果产品收购资料如下：试计算三种鲜果产品收购价格指数，说明该地区2013年较之2012年鲜果收购价格的提高程度，以及由于收购价格提高使当地农民增加的收入。
2、某企业2013年上半年进货计划执行情况如下表：试计算：（1）各季度进货计划完成程度。
（2）上半年进货计划完成情况。
（3）上半年累计计划进度执行情况。
3、按照某市城市社会发展十年规划，该市人均绿化面积要在2010年的人均4平方米的基础上十年后翻一番。
试问：（1）若在2020年达到翻一番的目标，每年的平均发展速度是多少？（2）若在2018年就达到翻一番的目标，每年的平均增长速度是多少？（3）若2011年和2012年的平均发展速度都为110%，那么后8年应该以怎样的平均发展速度才能实现这一目标？（4）假定2017年的人均绿化面积为人均6.6平方米，以2010年为基期，那么其平均年增长量是多少?4、设某总体服从正态分布，其标准差为12，现抽取了一个样本容量为400的子样，计算得平均值=21，试以显著性水平确定总体的平均值是否不超过20？（10分）1又知乙车间工人日产量的标准差为12件，日产量为40件，试根据资料说明：（1）哪一个车间的平均产量高。
统计学课后知识题目解析第五章指数
统计学课后知识题⽬解析第五章指数第五章指数⼀﹑单项选择题1.⼴义的指数是指反映A.价格变动的相对数B.物量变动的相对数C.总体数量变动的相对数D.各种动态相对数2.狭义的指数是反映哪⼀总体数量综合变动的相对数？A.有限总体B.⽆限总体C.简单总体D.复杂总体3.指数按其反映对象范围不同,可以分为A.个体指数和总指数B.数量指标指数和质量指标指数C.定基指数和环⽐指数D.平均指数和平均指标指数4.指数按其所表明的经济指标性质不同可以分为A.个体指数和总指数B.数量指标指数和质量指标指数C.定基指数和环⽐指数D.平均指数和平均指标指数5.按指数对⽐基期不同,指数可分为A.个体指数和总指数B.定基指数和环⽐指数C.简单指数和加权指数D.动态指数和静态指数6.下列指数中属于数量指标指数的是A.商品价格指数B.单位成本指数C.劳动⽣产率指数D.职⼯⼈数指数B.销售额指数C.职⼯⼈数指数D.劳动⽣产率指数8.由两个总量指标对⽐所形成的指数是A.个体指数B.综合指数C.总指数D.平均指数9.综合指数包括A.个体指数和总指数B.数量指标指数和质量指标指数C.定基指数和环⽐指数D.平均指数和平均指标指数10.总指数编制的两种基本形式是A.个体指数和综合指数B.综合指数和平均指数C.数量指标指数和质量指标指数D.固定构成指数和结构影响指数11.数量指标指数和质量指标指数的划分依据是A.指数化指标性质不同B.所反映的对象范围不同C.所⽐较的现象特征不同D.指数编制的⽅法不同12.编制综合指数最关键的问题是确定A.指数化指标的性质B.同度量因素及其时期C.指数体系D.个体指数和权数13.编制数量指标指数的⼀般原则是采⽤下列哪⼀指标作为同度量因素A.基期的质量指标B.报告期的质量指标C.报告期的数量指标D.基期的数量指标A.基期的质量指标B.报告期的质量指标C.报告期的数量指标D.基期的数量指标15.销售量指数中的指数化指标是A.销售量B.销售额C.销售价格D.数量指标16.单位产品成本指数中的同度量因素是A.单位产品成本B.总成本C.产量D.质量指标17.在由三个指数所组成的指数体系中,两个因素指数的同度量因素通常A.都固定在基期B.⼀个固定在基期,另⼀个固定在报告期C.都固定在报告期D.采⽤基期和报告期的平均18.拉⽒指数的同度量因素时期固定在A.基期B.报告期C.假定期D.任意时期19.派⽒指数的同度量因素时期固定在A.基期B.报告期C.假定期D.任意时期20.Σp1q1￣Σp0q1表明A.由于销售量的变化对销售额的影响B.由于价格的变化对销售额的影响C.由于销售量的变化对价格的影响A.由于价格的变化对销售额的影响B.由于销售量的变化对价格的影响C.由于销售量的变化对销售额的影响D.由于价格的变化对销售量的影响22. Σp0q1/Σp0q0表⽰A.价格⽔平不变的条件下,销售量综合变动的程度B.在报告期价格的条件下,销售量综合变动的程度C.综合反映多种商品物价变动程度D.综合反映商品销售额变动程度19.零售物价增长3%,零售商品销售量增长6%,则零售商品销售额增长A.9%B.9.18%C.18%D.2.91%24.若产量增加,⽽⽣产费⽤不变,则单位成本指数A.减少B.增加C.不变D.⽆法确定25.某企业⽣产费⽤报告期⽐基期增长了50%，产品产量增长了25%，则单位成本增长了A.25%B.2%C.75%D.20%26.若⼯资总额增长10%，平均⼯资下降5%，则职⼯⼈数A.增长15%B.增长5%C.增长15.8%D.下降5%27.假如播种⾯积报告期⽐基期下降5%，⽽平均亩产量却增长5%，则总产量报告期⽐基期A.增长B.下降28.平均指数是计算总指数的另⼀种形式,其计算基础A.数量指标指数B.质量指标指数C.综合指数D.个体指数29.综合指数和平均指数的联系表现在A.在⼀般条件下,两类指数间有变形关系B.在权数固定条件下,两类指数间有变形关系C.在⼀定权数条件下,两类指数间有变形关系D.在同度量因素固定条件下, 两类指数间有变形关系30.若将加权算术平均数指数变形为综合指数所⽤的特定权数是A.基期总额B.报告期总额C.假定期总额D.固定权数31.若将加权调和平均数指数变形为综合指数所⽤的特定权数是A.基期总额B.报告期总额C.假定期总额D.固定权数32.按个体价格指数和报告期销售额计算的价格指数是A.综合指数B.平均指标指数C.加权算术平均指数D.加权调和平均数指数33.按个体产量指数和基期总产值计算的产量指数是A.综合指数B.平均指标指数C.加权算术平均指数D.加权调和平均数指数34.因素分析法的⽅法论基础是A.指标体系B.指数体系35.我国现⾏的零售物价指数的编制主要采⽤A.个体指数的形式B.综合指数变形的平均指数形式C.综合指数形式主义D.固定权数的算术平均数指数形式36.某市1991年社会商品零售额为12000万元,1995年增加到15600万元.这四年中零售物价指数提⾼4%，则商品零售量指数为A.80%B.130%C.104%D.125%37.在指数体系中,总变动指数(对象指数)等于各因素指数A.之和B.之差C.之积D.之商38.在指数体系中,总变动绝对差额等于各因素变动绝对差额A.之和B.之差C.之积D.之商39.由两个平均指标对⽐所形成的指数是A.平均数指数B.个体指数C.综合指数D.平均指标指数40.固定构成指数反映A.总体结构变动对总体平均指标变动的影响B.总体各组⽔平变动对总体平均指标变动的影响C.总体平均指标的综合变动D.总体总量指标的综合变动41.结构影响指数的计算公式为42.已知劳动⽣产率可变构成指数为134.2%,职⼯⼈数结构影响指数为96.3%,则劳动⽣产率固定构成指数为A.139.36%D.39.36% 43.某⼚1997年单位产品成本⽐1996年提⾼了5.8%，产品产量结构影响指数为96%,则该⼚总平均单位成本A. 提⾼1.57%B.提⾼1.8%C.下降4%D.下降9.26% 44.两个不同时期的加权算术平均数对⽐所形成的指数称为 A.加权算术平均指数 B.加权调和平均指数 C.可变构成指数 D.综合指数⼆、多项选择题1.指数按照其所表明的指标性质不同可以分为A.个体指数B.总指数C.组指数D.数量指标指数E.质量指标指数 2.综合指数包括A.总指数B.平均指数C.数量指标指数D.质量指标指数E.平均指标指数111000000110110111000111....f f x f f x D f f x f f x C f f x f f x B f f x f f x A ∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑3.下列指数中属于数量指标指数的有A.销售量指数B.职⼯⼈数指数E.单位成本指数4.下列指数中属于质量指标指数的有A.销售价格指数B.销售额指数C.单位成本指数D.劳动⽣产率指数E.可变构成指数5.同度量因素的作⽤有A.平衡作⽤B.权数作⽤C.媒介作⽤D.同度量作⽤E.⽐较作⽤6.编制综合指数的⼀般原则是A.数量指标指数以基期质量指标为同度量因素B.数量指标指数以报告期质量指标为同度量因素C.质量指标指数以基期数量指标为同度量因素D.质量指标指数以报告期数量指标为同度量因素A.质量指标指数和数量指标指数都采⽤基期的对应指标为同度量因素7.编制综合指数要掌握的两个要点是A.引进同度量因素对复杂经济现象总体进⾏综合B.确定指数化因素C.将同度量因素固定，消除同度量因素变动的影响D.选择编制指数的⽅法E.明确指数的经济意义8.已知某商业企业基期销售额为100万元，报告期销售额⽐基* * 期增长14%，⼜知道以基期价格计算的报告期假定销售额为112万元，则通过计算可以知道A.销售量增长12%B.价格增长12%C.由于价格变化使销售额增加2万元D.由于销售量变化使销售额增加12万元E.由于销售量变化使销售额增加20万元B.综合反映价格变动的绝对额C.综合反映销售量变动的绝对额D.综合反映价格和销售量共同变动的绝对额E.综合反映由于多种价格变动⽽增减的销售额10.下列公式中属于拉⽒指数的有A.∑p1q0 ∑p0q0B.∑q1p1 ∑q0p1C.∑p1q1 ∑p0q1D.∑q1p0 ∑q0p0E.∑q1p1 ∑q0p011.下列公式中属于派⽒指数的有A.∑p1q0 ∑p0q0B.∑q1p1 ∑q0p1C.∑p1q1 ∑p0q1D.∑q1p0 ∑q0p0E.∑q1p1 ∑q0p012.加权算术平均数指数是⼀种A.总指数B.综合指数C.平均数指数D.平均指标指数E.个体指数加权平均数13.平均指数和综合指数的联系和区别表现为A.在解决复杂总体不能直接同度量问题的思想不同B.在运⽤资料的条件上不同C.综合指数是先综合后对⽐,⽽平均指数是先对⽐后综合D.在经济分析中的具体作⽤也有区别E.在⼀定的权数条件下,两类指数间有变形关系14.作为综合指数变形的平均指数应⽤的⼀般法则为A.数量指标指数必须采⽤基期总量指标为权数的加权算术平均指数的形式B.数量指标指数必须采⽤报告期总量指标为权数的加权算术平均指数的形式D.质量指标指数必须采⽤报告期总量指标为权数的加权调和平均指数的形式E.数量指标指数和质量指标指数所采⽤权数的时期可以采⽤不同时期15.在指数体系中,指数之间的数量对等关系表现在A.总量指数(对象指数)等于其因素指数的连乘积B.总量指数(对象指数)等于其因素指数的代数和C.总量指数(对象指数)等于其因素指数的⽐值D.总量指数的绝对增减额等于其因素指数绝对增减额的连乘积E.总量指数的绝对增减额等于其因素指数绝对增减额的代数和16.平均指标指数体系包括哪些指数？A.数量指标指数B.质量指标指数C.可变构成指数D.固定结构指数E.结构影响指数17.在指数体系中,同度量因素的选择标准是A.经济含义合理B.数学等式成⽴C.计算⽅法简便D.计算资料易取E.对⽐基期固定18.可变构成指数可以分解为A.数量指标指数B.质量指标指数C.固定结构指数D.结构影响指数E.平均指标指数19.可变构成指数体系的关系表现为A.可变构成指数等于结构影响指数乘以固定结构指数B.固定结构指数等于结构影响指数乘以可变构成指数C.固定结构指数等于可变构成指数除以结构影响指数20.运⽤指数体系进⾏因素分析时可以A.对总量指标进⾏因素分析B.对平均指标进⾏因素分析C.对相对指标进⾏因素分析D.从相对数⽅⾯进⾏因素分析E.从绝对数⽅⾯进⾏因素分析21.指数因素分析按指标表现形式不同可分为A.总量指标变动因素分析B.相对指标变动因素分析C.平均指标变动因素分析D.简单现象因素分析E.复杂现象因素分析22.适⽤于⾮全⾯资料编制的总指数是A.数量指标综合指数B.质量指标综合指数C.算术平均数指数D.调和平均数指数E.平均指标指数23.设表⽰产量；P表⽰价格，则在实际⼯作中下列式⼦哪些是正确的？A.∑p1q1 ∑p0q0B.∑q1p1 ∑q1p0C.∑p0q1 ∑p0q0D.∑q0p1 ∑q0p0E.∑q1p1 ∑q0p1三、填空题1.从狭义上讲,指数是表明数量综合变动的相对数。
题目：完整初一数学统计学难题解析
题目：完整初一数学统计学难题解析完整初一数学统计学难题解析
问题一
题目描述：在一个班级里，有30个学生。
其中有18个学生喜欢足球，12个学生喜欢篮球，5个学生既喜欢足球又喜欢篮球。
问有多少个学生既不喜欢足球也不喜欢篮球？
解析：
根据题目信息，我们可以得到以下等式：
总学生数 = 喜欢足球的学生数 + 喜欢篮球的学生数 - 既喜欢足球又喜欢篮球的学生数 + 既不喜欢足球也不喜欢篮球的学生数
代入已知值，设既不喜欢足球也不喜欢篮球的学生数为 x：
30 = 18 + 12 - 5 + x
解方程可得：
x = 5
所以，既不喜欢足球也不喜欢篮球的学生数为 5 个。
问题二
题目描述：小明做了一套30道数学测试题，他答对了25道题。
问小明的正确率是多少？
解析：
小明的正确率可以用答对的题数除以总题数来表示。
已知：
答对题数 = 25
总题数 = 30
正确率 = 答对题数 / 总题数
解题可得：
正确率= 25 / 30 ≈ 0.8333 (保留四位小数)
所以，小明的正确率约为 0.8333。
问题三
题目描述：在一场考试中，小明得了85分，班级平均分为78分，问小明的成绩相对于班级平均分来说是偏高还是偏低？
解析：
小明的成绩与班级平均分的相对关系可以通过比较两者的数值大小来确定。
已知：
小明的分数 = 85分
班级平均分 = 78分
小明的分数 > 班级平均分，所以小明的成绩相对于班级平均分来说是偏高的。
所以，小明的成绩相对于班级平均分来说是偏高的。
统计学计算题8个例题及答案
统计学计算题8个例题及答案
1.给定一组数据，X=(13,12,13,13,10,13,11)，求它的众数：
答：13（众数是出现次数最多的值）
2.给定一组数据，X=(1,2,3,4,5,6,7)，求它的中位数：
答：4（中位数是将一组数据按照大小顺序排列后位于正中间的一个数）
3.给定一组数据，X=(1,2,3,4,5,6,7)，求它的样本标准差：
答：（样本标准差S=√ [(∑(Xi−X平均数)2)/ (n−1)]，其中，Xi代表样本的每一项，X平均数是样本的平均值，n是样本的总观测值数量)
4.给定一组数据，X=(1,2,3,4,5,6,7,8,9)，求它的方差：
答：（方差σ^2=∑(Xi−X平均数)^2/n，其中，Xi代表样本的每一项，X平均数是样本的平均值，n是样本的总观测值数量）
5.给定一组数据，X=(21, 25, 28, 31, 34, 37, 40)，求它的算术平均数：
答：31（算术平均数是将样本中数据求和，再除以样本的个数得到的数）
6.给定一组数据，X=(1,2,3,4,5,6,7,8,9)，求它的期望：
答：5（期望是一组数据根据概率分布定义出的一种数学期望）
7.给定一组数据，X=(3,4,5,7,12,15,18)，求它的方差：
答：（方差σ^2=∑(Xi−X平均数)^2/n，其中，Xi代表样本的每一项，X平均数是样本的平均值，n是样本的总观测值数量）
8.给定一组数据，X=(7,7,7,7,8,8,9)，求它的众数：
答：7（众数是出现次数最多的值）。
应用统计学课后习题和参考答案解析
应用统计学课后习题与参考答案第一章一、选择题1．一个统计总体（D）。
A．只能有一个标志 B．只能有一个指标C．可以有多个标志 D．可以有多个指标2．对100名职工的工资收入情况进行调查，则总体单位是（D）。
A．100名职工 B．100名职工的工资总额C．每一名职工 D．每一名职工的工资 3．某班学生统计学考试成绩分别为65分、72分、81分和87分，这4个数字是（D）。
A．指标 B．标志C．变量 D．标志值4．下列属于品质标志的是（B）。
A．工人年龄 B．工人性别C．工人体重 D．工人工资5．某工业企业的职工数、商品销售额是（C）。
A．连续变量 B．离散变量C．前者是离散变量，后者是连续变量 D．前者是连续变量，后者是离散变量 6．下面指标中，属于质量指标的是（C）。
A．全国人口数 B．国内生产总值C．劳动生产率 D．工人工资7．以下指标中属于质量指标的是（C）。
A．播种面积 B．销售量C．单位成本 D．产量8．下列各项中属于数量指标的是（B）。
A．劳动生产率 B．产量C．人口密度 D．资金利税率二、简答题1．一项调查表明，消费者每月在网上购物的平均花费是200元，他们选择在网上购物的主要原因是“价格便宜”。
（1）这一研究的总体是什么？总体是“所有的网上购物者”。
（2）“消费者在网上购物的原因”是定类变量、定序变量还是数值型变量？分类变量。
（3）研究者所关心的参数是什么？所有的网上购物者的月平均花费。
（4）“消费者每月在网上购物的平均花费是200元”是参数还是统计量？统计量。
（5）研究者所使用的主要是描述统计方法还是推断统计方法？推断统计方法。
2．要调查某商场销售的全部冰箱情况，试指出总体、个体是什么？试举若干品质标志、数量标志、数量指标和质量指标。
总体：该商店销售的所有冰箱。
总体单位：该商店销售的每一台冰箱。
品质标志：型号、产地、颜色。
数量标志：容量、外形尺寸；数量指标：销售量、销售额。
质量指标：不合格率、平均每天销售量、每小时电消耗量。
统计学计算题解析
1、相对指标：计划数和实际数为相对数时计划完成程度如①劳动生产率（正指标）计划在上年的基础上提高10%，实际提高15%；②单位产品成本计划在上年基础上下降10%，实际下降15%劳动生产率计划完成=(1+15%)/(1+10%)=104.55% 单位产品成本计划完成=(1-15%)/(1-10%)=94.44%平均数:∑∑=fxf X =8400/200=42(万只/人)标准差： σ=∑-f fx x i 2)(=20012200=7.81(万只/人)标准差系数=7.81/42=18.60%3、某市工业企业有关分组资料如下:P102（注：产值利润率=实际利润/实际产值）要求:计算该市工业企业第一季度、第二季度和上半年平均产值利润率(1) 工业企业第一季度平均产值利润率%74.18225002050057002250025.02050015.05700075.0=++⨯+⨯+⨯(2)工业企业第二季度平均产值利润率(3) 工业企业上半年平均产值利润率 (0.075*5700+0.15*20500+0.25*22500+710+3514+2250) /(5700+20500+22500+9466.67+23426.67+9000)=15601.5/90593.34=17.22%4、(8%)某人存入银行人民币10万元， 20年后能够变为30万元 (1)如按单利计算，年利率为多少？ (2)如按复利计算，年利率为多少？(3)如按(2)利率计算20后取得50万元,最初存入人民币是多少?计算:单利 平均利率=[(30-10)/20]/10=10% 复利 年平均本利率=201030=105.65%平均利率=1-本利率=5.65%最初存入人民币=50/1.056520=50/3.0019=16.66(万元)5、有关资料如下：%45.1525.0225015.03514075.071022503514710=++++1.1计算第一季度女职工占职工平均比重=（214.29/2+244.71+229.13+235.29/2）/(714.29/2+764.71+739.13+735.29/2)=232.88/742.88=31.35%1.2计算第二季度女职工占职工平均比重=(235.29/2+218.57+224.64+244.71/2)/(735.29/2+728.57+724.64+764.71/2)=227.74/734.40=31.01%1.3计算上半年女职工占职工平均比重=(214.29/2+244.71+229.13+235.29+218.57+224.64+244.71/2)/(714.2 9/2+764.71+739.13+735.29+728.57+724.64+764.71/2)=230.31/738.64=31.18%2.1计算第一季度工人月劳动生产率=[(571428.57+743294.12+709565.22)/3]/[( 571.43/2+619.41+591.30+602.94/2)/3]=674762.64/599.30=1125.92(元/人)2.2计算第二季度工人月劳动生产率=[(663235.29+699428.57+695652.17)/3]/[( 602.94/2+582.86+579.71+611.76/2)/3]=686105.35/589.97=1162.95(元/人)2.3计算上半年工人月劳动生产率=[(571428.57+743294.12+709565.22+663235.29+699428.57+695652.17)/6 ]/[( 571.43/2+619.41+591.30+602.94+582.86+579.71+611.76/2)/6]=680433.99/594.64=1144.28(元/人)3.1计算第一季度工人劳动生产率= (571428.57+743294.12+709565.22)/[( 571.43/2+619.41+591.30+602.94/2)/3]=2024287.91/599.30=3377.75(元/人)3.2计算第二季度工人劳动生产率= (663235.29+699428.57+695652.17)/[( 602.94/2+582.86+579.71+611.76/2)/3]=2058316.04/589.97=3488.85(元/人)3.3计算上半年工人劳动生产率=(571428.57+743294.12+709565.22+663235.29+699428.57+695652.17) /[( 571.43/2+619.41+591.30+602.94+582.86+579.71+611.76/2)/6]=4082603.95/594.64=6865.67(元/人)6、某省对外贸易总额2000年比1997年增长7.9%，2001年比2000年增长4.5%，2002年又比2001年增长5%，2003—2006平均增长率为6%，试计算1997—2006年每年平均增长速度。
统计学计算题和答案完整版
统计学计算题和答案 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】三个企业生产的同一型号空调在甲、乙两个专卖店销售，有关资料如下：企业型号 价格 （元/台） 甲专卖店销售额（万元） 乙专卖店销售量（台） A 2500 340 B 3400 260 C 4100 200 合计——答案：2某企业甲、乙两个生产车间,甲车间平均每个工人日加工零件数为65件，标准差为11件；乙车间工人日加工零件数资料如下表。
试计算乙车间工人加工零件的平均数和标准差，并比较甲、乙两个生产车间哪个车间的平均日加工零件数更有代表性？日加工零件数（件） 60以下 60—70 70—80 80—90 90—100 工人数（人）59121410三、某地区2009—2014年GDP 资料如下表，要求： 1、计算2009—2014年GDP 的年平均增长量； 2、计算2009—2014年GDP 的年平均发展水平；年份 2009 2010 2011 2012 2013 2014 GDP （亿元）87431062711653147941580818362年平均增长速度：5100%280%100%22.9%x -=-= 年份2010 2011 2012 2013 2014 销售额（万元）320332340356380水平？答案： 2010年—2014年的数据有5项，是奇数，所以取中间为0，以1递增。
设定x 为-2、-1、0、1、2、年份/销售额（y ） x xy x2 2010 320 -2 -640 4 2011 332 -1 -332 1 2012 340 0 0 0 2013 356 1 356 1 2014 380 2 760 4合计 1728 0 144 10b=∑xy/∑x2=144/10=a=∑y/n=1728/5=y=+预测2016年，按照设定的方法，到2016年应该是5y=+*5=元五、某企业生产三种产品，2013年三种产品的总生产成本分别为20万元，45万元，35万元，2014年同2013年相比，三种产品的总生产成本分别增长8%，10%，6%，产量分别增长12%，6%，4%。
统计学计算题(有答案)
1、甲乙两班同时参加《统计学原理》课程的测试，甲班平均成绩为81分，标准差为9.5分，乙班的成绩分组资料如下：按成绩分组学生人数（人）60以下 460~70 1070~80 2580~90 1490~100 2计算乙班学生的平均成绩，并比较甲乙两班，哪个班的平均成绩更有代表性?静1 己5 甲册抽二。
也二93 Z Jti片■轨*■低4=?昭f4t/h= 1(1= 25,/, = 14.^ -1V f4*UH15*14f 144 N4 S+MU釘酿加样Mb !■ ,=^=^=0.1173 片1拆川备因加＜「m«i I'irwjtwft气tf]2、某车间有甲乙两个生产组，甲组平均每个人的日产量为36件，标准差为9.6件，乙组工人产量资料如下：日产量（件）工人数（人）15 1525 3835 3445 13要求：（1）计算乙组平均每个工人的日产量和标准差（2）比较甲乙两生产小组的日产量更有代表性战屮如 K 的平均日严洛更内世表性3月份 1 23 4 5 6 8 11 12 库存额6055 48 43 40 50 456068又知月日商品库存额为万元，试计算上半年，下半年和全年的平均商品库存额。
解：（1）该商店上半年商品库存额：8 泊（63/2+60+55M8+43+40+50/2） =50417 （万元） （2） 该商店下半年商品库存额：b ={[（50+45）/2]*2 + [（45+60>/2]*3 + [（60+68）/2]* 1 >5275 （万元）（3） 该商店全年商品库存额：C- （50.147+52.75） / 2-51.5835 （万元）4品名单位销售额2002比2001销售量增长（%）2001 2002电视 台 5000 8880 23 自行车辆4500 4200-7合计950013080要求：（）计算销售量总指标（2）计算由于销售量变动消费者增加或减少的支出金额工 K p 詔o[,23 x 5000 + ().93 x 4500 10335= -------------------- = --------------------------------------------- = ------------- =10S .79 %工 Pn% 5000 + 4500 9500ISxl5 + 25*38+35*34 +45<J3 dX)2'. fnr.^4 " !■<-h hlfln=0,267^629.5'U..VI5⑵山册吿员变功潇费者晏虫讨金敲= L K qPo<3o"LPo C5o =他饰9500-835（^<3）计霽苗种商品帝皆价格总指難和III十价格变动制悄您榊的誓响帥对飆.够见NS的思眛通过质11描标烷令指独号谓和平炖救持数处式之何的关帝壮得剋所需敎握”5、某商店两种商品的销售额和销售价格的变化情况如下：（万元）要求：（1）计算两件商品销售价格总指标和由于价格变动对销售额的影响绝对值（2）计算销售量总指数，计算由于销售变动消费者增加或减少的支出金额解，<”诙轴紳晦召也hl IJ2in w瀬的空，担对刃］I：I：船恪二对紀y p闭一工丄P4 =166-15032 = 15.67 万几k工PE工P0 工Pi%品備竹苗格总弗趙j-------------- =j ------------------= 寸几ItiJMSUI 和前顺的训算中y PnGi = 16()，卩“ =150.32由」旬％命苍城.占喑讪减❻的丸出伞触工卩％》几如=15°33-160 = -9厲76、某企业上半年产品量与单位成本资料如下:月份产量（千克）单位成本（元）12 73 2 3 72 34 71 4 3 73 54 69 6568要求：（1）计算相关系数，说明两个变量相关的密切程度（2）配合回归方程，指出产量每增加1000件时，单位成本平均变动多少?15033 160= 9335%,主"99二X + R 可审Ct• cao g* •<>»= 9*Z8 ・ r-zs •"=・i-z$: ・"=z 血二柬珂由 + 9=x （U -44 oooo MTT4君0 （ £》-竺N8 l 科刮站士寸孕刃衣 -4^4^ oooi nrrMT^TT=uitD “ X 岁⑷q 窪習日回Uh 耳雷宕F 丑xz8 T -ZS •"=•▲ fiiiZE ・"=gm （NR r-）-g/9Zfr= xq — « = □Z8 ・l 一 =（lN*lNy/l — GZ 〉/（9乙“INT/l -l 蔽l ） = a —严 M< M ・* M 二-心 MI/M 卜TRT-T RQTTOC6ZTZOt^E 卡 N9trSZ8^S 9 9ZN TQZtr 9T fi9* s6T^ ENWM 6 CX w卩"SIN TXFS 9T IXE9TZ ^8TS 6NZ £ Z 9" 6NW9frWZZTJLacNAA +申对侖< TT"3PTUtrl8^^OE=, 97^=18 * M<>=u<I>心M心M8^^OE=^7、根据企业产品销售额（万元）和销售利润率（％）资料计算出如下数据：（重点题目）n=7 X=18090 ' y=31.1X2=535500y2 =174.157 xy =9318要求：（1）确定以利润为因变量的直线回归方程（2）解释式中回归系数的经济含义（1）鞘定収利涓率为丙Z的立线冋旧方程：Y=-5. 5-K）, 037x（2）解释戌屮回归杀数的经济含突：产母制善额毎壊加1万元*钳您利満率平均増加6037^（3）肖常乜極为500万元时•利洞率为:¥=12. 9 寮8、某企业第二季度产品产量与单位成本资料如下:要求：（1）定量判断产量与单位成本间的相关程度（2）建立直线回归方程，并说明b的经济含义解：（1 ）所需计算数据见下表：月份产量单位成本45 634 57369 68916 25219276 340合计12210508352.57、根据企业产品销售额（万元）和销售利润率（％）资料计算出如下数据：（重点题目）因为，，所以产量每增加1000件时，即增加1单位时，单位成本的平均变动是：平均减少元。
统计学计算题例题(含答案)
1、某企业制定了销售额的五年计划， 该计划要求计划期的最后一年的年销售额应达到 1200万元。
实际执行最后两年情况如下表：请根据上表资料，对该企业五年计划的完成情况进行考核。
1、 计划完成相对数 =1410/1200*100%=117.5%该计划完成相对数指标为正指标， 计划完成相对数又大于 100% ，所以表示该计划超额完成。
从第 四年 5 月至第五年 4 月的一年的年销售额之和恰好为 1200 万元，所以该计划在第五年 4 月完成，提 前 8 个月完成。
2、 某地区制定了一个植树造林的五年计划，计划中设定的目标是五年累计植树造林面积为 2000 万 亩。
实际执行情况如下：请对该长期计划的完成情况进行考核。
2、 计划完成程度相对数 =2100/2000*100%=105%计划完成相对数指标大于100%, 且该指标为正指标 ， 所以该计划超额完成截止第五年第三季度累计完成 2000 万亩造林面积，所以提前 1 个 季 度 完 成3、某班学生统计学课程考试成绩情况如下表：请根据上述资料计算该班统计学课程的平均成绩、成绩的中位数、众数和成绩的标准差。
3、某企业职工年龄情况如下表：X 二三于=4740/62=76.45 （分）Me=70+ （62/2-18） *10/20=76.5 （分）Mo=70+（20 J5）70/［（2CM5）+（2CM8）］=77 」4 （分）G-7（55-76.45f *3 +⋯⋯+ （95^76.45f *6/62=10.45 （分）4、某学校有5000 名学生，现从中按重复抽样方法抽取250 名同学，调查其每周观看电视的小时数的情况，获得资料如下表：请根据上述资料，以95% 的概率保证程度对全校学生每周平均收看电视时间进行区间估计。
4> 样本平均数X= Sxf/Sf-l250/250-5样 ______________ __________二>/ 刀（好予f/（工f—1 ）二V 1136/249 二2. 14抽样平均误差U 二s/ Vn=0.14因为 F （t） =95%, 所以日.96抽样极限误差△ 二t U 二 1. 96*0. 14=0. 27 区间下限=5-0. 27=4. 73 区间上限二5+0. 27-5. 27全校学生每周平均收看电视的吋间在( 4.73,5.27) 小时之间，概率保证程度为95%5 、某企业对全自动生产线上的产品随机抽取1000 件进行检验，发现有45 件是不合格的,设定允许的极限误差为1.32% 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1、下表是某保险公司160名推销员月销售额的分组数据。
书p26（1）计算并填写表格中各行对应的向上累计频数；（2）计算并填写表格中各行对应的向下累计频数；（3）确定该公司月销售额的中位数。
按上限公式计算：Me=U-=18-0.22=17,78 2、某厂工人按年龄分组资料如下：p41要求：采用简捷法计算标准差。
《简捷法》3、试根据表中的资料计算某旅游胜地2004年平均旅游人数。
P50表：某旅游胜地旅游人数第 1 页/共 15 页4、某大学2004年在册学生人数资料如表3-6所示，试计算该大学2004年平均在册学生人数.5、已知某企业2004年非生产人员以及全部职工人数资料如下表所示，求该企业第四季度非生产人员占全部职工人数的平均比重。
表：某企业非生产人员占全部职工人数比重6、根据表中资料填写相应的指标值。
表：某地区1999~2004年国内生产总值发展速度计算表7、根据表中资料计算移动平均数，并填入相应的位置。
P618、根据表中资料计算移动平均数，并填入相应的位置。
P629、某百货商场某年上半年的零售额、商品库存额如下：（单位：百万元）试计算该商城该年上半年商品平均流转次数（注：商品流通次数=商品销售额/库存额；6月末商品库存额为24.73百万元）。
10、某地区2000-2004年粮食产量资料如下：p71要求：（1）用最小平方法拟合直线趋势方程（简洁法计算）；（2）预测2006年该地区粮食产量。
11、已知某地区2002年末总人口为9.8705万人，（1）若要求2005年末将人口总数控制在10.15万人以内，则今后三年人口年均增长率应控制在什么水平？（2）又知该地区2002年的粮食产量为3805.6万千克，若2005年末人均粮食产量要达到400千克的水平，则今后3年内粮食产量每年应平均增长百分之几？（3）仍按上述条件，如果粮食产量每年递增3%，2005年末该地区人口为10.15万人，则平均每人粮食产量可达到什么水平？12、根据表中数据对某商店的销售额变动进行两因素分析。
13、某商店三种商品销售额及价格变动资料如下：p113试计算：三种商品价格总指数和销售量总指数。
解:三种商品物价总指数：=105.74%销售量总指数=销售额指数÷价格指数=114.04%14、某商店资料如下：要求：分别分析价格和销售量对销售额的影响。
15、某市居民家庭人均收入服从μ=6000元，σ=1200元的正态分布，求该市居民家庭人均年收入：（1）在5000~7000元之间的概率；（2）超过8000元的概率；（3）低于3000元的概率。
（注：Φ（0.83）=0.7967，Φ（0.84）=0.7995，Φ（1.67）=0.95254，Φ（2.5）=0.99379）16、一种汽车配件的平均长度要求为12cm ，高于或低于该标准均被认为是不合格的。
汽车生产企业在购进配件时通常要对中标的汽车配件商提供的样品进行检验，以决定是否购进。
现对一个配件提供商提供的10个样本进行了检验，结果如下（单位：cm ）12.2 10.8 12.0 11.8 11.9 12.4 11.3 12.2 12.0 12.3假定该供货商生产的配件长度服从正态分布，在0.05的显著性水平下，检验该供货商提供的配件是否符合要求？（查t 分布单侧临界值表，262.2)9()9(025.0==t t α，2281.2)10(025.02==t t α；查正态分布双侧临界值表，96.105.0==z z α）。
17、假设考生成绩服从正态分布，在某地一次数学统考中随机抽取了36位考生的成绩，算得平均成绩为66.5分，标准差为15分。
在显著性水平05.0=α下，是否可以认为这次考试全体考生的成绩为70分？（查正态分布双侧临界值表得，96.105.0==z z α）18、某种纤维原有的平均强度不超过6g ，现希望通过改进工艺来提高其平均强度。
研究人员测得了100个关于新纤维的强度数据，发现其均值为6.35。
假定纤维强度的标准差仍保持为1.19不变，在5%的显著性水平下对该问题进行假设检验。
（645.105.0=z 96.1205.0=z ）（1）选择检验统计量并说明其抽样分布是什么样的？（2）检验的拒绝规则是什么？（3）计算检验统计量的值，你的结论是什么？19、一家瓶装饮料制造商想要估计顾客对一种新型饮料认知的广告效果。
他在广告前和广告后分别从市场营销区各抽选一个消费者随机样本，并询问这些消费者是否听说过这种新型饮料。
这位制造商想以10%的误差范围和95%的置信水平估计广告前后知道该新型饮料消费者的比例之差，他抽取的两个样本分别应包括多少人？(假定两个样本容量相等)（ 96.1205.02==z z α ）20、一家食品生产企业以生产袋装食品为主，每天的产量大约为8000袋左右。
按规定每袋的重量应为100g 。
为对产量质量进行监测，企业质监部门经常要进行抽检，以分析每袋重量是否符合要求。
现从某天生产的一批食品中随机抽取了25袋，测得每袋重量（单位：g ）如表所示。
表：25袋食品的重量已知产品重量服从正态分布，且总体标准差为10g 。
试估计该批产品平均重量的置信区间，置信水平为95%。
21、一家保险公司收集到由36投保人组成的随机样本，得到每个投保人的年龄数据如表所示。
试建立投保人年龄90%的置信区间。
表：36个投保人年龄的数据22、已知某种灯泡的寿命服从正态分布，现从一批灯泡中随机抽取16只，测得其使用寿命（单位：h）如下： 1510 1450 1480 1460 1520 1480 1490 14601480 1510 1530 1470 1500 1520 1510 1470建立该批灯泡平均使用寿命95%的置信区间。
23、某城市要估计下岗职工中女性所占的比例，随机抽取了100名下岗职工，其中65人为女性。
试以95%的置信水平估计该城市下岗职工中女性比例的置信区间。
24、一家食品生产企业以生产袋装食品为主，现从某天生产的一批食品中随机抽取了25袋，测得每袋重量如下表所示。
已知产品重量的分布服从正态分布。
以95%的置信水平建立该种食品重量方差的置信区间30、拥有工商管理学士学位的大学毕业生的年薪的标准差约为2000元，假定想要以95%的置信水平估计年薪的置信区间，希望边际误差为400元。
应抽取多大的样本容量？26、根据以往的生产统计，某种产品的合格率约为90%，现要求边际误差为5%，在求置信水平为95%的置信区间时，应抽取多少个产品作为样本？27、从一个标准差为5的总体中以重复抽样的方式抽出一个容量为40的样本，样本均值为25.（1）样本均值的抽样标准差是多少？（2）在95%的置信水平下，边际误差是多少？28、某快餐店想要估计每位顾客午餐的平均花费金额，在为期3周的时间里以重复抽样的方式选取49名顾客组成了一个简单随机样本。
（1）假定总体标准差为15元，求样本均值的抽样标准化差。
（2）在95%的置信水平下，求边际误差；（3）如果样本均值为120元，求总体均值在95%置信水平下的置信区间。
29、在一项家电调查中，随机抽取了200户居民，调查他们是否拥有某一品牌的电视机。
其中拥有该品牌电视机的家庭占23%。
求总体比例的置信区间，置信水平分别为90%和95%。
30、某居民小区共有居民500户，小区管理者准备采用一项新的供水设施，想了解居民赞成与否。
采取重复抽样方法随机抽取了50户，其中有32户赞成，18户反对。
（1）求总体中赞成该项改革的户数比例的置信区间，置信水平为95%。
（2）如果小区管理者预计赞成的比例达到80%，应抽取多少户进行调查？32、某超市想要估计每位顾客平均每次购物花费的金额。
根据过去的经验，标准差大约为120元，现要求以95%的置信水平估计每位顾客购物金额的置信区间，并要求边际误差不超过20元，应抽取多少位顾客作为样本？33、一种灌装饮料采用自动生产线生产，每罐的容量为255ml，标准差为5ml。
为检验每罐容量是否符合要求，质检人员在某天生产的饮料中随机抽取了40罐进行检验，测得每罐平均容量为255.8ml。
取显著性水平0.05，检验该天生产的饮料容量是否符合标准要求。
34、某一小麦品种的平均产量为5200kg/hm2。
一家研究机构对小麦品种进行了改良以期提高产量。
为检验改良后的新品种产量是否有显著提高，随机抽取了36个地块进行试种，得到的样本平均产量为5275 kg/hm2，标准差为120 kg/hm2。
试检验改良后的新品种产量是否有显著提高？（显著性水平为0.05）35、一种以休闲和娱乐为主题的杂志，声称其读者群中有80%为女性。
为验证这一说法是否属实，某研究部门抽取了由200人组成的一个随机样本，发现有146个女性经常阅读该杂志。
分别取显著性水平为0.05和0.01，检验该杂志读者群中女性的比例是否为80%。
36、啤酒生产企业采用自动生产线灌装啤酒，每瓶的装填量为640ml，但由于受某些不可控因素的影响，每瓶的装填量会有差异。
此时，不仅每瓶的平均装填量很重要，装填量的方差同样很重要。
如果方差很大，会出现装填量太多或太少的情况，这样要么生产企业不划算，要么消费者不满意。
假定生产标准规定每瓶装填量的标准差不应超过和不应低于4ml。
企业质检部门抽取了10瓶啤酒进行检验，得到的样本标准差为s=3.8ml。
试以0.10的显著性水平检验装填量的标准差是否符合要求？。