学习四元数笔记
一年级数学第四到第五单元笔记 人教版
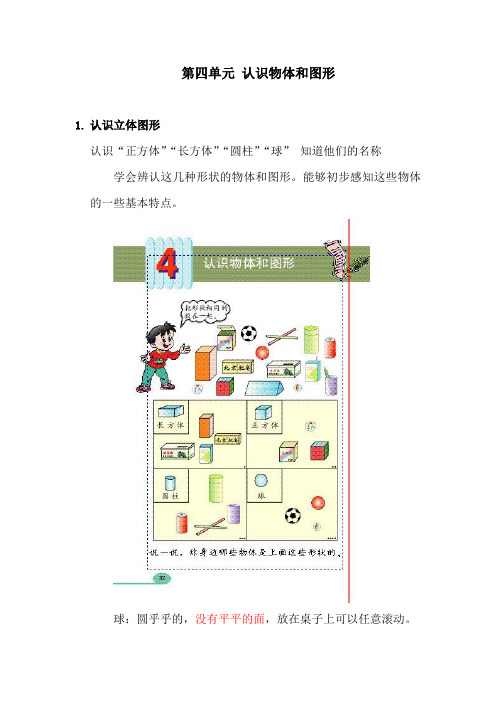
第四单元认识物体和图形1.认识立体图形认识“正方体”“长方体”“圆柱”“球”知道他们的名称学会辨认这几种形状的物体和图形。
能够初步感知这些物体的一些基本特点。
球:圆乎乎的,没有平平的面,放在桌子上可以任意滚动。
圆柱:直筒筒的,上下一样粗,两头是平平的一样大的圆形。
躺在桌子上是可以滚动的,立在桌子上就不能滚动了。
正方体:四四方方的,不能滚动。
有6个面,每个面的大小都是一样的,都是正方形。
长方体:长长方方的,无法滚动。
有6个面,每个面都是长方形,有时也可能有2个面是正方形。
重难点:(1)可以正确数出图形中物体的个数,包括能正确找出隐藏的物体。
图1:7 图2:5 图3:8(2)能够正确找出每种立体图形对应的平面图形。
(注意:根据一年级所学习的内容,球是不可以直接画出圆形的,因为球是曲面,和平面接触的部分只是一个点。
)第一行:选第三个第二行:选第二个第三行:选第一和第二个第四行:选第一个(3)认识正方体展开图理解与面1相对的是面3,两个面要相隔一个格子才能相对面。
(另附:三维展开图。
)2.认识平面图形认识“正方形”“长方形”“圆形”“三角形”知道他们的名称学会辨认这几种形状的物体和图形。
能够初步感知这些图形的一些基本特点。
圆:平平的圆圆的面正方形:四四方方的,有四个直直的角,四条边,并且每条边都相等长方形:长长方方的,也有四个直直的角,四条边,但边有长有短。
三角形:有三个角,三条边。
重难点:(1)能够正确的将图形折叠成其他图形A. 将正方形分成两个长方形B.将正方形分成两个三角形C.将三角形分成两个直角三角形D.将长方形分成两个正方形3.学会拼图能够将被分开的图形的两部分找出来,再拼成整体的图形。
(例如:半圆和半圆可以拼成整圆)教学方法:自制正方形,长方形,圆形,三角形的纸片,将他们剪开,放在一起,让孩子在其中找出被剪开的部分,然后拼起来。
以游戏的形式让孩子掌握知识。
第五单元分类1.单一标准的分类感知分类,观察课本38页图,发现:相同的东西放在一起,就叫分类。
四元数简介——精选推荐

四元数简介在我之前,⽹上各个博客各⼤⽹站都有很多关于四元数的介绍与讲解!但我总结了⼀下接三个字:看不懂!说实话!这真的是实话!举个例⼦:1.旋转,应该是三种坐标变换——缩放、旋转和平移,中最复杂的⼀种了。
⼤家应该都听过,有⼀种旋转的表⽰⽅法叫四元数。
按照我们的习惯,我们更加熟悉的是另外两种旋转的表⽰⽅法——矩阵旋转和欧拉旋转。
矩阵旋转使⽤了⼀个4*4⼤⼩的矩阵来表⽰绕任意轴旋转的变换矩阵,⽽欧拉选择则是按照⼀定的坐标轴顺序(例如先x、再y、最后z)、每个轴旋转⼀定⾓度来变换坐标或向量,它实际上是⼀系列坐标轴旋转的组合。
那么,四元数⼜是什么呢?简单来说,四元数本质上是⼀种⾼阶复数(听不懂了吧。
),是⼀个四维空间,相对于复数的⼆维空间。
我们⾼中的时候应该都学过复数,⼀个复数由实部和虚部组成,即x = a + bi,i是虚数单位,如果你还记得的话应该知道i^2 = -1。
⽽四元数其实和我们学到的这种是类似的,不同的是,它的虚部包含了三个虚数单位,i、j、k,即⼀个四元数可以表⽰为x = a + bi + cj + dk。
那么,它和旋转为什么会有关系呢?怎么样,看得懂吗?反正⼩编是被现实胖揍⼀顿!那么,今天我们要怎么来介绍这个四元数呢?我们来最简单暴⼒的!重新定义⼀下这个怪物四元数!Quaternion(四元数)⽤于计算和表⽰Unity旋转。
它们计算紧凑⾼效,不受万向节死锁的困扰,并且可以很⽅便快速地进⾏球⾯插值。
Unity内部使⽤四元数来表⽰所有的旋转。
注意重点:1,不受万向节死锁的困扰。
2,⽅便快速地进⾏球⾯插值。
3, Unity内部使⽤四元数来表⽰所有的旋转。
好了,现在你得重定义应该是这样的:定义:Quaternion(四元数)⽤于计算和表⽰Unity旋转。
就像当初数学⽼师告诉你∏(pai)⽤来表⽰圆周率⼀样!你有探究过∏(pai)是怎么算出来的吗?但是你们是不是都知道怎么利⽤圆周率计算圆的⾯积呢?类似的,对于初学者的我们,最重要的是现在要学会和记住四元数的使⽤⽅法。
四元数运动学笔记(1)旋转的表示

四元数运动学笔记(1)旋转的表⽰1.参考资料Quaternion kinematics for the error-state KFbarfoot《state estimation forrobotics》袁信、郑锷《捷联式惯性导航原理》以上书籍的下载链接链接:密码:jdsz2.旋转矩阵的性质2.1旋转矩阵定义frame1到frame2的旋转矩阵为,旋转矩阵是单位正交矩阵。
对于旋转矩阵的下标可以这样理解,等式右边是旋转矩阵转化后的新位置坐标,左右是上⼀时刻的位置坐标,因此旋转的叠加(积分)即在原来的基础上再左乘新的旋转矩阵。
z-y-x即图中3-2-1,是我看很多导航的书的表⽰⽅式,barfoot的书中以1-2-3旋转⽅式作为航空中常⽤的旋转⽅式,对⽐袁信的捷联惯导书和barfoot的书,两者每次旋转对应的旋转矩阵是相通的,只不过定义的旋转次序不同使得旋转矩阵的形式不太⼀样-欧拉⾓的⼤⼩和⽅向定义:barfoot书中每次旋转的旋转矩阵定义,和袁信书中⼀致。
以袁信书中的z-y-x即3-2-1的旋转⽅式表⽰的旋转矩阵,,这⾥frame1看作是n系,frame2看作是b系,则导航系n到机体系b的旋转矩阵()旋转矩阵的⼩⾓度表⽰:当旋转⾓都⽐较⼩时,利⽤三⾓函数的与欧拉⾓的近似,省略⼩量的⼆次以上部分,得到:2.2旋转矩阵的奇异点barfoot书中以1-2-3的旋转⽅式为例,如果中间那次旋转,则旋转就会变成绕1轴旋转,即旋转耦合在⼀起,即这次旋转的欧拉⾓⽆法恢复。
2.3旋转矩阵的微分⽅程哥⽒定理利⽤哥⽒定理推导旋转矩阵的微分⽅程3.向量叉乘与斜对称矩阵向量叉乘可以表⽰成向量的叉乘矩阵和向量相乘,叉乘矩阵是斜对称矩阵,这种表⽰在旋转相关公式⾥经常⽤到。
对于列向量a,b有:4.四元数4.1四元数表⽰四元数有很多表⽰⽅法,这⾥采⽤标量+向量的形式表⽰(scalar+vector)4.2四元数乘法两个四元数等于各个元素分别相乘,表⽰旋转的积分四元数乘法不满⾜交换律(commutative)四元数乘法满⾜结合律(associative)和分配律(distributive)两个四元数相乘可以表⽰为矩阵的形式利⽤四元数的结合律得到4.3四元数的性质单位1 四元数(Identity):共轭四元数:虚数部分符号相反单位四元数的逆等于其共轭四元数Loading [MathJax]/jax/output/HTML-CSS/jax.js。
四元数的初步总结

四元数的初步总结(一)前一阵子,以前公司的一位同事向我请教一段计算机图形程序中的算法,其中涉及齐次坐标和四元数。
齐次坐标问题到好讲解,但四元数方面以前所知几乎为零。
正好我看到齐民友在《复分析,可视化方法》译后记中提到的一本书:《高观点下的初等数学》([德]克莱因著,以下简称《初等数学》)当中有一段讲到四元数,于是就细读了一遍,把这个专题的整理笔记写下来。
但是那本书里有很多结果依靠繁杂的机械运算,让人看了不知道这样的结果是怎么得出来的。
因此我们这里用向量代数的观点重新审视四元数的一些结果,让四元数的特性看起来更直观,更自然。
另外还有一些我认为重要的有关四元数引入的背景知识,例如数域的扩充问题的证明,那本书里只有一部分提示,这里也试着补全一些。
一、四元数引入的理论背景将实数域扩充到复数域,并用复数来表示平面向量,用复数的加、乘运算表示平面向量的合成、伸缩和旋转变换,这些观念已经在中学课程中学过了。
那么,很自然的问题就是,在三维,或更高维空间中是否也有复数的类似物?也就是说,像扩充实数那样,在复数域的基础上添加一个或几个新的元素,并且让它们跟原来的复数做加减乘除,是否就可以得到一个新的数集,并且其中的元素还可以像复数域那样做加、减、乘、除运算,并满足通常复数的那些运算律,包括加法和乘法的交换律与结合律、乘法对加法的分配律等待?更进一步,我们是否可以期望用这样的数来表示三维或更高维空间中的伸缩和旋转,就像用复数表示平面向量的伸缩旋转那样方便?把问题说得明确一些,即是说,我们是否可以像得到复数域那样,在复数域中再添加一个新的元素(因此也是在实数基础上添加两个元素和),得到一个类似于复数集合,这个集合中的元素当时就是普通的复数,当时就是普通的实数,并且通常数的加减乘除运算及其性质都可以在这个集合上保持,即满足:1、对于任意两个数,它们的和是唯一确定的。
2、对于任意两个数,它们的积是唯一确定的。
3、存在一个数0,它具有性质:对于任意a,均有a+0=a。
四元数

定义两个四元数:
其中表示矢量 ;而表示矢量。
跟复数、向量和矩阵一样,两个四元数之和需要将不同的元素加起来。 加法遵循实数和复数的所有交换律和结合律。
威廉·卢云·哈密顿
明确地说,四元数是复数的不可交换延伸。如把四元数的集合考虑成多维实数空间的话,四元数就代表着一 个四维空间,相对于复数为二维空间。
四元数是除环(除法环)的一个例子。除了没有乘法的交换律外,除法环与域是相类的。特别地,乘法的结 合律仍旧存在、非零元素仍有逆元素。
四元数形成一个在实数上的四维结合代数(事实上是除法代数),并包括复数,但不与复数组成结合代数。 四元数(以及实数和复数)都只是有限维的实数结合除法代数。
不只如此,哈密顿还创造了向量的内外积。他亦把四元数描绘成一个有序的四重实数:一个纯量和向量的组 合。若两个纯量部为零的四元数相乘,所得的纯量部便是原来的两个向量部的纯量积的负值,而向量部则为向量 积的值,但它们的重要性仍有待发掘。
哈密顿之后继续推广四元数,并出了几本书。最后一本《四元数的原理》(Elements of Quaternions)于 他死后不久出版,长达八百多页。
非奇异表达(和例如欧拉角之类的表示相比)
比矩阵更紧凑(更快速)
单位四元数的对可以表示四维空间中的一个转动。
所有单位四元数的集合组成一个三维球和在乘法下的一个群(一个李群)。是行列式为1的实正交3×3正交 矩阵的群的双面覆盖,因为每两个单位四元数通过上述关系对应于一个转动。群和同构,是行列式为1的复酉 2×2矩阵的群。令为形为的四元数的集合,其中或者都是整数或者都是分子为奇数分母为2的有理数。集合是一 个环,并且是一个格。该环中存在 24个四元数,而它们是施莱夫利符号为的正二十四胞体的顶点。
四元数解析

四元数解析一、四元数是啥呢?嘿呀,四元数这个东西啊,可有点小神秘又有点小酷呢。
它就像是数学这个大乐园里一个超级独特的小天地。
四元数啊,其实是一种复数的扩展啦。
就好像我们本来有个小房子,然后突然给它加盖了好几层,变得超级酷炫。
二、四元数的构成它是由一个实数部分和三个虚数部分组成的哦。
这就好像是一个小团队,有一个队长(实数部分),还有三个特别的小伙伴(虚数部分)。
这三个虚数部分还都有着自己独特的小标识,它们可不是随便凑在一起的,而是有着非常奇妙的组合规则呢。
三、四元数的历史在数学的发展长河里,四元数的出现也是一段很有趣的故事。
有好多聪明的数学家们不断探索,就像探险家在未知的大陆上寻找宝藏一样。
经过很多人的努力,四元数才逐渐被发现和完善。
它在数学发展中可是有着很重要的地位,就像一颗璀璨的星星照亮了数学天空的一角。
四、四元数的用途1. 在计算机图形学里它可厉害了呢。
比如说在3D游戏的制作中,要让那些虚拟的角色动起来,转圈圈,四元数就能很好地来处理旋转的问题。
就像一个超级小助手,默默地在背后让游戏画面变得更加流畅和逼真。
2. 在物理学领域它也有自己的小舞台。
像是在研究一些物体的旋转运动的时候,四元数就可以简洁又高效地描述物体的状态。
这可比其他的方法有时候要方便很多呢。
五、四元数的计算它的计算规则有点像我们玩一种特别的数学游戏。
比如说加法、乘法之类的运算,都有着自己独特的小算法。
这些算法虽然刚开始学的时候可能有点绕,但只要你耐心去探索,就会发现其中的乐趣。
就像解开一道道有趣的小谜题一样。
六、四元数和其他数学概念的关系四元数和复数、向量这些数学概念都有着千丝万缕的联系。
它就像是一个大家庭里的一员,和其他成员之间有着相互的影响和作用。
复数可以说是四元数的小前辈,而四元数又对向量的发展有着一定的启发呢。
四元数

为什么使用四元数为了回答这个问题,先来看看一般关于旋转(面向)的描述方法-欧拉描述法。
它使用最简单的x,y,z值来分别表示在x,y,z轴上的旋转角度,其取值为0-360(或者0-2pi),一般使用roll,pitch,yaw来表示这些分量的旋转值。
需要注意的是,这里的旋转是针对世界坐标系说的,这意味着第一次的旋转不会影响第二、三次的转轴,简单的说,三角度系统无法表现任意轴的旋转,只要一开始旋转,物体本身就失去了任意轴的自主性,这也就导致了万向轴锁(Gimbal Lock)的问题。
还有一种是轴角的描述方法(即我一直以为的四元数的表示法),这种方法比欧拉描述要好,它避免了Gimbal Lock,它使用一个3维向量表示转轴和一个角度分量表示绕此转轴的旋转角度,即(x,y,z,angle),一般表示为(x,y,z,w)或者(v,w)。
但这种描述法却不适合插值。
那到底什么是Gimbal Lock呢?正如前面所说,因为欧拉描述中针对x,y,z的旋转描述是世界坐标系下的值,所以当任意一轴旋转90°的时候会导致该轴同其他轴重合,此时旋转被重合的轴可能没有任何效果,这就是Gimbal Lock,这里有个例子演示了Gimbal Lock,点击这里下载。
运行这个例子,使用左右箭头改变yaw 为90°,此时不管是使用上下箭头还是Insert、Page Up键都无法改变Pitch,而都是改变了模型的roll。
那么轴、角的描述方法又有什么问题呢?虽然轴、角的描述解决了Gimbal Lock,但这样的描述方法会导致差值不平滑,差值结果可能跳跃,欧拉描述同样有这样的问题。
什么是四元数四元数一般定义如下:q=w+xi+yj+zk其中w是实数,x,y,z是虚数,其中:i*i=-1j*j=-1k*k=-1也可以表示为:q=[w,v]其中v=(x,y,z)是矢量,w是标量,虽然v是矢量,但不能简单的理解为3D空间的矢量,它是4维空间中的的矢量,也是非常不容易想像的。
四元数计算法则

四元数计算法则
四元数是一种数学结构,用于描述三维空间的旋转和变换。
它由一个实部和三个虚部组成,可以表示为q = a + bi + cj + dk,其中i、j、k是虚数单位,满足i=j=k=ijk=-1。
四元数的加减法与复数相似,但是乘法则更加复杂。
四元数的乘法遵循以下法则:
1. 实部相乘,虚部相乘时,i=j=k=ijk=-1
2. i乘以j等于k,j乘以k等于i,k乘以i等于j
3. j乘以i等于-k,k乘以j等于-i,i乘以k等于-j
4. 任意两个虚数乘积可以表示为一个实数加上一个虚数
四元数的除法需要用到逆元,即q=q*/(q*q*),其中q*表示q的共轭。
四元数的共轭表示为q* = a - bi - cj - dk。
四元数的旋转可以通过四元数的乘法来实现。
以欧拉角为例,将欧拉角转换为四元数后,进行旋转就是将原始四元数与旋转四元数相乘。
同时,四元数也可以用于描述变换(如平移、缩放等),可以通过矩阵的方式表示。
总之,四元数是一种非常有用的数学工具,广泛应用于计算机图形学、虚拟现实、机器人控制等领域。
掌握四元数的计算法则,对于进行三维空间中的旋转和变换非常有帮助。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复数是由实数加上虚数单位i 组成,其中i^2 = -1 \,。
相似地,四元数都是由实数加上三个元素i、j、k 组成,而且它们有如下的关系:i^2 = j^2 = k^2 = ijk = -1 \,每个四元数都是1、i、j 和k 的线性组合,即是四元数一般可表示为a + bi + cj + dk \,。
四元数不像实数或复数那样,它的乘法是不可交换的,看乘数表四元数的优点是:表达式无奇点(和例如欧拉角之类的表示相比)比矩阵更简炼(也更快速)单位四元数的对可以表示四维空间中的一个转动。
以矩陣表示四元數[编辑]有兩種方法能以矩陣表示四元數,並以矩陣之加法、乘法應用於四元數之加法、乘法。
第一種是以二階複數矩陣表示。
若h = a + bi + cj + dk 則它的複數形式為:這種表示法有如下優點:所有複數(c = d = 0) 就相應於一個實矩陣。
四元數的絕對值的平方就等於矩陣的行列式。
四元數的共軛值就等於矩陣的共軛轉置。
對於單位四元數(|h| = 1) 而言,這種表示方式給了四維球体和SU(2)之間的一個同型,而後者對於量子力學中的自旋的研究十分重要。
(請另見泡利矩陣)第二種則是以四階實數矩陣表示:其中四元數的共軛等於矩陣的轉置。
(转载)四元数入门(2012-02-14 00:52:24)转载▼标签:computer graphic quaternion 四元数it 分类:学习(转载)四元数入门---------------------------------------------------------------------/showthread.asp?threadid=735114元数宝典这是国内找不到的超好文章。
(为什么大陆的4元数文章很垃圾呢?)(翻译中。
奉献给大家~~)70秒即懂,能使用,用四元数,4元数,阔特尼恩,Quaternion旋转(C) 中田亨(独立行政法人产业技术综合研究所数字人类研究中心研究员博士(工学))2003年11月25日★这个页面的对象读者想把三次元的旋转,用CG等定量地处理的人使用欧拉角(Euler Angles)的话,不懂得其道理的人卡尔丹角和欧拉角(Cardan Angles)不能区别的人对吉恩瓦尔洛克很困惑的人但是,对数学之类麻烦的事情很讨厌的人想要实例程序的人没有时间的人★旋转篇:我将说明使用了四元数(si yuan shu, quaternion)的旋转的操作步骤(1)四元数的虚部,实部和写法所谓四元数,就是把4个实数组合起来的东西。
4个元素中,一个是实部,其余3个是虚部。
比如,叫做Q的四元数,实部t而虚部是x,y,z构成,则像下面这样写。
Q = (t; x, y, z)又,使用向量V=(x,y,z),Q = (t; V)也可以这么写。
正规地用虚数单位i,j,k的写法的话,Q = t + xi + yj + zk也这样写,不过,我不大使用(2)四元数之间的乘法虚数单位之间的乘法ii = -1, ij = -ji = k (其他的组合也是循环地以下同文)有这么一种规则。
(我总觉得,这就像是向量积(外积),对吧)用这个规则一点点地计算很麻烦,所以请用像下面这样的公式计算。
A = (a; U)B = (b; V)AB = (ab - U·V; aV + bU + U×V)不过,“U·V”是内积,「U×V」是外积的意思。
注意:一般AB<>BA所以乘法的左右要注意!(3)3次元的坐标的四元数表示如要将某坐标(x,y,z)用四元数表示,P = (0; x, y, z)则要这么写。
另外,即使实部是零以外的值,下文的结果也一样。
用零的话省事所以我推荐。
(4)旋转的四元数表示以原点为旋转中心,旋转的轴是(α, β, γ)(但α^2 + β^2 + γ^2 = 1),(右手系的坐标定义的话,望向向量(α, β, γ)的前进方向反时针地)转θ角的旋转,用四元数表示就是,Q = (cos(θ/2); αsin(θ/2), βsin(θ/2), γsin(θ/2))R = (cos(θ/2); -αsin(θ/2), -βsin(θ/2), -γsin(θ/2))(另外R 叫Q 的共轭四元数。
)那么,如要实行旋转,则R P Q = (0; 答案)请像这样三明治式地计算。
这个值的虚部就是旋转之后的点的坐标值。
(另外,实部应该为零。
请验算看看)*未完。
instemast_REAL 2007-2-24 19:04:57注册: 2007-2 状态: Offline 1 Topinstemast_REALExp:124侦察兵发表于: 2007-2-24 19:06:00 档案| 短信| 树状| 收藏| 编辑| 删除| 引用--------------------------------------------------------------------------------Re:4元数宝典/// Quaternion.cpp/// (C) Toru Nakata, toru-nakata@aist.go.jp/// 2004 Dec 29#include <math.h>#include <iostream.h>/// Define Data typetypedef struct{double t; // real-componentdouble x; // x-componentdouble y; // y-componentdouble z; // z-component} quaternion;//// Kakezan 乘quaternion Kakezan(quaternion left, quaternion right) {quaternion ans;double d1, d2, d3, d4;d1 = left.t * right.t;d2 = -left.x * right.x;d3 = -left.y * right.y;d4 = -left.z * right.z;ans.t = d1+ d2+ d3+ d4;d1 = left.t * right.x;d2 = right.t * left.x;d3 = left.y * right.z;d4 = -left.z * right.y;ans.x = d1+ d2+ d3+ d4;d1 = left.t * right.y;d2 = right.t * left.y;d3 = left.z * right.x;d4 = -left.x * right.z;ans.y = d1+ d2+ d3+ d4;d1 = left.t * right.z;d2 = right.t * left.z;d3 = left.x * right.y;d4 = -left.y * right.x;ans.z = d1+ d2+ d3+ d4;return ans;}//// Make Rotational quaternion 求旋转四元quaternion MakeRotationalQuaternion(double radian, double AxisX, double AxisY, double AxisZ){quaternion ans;double norm;double ccc, sss;ans.t = ans.x = ans.y = ans.z = 0.0;norm = AxisX * AxisX + AxisY * AxisY + AxisZ * AxisZ;if(norm <= 0.0) return ans;norm = 1.0 / sqrt(norm);AxisX *= norm;AxisY *= norm;AxisZ *= norm;ccc = cos(0.5 * radian);sss = sin(0.5 * radian);ans.t = ccc;ans.x = sss * AxisX;ans.y = sss * AxisY;ans.z = sss * AxisZ;return ans;}//// Put XYZ into quaternion 把XYZ到四元quaternion PutXYZToQuaternion(double PosX, double PosY, double PosZ) {quaternion ans;ans.t = 0.0;ans.x = PosX;ans.y = PosY;ans.z = PosZ;return ans;}///// mainint main(){double px, py, pz;double ax, ay, az, th;quaternion ppp, qqq, rrr;cout << "Point Position (x, y, z) " << endl;cout << " x = ";cin >> px;cout << " y = ";cin >> py;cout << " z = ";cin >> pz;ppp = PutXYZToQuaternion(px, py, pz);while(1) {cout << "/nRotation Degree ? (Enter 0 to Quit) " << endl;cout << " angle = ";cin >> th;if(th == 0.0) break;cout << "Rotation Axis Direction ? (x, y, z) " << endl;cout << " x = ";cin >> ax;cout << " y = ";cin >> ay;cout << " z = ";cin >> az;th *= 3.1415926535897932384626433832795 / 180.0; ///Degree -> radian;qqq = MakeRotationalQuaternion(th, ax, ay, az);rrr = MakeRotationalQuaternion(-th, ax, ay, az);ppp = Kakezan(rrr, ppp);ppp = Kakezan(ppp, qqq);cout << "/nAnser X = " << ppp.x<< "/n Y = " << ppp.y<< "/n Z = " << ppp.z << endl;}return 0;}*未完。
