保持函数依赖的分解
模式分解

2.保持FD (函数依赖)的分解定义1:设F 是属性集U 上的FD 集,Z 是U 的子集,F 在Z 上的投影用πZ (F)表示,定义为πZ (F)={X →Y|X →Y ∈F +,且XY ⊆Z}定义2. 设},...{1K R R =ρ 是R 的一个分解,F 是R 上的FD 集,如果有)(1F R i ki π=Y ╞ F ,那么称分解ρ保持函数依赖集F 。
根据定义1,测试一个分解是否保持FD ,比较可行的方法是逐步验证F 中的每个FD 是否被)(1F R i ki π=Y 逻辑蕴涵。
如果F 的投影不蕴涵F ,而我们又用},...{1K R R =ρ表达R ,很可能会找到一个数据库实例σ 满足投影后的依赖,但不满足F 。
对σ的更新也有可能使r 违反FD 。
案例1:R (T#,TITLE ,SALARY )。
如果规定每个教师只有一个职称,并且每个职称只有 一个工资数目,那么R 上的FD 有T#→TITLE 和TITLE →SALARY 。
如果R 分解成ρ={R 1,R 2},其中R 1={T#,TITLE},R 2={T#,SALARY }。
则该分解具有无损连接性,但未保持函数依赖,丢失了依赖TITLE →SALARY 。
习题1:设关系模式R (ABC ),ρ={AB ,AC}是R 的一个分解。
试分析分别在F 1={A →B};F 2={A →C ,B →C},F 3={B →A},F 4={C→B,B→A}情况下, 是否具有无损分解和保持FD的分解特性。
算法1:分解成2NF模式集的算法设关系模式R(U),主码是W,R上还存在FD X→Z,并且Z是非主属性和X⊂W,那么W→Z就是非主属性对码的部分依赖。
此时,应把R分解成两个关系模式:R1(XZ),主码是X;R2(Y),其中Y=U-Z,主码仍为W,外码是X(参照R1)利用外码和主码的连接可以从R1和R2重新得到R。
如果R1和R2还不是2NF,则重复上述过程,一直到数据库模式中的每个关系模式都是2NF为止。
关系模式分解的无损连接和保持函数依赖

关系模式分解的无损连接和保持函数依赖一、引言关系模式是关系数据库中的核心元素之一,它描述了数据的结构和关系。
在设计关系数据库时,我们常常需要对关系模式进行分解,以满足数据库的需求。
本文将讨论关系模式分解的无损连接和保持函数依赖的相关概念和方法。
二、关系模式分解关系模式分解是将一个关系模式拆分成多个较小的关系模式的过程。
在分解关系模式时,我们需要考虑两个重要的性质:无损连接和保持函数依赖。
2.1 无损连接无损连接是指在关系模式分解后,通过对分解后的关系进行连接操作能够恢复原始关系模式。
换句话说,无损连接要求分解后的关系能够完整地保留原始关系中的所有信息。
2.2 保持函数依赖保持函数依赖是指在关系模式分解后,分解后的关系中依然能够保持原始关系中的函数依赖关系。
函数依赖是指一个属性或者属性集合的值决定了另一个属性或者属性集合的值。
三、关系模式分解的方法关系模式分解有多种方法,下面介绍三种常用的方法:自然连接、垂直分解和水平分解。
3.1 自然连接自然连接是指通过公共属性将两个或多个关系模式进行连接,得到一个具有完整信息的新关系模式。
自然连接的特点是能够保持原始关系中的所有信息和函数依赖。
3.2 垂直分解垂直分解是指根据属性集合的划分,将一个关系模式分解成多个关系模式。
垂直分解的优点是能够消除冗余数据,提高查询效率。
但是需要注意的是,垂直分解可能会造成关系丢失或信息损失。
3.3 水平分解水平分解是指将一个关系模式的元组进行水平划分,得到多个关系模式。
水平分解的特点是能够提高并发性能和容错性。
但是需要注意的是,水平分解可能会造成查询的复杂性增加和数据的分布不均衡。
四、关系模式分解的应用关系模式分解在实际的数据库设计中有着广泛的应用。
下面介绍两个例子以说明关系模式分解的应用。
4.1 学生课程关系考虑一个学生选课系统,其中包含学生和课程两个关系模式。
学生关系模式包括学生ID、姓名和年龄等属性,课程关系模式包括课程ID、课程名称和教师名称等属性。
数据库保持函数依赖的分解
2NG
a1
a2
a3
思考:不保持函数依赖的 分解会导致什么问题?
例: 分, G ) 职工工号 工资级别 工资数目 R上的FD集为: F= { N→S, /* 每个职工只有一个工资级别 */ S →G /* 一个工资级别只有一个工资数目*/ } 将R分解为:ρ ={ NS, SG }, ρ保持依赖?无损分解? 解:PNS(F)={N→S}, PSG(F)={S→G}。 因为PNS(F)∪PSG(F)= F, 所以ρ保持函数依赖; 也是无损分解:
1A 1AB 2AC a1 a1 2B a2 b22 3C b13 a3
例: 分解是否保持FD集,是否无损分解
设有关系模式:R(ABC), R上的FD集为: F= { C→B, B→A } 将R分解为:ρ ={ AB, AC }, ρ保持依赖?无损分解? 解:PAB(F)={B→A}, PAC(F)={C→A}。 ρ不保持依赖(丢失C→B) ; 也是损失分解:
问题:如何在保证无损和保持依赖的前提下,使分解所 得的关系模式集符合尽可能高的范式? 目前有三个算法: 1. 保持依赖且无损地分解成3NF关系模式集 2. 无损地分解成BCNF关系模式集 3. 无损地分解成4NF关系模式集(超出课程范围, 不讲)
则称分解ρ保持函数依赖集F。
两个函数依赖集F和G是等价的,当且仅当:
1) 凡是能够由F推出的FD都能够由G推出; 2) 凡是不能由F推出的FD也不能由G推出。
例: 分解是否保持FD集,是否无损分解
设有关系模式:R( N, S, G ) 职工工号 工资级别 工资数目 R上的FD集为: F= { N→S, /* 每个职工只有一个工资级别 */ S →G /* 一个工资级别只有一个工资数目*/ } 将R分解为:ρ ={ NS, NG }, ρ保持依赖?无损分解? 解:PNS(F)={N→S}, PNG(F)={N→G}。 因为根据N→S和N→G推不出S →G, 所以ρ不保持 函数依赖; 但是是无损分解:
规范化无损分解及保持函数依赖

AB BC CD
a1
a2
b13 a3 a3
b14 b24 a4
b 21 a 2 b31 b32
无损分解的测试方法
(2)把表格看成模式R的一个关系,反复检查F中每个FD在表格中是否成立, 若不成立,则修改表格中的值。修改方法如下: 对于F中一个FD X Y ,如果表格中有两行在X值上相等,在Y值上不相等, ai 那么把这两行在Y值上也改成相等的值。如果Y值中有一个是 ,那么另一 aj aj bij 个也改成 ;如果没有 ,那么用其中一个 替换另一个值(尽量把下标 ij改成较小的数)。一直到表格不能修改为止。 (3)若修改的最后一张表格中有一行全 是a,即 a1a 2 a n ,那么称ρ 相对于F 是无损分解,否则称有损分解。 A B C D
分解成3NF模式集既无损 又保持函数依赖的方法
① 对于关系模式R和R上成立的FD集F,先求出F的最小依赖集,然后再把最小依 赖集中那些左部相同的FD用合并性合并起来。 ② 对最小依赖集中每个FD X→Y去构成一个模式XY。 ③ 在构成的模式集中,如果每个模式都不包含R的候选键,那么把候选键作为一 个模式放入模式集中。
保持函数依赖的模式分解
设关系模式R<U,F>被分解为若干个关系模式 R1<U1,F1>,R2<U2,F2>,…,Rn<Un,Fn> (其中U=U1∪U2∪…∪Un,且不存在Ui Uj,Fi为F 在Ui上的投影),若F所逻辑蕴含的函数依赖一定
也由分解得到的某个关系模式中的函数依赖Fi所逻
辑蕴含,则称关系模式R的这个分解是保持函数依
, Rk 是R
例:设关系模式R(ABCD),R分解成 {AB, BC, CD} 。如果R上成立的函数依赖 集 F1 {B A, C D},那么ρ 相对于F 是否无损分解?如果R上成立的函数依赖集 1 F2 {A B, C D} 呢? (1)构建一张k行n列的表格,每 列对应一个属性 A j 1 j n ,每行 对应一个模式 R i 1 i K 。如 果 A j在 R i 中,那么在表格的第i行 第j列处填上符号 a j ,否则填上 bij。 A B C D
模式分解保持函数依赖的意义

系模式冗余度相对较大 ,需要对其进行分解 ,使其达
到更高一 级 的范 式 ,从 而 降 低 数 据 冗余 ,避 免 更 新 、 插 入和删 除异 常 ,这种过 程称 为规 范化 。
关 系 数据库 的逻 辑设 计原 理是 以减 小冗余 为 目标 的 ¨ 。范式 是符合 一定 级别 的关 系模 式 的集合 ,能 够
的 函数 依赖 ,只需要 考虑 该较 小关 系 的函数 依 赖 ,而 不 必连 接多个 较 小关 系 。一般 的 国内文 献重 点研 究 的
对关 系模 式施 加相 应 的数据 依赖 约束 ,已经成 为 衡量
2 c o l fC mp trS in e .S h o o o ue ce c ,Xiin U iest ,X ’n7 7 ,C ia da nvri y i 0 a 1 1 hn ) 0
Ab ta t No maiain c n i rv h oma o e re o eain h o g c e e o o iins a d sr c r l to a mp o e t e n r lfr d g e frlt str u h s h ma d c mp st z m o o , n
足不 同级 别 的范 式 ,常 用 的范 式 及相 互 联 系 为 :4 F N cB N C3 Fc2 Fc 1 F CF N N 。属 于较 低 级 别 范式 的关 N
保持 函数 依赖 的 意义 ,但是 没有 给 出严格 的证 明和易
于理解 的实例 。本 文证 明 了保 持 函数依 赖 的一个 定理 ,说 明了模 式 分解 保持 函数 依赖 的意 义是 在 减小
p n e ce sp o e e d n isi rv d, a d i i s o h tte sg f a c fp e e ain o n t n ld p n e ce o f c h n t s h wnt a h inic n eo r s r to ff ci a e e d n isdon taf tte i v u o e p ro a c fd t p ae i e u ig d t e u d n y T e c n rt n lss o n e a l u te o f ms efr n e o aa u d ts whl r d cn aa rd n a c . h o cee a ay i fa x mpe f rh r c n r m e i te c n lso h o cu in. Ke wo d n r aiain; s h ma d c mp sto y rs o m l to z c e e o o iin; p e ev t n o u cin ld p n e ce rs r ai ffn to a e e d n is o
关系模式分解的两种主要准则

关系模式分解的两种主要准则关系模式分解是数据库设计中非常重要的一个环节,它可以将一个复杂的关系模式分解成若干个更简单的关系模式,从而提高数据库的性能和可维护性。
在进行关系模式分解时,需要遵循一些准则,本文将介绍其中的两种主要准则。
一、函数依赖分解准则函数依赖是指一个或多个属性的值决定另一个属性的值。
在关系模式中,函数依赖是关系模式中数据之间的约束关系,也是关系模式分解的重要依据。
在进行函数依赖分解时,可以根据以下准则进行分解:1.不产生冗余数据:分解后的新关系模式不能产生冗余数据,即不能存在同一条数据在不同的关系模式中重复出现的情况。
2.保持原有的函数依赖关系:分解后的新关系模式应该能够与原有的函数依赖关系对应,保证数据的完整性和一致性。
3.尽可能保持关系模式的最小性:在函数依赖分解时,应该尽可能降低关系模式的冗余度,保持关系模式的最小性。
二、多值依赖分解准则多值依赖是指一个或多个属性的值决定另一组属性的值,这与函数依赖有所不同。
在进行多值依赖分解时,需要遵循以下准则:1.保持原有的多值依赖关系:分解后的新关系模式应该能够与原有的多值依赖关系对应,保证数据的完整性和一致性。
2.不产生冗余数据:分解后的新关系模式不能产生冗余数据,即不能出现同一条数据在不同的关系模式中重复出现的情况。
3.保留原有的关系模式属性:分解后的新关系模式应该保留原有的关系模式属性,且数据应该可以通过新关系模式及相应的联结操作还原到原有的关系模式中。
总结:以上是关系模式分解的两种主要准则,无论是进行函数依赖分解还是多值依赖分解,都需要遵循不产生冗余数据、保持原有的依赖关系以及保留原有属性的原则。
在分解过程中,不同的准则可能会产生冲突,此时需要根据实际情况进行权衡,选择最优的方案。
分解结果必须保证数据的完整性和一致性,还可以提高数据库的性能和可维护性。
关系模式分解的无损连接和保持函数依赖

关系模式分解的无损连接和保持函数依赖一、关系模式分解的概念关系模式分解是指将一个复杂的关系模式分解为若干个简单的关系模式的过程。
在实际应用中,由于某些原因(如性能、数据冗余等),需要将一个大型的关系模式分解成多个小型的关系模式,从而提高数据库系统的效率和可维护性。
二、无损连接和保持函数依赖在进行关系模式分解时,有两种重要的约束条件:无损连接和保持函数依赖。
无损连接是指在进行关系模式分解后,仍然能够通过连接操作得到原始数据集合。
保持函数依赖是指在进行关系模式分解后,仍然能够维护原始数据集合中所有函数依赖。
三、无损连接和保持函数依赖的定义1. 无损连接假设R是一个关系模式,R1和R2是R的两个投影。
如果存在一个连接操作J(R1,R2),使得J(R1,R2)中包含了所有R中元组,则称R1和R2对于R具有无损连接。
2. 保持函数依赖假设R是一个关系模式,F是R上的一组函数依赖集合。
如果对于F中任何一个函数依赖X→Y,都存在一个关系模式R1和R2,使得R=R1⋈R2,且X和Y分别属于R1和R2的属性集合,则称关系模式分解后,仍然能够维护原始数据集合中所有函数依赖。
四、无损连接和保持函数依赖的算法在进行关系模式分解时,需要考虑如何保证无损连接和保持函数依赖。
以下是两种常用的算法。
1. 剖析算法剖析算法是一种自顶向下的分解方法。
该方法首先将原始关系模式拆分成两个投影,并检查它们是否具有无损连接。
如果没有,则再次拆分,并重复该过程直到满足无损连接为止。
剖析算法的优点是简单易懂,容易实现。
但是缺点也很明显,即可能会产生大量冗余数据。
2. 合成算法合成算法是一种自底向上的分解方法。
该方法首先将原始关系模式拆分为多个小型关系模式,并检查它们是否能够维护原始数据集合中所有函数依赖。
如果不能,则将两个小型关系模式合并,并重复该过程直到满足保持函数依赖为止。
合成算法的优点是能够保证数据的最小化,减少数据冗余。
但是缺点也很明显,即实现难度较大。
数据库保持函数依赖的分解
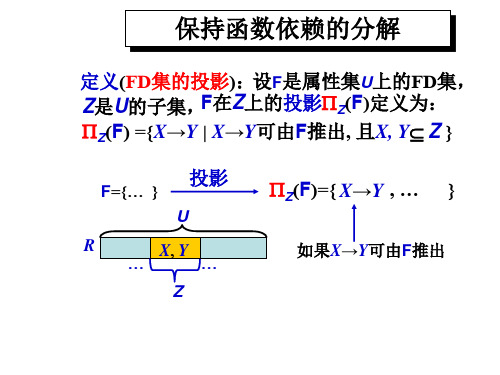
解:PAB(F)={A→B}, PAC(F)={ }。 ρ保持依赖; 也是无损分解:
1A 2B 3C 1AB a1 a2 b13 2AC a1 b22 a3
1A 2B 3C 1AB a1 a2 b13 2AC a1 a2 a3
例: 分解是否保持FD集,是否无损分解
设有关系模式:R(ABC), R上的FD集为: F= { A→B, B→C }
将R分解为:ρ ={ AB, AC }, ρ保持依赖?无损分解?
解:PAB(F)={A→B}, PAC(F)={A→C}。 ρ不保持依赖(丢失B→C); 但是是无损分解:
1A 2B 3C 1AB a1 a2 b13 2AC a1 b22 a3
1A 2B 3C 1AB a1 a2 b13 2AC a1 b22 a3
总结
根据是否保持依赖、是否无损分解将分解分成四类:
无损分解 保持依赖
说明
YES
YES
最好 (不丢失数据和依赖)
YES
NO 可接受 (丢失依赖, 会导致异常)
NO
YES
不能接受(丢失数据)
NO
NO
不能接受(丢失数据)
问题:如何在保证无损和保持依赖的前提下,使分解所 得的关系模式集符合尽可能高的范式?
例: 分解是否保持FD集,是否无损分解
设有关系模式:R( N,
S,
G)
职工工号 工资级别 工资数目
R上的FD集为:
F= {
N→S, /* 每个职工只有一个工资级别 */
S →G /* 一个工资级别只有一个工资数目*/
}
将R分解为:ρ ={ NS, NG }, ρ保持依赖?无损分解?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
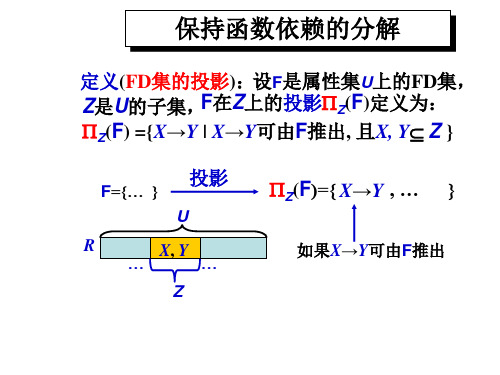
定义(FD集的投影):设F是属性集U上的FD集, F在Z上的投影PZ(F)定义为: Z是U的子集, PZ(F) ={X→Y | X→Y可由F推出, 且X, Y Z }
F={… } U R … X, Y Z … 如果X→Y可由F推出
投影
PZ(F)={ X→Y , …
}
例: FD集的投影
1A 1AB 2AC a1 a1 2B a2 b22 3C b13 a3
1A 1AB 2AC a1 a1
2B a2 a2
3C b13 a3
例: 分解是否保持FD集,是否无损分解
设有关系模式:R(ABC), R上的FD集为: F= { A→B, B→C } 将R分解为:ρ ={ AB, AC }, ρ保持依赖?无损分解? 解:PAB(F)={A→B}, PAC(F)={A→C}。 ρ不保持依赖(丢失B→C);但是是无损分解:
问题:如何在保证无损和保持依赖的前提下,使分解所 得的关系模式集符合尽可能高的范式? 目前有三个算法: 1. 保持依赖且无损地分解成3NF关系模式集 2. 无损地分解成BCNF关系模式集 3. 无损地分解成4NF关系模式集(超出课程范围, 不讲)
1N 1NS a1 2S a2 3G b13
2SG
b21
a2
a3
例: 分解是否保持FD集,是否无损分解
设有关系模式:R( N, S, G ) 职工工号 工资级别 工资数目 R上的FD集为: F= { N→S, /* 每个职工只有一个工资级别 */ S →G /* 一个工资级别只有一个工资数目*/ } 将R分解为:ρ ={ NS, SG }, ρ保持依赖?无损分解? 解:PNS(F)={N→S}, PSG(F)={S→G}。 因为PNS(F)∪PSG(F)= F, 所以ρ保持函数依赖; 也是无损分解:
1N 1NS a1 2S a2 3G b13
2NG
a1
a2
a3
思考:不保持函数依赖的 分解会导致什么问题?
例: 分解是否保持FD集,是否无损分解
设有关系模式:R( N, S, G ) 职工工号 工资级别 工资数目 R上的FD集为: F= { N→S, /* 每个职工只有一个工资级别 */ S →G /* 一个工资级别只有一个工资数目*/ } 将R分解为:ρ ={ NS, SG }, ρ保持依赖?无损分解? 解:PNS(F)={N→S}, PSG(F)={S→G}。 因为PNS(F)∪PSG(F)= F, 所以ρ保持函数依赖; 也是无损分解:
1N 1NS a1 2S a2 3G a3
2SG
b21
பைடு நூலகம்
a2
a3
例: 分解是否保持FD集,是否无损分解
设有关系模式:R(ABC), R上的FD集为: F= { A→B } 将R分解为:ρ ={ AB, AC }, ρ保持依赖?无损分解? 解:PAB(F)={A→B}, PAC(F)={ }。 ρ保持依赖; 也是无损分解:
1A 1AB 2AC a1 a1 2B a2 b22 3C b13 a3
总结
根据是否保持依赖、是否无损分解将分解分成四类: 无损分解 保持依赖 YES YES NO NO YES NO YES NO 说明 最好 (不丢失数据和依赖) 可接受 (丢失依赖, 会导致异常) 不能接受(丢失数据) 不能接受(丢失数据)
1N 1NS a1 2S a2 3G b13
2NG
a1
b22
a3
例: 分解是否保持FD集,是否无损分解
设有关系模式:R( N, S, G ) 职工工号 工资级别 工资数目 R上的FD集为: F= { N→S, /* 每个职工只有一个工资级别 */ S →G /* 一个工资级别只有一个工资数目*/ } 将R分解为:ρ ={ NS, NG }, ρ保持依赖?无损分解? 解:PNS(F)={N→S}, PNG(F)={N→G}。 因为根据N→S和N→G推不出S →G, 所以ρ不保持 函数依赖; 但是是无损分解:
设有关系模式R(ABCD), R上的FD集为: F = { A→B, B→C , D→B } 求PACD(F) 和PBD(F)
PACD(F)={ A→C , D→C }
PBD(F)={ D→B }
定义(保持函数依赖的分解): 设ρ={R1,…,Rk}是关 系模式R的一个分解,F是R上的FD集,如果: PR1(F)∪…∪ PRk(F)与F等价,
1A 1AB 2AC a1 a1 2B a2 b22 3C b13 a3
1A 1AB 2AC a1 a1
2B a2 a2
3C b13 a3
例: 分解是否保持FD集,是否无损分解
设有关系模式:R(ABC), R上的FD集为: F= { B→A } 将R分解为:ρ ={ AB, AC }, ρ保持依赖?无损分解? 解:PAB(F)={B→A}, PAC(F)={ }。 ρ保持依赖; 但是是损失分解:
1A 1AB 2AC a1 a1 2B a2 b22 3C b13 a3
例: 分解是否保持FD集,是否无损分解
设有关系模式:R(ABC), R上的FD集为: F= { C→B, B→A } 将R分解为:ρ ={ AB, AC }, ρ保持依赖?无损分解? 解:PAB(F)={B→A}, PAC(F)={C→A}。 ρ不保持依赖(丢失C→B) ; 也是损失分解:
则称分解ρ保持函数依赖集F。
两个函数依赖集F和G是等价的,当且仅当:
1) 凡是能够由F推出的FD都能够由G推出; 2) 凡是不能由F推出的FD也不能由G推出。
例: 分解是否保持FD集,是否无损分解
设有关系模式:R( N, S, G ) 职工工号 工资级别 工资数目 R上的FD集为: F= { N→S, /* 每个职工只有一个工资级别 */ S →G /* 一个工资级别只有一个工资数目*/ } 将R分解为:ρ ={ NS, NG }, ρ保持依赖?无损分解? 解:PNS(F)={N→S}, PNG(F)={N→G}。 因为根据N→S和N→G推不出S →G, 所以ρ不保持 函数依赖; 但是是无损分解:
