一般线性回归模型
logistic回归模型的一般形式

logistic回归模型的一般形式
logistic回归模型是一种广义的线性回归分析模型,常用于数据挖掘、疾病自动诊断、经济预测等领域。
其一般形式可表达为:logit(p) = α+β1*X1+β2*X2+β3*X3+.....+βk*Xk。
其中,logit(p)表示Y的对数发生比,p为Y事件发生的概率;α为常数项,βi(i=1,2,3,...,k)为自变量Xi的回归系数。
与传统的线性回归模型不同,logistic 模型中的因变量是分类变量而不是连续变量。
它反映了自变量对因变量的线性影响,常用于探讨引发疾病的危险因素,并根据危险因素预测疾病发生的概率等。
在实际应用中,logistic 回归模型的形式可能会根据具体问题和数据特点进行调整和扩展。
线性统计模型知识点总结

线性统计模型知识点总结一、线性回归模型1. 线性回归模型的基本思想线性回归模型是一种用于建立自变量和因变量之间线性关系的统计模型。
它的基本思想是假设自变量与因变量之间存在线性关系,通过对数据进行拟合和预测,以找到最佳拟合直线来描述这种关系。
2. 线性回归模型的假设线性回归模型有一些假设条件,包括:自变量与因变量之间存在线性关系、误差项服从正态分布、误差项的方差是常数、自变量之间不存在多重共线性等。
3. 线性回归模型的公式线性回归模型可以用如下的数学公式来表示:Y = β0 + β1X1 + β2X2 + ... + βnXn + ε,其中Y 是因变量,X是自变量,β是模型的系数,ε是误差项。
4. 线性回归模型的参数估计线性回归模型的参数估计通常使用最小二乘法来进行。
最小二乘法的目标是通过最小化残差平方和来寻找到最佳的模型系数。
5. 线性回归模型的模型评估线性回归模型的好坏可以通过很多指标来进行评价,如R-squared(R^2)、调整后的R-squared、残差标准差、F统计量等。
6. 线性回归模型的应用线性回归模型广泛应用于经济学、金融学、市场营销、社会科学等领域,用以解释变量之间的关系并进行预测。
二、一般线性模型(GLM)1. 一般线性模型的基本概念一般线性模型是一种用于探索因变量与自变量之间关系的统计模型。
它是线性回归模型的一种推广形式,可以处理更为复杂的数据情况。
2. 一般线性模型的模型构建一般线性模型与线性回归模型相似,只是在因变量和自变量之间的联系上,进行了更为灵活的变化。
除了线性模型,一般线性模型还可以包括对数线性模型、逻辑斯蒂回归模型等。
3. 一般线性模型的假设一般线性模型与线性回归模型一样,也有一些假设条件需要满足,如误差项的正态分布、误差项方差的齐性等。
4. 一般线性模型的模型评估一般线性模型的模型评估通常涉及到对应的似然函数、AIC、BIC、残差分析等指标。
5. 一般线性模型的应用一般线性模型可以应用于各种不同的领域,包括医学、生物学、社会科学等,用以研究因变量与自变量之间的关系。
线性回归模型的经典假定及检验修正

线性回归模型的经典假定及检验、修正一、线性回归模型的基本假定1、一元线性回归模型一元线性回归模型是最简单的计量经济学模型,在模型中只有一个解释变量,其一般形式是Y =β0+β1X 1+μ其中,Y 为被解释变量,X 为解释变量,β0与β1为待估参数,μ为随机干扰项。
回归分析的主要目的是要通过样本回归函数(模型)尽可能准确地估计总体回归函数(模型)。
为保证函数估计量具有良好的性质,通常对模型提出若干基本假设。
假设1:回归模型是正确设定的。
模型的正确设定主要包括两个方面的内容:(1)模型选择了正确的变量,即未遗漏重要变量,也不含无关变量;(2)模型选择了正确的函数形式,即当被解释变量与解释变量间呈现某种函数形式时,我们所设定的总体回归方程恰为该函数形式。
假设2:解释变量X 是确定性变量,而不是随机变量,在重复抽样中取固定值。
这里假定解释变量为非随机的,可以简化对参数估计性质的讨论。
假设3:解释变量X 在所抽取的样本中具有变异性,而且随着样本容量的无限增加,解释变量X 的样本方差趋于一个非零的有限常数,即∑(X i −X ̅)2n i=1n→Q,n →∞ 在以因果关系为基础的回归分析中,往往就是通过解释变量X 的变化来解释被解释变量Y 的变化的,因此,解释变量X 要有足够的变异性。
对其样本方差的极限为非零有限常数的假设,旨在排除时间序列数据出现持续上升或下降的变量作为解释变量,因为这类数据不仅使大样本统计推断变得无效,而且往往产生伪回归问题。
假设4:随机误差项μ具有给定X 条件下的零均值、同方差以及无序列相关性,即E(μi|X i)=0Var(μi|X i)=σ2Cov(μi,μj|X i,X j)=0, i≠j随机误差项μ的条件零均值假设意味着μ的期望不依赖于X的变化而变化,且总为常数零。
该假设表明μ与X不存在任何形式的相关性,因此该假设成立时也往往称X为外生性解释变量随机误差项μ的条件同方差假设意味着μ的方差不依赖于X的变化而变化,且总为常数σ2。
第五章线性回归模型的假设与检验

⎟⎟⎠⎞
于是
βˆ1 = ( X1′X1)−1 X1′y1 , βˆ2 = ( X 2′ X 2 )−1 X 2′ y2
应用公式(8.1.9),得到残差平方和
和外在因素.那么我们所要做的检验就是考察公司效益指标对诸因素的依赖关系在两个时间 段上是否有了变化,也就是所谓经济结构的变化.又譬如,在生物学研究中,有很多试验花费 时间比较长,而为了保证结论的可靠性,又必须做一定数量的试验.为此,很多试验要分配在 几个试验室同时进行.这时,前面讨论的两批数据就可以看作是来自两个不同试验室的观测 数据,而我们检验的目的是考察两个试验室所得结论有没有差异.类似的例字还可以举出很 多.
而刻画拟合程度的残差平方和之差 RSSH − RSS 应该比较小.反过来,若真正的参数不满足
(5.1.2),则 RSSH − RSS 倾向于比较大.因此,当 RSSH − RSS 比较大时,我们就拒绝假设(5.1.2),
不然就接受它.在统计学上当我们谈到一个量大小时,往往有一个比较标准.对现在的情况,我
们把比较的标准取为 RSS .于是用统计量 (RSSH − RSS) RSS 的大小来决定是接受假设
(5.1.2),还是拒绝(5.1.2). 定理 5.1.1 对于正态线性回归模型(5.1.1)
(a )
RSS
σ2
~
χ2 n− p
(b )
若假设(8.1.2)成立,则 (RSSH
− RSS)
σ2
~
χ2 n− p
得愈好.现在在模型(5.1.1)上附加线性假设(5.1.2),再应用最小二乘法,获得约束最小二乘估计
βˆH = βˆ − ( X ′X )−1 A′( A( X ′X )−1 A′)−1 ( Aβˆ − b)
第二章简单线性回归模型

4000
2037 2210 2325 2419 2522 2665 2799 2887 2913 3038 3167 3310 3510
2754
4500
2277 2388 2526 2681 2887 3050 3189 3353 3534 3710 3834
3039
5000 5500
2469 2924 2889 3338 3090 3650 3156 3802 3300 4087 3321 4298 3654 4312 3842 4413 4074 4165
Yi 与 E(Yi Xi )不应有偏差。若偏
差u i 存在,说明还有其他影响因素。
Xi
X
u i实际代表了排除在模型以外的所有因素对 Y 的影
响。 u i
◆性质 是其期望为 0 有一定分布的随机变量
重要性:随机扰动项的性质决定着计量经济分析结19
果的性质和计量经济方法的选择
引入随机扰动项 u i 的原因
特点:
●总体相关系数只反映总体两个变量 X 和 Y 的线性相关程度 ●对于特定的总体来说,X 和 Y 的数值是既定的,总体相关系
数 是客观存在的特定数值。
●总体的两个变量 X 和 Y的全部数值通常不可能直接观测,所
以总体相关系数一般是未知的。
7
X和Y的样本线性相关系数:
如果只知道 X 和 Y 的样本观测值,则X和Y的样本线性
计量经济学
第二章 一元线性回归模型
1
未来我国旅游需求将快速增长,根据中国政府所制定的 远景目标,到2020年,中国入境旅游人数将达到2.1亿人 次;国际旅游外汇收入580亿美元,国内旅游收入2500亿 美元。到2020年,中国旅游业总收入将超过3000亿美元, 相当于国内生产总值的8%至11%。
各种线性回归模型原理

各种线性回归模型原理线性回归是一种广泛应用于统计学和机器学习领域的方法,用于建立自变量和因变量之间线性关系的模型。
在这里,我将介绍一些常见的线性回归模型及其原理。
1. 简单线性回归模型(Simple Linear Regression)简单线性回归模型是最简单的线性回归模型,用来描述一个自变量和一个因变量之间的线性关系。
模型方程为:Y=α+βX+ε其中,Y是因变量,X是自变量,α是截距,β是斜率,ε是误差。
模型的目标是找到最优的α和β,使得模型的残差平方和最小。
这可以通过最小二乘法来实现,即求解最小化残差平方和的估计值。
2. 多元线性回归模型(Multiple Linear Regression)多元线性回归模型是简单线性回归模型的扩展,用来描述多个自变量和一个因变量之间的线性关系。
模型方程为:Y=α+β1X1+β2X2+...+βnXn+ε其中,Y是因变量,X1,X2,...,Xn是自变量,α是截距,β1,β2,...,βn是自变量的系数,ε是误差。
多元线性回归模型的参数估计同样可以通过最小二乘法来实现,找到使残差平方和最小的系数估计值。
3. 岭回归(Ridge Regression)岭回归是一种用于处理多重共线性问题的线性回归方法。
在多元线性回归中,如果自变量之间存在高度相关性,会导致参数估计不稳定性。
岭回归加入一个正则化项,通过调节正则化参数λ来调整模型的复杂度,从而降低模型的过拟合风险。
模型方程为:Y=α+β1X1+β2X2+...+βnXn+ε+λ∑βi^2其中,λ是正则化参数,∑βi^2是所有参数的平方和。
岭回归通过最小化残差平方和和正则化项之和来估计参数。
当λ=0时,岭回归变为多元线性回归,当λ→∞时,参数估计值将趋近于0。
4. Lasso回归(Lasso Regression)Lasso回归是另一种用于处理多重共线性问题的线性回归方法,与岭回归不同的是,Lasso回归使用L1正则化,可以使得一些参数估计为0,从而实现特征选择。
线性回归模型
线性回归模型1.回归分析回归分析研究的主要对象是客观事物变量之间的统计关系,它是建立在对客观事物进行大量试验和观察的基础上,用来寻找隐藏在那些看上去是不确定的现象中的统计规律性的方法。
回归分析方法是通过建立模型研究变量间相互关系的密切程度、结构状态及进行模型预测的一种有效工具。
2.回归模型的一般形式如果变量x_1,x_2,…,x_p与随机变量y之间存在着相关关系,通常就意味着每当x_1,x_2,…,x_p取定值后,y便有相应的概率分布与之对应。
随机变量y与相关变量x_1,x_2,…,x_p之间的概率模型为y = f(x_1, x_2,…,x_p) + ε(1)f(x_1, x_2,…,x_p)为变量x_1,x_2,…,x_p的确定性关系,ε为随机误差项。
由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
当概率模型(1)式中回归函数为线性函数时,即有y = beta_0 + beta_1*x_1 + beta_2*x_2 + …+ beta_p*x_p +ε (2)其中,beta_0,…,beta_p为未知参数,常称它们为回归系数。
当变量x个数为1时,为简单线性回归模型,当变量x个数大于1时,为多元线性回归模型。
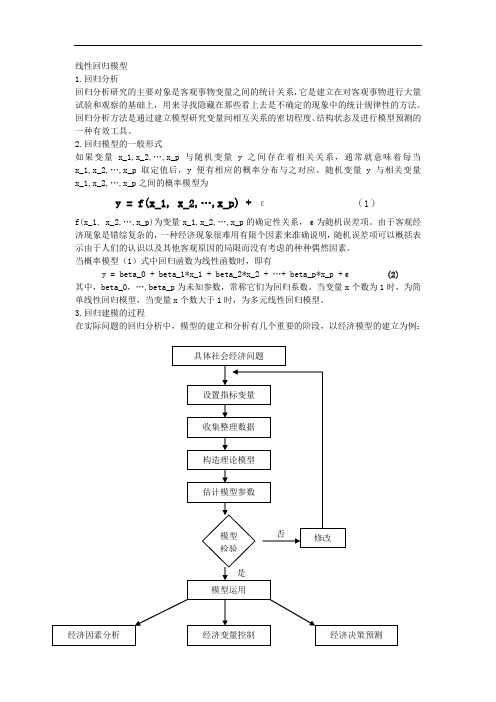
3.回归建模的过程在实际问题的回归分析中,模型的建立和分析有几个重要的阶段,以经济模型的建立为例:(1)根据研究的目的设置指标变量回归分析模型主要是揭示事物间相关变量的数量关系。
首先要根据所研究问题的目的设置因变量y,然后再选取与y有关的一些变量作为自变量。
通常情况下,我们希望因变量与自变量之间具有因果关系。
尤其是在研究某种经济活动或经济现象时,必须根据具体的经济现象的研究目的,利用经济学理论,从定性角度来确定某种经济问题中各因素之间的因果关系。
(2)收集、整理统计数据回归模型的建立是基于回归变量的样本统计数据。
一般线性回归分析案例

一般线性回归分析案例
案例背景:
在本案例中,我们要研究一个公司的运营数据,并探究它们之间的关
联性。
这家公司的运营数据包括:它的营业额(单位:万元)、产品质量
指数(QI)、客户满意度(CSI)和客户数量。
我们的目标是建立营业额
与其他变量之间的关联性模型,来预测公司未来的营业额。
资料收集:
首先,我们需要收集有关营业额、QI、CSI和客户数量的数据,以进
行分析。
从历史记录上可以收集到过去六个月的数据。
数据预处理:
接下来,我们需要对数据进行预处理,可以使用Excel进行格式整理,将数据归类分组,并计算总营业额。
建立模型:
接下来,我们就可以利用SPSS软件来建立一般线性回归模型,模型
表示为:Y=β0+β1X1+β2X2+…+βnXn。
其中,Y代表营业额,X1、
X2…Xn代表QI、CSI和客户数量等因素。
模型检验:
接下,我们要对模型进行检验,确定哪些因素与营业额有关联性,检
验使用R方和显著性检验确定系数的有效性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SPSS_迴歸:分析 → 迴歸方法 → 線性 指定 依變數 自變數
SAS_相關性: Analysis → Descriptive → Correlation Columns:指定 Correlations variables Correlation: ˇ Pearson
F
p-value
F*=MSR / MSE p
註: F* 值用於檢定 Y 與 X 諸變數是否有迴歸關聯
H 0 : 1 1 ... 0 H 1 : 0 for some i
p >α, 則結論為迴歸式不顯著。 p <α, 則結論為迴歸式顯著。
決定係數 (coef. of determination, R2)
較標準 。
R 2 1 SSE /(n p 1) SST O /(n 1)
預測變數相關性的影響:
➢ 由簡單相關係數矩陣可以看出變數間相關性之強度。 ➢ 由檢定 H0 : ρ= 0 vs. Ha : ρ ≠0 決定變數間是否相關; 若 p-值 < α,結論為顯著相關。 ➢ 兩預測變數的簡單相關係數相當大時,則其迴歸結果有共 線性的現象存在,此時迴歸式的不準度性很高,應做修正。 (p483)
第十八章 迴歸分析
一般線性迴歸模型 (GLM)
資料: (yi , x i1 , ……, x ip ) i=1,….,n 模式: Yi = β0+ β1X i1 +…….+ βpX ip+ εi,
i=1,….,n
其中
Yi β0 β1, …, βp Xij εij
為依變數 (dependent var.) 為截距 (intercept) 為係數
0.6582 0.5262
0.9902
diam; diam;
0.58814 0.76367 0.00347 1.00000 0.0211 0.0009 0.9902
age, high 對 diam的影響較強;treeno 與 diam相關性不顯著, age與 high 相關性很強,可能有共線性影響 。
多項式迴歸式; 如: E(Y) =β0+β1X1+ β2 X12
轉換變數迴歸式; 如: E(log(Y)) =β0+β1X1+β2 X2 E(Y) =β0+ β1 log(X1) + β2 X22
變異來源 迴歸 誤差
合計
變異數分析表
SS SSR SSE SSTO
df p n-p-1
n-1
MS MSR MSE
由 t-為經由其它變數
的調整後,Xi 對 Y 影響顯著。
係數之區間估計: βi 估計範圍在 bi ±tα/2;n-p-1 SE{bi}
【例 18.3b】 研究某林區樹木之年齡(X1),株高(X2),以及單位面積上 株數(X3) 對樹木直徑(Y)的影響。 Data : p481
SAS_迴歸: Analysis → Regression → Linear Columns:指定 Dependent variables Explanatory variables
變數間相關性
Pearson Correlation Coefficients, N = 15 Prob > |r| under H0: Rho=0
age
high treeno
diam;
age
1.00000 0.90793 0.12458 0.58814
age
<.0001 0.6582 0.0211
high high
0.90793 1.00000 0.17777 0.76367
<.0001
0.5262 0.0009
treeno treeno
0.12458 0.17777 1.00000 0.00347
R 2 SS 1 SS
SS
SS
說明 : 1. R2表示 Y 之總變異中由 X1,…,Xp 解釋的比例
2. 0≦R2≦1
3. R2 值的大小通常代表迴歸式解釋程度的多少。
評論 : 1. 增加 X 變數個數 , 一定使 R2 值增加 。 2. 高的 R2 值並不一定表示配套的模式適合 。 3. 有些學者建議以 X 變數個數調整後的校正判定係數( Ra2) 為比
兩個自變數的一階模式; 如: E(Y) =β0+β1X1+β2 X2 若 X1 對平均反應的效應和X2 無關, 而 X2 對平均反應的效應和 X1 無關, 則稱此兩自變數無交互作用 (no interaction), 即自變數對反應變數的效應是可加的 , 或無交互作用的。
迴歸係數的意義
參數β1:經過 X2 調整,平均反應(Y)隨 X1 之每一單位增加而改變的量。 參數β2:經過 X1 調整,平均反應(Y)隨 X2 之每一單位增加而改變的量。
兩個自變數含交互作用項的一階模式; 如: E(Y) =β0+β1X1+β2 X2 + β3X 1 X2
二次完全迴歸式; 如: E(Y)=β0+β1X1+ β2 X12 +β3 X2 + β4 X22 + β5X 1 X2 E(Y)為一曲面, 稱為 regression surface 或 response surface
考慮三個自變數的迴歸分析
Parameter Estimates
D
Variable Label
F
Intercept Intercept 1
age
age 1
high
high 1
treeno
treeno 1
Parameter Estimate 4.33469 -0.13272 0.09306
見例18.3b
相關係數與決定係數: • 相關係數量測兩變數間單純的相關性強度。 • 決定係數量測一變數與其他多個變數間的相關性強度。 • 在一個自變數問題上,決定係數是相關係數的平方值。
係數之顯著性與區間估計:
檢定第 i自變數(Xi)對依變數 (Y) 影響之顯著性:
H0 : βi = 0
Ha : βi ≠0
為預測變數 (independent var.) 為隨機誤差項 (error)
註解 :
線性迴歸模型意指其對參數為線性的方程式,有 p 個預測變數 , 可為數量或質性變數 。 E(Y) = β0+ β1X 1 +…….+ βp X p 估計式:Y= b0+ b1X 1 +…….+ bp X p
特殊模式
