3.求瞬时速度和加速度
考点一由纸带求瞬时速度和瞬时加速度
答案
• 解析 (1)由题图中所标纸带每段位移的大小,可知在相邻相等时 间内的位移差相等,可近似认为Δy=8 mm. • (2)由题图中的x轴作为时间轴,以纸带的宽度表示相等的时间间 隔T=0.1 s,每段纸带最上端中点对应v轴上的速度恰好表示每段 时间的中间时刻的瞬时速度,即vn=;因此可以用纸带的长度表 示每小段时间中间时刻的瞬时速度,将纸带上端中间各点连接起 来,可得到v-t图象,如图所示. • (3)利用图象求斜率 • 或用Δy=aT2均可 • 以求得小车的加速 • 度a=0.8 m/s2. • 答案 (1)相邻相等 • 的时间内的位移差 • 相等(2)见解析图 • (3)0.8 m/s2
• 若无法再做实验,可由以上信息推知: • (1)相邻两计数点的时间间隔为________ s; • (2)打C点时物体的速度大小为________m/s(取2位有效数 字); • (3)物体的加速度大小为____(用sA、sB、sD和f表示).
习题
• 在“测定匀变速直线运动的加速度”的实验中,用打点 计时器记录纸带运动的时间。计时器所用电源的频率为 50Hz,下图为一次实验得到的一条纸带,纸带上每相邻 的两计数点间都有四个点未画出,按时间顺序取0、1、2 3、4、5六个计数点,用米尺量出1、2、3、4、5点到0点 的距离如图所示(单位:cm)。由纸带数据计算可得计 数点4所代表时刻的即时速度大小v4=________m/s,小 车的加速度大小a=________m/s2
• • •
图实Ⅰ-9 (1)OD间的距离为________ cm. (2)图实Ⅰ-10是根据实验数据绘出的s-t2图线 (s为各计数点至同一起点的距离),斜率表示________, 其大小为________ m/s2(保留三位有效数字).
有关加速度的公式

有关加速度的公式加速度是描述物体在单位时间内速度改变的物理量。
它是一个矢量量,具有大小和方向。
在这篇文章中,将介绍加速度的定义、计算方法以及与速度和位移的关系。
首先,我们来定义加速度。
加速度(a)是速度(v)的变化率,即单位时间内速度的改变量。
具体来说,当一个物体的速度发生变化时,它产生了加速度。
加速度可以正也可以负,正表示速度增加,负表示速度减小。
通过观察一个物体在一段时间内速度的变化,我们可以计算出它的平均加速度。
平均加速度可以用以下公式计算:a=(v2-v1)/Δt其中a表示平均加速度,v2表示结束时的速度,v1表示开始时的速度,Δt表示时间间隔。
如果我们要计算瞬时加速度(即其中一时刻的加速度),我们需要缩小时间间隔至无穷小的极限。
根据微积分的原理,我们可以将时间间隔Δt趋近于0,使用微分符号(dt)表示。
此时,瞬时加速度可以用以下公式表示:a = dv / dt其中a表示瞬时加速度,dv表示无穷小时间间隔内的速度变化(即速度的微分),dt表示无穷小时间间隔(即时间的微分)。
除了上述的计算加速度的方法,还存在其他的计算加速度的公式。
这些公式可以根据不同的物理情境来使用。
一些常用的计算加速度的公式包括:1.牛顿第二定律:F=m*a在牛顿的第二定律中,力(F)与物体的质量(m)和加速度(a)成正比。
2.加速度与力的关系:a=F/m根据牛顿第二定律的公式,我们可以解出加速度。
3.圆周运动的加速度:a=(v^2)/r在圆周运动中,加速度与速度(v)的平方成正比,与半径(r)成反比。
此外,加速度还与速度和位移之间存在一些关系。
首先v=v0+a*t其中v表示最终速度,v0表示初始速度,a表示加速度,t表示时间。
其次,位移(x)与加速度(a)之间的关系可以用以下公式表示:x=x0+v0*t+1/2*a*t^2其中x表示最终位移,x0表示初始位移,v0表示初始速度,a表示加速度,t表示时间。
这个公式是基于匀加速运动的前提下得出的。
瞬时速度计算题

瞬时速度是指物体在某一瞬间的速度,可以通过以下公式计算:瞬时速度= Δs / Δt其中,Δs表示物体在时间间隔Δt内移动的距离。
如果给定了物体的位置函数s(t),则可以通过求导数来计算瞬时速度。
具体而言,对于一维运动,速度函数v(t)即为位置函数s(t)的导数。
下面是计算题:当然,我可以为您制定一些瞬时速度计算题。
以下是10个不同的问题:1. 一个汽车在t = 2秒时位于起点,t = 5秒时位于终点。
计算汽车在3秒到4秒之间的瞬时速度。
2. 一辆自行车以匀速从A点出发,经过2分钟后到达B点,距离为5公里。
计算自行车在第1分钟和第2分钟之间的瞬时速度。
3. 一个物体的位置函数为s(t) = 4t^2 - 3t + 2,其中t为时间(秒),s(t)为位置(米)。
求物体在t = 3秒时的瞬时速度。
4. 一架飞机以恒定速度飞行,已知它在t = 0时刻的位置为s(0) = 1000米,且在t = 5秒时刻的位置为s(5) = 2000米。
计算飞机在t = 4秒时的瞬时速度。
5. 一个人沿着直线道路以匀速行走,已知他从起点出发后15分钟后到达目的地,距离为2公里。
计算这个人在第7分钟和第8分钟之间的瞬时速度。
6. 一辆汽车在t = 0时刻的位置为s(0) = 10米,速度为v(t) = 3t^2 - 2t + 1(其中t 为时间,v(t)为速度)。
求汽车在t = 2秒时的瞬时速度。
7. 一个物体的位置函数为s(t) = 5t^3 - 2t^2 + 3t - 1,其中t为时间(秒),s(t)为位置(米)。
计算物体在t = 1秒时的瞬时速度。
8. 一架火箭以加速度a(t) = 2t + 3飞行,已知在t = 0时刻的速度为v(0) = 5m/s。
求火箭在t = 4秒时的瞬时速度。
9. 一个人沿着曲线路径行走,已知他在t = 0时刻的位置为s(0) = (1, 2),并且在t = 5秒时刻的位置为s(5) = (4, 6)。
打点计时器瞬时速度的计算公式

打点计时器瞬时速度的计算公式打点计时器是一种常用的测量时间的工具。
它通过记录物体经过两个或多个点的时间差来估算物体的瞬时速度。
在物理学中,瞬时速度是指物体在某一瞬间的瞬时速度。
本文将介绍打点计时器瞬时速度的计算公式以及相关内容。
一、打点计时器瞬时速度的计算公式打点计时器瞬时速度的计算公式可以通过以下步骤得出:1. 首先,选择一个起点和终点。
起点是物体开始运动的位置,终点是物体结束运动的位置。
2. 在起点和终点之间选择一个或多个点,作为记录点。
这些点的位置应尽可能接近于物体在该瞬间的位置。
3. 使用打点计时器记录物体经过每个记录点的时间。
打点计时器可以是手动的,也可以是自动的。
4. 根据记录的时间差计算物体在每个记录点的瞬时速度。
速度的计算公式为:速度=距离/时间。
5. 对于每个记录点,重复步骤4,得到物体在该点的瞬时速度。
6. 将所有记录点的瞬时速度进行整合,得到物体在整个运动过程中的瞬时速度变化。
二、打点计时器瞬时速度的应用打点计时器瞬时速度的计算公式在物理学和工程学中有着广泛的应用。
以下是一些应用实例:1. 运动学研究:打点计时器瞬时速度的计算公式可以用于研究物体的运动规律。
通过记录物体在不同时间点的瞬时速度,可以得出物体在不同时刻的加速度、位移等运动参数。
2. 交通工程:打点计时器瞬时速度的计算公式可以用于交通流量调查和交通信号优化。
通过记录车辆经过某个点的时间,可以估算出车辆在该点的瞬时速度,从而评估道路的通行能力和交通状况。
3. 运动训练:打点计时器瞬时速度的计算公式可以用于运动员的训练和竞技分析。
通过记录运动员在不同训练阶段和比赛阶段的瞬时速度,可以评估运动员的运动能力和技术水平,从而指导训练和制定竞技策略。
4. 物流管理:打点计时器瞬时速度的计算公式可以用于物流过程中的运输效率评估和优化。
通过记录货物在不同节点的瞬时速度,可以分析货物的运输时间和运输效率,从而提高物流运输的效益。
5. 航空航天:打点计时器瞬时速度的计算公式可以用于飞行器的轨迹规划和导航控制。
工程力学中的速度和加速度的计算方法

工程力学中的速度和加速度的计算方法工程力学是一门研究物体运动与受力关系的学科,其中计算速度和加速度是非常重要的内容。
在工程中,准确计算物体的速度和加速度对于分析和设计各种运动系统至关重要。
本文将介绍几种常用的速度和加速度的计算方法。
一、速度的计算方法速度是指物体在单位时间内所运动的距离。
在工程力学中,常用的速度计算方法包括瞬时速度和平均速度。
1. 瞬时速度瞬时速度是指物体在某一瞬间的速度,可以用物体位移对时间的导数来表示。
假设物体的位移函数为s(t),其中t表示时间,那么物体在时刻t的瞬时速度v(t)可以通过对位移函数求导来计算:v(t) = ds(t) / dt其中,ds(t)表示位移函数的微元,dt表示时间的微元。
通过对位移函数求导,我们可以得到物体在每个瞬间的瞬时速度。
这种方法适用于物体的位移函数是已知的情况。
2. 平均速度平均速度是指物体在某一时间段内的平均速度,可以用物体的位移和时间的比值来表示。
假设物体在时间段[t1, t2]内的位移为Δs,时间为Δt = t2 - t1,那么物体在时间段[t1, t2]内的平均速度v_avg可以用以下公式计算:v_avg = Δs / Δt平均速度适用于计算时间段内的物体平均速度,对于物体速度变化较大的情况,平均速度可能无法准确反映物体的运动状态。
二、加速度的计算方法加速度是指物体在单位时间内速度的变化量。
在工程力学中,常用的加速度计算方法包括瞬时加速度和平均加速度。
1. 瞬时加速度瞬时加速度是指物体在某一瞬间的加速度,可以用物体速度对时间的导数来表示。
假设物体的速度函数为v(t),那么物体在时刻t的瞬时加速度a(t)可以通过对速度函数求导来计算:a(t) = dv(t) / dt通过对速度函数求导,我们可以得到物体在每个瞬间的瞬时加速度。
这种方法适用于物体的速度函数是已知的情况。
2. 平均加速度平均加速度是指物体在某一时间段内的平均加速度,可以用物体的速度变化量和时间的比值来表示。
瞬时加速度的计算

A
在木板C 上,三者静置于地面,它们的质量之比是
1:2:3,设所有接触面都光滑,当沿水平面方向迅速抽
出木板C的瞬时,A和B的加速度大小分别为多大?
解:撤去木板C前, 对A、B球进行受力分析 C
B
kxmg ① Nkx2mg② kx
N
撤去木板C瞬时,A和B的重力及弹簧
A
的弹力不变 ,B物体受到的支持力突
例10. 竖直光滑杆上套有一个小球和两根弹簧,两弹簧的
M
一端各 与小球相连,另一端分别用销钉M N固定于杆上,
小球处于静止状态.若拔去销钉M的瞬间,小球的加速度
大小为12m/s2,若不拔去销钉M而拔去销钉N的瞬间,
小球的加速度
B. 22m/s2,方向竖直向下 C. 2m/s2, 方向竖直向上
瞬时加速度的计算
物体的加速度a与物体所受合外力F合瞬时对应。a为某一瞬时 的加速度,F合即为该时刻物体所受的合力。
求物体在某一时刻的瞬时加速度,关键是分析瞬时前后的受 力情况及其变化.先看不变量,再看变化量;加速度与合外力瞬 时一一对应.
轻绳(线、弹簧、橡皮绳)即其质量和重力均可视为等于零, 同一根绳(线、弹簧、橡皮绳)的两端及其中间各点的弹力大小 相等。
A
θB O
解F :O剪A断弹m簧gc前,o小t 球F受O力B 分析smi如ng图 所示.
弹簧在B处剪断瞬间, FOB立即消失, mg和FOA不变,小球将受到地面对它的 支持力N,它与重力平衡,小球受到的 FOA 合外力为FOA,根据牛顿第二定律得
aFOAgcot
m
θ FOB
mg
球和墙之间发生的是微小形变,弹簧发生的明显形变.发生微小形变产生 的弹力可以突变,发生明显形变产生的弹力发生变化需要一定的时间.
高三数学瞬时速度与瞬时加速度
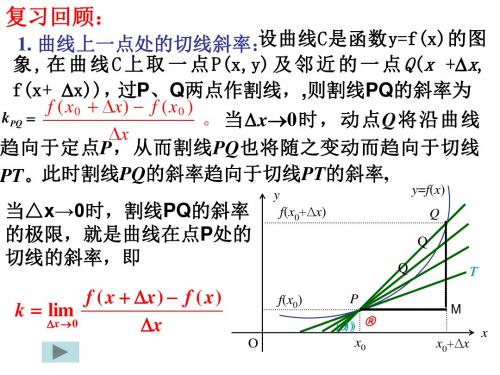
y f(x0+x) Q Q f(x0) O T
M
y=f(x) Q
f ( x + x ) f ( x ) k lim x 0 x
P
))) )a x0
x0+x
x
练习:曲线的方程为y=x2+1 ,求曲线在点P(1,2) 处的切线方程。 解:曲线在点P(1,2) 处的所用时间 的比称为平均速度。
平均速度反映物体在某一段时间段内 运动的快慢程度。那么如何刻画物体 在某一时刻运动的快慢程度?
3.1.2瞬时速度与瞬时 加速度
问题情境2:
跳水运动员从10m高跳台腾空到入水的过程 中,不同时刻的速度是不同的。假设t 秒后运动 员相对于水面的高度为H(t)=-4.9t2+6.5t+10,试 确定t=2s时运动员的速度。 (1)计算运动员在2s到2.1s(t∈[2,2.1])内的 平均速度。
v s f (t 0 + t ) f (t 0 ) a v 。 t t t
a
可作为物体在t0时刻的加速度的近似值, t 越小,
近似的程度就越好。所以当t0时,极限 就是物体在t0时刻的瞬时加速度,即
lim
t 0
v t
a
t t0
v lim t t o
H ( 2.1) H ( 2) v 13.59( m / s ) 2.1 2
(2)计算运动员在2s到2+⊿t s(t∈[2,2+⊿t])
内的平均速度。
时间区间 [2,2.1] [2,2.01] [2,2.001] [2,2.0001] [2,2.00001] [2,2.000001] 当△t→0时,
机械运动的速度和加速度计算

机械运动的速度和加速度计算机械运动是物理学中一个重要的研究领域,它涉及到速度和加速度的计算。
在这篇文章中,我们将探讨机械运动的速度和加速度的计算方法,以及它们在实际应用中的意义。
一、速度的计算速度是描述物体在单位时间内移动的距离的物理量。
在机械运动中,速度的计算可以通过两种方法进行:平均速度和瞬时速度。
平均速度是指物体在某段时间内移动的总距离与总时间的比值。
例如,如果一辆汽车在2小时内行驶了200公里,那么它的平均速度就是200公里/2小时=100公里/小时。
瞬时速度是指物体在某一瞬间的瞬时速度。
它可以通过计算物体在该瞬间的位移与时间的比值来获得。
例如,一辆汽车在某一瞬间的位移是10米,所花费的时间是0.1秒,那么它的瞬时速度就是10米/0.1秒=100米/秒。
在实际应用中,速度的计算对于控制和优化机械运动非常重要。
例如,在汽车行驶过程中,通过计算汽车的速度可以控制油门的大小,以达到安全和节能的目的。
二、加速度的计算加速度是描述物体在单位时间内速度变化的物理量。
在机械运动中,加速度的计算可以通过两种方法进行:平均加速度和瞬时加速度。
平均加速度是指物体在某段时间内速度变化的总量与总时间的比值。
例如,如果一辆汽车在5秒内从静止加速到60公里/小时,那么它的平均加速度就是(60公里/小时-0公里/小时)/5秒=12公里/小时^2。
瞬时加速度是指物体在某一瞬间的瞬时加速度。
它可以通过计算物体在该瞬间的速度变化与时间的比值来获得。
例如,一辆汽车在某一瞬间的速度变化是10米/秒,所花费的时间是1秒,那么它的瞬时加速度就是10米/秒/1秒=10米/秒^2。
加速度的计算在机械运动的控制和优化中也非常重要。
例如,在电梯的运行过程中,通过计算电梯的加速度可以控制电梯的平稳性和乘坐舒适度。
三、速度和加速度的关系速度和加速度之间存在着密切的关系。
根据物理学的基本原理,速度的变化率就是加速度。
换句话说,加速度是速度的导数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
一、求瞬时速度
求解依据:做匀变速直线运动的物体,一段时间中间时刻的瞬时速度等于这段时间内的平均速度。
表达式:v v t =2
平均速度的两种表达形式 t x
v = 20t v v v +=
求中间点的瞬时速度 t x
v t =
2
例如 OB
OB A t x v = 求端点的瞬时速度(以O 点为例) (1)先求A v 和B v ,然后根据 2
B
O A v v v +=
求出A v (2)先求A v 和加速度a ,OA A O at v v -=
相比两种解法,第一种简单。
二、求加速度依据:做匀变速直线运动的物体,在相邻相等时间间隔内的位移差为恒量。
表达式 2
a T x =∆ 逐差法求加速度
4段 21132T a x x =- 2
2242T a x x =- 2
2
1a a a +=
6段 2
1143T a x x =- 22253T a x x =- 23363T a x x =- 3
3
21a a a a ++=
1.偶数段逐差法求加速度
例 如图所示,某同学在做“研究匀变速直线运动”实验中,由打点计时器得到表示小车运动过程的一条清晰纸带,纸带上两相邻计数点的时间间隔为T =0.10s ,其中x 1=7.05cm 、x 2=7.68cm 、x 3=8.33cm 、x 4=8.95cm 、
x 5=9.61cm 、x 6=10.26cm ,则A 点处瞬时速度的大小是_______m/s ,小车运动的加速度计算表达式为________________,加速度的大小是_______m/s 2(计算结果保留两位有效数字)。
2.奇数段变偶数段逐差法求加速度
(01年全国)一打点计时器固定在斜面上某处,一小车拖着穿过打点计时器的纸带从斜面上滑下,如图所示.打出的纸带的一段如图所示.
已知打点计时器使用的交流电频率为50H Z ,利用纸带图给出的数据可求出小车下滑
的加速度a = . 4.00m/s 2 (3.90~4.10 m/s 2)
2
3.已知不相邻的两段相等时间内的位移求加速度
一条残缺的纸带如图所示,打点计时器所用交流电频率为50 Hz 。
在所选纸带上取某点为0号计数点,然后每5个点取一个计数点,根据测量数据及其标记符号计算加速度。
3.12m/s 2 练习
1.(04上海)用打点计时器研究物体的自由落体运动,得到如图一段纸带,测得AB=7.65cm , BC=9.17cm. 已知交流电频率是50Hz ,则打B 点时物体的瞬时速度为 m/s.如果实验测出的重力加速度值比公认值偏小,可能的原因是 .
2.10 下落过程中存在阻力等
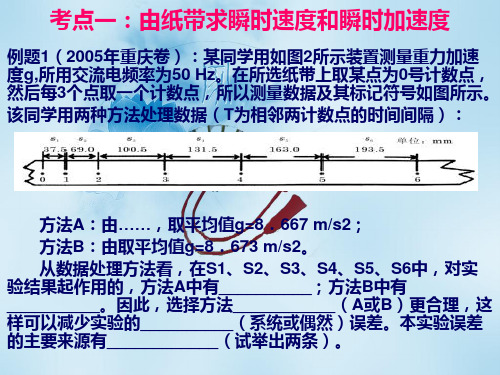
2.(06重庆)某同学用题图所示装置测量重力加速度g ,所用交流电频率为50 Hz 。
在所选纸带上取某点为0号计数点,然后每3个点取一个计数点,所以测量数据及其标记符号如题图所示。
该同学用两种方法处理数据(T 为相邻两计数点的时间间隔): 方法A :由,2121T S S g -=
,2232T S S g -=…,,2
565T
S S g -=取平均值g =8.667 m/s 2
;方法B :由,321
41T S S g -=
,32252T S S g -=,32
363T
S S g -=取平均值g =8.673 m/s 2。
从数据处理方法看,在S 1、S 2、S 3、S 4、S 5、S 6中,对实验结果起作用的,方法A 中
有__________;方法B 中有__________。
因此,选择方法___________(A 或B )更合理,这样可以减少实验的__________(系统或偶然)误差。
本实验误差的主要来源有____________(试举出两条)。
S 1 S 6;S 1 S 2 S 3 S 4 S 5 S 6 B 偶然 阻力(空气阻力 限位孔的阻力 复写纸的阻力等) 交流电频率波动 长度测量 数据处理方法等。
3.在测定匀变速直线运动的加速度实验中,用打点计时器记录纸带运动的时间计时器所用电源的频率为50Hz .图为做匀变速直线运动时,小车带动的纸带上记录的一些点,在每相邻的两点中间都有四个点未画出.按时间顺序取0、1、2、3、4、5六个点,用米尺量出1、2、3、4、5点到0点的距离分别是(单位:cm) ,由此可以得到小车的加速度大小为 m/s 2,方向为 。
(结果保留三位有效数字)
1.50 与运动方向相反
4.图为“验证机械能守恒定律”的装置图,实验中得到几条较为理想的纸带。
已知每条纸带上每5个点取一个计数点,即两计数点之间的时间间隔为0.1s ,依打点先后编为0,1,2,3,4,…….由于不小心,纸带都被撕断了,如图所示,根据给出的A 、B 、C 、D 四段纸带回答:
(1)在B 、C 、D 三段纸带中选出从纸带A 上撕下的那段应该是 .(填字母)
(2)纸带A 上,打点1时重物的速度 m/s.(结果保留三位有效数字) (1)C (2)3.47
x 1 x 6。
