FLUENT中壁面函数和近壁面模型
湍流流动的近壁处理详解

壁面对湍流有明显影响。
在很靠近壁面的地方,粘性阻尼减少了切向速度脉动,壁面也阻止了法向的速度脉动。
离开壁面稍微远点的地方,由于平均速度梯度的增加,湍动能产生迅速变大,因而湍流增强。
因此近壁的处理明显影响数值模拟的结果,因为壁面是涡量和湍流的主要来源。
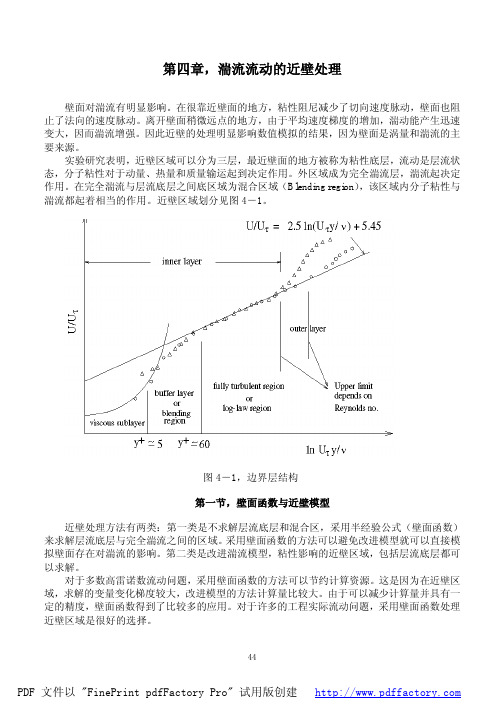
实验研究表明,近壁区域可以分为三层,最近壁面的地方被称为粘性底层,流动是层流状态,分子粘性对于动量、热量和质量输运起到决定作用。
外区域成为完全湍流层,湍流起决定作用。
在完全湍流与层流底层之间底区域为混合区域(Blending region),该区域内分子粘性与湍流都起着相当的作用。
近壁区域划分见图4-1。
图4-1,边界层结构第一节,壁面函数与近壁模型近壁处理方法有两类:第一类是不求解层流底层和混合区,采用半经验公式(壁面函数)来求解层流底层与完全湍流之间的区域。
采用壁面函数的方法可以避免改进模型就可以直接模拟壁面存在对湍流的影响。
第二类是改进湍流模型,粘性影响的近壁区域,包括层流底层都可以求解。
对于多数高雷诺数流动问题,采用壁面函数的方法可以节约计算资源。
这是因为在近壁区域,求解的变量变化梯度较大,改进模型的方法计算量比较大。
由于可以减少计算量并具有一定的精度,壁面函数得到了比较多的应用。
对于许多的工程实际流动问题,采用壁面函数处理近壁区域是很好的选择。
如果我们研究的问题是低雷诺数的流动问题,那么采用壁面函数方法处理近壁区域就不合适了,而且壁面函数处理的前提假设条件也不满足。
这就需要一个合适的模型,可以一直求解到壁面。
FLUENT提供了壁面函数和近壁模型两种方法,以便供用户根据自己的计算问题选择。
4.1.1壁面函数FLUENT 提供的壁面函数包括:1,标准壁面函数;2,非平衡壁面函数两类。
标准壁面函数是采用Launder and Spalding [L93]的近壁处理方法。
该方法在很多工程实际流动中有较好的模拟效果。
4.1.1.1 标准壁面函数根据平均速度壁面法则,有:**1ln()U Ey k = 4-1其中,1/41/2*/p pw U C k U μτρ≡,1/41/2*p pC k y y μρμ≡,并且k =0.42,是V on Karman 常数;E =9.81,是实验常数;p U 是P 点的流体平均速度;p k 是P 点的湍动能;p y 是P 点到壁面的距离;μ是流体的动力粘性系数。
「胡言」壁面函数与近壁面处理

「胡言」壁面函数与近壁面处理Fluent提供了众多的近壁面处理方法,这里简单扒一扒。
1y 的基本概念在临近壁面位置,法向速度非常大的梯度。
在非常小的壁面法向距离内,速度从相对较大的值下降到与壁面速度相同。
因此对于该区域内流场的计算,通常采用两种方式:(1)利用壁面函数法;(2)加密网格,利用壁面模型法。
对于这两类方法的选取,可以通过对于这两类方法的选取,可以通过y 来体现。
如图所示为近壁面位置无量纲速度分布情况。
图中横坐标所表示为无量纲壁面距离y ,纵坐标为无量纲速度u 。
其中:从图中看出,近壁面区域可分为3个区间:•粘性子层(Viscous sublayer region):黏性子层是一个紧贴壁面的极薄层,在该区域中,粘性力在动量、质量、能量交换过程中起主导地位,湍流剪切应力在该区域可以忽略不计。
该区域中的流动可看成层流流动,在平行于壁面方向上的速度分量沿壁面法向方向呈线性分布。
在该区域中,y <5。
•对数律层(log law region):对数律层位于近壁区域的最外层,在该区域中,湍流剪切应力占主导地位,粘性力几乎可以忽略,流动为充分发展湍流状态,流速近似成对数分布。
该区域中,y >60。
•过渡层(Buffer layer region):过渡层位于粘性子层与对数律层之间,该区域中粘性力与湍流剪切应力相当,流动状态极其复杂,难以用模型进行表达。
由于过渡层非常薄,工程中常将其合并到对数律层进行处理。
过渡层中y 在5~60之间。
对于近壁区域求解,主要集中在粘性子层的求解上,主要有两种方式:1、利用壁面模型直接求解粘性子层若想要求解粘性子层,则需要保证y 值小于1(建议接近1)。
由于y 直接影响第一层网格节点位置,因此对于求解粘性子层的情况,需要非常细密的网格,通常要求有10~20层边界层网格。
2、利用壁面函数近似处理。
对于湍流模型,需要选择低雷诺数湍流模型(如k-omega模型)。
FLUENT中文学习资料-建模与数值分析
4.1.1 壁面函数 FLUENT 提供的壁面函数包括:1,标准壁面函数;2,非平衡壁面函数两类。标准壁面函 数是采用 Launder and Spalding [L93]的近壁处理方法。该方法在很多工程实际流动中有较好的 模拟效果。 4.1.1.1 标准壁面函数 根据平均速度壁面法则,有:
U* = 1 ln( Ey* ) k
Gk ≈ τ w
τw ∂U =τw 1/ 4 1/ 2 ∂y kρC µ k p y p
4-5
耗散率不需要求解输运方程,直接用如下公式计算:
εp =
3/ 4 3/ 2 Cµ kp
ky p
4-6
以上所介绍的标准壁面函数是 FLUENT 程序的默认设置。标准壁面函数包含了定常剪切 和局部平衡假设条件,如果壁面有很强的压力梯度,并且很强的非平衡性,则我们可以选择非 平衡壁面函数方法。 4.1.1.2 非平衡壁面函数
* ( y* < yT )
4-3
* ( y* > yT )
其中 P 的计算采用下列公式[L93]
Pr Prt 4-4 − 1 Prt Pr & ′′ 壁面热流; Tp 近邻 其中, k f 是流体导热系数; ρ 是流体密度; c p 是流体定压比热; q π /4 A P= sin(π / 4) k
47
PDF 文件以 "FinePrint pdfFactory Pro" 试用版创建
衡壁面函数则把壁面函数方法推广到有压力梯度和非平衡的流动过程中。但是,如果流动情况 偏离了壁面函数的理想条件,则壁面函数就不合适了。如:高粘度流体流过狭窄的通道,壁面 由渗透的流动,大压力梯度并导致边界层分离的流动,由强体积力的流动,近壁区域三维性很 强的流动问题。 如果要成功解决上述问题, 必须采用改进模型的方法来模拟近壁流动。 FLUENT 提供了双层区模型(Two-Layer Zonal Model ) 。 4.1.1.3 双层区模型
Fluent物理模型概述

Fluent物理模型概述Fluent为各种不可压缩和可压缩、层流和湍流流体流动问题提供了全面的模拟能力。
可以进行稳态或瞬态分析。
在Fluent中,大量传输现象的数学模型(如传热和化学反应)与复杂几何模型的能力相结合。
Fluent应用实例包括:工艺设备层流非牛顿流;叶轮机械与汽车发动机部件的共轭传热;电站锅炉中煤粉燃烧的分析;外部空气动力学;通过压缩机、泵和风扇的流量;以及气泡塔和流化床中的多相流。
为了模拟工业设备和过程中的流体流动和相关的运输现象,本教程提供了各种有用的特性。
包括多孔介质、集总参数(风扇和热交换器)、流向周期性流动和传热、涡流和移动参考系模型。
模型的移动参照系系包括对单个或多个参照系建模的能力。
此外,还提供了一种时间精确的滑动网格方法,用于叶轮机械应用中的多级建模,例如,计算时间平均流场的混合平面模型。
Fluent中另一组非常有用的模型是一组自由面和多相流模型。
这些可用于分析气-液、气-固、液-固和气-液-固流动。
针对这类问题,Fluent提供了(VOF)、混合模型、欧拉模型以及离散相模型(DPM)。
DPM对分散相(粒子、液滴或气泡)进行拉格朗日轨迹计算,包括与连续相耦合。
多相流的例子包括明渠流、喷雾、沉降、分离和空化。
在Fluent模型中,鲁棒性和准确性是湍流模型至关重要的组成部分。
所提供的湍流模型具有广泛的适用性,而且还包括其他物理现象的影响,如浮力和压缩性。
通过使用壁面函数和分区处理模型来求解近壁区域。
各种传热模式可以模拟,包括自然对流、强迫对流、混合对流、多孔介质等。
辐射模型和一些子模型都是可以使用的,还可以计算燃烧。
Fluent的一个特别的优点是它能够使用多种模型来模拟燃烧现象,包括涡流耗散模型和概率密度函数模型。
还有许多其他模型对于反应流应用非常有用,包括煤和液滴燃烧、表面反应和污染物形成模型。
总之,fluent提供了丰富的模型让你来模拟你所感兴趣的问题。
对于所有流动,Fluent求解质量和动量守恒方程。
fluent基本物理模型介绍

基本物理模型本章介绍了FLUENT所提供的基本物理模型以及相关的定义和使用。
基本物理模型概述FLUENT提供了从不可压到可压、层流、湍流等很大范围模拟能力。
在FLUENT中,输运现象的数学模型与所模拟的几何图形的复杂情况是结合在一起的。
FLUENT应用的例子包括层流非牛顿流的模拟,涡轮机和汽车引擎的湍流热传导,锅炉内煤炭粉碎机的燃烧,可压射流,空气动力外流,以及固体火箭发动机的可压化学反应流。
为了与工业应用相结合,FLUENT提供了很多有用的功能。
如多孔介质,块参数(风扇和热交换),周期性流动和热传导,涡流,以及移动坐标系模型。
移动参考系模型可以模拟单一或者多个参考系。
FLUENT还提供了时间精度滑动网格方法以及计算时间平均流动流场的混合平面模型,滑动网格方法在模拟涡轮机多重过程中很有用。
FLUENT中另一个很有用的模型是离散相模型,这个模型何以用于分析喷雾和粒子流。
,多项流模型可以用于预测射流的破散以及大坝塌陷之后流体的运动,气穴现象,沉淀和分离。
湍流模型是FLUENT中很重要的一部分,湍流会影响到其它的物理现象如浮力和可压缩性。
湍流模型提供了很大的应用范围,而不需要对特定的应用做出适当的调节,而且它涵括了其它物理现象的影响,如浮力和可压缩性。
通过使用扩展壁面函数和区域模型,它可以对近壁面的精度问题有很好的考虑。
各种热传导模式可以被模拟,其中包括具有或不具有其它复杂性如变化热传导的,多孔介质的自然的、受迫的以及混合的对流。
模拟相应介质的辐射模型及子模型的设定通常可以将燃烧的复杂性考虑进来。
FLUENT一个最强大的功能就是它可以通过耗散模型或者和概率密度函数模型来模拟燃烧现象。
对于燃烧应用十分有用的其它模型也可以在FLUENT中使用,其中包括碳和液滴的燃烧以及污染形成模型。
连续性和动量方程对于所有的流动,FLUENT都是解质量和动量守恒方程。
对于包括热传导或可压性的流动,需要解能量守恒的附加方程。
FLUENT壁面函数的选择

FLUENT壁面函数的选择壁面函数问题1、无论是标准k—ε模型、RNGk—ε模型,还是Realizable k—ε模型,都是针对充分发展的湍流才有效的,也就是说,这些模型均是高Re数的湍流模型。
它们只能用于求解处于湍流核心区的流动。
而壁面函数是对近壁区的半经验描述,是对某些湍流模型的补充(近壁区对整体流动影响较大和低雷诺数Re的情况),通过壁面函数法和低Re数k—ε模型与标准k—ε模型和RNGk—ε模型配合,成功解决整个整个管道的流动计算问题。
2、在壁面区,流动情况变化很大。
解决这个问题目前有两个途径:一、是不对粘性影响比较明显的区域(粘性底层和过渡层)进行求解,而是用一组半经验的公式(即壁面函数)将壁面上的物理量与湍流核心区内的相应物理量联系起来。
这就是壁面函数法。
在划分网格的时候,不需要在壁面区加密,只需要把第一个节点布置在对数律成立的区域内,即配置在湍流充分发展区域。
如果要用到壁面函数的话,在define---modle--viscous面板里有near wall treatment一项。
可以选择标准壁面函数、不平衡壁面函数等。
二、是采用低Re数的k—ε模型来求解粘性底层和过渡层,此时需要在壁面区划分比较细密的网格,越靠近壁面,网格越细。
当局部湍流的Re数小于150时,就应该使用低Re数的k—ε模型。
总结:相对于低Re数的k—ε模型,壁面函数法计算效率高,工程实用性强。
但当流动分离过大或近壁面流动处于高压之下时,不是很理想。
在划分网格的时候,需要在壁面的位置设置边界层网格,原因也是如此。
为什么要用壁面函数??就是因为,k-epsilon模型中,k的boundary condition已知,在壁面上为零,而epsilon的boundary condition 在壁面上为一未知的非零量,如此如何来解两方程模型???所以,我们就需要壁面函数来确定至少第一内节点上的值,当然也包括壁面上的值。
实际上就是把epsilon方程的boundary condition放到了流体内部。
FLUENT中壁面函数-vs-近壁面模型

FLUENT中壁面函数 vs 近壁面模型在数值模拟中,如何有效处理固体壁面附近的流场一直是一个比较棘手的问题.一个稍复杂一点算例,简单更换一下壁面处理方法对计算结果都有较显著的影响,在缺少实验数据验证和流场涉及多种流动形态时,如何选择行之有效和经济合理的算法是一个艰难的考验,一般需要仔细考察流场与算法机理之间的契合度。
边界层分为层流边界层和湍流边界层,层流边界层为最靠近壁面或者层流流动时的边界层,对于一般湍流流动,两种边界层都有。
按参数分布规律划分时,边界层分为内区和外区,内区分为:粘性底层,Laminar sublayer(y+<5,Amano的三层模型),粘性起主导作用,在粘性支层中与壁面平行的速度与离开壁面的距离成线性关系(陶文铨,《数值传热学》);过渡层,Buffer region(5〈y+<30),湍流作用与粘性作用共同作用;对数律层,Log—law region(30〈y+),湍流起主导作用,无量纲速度与温度分布服从对数分布律;外区:惯性力主导,上限取决于雷诺数图1 边界层结构(引自中科大Fluent讲稿)FLUENT中有两种方法处理近壁面区域:A.壁面函数法。
不求解粘性影响内部区域(粘性子层及过渡层),使用一种称之为“wallfunction”的半经验方法去计算壁面与充分发展湍流区域之间的粘性影响区域.采用壁面函数法,省去了为壁面的存在而修改湍流模型.Fluent中的standard wallfunctions, scalable wall functions,Non—Equilibrium wall functions和Enhanced wall treatment都属于壁面函数法的模型。
B。
近壁模型法。
修改湍流模型以使其能够求解近壁粘性影响区域,包括粘性底层.此处使用的方法即近壁模型.(近壁模型不需要使用壁面函数,如一些低雷诺数模型,K—W 湍流模型是一种典型的近壁湍流模型)。
Fluent学习笔记之壁面网格与yplus的选择

壁面网格与y+的选择(参考官方手册ANSYS_Fluent_Theory_Guide19.2)大量的实验表明,近壁区域可以大致细分为三层。
在最内层,称为“粘性子层”,流动几乎是层流的,(分子)粘性在动量和热量或质量传递中起主导作用。
在被称为“湍流充分发展层”的外层,湍流起着主要作用。
最后,在粘性子层和湍流充分发展层之间有一个过渡区域,叫做“缓冲层”或“混合区”,在这里分子粘度和湍流的影响是同等重要的其中y+定义为y+≝ρuτy/μ其中uτ定义为uτ=√τw/ρ“壁面函数法”与“近壁模型法”传统的近壁区域建模方法有两种。
在第一种方法中,不解决粘度影响的内部区域(粘性子层和缓冲层)。
相反,被称为“壁面函数”的半经验公式被用来连接壁面和全紊流区域之间的粘滞区域。
使用壁面函数避免了需要修改湍流模型来考虑壁面的存在。
在另一种方法中,对湍流模型进行了修改,使粘滞区通过网格一直到壁面(包括粘滞子层)进行求解。
为了便于讨论,我们将其称为“近壁建模”方法。
这两种方法如图4.14所示。
图4.14: ANSYS Fluent中的近壁面处理所有壁面函数(scalable wall function除外)的主要缺点是在壁面法向网格细化的情况下,计算结果会恶化。
Y+小于15会逐渐导致壁面剪应力和壁面传热的误差增大。
但这已经是几年前的工业标准,ANSYS Fluent已经能够提供更先进的壁面方程,允许一致的网格细化没有恶化的结果。
对所有基于ω方程的湍流模型都采用这种与y+无关的公式。
对于基于ε-方程的模型,Menteri-Lechner和增强壁面处理(Enhanced Wall Treatment, EWT)具有相同的作用。
对y+不敏感的壁面处理也是Spalart-Allmaras模型的默认值,它允许你不用考虑近壁面的y+值而运行此模型。
只有当边界层的整体分辨率足够时,才能得到高质量的边界层数值结果。
这个要求实际上比实现特定的y+值更重要。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FLUENT中壁面函数和近壁面模型
技术邻作者:Jessica_4643
文章所包含相关领域及技术点:壁面函数、近壁面模型、fluent
在数值模拟中,如何有效处理固体壁面附近的流场一直是一个比较棘手的问题。
一个稍复杂一点算例,简单更换一下壁面处理方法对计算结果都有较显著的影响,在缺少实验数据验证和流场涉及多种流动形态时,如何选择行之有效和经济合理的算法是一个艰难的考验,一般需要仔细考察流场与算法机理之间的契合度。
边界层分为层流边界层和湍流边界层,层流边界层为最靠近壁面或者层流流动时的边界层,对于一般湍流流动,两种边界层都有。
按参数分布规律划分时,边界层分为内区和外区,内区分为:
粘性底层,Laminar sublayer(y+<5,Amano的三层模型),粘性起主导作用,在粘性支层中与壁面平行的速度与离开壁面的距离成线性关系(陶文铨,《数值传热学》);
过渡层,Buffer region(5<y+<30),湍流作用与粘性作用共同作用;
对数律层,Log-law region(30<y+),湍流起主导作用,无量纲速度与温度分布服从对数分布律;
外区:惯性力主导,上限取决于雷诺数
图1边界层结构(引自中科大Fluent讲稿)
FLUENT中有两种方法处理近壁面区域:
A.壁面函数法。
不求解粘性影响内部区域(粘性子层及过渡层),使用一种称之为“wall function”的半经验方法去计算壁面与充分发展湍流区域之间的粘性影响区域。
采用壁面函数法,省去了为壁面的存在而修改湍流模型。
Fluent中的standard wa ll functions,scalable wall functions,Non-Equilibrium wall functions和En hanced wall treatment都属于壁面函数法的模型。
B.近壁模型法。
修改湍流模型以使其能够求解近壁粘性影响区域,包括粘性底层。
此处使用的方法即近壁模型。
(近壁模型不需要使用壁面函数,如一些低雷诺数模型,K-W湍流模型是一种典型的近壁湍流模型)。
所有壁面函数(除scalable壁面函数外)的最主要缺点在于:沿壁面法向细化网格时,会导致数值结果恶化。
当y+小于15时,将会在壁面剪切力及热传递方面逐渐导致产生无界错误。
然而这是若干年前的工业标准,如今ANSYS FLUENT采取了措施提供了更高级的壁面格式,以允许网格细化而不产生结果恶化。
而y+无关的格式是默认的基于w方程的低湍流模型,其采用网格求解的方式计算近壁面粘性区域。
对于基于epsil on方程的模型,增强壁面函数(EWT)提供了相同的功能。
这一选项同样是SA模型所默认的,该选项允许用户使其模型与近壁面y+求解无关。
只有当所有的边界层求解都达到要求了才可能获得高质量的壁面边界层数值计算结果。
这一要求比单纯的几个Y+值达到要求更重要。
使用近壁模型法时,覆盖边界层的最小网格数量在10层左右,最好能达到20层。
还有一点需要注意的是,提高边界层求解常常可以取得稳健的数值计算结果,因为只需要细化壁面法向方向网格。
对于非结构网格,建议划分10~20层棱柱层网格以提高壁面边界层的预测精度。
棱柱层厚度应当被设计为保证有15层或更多网格节点。
另外,棱柱层大于边界层厚度是必要的,否则棱柱层会限制边界层的增长。
这可以在获得计算结果后,通过查看边界层中心的最大湍流粘度,该值提供了边界层的厚度(最大值的两倍位置即边界层的边)。
一些建议:(1)对于epsilon方程,使用enhanced壁面函数。
(2)若壁面函数有助于epsilon方程,则可以使用scalable壁面函数。
(3)对于基于w方程的模型,使用默认的增强壁面函数。
(4)SA模型,使用增强壁面处理。
文章后续内容可到技术邻平台继续观看,进入技术邻后在页面最上面搜索文章的原标题即可观看。
