第12章习题解答
运营管理第6版习题与参考答案_第12章

习题与参考答案_第12章一、名词解释1、作业计划答案:把企业的作业任务分解为短期的具体任务,规定每个环节(如车间、工段、生产线和工作站)、每个单位时间(周、日、班或小时)的具体任务,并组织计划的实施。
答案解析:略。
难易程度:易。
知识点:作业计划。
2、排序答案:确定各个作业在加工中心的处理顺序。
答案解析:略。
难易程度:易。
知识点:排序。
3、先到先服务准则(FCFS)答案:优先选择最早进入可排序列的作业,也就是按照作业到达的先后顺序进行加工。
答案解析:略。
难易程度:中。
知识点:先到先服务准则(FCFS)。
4、最短作业时间准则(SPT)答案:优先选择作业时间最短的作业。
答案解析:略。
难易程度:中。
知识点:最短作业时间准则(SPT)。
5、最早交货期准则(EDD)答案:优先选择完工期限最紧的作业。
答案解析:略。
难易程度:中。
知识点:最早交货期准则(EDD)。
6、最短松驰时间准则(SST)答案:优先选择松弛时间最短的作业。
答案解析:略。
难易程度:中。
知识点:最短松驰时间准则(SST)。
7、最长剩余作业时间准则(MWKR)答案:优先选择余下作业时间最长的作业。
答案解析:略。
难易程度:中。
知识点:最长剩余作业时间准则(MWKR)。
8、最短剩余作业时间准则(LWKR)答案:优先选择余下作业时间最短的作业。
答案解析:略。
难易程度:中。
知识点:最短剩余作业时间准则(LWKR)。
9、最多剩余作业数准则(MOPNR)答案:优先选择余下作业数最多的工件。
答案解析:略。
难易程度:中。
知识点:最多剩余作业数准则(MOPNR)。
10、最小临界比准则(SCR)答案:优先选择临界比最小的作业。
答案解析:略。
难易程度:中。
知识点:最小临界比准则(SCR)。
11、随机准则(Random)答案:随机地挑选出一项作业。
答案解析:略。
难易程度:中。
知识点:随机准则(Random)。
12、生产调度答案:生产调度部门,行使调度权力,协助各级行政领导指挥生产,协调各部门工作,处理生产中出现的问题。
组织胚胎学习题 第12章

第12章免疫系统一、A型题1.关于胸腺,哪项错误( )A.是培育T细胞的中枢淋巴器官B.在抗原刺激下,胸腺细胞增殖分化成T细胞C.培育中的胸腺细胞,只有5%能分化成初始T细胞D.胸腺小体仅分布于髓质2.胸腺上皮细胞的主要功能是( )A.向胸腺细胞呈递抗原信息B.形成网状纤维,构成胸腺支架C.分泌胸腺激素,培育T淋巴细胞D.分泌细胞因子,保护胸腺细胞3.血-胸腺屏障的血管周隙内常有( )A.白细胞B.胸腺细胞C.巨噬细胞D.成纤维细胞4.胸腺小体位于( )A.皮质和髓质B.皮质与髓质交界处C.髓质D.皮质5.关于胸腺,哪项错误( )A.属于中枢淋巴器官B.胸腺实质分为皮质和髓质C.髓质内有胸腺小体D.皮质内有许多淋巴小结6.淋巴结内毛细血管后微静脉主要分布于( )A.浅层皮质B.皮质与髓质交界处C.髓索D.副皮质区二、C型题A. T淋巴细胞C.两者皆是B.B淋巴细胞D.两者皆非7.在骨髓内早期分化( )8.在胸腺内早期分化( )9.表面有特异性抗原受体( )10.效应细胞分泌抗体( )11.类型多,分工细()三、X型题12.下列哪些细胞属于抗原提呈细胞( )A.巨噬细胞B.郎格汉斯细胞C.交错突细胞D.网状细胞13.属于单核吞噬细胞系统的有( )A.肺巨噬细胞B.小胶质细胞C.破骨细胞D.网状细胞14.血液内淋巴细胞进入淋巴组织的通道是( )A.脾血窦B.淋巴结的毛细血管后微静脉C.脾的边缘窦D.胸腺小体四、名词解释1.B细胞(B-lymphocyte)2.胸腺依赖区(thymus dependent area)五、论述题、1.试述单核吞噬细胞系统的组成、分布和功能特点。
2.简述淋巴细胞再循环的途径和意义。
【参考答案】一、A型题:1.B2.C3. C4. C5. D6.D二、C型题:7. B 8. A 9.C 10.B 11. A三、X型题:12. ABC 13. ABC 14. ABC四、名词解释1. B细胞(B-lymphocyte)即骨髓依赖淋巴细胞。
机械课后习题答案第12章习题及解答

(2) 由表 14.8 查得 fT=0.95,载荷负荷平稳,由表 14.9 查得 fF=1.0,对球轴承取=3, 对
滚子轴承=10/3。将以上有关数据代入下式
Lh
106 60n
fT C fPF
对球轴承
Lh
106 0.95 22800 3 60 1000 5880
833.1
h,
不满足要求,
再选 6408 (Cr=50200, C0r=37800),得
T 9.55106 P 9.55106 2.6 64661.4 N·mm
n
384
Ft 2T1 129322.8 2917.5 N d1 44.326
Fr 1107.5 N
Fa 864.2 N
(2) 计算轴向力
R2V=457.98 R1V=649.5 R1H= R2H =1458.75
由机械零件设计手册得 30307 圆锥滚子轴承的 Cr=71200 N, C0r=50200 N , Y = 1.9, e=0.31 表 14.12 可知圆锥滚子轴承轴承的内部轴向力 SA、SB 为
S1= R1/2Y=584/(2×1.9)=153.6 N S2= R2/2Y=1776/(2×1.9)=467.4 N
h
所选轴承型号为 N410 合适。
12.15一齿轮轴由一对 30206 轴承支承,支点间的跨距为 200 mm,齿轮位于两支点的中央。
已知齿轮模数 mn=2.5 mm,齿数 z1=17,螺旋角=16.5,传递功率 P=2.6 kW,齿轮轴
的转速 n=384r/min。试求轴承的额定寿命。
解: (1) 计算齿轮的作用力
每个轴承的径向载荷 R=5880 N,载荷平稳,工作温度 t=125C,预期寿命 Lh=5000 h,
《大学物理学》习题解答(第12章 静电场中的导体和电介质)(1)

(2)两输电线的电势差为 U
xR
E dl
R
Ed x
d R ln 0 R
(3)输电线单位长度的电容 C
U
0 / ln
d R d 0 / ln 4.86 1012 F R R
【12.9】半径为 R1 的导体球被围在内半径为 R2 、外半径为 R3 、相对电容率为 r 的介质球壳内,它们是同 球心的。若导体带电为 Q ,则导体内球表面上的电势为多少? 【12.9 解】先求各区域电场 (1)
Q 4 0 R3
( R3 r )
B 球壳为等势体,其电势为
V
R3
E dr
Q 4 0
R3
r
dr
2
【12.2】一导体球半径为 R1,外罩一半径为 R2 的同心薄导体球壳,外球壳所带总电荷为 Q,而内球的电势为 V0.求此系统的电势和电场分布。 【12.2 解】已知内球电势为 V0 ,外球壳带电 Q 。 (1)先求各区域的电场强度:设内球带电荷 q 。由高斯定理,有
E
U
z
2R
( 1 )一根带电 的输电线在两线之间、距其轴心 x 处 p 点的场强为
x
dx
p
E i 2 0 x
另一根带电 的输电线在 p 点产生的电场强度为
x
E
2 0 ( d x )
i
p 点的总电场强度为
E E E
d R
1 1 ( )i 2 0 x d x
E1 0
(r R1 ) ( R1 r R2 ) 4 r 2 D Q , D 0 r E3
第12章 习题(带答案)

9、垄断厂商利润最大化时( A C P=MR=MC; P>MR=MC;
10、完全垄断厂商的平均收益曲线为直线时,边际收益曲线也是直线。边际收益曲线的 斜率为平均收益曲线斜率的( A )。 A 2 倍; B 1/2 倍; C 1 倍; D 4 倍。
11、若一个管理机构对一个垄断厂商的限价正好使经济利润消失,则价格要等于( C )。 A C 边际收益; 平均成本; B D D B D 边际成本; 平均可变成本。 )。 取得最大利润; 上述情况都可能发生。 D )。
dTC 2Q 40 . dQ
该厂商实行三级价格歧视时利润最大化的原则可以写为 MR1=MR2=MC. 于是: 关于第一个市场: 根据 MR1=MC,有: 120-20Q1=2Q+40 关于第二个市场: 根据 MR2=MC,有: 7Q2=10 即 22Q1+2Q2=80
1 1 ),得 116=138( 1 )解得 ed ≈6 ed ed
所以,厂商长期均衡时主观需求曲线 d 上的需求的价格点弹性 ed ≈6. (3)令该厂商的线性的主观需求 d 曲线上的需求的函数形式 P=A-BQ,其中,A 表示该线 性需求 d 曲线的纵截距,-B 表示斜率.下面,分别求 A 值和 B 值. 根据线性需求曲线的点弹性的几何意义,可以有 ed
A.如果在某一行业中存在许多厂商,则这一市场是完全竞争的 B.如果厂商所面临的需求曲线是向下倾斜的,则这一市场是不完全竞争的 C.如果行业中所有厂商生产相同的产品,且厂商的数目大于 1,则这个市场是不完全竞争的 D.如果某一行业中有不止一家厂商,他们都生产相同的产品,都有相同的价格,则这个市场 是完全竞争的 2、垄断厂商面临的需求曲线是( A 向下倾斜的; A )。 B 向上倾斜的;
电工与电子技术第十二章习题详解(陶桓齐)华中科技大学出版社
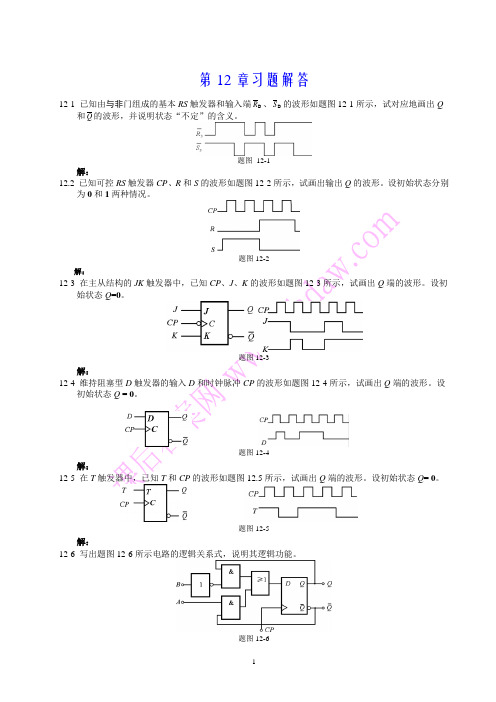
第12章习题解答12-1 已知由与非门组成的基本RS触发器和输入端D R、D S的波形如题图12-1所示,试对应地画出Q 和Q的波形,并说明状态“不定”的含义。
题图12-1解:12.2 已知可控RS触发器CP、R和S的波形如题图12-2所示,试画出输出Q的波形。
设初始状态分别为0和1两种情况。
题图12-2解:12-3 在主从结构的JK触发器中,已知CP、J、K的波形如题图12-3所示,试画出Q端的波形。
设初始状态Q=0。
题图12-3解:12-4 维持阻塞型D触发器的输入D和时钟脉冲CP的波形如题图12-4所示,试画出Q端的波形。
设初始状态Q = 0。
题图12-4解:12-5 在T触发器中,已知T和CP的波形如题图12.5所示,试画出Q端的波形。
设初始状态Q= 0。
题图12-5解:12-6 写出题图12-6所示电路的逻辑关系式,说明其逻辑功能。
题图12-6解:逻辑关系为:Q D AQ BQ==+所以其功能为JK触发器。
12-7 如题图12-7所示的电路和波形,试画出D端和Q端的波形。
设初始状态Q= 0。
题图12-7解:12-8 将主从型JK触发器转换为T'触发器有几种方案?画出外部连线图。
解:12-9 电路如题图12-9所示。
画出Q0端和Q1端在六个时钟脉冲CP作用下的波形。
设初态Q1=Q0= 0。
题图12-9解:12-10 用题图12.10(a)所给器件构成电路,并在示波器上观察到如图12.10(b)所示波形。
试问电路是如何连接的?请画出逻辑电路图。
(a) (b)题图12-10解:12-11 已知如题图12.11(a)所示电路的各输入端信号如题图12-11(b)所示。
试画出触发器输出端Q0和Q1的波形。
设触发器的初态均为0。
(a) (b)题图12-11解:12-12 已知电路和时钟脉冲CP及输入端A的波形如题图12-12所示,试画出输出端Q、1Q的波形。
假定各触发器初态为1。
(a ) (b )题图12-12解:12-13 已知题图12-13(a )所示电路中输入A 及CP 的波形如题图12-13(b )所示。
无机化学(上册):第12章 氧化还原与电化学 习题与答案

第12章氧化还原与电化学习题与详细答案1.计算下列化合物中右上角带“*”元素的氧化态:KCl*O3,NaCl*O,H2O*2,O*3,S*8,C*60,KO*2,Na2S*2O3,Cr*2O72-,S*4O62-,N*H4+,N*2H4,Fe*3O4,Ni*(CO)4,Na[Co*(CO)4],H[Mn*(CO)5],[Fe*(CN)6]4-,[Fe(N*CS)6]3-.解:+5 +1 -1 0 0 0 -½ +2 +6 +2.5 -3KCl*O3,NaCl*O,H2O*2,O*3,S*8,C*60,KO*2,Na2S*2O3,Cr*2O72-,S*4O62-,N*H4+,-2 +8/3 0 -1 -1 +2 -3N*2H4,Fe*3O4,Ni*(CO)4,Na[Co*(CO)4],H[Mn*(CO)5],[Fe*(CN)6]4-,[Fe(N*CS)6]3-.2.用“氧化数法”配平以下列各氧化还原反应的方程式;(8)-(15)同时用“离子-电子法”配平:(1)AgNO3(s) → Ag(s) + NO2(g) + O2(g)(2)(NH4)2Cr2O7(s) → N2(g) + Cr2O3(s)(3)H2O2(aq) → H2O(l) + O2(g)(4)Cu(s) + HNO3(稀)→ Cu(NO3)2 + NO(g)(5)CuS(s) + HNO3(浓)→ CuSO4 + NO2(g)(6)H2S(g) + H2SO4(浓)→ S(s) + SO2(g)(7)C(s) + H2SO4(浓)→ CO2(g) + SO2(g) + H2O(8)SO2(g) + MnO4-→ Mn2+ + SO42-(9)Cr2O72- + H2O2→ Cr3+ + O2(g)(10)CrO42- + CN-→ Cr(OH)3(s) + OCN-(11)Cl2(g) + CN- + OH-→ Cl- + OCN-(12)I2(s) + OH-→ I- + IO3-(13)I- + IO3-→ I2(s) + H2O(14)I2(s) + S2O32-→ I- + S4O62-(15)NaBiO3(s) + Mn2+ + H+→ Bi3+ + MnO4-解:(1)氧化数+1 +5 -2 0 +4 -2 02 AgNO3(s) = 2 Ag(s) + 2 NO2(g) + O2(g)(2)(NH4)2Cr2O7(s) = N2(g) + Cr2O3(s) + 4 H2O(3)2 H2O2(aq) = 2 H2O(l) + O2(g)(4)3 Cu(s) + 8 HNO3(稀)= 3 Cu(NO3)2 + 2 NO(g) + 4 H2O(5)CuS(s) + 8 HNO3(浓)= CuSO4 + 8 NO2(g) + 4 H2O(6)H2S(g) + H2SO4(浓)= S(s) + SO2(g) + 2 H2O(7)C(s) + 2 H2SO4(浓)→ CO2(g) + 2 SO2(g) + 2 H2O(8)“氧化数法”:5 SO2(g) + 2 MnO4- + 2 H2O = 2 Mn2+ + 5 SO42- + 4 H+“离子-电子法”:5 SO2(g) + 10 H2O = 5 SO42- + 20 H+ + 10 e2 MnO4- + 10 e + 16 H+ = 2 Mn2+ + 5 SO42-两式相加,得:5 SO2(g) + 2 MnO4- + 2 H2O = 2 Mn2+ + 5 SO42- + 4 H+(9)“氧化数法”:Cr2O72- + 3 H2O2 + 8 H+ = 2 Cr3+ + 3 O2(g) + 7 H2O“离子-电子法”:3 H2O2 = 3 O2(g) + 6 H+ + 6 eCr2O72- + 14 H+ + 6 e = 2 Cr3+ + 7 H2O两式相加,得:Cr2O72- + 3 H2O2 + 8 H+ = 2 Cr3+ + 3 O2(g) + 7 H2O (10)“氧化数法”:2 CrO42- + 3 CN- + 5 H2O = 2 Cr(OH)3(s) + 3 OCN- + 4 OH-“离子-电子法”:3 CN- + 6 OH- = 3 OCN- + 3 H2O + 6 e2 CrO42- + 8 H2O + 6 e = 2 Cr(OH)3(s) +10 OH-两式相加,得:2 CrO42- + 3 CN- + 5 H2O = 2 Cr(OH)3(s) + 3 OCN- + 4 OH- (11)“氧化数法”:Cl2(g) + CN- + 2 OH- = 2 Cl- + OCN- + H2O“离子-电子法”:CN- + 2 OH- = OCN- + H2O + 2 eCl2(g) + 2 e = 2 Cl- + H2O两式相加,得:Cl2(g) + CN- + 2 OH- = 2 Cl- + OCN- + H2O(12)“氧化数法”:3 I2(s) + 6 OH- = 5 I- + IO3- + 3 H2O“离子-电子法”:I2(s) + 12 OH- = 2 IO3- + 6 H2O + 10 e5 I2(s) + 10 e = 10 I-两式相加,约简系数,得:3 I2(s) + 6 OH- = 5 I- + IO3- + 3 H2O(13)“氧化数法”:5 I- + IO3- + 6 H+ = 3 I2(s) + 3 H2O“离子-电子法”:10 I- = 5 I2(s) + 10 e2 IO3- + 12 H+ + 10 e = I2(s) + 6 H2O两式相加,约简系数,得:5 I- + IO3- + 6 H+ = 3 I2(s) + 3 H2O(14)“氧化数法”:I2(s) + 2 S2O32- = 2 I- + S4O62-“离子-电子法”:2 S2O32- = S4O62- + 2 eI2(s) + 2 e = 2 I-两式相加,得:I2(s) + 2 S2O32- = 2 I- + S4O62-(15)“氧化数法”:5 NaBiO3(s) + 2 Mn2+ + 14 H+ = 5 Bi3+ + 5 Na+ + 2 MnO4- + 7 H2O “离子-电子法”:2 Mn2+ + 8 H2O= 2 MnO4- + 16 H+ + 10 e5 NaBiO3(s) + 30 H+ + 10 e = 5 Bi3+ + 5 Na+ + 15 H2O两式相加,得:5 NaBiO3(s) + 2 Mn2+ + 14 H+ = 5 Bi3+ + 5 Na+ + 2 MnO4- + 7 H2O 3.含氰(CN-)工业废水可以用漂白粉[有效成份Ca(ClO)2]或氯气或H2O2在碱性介质中进行氧化处理后排放,写出各反应方程式。
大学物理课后习题答案(上下册全)武汉大学出版社 第12章 习题解答

第12章 习题与答案12-1 在真空中波长为λ的单色光,在折射率为n 的透明介质中从A 沿某路径传播到B ,若A 、B 两点相位差为3π,则此路径AB 的光程为[ ]A. 1.5λ.B. 1.5λ/n .C. 1.5n .D. 3λ. [答案:A ]12-2 平行单色光垂直照射到薄膜上,经上下两表面反射的两束光发生干涉,若薄膜的厚度为e ,并且n 1<n 2>n 3,λ1为入射光在折射率为n 1的媒质中的波长,则两束反射光在相遇点的相位差为[ ]A. 2πn 2e / ( n 1λ1).B. 4πn 1e / ( n 2λ1)] +π.C. 4πn 2e / ( n 1λ1) ]+π.D. 4πn 2e / ( n 1λ1).[答案: C ]12-3 两块平玻璃构成空气劈形膜,左边为棱边,用单色平行光垂直入射.若上面的平玻璃以棱边为轴,沿逆时针方向作微小转动,则干涉条纹的[ ]A. 间隔变小,并向棱边方向平移.B. 间隔变大,并向远离棱边方向平移.C. 间隔不变,向棱边方向平移.D.间隔变小,并向远离棱边方向平移. [答案: A ]12-4 用劈尖干涉法可检测工件表面缺陷,当波长为λ的单色平行光垂直入射时,若观察到的干涉条纹如题12-4图所示,每一条纹弯曲部分的顶点恰好与其左边条纹的直线部分的连线相切,则工件表面与条纹弯曲处对应的部分[ ]A. 凸起,且高度为4λ.B. 凸起,且高度为2λ.C. 凹陷,且深度为2λ.D. 凹陷,且深度为4λ.[答案: C ]12-5 若把牛顿环装置(都是用折射率为1.52的玻璃制成的)由空气搬入折射率为1.33的水中,则干涉条纹[ ]A .中心暗斑变成亮斑. B. 间距变大. C. 间距变小. D. 间距不变. [答案: C ]题12-4图12-6 在光栅光谱中,假如所有偶数级次的主极大都恰好在单缝衍射的暗纹方向上,因而实际上不出现,那么此光栅每个透光缝宽度a 和相邻两缝间不透光部分宽度b 的关系为[ ] A. =3a b . B. =2a b . C. =a b . D. =0.5a b [答案: C ]12-7 对某一定波长的垂直入射光 衍射光栅的屏幕上只能出现零级和一级主极大,欲使屏幕上出现更高级次的主极大,应该[ ]A. 换一个光栅常数较小的光栅.B. 换一个光栅常数较大的光栅.C. 将光栅向靠近屏幕的方向移动.D. 将光栅向远离屏幕的方向移动.[答案: B ]12-8如果两个偏振片堆叠在一起,且偏振化方向之间夹角为60°,光强为I 0的自然光垂直入射在偏振片上,则出射光强为[ ]A. I 0 / 8.B. I 0 / 4.C. 3 I 0 / 8.D. 3 I 0 / 4.[答案: A ]12-9一束自然光自空气射向一块平板玻璃(如题12-9图),设入射角等于布儒斯特角i 0,则在上表面的出射光2是[ ]A. 自然光.B. 线偏振光且光矢量的振动方向平行于入射面.C. 线偏振光且光矢量的振动方向垂直于入射面.D. 部分偏振光.[答案: C ]12-10相干光的必要条件为________________________,________________________,________________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第12章习题解答12.1 求解下列本征值问题的本征值和本征函数1(1)()()0;(0)0,()0(2)()()0;(0)0,()0(3)()()0;()0,()0X x X x x x l X x X x x x l X x X x x a x b λλλ'''+===''''+===''+===【答案 2222121(1)(π),0,1,2,;()sin π22(2)(π),0,1,2,;()cos ππ(3)(π),1,2,;()sin ()n n n n n n n n n X x xl l n nn X x x l l n n n X x x a b a b aλλλ++=========---】12.2 长为l 的杆,一端固定;另一端受力0F 而伸长,求解放手杆的振动.【 答案 022011()π()π8122(1)cos sin π(21)n n n at n x F l YS n l l ∞=++-+∑】12.3 长为l 的的弦,两端固定,弦中张力为T . 在距一端为0x 的一点以力0F 把弦拉开,然后突然撤除此力,求弦的振动. 【答案初始位移=00()/(), (0)F l x x lT x x -<<,00000221()/()()2π1π(,)sin sin cosπn F x l x lT x x l F l n x n x n at u x t T n l l lπ∞==-<<=∑】12.4 一个长宽各为a 的方形膜,边界固定,膜的振动方程为 222222()0; (0,0)u u ux a y a t x y∂∂∂-+=<<<<∂∂∂2v 试求方形膜振动的本征频率.【答案,1,2,3,nm n m ν==】 12.5 求解细杆导热问题,杆长l ,两端保持为零度,初始温度分布为20|()/t u bx l x l ==-.【答案 2(21)π[]33081(21)πsin π(21)k a tl k b k x e k l+∞-=++∑】12.6 一根均匀弦两端固定在0,x x l ==处.假设初始时刻速度为零,而在初始时刻弦的形状是一条顶点为(/2,)l h 的抛物线。
试求弦振动的位移.【答案 33032(21)π(21)π(,)cos sin (21)πn h n at n xu x t n l l ∞=++=+∑】 12.7 解定解解问题22222, (0,),0 (1)(0,)(,)0 0 (2)(,0)(), x u ua x l t t x u t u l t t u x x ϕ∂∂=∈>∂∂==>= (3)(,0)(), (0,) (4)t u x x x l ψ⎧⎪⎪⎪⎨⎪⎪⎪⎩=∈解: 用分离变量法解,令(,)()() (5)u x t T t X x = 并将(5)代入(1),(2),得固有值问题 ''()()0 (6)(0)'()0 (7)X x X x X X l λ+=⎧⎨==⎩及 2()() (8)T t a T t λ+ 解(6)—(7)得 221()(), 0,1,2,2n n x n lλπ+== 21()sin , 0,1,2,2n n X x x n lπ+==将n λ代入(8)解得2121cossin , (0,1,2,)22n n n n n T C at D at n l lππ++=+=∴ (,)()() (0,1,2,)n n n u x t T t X x n ==叠加得212121(,)cossin sin (9)222n n n n n n u x t C at D at x l l l πππ∞=+++⎛⎫=+⎪⎝⎭∑ 令(9)满足(3),(4)得21(,0)()sin(10)2n n n u x x C x lϕπ∞=+==∑ 02121(,0)()sin (11)22t nn n n u x x Da x l lψππ∞=++==∑ 由Fourier 展式的唯一性知,n C 与212nn D a lπ+分别为()x ϕ与()x ψ关于021sin 2n n x l π∞=+⎧⎫⎨⎬⎩⎭的展开式系数. ∴ l0221 ()sin d (12) 2n n C x x x l lϕπ+=⎰002221()sin d (21)2421()sin d (0,1,2,) (13)(21)2ln ll n D x x xn a l l n x x x n n a lψππψππ+=⋅++==+⎰⎰所以,带有系数(12)~(13)的(9)即为定解问题(1)~(4)的形式解。
12.8 解定解问题22222110, 0, 02 (1)() 0<2 (2) r Ru u ur R r r r r u f θπθθθπ=⎧∂∂∂++=<<≤<⎪∂∂∂⎨⎪=≤⎩解: 这是圆域上的Laplace 方程第一边值问题.设(1)具有变量分离形式解(,)()() (3)u r F r θθ=Φ将(3)代入(1)得221''()()''()1()()r F r F r r F r rθλθ+Φ==-Φ- 令则有 ''()()0 (4)()(2)0 (5)θλθθθπΦ+Φ=⎧⎨Φ=Φ+=⎩及2''()'()()0 (6)(0) (7)r F r rF r F r F λ⎧+-=⎪⎨<+∞⎪⎩这里条件(5)是由区域的形状及(,)u r θ的单值性决定的。
即(,2)(,)u r u r θπθ+=成立。
((0,]r R ∈)。
而条件(7)是由问题的物理意义决定的,即(,)u r θ在圆心处有界。
问题(4)~(5)称为定解问题(1)~(2)的固有值问题。
解(4)~(5)得:2,0,1,2,n n n λ==0()1,()cos sin (1,2,)n n n a n b n n θθθθΦ=Φ=+=(,n n a b 为任意常数)将n λ代入(6)~(7)解得000()' (A'0F r A =≠为任意常数) n ()' (A'0 1,2nn n F r A r n =≠=为任意常数)∴ 0000(,)()()',2n A u r F r A θθ=Φ==(,)()()'(cos sin )n n n n n n n u r F r A r a n b n θθθθ=Φ=+cos sin (1,2,)nnn n A r n B r n n θθ=+=叠加得01(,)cos sin (8)2n n n n n n A u r A r n B r n θθθ∞==++∑令(8)满足(2)的得01(,()cos sin 2n n n n n A u R f A R n B R n θθθθ∞===++∑右端即为()f θ的Fourier 完全展示。
由于()f θ定义在[]02π,上,故应有(2)(),f f θπθ+=于是有2001() (9)A f d πθθπ=⎰201()cos (10)n n A f nd R πθθπ=⎰201()sin (11)n nB f nd R πθθπ=⎰(1,2,)n =带有系数(9)~(11)的(8)即为定解问题(1)~(2)的解。
()()()y x u y x u y x u ,,,21+=.12.9 解定解问题222220110 0, 0 (1)0 0<r<R (2)() r R u u ur R r r r r u u u f θθαθαθθ===∂∂∂++=<<<<∂∂∂=== 0<< (3)θα⎧⎪⎪⎪⎨⎪⎪⎪⎩解: 注意到方程就关于未知函数为线性齐次的,且在0θθα==与边界上具有线性齐次边界条件,故可用分离变量法求解。
为此,设(1)有非零解(,)()() (4)u r F r θθ=Φ 代入(1)并分离变量得2''()'()''()()()r F r rF r F r θλθ+Φ==--Φ 令即兴 2''()'()()0 (5)r F r rF r F r λ+-=令(4)满足(2)得(0)()0 (7) αΦ=Φ= (6)与(7)联立得''()()0 (6)(0)()0 (7) θλθαΦ+Φ=⎧⎨Φ=Φ=⎩注意问题的物理意义知,在0r =处,应满足条件 (0,,(0) (5)'u F θ<+∞有界故(5)与(5)'联立2''()'()()0 (5)(0) (5)'r F r rF r F r F λ⎧+-=⎪⎨<+∞⎪⎩(5)是一个二群众监督齐次欧拉方程,所带条件(5)'不具可叠加性。
故应由(6)~(7)确定λ值,即(6)(7)为定解问题(1)~(3)的固有值问题。
解解(6)~(7)得固有值 2()(), 1,2,n n x n πλα==固有函数系()sin , 1,2, n n n πθθαΦ==将2()()n n x πλα=代入(5),解(5)~(5)':令tr e =。
在(5)中变换自变量为t ,得22222d 0 (1,2,)d n n F n F n t πα-==其通解为2222(1,2,)n n ttn n n F C eD en ππαα-=+=即() (1,2,)n n n n n F r C r D rn ππαα-=+=由条件(5)'得0.n D =∴ () (1,2,)n n n F r C r n πα==于是 (,)sin (1,2,)n n n n u r C r n παπθθα==叠加这得1(,)sin(8)n n n n u r C r παπθθα∞==∑令(8)满足(3)得 1(,)sin () (9)n nn n u R C R f παπθθθα∞===∑(9)表明n n C R πα即为()f θ在[]0,α上Fourier 正弦展式的系数,即2()sin d (1,2,)n n n f C R n απαπθθθαα==⎰∴ 02()sind (1,2,)n n n C f n R απαπθθθαα==⎰代入(8)即得定解问题(1)~(3)的解。
12.10 解定解问题12221222212110 ,02 (1)()0 (2)() r r u u ur r r r r u f u f ρρρρθπθθθ==∂∂∂++=<<≤<∂∂∂=== 0<2 (3)θπ⎧⎪⎪⎪⎨⎪≤⎪⎪⎩解:这是圆环域12r ρρ<<上Laplacd 方程第一边值问题。
