第十二章相关与回归分析练习题
第12章 线性相关与回归

所以当计算出样本相关系数r后,
应对r是否来自ρ=0的总体作假设
检验,以判断两变量的总体是否有 直线相关关系。常用的假设检验方 法为t检验,其t值的计算公式为:
r 0 r tr 2 sr 1 r n2 n2
例10.2 对例10.1求得的r值作假
设检验。
1)建立假设并确定检验水准
如果我们主要目的是分析两变 量间是否存在直线相关关系,这时 我们就应进行x和y之间的线性相关
分析。如:我们要分析女大学身高
与体重之间的关系,通过散点图发
现两者有直线趋势,可对两个变量
进行线性相关分析。
直线相关(linear correlation): 是指两变量间存在的关系为直线关 系。又称为简单相关(simple
230 .455 r 0.8012 1000 .909 82.727
即表示男青年身高与前臂长之间存在正 相关关系。但还需作假设检验
三、相关系数的假设检验
相关系数r是根据样本资料计算
出来的,它是总体相关系数ρ的估
计值。若从ρ=0的总体中进行随机
抽样,抽取的样本相关系数也可能
不等于0,这是抽样误差所致。
(3,8365)和(21,36.06)两点,就 可做出本例的直线回归方程的图示。
ˆ 注意:直线必须通过( x ,y )和
纵轴上(0,a)两点,因此,这两点可
以用来核对回归直线绘制是否正确。
四、回归系数的假设检验
抽样研究中,计算出的回归系数 b为样本回归系数,故应考虑假设检 验的问题。即使我们从x、y的总体
r
( x x )( y y ) ( x x ) ( y y)
22Biblioteka l xy l xxl yy
社会统计学第十二章 相关与回归分析

2. 相关方向:正相关和负相关 所谓正相关关系是指一个变量的值增加时,另一变
量的值也增加。例如,受教育水平越高找到高薪水工作的 机会也越大。而负相关关系是指一个变量的值增加时,另 一变量的值却减少。例如,受教育水平越高,理想子女数 目越少。要强调的是,只有定序以上测量层次的变量才分 析相关方向,因为只有这些变量的值有高低或多少之分。 至于定类变量,由于变量的值并无大小、高低之分,故定 类变量与其他变量相关时就没有正负方向了。
父母智力 组合
优+优
优+劣 一般+一般
劣+劣
子女智力 子女智力
优秀
一般
71.6 25.4
33.6 42.7
18.6 66.9
5.4 34.4
子女智力 低下
3.0 23.7 14.5 60.2
通过列联表研究定类变量之间的关联性,这 实际上是通过相对频数条件分布的比较进行的。 如果对不同的X,Y的相对频数条件分布不同,且 和Y的相对频数边际分布不同,则两变量之间是 相关的。而如果变量间是相互独立的话,必然存 在着Y的相对频数条件分布相同,且和它的相对 频数边际分布相同。后者用数学式表示就是
r×c相对频数联合分布列联表
控制X,Y相对频数条件分布列联表
控制Y,X相对频数条件分布列联表
[例A1]试把下表所示的频数分布列联表,转 化为自变量受到控制的相对频数条件分布列联 表,并加以相关分析。
投票行为
受教育程度X
Y
大学以 大学以
FY
上
下
投票
160
129
289
弃权
7
61
68
合计:FX 167
r×c相对频数分布列联表的一般形式
在相对频数分布列联表中,各数据为各分类
12章 多元线性回归

统计学第十二章 多元线性回归一. 选择题1. 在多元线性回归分析中,t 检验是用来检验( ) A 总体线性关系的显著性 B.各回归系数的显著性 C.样本线性关系的显著性 D .H 0:β1=β2=…βk =02.在多元线性回归模型中,若自变量x i 对因变量y 的影响不显著,那么它的回归系数 βi 的取值( )A.可能为0B.可能为1C.可能小于0 D 可能大于13.在多元线性回归方程 y i ˆ=βˆ0+x 11ˆβ+x 22ˆβ+…+xkkβˆ中,回归系数βˆi表示( ) A.自变量x i 变动1个单位时,因变量y 的平均变动额为βˆiB.其他变量不变的条件下,自变量x i 变动1个单位时,因变量y的平均变动额为βˆiC.其他变量不变的条件下,自变量x i 变动1个单位时,因变量y的变动总额为βˆiD.因变量y 变动1个单位时,因变量x i 的变动总额为βˆi4.设自变量的个数为5个,样本容量为20。
在多元回归分析中,估计标准误差的自由度为( )A.20B.15C.14D.18 5.在多元回归分析中,通常需要计算调整的多重判定系数R a2,这样可以避免的值()A. 由于模型中自变量个数的增加而越来越接近1B. 由于模型中自变量个数的增加而越来越接近0C. 由于模型中样本容量的增加而越来越接近0D. 由于模型中样本容量的增加而越来越接近16.在多元线性回归分析中,如果F检验表明线性关系显著,则意味着()A.在多个变量中至少有一个自变量与因变量之间的线性关系显著B.所有的自变量与因变量之间的线性关系都显著C.在多个变量中至少有一个自变量与因变量之间的线性关系不显著D.所有的自变量与因变量之间的线性关系都不显著7.在多元线性回归分析中,如果t检验表明回归系数βi不显著,则意味着()A.整个回归方程的线性关系不显著B.整个回归方程的线性关系显著C.自变量x i与因变量之间的线性关系不显著D.自变量x i与因变量之间的线性关系显著8.设多元线性回归方程为Yˆ=βˆ0+x11ˆβ+x22ˆβ+…+xkkβˆ,若自变量x i的回归系数βˆi的取值接近0,这表明()A.因变量y对自变量ix的影响不显著B.因变量y对自变量ix的影响显著C.自变量ix对因变量y的影响不显著D.自变量x对因变量y的影响显著i9.一家出租汽车公司为确定合理的管理费用,需要研究出租车司机每天的收入(元)与他的行驶时间(小时)、行驶的里程(公里)之间的关系,为此随机调查了20位出租车司机,根据每天的收入(y)、行驶时间(x1)和行驶的里程(x2)的有关数据进行回归,得到下面的有关结果(a=0.05)根据上表计算的判定系数为()A. 0.9229B. 1.1483C. 0.3852D. 0.851610. 一家出租汽车公司为确定合理的管理费用,需要研究出租车四级每天的收入(元)与他的行驶时间(小时)、行驶的里程(公里)之间的关系,为此随机调查了20位出租车司机,根据每天的收入(y)、行驶时间(x1)和行驶的里程(x2)的有关数据进行回归,得到下面的有关结果(α=0.05)根据上表计算的估计标准误差为()A. 306.18B. 17.50C. 16.13D. 41.9311. 一家出租汽车公司为确定合理的管理费用,需要研究出租车司机每天的收入(元)与他的行驶时间(小时)、行驶的里程(公里)之间的关系,为此随机调查了20位出租车司机,根据每天的收入(y)、行驶时间(x1)和行驶的里程(x2)的有关数据进行回归,得到下面的有关结果(α=0.05)根据上表计算的用于检验线性关系的统计量F=()A. 306.18B. 48.80C. 5.74D. 41.9312.一家产品销售公司在30个地区设有销售分公司。
回归分析练习题及参考答案
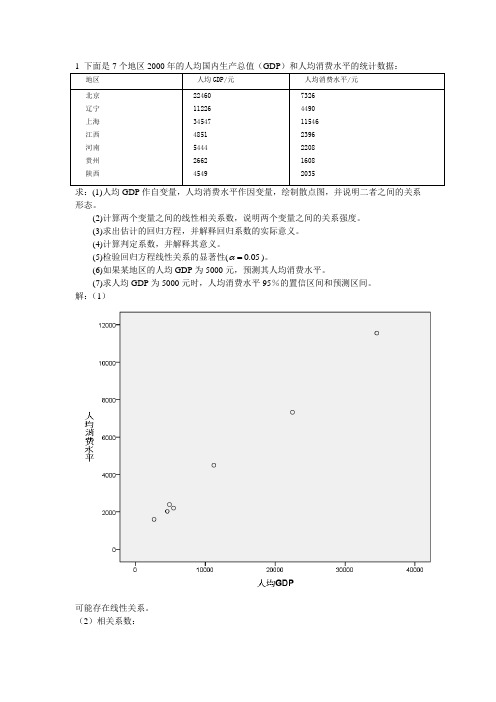
求:(1)人均GDP 作自变量,人均消费水平作因变量,绘制散点图,并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数,说明两个变量之间的关系强度。
(3)求出估计的回归方程,并解释回归系数的实际意义。
(4)计算判定系数,并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP 为5000元,预测其人均消费水平。
(7)求人均GDP 为5000元时,人均消费水平95%的置信区间和预测区间。
解:(1)可能存在线性关系。
(2)相关系数:(3)回归方程:734.6930.309y x=+回归系数的含义:人均GDP没增加1元,人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 (常量)734.693 139.540 5.265 0.003人均GDP(元)0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
模型摘要模型R R 方调整的R 方估计的标准差1 .998(a) 0.996 0.996 247.303a. 预测变量:(常量), 人均GDP(元)。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(5)F 检验:回归系数的检验:t 检验注意:图标不要原封不动的完全复制软件中的图标,要按规范排版。
系数(a)模型 非标准化系数标准化系数t 显著性B 标准误 Beta1(常量) 734.693 139.540 5.2650.003 人均GDP (元)0.3090.0080.99836.4920.000a. 因变量: 人均消费水平(元)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%(6)某地区的人均GDP 为5000元,预测其人均消费水平为 734.6930.30950002278.693y =+⨯=(元)。
(完整版)第十二章相关和回归分析练习试题

第十二章相关与回归分析一、填空1.如果两变量的相关系数为0,说明这两变量之间_____________。
2.相关关系按方向不同,可分为__________和__________。
3.相关关系按相关变量的多少,分为______和复相关。
4.在数量上表现为现象依存关系的两个变量,通常称为自变量和因变量。
自变量是作为(变化根据)的变量,因变量是随(自变量)的变化而发生相应变化的变量。
5.对于表现为因果关系的相关关系来说,自变量一般都是确定性变量,因变量则一般是(随机性)变量。
6.变量间的相关程度,可以用不知Y与X有关系时预测Y的全部误差E1,减去知道Y与X有关系时预测Y的联系误差E2,再将其化为比例来度量,这就是(削减误差比例)。
7.依据数理统计原理,在样本容量较大的情况下,可以作出以下两个假定:(1)实际观察值Y围绕每个估计值cY是服从();(2)分布中围绕每个可能的cY值的()是相同的。
7.已知:工资(元)倚劳动生产率(千元)的回归方程为xyc8010+=,因此,当劳动生产率每增长1千元,工资就平均增加 80 元。
8.根据资料,分析现象之间是否存在相关关系,其表现形式或类型如何,并对具有相关关系的现象之间数量变化的议案关系进行测定,即建立一个相关的数学表达式,称为(回归方程),并据以进行估计和预测。
这种分析方法,通常又称为(回归分析)。
9.积差系数r是(协方差)与X和Y的标准差的乘积之比。
二、单项选择1.欲以图形显示两变量X和Y的关系,最好创建(D )。
A 直方图 B 圆形图 C 柱形图 D 散点图2.在相关分析中,对两个变量的要求是( A )。
A 都是随机变量B 都不是随机变量C 其中一个是随机变量,一个是常数D 都是常数3. 相关关系的种类按其涉及变量多少可分为( )。
A. 正相关和负相关B. 单相关和复相关C. 线性相关和非线性相关D. 不相关、不完全相关、完全相关4.关于相关系数,下面不正确的描述是( B )。
第十二章 回归分析

回归分析
如果我们将存在相关的两个变量,一个作为自变 量,另一个作为因变量,并把两者之间不十分稳 定的、准确的关系,用数学方程式来表达,则可 利用该方程由自变量的值来估计、预测因变量的 估计值,这一过程称为回归分析。 相关表示两个变量之间的双向相互关系,回归表 示一个变量随另一个变量做不同程度变化的单向 关系。
• 线性回归的基本假设
– – – – 线性关系 正态分布 独立性假设 误差等分散性假设
• 回归方程的建立
– 步骤:1)作散点图;2)设直线方程;3)选定具体方 法,计算表达式中的a和b;4)将a和b代入表达式,得 到回归方程。 – 方法:1)平均数法;2)最小二乘法。 • 最小二乘法:在配置回归线时,回归系数b的确定原则是 使散布图上各点距回归线上相应点的纵向距离平方和为最 小,这种求b的方法即最小二乘法。
• 回归分析与相关分析的关系
– 理解: • 同属相关分析; • 对称设计与不对称设计。 – 回归系数与相关系数的关系 • 相关系数是两个回归系数的几何平均数。
第二节 一元线性回归方程的检验
• 估计误差的标准差
某一X值相对应的诸Y 值,是以Y的平均数YX 为中 ˆ 心呈正态分布的。而与某一X值相对应的回归值 Y 就是与该X值相对应的那些诸Y值的平均数YX的估 ˆ 计值。由 Y 估计YX 会有一定的误差。误差大小 与X值相对应的诸Y值分布范围有关,范围大,误 差大,估计的准确性、可靠性小,范围小,误差小, 估计的准确性、可靠性大。 ˆ 我们需要一个用来描述由Y 估计YX 时误差大小的 指标,即估计误差的标准差。平均数与标准差未知, 样本的无偏估计量为:
a YX Y bYX X
• 列回归方程式(见教材)
第十二章 简单回归分析

第十二章简单回归分析习题一、是非题1.直线回归反映两变量间的依存关系,而直线相关反映两变量间的相互线性伴随变化关系.2.对同一组资料,如相关分析算出的r越大,则回归分析算出的b值也越大. 3.对同一组资料,对r与b分别作假设检验,可得t r=t b4.利用直线回归估计X值所对应的Y值的均数置信区间时,增大残差标准差可以减小区间长度.5.如果直线相关系数r=0,则直线回归的SS残差必等于0.二、选择题1. 用最小二乘法确定直线回归方程的原则是各观察点距直线的( ).A.纵向距离之和最小 B. 纵向距离的平方和最小C. 垂直距离之和最小D.垂直距离的平方和最小E.纵向距离的平方和最大2.Y=14十4X是1~7岁儿童以年龄(岁)估计体质量(市斤)的回归方程,若体质量换成位kg,则此方程( )A 截距改变B 回归系数改变C 两者都改变D 两者都不改变E.相关系数改变4.直线回归系数假设检验,其自由度为( )A.n B. n-1C.n-2 D. 2n-1E.2(n-1)5.当r=0时,Y=a+b X回归方程中( )A a必大于零B a必大于XC a必等于零D a必大于YE a必等于b6.在多元线性回归分析中,反应变量总离均差平方和可以分解为两部分,残差是指( ).A.观察值与估计值之差B.观察值与平均值之差C.估计值与平均值的平方和之差D.观察值与平均值之差的平方和E.观察值与估计值之差的平方和三、筒答题1.用什么方法考察回归直线是否正确?2.简述回归系数方差分析Y的平方和与自由度的分解.3. 举例说明如何用直线回归方程进行预测和控制?4. 直线回归分析时怎样确定自变量和因变量?5. 简述曲线回归常用的几种曲线形式.。
第十二章相关与回归分析

第十二章 相关与回归分析四、名词解释1.消减误差比例变量间的相关程度,可以用不知Y 与X 有关系时预测Y 的误差0E ,减去知道Y 与X 有关系时预测Y 的误差1E ,再将其化为比例来度量。
将削减误差比例记为PRE 。
2. 确定性关系当一个变量值确定后,另一个变量值夜完全确定了。
确定性关系往往表现成函数形式。
3.非确定性关系在非确定性关系中,给定了一个变量值,另一个变量值还可以在一定范围内变化。
4.因果关系变量之间的关系满足三个条件,才能断定是因果关系。
1)连个变量有共变关系,即一个变量的变化会伴随着另一个变量的变化;2)两个变量之间的关系不是由其他因素形成的,即因变量的变化是由自变量的变化引起的;3)两个变量的产生和变化有明确的时间顺序,即一个在前,另一个在后,前者称为自变量,后者称为因变量。
5.单相关和复相关单相关只涉及到两个变量,所以又称为二元相关。
三个或三个以上的变量之间的相关关系则称为复相关,又称多元相关。
6.正相关与负相关正相关与负相关:正相关是指一个变量的值增加时,另一变量的值也增加;负相关是指一个变量的值增加时,另一变量的值却减少。
7.散点图散点图:将相关表所示的各个有对应关系的数据在直角坐标系上画出来,以直观地观察X 与Y 的相互关系,即得相关图,又称散点图。
8.皮尔逊相关系数r皮尔逊相关系数是协方差与两个随机变量X 、Y 的标准差乘积的比率。
9.同序对在观察X 序列时,如果看到i j X X <,在Y 中看到的是i j Y Y <,则称这一配对是同序对。
10.异序对在观察X 序列时,如果看到i j X X <,在Y 中看到的是i j Y >Y ,则称这一配对是异序对。
11.同分对如果在X 序列中,我们观察到i j X =X (此时Y 序列中无i j Y =Y ),则这个配对仅是X 方向而非Y 方向的同分对;如果在Y 序列中,我们观察到i jY =Y (此时X 序列中无i j X =X ),则这个配对仅是Y 方向而非X 方向的同分对;我们观察到i j X =X ,也观察到i j Y =Y ,则称这个配对为X 与Y 同分对。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二章相关与回归分析一、填空1.如果两变量的相关系数为0,说明这两变量之间_____________。
2.相关关系按方向不同,可分为__________和__________。
3.相关关系按相关变量的多少,分为______和复相关。
4.在数量上表现为现象依存关系的两个变量,通常称为自变量和因变量。
自变量是作为(变化根据)的变量,因变量是随(自变量)的变化而发生相应变化的变量。
5.对于表现为因果关系的相关关系来说,自变量一般都是确定性变量,因变量则一般是(随机性)变量。
6.变量间的相关程度,可以用不知Y与X有关系时预测Y的全部误差E1,减去知道Y与X有关系时预测Y的联系误差E2,再将其化为比例来度量,这就是(削减误差比例)。
7.依据数理统计原理,在样本容量较大的情况下,可以作出以下两个假定:(1)实际观察值Y围绕每个估计值cY是服从();(2)分布中围绕每个可能的cY值的()是相同的。
7.已知:工资(元)倚劳动生产率(千元)的回归方程为xyc8010+=,因此,当劳动生产率每增长1千元,工资就平均增加 80 元。
8.根据资料,分析现象之间是否存在相关关系,其表现形式或类型如何,并对具有相关关系的现象之间数量变化的议案关系进行测定,即建立一个相关的数学表达式,称为(回归方程),并据以进行估计和预测。
这种分析方法,通常又称为(回归分析)。
9.积差系数r是(协方差)与X和Y的标准差的乘积之比。
二、单项选择1.欲以图形显示两变量X和Y的关系,最好创建(D )。
A 直方图 B 圆形图 C 柱形图 D 散点图2.在相关分析中,对两个变量的要( A )。
A 都是随机变量B 都不是随机变量C 其中一个是随机变量,一个是常数D 都是常数3. 相关关系的种类按其涉及变量多少可分为( )。
A. 正相关和负相关B. 单相关和复相关C. 线性相关和非线性相关D. 不相关、不完全相关、完全相关4.关于相关系数,下面不正确的描述是( B )。
A当0≤≤r1时,表示两变量不完全相关; B当r=0时,表示两变量间无相关;C两变量之间的相关关系是单相关; D如果自变量增长引起因变量的相应增长,就形成正相关关系。
5. 当变量X按一定数量变化时,变量Y也随之近似地以固定的数量发生变化,这说明X与Y之间存在( )。
A. 正相关关系B. 负相关关系C. 直线相关关系D. 曲线相关关系6.当x按一定数额增加时,y也近似地按一定数额随之增加,那么可以说x与y之间存在( A )关系。
A 直线正相关B 直线负相关C 曲线正相关D 曲线负相关7.评价直线相关关系的密切程度,当r在0.5~0.8之间时,表示( C )。
A 无相关B 低度相关C 中等相关D 高度相关8.两变量的相关系数为0.8,说明( )A.两变量不相关B.两变量负相关C.两变量不完全相关D.两变量完全正相关9.两变量的线性相关系数为0,表明两变量之间( D )。
A 完全相关B 无关系C 不完全相关D 不存在线性相关10.兄弟两人的身高之间的关系是( )A.函数关系 B.因果关系 C.互为因果关系 D.共变关系11.身高和体重之间的关系是(C )。
A 函数关系 B 无关系 C 共变关系 D 严格的依存关系12.下列关系中,属于正相关关系得是(A )。
A 身高与体重B 产品与单位成本C 正常商品的价格和需求量D 商品的零售额和流通费率13如果变量x和变量y之间的皮尔逊相关系数为-1,说明这两个变量之间是()A.低度相关B.完全相关C.高度相关D.完全不相关28.定类变量的相关分析可以使用( )A. λ系数 B. ρ系数 C. r系数 D. τα系数14.相关分析和回归分析相辅相成,又各有特点,下面正确的描述有( D )。
A在相关分析中,相关的两变量都不是随机的;B在回归分析中,自变量是随机的,因变量不是随机的;C在回归分析中,因变量和自变量都是随机的;D在相关分析中,相关的两变量都是随机的。
15. 一元一次回归方程Y=a+bx中的a表示( )。
A. 斜率 B. 最小平均法 C. 回归直线 D. 截距16.当所有的观察值y都落在直线bxayc+=上时,则x与y之间的相关系数为( B )。
A、r=0B、r=1C、-1<r<1D、0<r<117.回归直线方程XC=c+dY,其中Y为自变量,则( )A.可以根据Y值推断XB.可以根据X值推断YC.可以互相推断D.不能进行推断18.对于有线性相关关系的两变量建立的直线回归方城Y=a+bx中,回归系数b ( B )。
A.肯定是正数B.显著不为0 C.可能为0 D.肯定为负数19.年劳动生产率x(千元)和工人工资y(元)之间的回归方程为y=10+70x,这意味着年劳动生产率每提高1千元时,工人工资平均()A.增加70元B.减少70元C.增加80元D.减少80元20产量X(千件)与单位成本Y(元)之间的回归方程为Y=77-3X,这表示产量每提高1000件,单位成本平均( )A.增加3元B.减少3000元C.增加3000元D.减少3元21.两变量X和Y的相关系数为0.8,则其回归直线的判定系数为( C )。
A 0.50 B 0.80 C 0.64 D 0.90 22.在完成了构造与评价一个回归模型后,我们可以( D )。
A 估计未来所需样本的容量B 计算相关系数和判定系数C 以给定的因变量的值估计自变量的值D 以给定的自变量的值估计因变量的值23.对相关系数的显著性检验,通常采用的是(①)① T检验② F检验③ Z 检验24.回归估计标准误差的计量单位与( )A.自变量相同B.因变量相同C.相关系数相同D.自变量、因变量及相关系数均不同25.在回归分析中,两个变量( D )。
A 都是随机变量B 都不是随机变量C 自变量是随机变量D 因变量是随机变量26.已知变量X和Y之间的关系如图所示,则变量X和Y的相关系数为(D )。
A、0.29B、-0.86C、1.04D、0.9127.一元线性回归模型和多元线性回归模型的区别在于只有一个(B )。
A 因变量B 自变量C 相关系数D 判定系数28.以下指标恒为正的是( D )。
A 相关系数r B 截距a C 斜率b D 复相关系数29.对两变量进行回归分析时,( )A.前提是两变量之间存在较高的相关关系B.其中任一变量都可以成为自变量或因(依)变量C.两变量都是随机变量D.一变量是随机变量,另一变量是非随机变量E.一变量是自变量,另一变量是因(依)变量三、多项选择1.判定现象之间有无相关系数的方法是( ABC )。
A、对客观现象作定性分析B、编制相关表C、绘制相关图D、计算相关系数E、计算估计标准误2.回归分析和相关分析的关系是(ABE )。
A 回归分析可用于估计和预测B 相关分析是研究变量之间的相互依存关系的密切程度C 回归分析中自变量和因变量可以互相推导并进行预测D 相关分析需区分自变量和因变量E 相关分析是回归分析的基础3.关于积差系数,下面正确的说法是(ABCD )。
A 积差系数是线性相关系数B 在积差系数的计算公式中,变量X 和Y 是对等关系C 积差系数具有PRE 性质D 在积差系数的计算公式中,变量X 和Y 都是随机的 4.关于皮尔逊相关系数,下面正确的说法是(ACE )。
A 皮尔逊相关系数是线性相关系数B 积差系数能够解释两变量间的因果关系C r 公式中的两个变量都是随机的D r 的取值在1和0之间E 皮尔逊相关系数具有PRE 性质,但这要通过r 2加以反映 5.简单线性回归分析的特点是( ABE )。
A 两个变量之间不是对等关系B 回归系数有正负号C 两个变量都是随机的D 利用一个回归方程,两个变量可以互相推算E 有可能求出两个回归方程 6.反映某一线性回归方程y=a+bx 好坏的指标有(ABD )。
A 相关系数B 判定系数C b 的大小D 估计标准误E a 的大小7.模拟回归方程进行分析适用于(ACDE )。
A 变量之间存在一定程度的相关系数B 不存在任何关系的几个变量之间C 变量之间存在线性相关D 变量之间存在曲线相关E 时间序列变量和时间之间8.判定系数r 2=80%和含义如下(ABC )。
A 自变量和因变量之间的相关关系的密切程度B 因变量y 的总变化中有80%可以由回归直线来解释和说明C 总偏差中有80%可以由回归偏差来解释D 相关系数一定为0.64E 判定系数和相关系数无关 9.以下指标恒为正的是(BC )。
A 相关系数B 判定系数C 复相关系数D 偏相关系数E 回归方程的斜率 10.一元线性回归分析中的回归系数b 可以表示为(BC )。
A 两个变量之间相关关系的密切程度B 两个变量之间相关关系的方向C 当自变量增减一个单位时,因变量平均增减的量D 当因变量增减一个单位时,自变量平均增减的量E 回归模型的拟合优度11.关于回归系数b ,下面正确的说法是(AE )。
A b 也可以反映X 和Y 之间的关系强度。
;B 回归系数不解释两变量间的因果关系; C b 公式中的两个变量都是随机的; D b 的取值在1和-1之间;E b 也有正负之分。
12、如果两个变量之间有一定的相关性,则以下结论中正确的是 ( ①②③ )①、回归系数b 的绝对值大于零 ②、判定系数2R 大于零 ③、相关系数r 的绝对值大于0.313、当所有的观察值都落在回归直线x y ββ10+=上时,下述备选答案成立的有(②③ )①r=0 ② ∣r ∣= 1 ③s y =0五、判断题1.相关关系和函数关系都属于完全确定性的依存关系。
( )2.不管相关关系表现形式如何,当r =1时,变量X 和变量Y 都是完全相关。
(√ ) 3.不管相关关系表现形式如何,当r =0时,变量X 和变量Y 都是完全不相关。
(× )4.若x 与y 之间的相关系数r=-0.9,表示二者“不相关”。
( )5.通过列联表研究定类变量之间的关联性,这实际上是通过相对频数条件分布的比较进行的。
而如果两变量间是相关的话,必然存在着Y 的相对频数条件分布相同,且和它的相对频数边际分布相同。
(× )6.如果众数频数集中在条件频数分布列联表的同一行中,λ系数便会等于0,从而无法显示两变量之间的相关性。
( √ )7.由于削减误差比例的概念不涉及变量的测量层次,因此它的优点很明显,用它来定义相关程度可适用于变量的各测量层次。
( √ )8.不论是相关分析还是回归分析,都必须确定自变量和因变量。
( )9.从分析层次上讲,相关分析更深刻一些。
因为相关分析具有推理的性质,而回归分析从本质上讲只是对客观事物的一种描述,知其然而不知其所以然。
(× ) 10、 在回归分析中,通常假定N ~ε (0, σ2)。
