位似图形的坐标变化规律
合集下载
第15讲 位似图形
第15讲位似图形目标导航课程标准1.了解位似图形、位似中心的概念，掌握位似图形的性质，理解位似变换是特殊的相似变换。
2.会画位似图形，能够利用位似把一个图形放大或缩小。
3.掌握位似图形坐标的变化规律，会利用这个规律求某些特殊点的坐标。
知识精讲知识点01 位似多边形的有关概念一般地，如果两个相似多边形任意一组对应顶点A，A 所在的直线都，且有，那么这样的两个多边形叫做位似多边形，点O叫做。
实际上，k就是这两个相似多边形的相似比。
注意：位似图形与相似图形的区别位似图形是一种特殊的相似图形，而相似图形未必能构成位似图形。
知识点02 位似图形的性质（1）位似图形上任意一对对应点到的距离之比等于相似比；（2) 位似图形上的每组和在同一条直线上；（3）位似图形的对应线段。
（4）位似图形是特殊的相似图形，因此位似图形具有。
知识点03 位似图形的画法1．位似变换利用位似图形的性质将一个图形进行或叫做位似变换。
2．画位似图形的一般步骤（1）确定位似中心。
（2）确定原图形的，通常是多边形的顶点。
（3）分别原图形中的和，并延长（或截取）。
（4）根据已知的相似比，确定所画位似图形 的位置。
（5） 各点，得到放大或缩小后的图形。
3．实例知识点04 平面直角坐标系中的位似变换1．位似多边形对应点的坐标的变化规律在平面直角坐标系中，将一个多边形每个顶点的横坐标、纵坐标都乘同一个数)0( k k ，则所对应的图形与原图形位似，位似中心是 ，它们的相似比为 。
2．平移、轴对称、旋转与位似变换的坐标变化规律 名称 变换规律变换方式平移对应点的横坐标（或纵坐标）加上（或减去）平移的单位长度全等变换轴对称 若以x 轴为对称轴，则对应点的横坐标相等，纵坐标互为相反数；若以y 轴为对称轴，则对应点的纵坐标相等，横坐标互为相反数。
旋转若一个图形绕原点旋转180，则旋转前后两个图形对应点的横坐标与纵坐标均互为相反数。
位似当以原点为位似中心时，变换前后两个图形对应点的横坐标、纵坐标之比的绝对值均等于相似比。
1.4图形的位似
B’
课本P30习题:第1,2题 学案跟踪训练：1
A
A`
O
B` C
A
C` C
∴△ A’B’C’就是所求作图形。
B C
A`
D
B
O
E
O
C`
B`
F
C
A
∴△ A’B’C’就是所求作图形。
∴△ DEF就是所求作图形。
A
A
A`
o
D
E B B C
∴△ ADE就是所求作图形。
B`
C`
C
∴△ A’B’C’就是所求作图形。
如何画位似图形？ 1、关键是确定位似中心 2、先连结顶点与位似中心 3、然后按比例确定对应点的位置 4、再连结对应点
A2
●
B2
●
C C1 A2
(0,4) B1
B (6,4)
O B2 C2
A1
A (6,0)
以坐标原点为位似中心的位似变换的坐标规律：
原来图形上点的坐标为（x，y）， 所求图形上点的坐标为（a, b）, 所求图形与原来图形的位似比为 k， 那么： a k或 k x b k或 k y
C 1 ●
B1
●
A1
A ′ ●
B′
●
●
C′
(x,y) (1,2)
(3,0) 4,0)
x 4 1 3 y 4 2 3
C ●2 B2●●源自A2B2●
C2
●
A2●
●
A1 (4,0)
● ●
C1 (2,-2)
B1 (6,-2)
●
A1
●
B1
如果两个多边形是位似图 形，那么图形上任意一对 对应点到位似中心的距离 之比等于对应边的比。 注意： 1、位似图形是相似图形 的特殊情形，其相似比又 叫做它们的位似比. 2、位似图形的对应点和 位似中心在同一条直线上.
专项练习图形的位似变换与坐标
专项练习图形的位似变换与坐标
目 录
• 位似变换基本概念与性质 • 平面直角坐标系中位似变换 • 三角形和四边形位似变换探讨 • 函数图像在位似变换下性质研究 • 实际应用问题中位似变换思想运用 • 总结回顾与拓展延伸
01 位似变换基本概念与性质
位似变换定义及特点
位似变换定义
如果两个图形不仅是相似图形，而且每组对应点的连线交于 一点，对应边互相平行（或在一条直线上），那么这两个图 形叫做位似图形。这个点叫做位似中心，这时的相似比又称 为位似比。
02 平面直角坐标系中位似变 换
平面直角坐标系简介
平面直角坐标系定义
点的坐标
在平面内画两条互相垂直、原点重合 的数轴，组成平面直角坐标系。
平面内一点P的坐标由一对有序实数 (x,y)确定，其中x是点P到y轴的距离， y是点P到x轴的距离。
坐标轴及象限
水平数轴称为x轴或横轴，垂直数轴称 为y轴或纵轴。坐标轴将平面分为四个 象限。
然保持。
渐近线变换规律
反比例函数的渐近线在位似变换 下也会进行相应的平移和缩放，
但渐近线的斜率不会改变。
05 实际应用问题中位似变换 思想运用
几何证明题中位似变换思想运用
利用位似变换证明线段比例关系
01
通过构造位似图形，证明两条线段之间的比例关系，进而解决
几何证明问题。
利用位似变换证明角度相等关系
位似图形特点
两个位似图形中每组对应顶点所在的直线都交于一点，这个 交点叫做位似中心，图形上任意一对对应点到位似中心的距 离之比等于相似比。
相似比与位似中心关系
相似比
在位似变换中，如果两个相似图形的对应边长之比相等，那么这个比值就叫做 相似比。
位似中心与相似比关系
目 录
• 位似变换基本概念与性质 • 平面直角坐标系中位似变换 • 三角形和四边形位似变换探讨 • 函数图像在位似变换下性质研究 • 实际应用问题中位似变换思想运用 • 总结回顾与拓展延伸
01 位似变换基本概念与性质
位似变换定义及特点
位似变换定义
如果两个图形不仅是相似图形，而且每组对应点的连线交于 一点，对应边互相平行（或在一条直线上），那么这两个图 形叫做位似图形。这个点叫做位似中心，这时的相似比又称 为位似比。
02 平面直角坐标系中位似变 换
平面直角坐标系简介
平面直角坐标系定义
点的坐标
在平面内画两条互相垂直、原点重合 的数轴，组成平面直角坐标系。
平面内一点P的坐标由一对有序实数 (x,y)确定，其中x是点P到y轴的距离， y是点P到x轴的距离。
坐标轴及象限
水平数轴称为x轴或横轴，垂直数轴称 为y轴或纵轴。坐标轴将平面分为四个 象限。
然保持。
渐近线变换规律
反比例函数的渐近线在位似变换 下也会进行相应的平移和缩放，
但渐近线的斜率不会改变。
05 实际应用问题中位似变换 思想运用
几何证明题中位似变换思想运用
利用位似变换证明线段比例关系
01
通过构造位似图形，证明两条线段之间的比例关系，进而解决
几何证明问题。
利用位似变换证明角度相等关系
位似图形特点
两个位似图形中每组对应顶点所在的直线都交于一点，这个 交点叫做位似中心，图形上任意一对对应点到位似中心的距 离之比等于相似比。
相似比与位似中心关系
相似比
在位似变换中，如果两个相似图形的对应边长之比相等，那么这个比值就叫做 相似比。
位似中心与相似比关系
第2课时坐标系中的位似图形
旋转和位似，你能说出它们之间的异同吗？在图所示 的图案中，你能找到这些变换吗？
探究
在平面直角坐标系中,有两点A(6,3),B(6,0),以 原点O为位似中心,相似比为1:3,把线段AB缩小.
y A′(2,1), B′(2,0)
A
A'
o
B'
B
x
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以 原点O为位似中心,相似比为1:3,把线段AB缩小.
A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
y
A
C
B
x
o
B”
A”
知识要点
在平面直角坐标系中，如果位似变换 是以原点为位似中心，相似比为k，那么 位似图形对应点的坐标的比等于k或-k，则 像上的对应点的坐标为（kx，ky）或（－ kx，－ky）.
例题
在平面直角坐标系中, 四边形ABCD的四个顶点的坐标分
y A′(2,1),B′(2,0) A〞(-2,-1),B(-2,0)
A
A&#
x
A〞
观察对应点之间的坐标的变化,你有什么发现?
探究
放大后对应点的坐标分别是多少?
在平面直角坐标系中, △ABC三个顶点的坐标分 别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相 似比为2画它的位似图形.
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 ) y
A' 6
还有其他办法吗?
4 A
3
2
B'
C
1
B
o
2
4
6
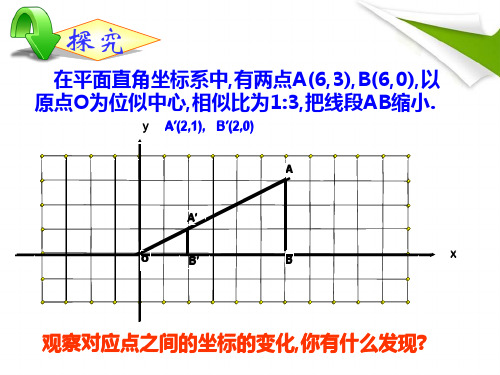
探究
在平面直角坐标系中,有两点A(6,3),B(6,0),以 原点O为位似中心,相似比为1:3,把线段AB缩小.
y A′(2,1), B′(2,0)
A
A'
o
B'
B
x
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,有两点A(6,3),B(6,0),以 原点O为位似中心,相似比为1:3,把线段AB缩小.
A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
y
A
C
B
x
o
B”
A”
知识要点
在平面直角坐标系中，如果位似变换 是以原点为位似中心，相似比为k，那么 位似图形对应点的坐标的比等于k或-k，则 像上的对应点的坐标为（kx，ky）或（－ kx，－ky）.
例题
在平面直角坐标系中, 四边形ABCD的四个顶点的坐标分
y A′(2,1),B′(2,0) A〞(-2,-1),B(-2,0)
A
A&#
x
A〞
观察对应点之间的坐标的变化,你有什么发现?
探究
放大后对应点的坐标分别是多少?
在平面直角坐标系中, △ABC三个顶点的坐标分 别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相 似比为2画它的位似图形.
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 ) y
A' 6
还有其他办法吗?
4 A
3
2
B'
C
1
B
o
2
4
6
位似图形的坐标变化规律(课件)-2023-2024学年九年级数学下册同步精品课堂(人教版)
C″
B″
例2.如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位
似中心的位似图形，且相似比为1:3，点A，B，E在x轴上.
(1)若点F的坐标为(4.5, 3),直接写出点A和点C的坐标;
(2)若正方形BEFG的边长为6，求点C的坐标.
解:
1
3
(1)A( ，0)，C( ,
2
2
1)
1.理解平面直角坐标系中，位似图形对应点的坐标之间的联系．
2.会用图形的坐标的变化表示图形的位似变换，掌握把一个图形按一定比
例放大或缩小后，点的坐标变化的规律.
(重点、难点)
3.了解四种图形变换 (平移、轴对称、旋转和位似) 的异同，并能在复杂
图形中找出这些变换.
位似
1.如图，若AB∥CD，则△OAB___△OCD，△OAB与△OCD是_____图形，点O是
分别得A'(8，-10) ,B'(12, 0),O' (0,0) ,
或A'(-8,10),B'(-12,0)，O'(0,0).
3.将平面直角坐标系中某个图案的各点坐标作如下变化,其中属于位似变换
的是( C )
A.将各点的纵坐标乘2,横坐标不变
B.将各点的坐标除以2，纵坐标不变
C.将各点的横坐标、纵坐标都乘2
(3，6)，C(－3，3). 以原点O为位似中心，画出四边形OABC的位似图形，
使它与四边形OABC的相似是2:3.
画法二：将四边形OABC各顶点的坐标都
2
乘 ；在平面直角坐标系中描点O(0，
3
0)，A″(－4，0)，B″(－2，－4)，C″(2，
－2)，用线段顺次连接O，A″，B″，C″.
【教育资料】第2课时 位似图形的坐标变化规律学习专用
图27－3－61
5.已知△ABC三顶点的坐标分别为A(0，2)，B(3，3)，C(2，1).
(1)画出△ABC；
(2)以点B为位似中心，将△ABC放大到原来的2倍，在网格图中画出放大后的图形△A1BC1；
(3)写出点A的对应点A1的坐标.
通过设置达标测评，进一步巩固所学新知，同时检测学习效果，做到“堂堂清”.
问题：如图27－3－57，△AOC三个顶点的坐标分别为A(2，4)，O(0，0)，C(5，0)，以点O图27－3－57
为位似中心，相似比为2，将△AOC放大，观察对应顶点坐标的变化，你有什么发现？
2.总结位似图形的坐标变化规律：
师生活动：教师组织学生以小组的形式进行探究，得到位似变换中对应点的坐标变化规律，教师多媒体演示，对表现优秀的学生进行表扬.
师生活动：师生共同总结位似、平移、轴对称、旋转等图形变换的基本变换规律：
位似的变换规律前面已给出；平移是横、纵坐标加上或减去平移的单位；轴对称若以x轴为对称轴则对应点的横坐标相等，纵坐标互为相反数，若以y轴为对称轴则反之；旋转是一个图形绕原点旋转180°形成中心对称时，横纵坐标都互为相反数.
未来两年大学生活的计划2.联系新旧知识，进行归纳总结，形成知识体系.
活动
四：
课堂
总结
反思
【达标测评】
1.已知线段AB两端点A(4，6)，B(8，2)，以原点O为位似中心，在第一象限内将线段AB缩小为原来的 后得到线段CD，点A的对应点为点C，则端点C的坐标为(A)
A.(2，3)B．(2，1)C．(4，3)D．(4，1)
2.如图27－3－60，△ABO缩小后变为△A′B′O，其中点A，B的对应点分别为A′，B′，点A′，B′均在图中格点上，若线段AB上有一点P(m，n)，则点P在A′B′上的对应点P′的坐标为(D)
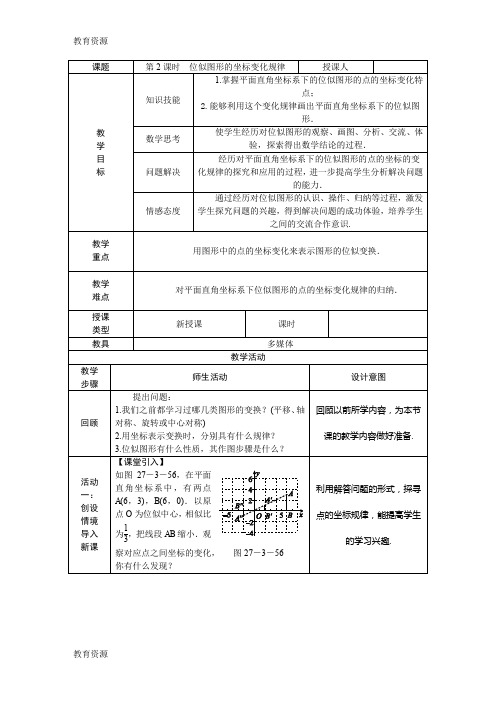
5.已知△ABC三顶点的坐标分别为A(0，2)，B(3，3)，C(2，1).
(1)画出△ABC；
(2)以点B为位似中心，将△ABC放大到原来的2倍，在网格图中画出放大后的图形△A1BC1；
(3)写出点A的对应点A1的坐标.
通过设置达标测评，进一步巩固所学新知，同时检测学习效果，做到“堂堂清”.
问题：如图27－3－57，△AOC三个顶点的坐标分别为A(2，4)，O(0，0)，C(5，0)，以点O图27－3－57
为位似中心，相似比为2，将△AOC放大，观察对应顶点坐标的变化，你有什么发现？
2.总结位似图形的坐标变化规律：
师生活动：教师组织学生以小组的形式进行探究，得到位似变换中对应点的坐标变化规律，教师多媒体演示，对表现优秀的学生进行表扬.
师生活动：师生共同总结位似、平移、轴对称、旋转等图形变换的基本变换规律：
位似的变换规律前面已给出；平移是横、纵坐标加上或减去平移的单位；轴对称若以x轴为对称轴则对应点的横坐标相等，纵坐标互为相反数，若以y轴为对称轴则反之；旋转是一个图形绕原点旋转180°形成中心对称时，横纵坐标都互为相反数.
未来两年大学生活的计划2.联系新旧知识，进行归纳总结，形成知识体系.
活动
四：
课堂
总结
反思
【达标测评】
1.已知线段AB两端点A(4，6)，B(8，2)，以原点O为位似中心，在第一象限内将线段AB缩小为原来的 后得到线段CD，点A的对应点为点C，则端点C的坐标为(A)
A.(2，3)B．(2，1)C．(4，3)D．(4，1)
2.如图27－3－60，△ABO缩小后变为△A′B′O，其中点A，B的对应点分别为A′，B′，点A′，B′均在图中格点上，若线段AB上有一点P(m，n)，则点P在A′B′上的对应点P′的坐标为(D)
《图形的位似》课件1
y C' B'
B(A')
A
C
D
O
D' x
课堂小结
定理
平面直角坐标系 中的位似变化
在平面直角坐标系中，将一个多边形每个顶点的横 坐标、纵坐标都乘同一个数k(k≠0)，所对应的图形 与原图形位似，位似中心是坐标原点，它们的相似 比位|k|.
画图
0)，A(6，0),B(3，6),C(-3，3).以原点O为位似中心，画出四边形 OABC的位似图形，使它与四边形OABC的相似是2:3.
y B B'
画法一：如右图所示， 解：将四边形OABC各顶点的
2 坐标都乘 ；在平面直角坐标 3
4
C
2 C'
系中描点O(0,0), A'(4,0),B'(2,4)
例1：在平面直角坐标系中，△OAB三个顶点的坐标分别为O(0,0), A(3，0),B(2，3)
6 y 4 A 2 -4 -2 O -2 2 B 4 x B'
A'
（1）将点O,A,B的横坐标、 纵坐标都乘2，得到三个点，
以这三个点位为顶点的三角
形与△OAB位似吗？如果位 似，指出位似中心和相似比. 位似,位似中心为原点O， 位似比为1:2
-4
-6
y 4
（2）如果将点O,A,B的横 坐标、纵坐标都乘以-2.
B' -4 -2
A
2 O
-2 -4 2 B 4 x
A' 定理 在平面直角坐标系中，将一个多边形每个顶点的横坐标、纵坐标 都乘同一个数k(k≠0)，所对应的图形与原图形位似，位似中心是坐标原
点，它们的相似比位|k|.
例2：在平面直角坐标系中，四边形OABC的顶点坐标分别为O(0，
B(A')
A
C
D
O
D' x
课堂小结
定理
平面直角坐标系 中的位似变化
在平面直角坐标系中，将一个多边形每个顶点的横 坐标、纵坐标都乘同一个数k(k≠0)，所对应的图形 与原图形位似，位似中心是坐标原点，它们的相似 比位|k|.
画图
0)，A(6，0),B(3，6),C(-3，3).以原点O为位似中心，画出四边形 OABC的位似图形，使它与四边形OABC的相似是2:3.
y B B'
画法一：如右图所示， 解：将四边形OABC各顶点的
2 坐标都乘 ；在平面直角坐标 3
4
C
2 C'
系中描点O(0,0), A'(4,0),B'(2,4)
例1：在平面直角坐标系中，△OAB三个顶点的坐标分别为O(0,0), A(3，0),B(2，3)
6 y 4 A 2 -4 -2 O -2 2 B 4 x B'
A'
（1）将点O,A,B的横坐标、 纵坐标都乘2，得到三个点，
以这三个点位为顶点的三角
形与△OAB位似吗？如果位 似，指出位似中心和相似比. 位似,位似中心为原点O， 位似比为1:2
-4
-6
y 4
（2）如果将点O,A,B的横 坐标、纵坐标都乘以-2.
B' -4 -2
A
2 O
-2 -4 2 B 4 x
A' 定理 在平面直角坐标系中，将一个多边形每个顶点的横坐标、纵坐标 都乘同一个数k(k≠0)，所对应的图形与原图形位似，位似中心是坐标原
点，它们的相似比位|k|.
例2：在平面直角坐标系中，四边形OABC的顶点坐标分别为O(0，
人教版初三数学下册位似图形的坐标变化规律
例题.在平面直角坐标系中, 四边形ABCD的四个顶点的坐
标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以 原点O为位似中心,相似比为1/2的位似图形.
y
A
D
A′
B
D′
B′
x
C
C′
o
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 ) A′( 3,-3 ), B′( 4,-1 ), C′( 2,0 ), D′( 1,-2)
解析:根据以原点为位似图形的坐标特征，可得C，D点横、 纵坐标为A，B点横、纵坐标的同一个倍数的只有D.故选D.
3.如图所示，原点O是△ABC和△A1B1C1的位似中心，点A(1，0)与A1(-2，0)
是对应点，△ABC的面积是
3 2
，则△Aபைடு நூலகம்B1C1的面积是
6
.
解析:∵原点O是△ABC和△A1B1C1的位似中心，点A(1，
B 2D 4 6 8
-4
-6
-8
2.已知线段AB和CD，依据下列点的坐标，能判断AB和CD是以原点为
位似中心的位似图形的是 ( D )
A.A(2，3)，B(-1，1)，C(4，3)，D(-2，1) B.A(1，-5)，B(-1，-2)，C(1，-10)，D(-1，-4) C.A(-4，5)，B(2，-2)，C(4，5)，D(-2，-2) D.A(2，0)，B(-1，0)，C(-4，0)，D(2，0)
3）位似图形中的对应线段平行或在同一条直线上
3.利用位似可以把一个图形放大或缩小
复习回顾
如何把三角形ABC放大为原来的2倍?
E
B
O
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例题.在平面直角坐标系中, 四边形ABCD的四个顶点的坐标
分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个 以原点O为位似中心,相似比为1/2的位似图形.
y
A
D
A′
B
D′
B′
x
C
C′
o
A′( -3,3 ), B′( -4,1 ), C′( -2,0 ), D′( -1,2 ) A′( 3,-3 ), B′( 4,-1 ), C′( 2,0 ), D′( 1,-2)
想一想？
1、如果把位似图形放到直角坐标系中， 又如何去探究位似变换与坐标之间的关系呢？
在平面直角坐标系中,有两点A(6,3),B(6,0),
以原点O为位似中心,相似比为1:3,把线段AB
缩小.
y
A′(2,1),
B′(2,0)
6
A〞(-2,-1),
4
2
B〞(-2,0)
B′ ′
-6 -4 -2 o
A′ ′ -2
B、位似图形上任意两点与位似中心的距离 之比等于位似比。
C、两个正方形是位似图形。
D、位似图形是具有某种特殊位置的相似图 形。
在前面我们学习了在平面直角坐
标系中，如何用坐标表示某些平移、 轴对称、旋转（中心对称）等变换， 相似也是一种图形的变换，一些特殊 的相似（如位似）也可以用图形坐标 的变化来表示．
B 2D 4 6 8
Байду номын сангаас
-4
-6
-8
2.已知线段AB和CD，依据下列点的坐标，能判断AB和CD是以原点为
位似中心的位似图形的是 ( D )
A.A(2，3)，B(-1，1)，C(4，3)，D(-2，1) B.A(1，-5)，B(-1，-2)，C(1，-10)，D(-1，-4) C.A(-4，5)，B(2，-2)，C(4，5)，D(-2，-2) D.A(2，0)，B(-1，0)，C(-4，0)，D(2，0)
27.3.2位似图形的坐标变化规律
复习回顾
1.什么叫位似图形?
如果两个图形不仅相似,而且对应顶点的连线 相交于一点,像这样的两个图形叫做位似图形, 这 个点叫做位似中心, 这时的相似比又称为位似比.
2.位似图形的性质
1)位似图形可能在位似中心的同侧，也可能在 位似中心的异侧
3）位似图形中的对应线段平行或在同一条直线上
3.利用位似可以把一个图形放大或缩小
复习回顾
如何把三角形ABC放大为原来的2倍?
E
B
O
C
F
A
D
D
O F
B C
A
E
对应点连线都交于_位__似___中__心____ 对应线段___平___行__或__在___一__条__直___线__上_________
判断下列命题正确的是（D ） A、对应边都平行能得到两个图形是位似图形。
至此，我们已经学习了四种变换：平移、轴对称、旋转和 位似，你能说出它们之间的异同吗？在图所示的图案中， 你能找到这些变换吗？
练习
检测检反测馈反馈
1. 如图表示△AOB和把它缩小后得到的△COD，求它们的
相似比．
8A
点D的横坐标为2 点B的横坐标为5
相似比为
2 5
6
4C
2
-8 -6 -4 -2 O -2
解析:根据以原点为位似图形的坐标特征，可得C，D点横、 纵坐标为A，B点横、纵坐标的同一个倍数的只有D.故选D.
3.如图所示，原点O是△ABC和△A1B1C1的位似中心，点A(1，0)与A1(-2，0)
是对应点，△ABC的面积是
3 2
，则△A1B1C1的面积是
6
.
解析:∵原点O是△ABC和△A1B1C1的位似中心，点
A(1，0)与A1(-2，0)是对应点，∴△ABC和△A1B1C1
的相似比为 1 ，由相似三角形的面积比等于相似比
2
的平方，得△A1B1C1的面积是
3 2
×4=6.故填6.
课堂小结
一般的，在平面直角坐标系中，如果以 原点为位似中心，画出一个与原图形位似且 位似比为k的图形，那么与原图形上的点 （ x ， y ）对应的位似图形上的点的坐标 为（kx , ky) 或 (-kx , -ky)
观察对应点之间的 坐标的变化,你有
-4
什么发现?
-6
A A′
2B′ 4 B6 x
在平面直角坐标系中, △ABC三个顶点的坐 标分别为A(2,3),B(2,1),C(6,2),以原点O 为位似中心,相似比为2画它的位似图形.
放大后对应点的坐标分别是多少?
y
A′(4 ,6 ),
6
A′
4A
C′
B′(4 ,2 ),
2
C′(12,观4坐还察)标有对-的12其应-变10他点化-8办之,-你6法间-有4吗的-?2
B′ ′
o
-2
什C′′么发现?
-4
B′ B
24
C
6 8 10 12 x
A′ ′ -6
在平面直角坐标系中，如果位似变换是以原点为位似中心， 相似比为k，那么位似图形对应点的坐标的比等于k或－k．
结论：在平面直角坐标系中, 以原点O为位似中心,位似比为 k,若原图形上点A的坐标为（x，y），那么位似图形对应点 A’的坐标为（kx，ky）或（-kx，-ky）