质点运动学动力学作业问题
质点运动学动力学作业解

t = 2h = 2s 10
4.如图所示,质量 m 为 0.1kg 的木块,在一个水平面上 和一个倔强系数k 为 20Nm-1 的轻弹簧碰撞,木块将弹簧
由原长压缩了0.4m。假设木块与水平面间的滑动摩擦系数
µk 为0.25,问在将要发生碰撞时木块的速率 υ 为多少?
动能定理
−
frx −
1 2
kx2
3.一质点从静止(t=0)出发,沿半径 R = 3m 的圆周运动,
切向加速度大小保持不变,为 at = 3ms-2。在t时刻,其
总加速度恰与半径成45°角,此时 t =_______ ,此时,
质点的速度大小为_______,质点的加速度大小为 ______。
解:切向加速度不变
at
=
dυ dt
= 不变
∆E = 0
MgLsin
α
=
1 2
Mυ02
(1)
过垂程 直二x:方发向炮,。则由沿于x爆方炸向产动生量的守作恒用。力很大,重力px
m
α
υ
Mυ0 = mυ cos α (2)
由式(1)、(2)解出 υ = M
2gL sin α
m cos α
四、证明题
一艘正在沿直线行驶的电艇,在发动机关闭后,其加速度 方向与速度方向相反,大小与速度平方成正比,即 dυ = −kυ2
2
3
3
解: υ = (4 + t 2 ) = dx
[C]
dt
dx = (4 + t 2 )dt
x = 4t + 1 t3 + C 3
当t =3s时,质点位于 x = 9m 处 C = 9 − 4× 3 − 1 × 33 = −12 3
第2章质点动力学作业解答2

M
从小木块开始下落到脱离大木块 过程中,水平方向没有外力作用,
题 2.23 图
所以,水平方向系统的动量守恒,即:
0mv1Mv2
得到:v 2
m M
v1
(1)
考察小木块、大木块和地球组成的系统,在小木块开始下落
到脱离大木块过程中,没有外力和非保守内力做功,机械能
保持守恒,取小木块脱离大木块时的位置为势能零点,有:
V 2mgRm s) mM
教材上册P67习题2.17 设 F7i6j(N );(1) 当一质点
从原点运动到 r 3 i 4 j 1 6 k ( m )时,求 F 所做的功。(2)如
果质点到 r 处时需 0.6 s ,试求平均功率;(3)如果质点的质Βιβλιοθήκη 为1 kg ,试求动能的变化。
解:(1)根据功的定义式 W Fdr,得:
3
4
16
W0 7dx06dy+00dz
= 7 ( 3 0 ) 6 (4 0 ) 0 = 45(J)
(负号表示该力做负功)
(2)根据平均功率的定义式 P W ,得: t
P 4 5 75(W) (负号表示该力的功率是负的) 0 .6
(3)已知 m = 1 kg , 根据动量定理 W =ΔEk ,得动能的变化 ΔEk 为:
EkW45J (负号表示动能减少)
教材上册P67习题2.23 质量为M的大木块具有半径为R的四分
之一弧形槽,如题2.23图所示;质量为m的小立方体从曲面的顶端 滑下,大木块放在光滑的水平面上,二者
m
都作无摩擦的运动,而且都从静止开始,
求小木块脱离大木块时的速度。
解: 考察小木块和大木块组成的系统,
解:由机械能守恒得:m gR1 2M V M 21 2m V m 2 ①
01 质点运动学和动力学习题答案

(2)由题知:
������������ ������ ������ = − ������ ������������
������ ������������
������ ������
∫
������0
dt dv A Bv
t
v
dt
dv
0
0 A Bv
t 1 [ln( A Bv) ln A] B
即: v A (1 eBt ) B
(2) v dy A (1 eBt ) dy A (1 eBt )dt
dt B
B
y
dy
t A (1 eBt )dt
(2)������ = |���⃑���| = 2√16������2 + 1
���⃑��� = ���������⃑⃑��� = 8���⃑���
������������
������������
32������
������������ = ������������ = √16������2 + 1
������d������, 1
������0
−
1 ������
=
−
1 2
������������2
������
=
2
2������0 + ������������0������2
4.t=1s
分析:由 an
a ,������
= ������������������, a
v2 R
可得。
质点动力学习题解答
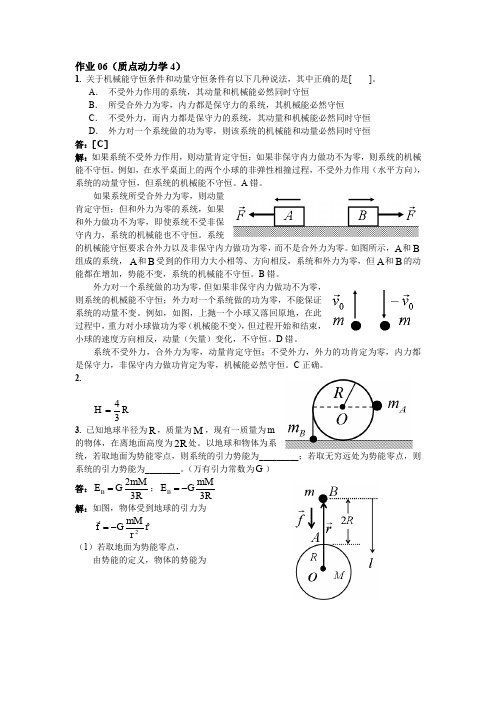
作业06(质点动力学4)1. 关于机械能守恒条件和动量守恒条件有以下几种说法,其中正确的是[ ]。
A . 不受外力作用的系统,其动量和机械能必然同时守恒B . 所受合外力为零,内力都是保守力的系统,其机械能必然守恒C . 不受外力,而内力都是保守力的系统,其动量和机械能必然同时守恒D . 外力对一个系统做的功为零,则该系统的机械能和动量必然同时守恒答:[C ]解:如果系统不受外力作用,则动量肯定守恒;如果非保守内力做功不为零,则系统的机械能不守恒。
例如,在水平桌面上的两个小球的非弹性相撞过程,不受外力作用(水平方向),系统的动量守恒,但系统的机械能不守恒。
A 错。
如果系统所受合外力为零,则动量肯定守恒;但和外力为零的系统,如果和外力做功不为零,即使系统不受非保守内力,系统的机械能也不守恒。
系统的机械能守恒要求合外力以及非保守内力做功为零,而不是合外力为零。
如图所示,A 和B 组成的系统,A 和B 受到的作用力大小相等、方向相反,系统和外力为零,但A 和B 的动能都在增加,势能不变,系统的机械能不守恒。
B 错。
外力对一个系统做的功为零,但如果非保守内力做功不为零,则系统的机械能不守恒;外力对一个系统做的功为零,不能保证系统的动量不变。
例如,如图,上抛一个小球又落回原地,在此过程中,重力对小球做功为零(机械能不变),但过程开始和结束,小球的速度方向相反,动量(矢量)变化,不守恒。
D 错。
系统不受外力,合外力为零,动量肯定守恒;不受外力,外力的功肯定为零,内力都是保守力,非保守内力做功肯定为零,机械能必然守恒。
C 正确。
2.R H 34= 3. 已知地球半径为R ,质量为M ,现有一质量为m的物体,在离地面高度为R 2处。
以地球和物体为系统,若取地面为势能零点,则系统的引力势能为_________;若取无穷远处为势能零点,则系统的引力势能为________。
(万有引力常数为G )答:R mM G E B 32=;RmM G E B 3-= 解:如图,物体受到地球的引力为r rmM G f ˆ2-= (1)若取地面为势能零点,由势能的定义,物体的势能为R mM G l d l R mM Gl fd l d f E R A B A B B 32)3(202)()()()(=-==⋅=⎰⎰⎰(2)若取无穷远处为势能零点,由势能的定义,物体的势能为R mM G r d r mM Gr fd l d f E R B B B 332)()()()(-=-=-=⋅=⎰⎰⎰∞∞∞4. 如图所示,一水平放置的轻弹簧,劲度系数为k ,其一端固定,另一端系一质量为m 的滑块A ,A 旁又有一质量相同的滑块B 。
质点动力学习题解答2

作业04(质点动力学2)1. 质量为m 、速度大小为V 的质点受到某个力作用后,其速度的大小未变,但方向改变了θ,则这个力的冲量大小为[ ]。
A.)2/cos(2θmvB. )2/sin(2θmvC. )2/cos(θmvD. )2/sin(θmv 答:[B ]解:如图,由动量定理,冲量等于动量的变化 im v j m v i m v i m v j m v i m v v m v m v m I -+=-+=-=∆=θθθθsin cos sin cos /// 冲量的大小为 )2/s i n (2c o s 22s i n )c o s (222θθθθv m mv v v v m I I =-=+-==2. 一质量为kg m 60=的人静止站在一条质量为kg M 300=、且正以12-⋅=s m V 的速率向湖岸驶进的小木船上,湖水是静止的,其阻力不计。
现在人相对于船以一水平速度v 沿船的前进方向向河岸跳去,该人起跳后,船速减为原来的一半,v 应该是[ ]A. 12-⋅s mB. 13-⋅s mC. 15-⋅s mD. 16-⋅s m答:[C ]解:以地面为参考系。
人与船为系统。
人相对于地面的起跳速度为v V +,起跳后,船向岸边运动的速度为2/V ;原来人与船以水平速度V 一起向岸边运动。
水平方向不受外力 V M m MV v V m )(21)(+=++,)(5602230022-⋅=⨯⨯==s m m MV v 也可以原船为参考系(也是惯性系),人与船为系统。
人相对于原船的起跳速度为v ,起跳后,船相对于原船的运动速度为2/V -;在原船参考系中,起跳前,人与船静止。
水平方向不受外力,由动量守恒,得到VM mv 210-=,)(5602230022-⋅=⨯⨯==s m m MV v 3. 下列叙述中正确的是[ ]A. 质点的动量不变,则动能也不变。
B 质点的动能不变,则动量也不变C. 质点的动量变化,则动能也一定变化。
大学物理力学一、二章作业答案-一质点的运动方程为x=cos2

第一章质点运动学一、选择题1、一质点在xoy 平面内运动,其运动方程为x2,式中 a、、at , y b ct b c 均为常数。
当运动质点的运动方向与x 轴成 450角时,它的速率为 [ B ] 。
A. a;B.2a;C. 2c;D.a24c 2。
2、设木块沿光滑斜面从下端开始往上滑动,然后下滑,则表示木块速度与时间关系的曲线是图 1-1 中的 [ D ]。
v v v vt t t tA B C D图1-13、一质点的运动方程是r R cos ti Rsin tj ,R、为正常数。
从t=/到 t=2/ 时间内该质点的路程是[ B]。
A .2R;B.R;C. 0;D.R。
4、质量为 0.25kg 的质点,受F t i(N) 的力作用, t=0 时该质点以v =2 j m/s 的速度通过坐标原点,该质点任意时刻的位置矢量是[B]。
A . 2 t2i +2j m;B. 2 t3i2tj m;3C.3t4 i2t 3 j ;D.条件不足,无法确定。
43二、填空题1、一质点沿 x 轴运动,其运动方程为x52t t 2(x以米为单位,t以秒为单位)。
质点的初速度为2m/s,第 4 秒末的速度为-6m/s,第 4 秒末的加速度为2。
-2m/s2、一质点以(m/s)的匀速率作半径为5m的圆周运动。
该质点在5s 内的平均速度的大小为2m/s,平均加速度的大小为2m / s2。
53、一质点沿半径为 0.1m的圆周运动,其运动方程为2t 2(式中的θ以弧度计,t以秒计),质点在第一秒末的速度为0.2m/s,切向加速度为0.2m/s2。
4、一质点沿半径1m的圆周运动,运动方程为θ=2+3t 3,其中θ以弧度计,t 以秒计。
T=2s时质点的切向加速度为36m/s 2;当加速度的方向和半径成45o 角时角位移是3rad 。
85、飞轮半径 0.4m ,从静止开始启动,角加速度β=0.2rad/s 2。
t=2s 时边缘各点的速度为0.16m/s ,加速度为 0.102m/s 2。
质点动力学例题

解 F T sinθ 0
T cosθ mg 0
F mg tanθ
A
F
dr
F
cosθ
ds
mg tanθ cosθ ds θ0 mg tanθ cosθ dθ
0
Lθ T
F
G
y
1 mgLcosθ 0
x
例18 已知 m = 2kg , 在 F = 12t 作用下由静止做直线运动.
o
(a)
x
(b)
例题 2-6图
解:直接用动量定理的矢量形式求解。垒球被击中前后的动量
和 p1 mv的1 矢量p2关系m。v2
Ft、mv2、mv1 组成矢量三角形。由题意可知
mv1 mv2 mv
a 1 30
2
F t 2mv cos
F 2mv cos
t
2 0.14 40 cos 30
f
M
v f ( M 1)
Mt
例6 质量分别为 m1 和 m2 的两物体用轻细绳相连接后,悬挂在 一个固定在电梯内的定滑轮的两边。滑轮和绳的质量以及
所有摩擦均不计。当电梯以 a0=g/2 的加速度下降时。
求 m1 和 m2 的加速度和绳中的张力。 解 取电梯为参考系
对m1 有 m1g T m1a0 m1a'
求 时刻 t ,A 的瞬时加速度
解 选A车M和t时间内抽至A
A
v
B
u
车的水m为研究系统,
A
水平方向上动量守恒
Mv mu (M m)v
v Mv mu M m
v v v mu v
M m
v m u v
M
a lim v dm u v 6 u v
质点动力学习题答案

l
m
v0
T
m
v02 l
2g
3g cos
2-9. 质量均为M的三条小船以相同的速率 v 沿一直线同
向航行,从中间的小船向前后两船同时以相同速率 u
(相对于该船)抛出质量同为 m 的小包。从小包被抛出
至落入前后船的过程中,试分别对前、中、后船建立动
量守恒方程。
(2)解:物体系的加速度:
a (mA mB )g mC g
f
T
(mA mB mC )
1.1 m s2
分析物体C,T mC g mCa
代入数据解得:T 1.7 N
2-7. 已知条件如图,求物体系的加速度和A、B两绳中的 张力。绳与滑轮的质量和所有摩擦不计。
解:物体系的加速度:
a 2mg cos 45 mg 2m m 2m
解:设小包抛出之后,三船的速度分别变为 v前 ,v中 ,v后
Mv m(v u)
(M
m)v前
v前
v
m M m
u
Mv m(v u) m(v u) (M 2m)v中 v中 v
m Mv m(v u) (M m)v后 v后 v M m u
2-10. 一质量为0.25kg的小球以20m/s的速度和45°的 仰角投向竖直放置的木板,设小球与木板碰撞时间为
0.05s,反弹角与入射角相等,小球速率不变,求木板
对小球的冲力。
y
解:建立直角坐标系:
P mv mv0
0.25
20
i
20
j 0.25
20
i
20
j
45
x
2
2
2
2
7.07i
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C 9 4 3 1 33 12 3
故选 [ C ]。
凌亚文
大学物理第一学期作业中的问题
4.有A、B两辆车在同一直线轨道上同向行驶。A车以1
匀速运动,B车在后。当B车与A车距离为d时,B以2 开始做匀减速运动,其加速度为a,B车速度2 比A车速
度 大1,那么两车不会相撞的最小距离为
解: (1)以升降机为参考系
a物对机 a物对地 a地对机
9.8 0.2 10
匀加速运动
h
1 2
a物对机t 2
t 2h 2s 10
a机对地
h
凌亚文
大学物理第一学期作业中的问题
(2)以地面为参考系 向上为X轴正方向
以x1和x2分别表示任一t时刻螺钉和底板的位置
螺钉的运动 :
凌亚文
大学物理第一学期作业中的问题
8.质量为 m的物体,从高出弹簧上端 h 处由静止自由下落到
竖直放置在地面上的轻弹簧上,弹簧的倔强系数为 k,则弹簧
被压缩的最大距离 x ?
解: 初态体系总能量为:
mgh mgx
末态体系总能量为:
mgh mgx 1 kx2
2
1 kx2 2
x mg k
凌亚文
大学物理第一学期作业中的问题
7.一斜面倾角为 ,用与斜面成 角的恒力F将一质量为 m
h 的物体沿斜面拉升了高度 ,物体与斜面间的摩擦系数为
,摩擦力在此过程中所作的功 Wf ?
解:
Ar
frL
fr
h
s in
fr N
N mg cos - F sin
A mgh ctg Fh sin s in
fr mg N
fr mR2
N m 2 m (R)2
R
R
g R
凌亚文
大学物理第一学期作业中的问题
6.一光滑的内表面半径为 10cm 的半球形碗,以匀角速度
绕其对称轴 OC 旋转,已知放在碗内表面上的一个小球
P 相对碗静止,其位置高于碗底 4cm ,则由此可推知
x1
x10
0t
1 2
gt 2
电梯底板的运动 :
x2
x20
0t
1 at 2 2
x10 x20 d 20(cm)
x1=x2
d 1 (g a)t 2 2
t 2x0 2 20 2s g a 9.8 0.2
凌亚文
大学物理第一学期作业中的问题
4.如图所示,质量 m 为 0.1kg 的木块,在一个水平面上和 一个倔强系数k 为 20Nm-1 的轻弹簧碰撞,木块将弹簧由原
碗旋转的角速度约为
解: N cos mr2
N sin mg
r Rcos
tan R h
r
ω=12.78 rad·s-1≈13 rad·s-1
凌亚文
大学物理第一学期作业中的问题
7. 质量为 m 的质点。以不变速率沿图中正三角形ABC 的水平光滑轨道运动。
求 质点越过A角时,轨道作用于质点的冲量。
t
t
tt
解: 质点在 2t 时间间隔内,正好转两圈,回到原点
平均速度的大小为零
平均速率的大小为
2 2R 2R
2t
t
故选 [ B ]。
凌亚文
大学物理第一学期作业中的问题
3. 一质点沿X轴运动,其速度与时间的关系为 (4 t 2 )
m/s,且当t =3s时,质点位于 x = 9m 处,则质点的运动方程为
解 由动量定理
I
P
m 2
m 1
x 方向
I x m2 x m1x 0
y 1
A
3
x
2
y 方向
C
B
Iy
m2 y
m 1 y
2m sin
3
冲量
I 3mj
3m
凌亚文
大学物理第一学期作业中的问题
8.一F质F点0 (在xi如 图yj)所作示用的在坐质标点平上面。内在作该圆质周点运从动坐,标有原一点力运动
M
dx dt
h1 h2 x x x
dx
dt
x h1 x h1 h2
M
h1
h1 h2
凌亚文
大学物理第一学期作业中的问题
2.在半径为 R 的圆周上运动的质点,其速率与时间的关系为
ct 2 (式中c为常数),则: 从t=0到t时刻质点走过的路程S(t)=? t 时刻质点的切向加速度 a ? t 时刻质点的法向加速度 an ?
解: 质地 质斜 斜地
x方向 x x u 2gh cos u h
y方向 y y 2ghsin
y
x
u
2 x
2 y
u2 2gh 2u
2gh cos
arctg y arctg 2ghsin
x
2ghcos u
凌亚文
大学物理第一学期作业中的问题
3. 一升降机以加速度a = 0.2 ms-2上升,在升降机上升的过 程中,有一螺钉从升降机的天花板上松动并脱落,升降机 的天花板与底板相距 d = 20m,求螺钉从天花板落到底板 所需的时间。(取g = 9.8 ms-2)
分析 相对升降机,螺母作初速为0的落体运动,运动距离20m
凌亚文
大学物理第一学期作业中的问题
6.图中所示的装置中,略去一切摩擦力以及滑轮和绳的质 量,且绳不可伸长,则 m1 质量为的物体的加速度
m1 : m1a1 T m2 : m2a2 m2g T
T 2T a1 2a2
a1
2m2 g 4m1 m2
N
m1
T
m1g
T’
m2 m2g
到(0,2R)位置过程中,力对它所作的功为
解
dA
F
ds
F
dl
F
dr
dA
F
dr
(F0
xi
F0
yj )
(dxi
dyj )
dA F0xdx F0 ydy
y
0
2R
A dA 0 F0xdx 0 F0 ydy
A
沿水平直线行走,如图所示。则他的头顶在地上的影子
M 点沿地面移动的速度
解:
M
dx dt
h1 h2 x x
x h1 x h2
dx h1 dx dt h2 dt
d(x dt
x)
dx dt
dx dt
M
dx dt
M
h1
h1 h2
凌亚文
大学物理第一学期作业中的问题
大学物理第一学期作业中的问题
质点运动学、动力学 作业中问题
凌亚文
一、选择题
大学物理第一学期作业中的问题
1.一小球沿斜面向上运动,其运动方程为 S 5 4t t 2
(SI), 则小球运动到最高点的时刻是
(A) t =4s ; (B) t =2s ;(C) t =8s ;(D) t =5s
解:切向加速度不变
at
d dt
不变
att
a 45° at
2
an
an R
总加速度恰与半径成45°角,说明: an at
at
at2t 2 R
得出: t = 1s
凌亚文
大学物理第一学期作业中的问题
an at 3 m / s2 att 3m / s
an at
1 2
F0 (2R)2
2F0 R2
x
O
凌亚文
大学物理第一学期作业中的问题
9.一质量为m的质点,在半径为R的半球形容器中,由静止 开始自边缘上的A点滑下,到达最低点B点时,它对容器的 正压力数值为N ,则质点自A滑到B的过程中,摩擦力对其 作的功为 解 质点系: 质点+容器
动能定理:
A外 A内 A重 A摩 E动
解:
y(t) ?
y
dy dt
凌亚文
大学物理第一学期作业中的问题
y(t) ?
已知: H h dx
dt
l 变量
l H h y y l H h (H h)2 x2 H h
x t
y
72.25 t2 8.5
y
dy dt
t 72.25 t 2
(A) x 2t ;3(B) x 4t 1 t;2(C)
2
解: (4 t 2 ) dx
dt
x 4t 1 t 3 12 ; (D) x 4t 1 t 3 12
3
3
dx (4 t2 )dt
x 4t 1 t3 C 3
当t =3s时,质点位于 x = 9m 处
( mg )2 2 mg h
k
k
凌亚文
三、计算题
大学物理第一学期作业中的问题
1.一质点从静止开始作直线运动,开始加速度为a ,此后加速 度随时间均匀增加,经过时间τ后,加速度为 2a ,经过时间 2τ后,加速度为 3a ,···。求经过时间 nτ后,该质点的加速度 和走过的距离。
