全版三角形三线定理.ppt
合集下载
三线合一等腰三角形ppt课件
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
情景引入：
小学时，我们学习过等腰三角形的初步知识，现在 我们进一步研究有关等腰三角形的知识。
探究新知：
请同学们把一张长方形纸对折，并剪去阴影部分， 再把它展开，得到的△ABC有什么特点？
拓展提高:
. 1 等腰三角形的顶角等于一个底角的4倍时, 则顶角为____度．
2 如图(2) 在△ABC中, AB＝AC, CD⊥AB于D, 则下列判断正确的是 A.∠A＝∠B B.∠A＝∠ACD C.∠A＝∠DCB D.∠A＝2∠BCD
3 如图(3), 已知：点D,E在△ABC的边BC上,AB=AC,AD=AE. 求证：BD=CE
你从以上的证明中还能得出什么结论？
性质：
1 等腰三角形两个底角相等（简写为“等边对等角”）
2 等腰三角形顶角平分线、底边上 的中线、底边上的高相互重合。 （简称“等腰三角形三线合一”）
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
在△ABC中，∠A=36 ° ∠ABC=∠C=72 °
巩固训练 经营者提供商品或者服务有欺诈行为的，应当按照消费者的要求增加赔偿其受到的损失，增加赔偿的金额为消费者购买商品的价款或接受服务的费用
1、等腰三角形的一个角是40度，它的另外两个角 的度数是多少呢？
2、等腰三角形的一个角是100度，它的另外两 个角的度数是多少呢？
A A
D
B 图(2)
B C
D 图(3)
情景引入：
小学时，我们学习过等腰三角形的初步知识，现在 我们进一步研究有关等腰三角形的知识。
探究新知：
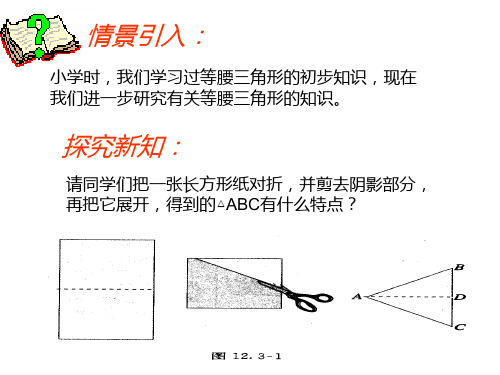
请同学们把一张长方形纸对折，并剪去阴影部分， 再把它展开，得到的△ABC有什么特点？
拓展提高:
. 1 等腰三角形的顶角等于一个底角的4倍时, 则顶角为____度．
2 如图(2) 在△ABC中, AB＝AC, CD⊥AB于D, 则下列判断正确的是 A.∠A＝∠B B.∠A＝∠ACD C.∠A＝∠DCB D.∠A＝2∠BCD
3 如图(3), 已知：点D,E在△ABC的边BC上,AB=AC,AD=AE. 求证：BD=CE
你从以上的证明中还能得出什么结论？
性质：
1 等腰三角形两个底角相等（简写为“等边对等角”）
2 等腰三角形顶角平分线、底边上 的中线、底边上的高相互重合。 （简称“等腰三角形三线合一”）
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
在△ABC中，∠A=36 ° ∠ABC=∠C=72 °
巩固训练 经营者提供商品或者服务有欺诈行为的，应当按照消费者的要求增加赔偿其受到的损失，增加赔偿的金额为消费者购买商品的价款或接受服务的费用
1、等腰三角形的一个角是40度，它的另外两个角 的度数是多少呢？
2、等腰三角形的一个角是100度，它的另外两 个角的度数是多少呢？
A A
D
B 图(2)
B C
D 图(3)
三角形内角和ppt课件完整版
度或边长。
余弦函数
cosA = b/c，表示邻边与斜边的 比值，同样用于直角三角形中。
正切函数
tanA = a/b，表示对边与邻边的比 值，常用于求解直角三角形的角度。
三角函数在解三角形中应用
已知两边及夹角求第三边
01
利用正弦定理或余弦定理求解。
已知三边求角度
02
利用余弦定理求解角度，再结合三角形内角和为180度求解其他
算错误。
公式选择
根据已知条件选择合适的公式 进行计算，避免使用错误的公
式导致结果不准确。
精度问题
在计算过程中要注意精度问题， 避免因舍入误差导致结果不准
确。
06
总结回顾与拓展延伸
关键知识点总结回顾
三角形的内角和定义 三角形三个内角的度数之和等于180度。
三角形内角和定理的证明 可以通过多种方法证明，如平行线性质、外角性质等。
角度。
已知两角及一边求其他边和角
03
利用正弦定理和三角形内角和求解。
边长比例与角度关系探讨
边长比例对角度的影响
在三角形中，边长比例的变化会影响角度 的大小，如等腰三角形底角相等。
VS
角度对边长比例的影响
角度的变化也会影响三角形的边长比例， 如直角三角形中，30度角所对的直角边等 于斜边的一半。
典型问题解决方法分享
建筑设计
建筑设计中经常涉及到三角形的面积计算，如屋顶、窗户等部分的 设计。
物理问题
在物理问题中，三角形的面积计算也经常出现，如求解力的大小和方 向等。
误区提示和易错点剖析
01
02
03
04
底和高的对应
在计算三角形面积时，一定要 注意底和高的对应关系，避免
余弦函数
cosA = b/c，表示邻边与斜边的 比值，同样用于直角三角形中。
正切函数
tanA = a/b，表示对边与邻边的比 值，常用于求解直角三角形的角度。
三角函数在解三角形中应用
已知两边及夹角求第三边
01
利用正弦定理或余弦定理求解。
已知三边求角度
02
利用余弦定理求解角度，再结合三角形内角和为180度求解其他
算错误。
公式选择
根据已知条件选择合适的公式 进行计算，避免使用错误的公
式导致结果不准确。
精度问题
在计算过程中要注意精度问题， 避免因舍入误差导致结果不准
确。
06
总结回顾与拓展延伸
关键知识点总结回顾
三角形的内角和定义 三角形三个内角的度数之和等于180度。
三角形内角和定理的证明 可以通过多种方法证明，如平行线性质、外角性质等。
角度。
已知两角及一边求其他边和角
03
利用正弦定理和三角形内角和求解。
边长比例与角度关系探讨
边长比例对角度的影响
在三角形中，边长比例的变化会影响角度 的大小，如等腰三角形底角相等。
VS
角度对边长比例的影响
角度的变化也会影响三角形的边长比例， 如直角三角形中，30度角所对的直角边等 于斜边的一半。
典型问题解决方法分享
建筑设计
建筑设计中经常涉及到三角形的面积计算，如屋顶、窗户等部分的 设计。
物理问题
在物理问题中，三角形的面积计算也经常出现，如求解力的大小和方 向等。
误区提示和易错点剖析
01
02
03
04
底和高的对应
在计算三角形面积时，一定要 注意底和高的对应关系，避免
三角形的三条重要线段PPT课件
04
典型例题分析与讲解
中线相关例题分析
解题思路
利用中线性质，将AD与AB、 AC的长度联系起来，通过不等 式求解。
解题思路
通过构造平行线，利用中线与 平行线的关系证明三线交于一 点。
例题1
已知三角形ABC中，D为BC中 点，AD为中线，求AD的长度 范围。
知识点
中线定义及性质，三角形不等 式。
知识点
绘制锐角三角形、直 角三角形和钝角三角 形
利用不同颜色或线型 区分三条线段，增强 视觉效果
在每个三角形中标出 角平分线、中线和高 线
测量和比较不同类型三角形中各条线段长度
使用测量工具（如直尺、量角 器等）测量各条线段的长度
比较同一三角形中不同线段长 度，观察规律
比较不同三角形中相同类型线 段的长度，分析差异原因
02
三角形中的三条重要线段
中线定义及性质
01
02
03
定义
连接三角形任意两边中点 的线段叫做三角形的中线。
性质
三角形的中线平分三角形 的面积，即三角形的面积 被中线分为两个相等的部 分。
应用
中线常用于解决与三角形 面积、重心有关的问题。
角平分线定义及性质
Байду номын сангаас定义
从一个角的顶点出发，把这个角分成 相等的两个角的射线叫做角的平分线。
距离和高度差。
03
日常生活
在日常生活中，许多物品的形状和结构都与三角形及其线段有关，如自
行车支架、相机三脚架等。了解这些性质有助于我们更好地理解和利用
这些物品。
THANKS
感谢观看
04
例题2
在三角形ABC中，角A的平分线AD与 BC交于点D，求证：三角形ABD与三 角形ACD的面积之比等于BD/CD。
高考数学一轮复习课件 解三角形中的“三线”技巧问题(共11张PPT)
2017年 题11 题16 题17（角平分线）
2016年 题4 题15
题9（高线）
2015年 题16 题17（角平分线）
纵观近几年的全国高考，在“三角函数与解三角形”的 考查中，不仅要关注传统的“边角互化”，更要关注对“平 面图形的分析”。三角形的中线、高线、角平分线作为三角 形中的三条重要线段，以它们为背景的题目屡见不鲜。
中线
三角形中，连结一个顶点和它所对边的中点的连线段叫做三角形 A
的中线。
B
D
C
高线 从三角形一个顶点向它的对边（或对边所在的直线）作垂线，顶
点和垂足间的线段叫做C
三角形的一个角的平分线与这个角的对边相交，连结这个角
的顶点和交点的线段叫做三角形的角平分线。（也叫三角形 A
的内角平分线。）
NEWYORK
B
C
直击高考
1（. 2015年课标Ⅱ）在ΔABC中，D是BC上的点，AD平分BAC，BD 2DC. (1)求 sinB ;
sinC (2)若BAC 60O，求B.
A
B
C D
NEWYORK
直击高考
2（. 2017 年全国卷 Ⅲ）如图，在 ΔABC中，A 120 o , a 2 7，b 2，D是BC上的点， AD AC，求ΔABD的面积.
2019届高三年级数学一轮总复习 《解三角形》专题
解三角形中的“三线”问题
回顾
正弦定理：a b c sinA sinB sinC
余弦定理：a 2 b2 c 2 2bc cosA b2 a 2 c 2 2ac cosB c 2 a 2 b2 2ab cosC
解三角形： ①已知三角形的一边及两角，可用正弦定理 ②已知三角形的两边及一边的对角，可用正弦定理或余弦定理
三角形的分类完整ppt课件
判定
三条边长度都不相等的三 角形是不等边三角形
特殊类型三角形对比
等腰三角形与等边三角形的区别与联系
等腰三角形至少有两边相等，而等边三角形三边都相等；等边三角形是特殊的等腰 三角形，但等腰三角形不一定是等边三角形。
不等边三角形与其他三角形的区别
不等边三角形的三边长度都不相等，而其他类型的三角形至少有两边长度相等。
三角形外角性质
三角形外角的定义
三角形的一边与另一边的延长线组 成的角，叫做三角形的外角。
三角形外角性质
三角形的外角等于与它不相邻的两 个内角的和；三角形的一个外角大 于任何一个与它不相邻的内角。
三角形不等式定理
三角形不等式定理
任意两边之和大于第三边，任意 两边之差小于第三边。
推论1
在三角形中，如果两边之和等于 第三边，那么这个三角形不存在。
01
有一个内角等于90度
02
两直角边相等
03
斜边等于直角边的√2倍
04
具有对称性，关于斜边的中垂线对称
03 按边分类
等腰三角形
定义
01
有两边长度相等的三角形
性质
02
两等边所对的两内角相等；底边上的中线、高线和顶角的平分
线“三线合一”
判定
03
有两条边相等的三角形是等腰三角形；有两个内角相等的三角
形是等腰三角形
已知两边及夹角求其他元素
通过正弦定理，可以求解三角形的其他边或角。
判断三角形形状
结合正弦定理和已知条件，可以判断三角形的形状（如锐角、直角 或钝角三角形）。
余弦定理在解三角形中应用
余弦定理的公式表达
在任意三角形ABC中，有$a^2 = b^2 + c^2 - 2bccos A$，以及相应的其他两个式子。
2024版三角形的三线及中位线课件通用[1]
![2024版三角形的三线及中位线课件通用[1]](https://img.taocdn.com/s3/m/f5c08ac803d276a20029bd64783e0912a3167c6d.png)
利用高线证明三角形全等或相似
在证明两个三角形全等或相似时，有时需要利用高线的性质来证明对应边或对应角相等。
2024/1/28
利用高线解决与三角形有关的实际问题
在实际问题中，如测量、建筑等领域，经常需要利用三角形的性质来解决问题。高线作为三 角形的重要性质之一，在这些问题的解决过程中发挥着重要作用。
17
2024/1/28
三角形定义
由不在同一直线上的三条线段首尾 顺次连接所组成的封闭图形。
三角形分类
按边可分为不等边三角形、等腰三 角形和等边三角形；按角可分为锐 角三角形、直角三角形和钝角三角 形。
4
三角形内角和定理
三角形内角和定理
三角形的三个内角之和等于180°。
内角和定理的推论
直角三角形的两个锐角互余；一个三角形中至少有两个锐角。
高线的性质
直角三角形三条高线的交点恰好是 三角形的直角顶点。
高线定义：从三角形的一个顶点向 它的对边所在的直线作垂线，顶点 和垂足之间的线段叫做三角形的高 线，简称为三角形的高。
2024/1/28
锐角三角形三条高线交于三角形内 部一点。
钝角三角形中，两条高线所在直线 的交点在三角形外部。
14
高线长度计算公式
2024/1/28
5
三角形外角性质
三角形外角定义
三角形的一个外角等于与它不相邻的 两个内角的和。
三角形外角性质
三角形的外角大于任何一个与它不相邻 的内角。
2024/1/28
6
特殊三角形性质
等腰三角形性质
两腰相等，两底角相等；底边上 的高、中线及顶角的平分线互相
重合（三线合一）。
2024/1/28
等边三角形性质
上海初中 三角形的三线及中位线课件
例题： 例题： 求证三角形的一条中位线与第 三边上的中线互相平分． 三边上的中线互相平分．
已知： 如图所示，在△ABC中，AD＝DB，BE＝EC，AF ＝FC． 求证： AE、DF互相平分． 连结DE、EF． 证明 连结 ∵ AD＝DB，BE＝EC， ∴ DE∥AC（三角形的中位线平行 于第三边并且等于第三边的一 半）． 同理EF∥AB． ∴四边形ADEF是平行四边形． ∴ AE、DF互相平分（平行四边形 的对角线互相平分）．
A２
C１ B２ C
分析：填表 分析：
次序 1 2 3 ……
B
n
B１
所得三角 形周长 所得三角 形面积
1 2 1 4
a s
1 4 1 16
a s
1 8 1 64
a s
……
……
1 n 2 1 n 4
a s
• 12. 如图，在△ABC中，D是BC中点，N是 AD中点，M是BN中点，P是MC的中点。 • 求证：S△MNP＝ 1/8 S△ABC
A D O B F C E A A D O B F C O B D C
E
E
F
已知：如图， 的角平分线BM、 练习： 已知：如图，△ABC的角平分线 、CN 的角平分线 相交于点P. 相交于点 求证： 到三边AB、 、 的距离相等 的距离相等. 求证：点P到三边 、BC、CA的距离相等 到三边 证明：过点 作 分别垂直于AB、 、 ， 证明：过点P作PD 、PE、PF分别垂直于 、BC、CA， 、 分别垂直于 垂足为D、 、 垂足为 、E、F 的角平分线， ∵BM是△ABC的角平分线，点P在BM上 是 的角平分线 在 上 ∴PD=PE 在角平分线上的点到角的两边的距离相等） （在角平分线上的点到角的两边的距离相等） A 同理 PE=PF. D ∴ PD=PE=PF. F 即点P到边 到边AB、 、 即点 到边 、BC、 N PM CA的距离相等 的距离相等
三线垂直定理
三线垂直定理1. 引言三线垂直定理是几何学中的一个重要原理，用于描述三角形内部各个线段之间的关系。
它是基础几何学中的一个重要概念，不仅在数学教育中被广泛教授，也在实际问题中有着广泛的应用。
本文将对三线垂直定理进行全面详细、完整且深入的讨论。
2. 三线垂直定理的表述三线垂直定理又称为欧拉定理，它描述了三角形内部几条特殊线段之间的关系。
具体而言，对于任意一个三角形ABC，它的三条特殊线段：高、中线和垂心连线，在一个点上相交，并且相交点与三个顶点连成的线段互相垂直。
图1：欧拉定理示意图（图片来源：维基百科）3. 欧拉定理证明3.1 高与中线相交于垂心首先证明高与中线相交于垂心。
设高所在直线为AD（D为BC的垂足），中线所在直线为BE（E为AC的中点）。
我们需要证明AD与BE相交于一个点O，并且AO与BO互相垂直。
考虑△ABC，由于D是BC的垂足，所以AD⊥BC。
又因为E是AC的中点，所以BE平分∠CBA。
假设AD与BE相交于点O，我们需要证明AO⊥BO。
由于△ADC和△BEC是等腰三角形（AD = CD，BE = CE），所以∠DAC = ∠DCA 和∠EBC = ∠ECB。
又因为∠ABC = ∠ADC + ∠BEC（内角和等于外角）, 所以∠ABC = (∠DAC + ∠DCA) + (∠EBC + ∠ECB) = 180°。
根据反证法可知，若AO不⊥BO，则∠ABC ≠ 180°，与前述结论矛盾。
因此，AO⊥BO成立。
3.2 垂心连线接下来证明垂心连线也经过点O。
设垂心所在直线为CF（F为AB的垂足），我们需要证明CF经过点O。
考虑△ABC，由于F是AB的垂足，所以CF⊥AB。
同样地，根据前述证明可知CO⊥AB。
我们需要证明CF经过点O，即证明CO⊥CF。
假设CO与CF不垂直，则存在一条直线DE与CO和CF分别相交于点D和E，并且CD ≠ CE。
考虑△ABC，由于F是AB的垂足，所以∠ACF = 90°。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A
∵BE是△ABC的角平分线
∴∠ABE=_∠_C_B_E_
=
1 2
_∠_A_B_C_
F
E
O
∵CF是△ABC的角平分线
B
∴∠ACB=2__∠__A_C_F=2__∠_B_C_F_
D
C
三角形的角平分线与角的
思
平分线有什么区别？
考
三角形的角平分线是一条线段 , 角 的平分线是一条射线课件.
基础练习
1、点D是△ABC的BC边上的一点。 A ∵BD=CD，
课件
三角形的角平分线
在三角形中，一个内角的角平分线与它的对边相交，
这个角的顶点与交点之间的线段 叫做三角形的角平分线。
,
A
∵AD是 △ ABC的角平分线
●
∴∠ BAD = ∠ CAD = ２１∠BAC （角平分线的定义）
B
︶
●
D
C
三角形的三条角平分线相交于一点,交点在三 角形的内部。
课件ቤተ መጻሕፍቲ ባይዱ
角平分线的理解
课件B
D
C
三角形的高
(2)怎样画下面三角形的高线？（画法
）A
A
A
G
F
B
E
CB
D
F
CB
CD E
课件
三角形的中线
在三角形中,连接一个顶点与它对边中点的线段
叫做这个三角形这边的中,线 .
A 重心
●
∵AD是△ ABC的中线
F
E O
∴BD=CD= 12BC（中线的定义B）
●
D
C
三角形的三条中线相交于一点,交点在三角形的内部.
课件
三角形的高
从三角形的一个顶点 向它的对边 所在直线作垂线，顶点 和垂足 之间的线段 叫做三角形这边的高，
简称三角形的高。 B
如图, 线段AD是BC边上的高.
A
0
1
01 23 4 5
2
3
4
5
6
7
8
9
01 23 4 5
10
D
C
任意画一个锐角△ABC,
A
请你画出BC边上的高.
注意 ! 标明 垂直的记号 和垂足的字母.
=
∠ BAC
2
。
(2) ∵AM是△ABC的中线，
∴ BM = CM = 1 BC 。
A
2
（3）∵AH是△ABC的高，
∴∠AHC=∠ AHB =90°
B
MDH C
课件
迁移提升
5、如图，BD=DE=EF=FC。 AD是△A__B_E_的中线，
_A__F_是△AEC的中线，
A
AE是△A__B_C_和△_A__D_F_的中线。
课件
∴线段AD是△ABC的中__线_
B
D
C
∵∠BAD=∠CAD，
A
∴线段AD是△ABC的角__平__分_ 线
B
D
C
A
∵∠ADC=90°，
∴线段AD是△ABC的_高__
课件
B
D
C
2、如图，AD、AM、AH分别是△ABC的角平分线、中 线、高。
（1）∵AD是△ABC的角平分线，
1
∴∠ BAD =∠ DAC
B
D课件
E
FC
总结归纳
• 1、三角形中的三条线段是:
•
高线、角平分线、中线
• 2、三角形中的高、角平分线、中线都是线段
• 3、锐角三角形的三条高交与一点，此点在三角形 的内部；直角三角形的三条高交与直角顶点；钝 角三角形 的三条高也交与一点，此点在三角形
• 外部
• 4、三角形的一条中线分成的两个三角形面积相等