判断推理逻辑判断
判断推理常用公式
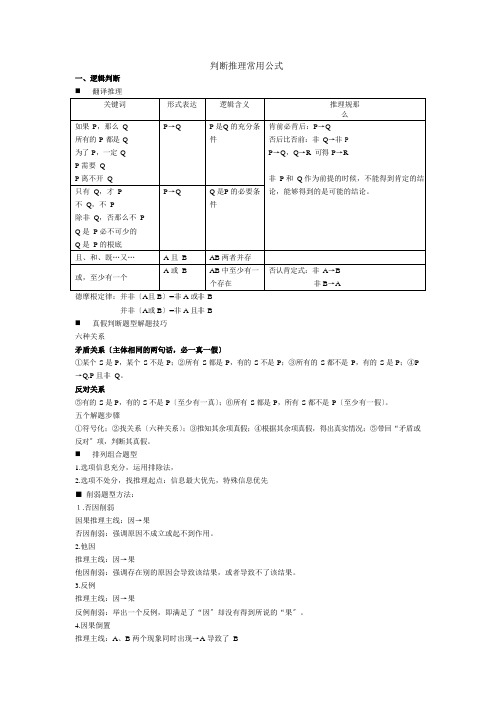
判断推理常用公式
一、逻辑判断
⏹翻译推理
德摩根定律:并非〔A且B〕=非A 或非B
并非〔A或B〕=非A 且非B
⏹真假判断题型解题技巧
六种关系
矛盾关系〔主体相同的两句话,必一真一假〕
①某个S 是P,某个S 不是P;②所有S 都是P,有的S 不是P;③所有的S 都不是P,有的S 是P;④P →Q,P 且非Q。
反对关系
⑤有的S 是P,有的S 不是P〔至少有一真〕;⑥所有S 都是P,所有S 都不是P〔至少有一假〕。
五个解题步骤
①符号化;②找关系〔六种关系〕;③推知其余项真假;④根据其余项真假,得出真实情况;⑤带回“矛盾或反对〞项,判断其真假。
⏹排列组合题型
1.选项信息充分,运用排除法,
2.选项不处分,找推理起点:信息最大优先,特殊信息优先
■削弱题型方法:
1.否因削弱
因果推理主线:因→果
否因削弱:强调原因不成立或起不到作用。
2.他因
推理主线:因→果
他因削弱:强调存在别的原因会导致该结果,或者导致不了该结果。
3.反例
推理主线:因→果
反例削弱:举出一个反例,即满足了“因〞却没有得到所说的“果〞。
4.因果倒置
推理主线:A、B 两个现象同时出现→A 导致了B。
判断推理逻辑推理常考知识点

判断推理逻辑推理常考知识点一、逻辑推理基本概念。
1. 命题。
- 定义:可以判断真假的陈述句。
例如“今天是晴天”就是一个命题。
- 简单命题:不能再分解为更简单命题的命题。
像“小明是学生”。
- 复合命题:由简单命题通过逻辑联结词组合而成的命题。
如“小明是学生并且小红是老师”,其中“并且”就是逻辑联结词。
2. 逻辑联结词。
- 且(∧):表示两个命题同时成立。
例如,命题p:小明是男生,命题q:小明是学生,那么p∧q表示小明是男生并且是学生。
当p和q都为真时,p∧q才为真。
- 或(∨):表示两个命题至少有一个成立。
比如命题p:今天是周一,命题q:今天是周二,p∨q表示今天是周一或者是周二。
只要p、q中有一个为真,p∨q就为真。
- 非(¬):对一个命题进行否定。
若命题p:小李是好人,那么¬p:小李不是好人。
p为真时,¬p为假;p为假时,¬p为真。
3. 充分条件与必要条件。
- 充分条件:如果有事物情况A,则必然有事物情况B;如果没有事物情况A,但未必没有事物情况B,A就是B的充分而不必要的条件,简称充分条件。
例如,如果天下雨(A),那么地面湿(B),天下雨是地面湿的充分条件。
- 必要条件:如果没有事物情况A,则必然没有事物情况B;如果有事物情况A而未必有事物情况B,A就是B的必要而不充分的条件,简称必要条件。
只有年满18周岁(A),才能有选举权(B),年满18周岁是有选举权的必要条件。
1. 三段论推理。
- 定义:由两个包含着一个共同项的性质判断作前提,得出一个新的性质判断为结论的演绎推理。
例如:所有的金属都能导电(大前提),铜是金属(小前提),所以铜能导电(结论)。
- 规则:- 在一个三段论中,有且只能有三个不同的项。
- 中项在前提中至少要周延一次。
- 在前提中不周延的项,在结论中也不得周延。
- 如果前提中有一个是否定的,那么结论也是否定的;如果结论是否定的,那么前提中必有一个是否定的。
完整版逻辑判断推理技巧大全

逻辑判断推理技巧大全一、演绎推理1.指的是通过一些的前提来论证从而推断出某个结论。
2.基本原则:头脑清空原则(按人家来,不要按自己的来)题设为真原则(人家题设说的是绝对不可怀疑的)形式统一原则3.解题步骤:(1)看问题,定题型;(2)看题目,做简化;(3)据技巧,得答案。
4.演绎推理的分类:(1)论证类——加强论证型——减弱论证型(2)结论类——形式推理结论类:侧重规则的考察——日常推理结论类:侧重脉络的考察(一)形式推理结论类1.分类:有真有假型;翻译推理型(强调对于肯定确定信息的认识);排列组合型(匹配型的题型);集合运算型(很像数学的一种题型)2.有真有假型:1)首先看矛盾;其次看包容;然后看反对;最后带题中(实在不行就代入排除法)(2)矛盾关系:必然一真一假,两者构成整个全集,如生和死;——A:其矛盾关系为否AA且B:其矛盾关系为否(A且B)即否A或否BA或B:其矛盾关系为否(A或B)即否A且否BA能够推出B :其矛盾关系为A且否B所有:其矛盾关系为有的不必然:其矛盾关系为可能不——即首先要寻找矛盾关系,然后根据题目中的真假结论来得出其他几个关系的真假,从而得出相应的最后答案——能用在很多地方,不光是在这里。
比如说在后来的削弱关系中,矛盾是最强的削弱关系——构成矛盾关系的主体一定相同,这是观察矛盾关系的一个重要判断指标。
(3)包容关系:——当不能发现矛盾关系时,我们就要看包容关系,即寻找看几个关系之间是否存在包容。
——即要寻找包容关系,几个关系如果为包容关系,则他们同时为真或为假(这和矛盾关系刚好相反),然后根据题目中的真假结论来得出其他几个关系的真假,从而得出相应的最后答案。
--- 若A能推出B:则包容关系为若A为真则B为真+若B为假则A为假只有一真,则 A 必为假——即“一真前假” 只有一假,则 B 必为真——即“一假后真”所有:则包容关系是能够推出某人、有的A且B:则包容关系是能过推出A (B)、A或者B(4)反对关系:——对于两个“有的” 的反对关系,“必有一真”;对于两个“所有” 的反对关系,“必有一假”;(5)当题目中有多真多假时,可以利用矛盾或包容或反对关系将其转化为一个真或假再解。
行测逻辑判断推理公式

行测逻辑判断推理公式
行测逻辑判断推理涉及到一些常用的公式,具体如下:
1. 充分必要条件公式:表示条件A是事件B发生的充分条件,也是事件B 发生的必要条件。
常见的充分必要条件公式有以下几种形式:
如果A,则B;反之,如果非B,则非A。
A是B的充分必要条件,可以表示为A↔B。
A是B的充分条件,可以表示为A→B。
B是A的必要条件,可以表示为B→A。
2. 命题逻辑公式:通过对命题的逻辑连接和推理,来判断命题的真假。
常见的命题逻辑公式有以下几种形式:
与(∧):表示两个命题都为真时,结果为真;一方为假时,结果为假。
或(∨):表示两个命题有一个为真时,结果为真;两个都为假时,结果为假。
非(¬):表示对一个命题否定,即取反。
蕴含(→):表示如果A成立,则B也成立。
等价(↔):表示A成立当且仅当B成立。
3. 翻译推理:
“如果...就...” 翻译规则:前句推出后句。
“只有...才...” 翻译规则:后句推出前句。
“且” 口诀:全真为真,一假全假。
“或” 口诀:一真既真,全假为假。
4. 逆否命题:肯前必肯后,否后必否前。
否前肯后无必然结果,只能推出可能性结果。
5. 摩根定公式:
-(A 且 B)=-A 或-B
-(A 或 B)=-A 且-B
这些公式在行测逻辑判断推理中应用广泛,可以帮助考生快速准确地解答相关题目。
公务员考试行测判断推理之逻辑推理

公务员考试⾏测判断推理之逻辑推理⼀、假⾔命题1.如果那么(前推后):肯前肯后,否后否前2.只有才(后推前):肯前肯后,否后否前⼆、联⾔命题1. A且B为真,则AB均为真2. A且B为假,则AB⾄少⼀个为假三、选⾔命题1. A或B为真,则AB⾄少⼀个为真2. A或B为假,则AB均为假3.不相容选⾔命题:要么A真B假,要么A假B真四、三个定理1.逆否定理:A推B è -B 推 –A2.摩根定理:1) - (A或B) = -A 且 -B2) - (A且B) = -A 或 –B3.鲁滨逊定理: - (A 推 B) = A 且 -B五、集合推理1.四个基本1)所有A都是B 》A推B2)所有A都不是B 》A推-B3)有的A是B 》有的A推B4)有的A不是B 》有的A推-B2.三个换位1)所有A都是B 》有的B是A2)所有A都不是B 》所有B都不是A3)有的A是B 》有的B是A4)有的A不是B 》不能换位3.两个推出1)所有A都是B 》某个A是B 》有的A是B2)所有A都不是B 》某个A不是B 》有的A不是B4.⼀个递推1) A 推 B ,所有B 推 C 》A推C六、模态命题1.并⾮可能 = 必然不2.并⾮所有 = 有的不3.移动否定词,所有变有的,有的变所有,可能变必然,必然变可能七、真假推理1.⽭盾关系1)某个是和某个不是2)所有的A都是B和有的A不是B3)所有的A都不是B和有的A是B4) A推B和A且-B5) A且B和-A或-B6) A或B和-A且-B2.反对关系1)所有的A都不是B和所有的A都是B2)有的A是B和有的A不是B3.包容关系所有都是(不是)》某个是(不是)》有些是(不是)A且B 》 A(B)》 A或B⼋、四个原则1.话题⼀致原则2.整体优先原则3.可能优先原则4.敏感词汇原则九、七种逻辑关系1.对应关系2.条件关系3.属性关系4.全同关系5.并列关系6.包容关系7.交叉关系更多精彩,关注秋风!。
判断推理知识点梳理

判断推理知识点梳理.判断推理知识点梳理(念卿児)一、总知识体系逻辑判断。
1.类比推理。
2.图形推理。
3.定义判断。
4.二、逻辑判断知识点(一)翻译推理假言命题1.)关联词替换表达2(。
就。
就。
前推后:如果。
就。
;只要。
;要。
①。
后推前:只有。
才。
;除非。
否则不②离不开///不明确:必不可少必须基础、前提必要条件/③“不能没有的项”放在“→”后边2.联言命题与选言命题(2)德摩根定律B 且﹣=﹣A ﹣(A或B)①B或﹣﹣AB且﹣(A)=②(二)集合推理三个换位个基本2.1.4。
(单项不可逆)1()所有的S都是P。
(1)有的P是S=>(双项可逆))所有的(2)所有的S都不是P。
(2P都不是S。
<=>(双项可逆))有的S是P。
(3)有的P是S。
(3<=>)不让换。
有的(4)S不是P。
×(4 两个推出3.。
是都是P。
SP。
S是P(1)所有的S有的=> => 某个。
S不是P S不是P(2)所有的S都不是P有的=> 某个=>(箭头方向不可逆)某个所有有的=> =>一个递推4.C →B→C, AA(1)递推公式:→B,=>2()成立条件:“B”必须指“所有”(三)真假判断,关键是“其余”首先找“矛盾”必有一真,必有一假&矛盾关系:(四)论证类 1.论证的基本结构及思路(1)找论点引导词:因此、所以、认为、观点是、建议、倡导、表明、说明、结果是。
①首尾句原则② 2)表立场( => 削弱加强反对支持 => ②①)根据强度选答案(3 本身方法的强弱关联性②①加强论证类2.最强☆☆☆☆☆)搭桥:建构联系1(.(2)排除他因:加强可能性控制变量A无B有(3)对比试验:有AB,无4)加强论据:(解释原因举例子加强原有论据:/①补充新论据②。
部分重复/同义转换(5)重复论点: 3.削弱论证类最强☆☆☆☆☆(1)因果倒置☆☆☆☆☆最强)否论点(否前提)(2 特点:不能没有次强)拆桥☆☆☆(3 次强)对比试验:☆☆☆(4 A无B,有有A有B①控制变量有B 有A有B,无A ②最弱☆(5)另有他因(6)否论据:☆最弱质疑原论据①提出反向论据②(五)原因解释1.题目形式(1)无关联词(2)设问形式:原因、解释2.解题规范(1)明确目标(2)选项验证(六)日常推理(日常推理没有关联词,翻译推理有关联词)1.主题一致:话题必须聚焦2.主体一致:无关概念必须排除(无中生有/偷换概念/扩大范围)3.优选“可能”4.整体优先:(1)整体>部分(2)主旨>句子(七)分析推理选项信息充分1.(1)直接排除(2)代入排除2.选项信息不充分(1)最大信息优先(2)肯定信息标注3.材料题(1)题干结论:应用所有(2)题目结论:通常不可用三、类比推理知识点(一)三种题型1.两词型2.括号型:选项代入(1)主线:横看/词义(2)辅线:竖看/词性3.三词型(二)七种关系1.同一关系古、今/中、外/雅、俗/自称、他称/书面、口头2.交叉关系3.并列关系:一个概念在一个分类标准下进行分类(1)矛盾关系(2)反对关系4.包容关系:种属关系/组成关系5.属性关系:必然属性/或然属性6.对应关系:一一对应/非一一对应7.条件关系:找方向、找“必要”(三)两种技巧1.造句子2.想逻辑四、图形推理知识点(一)位置类:图形组成相同1.平移(1)方向:上、下、左、右;顺时针、逆时针(2)距离:等差数列(常数列)旋转2.(1)方向:顺时针、逆时针(2)度数:30、45、60、90、120、150、1803.翻转:横/纵4.静态位置(1)上、下、左、右、前、后、内、外(2)相离、相交、相切(3)平行、垂直(4)面积大小(二)样式类:图形组成相似1.遍历(缺啥补啥)(1)分层:九宫格一行遍历一层(2)层与层之间的组成元素完全相同(3)层与层之间找元素的全集2.运算(1)规则运算:加、减、同、异&同:无关图形的大小、比例、面积(2)特殊运算:没有任何既定运算规则①所有的运算规则都要在题目中总结并在题目中运算②加法交换律不适用③(三)数量类:图形组成凌乱1.点(1)通常情况下端点不数(2)点分为:交点、切点、顶点(3)先数所有的点,再数某一类点(4)重点:曲线和直线的交点2.线(1)直线(2)曲线(3)直线与曲线之和 4)笔画(相关知识点:一笔画问题 1)简单图:直接画(奇点个数是0或者的图形可以一笔画2奇点:2()复杂图:数奇点:从一个点引出线的条数是奇数&切多边形:内部能,整图能;内部不能,整图不能。
逻辑判断推理技巧大全

逻辑判断推理技巧大全一、演绎推理1.指的是通过一些的前提来论证从而推断出某个结论。
2.基本原则:头脑清空原则(按人家来,不要按自己的来)题设为真原则(人家题设说的是绝对不可怀疑的)形式统一原则3.解题步骤:(1)看问题,定题型;(2)看题目,做简化;(3)据技巧,得答案。
4.演绎推理的分类:(1)论证类——加强论证型——减弱论证型(2)结论类——形式推理结论类:侧重规则的考察——日常推理结论类:侧重脉络的考察(一)形式推理结论类1.分类:有真有假型;翻译推理型(强调对于肯定确定信息的认识);排列组合型(匹配型的题型);集合运算型(很像数学的一种题型)2.有真有假型:(1)首先看矛盾;其次看包容;然后看反对;最后带题中(实在不行就代入排除法)(2)矛盾关系:必然一真一假,两者构成整个全集,如生和死;——A:其冲突干系为否AA且B:其冲突干系为否(A且B)即否A或否BA或B:其冲突干系为否(A或B)即否A且否BA能够推出B:其矛盾关系为A且否B所有:其冲突干系为有的不必然:其矛盾关系为可能不——即第一要寻觅冲突干系,然后根据题目中的真假结论来得出其他几个干系的真假,从而得出响应的最后答案——能用在很多地方,不光是在这里。
比如说在后来的削弱关系中,矛盾是最强的削弱关系——构成矛盾关系的主体一定相同,这是观察矛盾关系的一个重要判断指标。
(3)包容关系:——当不能发现冲突干系时,我们就要看包涵干系,即寻觅看几个干系之间是否存在包涵。
——即要寻觅包涵干系,几个干系如果为包涵干系,则他们同时为真或为假(这和冲突干系恰好相反),然后根据题目中的真假结论来得出其他几个干系的真假,从而得出响应的最后答案。
——若A能推出B:则包容关系为若A为真则B为真+若B为假则A为假只有一真,则A必为假——即“一真前假”只有一假,则B必为真——即“一假后真”——所有:则包容关系是能够推出某人、有的A且B:则包容关系是能过推出A(B)、A或者B(4)否决干系:——对于两个“有的”的否决干系,“必有一真”;对于两个“所有”的反对关系,“必有一假”;(5)当题目中有多真多假时,可以利用矛盾或包容或反对关系将其转化为一个真或假再解。
判断推理逻辑判断推理口诀

判断推理逻辑判断推理口诀
一、判断推理逻辑判断推理口诀
嘿,宝子们!今天咱们来唠唠判断推理逻辑判断推理口诀呀。
1. 肯前必肯后,否后必否前
这就像是一个规则,要是前面的条件成立,那后面的结果肯定就会出现。
反过来呢,如果后面的结果不成立,那前面的条件肯定也不成立啦。
比如说,如果是下雨(前)就会地湿(后),要是地没湿,那就肯定没下雨。
2. 否前肯后推可能
要是前面的条件不成立,或者后面的结果成立了,那这个时候呀,只能说有这种可能性,不能确定一定是怎么回事。
就好比说,不下雨的时候,地有可能湿(因为可能有人泼水之类的),地湿的时候,也不一定就是下雨导致的。
3. 两个所有至少一假
如果有两个都是说“所有”的情况,那这里面至少有一个是假的哦。
比如说,所有的苹果都是红的,所有的苹果都是绿的,这俩肯定有一个是错的呀。
4. 两个有的至少一真
要是出现两个都是“有的”的说法,那这里面至少有一个是真
的呢。
像有的花是红色的,有的花是白色的,这两个说法里至少有一个是真的。
5. 所有可以推有的
要是所有的东西都有某个特征,那肯定有的东西就有这个特征啦。
就像所有的鸟都会飞,那当然有的鸟会飞咯。
6. 必然推可能
如果一件事是必然会发生的,那它肯定是有可能发生的啦。
比如说,太阳必然从东方升起,那太阳肯定是有可能从东方升起的呀。
宝子们,把这些口诀记住,做判断推理的时候就会轻松不少呢!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全面大于片面
结论型题目(排除主观项,含有“可能”,“一些”的词语)
推出推出
矛盾
有的A是B.........................下反对.............................有的A不是B
“所有A是B”与“有的A不是B”、“.所有A不是B”与“有的A是B”必有一真一假
“所有A是B”与“.所有A不是B”必有一假(可以同假)
“有的A不是B”与“有的A是B”必有一真(可以同真)
有些A是B有些B是A
有些A不是B
特殊词量(少数,大部分,一半)作为量项引导命题,不能换位
三段论推理(两个直言命题作为前提/一个直言命题作为结论)
(两个前提包含三个概念/前提和结论中,每个概念都出现两次)
两条常用规则一特得特:两个前提不能都是特称命题(含有“有的”命题)
只有一个前提是特称,结论也是特称
A B
交叉关系(两个概念的外延有重合部分,也有不重合部分)
A B
真包含(于)关系 A
B
②用概念间关系表示直言命题
直言命题(简单命题),是断定对象是否具有某种性质的单句
直言命题的对当关系(不同直言命题之间在真假方面所存在的制约关系)
所有A是B.......................反对..........................所有A不是B
正确选项起到正反两方面的评价作用,
(则一方面起支持作用,一方面起削弱作用)
直接评价论证方法(给出一个论证或一段对话,概括或指出其中逻辑错误)
寻找相似的逻辑结构: 论证推理,分析题干和选项的论证方式
命题推理,分析题干和选项的句子结构
找争论的焦点(给出对话,找出两人所争论的焦点)
焦点必须与双方所述内容具有相关性
加强型(题干由于论据不够充分而不足以得出该结论,要求
选出能够(或不能)加强题干的选项)
前提型(特殊的加强型题目,要求选出能够(或不能)成为题
干前提或假设的选项,正确选项是论证成立的必要条件)
①题干论证结构分析(了解论证的结构及常见类型 找到漏洞 )
(削弱—具体指出漏洞/加强—尽量弥补漏洞)
论据(用什么来证明论点)论证方式(如何用论据来证明论点)论点(结论)(论证什么)
反应条件的肢命题在前,称为前件
反应结果的肢命题在前,称为后件
一、定义及真假关系①充分条件(条件P存在时,结论Q一定成立,P是Q的充分)
(如果P,那么Q(P Q))
(只要…就,若….则,….必须…)
②必要条件(条件P不存在,结论Q一定不成立)
(只有P,才Q(P Q))
(不…不…,除非,否则不,没有….就没有…)
从题干数据出发,补充评价观点所需要的其他相关数据使结论成立
③因果论证(通过揭示事物之间存在的因果联系而得出某种观点)(求异法,对比得出因果)
某一事件与另一事件的发生(或不发生),推出两个事件的因果关系
两个比较场合中出现的不同情况必须是唯一的
两个比较场合中唯一不同的情况可能只是被研究对象的部分原因
削弱:指出题干因果关系不成立、“因果倒置”、除了原因条件外有其他不同的条件、
焦点必须是双方在该论题上的观点构成对抗
结论型(类似于言语理解与表达的片段阅读题)
错误选项:无中生有,过度推断(由题干信息无法客观推出的选项),
偷换概念,与题干信息相矛盾的选项,
违反假言推理规则的选项
正确选项:既可能是对题干材料整体内容的概括,也可能对题干某一细节概括
选项分析①识别迷惑选项: 偷换概念
②归纳论证(从一系列个别性的前提出发,引申出一般性结论)
某类对象的每一个对象(部分对象)都具有或不具有属性A
所以,该类对象的全体都具有或不具有属性A
削弱:指出所调查的样本或部分特殊,没有代表性,不能推广到整体
指出与整体相关的其他事实,这一事实足以影响整体
加强:说明样本选择正确,具有代表性或样本数量充足
当两者之间存在的不同属性与推知属性没有必然联系时,削弱力度较弱
加强:指出两者之间具有很高的相似性
⑥非论证 削弱:直接指出论点/论据错误; 指出方法不可行或达不到目的
加强:直接指出论点/论据正确; 说明方法是可行的
解释型(给出某一个事实或论证的描述(结论、现象、矛盾或差异),
找出最能够合理解释题干的选项)
推理规则:肯定前件则肯定后件,否定后件则否定前件
否定前件不能否定后件,肯定后件不能肯定前件
②必要条件:无P必无Q,有Q必有P
P Q=非P非Q(否定前件)=Q P(肯定后件)
(只有P,才Q=如果非P,那么非Q=如果Q,那么P)
推理规则:否定前件则否定后件,肯定后件则肯定前件
肯定前件不能肯定后件,否定后件不能否定前件
通常情况,论点(结论)会出现在段首或段尾,是专家的看法,也可能是某些研究的结果
论证分析方法 找提示词:“因此、据此、说明、认为、推测、建议”后是论点
“因为、由于、假如、理由是、调查、统计、实验、研究”后是论据
分析因果联系:论据(支持论点),作为原因或现象
论点(根据论据得出的观点),作为结果或对对象的总结概括
诉诸权威(无实质证据,以身份是否权威来说明问题)
(不是出现“权威”、“专家”字样)
诉诸无知(通过说明没有证据证明为真来削弱论证)
诉诸众人(不是出现“很多”)(仅是主观看法或主观行为)
不当类比/特殊比例(选项仅仅相对于其他选项来,
其程度较弱)
②选项比较原则 削弱型题目(加强型题目/解释型题目)
直接大于间接
一、必然性推理概念间关系
直言命题的对当关系
直言命题的变形推理
三段论推理
联言命题与选言命题
假言命题
模态命题
智力推理
概念间关系(概念,是构成命题与推理的基础,只有表达了一类事物的词语才是概念)
①四种概念间关系(概念所表达的事物范围 概念的外延)
全同关系(两个概念的外延完全相同)
A B
全异关系(两个概念的外延完全不同,无重合)
(P或者Q)
联结词:表选择关系(或者…或者)
b.不相容选言命题(有且只有一种情况存在/要么P,要么Q)
“或…或..”,二者不可兼得
联言命题与相容选言命题是相互矛盾命题
二、推理规则①联言命题:一个联言命题为真构成其的每个肢命题为真
否定一个肢命题否定联言命题
否定联言命题 否定一个肢命题
②选言命题
假言命题(带有假设性的命题,包含两个肢命题)
一否得否:两个前提不能都是否定命题
只有一个前提是否定,结论也是否定
联言命题与选言命题
复言命题(有两个或多个单句通过联结词联结的命题)联言命题
选言命题
假言命题
一、定义及真假关系①联言命题(多做做情况同时存在/P并且Q)
联结词:表并列、递进、转折、顺承等关系
(虽然…但是/既…又)
②选言命题
a.相容选言命题(至少有一种情况存在,可以同时存在)
一个命题前面+“并非”=这个命题的矛盾命题
所有与有的互换,有“不”的去掉,没“不”的加上
直言命题的变形推理(通过改变前提中直言命题的联项或主项与谓项的关系结论)
①换质推理(换一种说法)
双重否定表示肯定
将“不是”改为“是”或将“是”改为“不是”
②换位推理(倒过来说)所有A是B有些B是A
所有A不是B所有B不是A
③充分必要条件(P既是Q的充分,又是Q的必要)
(P当且仅当Q(P Q))
(若…则…,且若不…则不…,当且仅当…才…)
区别:充分条件(有P必有Q)
必有条件(无P必无Q)
充分必要条件(P、Q同时成立或不成立)
二、推理规则:
①充分条件:有P必有Q,无Q必无P
P Q(肯定前件)=非Q非P(否定后件)
(如果P,那么Q=如果非Q,那么非P)
这种差异可能并不明显,需要特别注意从论据到论点是否偷换了概念
加强:通过“搭桥”,在论点与论据之间建立联系
排除他因,即排除其他因素的影响,从而使两者之间存在联系
⑤类比论证(通过“打比方”得出结论/
通过已知事物与跟它有某些相同特点的事物进行比较推理)
可靠性主要与对象之间的相似性相关
削弱:指出两者之间在其他方面并不相似或存在影响性质的其他因素
否一推一:除非P,否则Q=如果非P,那么Q=只有P,才非Q=如果非Q,那么P
三、复杂推理假言连锁推理:P Q R,所以,P R
二难推理:A C,B C,A或B,则C
大部分条件句可看成A B,而A是B的必不可少/必要/前提条件=只有A,才B
模态命题(含有“必然”、“可能”等模态词的命题)
“必然P”和“可能非P”(矛盾命题,必有一真一假)
指出原因条件相同时,结果也可能不同
加强:从反面场合加强,即指出原因条件不存在时,结果也不存在
排除他因,即说明除了题干原因之外的其他条件是相同的
④跳跃论证(论据与论点之间存在明显的跳跃,不是一种论证方法)
推不出,需要增加一个隐含假设/论据与论点的关键词不同
削弱:指出这一跳跃不成立,即两者之间没有联系或差异
智力推理(朴素逻辑)(真假、匹配、排序和与数字结合)
①假设、代入、排除法
②找突破口(某个确定条件、比较特殊的条件或者
某个对象(条件)被反复提及)
③图表法
二、可能性推理 削弱、加强、前提型
解释型
评价型
结论型
选项分析
削弱、加强、前提型 削弱型(题干给出一个完整的论证,要求从备选项中
寻找最能(或不能)反驳或削弱题干论证的选项)
要点:正确选项必须能够解释题干现象或矛盾发生的原因
正确选项必须与题干现象或矛盾相关,不能否定或无视题干事实
正确选项必须能够包容题干所述的矛盾双方,且与人们的常识相符
