列主元高斯消去法和列主元三角分解法解线性方程
Gauss列主元素消去法实验

Lab06.Gauss 列主元素消去法实验【实验目的和要求】1.使学生深入理解并掌握Gauss 消去法和Gauss 列主元素消去法步骤; 2.通过对Gauss 消去法和Gauss 列主元素消去法的程序设计,以提高学生程序设计的能力;3.对具体问题,分别用Gauss 消去法和Gauss 列主元素消去法求解。
通过对结果的分析比较,使学生感受Gauss 列主元素消去法优点。
【实验内容】1.根据Matlab 语言特点,描述Gauss 消去法和Gauss 列主元素消去法步骤。
2.编写用不选主元的直接三角分解法解线性方程组Ax=b 的M 文件。
要求输出Ax=b 中矩阵A 及向量b ,A=LU 分解的L 与U ,det A 及解向量x 。
3.编写用Gauss 列主元素消去法解线性方程组Ax=b 的M 文件。
要求输出Ax=b 中矩阵A 及向量b 、PA=LU 分解的L 与U 、det A 及解向量x ,交换顺序。
4.给定方程组(1) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--11134.981.4987.023.116.427.199.103.601.3321x x x(2) ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----15900001.582012151********.23107104321x x x x 先用编写的程序计算,再将(1)中的系数3.01改为3.00,0.987改为0.990;将(2)中的系数2.099999改为2.1,5.900001改为9.5,再用Gauss 列主元素消去法解,并将两次计算的结果进行比较。
【实验仪器与软件】1.CPU 主频在1GHz 以上,内存在128Mb 以上的PC ;2.Matlab 6.0及以上版本。
实验讲评:实验成绩:评阅教师:200 年 月 日Lab06.Gauss 列主元素消去法实验第一题:1、算法描述:Ⅰ、Gauss 消去法由书上定理5可知 设Ax=b ,其中A ∈R^(n(1)如果()0(1,2,....,1)k kka k n ≠=-,则可通过高斯消去法将Ax=b 约化为等价的 角形线性方程组,且计算公式为:① 消元计算(k=1,2,….,n-1)()()(1)()()(1)()()/,1,...,,,,1,...,,,1,...,.k k ik ik kk k k k ij ij ik kj k k k iiik k m a a i k n a a m a i j k n b b m b i k n ++==+=-=+=-=+② 回带公式()()()()()1/,()/,1,...,2,1.n n n n nn ni i i i iii j ii j i x b a x ba x a i n =+==-=-∑(2)如果A 为非奇异矩阵,则可通过高斯消去法将方程组Ax=b 约化方程组为上三角矩阵以上消元和回代过程总的乘除法次数为332333nn nn +-≈,加减法次数为32353263nnn n+-≈以上过程就叫高斯消去法。
列主元三角分解法例题解析

列主元三角分解法例题解析列主元三角分解法是一种用于求解线性方程组的方法。
它将系数矩阵A分解为一个下三角矩阵L和一个上三角矩阵U,使得A=LU。
在该分解过程中,每一步选取一个列主元,确保主元所在的列进行了交换,以避免出现除以零的情况。
接下来,我将通过一个例题来详细解析列主元三角分解法的具体步骤和计算过程。
假设有如下线性方程组:2x1+3x2-x3=94x1+4x2-3x3=12x1-x2+6x3=12首先,将方程组转化为矩阵形式:Ax=b。
A=[[2,3,-1],[4,4,-3],[2,-1,6]]b=[9,1,12]接下来,我们开始进行列主元三角分解的计算过程。
第一步:选取第一列的主元,并确保主元所在的行是当前列中绝对值最大的。
在第一列中,主元为4。
由于4所在的行已经是绝对值最大的行,因此不需要进行行交换。
第二步:通过高斯消元法,将主元所在列下方的元素消为零。
将第二行乘以2并减去第一行的两倍,得到新的第二行:[0,-2,1]将第三行乘以1并减去第一行的一倍,得到新的第三行:[0,-4,7]更新后的矩阵A为:[[2,3,-1],[0,-2,1],[0,-4,7]]第三步:重复上述过程,选取第二列的主元,并确保主元所在的行是当前列中绝对值最大的。
在第二列中,主元为-4。
由于-4所在的行已经是绝对值最大的行,因此不需要进行行交换。
第四步:通过高斯消元法,将主元所在列下方的元素消为零。
将第三行乘以2并加上第二行的两倍,得到新的第三行:[0,0,15]更新后的矩阵A为:[[2,3,-1],[0,-2,1],[0,0,15]]现在,我们已经得到了分解后的矩阵U:U=[[2,3,-1],[0,-2,1],[0,0,15]]接下来,我们需要求解下三角矩阵L。
L的主对角线元素都为1,而且L的非零元素是通过进行消元操作得到的。
根据之前的计算过程,可以得到L的非零元素:l21=2/4=0.5l31=2/2=1l32=4/2=2因此,L的形式为:L=[[1,0,0],[0.5,1,0],[1,2,1]]最后,我们可以将原始方程组写成LUx=b的形式,并求解出x的值。
Guass列选主元消去法和三角分解法

Guass列选主元消去法和三⾓分解法 最近数值计算学了Guass列主消元法和三⾓分解法解线性⽅程组,具体原理如下:1、Guass列选主元消去法对于AX =B1)、消元过程:将(A|B)进⾏变换为,其中是上三⾓矩阵。
即:k从1到n-1a、列选主元选取第k列中绝对值最⼤元素作为主元。
b、换⾏c、归⼀化d、消元2)、回代过程:由解出。
2、三⾓分解法(Doolittle分解)将A分解为如下形式由矩阵乘法原理a、计算U的第⼀⾏,再计算L的第⼀列b、设已求出U的1⾄r-1⾏,L的1⾄r-1列。
先计算U的第r⾏,再计算L的第r列。
a)计算U的r⾏b)计算L的r列C#代码: 代码说明:Guass列主消元法部分将计算出来的根仍然储存在增⼴矩阵的最后⼀列,⽽Doolittle分解,将分解后的结果也储存⾄原来的数组中,这样可以节约空间。
using System;using System.Windows.Forms;namespace Test{public partial class Form1 : Form{public Form1(){InitializeComponent();}private void Cannel_Button_Click(object sender, EventArgs e){this.textBox1.Clear();this.textBox2.Clear();this.textBox3.Clear();boBox1.SelectedIndex = -1;}public double[,] GetNum(string str, int n){string[] strnum = str.Split(' ');double[,] a = new double[n, n + 1];int k = 0;for (int i = 0; i < n; i++){for (int j = 0; j < strnum.Length / n; j++){a[i, j] = double.Parse((strnum[k]).ToString());k++;}}return a;}public void Gauss(double[,] a, int n){int i, j;SelectColE(a, n);for (i = n - 1; i >= 0; i--){for (j = i + 1; j < n; j++)a[i, n] -= a[i, j] * a[j, n];a[i, n] /= a[i, i];}}//选择列主元并进⾏消元public void SelectColE(double[,] a, int n){int i, j, k, maxRowE;double temp; //⽤于记录消元时的因数for (j = 0; j < n; j++){maxRowE = j;for (i = j; i < n; i++)if (System.Math.Abs(a[i, j]) > System.Math.Abs(a[maxRowE, j]))maxRowE = i;if (maxRowE != j)swapRow(a, j, maxRowE, n); //与最⼤主元所在⾏交换//消元for (i = j + 1; i < n; i++){temp = a[i, j] / a[j, j];for (k = j; k < n + 1; k++)a[i, k] -= a[j, k] * temp;}}return;}public void swapRow(double[,] a, int m, int maxRowE, int n){int k;double temp;for (k = m; k < n + 1; k++){temp = a[m, k];a[m, k] = a[maxRowE, k];a[maxRowE, k] = temp;}}public void Doolittle(double[,] a, int n){for (int i = 0; i < n; i++){if (i == 0){for (int j = i + 1; j < n; j++)a[j, 0] = a[j, 0] / a[0, 0];}else{double temp = 0, s = 0;for (int j = i; j < n; j++){for (int k = 0; k < i; k++){temp = temp + a[i, k] * a[k, j];}a[i, j] = a[i, j] - temp;}for (int j = i + 1; j < n; j++){for (int k = 0; k < i; k++){s = s + a[j, k] * a[k, i];}a[j, i] = (a[j, i] - s) / a[i, i];}}}}private void Exit_Button_Click(object sender, EventArgs e){this.Close();}private void Confirm_Button_Click(object sender, EventArgs e){if (this.textBox2.Text.Trim().ToString().Length == 0){this.textBox2.Text = this.textBox1.Text.Trim();}else{this.textBox2.Text = this.textBox2.Text + "\r\n" + this.textBox1.Text.Trim();}this.textBox1.Clear();}private void Calculate_Button_Click(object sender, EventArgs e){string str = this.textBox2.Text.Trim().ToString();string myString = str.Replace("\n", " ").Replace("\r", string.Empty);double[,] a = new double[this.textBox2.Lines.GetUpperBound(0) + 1, this.textBox2.Lines.GetUpperBound(0) + 2];a = GetNum(myString, this.textBox2.Lines.GetUpperBound(0) + 1);if (boBox1.Text == "Guass列主消元法"){Gauss(a, this.textBox2.Lines.GetUpperBound(0) + 1);for (int i = 0; i < this.textBox2.Lines.GetUpperBound(0) + 1; i++){this.textBox3.Text = this.textBox3.Text + "\r\nX" + (i + 1) + "=" + a[i, this.textBox2.Lines.GetUpperBound(0) + 1]; }}else if (boBox1.Text == "Doolittle三⾓分解法"){this.textBox3.Enabled = true;Doolittle(a, this.textBox2.Lines.GetUpperBound(0) + 1);bel3.Text = "分解后的结果:";this.textBox3.Clear();this.textBox3.Text += "L矩阵:\r\n";for (int i = 0; i < this.textBox2.Lines.GetUpperBound(0) + 1; i++) {for (int j = 0; j < this.textBox2.Lines.GetUpperBound(0) + 1; j++) {if (j < i){this.textBox3.Text += a[i, j].ToString() + "\t";}else if (i == j){this.textBox3.Text += "1\t";}else{this.textBox3.Text += "0\t";}}this.textBox3.Text += "\r\n";}this.textBox3.Text += "\r\nU矩阵:\r\n";for (int i = 0; i < this.textBox2.Lines.GetUpperBound(0) + 1; i++) {for (int j = 0; j < this.textBox2.Lines.GetUpperBound(0) + 1; j++) {if (j >= i){this.textBox3.Text += a[i, j].ToString() + "\t";}else{this.textBox3.Text += "0\t";}}this.textBox3.Text += "\r\n";}}}private void textBox1_KeyDown(object sender, KeyEventArgs e){if (e.KeyCode == Keys.Enter){if (this.textBox1.Text.Trim().ToString().Length == 0){Calculate_Button_Click(sender, e);}else{Confirm_Button_Click(sender, e);}}}private void button1_Click(object sender, EventArgs e){this.textBox2.Enabled = true;}}} 运⾏截图: ⾄此完毕。
范数-摆脱课本繁琐的公式,比较好懂
p
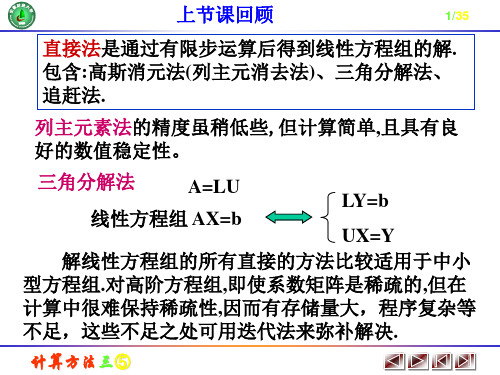
范数的特殊情况。 注:前三种范数都是p—范数的特殊情况。其中 前三种范数都是 范数的特殊情况
|| X ||∞ = lim || X || p
p →∞
计算方法三 计算方法三⑤
向量范数的连续性: 向量范数的连续性
5/35
定理3.3 设f(X)=||X||为Rn上的任一向量范数 则f(X) 定理 为 上的任一向量范数,则 的分量x 的连续函数. 为X的分量 1,x2,…,xn的连续函数 的分量
lim x i = xi (i = 1,2,..., n)
(k ) k →∞
则称向量X= (x1,x2,...,xn)T为向量序列 则称向量 , {X(k)}的极限,或者说向量序列 (k)}收敛 的极限, 的极限 或者说向量序列{X 收敛 于向量X, 于向量 ,记为
lim X
k →∞
(k )
=X 或 X
(k )
→ X (k → ∞)
计算方法三 计算方法三⑤
计算方法三 计算方法三⑤
x1 (k ) ( k ) x2 X = ………… M x (k ) n (k ) x1 x1 (k ) x2 ( k ) x2 X = → = M M x (k ) x n n
几种常用的矩阵范数: 几种常用的矩阵范数:
n
13/35
a11 a21 设 A= ⋅⋅⋅ a n1
a12 ⋅⋅⋅ a1n A 1 = max∑aij 列范数 1≤j≤n i=1 n a22 ⋅⋅⋅ a2n A ∞ = max∑aij 行范数 ⋅⋅⋅ ⋅⋅⋅ ⋅⋅⋅ 1≤i≤n j=1 T an2 ⋅⋅⋅ ann A 2 = λ (A A) max AF =
列主元消去法和三角分解法之间的关系

主题:列主元消去法和三角分解法之间的关系一、概述上线性代数领域中,列主元消去法和三角分解法是两种常用的矩阵求解方法。
它们都是用于解线性方程组的工具,但在实际应用中有着不同的特点和适用范围。
本文将通过对列主元消去法和三角分解法的理论基础、求解步骤和应用场景进行比较和分析,旨在探讨它们之间的关系。
二、列主元消去法的基本原理和步骤1. 列主元消去法概述列主元消去法是一种用于求解线性方程组的方法,其基本思想是通过逐步消元的方式将增广矩阵转化为上三角形矩阵,最终获得方程组的解。
其核心步骤包括选取主元、消元和回代。
2. 列主元消去法的求解步骤(1)选取主元:在每一列中选取绝对值最大的元素作为主元,以确保消元过程中不会出现除以零的情况。
(2)消元:通过一系列行变换操作,将矩阵转化为上三角形矩阵。
(3)回代:从最后一行开始,依次求解未知数的值。
三、三角分解法的基本原理和步骤1. 三角分解法概述三角分解法是一种将矩阵分解为下三角矩阵和上三角矩阵的求解方法,其基本思想是通过矩阵的分解降低方程组求解的复杂度。
2. 三角分解法的求解步骤(1)矩阵的LU分解:将系数矩阵A分解为下三角矩阵L和上三角矩阵U,使得A=LU。
(2)求解Ly=b:先通过前代法求解Ly=b,得到y。
(3)求解Ux=y:再通过回代法求解Ux=y,得到方程组的解x。
四、列主元消去法与三角分解法的关系比较1. 算法思想比较(1)列主元消去法是通过逐步消元将增广矩阵转化为上三角形矩阵,直接求解方程组的解。
(2)三角分解法是通过将矩阵分解为下三角矩阵和上三角矩阵,再进行前代和回代求解方程组的解。
2. 适用范围比较(1)列主元消去法适用于一般的线性方程组求解,能够处理任意形状的矩阵。
(2)三角分解法适用于特定类型的线性方程组求解,对称正定矩阵具有较好的稳定性,求解速度较快。
3. 数值稳定性比较(1)列主元消去法在计算过程中容易出现主元选取不当导致的数值不稳定性问题,需要进行主元选取和行变换的操作。
线性代数求解方法和技巧

线性代数求解方法和技巧线性代数是数学中重要的一个分支,研究向量空间、线性变换和线性方程组等内容。
在实际问题中,我们常常需要用线性代数的方法来解决问题,因此掌握线性代数的求解方法和技巧对于理解和应用数学是非常重要的。
首先,我们讨论线性方程组的求解方法。
线性方程组是由一组线性方程组成的方程组,其中每个方程的未知数的次数都为1。
对于n个未知数和m个方程的线性方程组,我们有以下几种常用的求解方法:1. 列主元消元法:这是最常用的线性方程组求解方法之一。
它的基本思想是通过行变换将线性方程组化为一个三角形式,进而求解得到方程组的解。
在进行行变换时,要选择合适的列主元,即选择主元元素绝对值最大的一列作为主元素。
2. 矩阵求逆法:对于一个可逆的n阶方阵A,我们可以通过求A的逆矩阵来求解线性方程组Ax=b。
具体地,我们首先通过高斯消元法将方程组化为三角形式,然后根据三角形式的矩阵求逆公式来求解x。
3. LU分解法:对于一个n阶非奇异矩阵A,我们可以将其分解为一个下三角矩阵L和一个上三角矩阵U的乘积,即A=LU。
接着,我们可以通过LU分解来求解线性方程组Ax=b。
具体地,我们首先通过LU分解将方程组化为Lc=b和Ux=c两个方程组,然后依次求解这两个方程组得到x的值。
除了以上的求解方法,还有一些线性方程组的特殊情况和对应的求解方法:1. 齐次线性方程组:如果线性方程组右边的常数项都为0,即b=0,那么我们称为齐次线性方程组。
对于齐次线性方程组,其解空间是一个向量空间。
我们可以通过高斯消元法来求解齐次线性方程组,先将其化为三角形式,然后确定自由未知量的个数,最后确定解空间的基底。
2. 奇异线性方程组:如果线性方程组的系数矩阵A是奇异矩阵,即det(A)=0,那么我们称为奇异线性方程组。
对于奇异线性方程组,其解可能不存在,或者存在无穷多解。
我们可以通过计算矩阵A的秩来确定线性方程组的解的情况。
另外,在实际问题中,我们可能会遇到大规模的线性方程组,这时候求解方法和技巧还需要考虑到计算效率的问题。
实验三 高斯消去法和三角分解法1

实验报告实验三 高斯消去法与矩阵的三角分解一、实验目的1、掌握列主元素消去法,并且能够用MATLAB 编写相关程序,实现高斯消去法的求解。
2、能够用矩阵理论理解与研究高斯消去法,通过对矩阵的初等变换实现高斯消去法。
3、学会矩阵的三角分解,并且能够用MATLAB 编写相关程序,实现矩阵的三角分解,解方程组。
二、上机内容⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡2822171310871234567112345611123451111234111112311111121111111764321x x x x x x1、用列主元素高斯消去法求解方程组。
2、用列主元消去法求解方程组(实现PA=LU) 要求输出: (1)计算解X;(2)L,U;(3)正整型数组IP(i),(i=1,···,n) (记录主行信息)。
三、实验原理1、列主元素消去法用高斯消去法求解方程组时,为了减小误差,在消去的过程中要避免用绝对值较小的主元素。
因此在高斯消去法的每一步应该在系数矩阵货消去后的低阶矩阵中选取绝对值较大的元素作为主元素,保持|m ik |<=1,以减小计算过程中的舍入误差对计算解的影响。
此方法为完全主元素消去法。
完全主元素消去法在选主元素时花费一定的计算机时间,因此实际计算中常用列主元消去法。
列主元消去法在每次选主元时,仅依次按列选取绝对值最大的元素作为主元素,且仅交换两行,再进行消元计算。
装订 线第k步计算如下:对于k=1,2,…,n-1(1)按列选主元:即确定t使(2)如果t≠k,则交换[A,b]第t行与第k行元素。
(3)消元计算(4)回代求解计算流程图回代求解 b=b/a (当a nn ≠0)b ←(b -∑a x )/adet=a nn *det输出计算解及行列式及detk=1,2,…,n-1输入n ,A,b,εdet=1按列主元|a i(k),k |=max|a ik |C 0=a i(k),k换行 a ik a i(k)j(j=k,…n ) b k b j(k), 消元计算 (i=k+1,…,n ) a ik=a ik -a kk *m ik a ij=a ij -a kj *m ik (j=k+1,…,n )|C 0|<εi k =kdet=a kk det否否是是k<=n-1输出det(A)=0停机停机2. 矩阵的三角分解法 (1)定理设 n n R A ⨯∈ 。
常见的线性代数求解方法

常见的线性代数求解方法
1.列主元消去法
列主元消去法是一种经典的求解线性方程组的方法。
它通过将
方程组转化为上三角矩阵的形式来求解。
这个方法的关键在于选取
主元的策略。
一种常见的选取主元的策略是选择当前列中绝对值最
大的元素作为主元,然后进行消去操作,直到将矩阵转化为上三角
矩阵。
2.高斯-约当消去法
高斯-约当消去法是另一种常见的线性方程组求解方法。
它通
过消去矩阵的下三角部分来将线性方程组转化为上三角矩阵的形式。
这个方法也需要选择主元,常见的选择策略是选取当前行中绝对值
最大的元素作为主元,然后进行消去操作。
3.LU分解法
LU分解法是将矩阵分解为一对矩阵的乘积的方法。
这个方法的思想是先将矩阵分解为一个下三角矩阵和一个上三角矩阵,然后通过求解上三角矩阵和下三角矩阵的两个方程组来求解原始的线性方程组。
4.Jacobi迭代法
Jacobi迭代法是一种迭代求解线性方程组的方法。
它通过将原始的线性方程组转化为一个对角矩阵和另一个矩阵的乘积的形式,然后通过迭代求解这个对角矩阵和另一个矩阵的方程组来逼近线性方程组的解。
5.Gauss-Seidel迭代法
Gauss-Seidel迭代法是另一种迭代求解线性方程组的方法。
它与Jacobi迭代法类似,但是在每一次迭代中,它使用前一次迭代得到的部分解来更新当前的解。
这个方法通常比Jacobi迭代法收敛得更快。
以上是一些常见的线性代数求解方法。
每种方法都有其特点和适用范围,我们可以根据具体情况选择合适的方法来求解线性方程组的问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算方法实验报告1课题名称用列主元高斯消去法和列主元三角分解法解线性方程目的和意义高斯消去法是一个古老的求解线性方程组的方法,但由它改进得到的选主元的高斯消去法则是目前计算机上常用的解低阶稠密矩阵方程组的有效方法;用高斯消去法解线性方程组的基本思想时用矩阵行的初等变换将系数矩阵A 约化为具有简单形式的矩阵上三角矩阵、单位矩阵等,而三角形方程组则可以直接回带求解 用高斯消去法解线性方程组b Ax =其中A ∈Rn ×n 的计算量为:乘除法运算步骤为32(1)(1)(21)(1)(1)262233n n n n n n n n n n nMD n ----+=+++=+-,加减运算步骤为(1)(21)(1)(1)(1)(25)6226n n n n n n n n n n AS -----+=++=;相比之下,传统的克莱姆法则则较为繁琐,如求解20阶线性方程组,克莱姆法则大约要19510⨯次乘法,而用高斯消去法只需要3060次乘除法;在高斯消去法运算的过程中,如果出现absAi,i 等于零或过小的情况,则会导致矩阵元素数量级严重增长和舍入误差的扩散,使得最后的计算结果不可靠,所以目前计算机上常用的解低阶稠密矩阵方程的快速有效的方法时列主元高斯消去法,从而使计算结果更加精确; 2、列主元三角分解法高斯消去法的消去过程,实质上是将A 分解为两个三角矩阵的乘积A=LU,并求解Ly=b 的过程;回带过程就是求解上三角方程组Ux=y;所以在实际的运算中,矩阵L 和U 可以直接计算出,而不需要任何中间步骤,从而在计算过程中将高斯消去法的步骤进行了进一步的简略,大大提高了运算速度,这就是三角分解法采用选主元的方式与列主元高斯消去法一样,也是为了避免除数过小,从而保证了计算的精确度计算公式1、 列主元高斯消去法设有线性方程组Ax=b,其中设A 为非奇异矩阵;方程组的增广矩阵为第1步k=1:首先在A 的第一列中选取绝对值最大的元素1l a ,作为第一步的主元素:111211212222112[,]n n n l n nn n a a a a b a a a b a a a b ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦a b然后交换A,b 的第1行与第l 行元素,再进行消元计算;设列主元素消去法已经完成第1步到第k -1步的按列选主元,交换两行,消元计算得到与原方程组等价的方程组 Akx=bk第k 步计算如下:对于k=1,2,…,n -11按列选主元:即确定t 使 2如果t ≠k,则交换A,b 第t 行与第k 行元素; 3消元计算消元乘数mik 满足:4回代求解2、 列主元三角分解法 对方程组的增广矩阵 经过k -1步分解后,可变成如下形式:111max 0l i i n a a ≤≤=≠(1)(1)(1)(1)(1)1112111(2)(2)(2)(2)22222()(()1)()()()()()1,1()(,)()[,][,] k k k k nk k nk n k k k k k kk kn k k k k n k k k n nn a a a a b a a a b a a b a b b a a a +++⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥→=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A b A b ()()max 0k k tk ik k i na a ≤≤=≠,(1,,)ik ik ik kka a m i k n a ←=-=+, (,1,,), (1,,)ij ij ik kji i ik k a a m a i j k n b b m b i k n ←+=+⎧⎨←+=+⎩⎪⎪⎩⎪⎪⎨⎧--=-←←∑+=)1,,2,1(,)(1n n i a x a b x a b x ii n i j j ij i i nnn n [,]A A b =11121,11111222,122221,11,1,1,211,11,2121,112,112,1k k k k k k k j n k k j n k k k i i i k n n kk kj kn k ik ij in i nknjk k k j k n n nnk k n a a a b A a u u u u u u y l l l l l l ll l l l u u u u u y u u u u y a a b a a b l a -------------⎡→⎣⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎦第k 步分解,为了避免用绝对值很小的数kku 作除数,引进量1111 (,1,,;1,2,,) ()/ (1,2,,;1,2,,)k kj kj km mj m k ik ik im mk kkm u a l u j k k n k n l a l u u i k k n k n -=-=⎧=-=+=⎪⎪⎨⎪=-=++=⎪⎩∑∑11(,1,,)k i ik im mk m s a l u i k k n -==-=+∑,于是有kk u =ks ;如果 ,则将矩阵的第t 行与第k 行元素互换,将i,j 位置的新元素仍记为jjl 或jja ,然后再做第k 步分解,这时列主元高斯消去法程序流程图max t ik i n s s ≤≤= ()/ 1,2,,)1 (1,2,,),kk k k t iki k ik u s s s l s s i k k n l i k k n ===++≤=++即交换前的,(且列主元高斯消去法Matlab主程序function x=gauss1A,b,c %列主元法高斯消去法解线性方程Ax=bif lengthA~=lengthb %判断输入的方程组是否有误disp'输入方程有误'return;enddisp'原方程为AX=b:' %显示方程组Abdisp'------------------------'n=lengthA;for k=1:n-1 %找列主元p,q=maxabsAk:n,k; %找出第k列中的最大值,其下标为p,qq=q+k-1; %q在Ak:n,k中的行号转换为在A中的行号if absp<cdisp'列元素太小,detA≈0';break;elseif q>ktemp1=Ak,:; %列主元所在行不是当前行,将当前行与列主Ak,:=Aq,:; 元所在行交换包括bAq,:=temp1;temp2=bk,:;bk,:=bq,:;bq,:=temp2;end%消元for i=k+1:nmi,k=Ai,k/Ak,k; %Ak,k将Ai,k消为0所乘系数Ai,k:n=Ai,k:n-mi,kAk,k:n; %第i行消元处理bi=bi-mi,kbk; %b消元处理endenddisp'消元后所得到的上三角阵是'A %显示消元后的系数矩阵bn=bn/An,n; %回代求解for i=n-1:-1:1bi=bi-sumAi,i+1:nbi+1:n/Ai,i;endclear x;disp'AX=b的解x是' x=b;调用函数解题列主元三角分解法程序流程图列主元三角分解法Matlab主程序①自己编的程序:function x=PLUA,b,eps %定义函数列主元三角分解法函数if lengthA~=lengthb %判断输入的方程组是否有误disp'输入方程有误'return;enddisp'原方程为AX=b:' %显示方程组Abdisp'------------------------'n=lengthA;A=A b; %将A与b合并,得到增广矩阵for r=1:nif r==1for i=1:nc d=maxabsA:,1; %选取最大列向量,并做行交换if c<=eps %最大值小于e,主元太小,程序结束break;elseendd=d+1-1;p=A1,:;A1,:=Ad,:;Ad,:=p;A1,i=A1,i;endA1,2:n=A1,2:n;A2:n,1=A2:n,1/A1,1; %求u1,ielseur,r=Ar,r-Ar,1:r-1A1:r-1,r; %按照方程求取ur,iif absur,r<=eps %如果ur,r小于e,则交换行p=Ar,:;Ar,:=Ar+1,:;Ar+1,:=p;elseendfor i=r:nAr,i=Ar,i-Ar,1:r-1A1:r-1,i; %根据公式求解,并把结果存在矩阵A中endfor i=r+1:nAi,r=Ai,r-Ai,1:r-1A1:r-1,r/Ar,r; %根据公式求解,并把结果存在矩阵A中endendendy1=A1,n+1;for i=2:nh=0;for k=1:i-1h=h+Ai,kyk;endyi=Ai,n+1-h; %根据公式求解yiendxn=yn/An,n;for i=n-1:-1:1h=0;for k=i+1:nh=h+Ai,kxk;endxi=yi-h/Ai,i; %根据公式求解xiendAdisp'AX=b的解x是'x=x'; %输出方程的解②可直接得到P,L,U并解出方程解的的程序查阅资料得子函数PLU1,其作用是将矩阵A分解成L乘以U的形式;PLU2为调用PLU1解题的程序,是自己编的Ⅰ.function l,u,p=PLU1A %定义子函数,其功能为列主元三角分解系数矩阵A m,n=sizeA; %判断系数矩阵是否为方阵if m~=nerror'矩阵不是方阵'returnendif detA==0 %判断系数矩阵能否被三角分解error'矩阵不能被三角分解'endu=A;p=eyem;l=eyem; %将系数矩阵三角分解,分别求出P,L,Ufor i=1:mfor j=i:mtj=uj,i;for k=1:i-1tj=tj-uj,kuk,i;endenda=i;b=absti;for j=i+1:mif b<abstjb=abstj;a=j;endendif a~=ifor j=1:mc=ui,j;ui,j=ua,j;ua,j=c;endfor j=1:mc=pi,j;pi,j=pa,j;pa,j=c;endc=ta;ta=ti;ti=c;endui,i=ti;for j=i+1:muj,i=tj/ti;endfor j=i+1:mfor k=1:i-1ui,j=ui,j-ui,kuk,j;endendendl=trilu,-1+eyem;u=triuu,0Ⅱ.function x=PLU2A,b %定义列主元三角分解法的函数l,u,p=PLU1A %调用PLU分解系数矩阵A m=lengthA; %由于A左乘p,故b也要左乘p v=b;for q=1:mbq=sumpq,1:mv1:m,1;endb1=b1 %求解方程Ly=b for i=2:1:mbi=bi-sumli,1:i-1b1:i-1;endbm=bm/um,m; %求解方程Ux=y for i=m-1:-1:1bi=bi-sumui,i+1:mbi+1:m/ui,i;endclear x;disp'AX=b的解x是' x=b;调用函数解题①②编程疑难这是第一次用matlab编程,对matlab的语句还不是非常熟悉,因此在编程过程中,出现了许多错误提示;并且此次编程的两种方法对矩阵的运算也比较复杂;问题主要集中在循环控制中,循环次数多了一次或者缺少了一次,导致数据错误,一些基本的编程语句在语法上也会由于生疏而产生许多问题,但是语句的错误由于系统会提示,比较容易进行修改,数据计算过程中的一些逻辑错误,比如循环变量的控制,这些系统不会提示错误,需要我们细心去发现错误,不断修正,调试;。
