电路分析答案第五章
电路分析(四川邮电职业技术学院)知到章节答案智慧树2023年

电路分析(四川邮电职业技术学院)知到章节测试答案智慧树2023年最新绪论单元测试1.《电路分析》这门课程涵盖了很多专业参考答案:对第一章测试1.将电能转换成热能的理想元件是()参考答案:电阻2.国际单位制中,电压的基本单位是()。
参考答案:伏特3.电压参考方向的设定,必须满足下列哪个条件参考答案:任意设定4.电路中,规定电位降低的方向为电压的实际方向。
参考答案:对5.传送、转换电能的速率叫做电功率。
参考答案:对6.元件电压与电流的关系曲线叫做元件的伏安特性参考答案:对7.电阻的倒数叫做电导参考答案:对8.网孔是指其内部不含任何支路的回路。
参考答案:对9.理想电流源其输出电流总保持定值或为一定的时间函数,与其端电压无关。
参考答案:对10.KCL告诉我们,对于集中参数电路,任意时刻,连接在任一节点的各支路电流的代数和恒不为0。
参考答案:错第二章测试1.直流电路中,并联电路的总电流一定比各支路电流要大。
参考答案:对2.含有受控源的二端网络,其等效电阻可以是正值也可以是负值。
参考答案:对3.两个线性电路等效,是指二者对外电路的作用完全相同。
参考答案:对4.两个电阻串联接到某理想电压源上,则电阻大者消耗的功率就大。
参考答案:对5.二端网络A与二端网络B互为等效,则电路A与电路B具有相同的关系。
参考答案:电压、电流6.实际电压源变换成实际电流源时,Is参考方向应该指向电压源的极。
参考答案:正极7.把一个量程为1V的电压表改装成量程为10V的电压表,可以采用的措施。
参考答案:串联一个电阻分压8.电压大小和极性不一致的理想电压源也可以并联。
参考答案:错9.Δ形电路的三个电阻相等且为9Ω,变换为Y形电路时,Y形电路的三个电阻也相等且为Ω。
参考答案:310.有三条支路,之路中的电阻都为1Ω,则三条支路并联后两端的电阻为Ω。
1/3第三章测试1.三个或三个以上支路的汇交点称为节点。
参考答案:对2.平面电路内部不含有支路的回路称之为网孔。
电路分析(中国石油大学(华东))智慧树知到课后章节答案2023年下中国石油大学(华东)

电路分析(中国石油大学(华东))智慧树知到课后章节答案2023年下中国石油大学(华东)中国石油大学(华东)绪论单元测试1.学好《电路》课的意义()答案:《电路》是电类专业(自动化、电气工程、电子与信息工程、通信等专业)的第一门专业基础课,有着非常重要的地位。
;《电路》课程的掌握程度对于后续专业课程的学习,有着举足轻重的作用。
;《电路》也是多数电类专业研究生入学考试课。
第一章测试1.电流的参考方向为()。
答案:沿电路任意选定的某一方向2.图示电路,求u:()。
答案:-4V3.基尔霍夫电流定律应用于()。
答案:节点4.在有n个节点,b条支路的连通电路中,可以列出独立KCL方程的个数为()。
答案:n-15.图示电路中,直流电压表和电流表的读数分别为4V及1A,则电阻R为()。
答案:76.图示电路中电压U为()。
答案:2V7.图示电路中电压U AB为()。
答案:-16V8.电路中b、c两点间的电压U bc为()。
答案:2V9.图示为某电路中的一个回路,其KCL方程为()。
答案:R1I1-R2I2-R3I3+R4I4=U S1+U S2-U S3-U S410.图示电路中电压U S为()。
答案:4V第二章测试1.图示电路中的I为()。
答案:2A2.电路如图所示,短路线中的电流I为()。
答案:10A3.图示直流电路中,已知a点电位为5V,则参考点为()。
答案:c点4.图示电路中的电流I为()。
答案:0A5.图示电阻串联电路中,U=U1-U2+U3,再根据欧姆定律,可求出等效电阻R为()。
答案:R1+R2+R36.在下列各图中,与图(N)所示伏安特性相对应的电路是()。
答案:(B)7.图示电路的开路电压Uoc为()。
答案:-2V8.图示电路中电位VA为()。
答案:4V9.如图所示电路中I1为()。
答案:2A10.图示电路的电压U与电流I的关系为()。
答案:U=-1-3I第三章测试1.各点电位的高低是()的,而两点之间的电压值是()的。
电路分析 张永瑞 王松林 答案

uL (t)
=
L
diL (t) dt
=
−20e−5t
A
5.14 如题 5.14 图所示电路,t < 0 已处于稳态,当 t = 0 时开关 S 闭合,求 t ≥ 0
时的电流 i(t) 。 解:在 t ≥ 0 ,开关闭合,根据电路的
特殊性,电流 i(t) 可以看成电压源和电容 初始储能作用的叠加。可利用三要素公式 进行求解:
iC
(t )
=
C
duC (t) dt
=
1.2e−2t
A
u(t) = uC (t) + iC (t)R = 6(1− e−2t ) + 4.8e−2t = (6 −1.2e−2t )V
4Ω
iC +
0.1F
uC
-
5.9 如题 5.9 图所示电路,t < 0 时已处于稳态。当 t = 0 时开关 S 闭合,求 t ≥ 0
零状态响应方程为:
duC (t) dt
+
2uC
(t)
=
12
uC (0+ ) = 0
其齐次为:
Ke−2t
4
其特解为:
A0 代入方程有: 2 A0 = 12
通解为:
uCzs (t) = Ke−2t + 6
代入初始条件: 0 = K + 6 K = −6
得:
uCzs (t) = 6(1− e−2t )V
+ 25V 1F -
S +
uC 5Ω
-
5.13 如题 5.13 图所示电路,t < 0 已处于稳态,当 t = 0 时开关 S 打开,求 t ≥ 0
电路分析基础第四版课后习题答案
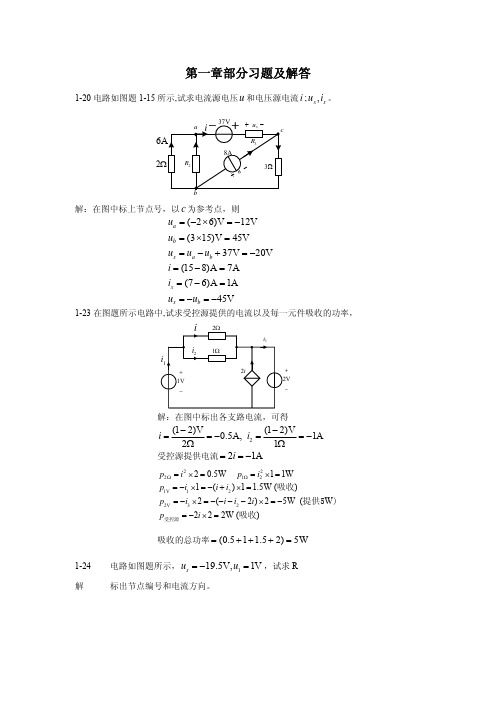
i
i1
+ 1V −
2Ω
i3
i2
1Ω
2i
+ 2V −
解:在图中标出各支路电流,可得
(1 − 2)V (1 − 2)V = −0.5A, i2 = = −1A 2Ω 1Ω 受控源提供电流 = 2i = −1A i=
p2 Ω = i 2 × 2 = 0.5W
为确定 R,需计算 i4 ,
uce = ucd + ude = 0 ⇒ ude = −ucd = −10u1 = −10V
故
i3 =
udc = −2.5A, i4 = is − i3 = (−3.5 + 2.5)A = −1A 4 R = 0Ω 由此判定
1-33
试用支路电流法求解图题所示电路中的支路电流 i1 , i2 , i3 。
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2
⎧25i1 − 20i2 − 5i3 = 50 ⎪ 代入并整理得: ⎨−5i1 + 9i2 − 4i3 = 0 解得 ⎪−5i − 4i + 10i = 0 2 3 ⎩ 1
受控源电压 受控源功率
⎧i1 = 29.6A ⎨ ⎩i2 = 28A
i2
3Ω
i3
gu
2−5
解
设网孔电流为 i1 , i2 , i3 ,则 i3 = − gu A = −0.1u A ,所以只要列出两个网孔方程
27i1 − 18i2 = 42 −18i1 + 21i2 − 3(−0.1u A ) = 20
因 u A = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
电路分析第五版答案

电路分析第五版答案第一章简介1.1 电路分析的重要性•电路分析是电气工程的基础课程之一,是理解电路原理和设计电路的关键。
•电路分析可以帮助我们了解电流、电压、功率等基本概念,并掌握电路元件的特性和相互关系。
1.2 本书的结构和内容本书共分为八个章节:1.第一章简介2.第二章基本电路定律3.第三章电阻电路4.第四章电容电路5.第五章电感电路6.第六章交流电路分析7.第七章双端口网络8.第八章共模与差模分析第二章基本电路定律2.1 基本电路定律的概述电路中的电压和电流遵循一些基本定律,包括:•基尔霍夫电流定律(KCL)•基尔霍夫电压定律(KVL)•电阻定律(Ohm’s Law)2.2 基尔霍夫电流定律(KCL)根据基尔霍夫电流定律,任何节点处的电流代数和必须等于零。
这可以用公式表示为:$$\\sum_{i=1}^n I_i = 0$$2.3 基尔霍夫电压定律(KVL)根据基尔霍夫电压定律,电路中任何回路的电压总和必须等于零。
这可以用公式表示为:$$\\sum_{i=1}^n V_i = 0$$2.4 电阻定律(Ohm’s Law)根据电阻定律,电阻的电压和电流之间存在线性关系。
这可以用公式表示为:V=VV其中,V表示电阻两端的电压,I表示通过电阻的电流,R 表示电阻的阻值。
第三章电阻电路3.1 电阻的基本性质•电阻是电路中常见的元件,用于限制电流的流动。
•电阻的阻值可以通过颜色代码或万用表进行测量。
3.2 串联电阻和并联电阻•串联电阻是将电阻依次连接在一起,电流从一个电阻流向下一个电阻。
•并联电阻是将电阻并排连接在一起,电流可以通过多个路径流动。
3.3 电阻网络的简化•电阻网络可以用串联和并联的组合来简化。
•通过串并联电阻的变换,可以将复杂的电阻网络简化为更简单的形式。
第四章电容电路4.1 电容的基本性质•电容是一种能够存储电荷的元件。
•电容的电压和电荷之间存在线性关系。
4.2 电容充放电过程•当电容器被连接到电池正极时,电容开始充电。
电路分析基础第四版课后习题第四章第五章第六章答案
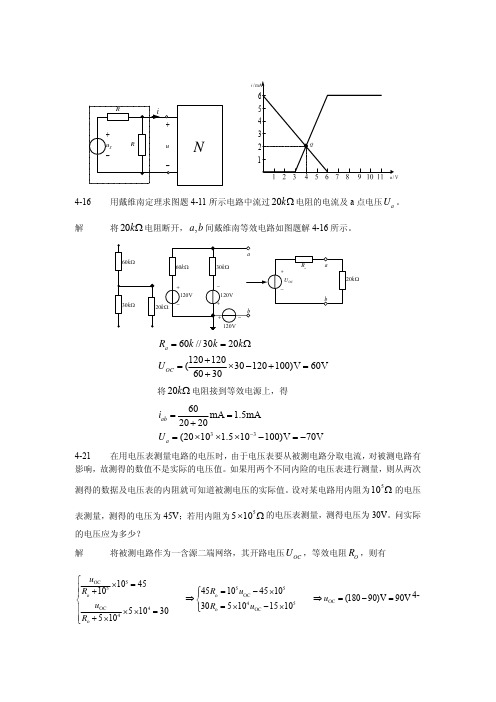
/i4-16 用戴维南定理求图题4-11所示电路中流过20k Ω电阻的电流及a 点电压。
a U 解将电阻断开,间戴维南等效电路如图题解4-16所示。
20k Ω,a bk Ω60//3020120120(30120100)V 60V6030a OCR k k k U ==Ω+=×−+=+ 将电阻接到等效电源上,得20k Ω3360mA 1.5mA2020(2010 1.510100)V 70V ab a i U −==+=×××−=− 4-21 在用电压表测量电路的电压时,由于电压表要从被测电路分取电流,对被测电路有影响,故测得的数值不是实际的电压值。
如果用两个不同内险的电压表进行测量,则从两次测得的数据及电压表的内阻就可知道被测电压的实际值。
设对某电路用内阻为的电压表测量,测得的电压为45V ;若用内阻为510Ω5510×Ω的电压表测量,测得电压为30V 。
问实际的电压应为多少? 解将被测电路作为一含源二端网络,其开路电压,等效电阻OC U O R ,则有5OC 555o o OC OC 454OCo OC 4o 10451045104510(18090)V 90V 30510151051030510u R R u u u R u R ⎧×=⎪⎧+=−×⎪⎪⇒⇒=⎨⎨=×−×⎪⎪⎩××=⎪+×⎩−=4-28 求图题4-20所示电路的诺顿等效电路。
已知:12315,5,10,R R R =Ω=Ω=Ω。
10V,1A S S u i ==解对图题4-20所示电路,画出求短路电流和等效内阻的电路,如下图所示SC i对左图,因ab 间短路,故0,0i i α==,10A 0.5A 155SC i ==+ 对右图,由外加电源法,106ab R α=Ω− 4-30 电路如图题4-22所示。
电路分析基础(浙江大学)智慧树知到课后章节答案2023年下浙江大学

电路分析基础(浙江大学)智慧树知到课后章节答案2023年下浙江大学浙江大学第一章测试1.实现电能的输送和变换的电路称为____电路。
()答案:电工2.图示电路中电流 I 的大小为:()。
答案:4A3.两个电容C1=3μF,C2=6μF串联时,其等效电容值为_____μF()。
答案:24.图示电路中a、b端的等效电阻Rab在开关K打开与闭合时分别为_____。
()答案:10Ω,10Ω5.电路理论的研究对象是()。
答案:模型化电路第二章测试1.具有n个节点,b条支路的连通图G,其独立节点数为:()答案:n-12.受控源在叠加定理时,下列说法正确的是()。
答案:受控源不能当独立源单独作用3.最大功率传输定理说明,当负载电阻RL等于电源内阻RS时,负载可获得最大功率,该定理成立的条件是()。
答案:电源电压和其内阻不变,负载RL可变4.下图电路中,Is=0时,I=2A,则当Is=8A时,I为___ 安。
()答案:85.若电流表A示数为0,则R与I的值分别为:()答案:6Ω,2.5A第三章测试1.在交流电路中,直流电路的各种定理和分析方法,只要用____形式代替各种物理量,则直流电路的各种定理和分析方法都可适用。
()答案:相量2.已知负载阻抗为Z=10∠60°Ω,则该负载性质为____。
()答案:感性3.图示串联谐振电路的品质因数Q等于:____。
()答案:104.RLC串联谐振电路品质因数Q=100,若UR=10mV,则电源电压U=____,电容两端电压UC=____。
()答案:0.01V ; 1V5.理想变压器匝数比为N1:N2, 求ab端的等效阻抗()答案:第四章测试1.下列说法正确的是:()答案:正确找出非正弦周期量各次谐波的过程称为谐波分析法。
2.()答案:24W3.在非正弦周期电路中,电磁系或者电动系仪表测量的是非正弦的________()。
答案:有效值4.()答案:0.775A5.下列说法正确的是:()。
电路分析基础(第四版)张永瑞答案第5章
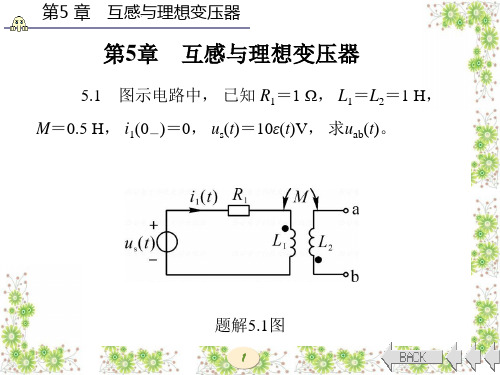
第5 章 互感与理想变压器 解 自耦变压器对求 U1、I1、U2、I2 来说可以等效为题解
5.9图所示的理想变压器。 设a端到c端的匝数为N1, b端到c端 的匝数为N2, 显然, 有
N1 U1 220 1.1 N2 U2 200
41
第5 章 互感与理想变压器
设 U2 2000 V , 则
题解5.7图
36
第5 章 互感与理想变压器 5.8 求题5.8图所示的两个电路从ab端看的等效电感Lab。
题5.8图
37
第5 章 互感与理想变压器 解 应用互感T形去耦等效, 将题5.8图(a)、 题5.8图(b)分
别等效为题解5.8图(a)、 题解5.8图(b)。 图 (a): Lab=1+2∥2=2 H 图 (b): Lab=1+[4+(-1)]∥(2+4)+3=6 H
题解5.6图
33
第5 章 互感与理想变压器 5.7 题5.7图所示为全耦合空芯变压器, 求证:当次级短
路时从初级两端看的输入阻抗Zin=0; 当次级开路时从初级两 端看的输入阻抗Zin=jωL1。
题5.7图
34
第5 章 互感与理想变压器
证明 k=1知互感 M L1L2 。 画T形去耦等效电路并
R r1 r2 Z cosjz 300.8 24
阻抗Z中的电抗即相串联的两个互感线圈等效电感的感抗
X L Z sinjz 30 1 0.82 18
等效电感
L X L 18 57.3mH
2 f 100
25
第5 章 互感与理想变压器
由于是顺接,
0.5
d i1 dt
(2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 习题5.1 如题5.1图所示电路,0t <时已处于稳态。
当0t =时开关S 打开,求初始值(0)C u +和(0)C i +。
解:根据电容电压不能突变,有: 4(0)6424C u V -=⨯=+ S 打开时有: (0)(0)4C C u u V +-== 可得: 1(0)(0)0.814C C i u A ++=-⨯=-+5.2 如题5.2图所示电路,0t <时已处于稳态。
当0t =时开关S 闭合,求初始值(0)L u +、(0)C i +和(0)i +。
解:0t <时处于稳态,有: 12(0)148L i A -==+ (0)(0)88C L u i V --=⨯=根据电容电压、电感电流不能突变,当开关S 闭合有:12(0)12(0)(0)144C C C u u i A +-+--=== (0)(0)4(0)(0)8148184L C C L u i u i V ++++=⨯+-⨯=⨯+-⨯= (0)(0)(0)112C L i i i A +++=+=+=5.3 如题5.3图所示电路,0t <时已处于稳态。
当0t =时开关S 闭合,求(0)L i +和(0)Ldi dt+。
解:0t <时,A Vi L 144)0(=Ω=- 有: A i i L L 1)0()0(==-+5.4 如题5.4图所示电路,电压表的内阻10V R k =Ω,量程为100V 。
开关S 在0t =时打开,问开关打开时,电压表是否会损坏?解:当开关闭合时,有:24==6(0)4L L i A i -=当开关打开时,有:(0)(0)6L L i i A +-==所产生的电压为: (0)61060V L V u i R k kV +=⨯=⨯Ω=可见超出了电压表的量程,因此电压表会损坏。
5.5 如题5.5图所示电路,0t <时已处于稳态。
当0t =时开关S 打开,求初始值(0)C u +和1(0)L i +、2(0)L i +。
解:开关闭合时,0C i = 110(0)223L i A -==+ 3Ω电阻上的电压为:31(0)36R L u i V -=⨯= 所以有 3(0)6C R u u V -==根据电容电压不能突变,开关打开时可得:(0)(0)6C C u u V +-==2110(0)(0)(0)122C L L u i i A +++-===+5.6 如题5.6图所示电路,0t <时已处于稳态。
当0t =时开关S 从1打到2,试求0t ≥时电流()i t ,并画出其波形。
解:开关S 位于1时,有: 36(0)7.51536C u V -⨯=⨯=+ 开关S 位于2时,建立()C u t 的方程:()()C R u t u t = ()R u t 为等效电阻33//65R =+=Ω的电压 而 ()()()C R C du t u t i t R RCdt=-=-可得微分方程:()1()0C C du t u t dt RC+= 初始条件: (0)(0)15C C u u V +-== 解方程: 特征根为12RCλ=-=- 则有: 2()t C u t Ke -= 代入初始条件可得: 15K = 得: 2()15t C u t e -= 根据分流关系,可得:22()616()15233//63659t t C u t i t e e A --=⨯=⨯⨯=++5.7 如题5.7图所示电路,电感初始储能为零,当0t =时开关S 闭合,试求0t ≥时电流()L i t ,并画出其波形。
解:已知(0)0L i -= 当开关闭合时,有:11()3()()L i t i t i t += 11()()4L i t i t =根据KVL 有: 1()8()()S L u t i t u t =⨯+ ()()L L di t u t L dt= 整理可得:()2()4L L di t i t dt+= (0)(0)0L L i i +-== 方程的齐次解为: 2()t Lh i t Ke -= 方程的特解为: 0()Ly i t A = 代入方程有: 024A = 可得:02A = 全解为: 2()()()2t L Lh Ly i t i t i t Ke -=+=+ 代入初始条件,可得: 2K =- 得: 2()2(1)t L i t e A -=-5.8 如题5.8图所示电路,电容初始储能为零,当0t =时开关S 闭合,试求0t ≥时的()C u t 、()C i t 和()u t 。
解:已知(0)0C u -=开关闭合时,将电路等效为简单的RC 串联, 以()C u t 建立方程,有:()11()()C C S du t u t u t dt RC RC+= 代入参数有:()2()12C C du t u t dt+= (0)(0)0C C u u +-== 方程齐次解为: 2t Ke -方程的特解为: 0A 代入方程可知 06A =所以有: 2()6t C u t Ke -=+ 代入初始条件可得: 6K =- 得: 2()6(1)t C u t e V -=-2()() 1.2t C C du t i t Ce A dt-== 222()()()6(1) 4.8(6 1.2)t t t C C u t u t i t R e e e V ---=+=-+=-5.9 如题5.9图所示电路,0t <时已处于稳态。
当0t =时开关S 闭合,求0t ≥时电压()C u t 和电流()i t 的零输入响应和零状态响应。
解:设C=0.1F ,开关闭合时建立方程,有:()()C C du t i t C dt=3()()(3//6)[()()]C C S C i t u t i t i t +=-两式整理可得:()2()4()C C S du t u t i t dt+= 电容初始电压为: (0)(0)339C C u u V +-==⨯= 零输入响应方程为:()2()0C C du t u t dt+= (0)9C u V += 解的形式为: 2()t Czi u t Ke -= 代入初始条件可得: 9K = 得: 2()9t Czi u t e V -= 零状态响应方程为: ()2()12C C du t u t dt+= (0)0C u += 其齐次为: 2t Ke -其特解为: 0A 代入方程有: 0212A = 可知:06A = 通解为: 2()6t Czs u t Ke -=+ 代入初始条件: 06K =+ 6K =- 得: 2()6(1)t Czs u t e V -=-根据分流关系,可知电流()i t 的零输入响应为:2()3()0.63(3//6)36t Czi zi u t i t e A -=⨯=++再根据回路列KVL 方程:6()()5()3[()()]3zs Czs zs zs S i t u t i t i t i t -=+- 整理可得: 2()9()(10.4)15t Czs zs u t i t e A -+==-5.10 如题5.10图所示电路,0t =时开关S 位于1,电路已处于稳态。
当0t =时开关S 闭合2,求0t ≥时电流()L i t 和电压()u t 的零输入响应和零状态响应。
解:0t <时有: 366(0)363//636L i A -=⨯=++0t ≥时建立方程,有:()3()()()3L L L S u t i t i t i t ++=()()L L di t u t Ldt= 整理可得微分方程为:()2()2L L di t i t dt+= 零输入响应: 2()t Lzi i t Ke -= 代入初始条件 (0)3L i K +== 可得: 2()3t Lzi i t e A -=2()()3()9t L zi L di t u t i t Le V dt-=+=- 零状态响应: ()+Lzs i t =齐次解特解 齐次解: 2()t Lzsy i t Ke -=特解: ()Lzip i t A = 代入方程可得: 1A = 则: 2()t Lzs i t Ke -=+1由初始条件(0)0Lzs i +=,可知1K =- 得: 2()(1t Lzs i t e -=-)2()()3()3(1)t Lzs zs Lzs di t u t i t L e V dt-=+=+5.11 如题5.11图所示电路,0t <已处于稳态,当0t =时开关S 打开,求0t ≥时电流()L i t 的零输入响应、零状态响应和全响应。
解:0t <时根据叠加原理有:3(6//6//6)615(0)6//666//623L i A -⨯=-⨯=+⑴ 零输入响应,其方程为:0=+L L i L R dt di 35)0()0(==-+L L i i Ω=+=1266R 方程解为: τtL Ket i -=)( 41123===R L τ 代入初始条件: 35)0(==+K i L零输入相应为: t L e t i 435)(-= 0t ≥⑵ 零状态响应(等效电路如右),其方程为:6=+L L i LRdt di Ω=+=1266R 0)0(=+L i齐次解为: τtLh Ke t i -=)( 41123===R L τ 特解为: A t i Lp =)( 代入方程可得: 23=A 则零状态相应为: 23)(4+=-t L Ke t i 代入初始条件可得: 23-=K有: )(t L e t i 4-123)(-= 0t ≥⑶ 全响应为:)(零状态相应零输入相应t t L e e t i 44-12335)(--+=+= 0t ≥5.12 如题5.12图所示电路,0t <已处于稳态,当0t =时开关S 闭合,闭合后经过10s 后,开关又打开,求0t ≥时()C u t 。
解:5.13 如题5.13图所示电路,0t <已处于稳态,当0t =时开关S 打开,求0t ≥时()L i t 和()L u t 。
解:0t <时,有:55(0)3+12A 5555L i -==++S 打开,t →∞时有:55()3+11515515L i A ∞==++ 电路的时间常数为: 41=55+105L R τ==+ (0)(0)2A L L i i +-== 根据三要素公式,可知:5()()[(0)()](1)tt L L L L i t i i i ee A τ--+=∞+-∞=+5()()20t L L di t u t L e A dt-==-5.14 如题5.14图所示电路,0t <已处于稳态,当0t =时开关S 闭合,求0t ≥时的电流()i t 。
