正弦定理与余弦定理
正弦定理和余弦定理
的面积．
思维启迪
解析
探究提高
(1)根据所给等式的结构特点利 用余弦定理将角化边进行变形 是迅速解答本题的关键． (2) 熟 练 运 用 余 弦 定 理 及 其 推 论，同时还要注意整体思想、方 程思想在解题过程中的运用．
基础知识
题型分类
(2)a＝ 2Rsin A ，b＝ 2Rsin B ，
也较大，即在 △ABC
a c＝ 2Rsin C ；(3)sin A＝ 2R ，sin B
b
c
中，A>B⇔a>b⇔ sin A>sin B.
＝ 2R ，sin C＝ 2R 等形式，以
解决不同的三角形问题．
动画展示
基础知识
题型分类
思想方法
练出高分
基础知识·自主学习
题型一
利用正弦定理解三角形
【例 1】 在△ABC 中，a＝ 3，b＝ 2， 思维启迪
解析
探究提高
B＝45°.求角 A、C 和边 c.
(1)已知两角及一边可求第三角， 解这样的三角形只需直接用正弦
定理代入求解即可．
(2)已知两边和一边对角，解三角 形时，利用正弦定理求另一边的
对角时要注意讨论该角，这是解
况如下：
形的形状，主要有两种
A 为锐角
A 为钝角 或直角
途径：
(1)化边为角；(2)化角为边，
图形
并常用正弦(余弦)定理实施
关系
bsin A
a＝bsin A
式
<a<b
解的 个数
一解
两解
a≥b 一解
a>b 一解
边、角转换．
正弦定理和余弦定理
正弦定理和余弦定理在△ABC中，若角A，B，C所对的边分别是a，b，c，R为△ABC外接圆半径，则有正弦定理和余弦定理：正弦定理：a/sinA = b/sinB = c/sinC = 2R余弦定理：a^2 = b^2 + c^2 - 2bccosA；b^2 = c^2 + a^2 - 2cacosB；c^2 = a^2 + b^2 - 2abcosC可以通过变形得到以下公式：cosA = (b^2 + c^2 - a^2) / 2bc；cosB = (c^2 + a^2 - b^2) / 2ac；cosC = (a^2 + b^2 - c^2) / 2ab同时还有以下关系：a = 2RsinA；b = 2RsinB；c = 2RsinCa:b:c =asinB = bsinA；bsinC = csinB；asinC = csinAABC的面积S = absinC = bcsinA = acsinB = r其中r为三角形内切圆半径，可以通过S = (a + b + c)r得到。
选择题：1.在△ABC中，已知a = 2，b = 6，A = 45°，则满足条件的三角形有2个。
2.在△ABC中，A = 60°，AB = 2，且△ABC的面积为3，则BC的长为3.3.已知在△ABC中，a = x，b = 2，B = 45°，若三角形有两解，则x的取值范围是2＜x＜22.4.已知锐角三角形的边长分别为1，3，x，则x的取值范围是(8,10)。
注：原文中存在格式错误，已经进行修正。
整理得2c=b+bc，因为c≠0，所以等式两边同时除以c，得到2=c+b，解得c=2/(b+1)。
在△ABC中，已知内角A、B、C所对的边分别为a、b、c，且△ABC的面积为315，b-c=2，cosA=1/4，求a的值。
解析：由cosA=1/4，得到sinA=√15/4，S△ABC=bcsinA=bc*√15/4=315，因此bc=24.又因为b-c=2，所以b^2-2bc+c^2=4，联立解得b^2+c^2=52.由余弦定理得，a=b+c-2bccosA=52-2*24*(1/4)=64，因此a=8.在△ABC中，已知内角A、B、C所对的边分别为a、b、c，且A=π/4，b^2-a^2=c^2/2.1)求tanC的值；2)若△ABC的面积为3，求b的值。
正弦定理和余弦定理
正弦定理和余弦定理一、基础知识1．正弦定理asin A＝bsin B＝csin C＝2R(R为△ABC外接圆的半径)．正弦定理的常见变形(1)a＝2R sin A，b＝2R sin B，c＝2R sin C；(2)sin A＝a2R，sin B＝b2R，sin C＝c2R；(3)a∶b∶c＝sin A∶sin B∶sin C；(4)a＋b＋csin A＋sin B＋sin C＝asin A.2．余弦定理a2＝b2＋c2－2bc cos A；b2＝c2＋a2－2ca cos B；c2＝a2＋b2－2ab cos C. 3．三角形的面积公式(1)S△ABC＝12ah a(h a为边a上的高)；(2)S△ABC＝12ab sin C＝12bc sin A＝12ac sin B；(3)S＝12r(a＋b＋c)(r为三角形的内切圆半径)．二、常用结论汇总——规律多一点1．三角形内角和定理在△ABC中，A＋B＋C＝π；变形：A＋B2＝π2－C2.2．三角形中的三角函数关系(1)sin(A＋B)＝sin C；(2)cos(A＋B)＝－cos C；(3)sin A＋B2＝cosC2；(4)cosA＋B2＝sinC2.3．三角形中的射影定理在△ABC 中，a ＝b cos C ＋c cos B ；b ＝a cos C ＋c cos A ；c ＝b cos A ＋a cos B . 4．用余弦定理判断三角形的形状在△ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，当b 2＋c 2－a 2>0时，可知A 为锐角；当b 2＋c 2－a 2＝0时，可知A 为直角；当b 2＋c 2－a 2<0时，可知A 为钝角．第一课时 正弦定理和余弦定理(一) 考点一 利用正、余弦定理解三角形考法(一) 正弦定理解三角形[典例] (1)(优质试题·江西重点中学联考)在△ABC 中，a ＝3，b ＝2，A ＝30°，则cos B ＝________.(2)设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .若a ＝3，sin B ＝12，C ＝π6，则b ＝________.[解析] (1)由正弦定理可得sin B ＝b sin A a ＝2×sin 30°3＝13，∵a ＝3>b ＝2，∴B <A ，即B 为锐角，∴cos B ＝1－sin 2B ＝223.(2)∵sin B ＝12且B ∈(0，π)，∴B ＝π6或B ＝5π6， 又∵C ＝π6，∴B ＝π6，A ＝π－B －C ＝2π3. 又a ＝3，由正弦定理得a sin A ＝bsin B ， 即3sin 2π3＝b sin π6，解得b ＝1. [答案] (1)223 (2)1 考法(二) 余弦定理解三角形[典例] (1)(优质试题·山西五校联考)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若b cos A ＋a cos B ＝c 2，a ＝b ＝2，则△ABC 的周长为( )A ．7.5B ．7C ．6D ．5(2)(优质试题·泰安二模)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且c －b 2c －a ＝sin Asin B ＋sin C，则角B ＝________. [解析] (1)∵b cos A ＋a cos B ＝c 2，∴由余弦定理可得b ·b 2＋c 2－a22bc ＋a ·a 2＋c 2－b 22ac ＝c 2，整理可得2c 2＝2c 3，解得c ＝1，则△ABC 的周长为a ＋b ＋c ＝2＋2＋1＝5.(2)由正弦定理可得c －b 2c －a＝sin Asin B ＋sin C ＝ab ＋c，∴c 2－b 2＝2ac －a 2，∴c 2＋a 2－b 2＝2ac ， ∴cos B ＝a 2＋c 2－b 22ac ＝22，∵0<B <π，∴B ＝π4.[答案] (1)D (2)π4[专题训练]1.△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若b 2＝ac ，c ＝2a ，则cos C ＝( )A.24 B ．－24 C.34D ．－34解析：选B 由题意得，b 2＝ac ＝2a 2，即b ＝2a ，∴cos C ＝a 2＋b 2－c 22ab ＝a 2＋2a 2－4a 22a ×2a＝－24.2.△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知sin B ＋sin A (sin C －cos C )＝0，a ＝2，c ＝2，则C ＝( )A.π12B.π6C.π4D.π3解析：选B 因为sin B ＋sin A (sin C －cos C )＝0， 所以sin(A ＋C )＋sin A sin C －sin A cos C ＝0，所以sin A cos C ＋cos A sin C ＋sin A sin C －sin A cos C ＝0，整理得sin C (sin A ＋cos A )＝0.因为sin C ≠0，所以sin A ＋cos A ＝0，所以t a n A ＝－1， 因为A ∈(0，π)，所以A ＝3π4，由正弦定理得sin C ＝c ·sin A a ＝2×222＝12， 又0＜C ＜π4，所以C ＝π6.3.在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知sin 2B ＋sin 2C ＝sin 2A ＋sin B sin C .(1)求角A 的大小；(2)若cos B ＝13，a ＝3，求c 的值． 解：(1)由正弦定理可得b 2＋c 2＝a 2＋bc ， 由余弦定理得cos A ＝b 2＋c 2－a 22bc ＝12， 因为A ∈(0，π)，所以A ＝π3. (2)由(1)可知sin A ＝32，因为cos B＝13，B为△ABC的内角，所以sin B＝223，故sin C＝sin(A＋B)＝sin A cos B＋cos A sin B＝32×13＋12×223＝3＋226.由正弦定理asin A＝csin C得c＝a sin Csin A＝3×(3＋22)32×6＝1＋263.考点二判定三角形的形状[典例](1)设△ABC的内角A，B，C所对的边分别为a，b，c，若b cos C ＋c cos B＝a sin A，则△ABC的形状为()A．锐角三角形B．直角三角形C．钝角三角形D．不确定(2)在△ABC中，角A，B，C的对边分别为a，b，c，若sin Asin B＝ac，(b＋c＋a)(b＋c－a)＝3bc，则△ABC的形状为()A．直角三角形B．等腰非等边三角形C．等边三角形D．钝角三角形[解析](1)法一：因为b cos C＋c cos B＝a sin A，由正弦定理知sin B cos C＋sin C cos B＝sin A sin A，得sin(B＋C)＝sin A sin A.又sin(B＋C)＝sin A，得sin A＝1，即A＝π2，因此△ABC是直角三角形．法二：因为b cos C ＋c cos B ＝b ·a 2＋b 2－c 22ab ＋c ·a 2＋c 2－b 22ac ＝2a 22a ＝a ，所以a sin A ＝a ，即sin A ＝1，故A ＝π2，因此△ABC 是直角三角形．(2)因为sin A sin B ＝a c ，所以a b ＝ac ，所以b ＝c .又(b ＋c ＋a )(b ＋c －a )＝3bc ，所以b 2＋c 2－a 2＝bc ， 所以cos A ＝b 2＋c 2－a 22bc ＝bc 2bc ＝12.因为A ∈(0，π)，所以A ＝π3，所以△ABC 是等边三角形． [答案] (1)B (2)C[变透练清]1.(变条件)若本例(1)条件改为“a sin A ＋b sin B <c sin C ”，那么△ABC 的形状为________．解析：根据正弦定理可得a 2＋b 2<c 2，由余弦定理得cos C ＝a 2＋b 2－c 22ab <0，故C 是钝角， 所以△ABC 是钝角三角形． 答案：钝角三角形2.(变条件)若本例(1)条件改为“c －a cos B ＝(2a －b )cos A ”，那么△ABC 的形状为________．解析：因为c －a cos B ＝(2a －b )cos A ， C ＝π－(A ＋B )，所以由正弦定理得sin C －sin A cos B ＝2sin A cos A －sin B ·cos A ， 所以sin A cos B ＋cos A sin B －sin A cos B ＝2sin A cos A －sin B cos A ， 所以cos A (sin B －sin A )＝0，所以cos A＝0或sin B＝sin A，所以A＝π2或B＝A或B＝π－A(舍去)，所以△ABC为等腰或直角三角形．答案：等腰或直角三角形3.(变条件)若本例(2)条件改为“cos Acos B＝ba＝2”，那么△ABC的形状为________．解析：因为cos Acos B＝ba，由正弦定理得cos Acos B＝sin Bsin A，所以sin 2A＝sin 2B.由ba＝2，可知a≠b，所以A≠B.又因为A，B∈(0，π)，所以2A＝π－2B，即A＋B＝π2，所以C＝π2，于是△ABC是直角三角形．答案：直角三角形[课时跟踪检测]A级1．在△ABC中，内角A，B，C的对边分别为a，b，c.若sin Aa＝cos Bb，则B的大小为()A．30°B．45°C．60°D．90°解析：选B由正弦定理知，sin Asin A＝cos Bsin B，∴sin B＝cos B，∴B＝45°.2．在△ABC中，内角A，B，C的对边分别为a，b，c.已知b＝40，c＝20，C＝60°，则此三角形的解的情况是()A．有一解B．有两解C．无解D．有解但解的个数不确定解析：选C 由正弦定理得b sin B ＝csin C ， ∴sin B ＝b sin Cc ＝40×3220＝3>1.∴角B 不存在，即满足条件的三角形不存在．3．(优质试题·重庆六校联考)在△ABC 中，cos B ＝ac (a ，b ，c 分别为角A ，B ，C 的对边)，则△ABC 的形状为( )A ．直角三角形B ．等边三角形C ．等腰三角形D ．等腰三角形或直角三角形解析：选A 因为cos B ＝a c ，由余弦定理得a 2＋c 2－b 22ac ＝a c ，整理得b 2＋a2＝c 2，即C 为直角，则△ABC 为直角三角形．4．在△ABC 中，a ，b ，c 分别是内角A ，B ，C 的对边．若b sin A ＝3c sin B ，a ＝3， cos B ＝23，则b ＝( )A ．14B ．6 C.14D. 6解析：选D ∵b sin A ＝3c sin B ⇒ab ＝3bc ⇒a ＝3c ⇒c ＝1，∴b 2＝a 2＋c 2－2ac cos B ＝9＋1－2×3×1×23＝6，∴b ＝ 6.5．(优质试题·莆田调研)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，若a sin B cos C ＋c sin B cos A ＝12b ，且a >b ，则B ＝( )A.π6B.π3C.2π3D.5π6解析：选A ∵a sin B cos C ＋c sin B cos A ＝12b ，∴根据正弦定理可得sin A sinB cosC ＋sin C sin B cos A ＝12sin B ，即sin B (sin A cos C ＋sin C cos A )＝12sin B ．∵sin B ≠0，∴sin(A ＋C )＝12，即sin B ＝12.∵a >b ，∴A >B ，即B 为锐角，∴B ＝π6.6．(优质试题·山西大同联考)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若2(b cos A ＋a cos B )＝c 2，b ＝3,3cos A ＝1，则a ＝( )A. 5 B ．3 C.10D ．4解析：选B 由正弦定理可得2(sin B cos A ＋sin A cos B )＝c sin C ， ∵2(sin B cos A ＋sin A cos B )＝2sin(A ＋B )＝2sin C ，∴2sin C ＝c sin C ，∵sin C >0，∴c ＝2，由余弦定理得a 2＝b 2＋c 2－2bc cos A ＝32＋22－2×3×2×13＝9，∴a ＝3.7．在△ABC 中，AB ＝6，A ＝75°，B ＝45°，则AC ＝________. 解析：C ＝180°－75°－45°＝60°， 由正弦定理得AB sin C ＝AC sin B ， 即6sin 60°＝AC sin 45°，解得AC ＝2. 答案：28．设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且a ＝2，cos C ＝－14，3sin A ＝2sin B ，则c ＝________.解析：∵3sin A ＝2sin B ，∴3a ＝2b . 又∵a ＝2，∴b ＝3.由余弦定理可知c 2＝a 2＋b 2－2ab cos C ， ∴c 2＝22＋32－2×2×3×⎝ ⎛⎭⎪⎫－14＝16，∴c ＝4.答案：49．(优质试题·浙江高考)在△ABC中，角A，B，C所对的边分别为a，b，c.若a＝7，b＝2，A＝60°，则sin B＝________，c＝________.解析：由正弦定理asin A＝bsin B，得sin B＝ba·sin A＝27×32＝217.由余弦定理a2＝b2＋c2－2bc cos A，得7＝4＋c2－4c×cos 60°，即c2－2c－3＝0，解得c＝3或c＝－1(舍去)．答案：217 310．在△ABC中，a，b，c分别为角A，B，C所对的边，sin A，sin B，sin C 成等差数列，且a＝2c，则cos A＝________.解析：因为sin A，sin B，sin C成等差数列，所以2sin B＝sin A＋sin C．由正弦定理得a＋c＝2b，又因为a＝2c，可得b＝32c，所以cos A＝b2＋c2－a22bc＝94c2＋c2－4c22×32c2＝－14.答案：－1 411．在△ABC中，内角A，B，C的对边分别为a，b，c，且A＝2B.(1)求证：a＝2b cos B；(2)若b＝2，c＝4，求B的值．解：(1)证明：因为A＝2B，所以由正弦定理asin A＝bsin B，得asin 2B＝bsin B，所以a＝2b cos B.(2)由余弦定理，a2＝b2＋c2－2bc cos A，因为b＝2，c＝4，A＝2B，。
正弦定理、余弦定理对比表
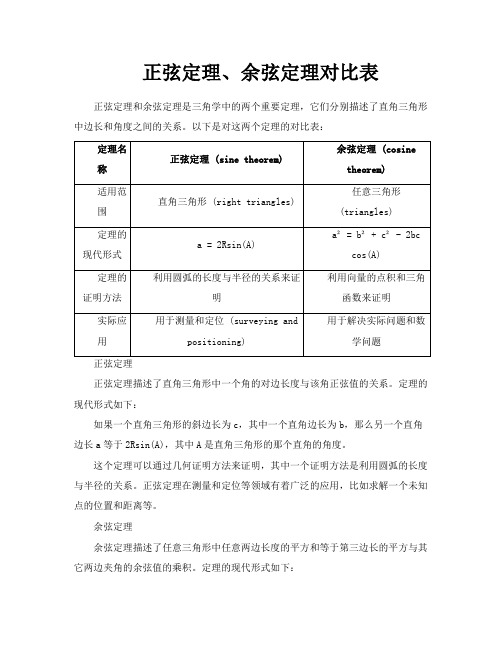
正弦定理、余弦定理对比表正弦定理和余弦定理是三角学中的两个重要定理，它们分别描述了直角三角形中边长和角度之间的关系。
以下是对这两个定理的对比表：正弦定理描述了直角三角形中一个角的对边长度与该角正弦值的关系。
定理的现代形式如下：如果一个直角三角形的斜边长为c，其中一个直角边长为b，那么另一个直角边长a等于2Rsin(A)，其中A是直角三角形的那个直角的角度。
这个定理可以通过几何证明方法来证明，其中一个证明方法是利用圆弧的长度与半径的关系。
正弦定理在测量和定位等领域有着广泛的应用，比如求解一个未知点的位置和距离等。
余弦定理余弦定理描述了任意三角形中任意两边长度的平方和等于第三边长的平方与其它两边夹角的余弦值的乘积。
定理的现代形式如下：对于一个三角形ABC，如果角A的对边长度为a，角B的对边长度为b，角C 的对边长度为c，那么有以下等式成立：a² = b² + c² - 2bc cos(A)。
这个定理可以通过代数证明方法来证明，其中一个证明方法是利用向量的点积和三角函数。
余弦定理在解决实际问题和数学问题中有着广泛的应用，比如求解一个三角形的面积和周长等。
对比总结正弦定理和余弦定理都是描述三角形中边长和角度之间关系的定理。
正弦定理适用于直角三角形，而余弦定理适用于任意三角形。
在应用领域方面，正弦定理主要用于测量和定位，而余弦定理则主要用于解决实际问题和数学问题。
此外，正弦定理的证明方法比较直观和几何化，而余弦定理的证明方法则比较代数化。
在实际应用中，如果知道三角形的一个角度和任意两边长度，我们可以使用正弦定理或余弦定理来求解第三条边长；如果知道三角形的三条边长，我们可以使用余弦定理来求解任意一个角度。
因此，正弦定理和余弦定理在解三角形的问题中是密不可分的。
三角形中的正弦定理与余弦定理
三角形中的正弦定理与余弦定理正文：三角形中的正弦定理与余弦定理三角形是几何学中最基本的图形之一，它包含了很多重要的定理和公式。
在三角形的研究中，正弦定理和余弦定理是两个非常重要且常用的公式。
它们可以帮助我们计算三角形的各种属性，如边长、角度等。
本文将详细介绍这两个定理的含义、推导过程，并给出实际应用的一些例子。
一、正弦定理正弦定理是指在一个三角形中，三条边与三个对应的正弦值之间存在一定的关系。
设三角形的三条边分别为a、b、c，对应的角度为A、B、C，则正弦定理可以表达为：a/sinA = b/sinB = c/sinC其中，sinA、sinB、sinC分别为三个角的正弦值。
这个定理实际上是在说明了三角形的三个边的长度与对应的角度之间存在一定的比例关系。
如果我们已知了三角形的一个角度和两个对应的边长，就可以利用正弦定理来计算第三个边的长度。
例如，已知三角形ABC中，角A的度数为30°，边AB的长度为3，边AC的长度为4，我们可以利用正弦定理求解边BC的长度。
根据正弦定理，我们有：BC/sinA = AC/sinC代入已知条件，得到：BC/sin30° = 4/sinC进一步计算可得：BC = 4*sin30°/sinC ≈ 4*0.5/sinC = 2/sinC通过这个简单的计算过程，我们可以求解出BC的长度。
正弦定理在实际应用中非常有用，可以帮助我们解决各种与三角形边长相关的问题。
二、余弦定理余弦定理是指在一个三角形中，三条边与一个对应的角度之间存在一定的关系。
设三角形的三条边分别为a、b、c，对应的角度为A、B、C，则余弦定理可以表示为：c^2 = a^2 + b^2 - 2ab*cosC这个定理实际上是在说明了三角形的三个边的长度与对应的角度之间存在一定的关系。
利用余弦定理，我们可以计算三角形的一个边长，当已知该边的两个对应角度和另一边的长度时。
例如，已知三角形ABC中，边AB的长度为3，边AC的长度为4，角C的度数为60°，我们可以利用余弦定理来计算边BC的长度。
余弦定理与正弦定理的推导
余弦定理与正弦定理的推导三角函数是数学中重要且常用的概念，其中余弦定理和正弦定理是解决三角形问题的基本工具。
本文将介绍余弦定理和正弦定理的推导过程，并探讨其应用。
一、余弦定理的推导余弦定理用于计算三角形任意一边的长度，其表达式为：c² = a² + b² - 2ab * cos(C)其中，a、b、c 分别表示三角形的三条边的长度，C 表示夹角C的度数。
我们假设有一个三角形ABC，令 a=BC，b=AC，c=AB，角A的度数为α，角B的度数为β，角C的度数为γ。
根据三角形的角度关系可知，α = 180° - β - γ。
根据余弦定理的定义可得：c² = a² + b² - 2ab * cos(C)将 a=BC，b=AC，c=AB 代入，得到：AB² = BC² + AC² - 2 × BC × AC × cos(γ)将γ 替换为α+β，得到：AB² = BC² + AC² - 2 × BC × AC × cos(α+β)使用余弦的和差化简公式可得：AB² = BC² + AC² - 2 × BC × AC × [cosα*cosβ - sinα*sinβ]再利用三角函数的定义可得：AB² = BC² + AC² - 2 × BC × AC × [cosα*cosβ - (1 - cos²α)(1 -cos²β)^(1/2)]经过化简，我们可以得到最终的余弦定理表达式：AB² = BC² + AC² - 2 × BC × AC × cosα*cosβ + 2 × BC × AC ×sinα*sinβ二、正弦定理的推导正弦定理用于计算三角形的边长与角度的关系，其表达式为：a/sinA = b/sinB = c/sinC根据这个定理，我们可以推导出正弦定理的表达式。
三角形正弦定理和余弦定理
三角形正弦定理和余弦定理三角形正弦定理和余弦定理是几何学中的重要定理。
它们可以用来解决三角形中任意两边和夹角的求解问题。
两个定理都是基于三角形的基本定义而推导出来的，都有它们自己的特点，可以帮助我们解决复杂的几何问题。
三角形正弦定理由法国数学家Adrien-Marie Legendre于1786年提出，它定义了三角形的正弦和余弦值之间的关系：a/sinA = b/sinB = c/sinC，其中a,b,c分别表示三角形的三边，A,B,C分别表示三边所对应的角。
它可以用来求解三角形的任意两边和夹角的大小。
余弦定理，又称余弦公式，是由18世纪英国数学家John Wallis发现的，它定义了三角形的余弦值之间的关系：a^2 =b^2 + c^2 - 2bc*cosA，其中a,b,c分别表示三角形的三边，A表示两边之间的夹角。
它可以用来求解三角形的任意两边的长度。
三角形正弦定理和余弦定理是几何学中的重要定理，它们可以用来解决三角形中任意两边和夹角的求解问题，帮助我们求解复杂的几何问题。
它们的精确性和准确性，使得它们在几何学中具有重要的作用，也被广泛应用于现代数学和工程学中。
例如，它们可以用来求解地球表面上两点之间的距离，这是很多工程学上的应用，比如建筑、测量等应用都会用到三角形正弦定理和余弦定理。
此外，它们还可以用来解决圆柱体、球体和其他几何体的体积、表面积等问题，也是工程学中重要的计算公式。
三角形正弦定理和余弦定理都是几何学的重要定理，它们可以用来解决三角形中任意两边和夹角的求解问题，它们的精确性和准确性使得它们在几何学中具有重要的作用，也被广泛应用于现代数学和工程学中，比如求解两点之间的距离，求解圆柱体、球体和其他几何体的体积、表面积等问题，都是重要的工程学计算公式。
正弦定理和余弦定理
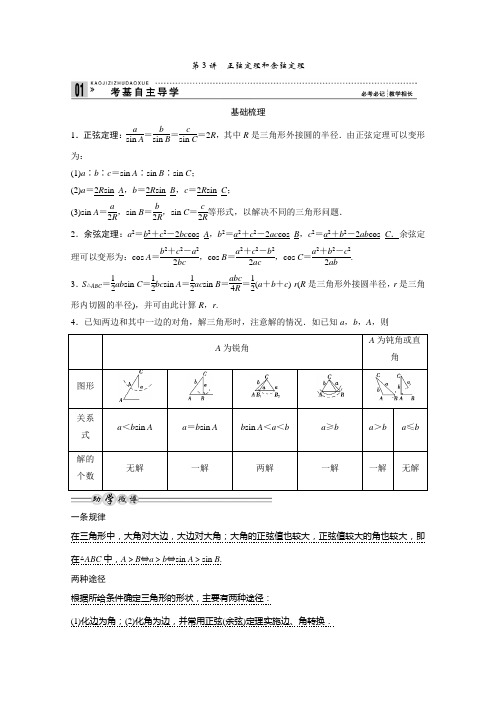
第3讲 正弦定理和余弦定理基础梳理1．正弦定理：a sin A ＝b sin B ＝csin C ＝2R ，其中R 是三角形外接圆的半径．由正弦定理可以变形为：(1)a ∶b ∶c ＝sin A ∶sin B ∶sin C ；(2)a ＝2R sin_A ，b ＝2R sin_B ，c ＝2R sin_C ；(3)sin A ＝a 2R ，sin B ＝b 2R ，sin C ＝c2R等形式，以解决不同的三角形问题．2．余弦定理：a 2＝b 2＋c 2－2bc cos_A ，b 2＝a 2＋c 2－2ac cos_B ，c 2＝a 2＋b 2－2ab cos_C ．余弦定理可以变形为：cos A ＝b 2＋c 2－a 22bc ，cos B ＝a 2＋c 2－b 22ac ，cos C ＝a 2＋b 2－c 22ab.3．S △ABC ＝12ab sin C ＝12bc sin A ＝12ac sin B ＝abc 4R ＝12(a ＋b ＋c )·r (R 是三角形外接圆半径，r 是三角形内切圆的半径)，并可由此计算R ，r .4．已知两边和其中一边的对角，解三角形时，注意解的情况．如已知a ，b ，A ，则A 为锐角A 为钝角或直角图形关系 式 a ＜b sin Aa ＝b sin Ab sin A ＜a ＜b a ≥ba ＞ba ≤b解的 个数无解 一解 两解 一解 一解 无解一条规律在三角形中，大角对大边，大边对大角；大角的正弦值也较大，正弦值较大的角也较大，即在△ABC 中，A ＞B ⇔a ＞b ⇔sin A ＞sin B . 两种途径根据所给条件确定三角形的形状，主要有两种途径：(1)化边为角；(2)化角为边，并常用正弦(余弦)定理实施边、角转换．双基自测1．(人教A 版教材习题改编)在△ABC 中，A ＝60°，B ＝75°，a ＝10，则c 等于( )． A ．5 2 B ．10 2 C.1063D ．5 6解析 由A ＋B ＋C ＝180°，知C ＝45°， 由正弦定理得：a sin A ＝c sin C ，即1032＝c 22.∴c ＝1063.答案 C2．在△ABC 中，若sin A a ＝cos B b ，则B 的值为( )．A ．30°B ．45°C ．60°D ．90° 解析 由正弦定理知：sin A sin A ＝cos Bsin B ，∴sin B ＝cos B ，∴B ＝45°. 答案 B3．(2011·郑州联考)在△ABC 中，a ＝3，b ＝1，c ＝2，则A 等于( )． A ．30° B ．45° C ．60° D ．75° 解析 由余弦定理得：cos A ＝b 2＋c 2－a 22bc ＝1＋4－32×1×2＝12，∵0＜A ＜π，∴A ＝60°. 答案 C4．在△ABC 中，a ＝32，b ＝23，cos C ＝13，则△ABC 的面积为( )．A ．3 3B ．2 3C ．4 3 D. 3 解析 ∵cos C ＝13，0＜C ＜π，∴sin C ＝223，∴S △ABC ＝12ab sin C＝12×32×23×223＝4 3.答案 C5．已知△ABC 三边满足a 2＋b 2＝c 2－3ab ，则此三角形的最大内角为________． 解析 ∵a 2＋b 2－c 2＝－3ab ， ∴cos C ＝a 2＋b 2－c 22ab ＝－32，故C ＝150°为三角形的最大内角． 答案 150°考向一 利用正弦定理解三角形【例1】►在△ABC 中，a ＝3，b ＝2，B ＝45°.求角A ，C 和边c .[审题视点] 已知两边及一边对角或已知两角及一边，可利用正弦定理解这个三角形，但要注意解的判断．解 由正弦定理得a sin A ＝b sin B ，3sin A ＝2sin 45°，∴sin A ＝32. ∵a ＞b ，∴A ＝60°或A ＝120°.当A ＝60°时，C ＝180°－45°－60°＝75°， c ＝b sin C sin B ＝6＋22；当A ＝120°时，C ＝180°－45°－120°＝15°， c ＝b sin C sin B ＝6－22.(1)已知两角一边可求第三角，解这样的三角形只需直接用正弦定理代入求解即可．(2)已知两边和一边对角，解三角形时，利用正弦定理求另一边的对角时要注意讨论该角，这是解题的难点，应引起注意．【训练1】 (2011·北京)在△ABC 中，若b ＝5，∠B ＝π4，tan A ＝2，则sin A ＝________；a ＝________.解析 因为△ABC 中，tan A ＝2，所以A 是锐角， 且sin Acos A＝2，sin 2A ＋cos 2A ＝1，联立解得sin A ＝255，再由正弦定理得a sin A ＝bsin B ，代入数据解得a ＝210. 答案255210 考向二 利用余弦定理解三角形【例2】►在△ABC 中，a 、b 、c 分别是角A 、B 、C 的对边，且cos B cos C ＝－b2a ＋c .(1)求角B 的大小；(2)若b ＝13，a ＋c ＝4，求△ABC 的面积． [审题视点] 由cos B cos C ＝－b2a ＋c，利用余弦定理转化为边的关系求解． 解 (1)由余弦定理知：cos B ＝a 2＋c 2－b 22ac ，cos C ＝a 2＋b 2－c 22ab.将上式代入cos B cos C ＝－b2a ＋c 得：a 2＋c 2－b 22ac ·2ab a 2＋b 2－c 2＝－b 2a ＋c ， 整理得：a 2＋c 2－b 2＝－ac . ∴cos B ＝a 2＋c 2－b 22ac ＝－ac 2ac ＝－12.∵B 为三角形的内角，∴B ＝23π.(2)将b ＝13，a ＋c ＝4，B ＝23π代入b 2＝a 2＋c 2－2ac cos B ，得b 2＝(a ＋c )2－2ac －2ac cos B ， ∴13＝16－2ac ⎝⎛⎭⎫1－12，∴ac ＝3. ∴S △ABC ＝12ac sin B ＝334.(1)根据所给等式的结构特点利用余弦定理将角化边进行变形是迅速解答本题的关键．(2)熟练运用余弦定理及其推论，同时还要注意整体思想、方程思想在解题过程中的运用． 【训练2】 (2011·桂林模拟)已知A ，B ，C 为△ABC 的三个内角，其所对的边分别为a ，b ，c ，且2cos 2 A2＋cos A ＝0.(1)求角A 的值；(2)若a ＝23，b ＋c ＝4，求△ABC 的面积． 解 (1)由2cos 2 A2＋cos A ＝0，得1＋cos A ＋cos A ＝0， 即cos A ＝－12，∵0＜A ＜π，∴A ＝2π3.(2)由余弦定理得，a 2＝b 2＋c 2－2bc cos A ，A ＝2π3，则a 2＝(b ＋c )2－bc ， 又a ＝23，b ＋c ＝4， 有12＝42－bc ，则bc ＝4， 故S △ABC ＝12bc sin A ＝ 3.考向三 利用正、余弦定理判断三角形形状【例3】►在△ABC 中，若(a 2＋b 2)sin(A －B )＝(a 2－b 2)sin C ，试判断△ABC 的形状． [审题视点] 首先边化角或角化边，再整理化简即可判断． 解 由已知(a 2＋b 2)sin(A －B )＝(a 2－b 2)sin C ， 得b 2[sin(A －B )＋sin C ]＝a 2[sin C －sin(A －B )]， 即b 2sin A cos B ＝a 2cos A sin B ，即sin 2B sin A cos B ＝sin 2A cos B sin B ，所以sin 2B ＝sin 2A ， 由于A ，B 是三角形的内角． 故0＜2A ＜2π，0＜2B ＜2π. 故只可能2A ＝2B 或2A ＝π－2B ， 即A ＝B 或A ＋B ＝π2.故△ABC 为等腰三角形或直角三角形．判断三角形的形状的基本思想是；利用正、余弦定理进行边角的统一．即将条件化为只含角的三角函数关系式，然后利用三角恒等变换得出内角之间的关系式；或将条件化为只含有边的关系式，然后利用常见的化简变形得出三边的关系． 【训练3】 在△ABC 中，若a cos A ＝b cos B ＝c cos C；则△ABC 是( )． A ．直角三角形 B ．等边三角形 C ．钝角三角形D ．等腰直角三角形解析 由正弦定理得a ＝2R sin A ，b ＝2R sin B ，c ＝2R sin C (R 为△ABC 外接圆半径)． ∴sin A cos A ＝sin B cos B ＝sin C cos C. 即tan A ＝tan B ＝tan C ，∴A ＝B ＝C . 答案 B考向三 正、余弦定理的综合应用【例3】►在△ABC 中，内角A ，B ，C 对边的边长分别是a ，b ，c ，已知c ＝2，C ＝π3.(1)若△ABC 的面积等于3，求a ，b ；(2)若sin C ＋sin(B －A )＝2sin 2A ，求△ABC 的面积．[审题视点] 第(1)问根据三角形的面积公式和余弦定理列出关于a ，b 的方程，通过方程组求解；第(2)问根据sin C ＋sin(B －A )＝2sin 2A 进行三角恒等变换，将角的关系转换为边的关系，求出边a ，b 的值即可解决问题．解 (1)由余弦定理及已知条件，得a 2＋b 2－ab ＝4.又因为△ABC 的面积等于3，所以12ab sin C ＝3，得ab ＝4，联立方程组⎩⎪⎨⎪⎧a 2＋b 2－ab ＝4，ab ＝4，解得⎩⎪⎨⎪⎧a ＝2，b ＝2. (2)由题意，得sin(B ＋A )＋sin(B －A )＝4sin A cos A ， 即sin B cos A ＝2sin A cos A . 当cos A ＝0，即A ＝π2时，B ＝π6，a ＝433，b ＝233；当cos A ≠0时，得sin B ＝2sin A ， 由正弦定理，得b ＝2a .联立方程组⎩⎪⎨⎪⎧a 2＋b 2－ab ＝4，b ＝2a ，解得⎩⎨⎧a ＝233，b ＝433.所以△ABC 的面积S ＝12a b sin C ＝233.正弦定理、余弦定理、三角形面积公式对任意三角形都成立，通过这些等式就可以把有限的条件纳入到方程中，通过解方程组获得更多的元素，再通过这些新的条件解决问题． 【训练3】 (2011·北京西城一模)设△ABC 的内角A ，B ，C 所对的边长分别为a ，b ，c ，且cos B ＝45，b ＝2.(1)当A ＝30°时，求a 的值；(2)当△ABC 的面积为3时，求a ＋c 的值． 解 (1)因为cos B ＝45，所以sin B ＝35.由正弦定理a sin A ＝b sin B ，可得a sin 30°＝103，所以a ＝53.(2)因为△ABC 的面积S ＝12ac ·sin B ，sin B ＝35，所以310ac ＝3，ac ＝10.由余弦定理得b 2＝a 2＋c 2－2ac cos B ，得4＝a 2＋c 2－85ac ＝a 2＋c 2－16，即a 2＋c 2＝20.所以(a ＋c )2－2ac ＝20，(a ＋c )2＝40. 所以a ＋c ＝210.第7讲 正弦定理、余弦定理应用举例基础梳理1．用正弦定理和余弦定理解三角形的常见题型测量距离问题、高度问题、角度问题、计算面积问题、航海问题、物理问题等． 2．实际问题中的常用角 (1)仰角和俯角在视线和水平线所成的角中，视线在水平线上方的角叫仰角，在水平线下方的角叫俯角(如图(1))．(2)方位角指从正北方向顺时针转到目标方向线的水平角，如B点的方位角为α(如图(2))．(3)方向角：相对于某正方向的水平角，如南偏东30°，北偏西45°，西偏东60°等．(4)坡度：坡面与水平面所成的二面角的度数．一个步骤解三角形应用题的一般步骤：(1)阅读理解题意，弄清问题的实际背景，明确已知与未知，理清量与量之间的关系．(2)根据题意画出示意图，将实际问题抽象成解三角形问题的模型．(3)根据题意选择正弦定理或余弦定理求解．(4)将三角形问题还原为实际问题，注意实际问题中的有关单位问题、近似计算的要求等．双基自测1．(人教A版教材习题改编)如图，设A，B两点在河的两岸，一测量者在A所在的同侧河岸边选定一点C，测出AC的距离为50 m，∠ACB＝45°，∠CAB＝105°后，就可以计算出A，B 两点的距离为()．A．50 2 m B．50 3 m C．25 2 m D.2522m解析由正弦定理得ABsin∠ACB＝ACsin B，又∵B＝30°∴AB＝AC·sin∠ACBsin B＝50×2212＝502(m)．答案 A2．从A处望B处的仰角为α，从B处望A处的俯角为β，则α，β的关系为()．A ．α＞βB ．α＝βC ．α＋β＝90°D ．α＋β＝180° 解析 根据仰角与俯角的定义易知α＝β. 答案 B3．若点A 在点C 的北偏东30°，点B 在点C 的南偏东60°，且AC ＝BC ，则点A 在点B 的( )． A ．北偏东15° B ．北偏西15° C ．北偏东10° D ．北偏西10°解析 如图．答案 B4．一船向正北航行，看见正西方向相距10海里的两个灯塔恰好与它在一条直线上，继续航行半小时后，看见一灯塔在船的南偏西60°，另一灯塔在船的南偏西75°，则这艘船的速度是每小时( )． A ．5海里 B ．53海里 C ．10海里D ．103海里解析 如图所示，依题意有∠BAC ＝60°，∠BAD ＝75°，所以∠CAD ＝∠CDA ＝15°，从而CD ＝CA ＝10(海里)，在Rt △ABC 中，得AB ＝5(海里)， 于是这艘船的速度是50.5＝10(海里/时)．答案 C5．海上有A ，B ，C 三个小岛，测得A ，B 两岛相距10海里，∠BAC ＝60°，∠ABC ＝75°，则B ，C 间的距离是________海里．解析 由正弦定理，知BC sin 60°＝AB sin (180°－60°－75°).解得BC ＝56(海里)．答案 5 6考向一 测量距离问题【例1】►如图所示，为了测量河对岸A ，B 两点间的距离，在这岸定一基线CD ，现已测出CD ＝a 和∠ACD ＝60°，∠BCD ＝30°，∠BDC ＝105°，∠ADC ＝60°，试求AB 的长． [审题视点] 在△BCD 中，求出BC ，在△ABC 中，求出AB .解 在△ACD 中，已知CD ＝a ，∠ACD ＝60°，∠ADC ＝60°，所以AC ＝a .∵∠BCD ＝30°，∠BDC ＝105°∴∠CBD ＝45°在△BCD 中，由正弦定理可得BC ＝a sin 105°sin 45°＝3＋12a .在△ABC 中，已经求得AC 和BC ，又因为∠ACB ＝30°，所以利用余弦定理可以求得A ，B 两点之间的距离为AB ＝AC 2＋BC 2－2AC ·BC ·cos 30°＝22a . (1)利用示意图把已知量和待求量尽量集中在有关的三角形中，建立一个解三角形的模型．(2)利用正、余弦定理解出所需要的边和角，求得该数学模型的解．【训练1】 如图，A ，B ，C ，D 都在同一个与水平面垂直的平面内，B 、D 为两岛上的两座灯塔的塔顶，测量船于水面A 处测得B 点和D 点的仰角分别为75°，30°，于水面C 处测得B 点和D 点的仰角均为60°，AC ＝0.1 km.试探究图中B 、D 间距离与另外哪两点间距离相等，然后求B ，D 的距离．解 在△ACD 中，∠DAC ＝30°，∠ADC ＝60°－∠DAC ＝30°，所以CD ＝AC ＝0.1 km.又∠BCD ＝180°－60°－60°＝60°，故CB 是△CAD 底边AD 的中垂线，所以BD ＝BA . 又∵∠ABC ＝15°在△ABC 中，AB sin ∠BCA ＝AC sin ∠ABC ， 所以AB ＝AC sin 60°sin 15°＝32＋620(km)， 同理，BD ＝32＋620(km)． 故B 、D 的距离为32＋620km. 考向二 测量高度问题【例2】►如图，山脚下有一小塔AB ，在塔底B 测得山顶C 的仰角为60°，在山顶C 测得塔顶A 的俯角为45°，已知塔高AB ＝20 m ，求山高CD .[审题视点] 过点C 作CE ∥DB ，延长BA 交CE 于点E ，在△AEC 中建立关系．解如图，设CD ＝x m ，则AE ＝x －20 m ，tan 60°＝CD BD ， ∴BD ＝CD tan 60°＝x 3＝33x (m)． 在△AEC 中，x －20＝33x ， 解得x ＝10(3＋3) m ．故山高CD 为10(3＋3) m.(1)测量高度时，要准确理解仰、俯角的概念；(2)分清已知和待求，分析(画出)示意图，明确在哪个三角形内应用正、余弦定理．【训练2】 如图所示，测量河对岸的塔高AB 时，可以选与塔底B 在同一水平面内的两个测点C 与D ，现测得∠BCD ＝α，∠BDC ＝β，CD ＝s ，并在点C 测得塔顶A 的仰角为θ，求塔高AB .解 在△BCD 中，∠CBD ＝π－α－β， 由正弦定理得BC sin ∠BDC ＝CD sin ∠CBD ， 所以BC ＝CD sin ∠BDC sin ∠CBD ＝s ·sin βsin (α＋β)在Rt △ABC 中，AB ＝BC tan ∠ACB ＝s tan θsin βsin (α＋β). 考向三 正、余弦定理在平面几何中的综合应用【例3】►如图所示，在梯形ABCD 中，AD ∥BC ，AB ＝5，AC ＝9，∠BCA ＝30°，∠ADB ＝45°，求BD 的长．[审题视点] 由于AB ＝5，∠ADB ＝45°，因此要求BD ，可在△ABD 中，由正弦定理求解，关键是确定∠BAD 的正弦值．在△ABC 中，AB ＝5，AC ＝9，∠ACB＝30°，因此可用正弦定理求出sin ∠ABC ，再依据∠ABC 与∠BAD 互补确定sin ∠BAD 即可． 解 在△ABC 中，AB ＝5，AC ＝9，∠BCA ＝30°.由正弦定理，得AB sin ∠ACB ＝AC sin ∠ABC， sin ∠ABC ＝AC ·sin ∠BCA AB ＝9sin 30°5＝910. ∵AD ∥BC ，∴∠BAD ＝180°－∠ABC ，于是sin ∠BAD ＝sin ∠ABC ＝910. 同理，在△ABD 中，AB ＝5，sin ∠BAD ＝910， ∠ADB ＝45°，由正弦定理：AB sin ∠BDA ＝BD sin ∠BAD， 解得BD ＝922.故BD 的长为922. 要利用正、余弦定理解决问题，需将多边形分割成若干个三角形，在分割时，要注意有利于应用正、余弦定理．【训练3】 如图，在△ABC 中，已知∠B ＝45°，D 是BC 边上的一点，AD ＝10，AC ＝14，DC ＝6，求AB 的长．解 在△ADC 中，AD ＝10，AC ＝14，DC ＝6，由余弦定理得cos ∠ADC ＝AD 2＋DC 2－AC 22AD ·DC＝100＋36－1962×10×6＝－12，∴∠ADC ＝120°，∴∠ADB ＝60°. 在△ABD 中，AD ＝10，∠B ＝45°，∠ADB ＝60°，由正弦定理得AB sin ∠ADB ＝AD sin B， ∴AB ＝AD ·sin ∠ADB sin B ＝10sin 60°sin 45°＝10×3222＝5 6.。
高中数学必修五-正弦定理与余弦定理
正弦定理与余弦定理知识集结知识元正弦定理公式知识讲解1．正弦定理【知识点的知识】1．正弦定理和余弦定理定理正弦定理余弦定理内容＝2R（R是△ABC外接圆半径）a2＝b2+c2﹣2bc cos A，b2＝a2+c2﹣2ac cos B，c2＝a2+b2﹣2ab cos C变形形式①a＝2R sin A，b＝2R sin B，c＝2R sin C；②sin A＝，sin B＝，sin C＝；③a：b：c＝sin A：sin B：sin C；④a sin B＝b sin A，b sin C＝c sin B，a sin C＝c sin A cos A＝，cos B＝，cos C＝解决三角形的问题①已知两角和任一边，求另一角和其他两条边；②已知两边和其中一边的对角，求另一边和其他两角①已知三边，求各角；②已知两边和它们的夹角，求第三边和其他两角在△ABC中，已知a，b和角A时，解的情况A为锐角A为钝角或直角图形关系式a＝b sin A b sin A＜a＜b a≥b a＞b一解两解一解一解解的个数由上表可知，当A为锐角时，a＜b sin A，无解．当A为钝角或直角时，a≤b，无解．2、三角形常用面积公式1．S＝a•h a（h a表示边a上的高）；2．S＝ab sin C＝ac sin B＝bc sin A．3．S＝r（a+b+c）（r为内切圆半径）．【正余弦定理的应用】1、解直角三角形的基本元素．2、判断三角形的形状．3、解决与面积有关的问题．4、利用正余弦定理解斜三角形，在实际应用中有着广泛的应用，如测量、航海、几何等方面都要用到解三角形的知识（1）测距离问题：测量一个可到达的点到一个不可到达的点之间的距离问题，用正弦定理就可解决．解题关键在于明确：①测量从一个可到达的点到一个不可到达的点之间的距离问题，一般可转化为已知三角形两个角和一边解三角形的问题，再运用正弦定理解决；②测量两个不可到达的点之间的距离问题，首先把求不可到达的两点之间的距离转化为应用正弦定理求三角形的边长问题，然后再把未知的边长问题转化为测量可到达的一点与不可到达的一点之间的距离问题．（2）测量高度问题：解题思路：①测量底部不可到达的建筑物的高度问题，由于底部不可到达，因此不能直接用解直角三角形的方法解决，但常用正弦定理计算出建筑物顶部或底部到一个可到达的点之间的距离，然后转化为解直角三角形的问题．②对于顶部不可到达的建筑物高度的测量问题，我们可选择另一建筑物作为研究的桥梁，然后找到可测建筑物的相关长度和仰、俯角等构成三角形，在此三角形中利用正弦定理或余弦定理求解即可．点拨：在测量高度时，要理解仰角、俯角的概念．仰角和俯角都是在同一铅锤面内，视线与水平线的夹角．当视线在水平线之上时，成为仰角；当视线在水平线之下时，称为俯角．例题精讲正弦定理公式例1.已知△ABC中，角A，B，C所对的边分别是a，b，c．若A=45°，B=30°，a=，则b=（）A．B．1 C．2 D．例2.在△ABC中，角A，B，C的对边分别为a，b，c，若，则B=（）A．B．C．D．或例3.在△ABC中，已知三个内角为A，B，C满足sin A：sin B：sin C=3：5：7，则C=（）A．90°B．120°C．135°D．150°利用正弦定理解三角形知识讲解【正余弦定理的应用】1、解直角三角形的基本元素．2、判断三角形的形状．3、解决与面积有关的问题．4、利用正余弦定理解斜三角形，在实际应用中有着广泛的应用，如测量、航海、几何等方面都要用到解三角形的知识例题精讲利用正弦定理解三角形例1.在△ABC中，a，b，c是内角A，B，C所对的边．若a>b，则下列结论不一定成立的（）A．A>B B．sin A>sin BC．cos A<cos B D．sin2A>sin2B例2.在△ABC中，角A，B，C的对边分别是a，b，c，且，则角A的大小为（）A．B．C．D．例3.在△ABC中，三内角A，B，C的对边分别为a，b，c，若sin B =b sin A，则a=（）A ．B ．C．1 D．三角形面积公式的简单应用知识讲解1．余弦定理【知识点的知识】1．正弦定理和余弦定理定理正弦定理余弦定理内容＝2R（R是△ABC外接圆半径）a2＝b2+c2﹣2bc cos A，b2＝a2+c2﹣2ac cos B，c2＝a2+b2﹣2ab cos C变形形式①a＝2R sin A，b＝2R sin B，c＝2R sin C；②sin A＝，sin B＝，sin C＝；③a：b：c＝sin A：sin B：sin C；④a sin B＝b sin A，b sin C＝c sin B，a sin C＝c sin A cos A＝，cos B＝，cos C＝解决三角形的问题①已知两角和任一边，求另一角和其他两条边；②已知两边和其中一边的对角，求另一边和其他两角①已知三边，求各角；②已知两边和它们的夹角，求第三边和其他两角A为锐角A为钝角或直角图形关系式a＝b sin A b sin A＜a＜b a≥b a＞b 解的个数一解两解一解一解由上表可知，当A为锐角时，a＜b sin A，无解．当A为钝角或直角时，a≤b，无解．例题精讲三角形面积公式的简单应用例1.已知△ABC的内角A，B，C的对边分别为a，b，c，且（a+b）2=c2+ab，B=30°，a=4，则△ABC的面积为（）A．4 B．3C．4D．6例2.设△ABC的三个内角A，B，C成等差数列，其外接圆半径为2，且有，则三角形的面积为（）A．B．C．或D．或例3.在△ABC中角ABC的对边分别为a、b、c，cos C=，且a cos B+b cos A=2，则△ABC面积的最大值为（）A．B．C．D．利用余弦定理解三角形当堂练习填空题练习1.如图，O在△ABC的内部，且++3=，则△ABC的面积与△AOC的面积的比值为_____．练习2.锐角△ABC的内角A，B，C的对边分别为a，b，c，已知c2-8=（a-b）2，a=2c sin A，则△ABC的面积为____．练习3.在△ABC中，内角A，B，C的对边分别为a，b，c，已知，则的最大值是____．解答题练习1.'在△ABC中，角A，B，C所对的边分别为a，b，c，且满足．（1）求角B的大小；（2）若D为AC的中点，且BD=1，求S△ABC的最大值．'练习2.'在△ABC中，角A、B、C的对边分别是a、b、c，若（a+c）sin B-b sin C=b cos A．（1）求角A；（2）若△ABC的面积为4，a=6，求△ABC的周长．'练习3.'△ABC内角A，B，C所对的边分别为a，b，c．若。
正弦定理余弦定理知识点总结及最全证明
正弦定理余弦定理知识点总结及最全证明正弦定理概述：正弦定理是三角形的一个重要定理，它描述了三角形中各边与其相对的正弦值之间的关系。
正弦定理可以用于求解任意三角形的边长或角度。
正弦定理表达式：在一个三角形ABC中，有以下正弦定理的表达式：a/sin(A) = b/sin(B) = c/sin(C)其中，a、b、c分别表示三角形的边长，A、B、C表示三角形的角度。
正弦定理表明，三角形的任意一边的长度与这条边相对的角的正弦值成正比。
正弦定理的证明：可以使用数学推导来证明正弦定理。
这里给出一种较为详细的证明方法。
证明：1. 通过三角形的边长关系：a = b * sin(A) / sin(B)和c = b *sin(C) / sin(B)，可得到以下关系式：a * sin(B) = b * sin(A)和c * sin(B) = b * sin(C)2.利用向量叉积原理知识，假设D为线段BC上的一点，则由向量的垂直性知：向量BD与向量AD是垂直的，向量CD与向量AD是垂直的。
3. 记向量AD为向量a，向量BD为向量b，向量CD为向量c，由向量b与向量a的垂直性可得：向量b·向量a = ，b， * ，a， *sin(∠BA) = b * AD * sin(∠BA)。
4. 同理，由向量c与向量a的垂直性可得：向量c·向量a = ，c，* ，a，* sin(∠CA) = c * AD * sin(∠CA)。
5. 因为∠C + ∠A = ∠BA，即∠CA + ∠BA = 180°，所以sin(∠BA) = sin(∠CA)。
所以有b * AD * sin(∠BA) = c * AD *sin(∠CA)。
6. 即有b * AD * sin(∠BA) = c * AD * sin(∠BA)，那么b = c，所以定理得证。
余弦定理概述：余弦定理是三角形的另一个重要定理，它描述了三角形中各边与其相对的角之间的关系。
正弦定理余弦定理
03
正弦定理与余弦定理的关 联
正弦定理与余弦定理的相似之处
01
两者都是关于三角形边角关系的定理，是三角学中 的基本定理之一。
02
它们都可以用来解决与三角形相关的问题，如求角 度、边长等。
03
正弦定理和余弦定理在形式上具有一定的对称性， 反映了三角形的内在规律。
正弦定理与余弦定理的不同之处
01
02
03
正弦定理主要应用于求解三角形 的角度，特别是当已知两边及其 夹角时；而余弦定理则更常用于 求解三角形的边长，特别是当已 知两角及一边时。
正弦定理中的角度是通过正弦函 数来表达的，而余弦定理中的角 度则是通过余弦函数来表达的。
正弦定理和余弦定理在应用上有 一定的互补性，可以根据具体问 题选择使用。
总结词
余弦定理是三角形中一个重要的定理，它描述了三角形各边与其对应角余弦值之间的关系。
详细描述
余弦定理是三角学的基本定理之一，它指出在任意三角形ABC中，任意一边的平方等于其他两边的平 方和减去两倍的另一边的长度与相邻两边的乘积。数学公式表示为：a^2 = b^2 + c^2 - 2bc cos(A) 。
交流电
交流电的电压和电流是时间的正 弦函数，这使得正弦定理在电力 系统中有着广泛的应用。
声学
声音的传播和反射可以用正弦和 余弦函数来描述，这使得余弦定 理在声学中有重要应用。
三角函数在工程中的应用
1 2
结构设计
在建筑和机械设计中，正弦和余弦定理常被用来 计算角度、长度等参数，以确保结构的稳定性和 安全性。
余弦定理的应用
总结词
余弦定理在解决三角形问题中具有广泛 的应用，包括求解角度、判断三角形的 形状以及解决实际问题等。
正弦定理和余弦定理-PPT课件
22
类型一
正弦定理和余弦定理的应用
解题准备:
1.正弦定理和余弦定理揭示的都是三角形的边角关系,根据题 目的实际情况,我们可以选择其中一种使用,也可以综合起 来运用.
2.在求角时,能用余弦定理的尽量用余弦定理,因为用正弦定 理虽然运算量较小,但容易产生增解或漏解.
23
3.综合运用正､余弦定理解三角形问题时,要注意以下关系式
32
∵0<A<π,0<B<π,∴sin2A=sin2B
∴2A=2B或2A=π-2B,即A=B或A+B= .
2
∴△ABC是等腰三角形或直角三角形.
33
解法二:同解法一可得2a2cosAsinB=2b2cosBsinA,
由正、余弦定理得
a2b•
b2
c2
a
2
=b2a•
a2 c2 b2
2bc
2ac
1 2 3 2 1 3.
2
2
(2)当|BC|=4时,S△=
1 2
|AB|·|BC|·sinB
1 2 3 4 1 2 3.
2
2
∴△ABC的面积为 2 3 或 3.
27
[反思感悟]本题主要考查正弦定理､三角形面积公式及分类 讨论的数学思想,同时也考查了三角函数的运算能力及推 理能力.
28
40
设云高CM x m,则CE x h,
DE x h, AE x h .
tan
又AE x h , x h x h
tan tan tan
解得x tan tan gh hgsin( ) m.
tan tan
sin( )
41
[反思感悟]在测量高度时,要理解仰角､俯角的概念.仰角和俯 角都是在同一铅垂面内,视线与水平线的夹角,当视线在水 平线之上时,称为仰角;当视线在水平线之下时,称为俯角.
正弦定理和余弦定理
用 (2015· 新课标全国卷Ⅰ)已知 a，b，c 分别为△ABC 内角 A，B，
C 的对边，sin B＝2sin Asin C. (1)若 a＝b，求 cos B； (2)设 B＝90° ，且 a＝ 2，求△ABC 的面积．
2
[听前试做]
(1)由题设及正弦定理可得 b2＝2ac.
又 a＝b，可得 b＝2c，a＝2c. a2＋c2－b2 1 由余弦定理可得 cos B＝ ＝ . 2ac 4 (2)由(1)知 b2＝2ac. 因为 B＝90° ，由勾股定理得 a2＋c2＝b2， 故 a2＋c2＝2ac，进而可得 c＝a＝ 2. 1 所以△ABC 的面积为 × 2× 2＝1. 2
[方法技巧] 1．在利用正、余弦定理解决三角形问题时，应熟练掌握和 A B C π 运用内角和定理：A＋B＋C＝π， ＋ ＋ ＝ 中互补和互余的情 2 2 2 2 况，结合诱导公式可以减少角的种数． 2．在△ABC 中，A>B⇔a>b⇔sin A>sin B⇔cos A<cos B.
1． 判断下列结论的正误． (正确的打“√”， 错误的打“×”) (1)在△ABC 中，若 sin A>sin B，则 A>B.( )
思
(2)在△ ABC 的六个元素中，已知任意三个元素可求其他元 素．( ) )
(3)在△ABC 中，有 sin A＝sin(B＋C)．(
(4)在△ABC 中， 若 a2＋b2<c2， 则△ABC 为钝角三角形． ( 1 (5)公式 S＝ absin C 适合求任意三角形的面积．( 2 )
1.解析：
依据题设条件的特点，由正弦定理，
得 sin Bcos C＋cos Bsin C＝sin2A，有 sin(B＋C)＝sin2A， 从而 sin(B＋C)＝sin A＝sin2A，解得 sin A＝1， π ∴A＝ ，故选 B. 2
高中数学 正余弦定理
正弦定理和余弦定理一：基础知识理解 1．正弦定理(1)S ＝12ah (h 表示边a 上的高)；(2)S ＝12bc sin A ＝12ac sin B ＝12ab sin C ；(3)S ＝12r (a ＋b ＋c )(r 为三角形的内切圆半径)．二：基础知识应用演练1．(2012·广东高考)在△ABC 中，若∠A ＝60°，∠B ＝45°，BC ＝32，则AC ＝( ) A ．43 B ．2 3 C. 3D.322．在△ABC 中，a ＝3，b ＝1，c ＝2，则A 等于( ) A ．30° B ．45° C ．60°D ．75°3．(教材习题改编)在△ABC 中，若a ＝18，b ＝24，A ＝45°，则此三角形有( )A ．无解B ．两解C ．一解D ．解的个数不确定4．(2012·陕西高考)在△ABC 中，角A ，B ，C 所对边的长分别为a ，b ，c .若a ＝2，B ＝π6，c ＝23，则b ＝________.5．△ABC 中，B ＝120°，AC ＝7，AB ＝5，则△ABC 的面积为________．解析：1选B 由正弦定理得：BC sin A ＝AC sin B ，即32sin 60°＝AC sin 45°，所以AC ＝3232×22＝2 3.2选C ∵cos A ＝b 2＋c 2－a 22bc ＝1＋4－32×1×2＝12，又∵0°<A <180°，∴A ＝60°.3 选B ∵a sin A ＝b sin B ，∴sin B ＝b a sin A ＝2418sin 45°，∴sin B ＝223.又∵a <b ，∴B 有两个．4 由余弦定理得b 2＝a 2＋c 2－2ac cos B ＝4＋12－2×2×23×32＝4，所以b ＝2.答案：2 5、解析：设BC ＝x ，由余弦定理得49＝25＋x 2－10x cos 120°，整理得x 2＋5x －24＝0，即x ＝3. 因此S △ABC ＝12AB ×BC ×sin B ＝12×3×5×32＝1534. 答案：1534小结：(1)在三角形中，大角对大边，大边对大角；大角的正弦值也较大，正弦值较大的角也较大，即在△ABC 中，A >B ⇔a >b ⇔sin A >sin B .(2)在△ABC 中，已知a 、b 和A 时，解的情况如下：A 为锐角A 为钝角 或直角图形关系式 a ＝b sin A b sin A <a <ba ≥b a >b 解的个数一解两解一解一解（1）利用正弦、余弦定理解三角形[例1] (2012·浙江高考)在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且b sin A ＝3a cos B . (1)求角B 的大小； (2)若b ＝3，sin C ＝2sin A ，求a ，c 的值．解析：(1)由b sin A ＝3a cos B 及正弦定理a sin A ＝b sin B ，得sin B ＝3cos B ，所以tan B ＝3，所以B ＝π3. (2)由sin C ＝2sin A 及a sin A ＝csin C ，得c ＝2a .由b ＝3及余弦定理b 2＝a 2＋c 2－2ac cos B ，得9＝a 2＋c 2－ac . 所以a ＝3，c ＝2 3. 思考一下：在本例(2)的条件下，试求角A 的大小．方法小结：1．应熟练掌握正、余弦定理及其变形．解三角形时，有时可用正弦定理，有时也可用余弦定理，应注意用哪一个定理更方便、简捷．2．已知两角和一边，该三角形是确定的，其解是唯一的；已知两边和一边的对角，该三角形具有不唯一性，通常根据三角函数值的有界性和大边对大角定理进行判断．试题变式演练1．△ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，a sin A sin B ＋b cos 2A ＝2a .(1)求b a；(2)若c 2＝b 2＋3a 2，求B .解：(1)由正弦定理得，sin 2A sin B ＋sin B cos 2A ＝ 2sin A ，即sin B (sin 2A ＋cos 2A )＝2sin A . 故sin B ＝ 2sin A ，所以ba＝ 2.(2)由余弦定理和c 2＝b 2＋3a 2，得cos B ＝(1＋3)a2c .由(1)知b 2＝2a 2，故c 2＝(2＋3)a 2.可得cos 2B ＝12，又cos B >0，故cos B ＝22，所以B ＝45°.（2）利用正弦、余弦定理判定三角形的形状[例2] 在△ABC 中a ，b ，c 分别为内角A ，B ，C 的对边，且2a sin A ＝(2b ＋c )sin B ＋(2c ＋b )sin C . (1)求A 的大小；(2)若sin B ＋sin C ＝1，试判断△ABC 的形状．[解析] (1)由已知，根据正弦定理得2a 2＝(2b ＋c )·b ＋(2c ＋b )c ，即a 2＝b 2＋c 2＋bc . 由余弦定理得a 2＝b 2＋c 2－2bc cos A ，故cos A ＝－12，∵0<A <180°，∴A ＝120°.(2)由(1)得sin 2A ＝sin 2B ＋sin 2C ＋sin B sin C ＝34 又sin B ＋sin C ＝1，解得sin B ＝sin C ＝12.∵0°<B <60°，0°<C <60°，故B ＝C ， ∴△ABC 是等腰的钝角三角形．方法小结：依据已知条件中的边角关系判断三角形的形状时，主要有如下两种方法：(1)利用正、余弦定理把已知条件转化为边边关系，通过因式分解、配方等得出边的相应关系，从而判断三角形的形状；(2)利用正、余弦定理把已知条件转化为内角的三角函数间的关系，通过三角函数恒等变形，得出内角的关系，从而判断出三角形的形状，此时要注意应用A ＋B ＋C ＝π这个结论．[注意] 在上述两种方法的等式变形中，一般两边不要约去公因式，应移项提取公因式，以免漏解．试题变式演练 (2012·安徽名校模拟)已知△ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，向量m ＝(4，－1)，n ＝⎝⎛⎭⎫cos 2A 2，cos 2A ，且m ·n ＝72. (1)求角A 的大小；(2)若b ＋c ＝2a ＝23，试判断△ABC 的形状．解：(1)∵m ＝(4，－1)，n ＝⎝⎛⎭⎫cos 2A2，cos 2A ， ∴m ·n ＝4cos 2A 2－cos 2A ＝4·1＋cos A 2－(2cos 2A －1)＝－2cos 2A ＋2cos A ＋3.又∵m ·n ＝72，∴－2cos 2A ＋2cos A ＋3＝72，解得cos A ＝12.∵0<A <π，∴A ＝π3.(2)在△ABC 中，a 2＝b 2＋c 2－2bc cos A ，且a ＝3，∴(3)2＝b 2＋c 2－2bc ·12＝b 2＋c 2－bc .①又∵b ＋c ＝23， ∴b ＝23－c ，代入①式整理得c 2－23c ＋3＝0，解得c ＝3，∴b ＝ 3，于是a ＝b ＝c ＝ 3，即△ABC 为等边三角形．（3）与三角形面积有关的问题[例3] (2012·新课标全国卷)已知a ，b ，c 分别为△ABC 三个内角A ，B ，C 的对边，a cos C ＋3a sin C －b －c ＝0.(1)求A ；(2)若a ＝2，△ABC 的面积为3，求b ，c .[解] (1)由a cos C ＋3a sin C －b －c ＝0及正弦定理得sin A cos C ＋3sin A sin C －sin B －sin C ＝0. 因为B ＝π－A －C ， 所以3sin A sin C －cos A sin C －sin C ＝0. 由于sin C ≠0，所以sin ⎝⎛⎭⎫A －π6＝12. 又0＜A ＜π，故A ＝π3. (2)△ABC 的面积S ＝12bc sin A ＝3，故bc ＝4.而a 2＝b 2＋c 2－2bc cos A ，故b 2＋c 2＝8. 解得b ＝c ＝2. 方法小结：1．正弦定理和余弦定理并不是孤立的．解题时要根据具体题目合理选用，有时还需要交替使用． 2．在解决三角形问题中，面积公式S ＝12ab sin C ＝12bc sin A ＝12ac sin B 最常用，因为公式中既有边也有角，容易和正弦定理、余弦定理结合应用．试题变式演练 (2012·江西重点中学联考)在△ABC 中，12cos 2A ＝cos 2A －cos A .(1)求角A 的大小；(2)若a ＝3，sin B ＝2sin C ，求S △ABC .解：(1)由已知得12(2cos 2A －1)＝cos 2A －cos A ，则cos A ＝12.因为0<A <π，所以A ＝π3.(2)由b sin B ＝c sin C ，可得sin B sin C ＝b c＝2， 即b ＝2c . 所以cos A ＝b 2＋c 2－a 22bc ＝4c 2＋c 2－94c 2＝12， 解得c ＝3，b ＝23，所以S △ABC ＝12bc sin A ＝12×23×3×32＝332.课后强化与提高练习（基础篇-必会题）1．在△ABC 中，a 、b 分别是角A 、B 所对的边，条件“a <b ”是使“cos A >cos B ”成立的( ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件2．(2012·泉州模拟)在△ABC 中，a ，b ，c 分别是角A ，B ，C 所对的边．若A ＝π3，b ＝1，△ABC 的面积为32，则a 的值为( ) A ．1 B ．2 C.32D. 33．(2013·“江南十校”联考)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知a ＝23，c ＝22，1＋tan A tan B ＝2c b，则C ＝( )A ．30°B ．45°C ．45°或135°D ．60°4．(2012·陕西高考)在△ABC 中 ，角A ，B ，C 所对边的长分别为a ，b ，c ，若a 2＋b 2＝2c 2，则cos C 的最小值为( )A.32B.22C.12D ．－125．(2012·上海高考)在△ABC 中，若sin 2 A ＋sin 2B <sin 2C ，则△ABC 的形状是( ) A ．锐角三角形 B ．直角三角形 C ．钝角三角形D ．不能确定6．在△ABC 中，角A 、B 、C 所对的边分别是a 、b 、c .若b ＝2a sin B ，则角A 的大小为________． 解析：由正弦定理得sin B ＝2sin A sin B ，∵sin B ≠0，7．在△ABC 中，若a ＝3，b ＝3，A ＝π3，则C 的大小为________．8．(2012·北京西城期末)在△ABC 中，三个内角A ，B ，C 的对边分别为a ，b ，c .若b ＝25，B ＝π4，9．(2012·北京高考)在△ABC 中，若a ＝2，b ＋c ＝7，cos B ＝－14，则b ＝________.10．△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，a sin A ＋c sin C －2a sin C ＝b sin B . (1)求B ；(2)若A ＝75°，b ＝2，求a ，c .11．(2013·北京朝阳统考)在锐角三角形ABC 中，a ，b ，c 分别为内角A ，B ，C 所对的边，且满足3a －2b sin A ＝0.(1)求角B 的大小；(2)若a ＋c ＝5，且a >c ，b ＝7，求AB u u u r ·AC u u ur 的值．12．(2012·山东高考)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，已知sin B (tan A ＋tan C )＝tan A tan C .(1)求证：a ，b ，c 成等比数列； (2)若a ＝1，c ＝2，求△ABC 的面积S .课后强化与提高练习（提高篇-选做题）1．(2012·湖北高考)设△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c .若三边的长为连续的三个正整数，且A >B >C ，3b ＝20a cos A ，则sin A ∶sin B ∶sin C 为( )A ．4∶3∶2B ．5∶6∶7C ．5∶4∶3D ．6∶5∶42．(2012·长春调研)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知4sin 2A ＋B 2－cos 2C ＝72，且a ＋b ＝5，c ＝7，则△ABC 的面积为________．3．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且满足(2b －c )cos A －a cos C ＝0. (1)求角A 的大小；(2)若a ＝3，S △ABC ＝334，试判断△ABC 的形状，并说明理由．选做题1．已知a ，b ，c 分别是△ABC 的三个内角A ，B ，C 所对的边．若a ＝1，b ＝3，A ＋C ＝2B ，则sin C＝________.2．在△ABC 中，a ＝2b cos C ，则这个三角形一定是( ) A ．等腰三角形 B ．直角三角形 C ．等腰直角三角形D ．等腰或直角三角形3．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知 cos 2C ＝－14.(1)求sin C 的值；(2)当a ＝2,2sin A ＝sin C 时，求b 及c 的长．4．设△ABC 的内角A ，B ，C 所对的边长分别为a ，b ，c ， 且cos B ＝45，b ＝2.(1)当A ＝30°时，求a 的值；(2)当△ABC 的面积为3时，求a ＋c 的值．课后强化与提高练习（基础篇-必会题）解析1解析：选C a <b ⇔A <B ⇔cos A >cos B .2解析：选D 由已知得12bc sin A ＝12×1×c ×sin π3＝32，解得c ＝2，则由余弦定理可得a 2＝4＋1－2×2×1×cos π3＝3⇒a ＝ 3.3解析：选B 由1＋tan A tan B ＝2cb 和正弦定理得cos A sin B ＋sin A cos B ＝2sin C cos A ，即sin C ＝2sin C cos A ，所以cos A ＝12，则A ＝60°.由正弦定理得23sin A ＝22sin C ，则sin C ＝22，又c <a ，则C <60°，故C ＝45°. 4解析：选C 由余弦定理得a 2＋b 2－c 2＝2ab cos C ，又c 2＝12(a 2＋b 2)，得2ab cos C ＝12(a 2＋b 2)，即cosC ＝a 2＋b 24ab ≥2ab 4ab ＝12.6解析：选C 由正弦定理得a 2＋b 2<c 2，所以cos C ＝a 2＋b 2－c 22ab<0，所以C 是钝角，故△ABC 是钝角三角形．∴sin A ＝12，∴A ＝30°或A ＝150°.答案：30°或150°7解析：由正弦定理可知sin B ＝b sin Aa ＝3sinπ33＝12，所以B ＝π6或5π6(舍去)，所以C ＝π－A －B ＝π－π3－π6＝π2.答案：π28解析：根据正弦定理得b sin B ＝c sin C ，则c ＝b sin Csin B＝22，再由余弦定理得b 2＝a 2＋c 2－2ac cos B ，即a 2－4a －12＝0，(a ＋2)(a －6)＝0，解得a ＝6或a ＝－2(舍去)．答案：22 69解析：根据余弦定理代入b 2＝4＋(7－b )2－2×2×(7－b )×⎝⎛⎭⎫－14，解得b ＝4.答案：4 10解：(1)由正弦定理得a 2＋c 2－2ac ＝b 2.由余弦定理得b 2＝a 2＋c 2－2ac cos B . 故cos B ＝22，因此B ＝45°. (2)sin A ＝sin(30°＋45°)＝sin 30°cos 45°＋cos 30°sin 45°＝2＋64. 故a ＝b ×sin A sin B ＝2＋62＝1＋3，c ＝b ×sin C sin B ＝2×sin 60°sin 45°＝ 6.11解：(1)因为3a －2b sin A ＝0，所以 3sin A －2sin B sin A ＝0，因为sin A ≠0，所以sin B ＝32.又B 为锐角，所以B ＝π3. (2)由(1)可知，B ＝π3.因为b ＝ 7.根据余弦定理，得7＝a 2＋c 2－2ac cos π3，整理，得(a ＋c )2－3ac ＝7.由已知a ＋c ＝5，得ac ＝6.又a >c ，故a ＝3，c ＝2. 于是cos A ＝b 2＋c 2－a 22bc ＝7＋4－947＝714，所以AB u u u r ·AC u u u r ＝|AB u u u r |·|AC u u ur |cos A ＝cb cos A＝2×7×714＝1. 12解：(1)证明：在△ABC 中，由于sin B (tan A ＋tan C )＝ tan A tan C ，所以sin B ⎝⎛⎭⎫sin A cos A ＋sin C cos C ＝sin A cos A ·sin Ccos C ， 因此sin B (sin A cos C ＋cos A sin C )＝sin A sin C ， 所以sin B sin(A ＋C )＝sin A sin C . 又A ＋B ＋C ＝π，所以sin(A ＋C )＝sin B ，因此sin 2B ＝sin A sin C .由正弦定理得b 2＝ac ，即a ，b ，c 成等比数列．(2)因为a ＝1，c ＝2，所以b ＝2，由余弦定理得cos B ＝a 2＋c 2－b 22ac ＝12＋22－22×1×2＝34， 因为0<B <π，所以sin B ＝1－cos 2B ＝74， 故△ABC 的面积S ＝12ac sin B ＝12×1×2×74＝74. 课后强化与提高练习（提高篇-选做题）解析1解析：选D 由题意可得a >b >c ，且为连续正整数，设c ＝n ，b ＝n ＋1，a ＝n ＋2(n >1，且n ∈N *)，则由余弦定理可得3(n ＋1)＝20(n ＋2)·(n ＋1)2＋n 2－(n ＋2)22n (n ＋1)，化简得7n 2－13n －60＝0，n ∈N *，解得n ＝4，由正弦定理可得sin A ∶sin B ∶sin C ＝a ∶b ∶c ＝6∶5∶4.2解析：因为4sin 2A ＋B 2－cos 2C ＝72，所以2[1－cos(A ＋B )]－2cos 2C ＋1＝72， 2＋2cos C －2cos 2C ＋1＝72，cos 2C －cos C ＋14＝0，解得cos C ＝12.根据余弦定理有cos C ＝12＝a 2＋b 2－72ab， ab ＝a 2＋b 2－7,3ab ＝a 2＋b 2＋2ab －7＝(a ＋b )2－7＝25－7＝18，ab ＝6，所以△ABC 的面积S △ABC ＝12ab sin C ＝12×6×32＝332.答案：3323解：(1)法一：由(2b －c )cos A －a cos C ＝0及正弦定理，得(2sin B －sin C )cos A －sin A cos C ＝0，∴2sin B cos A －sin(A ＋C )＝0，sin B (2cos A －1)＝0. ∵0<B <π，∴sin B ≠0，∴cos A ＝12.∵0<A <π，∴A ＝π3. 法二：由(2b －c )cos A －a cos C ＝0，及余弦定理，得(2b －c )·b 2＋c 2－a 22bc －a ·a 2＋b 2－c 22ab＝0， 整理，得b 2＋c 2－a 2＝bc ，∴cos A ＝b 2＋c 2－a 22bc ＝12，∵0<A <π，∴A ＝π3. (2)∵S △ABC ＝12bc sin A ＝334， 即12bc sin π3＝334，∴bc ＝3，①∵a 2＝b 2＋c 2－2bc cos A ，a ＝3，A ＝π3， ∴b 2＋c 2＝6，②由①②得b ＝c ＝3，∴△ABC 为等边三角形．选择题解析1解析：在△ABC 中，A ＋C ＝2B ，∴B ＝60°.又∵sin A ＝a sin B b ＝12，∴A ＝30°或150°(舍)，∴C ＝90°，∴sin C ＝1.答案：12解析：选A 法一：(化边为角)由正弦定理知：sin A ＝2sin B cos C ，又A ＝π－(B ＋C )，∴sin A ＝sin(B ＋C )＝2sin B cos C .∴sin B cos C ＋cos B sin C ＝2sin B cos C ，∴sin B cos C －cos B sin C ＝0，∴sin(B －C )＝0.又∵B 、C 为三角形内角，∴B ＝C .法二：(化角为边)由余弦定理知cos C ＝a 2＋b 2－c 22ab， ∴a ＝2b ·a 2＋b 2－c 22ab ＝a 2＋b 2－c 2a， ∴a 2＝a 2＋b 2－c 2，∴b 2＝c 2，∴b ＝c .3解：(1)因为cos 2C ＝1－2sin 2C ＝－14，且0<C <π， 所以sin C ＝104. (2)当a ＝2,2sin A ＝sin C 时，由正弦定理a sin A ＝c sin C ，得c ＝4.由cos 2C ＝2cos 2C －1＝－14，及0<C <π得cos C ＝±64. 由余弦定理c 2＝a 2＋b 2－2ab cos C ，得b 2±6b －12＝0，解得b ＝6或26，所以⎩⎨⎧ b ＝6，c ＝4或⎩⎨⎧b ＝26，c ＝4.4 解：(1)因为cos B ＝45，所以sin B ＝35. 由正弦定理a sin A ＝b sin B ，可得a sin 30°＝103，所以a ＝53. (2)因为△ABC 的面积S ＝12ac ·sin B ，sin B ＝35，所以310ac ＝3，ac ＝10. 由余弦定理得b 2＝a 2＋c 2－2ac cos B ，得4＝a 2＋c 2－85ac ＝a 2＋c 2－16，即a 2＋c 2＝20. 所以(a ＋c )2－2ac ＝20，(a ＋c )2＝40.所以a ＋c ＝210.。
三角函数中的正弦定理和余弦定理总结
三角函数中的正弦定理和余弦定理总结
正弦定理是三角函数中非常重要的一条定理，它描述了三角形
中各边和角之间的关系。
根据正弦定理，对于任意一个三角形，其
三条边a、b、c和对应的角A、B、C之间满足以下关系：
a / sin(A) =
b / sin(B) =
c / sin(C)
其中，sin(A)表示角A对应的正弦值，其他的sin(B)和sin(C)表示类似含义。
由正弦定理可以推导出余弦定理，它也是三角函数中一条重要
的定理。
余弦定理描述了三角形中三边和角之间的关系。
根据余弦
定理，对于任意一个三角形，其三条边a、b、c和对应的角A、B、C之间满足以下关系：
c^2 = a^2 + b^2 - 2ab * cos(C)
其中，cos(C)表示角C的余弦值，其他的cos(A)和cos(B)表示
类似含义。
正弦定理和余弦定理是求解三角形的重要工具，可以帮助我们计算未知边长或角度。
在实际问题中，常常需要利用这两个定理来解决对角度或边长的求解问题。
总之，正弦定理和余弦定理是三角函数中非常重要的定理，它们通过描述三边与三角形内角之间的关系，为我们解决三角形相关问题提供了有效的方法和工具。
第五章第六节正弦定理和余弦定理课件共58张PPT
A，bsin
C＝csin
B，
cos
C＝a2＋2ba2b－c2
2.三角形中常用的面积公式
(1)S＝12 ah(h 表示边 a 上的高)；
(2)S＝12
1
1
bcsin A＝___2__a_c_s_in_B____＝__2__a_b_si_n_C___；
(3)S＝12 r(a＋b＋c)(r 为三角形的内切圆半径).
解析： 在△ABC 中， 由余弦定理及 a＝2 2 ，b＝5，c＝ 13 ，有 cos
C＝a2＋2ba2b－c2
＝
2 2
π .又因为 C∈(0，π)，所以 C＝ 4
.
π 在△ABC 中，由正弦定理及 C＝ 4 ，a＝2 2 ，c＝ 13 ，可得 sin A＝
a sin C c
＝2 1313
.
答案：
π 4
变形
(1)a＝2R sin A，b＝_2_R_s_in_B___，c＝ __2_R_s_in_C___；
cos A＝b2＋2cb2c－a2
；
(2)a∶b∶c＝_si_n_A_∶__s_i_n_B_∶__s_in_C___； cos B＝c2＋2aa2c－b2 ；
(3)asin B＝bsin asin C＝csin A
考点·分类突破
⊲学生用书 P84
利用正弦、余弦定理解三角形
(1)(2020·全国卷Ⅲ)在△ABC 中，cos C＝23 ，AC＝4，BC＝3，则
tan B＝( )
A． 5
B．2 5
C．4 5
D．8 5
(2)(2020·广东省七校联考)若△ABC 的内角 A，B，C 所对的边分别为 a，
b，c，已知 2b sin 2A＝3a sin B，且 c＝2b，则ab 等于( )
三角形的余弦定理与正弦定理
三角形的余弦定理与正弦定理三角形是几何学中最基本的形状之一。
在研究三角形的性质和特征时，余弦定理和正弦定理起到了重要的作用。
它们是利用三角形的边长和角度之间的关系来解决各种三角形问题的工具。
本文将详细介绍三角形的余弦定理与正弦定理的定义、公式推导和应用。
一、余弦定理余弦定理是描述三角形边长与角度关系的定理。
对于任意三角形ABC，假设a、b、c分别表示BC、AC和AB的边长，而∠A、∠B和∠C分别表示三角形的内角A、B和C，则余弦定理可以表示为以下公式：c² = a² + b² - 2ab·cosCb² = a² + c² - 2ac·cosBa² = b² + c² - 2bc·cosA其中，cosA、cosB和cosC分别表示角A、B和C的余弦值。
推导过程：我们可以通过向三角形ABC引入高，再利用勾股定理和直角三角形的性质推导余弦定理。
设三角形ABC的高为h，起点为顶点A，终点为D，连接BD和CD，如图所示。
[图示]由于三角形ADC为直角三角形，根据勾股定理，我们可以得到：AC² = AD² + CD² ------ (1)在三角形ABD中，我们可以应用勾股定理得到：AB² = AD² + BD² ------ (2)注意到BD = BC - CD，将其代入式(2)，我们可以得到：AB² = AD² + (BC - CD)²= AD² + BC² + CD² - 2BC·CD ------ (3)由于三角形ABC为平面图形，AD ⊥ BC，所以∠ADC = ∠C。
根据余弦定理，我们可以得到：CD² = AC² + AD² - 2AC·AD·cosC ------ (4)将式(1)代入式(4)，我们可以得到：CD² = (AD² + CD²) + AD² - 2√(AD² + CD²)√AD·cosC= 2AD² + CD² - 2AD·CD·cosC将式(4)代入式(3)，我们可以得到：AB² = 2AD² + BC² - 2BC·CD + 2AD² - 2√(AD² + CD²)√AD·cosC= 4AD² + BC² - 2BC·CD - 2√(AD² + CD²)√AD·cosC= 4AD² + BC² - 2BC·CD - 2AC·AD·cosC由于三角形为平面图形，所以CD = BC·cosA，代入上式得：AB² = 4AD² + BC² - 2BC²·cosA - 2AC·AD·cosC= 4AD² + BC² - 2BC²·cosA - 2AC²·cosC= 4AD² + BC² - 2AC²·cosC - 2BC²·cosA由几何性质可知，4AD² = c²，所以：c² = a² + b² - 2ab·cosC ------ (5)同理，可以推导出余弦定理的其他两个公式。
余弦定理与正弦定理
余弦定理与正弦定理余弦定理和正弦定理是解决三角形中边长和角度之间关系的重要定理。
它们在三角学中有着广泛的应用，能够帮助我们计算未知边长或角度。
本文将介绍余弦定理和正弦定理的定义、公式以及应用，并探讨它们的区别和联系。
一、余弦定理的定义和公式余弦定理是在三角形中，通过已知边长和夹角计算其他边长的定理。
它的定义如下：在三角形ABC中，设三条边分别为a、b、c，对应的夹角分别为A、B、C，则余弦定理的公式为：c² = a² + b² - 2abcosC其中，c为三角形对应于角C的边长，a和b为与角C相邻的两条边长，cosC为角C的余弦值。
二、正弦定理的定义和公式正弦定理是在三角形中，通过已知两个角度和一个边长计算其他边长的定理。
它的定义如下：在三角形ABC中，设三条边分别为a、b、c，对应的夹角分别为A、B、C，则正弦定理的公式为：a/sinA = b/sinB = c/sinC其中，a、b、c为三角形的边长，A、B、C为对应的角度。
三、余弦定理和正弦定理的应用1. 通过余弦定理计算未知边长或角度：- 已知两边长和夹角：可以使用余弦定理计算第三条边长，或者计算其他两个角度。
- 已知三边长：可以使用余弦定理计算其中一个角度。
2. 通过正弦定理计算未知边长或角度：- 已知两角度和一个边长：可以使用正弦定理计算其他两条边长。
- 已知一个角度和两边长：可以使用正弦定理计算另外两个角度。
四、余弦定理与正弦定理的区别和联系余弦定理和正弦定理在解决三角形问题时具有不同的应用场景。
余弦定理适用于已知边长和夹角的情况，可以求解缺失的边长或角度。
而正弦定理适用于已知两个角度和一个边长的情况，同样可以求解其他边长或角度。
此外，两个定理之间也存在一定的联系。
通过余弦定理可以推导出正弦定理，而正弦定理也可以推导出余弦定理。
在解决问题时，可以根据具体情况选择使用其中一个定理进行计算。
总结：余弦定理和正弦定理是解决三角形中边长和角度之间关系的重要定理。
三角形的余弦定理与正弦定理
三角形的余弦定理与正弦定理三角形的几何学是数学中一个重要的分支，其中，余弦定理和正弦定理是解决三角形问题的关键工具。
余弦定理用于计算三角形的边长或角度，而正弦定理用于计算三角形的边长和角度之间的关系。
首先，我们先来看余弦定理。
对于任意一个三角形ABC，假设其三条边分别为a、b和c，对应的内角分别为A、B和C。
余弦定理的定义如下：c^2 = a^2 + b^2 - 2ab*cos(C)a^2 = b^2 + c^2 - 2bc*cos(A)b^2 = a^2 + c^2 - 2ac*cos(B)可以看到，余弦定理根据三边的长度和对应的内角的余弦值，计算了第三个边的平方。
这个定理可以帮助我们在已知三条边或者两条边和一个夹角的情况下，计算出剩余的边或者夹角的大小。
接下来，我们来看正弦定理。
对于任意一个三角形ABC，其中边长分别为a、b和c，对应的内角为A、B和C。
正弦定理的定义如下：a/sin(A) = b/sin(B) = c/sin(C)正弦定理表明，在一个三角形中，每个边的长度与对应的角的正弦值成比例。
如果我们已经知道三个角的大小，或者两个角的大小和一个边的长度，我们就可以通过正弦定理计算出其他的边长或角度。
下面，我们通过几个例子来进一步说明余弦定理和正弦定理的应用。
例子1：已知一个三角形的两条边分别为5和8，夹角为60度，求第三边的长度。
根据余弦定理，我们有：c^2 = a^2 + b^2 - 2ab*cos(C)c^2 = 5^2 + 8^2 - 2*5*8*cos(60)c^2 = 25 + 64 - 80*cos(60)c^2 = 89 - 40c^2 = 49c = 7所以，第三边的长度为7。
例子2：已知一个三角形的两个角分别为30度和45度，以及其中一个角的对边长度为6，求其他两个边的长度。
根据正弦定理，我们有：a/sin(A) = b/sin(B) = c/sin(C)在这个问题中，我们已经知道两个角的大小和一个角的对边长度，我们需要求解其他两个边的长度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
精心整理
正弦定理与余弦定理
一、三角形中的各种关系
设ABC ∆的三边分别是,,a b c ，与之对应的三个角分别是,,A B C .则有如下关系： 1、三内角关系
三角形中三内角之和为π（三角形内角和定理），即A B C π++=，； 2、边与边的关系
三角形中任意两条边的和都大于第三边，任意两条边的差都小于第三边,即
,,a b c a c b b c a +>+>+>；,,a b c a c b b c a -<-<-<；
3、边与角的关系 （1）正弦定理
三角形中任意一条边与它所对应的角的正弦之比都相等，即
2sin sin sin a b c
R A B C
===（这里，R 为ABC ∆外接圆的半径）. 注1：（I ）正弦定理的证明：
在ABC ∆中，设,,BC a AC b AB c ===, 证明：2sin sin sin a b c
R A B C
===（这里，R 为ABC ∆外接圆的半径）
证：法一（平面几何法）：
在ABC ∆中，作CH AB ⊥，垂足为H 则在Rt AHC ∆中，sin CH A AC =
；在Rt BHC ∆中，sin CH
B BC
=
sin ,sin CH b A CH a B ∴==sin sin b A a B ⇒=即
sin sin a b
A B
=
同理可证：
sin sin b c
B C
=
于是有
sin sin sin a b c
A B C
==
正弦定理指出了任意三角形中三边与其对应角的正弦值之间的一个关系式，也就是任意三角形的边角关系.
（Ⅲ）正弦定理适用的范围：
（i ）已知三角形的两角及一边，解三角形；
（ii ）已知三角形的两边及其中一边所对应的角，解三角形；
（iii ）运用::sin :sin :sin a b c A B C =解决角之间的转换关系. 注2：正弦定理的一些变式： （i ）::sin :sin :sin a b c A B C =； （ii ）sin ,sin ,sin 222a b c
A B C R R R
=
==
；
. （2）余弦定理
三角形中任意一条边的平方等于其他两条边平方的和减去这两条边与它们夹角的余弦的乘积的2倍，即
2222cos a b c bc A =+-，2222cos b c a ca B =+-，2222cos c a b ab C =+-.
注1：（I ）余弦定理的证明： 法一（平面几何法）
在ABC ∆中，作CH AB ⊥，垂足为H 则在Rt AHC ∆中，sin CH CH A AC b =
=；cos AH AH
A AC b
==
注3：常选用余弦定理判定三角形的形状；
注4：求解三角形中含有边角混合关系的问题时，常运用正弦定理、余弦定理实现边角互化.
例1.在ABC ∆中，三边长为连续的正整数，且最大角是最小角的2倍，求此三角形的三边长. 例2.如下图所示，在四边形ABCD 中，已知,10AD CD AD ⊥=,14AB =，
60O BDA ∠=，135O BCD ∠=,求BC 的长.
例3.在ABC ∆中，已知7
5,4,cos()8
BC AC A B ==-=
，则cos C =()
A.
1116（3（i （ii （iii . 例1.（1（2cos71例2.在ABC ∆中，内角,,A B C 对应的边分别是,,a b c ，已知2222a c b +=.
(1)若4
B π
=
，且A 为钝角，求内角A 与C 的大小；
（2）若2b =，求ABC ∆面积的最大值.
二、关于三角形内角的常用三角恒等式
由三角形内角和定理：A B C π++=，有()A B C π=-+ 由此可得到：sin sin()A B C =+,cos cos()A B C =-+；
又
222
A B C
π+=-
，
（1（2（3注： ①若②若 ①若②a b ≤，则无解.
四、三角形形状的判定方法 （1）角的判定； （2）边的判定；
（3）综合判定； （4）余弦定理判定.
注：余弦定理判定法：若c 是ABC ∆的最大边，则： ①222a b c +>⇔ABC ∆是锐角三角形； ②222a b c +<⇔ABC ∆是钝角三角形；
③2a 注：⇔1.设
2.A.
5183.在4、在ABC ∆中，4B π
=
，BC 边上的高等于1
3
BC ，则cos A =_____. 5、ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c .若4cos 5A =
，5
cos 13
C =，1a =，则b =_____.
6、已知ABC ∆的三边长分别为3，5，7，则该三角形的外接圆半径等于_____.
7、在△ABC 中，已知B=45°,D 是BC 边上的一点，AD=10,AC=14,DC=6，求AB 的长. 8、在ABC ∆中，内角,,A B C 对应的边分别为,,a b c ，已知
2,3
c C π
==
.
（1）若ABC ∆3，求,a b ；
（2）若sin sin()2sin 2C B A A +-=，求ABC ∆的面积.
9、设函数2()sin cos sin ()4f x x x x π
=--（x R ∈）.
（1）求函数()f x 的单调区间；
（2）在锐角ABC ∆中，角A ，B ，C 所对应的边分别为a ，b ，c .若()02
C
f =，2c =，求ABC
∆面积的最大值.
10、已知向量3
(,sin )2
m x =u r ，(1,sin 3cos )n x x =+r ，函数()f x m n =⋅u r r .
（1）试求函数()f x 的单调递增区间；
（2）若ABC ∆的三个内角A ，B ，C 所对应的边分别为a ，b ，c ，内角B 满足()3f B =，且
3b =，试求ABC ∆面积的最大值.
11、在ABC ∆中，角A ，B ，C 所对应的边分别为a ，b ，c ，且4a =，3cos 4
A =
，57
sin B =
，4c >. （1）求b ；
（2）求ABC ∆的周长.
12、设ABC ∆三个内角A ，B ，C 所对的边分别为a ，b ，c .已知3
c π
=
，cos cos a A b B =.
（1）求角A 的大小；
（2）如图所示，在ABC ∆的外角ACD ∠内取一点P ，使得2PC =.过点P 分别作直线CA 、CD 的垂线，垂足分别是M 、N .设PCA α∠=，求
.
13、ABC ∆的内角,,A B C 的对边分别为,,a b c .（1）求C ；
（2）若c =ABC ∆∆14（1（215、)
B 平行（1（216A ，B （1（2【解析】（1）在OB
C ∆中，1)BC =，OB OC ==由余弦定理，有222cos 2OB OC BC BOC OB OC +-∠====⋅∴6
BOC π
∠=
于是
的长为
22
426
3
π
⨯=
（2）设AOC θ∠=，2
(0,)3
θπ∈
则2
3
BOC πθ∠=-
AOC BOC OACB S S S ∆∆=+四边形又2
(0,)3
θπ∈
∴5(,)666π
ππθ∈ 故当62
π
π
θ+
=
，即3
π
θ=
时，四边形OACB 的面积最大，且最大值为163
17、在△ABC 中，若2AB =，2AC BC =，求ABC S ∆的最大值.
【解析】（法一）由余弦定理，有222222
424cos 244a c b a a a B ac a a +-+--===
又由三角形三边关系，有：a b c a c b +>⎧⎨+>⎩，即22
22a a a a
⎧+>⎪⎨
+>⎪⎩222222a ⇒-<<+ 故当212a =，即23a =时，ABC S ∆最大，且max 128
[]82216
ABC S ∆=
== （法二）∵22
22
a b c a a p ++++=
= ∴222222
a a a a p a a +-+-=
-= 于是由海伦公式，有：()()()ABC S p p a p b p c ∆=---
精心整理
精心整理
又由三角形三边关系，有：a b c a c b +>⎧⎨+>⎩
，即22a a ⎧>⎪⎨+>⎪
⎩22a ⇒<< 故当212a =
，即a =ABC S ∆
最大，且max []ABC S ∆===。