两因素方差分析检验
双因素试验的方差分析

i 1
j 1
要判断因素A,B及交互作用AB对试验结果是否 有显著影响,即为检验如下假设是否成立:
H01 :1 2 a 0
H02 : 1 2 b 0
H03 : ij 0 i 1, 2, , a; j 1, 2, ,b
➢ 总离差平方和的分解定理 仿单因素方差分析的方法,考察总离差平方和
a
Ti.2
b,
i1
p T 2 ab ,
DB
b
T.
2 j
a,
j1
ab
R
X
2 ij
i1 j1
例1 设甲、乙、丙、丁四个工人操作机器Ⅰ、Ⅱ、Ⅲ各一天, 其产品产量如下表,问工人和机器对产品产量是否有显著 影响?
机器 B 工人 A
ⅠⅡ
Ⅲ
甲
50 63 52
乙
47 54 42
丙
47 57 41
F值
F 值临介值
因素A 因素B
SS A SSB
df A
MS A
SS A df A
FA
MS A MSE
df B
MSB
Байду номын сангаас
SSB df B
FB
MSB MSE
F (a 1 ,
ab n 1) F (b 1 ,
ab n 1)
A B
误差 总和
SS AB
SSE SST
df AB df E dfT
MS AB SS AB
F0.01 3,6 9.78 F0.05 3,6 4.76 F0.01 2,6 10.92
FB F0.01 2,6
结论:工人对产品的产量有显著影响, 机器对产品的产量有极显著影响。
无交互影响的双因素方差分析

1、无交互影响的双因素方差分析如果某一试验结果受到A和B两个因素的影响,这两个因素分别可取K和M个水平,则双因素分析实际上就是要比较因素A的K个水平的均值之间是否存在显著差异,因素B 的M个水平的均值之间是否存在显著差异。
假定试验的结果如下表所示(在假定两个因素无交互影响的情形下,通常采用不重复试验)。
表9-8 无交互影响的双因素分析试验观察值无交互影响的双因素方差分析结果如下表:表9-9 无交互影响的双因素分析表在显著性水平α下,如果F > 临界值Fα,则拒绝原假设,认为差异显著。
小案例9-1:有4个品牌的彩电在5个地区销售,为分析彩电的品牌(品牌因素)和销售地区(地区因素)对销售量的影响,对每个品牌在各地区的销售量取得表9-10的数据。
试分析品牌和销售地区对彩电的销售量是否有显著影响?(α=0.05)表9-10 不同品牌的彩电在5个地区的销售量数据提出假设:对品牌因素提出的假设为:H0:m1=m2=m3=m4 (品牌对销售量无显著影响)H1:mi (i =1,2, …, 4) 不全相等(有显著影响)对地区因素提出的假设为:H0:m1=m2=m3=m4=m5 (地区对销售量无显著影响)H1:mj (j =1,2,…,5) 不全相等(有显著影响)表9-11 方差分析表结论:F品牌=18.10777>Fα=3.4903,拒绝原假设H0,说明彩电的品牌对销售量有显著影响。
F地区=2.100846<Fα=3.2592,不拒绝原假设H0,无证据表明销售地区对彩电的销售量有显著影响。
资料来源:贾俊平、何晓群、金勇进,《统计学》[M].北京: 中国人民大学出版社,2004.10第2版。
论文—双因素试验的方差分析

X ijk ~ N (ij , 2 ) ( ij 和 2 未 知 ), 记 X ijk i = ijk , 即 有
ijk X ij ijk ~ N (0, 2 ), 故 X ijk ijk 可视为随机误差. 从而得到如下数学模型
X ijk ij ijk, ijk ~ N(0, 2), 各 ijk 相互独立, i 1, , r; j 1, , s; k 1, , t;
1 st
1 rt
X
j 1 k 1
r t
s
t
ijk
,i=1,2, ,r,
X
j =
X
i 1 k 1
类似地,引入记号: , i , j , i , j , 易见
i 1
r
i 0 ,
j 1
s
j
0.
为水平 B j 的效应. 这样可以将
仍称 为总平均,称 i 为水平 A i 的效应,称 成
ij
j
ij
表示
= + i + j +
ij
( i 1, , r; j 1, , s ) ,
(3)
与无重复试验的情况类似,此类问题的检验方法也是建立在偏差平方和的分解上的。 2. 偏差平方和及其分解 引入记号: X =
1 rst
X
i 1 j 1 k 1
r
s
t
ijk
,
X
ij =
1 X ijk ,i=1,2, ,r,j=1,2, ,s, t k 1
t
X
i =
试 验 结 因 素 果 A 因 素 B
6-2双因素方差分析

• H0:m1=m2=m3=m4=m5 (地区对销售量无显著影响) • H1:mj (j =1,2,…,5) 不全相等 (有显著影响)
【例】有4个品牌的彩电在5个地区销售,为分析彩电的品牌( 品牌因素)和销售地区(地区因素)对销售量的影响,对每显著 个品牌在各地区的销售量取得以下数据。试分析品牌和销售 地区对彩电的销售量是否有显著影响?(=0.05)
5. 误差项平方和: SSE SST SSR SSC SSRC
SST=SSR+SSC+SSRC+SSE
可重复双因素方差分析表
(基本结构)
误差来源 平方和 自由度
(SS)
(df)
均方 (MS)
F值
P值
F 临界值
行因素 列因素 交互作用
误差
SSR SSC SSRC SSE
k-1 MSR FR r-1 MSC FC (k-1)(r-1) MSRC FRC kr(m-1) MSE
replication)
3. 如果除了行因素和列因素对试验数据的单
独影响外,两个因素的搭配还会对结果产 生一种新的影响,这时的双因素方差分析
称为有交互作用的双因素方差分析或可重 复 双 因 素 方 差 分 析 (Two-factor with
replication )
双因素方差分析的基本假定
1. 每个总体都服从正态分布 ▪ 对于因素的每一个水平,其观察值是来自正态分布
不同品牌的彩电在5个地区的销售量数据
品牌因素 地区1
地区因素 地区2 地区3 地区4
品牌1
365
350
343
340
品牌2
345
368
363
3两因素试验资料的方差分析 重点
第三节两因素试验资料的方差分析两因素试验资料的方差分析是指对试验指标同时受到两个试验因素作用的试验资料的方差分析。
两因素试验按水平组合的方式不同,分为交叉分组和系统分组两类,因而对试验资料的方差分析方法也分为交叉分组方差分析和系统分组方差分析两种,现分别介绍如下。
一、交叉分组资料的方差分析设试验考察A、B两个因素,A因素分个水平,B因素分b个水平。
所谓交叉分组是指A因素每个水平与B因素的每个水平都要碰到,两者交叉搭配形成b个水平组合即处理,试验因素A、B在试验中处于平等地位,试验单位分成b个组,每组随机接受一种处理,因而试验数据也按两因素两方向分组。
这种试验以各处理是单独观测值还是有重复观测值又分为两种类型。
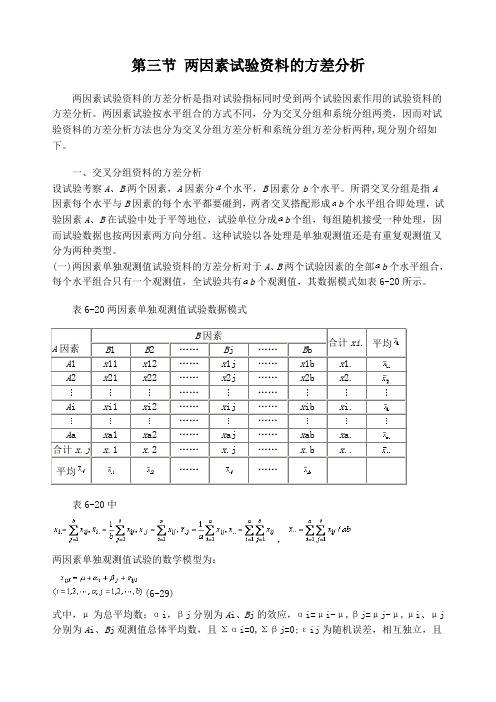
(一)两因素单独观测值试验资料的方差分析对于A、B两个试验因素的全部b个水平组合,每个水平组合只有一个观测值,全试验共有b个观测值,其数据模式如表6-20所示。
表6-20两因素单独观测值试验数据模式平均平均表6-20中,两因素单独观测值试验的数学模型为:(6-29)式中,μ为总平均数;αi,βj分别为A i、B j的效应,αi=μi-μ,βj=μj-μ,μi、μj 分别为A i、B j观测值总体平均数,且Σαi=0,Σβj=0;εij为随机误差,相互独立,且服从N(0,σ2)。
交叉分组两因素单独观测值的试验,A因素的每个水平有b次重复,B因素的每个水平有次重复,每个观测值同时受到A、B两因素及随机误差的作用。
因此全部b个观测值的总变异可以剖分为A因素水平间变异、B因素水平间变异及试验误差三部分;自由度也相应剖分。
平方和与自由度的剖分式如下:(6-30)各项平方和与自由度的计算公式为矫正数总平方和A因素平方和B因素平方和(6-31)误差平方和SS e=SS T-SS A-SS B总自由度dfT=ab-1A因素自由度dfA=a-1B因素自由度dfB=b-1误差自由度dfe=dfT-dfA-dfB=(a-1)(b-1)相应均方为【例6.5】为研究雌激素对子宫发育的影响,现有4窝不同品系未成年的大白鼠,每窝3只,随机分别注射不同剂量的雌激素,然后在相同条件下试验,并称得它们的子宫重量,见表6-21,试作方差分析。
双因素试验方差分析

SS E df E
SST
注意
df E dfT df A f B , SSE SST SSA SSB
各因素离差平方和的自由度为水平数减一,总平方 和的自由度为试验总次数减一。
双因素(无交互作用)试验的方差分析表
简便计算式:
SS A DA p, SSB DB p
双因素试验的方差分析
在实际应用中,一个试验结果(试验指标)往往 受多个因素的影响。不仅这些因素会影响试验结果, 而且这些因素的不同水平的搭配也会影响试验结果。 例如:某些合金,当单独加入元素A或元素B时, 性能变化不大,但当同时加入元素A和B时,合金性 能的变化就特别显著。 统计学上把多因素不同水平搭配对试验指标的 影响称为交互作用。交互作用在多因素的方差分析 中,把它当成一个新因素来处理。 我们只学习两个因素的方差分析,更多因素的 问题,用正交试验法比较方便。
双因素无重复(无交互作用)试验资料表
因素 B 因素 A
B1
X 11 ... X a1
B2
X 12 ... X a2
... Bb
... ... ... X 1b ... X ab
Ti. X ij X i. T b i.
j 1
b
A1 ... Aa
a b i 1 j 1
1 b i ij i 水平Ai对试验结果的效应 a j 1 1 a j ij j 水平Bj对试验结果的效应 b i 1 试验误差 ij X ij ij
特性:
i 1
a
i
0;
j 1
b
j
0; ij ~ N 0,
两因素重复测量方差分析,史上最详细SPSS教程!

两因素重复测量方差分析,史上最详细SPSS教程!一、问题与数据研究者想知道短期(2周)高强度锻炼是否会减少C反应蛋白(C-Reactive Protein, CRP)的浓度。
研究者招募了12名研究对象,并让研究对象参与两组试验:对照试验和干预试验。
在对照试验中,研究对象照常进行日常活动;在干预试验中,研究对象每天进行45分钟的高强度锻炼,每组试验持续2周,两组试验中间间隔足够的时间。
CRP的浓度在每组试验中共测量了3次:试验开始时的CRP 浓度、试验中的CRP浓度(1周)和试验结束时的CRP浓度(2周)。
这三个时间点代表了受试者内因素“时间”的三个水平,因变量是CRP的浓度,单位是mg/L。
con_1、con_2和con_3分别代表对照试验开始时、对照试验中和对照试验结束时研究对象的CRP浓度,int_1、int_2和int_3分别代表干预试验开始时、干预试验中和结束时研究对象的CRP浓度。
部分数据如下:二、对问题的分析使用两因素重复测量方差分析(Two-way Repeated Measures Anova)进行分析时,需要考虑5个假设。
对研究设计的假设:假设1:因变量唯一,且为连续变量;假设2:有两个受试者内因素(Within-Subject Factor),每个受试者内因素有2个或以上的水平。
注:在重复测量的方差分析模型中,对同一个体相同变量的不同次观测结果被视为一组,用于区分重复测量次数的变量被称为受试者内因素,受试者内因素实际上是自变量。
对数据的假设:假设3:受试者内因素的各个水平,因变量没有极端异常值;假设4:受试者内因素的各个水平,因变量需服从近似正态分布;假设5:对于受试者内因素的各个水平组合而言,因变量的方差协方差矩阵相等,也称为球形假设。
三、思维导图(点击图片看清晰大图)四、SPSS操作两因素重复测量方差分析的操作1. 在主菜单下点击Analyze > General Linear Model > Repeated measures...,如下图所示:2. 出现Repeated Measures Define Factor(s)对话框,如下图所示:3. 在Within-Subject Factor Name:中将“factor1”更改为treatment,因为研究对象共进行了2组试验,在Number of Levels:中填入2;4. 点击Add,出现下图:5. 在Within-Subject Factor Name:中填入time,因为研究对象的CRP水平在每组试验中共测量了3次,在Number ofLevels:中填入3,点击Add;6. 点击Define,出现下图Repeated Measures对话框;7. 如下图所示,Within-Subjects Variables后面的括号内是受试者内因素的名字,将左侧六个变量均选入右侧框中,如下图所示:8. 点击Plots,出现Repeated Measures: Profile Plots 对话框,如下图所示:9. 将time选入Horizontal Axis:框中,将treatment选入Separate Lines:框中;10. 点击Add,出现下图,点击Continue;11. 点击Save,出现Repeated Measures: Save对话框;12. 在Residuals下方选择Studentized,如下图所示,点击Continue;13. 点击Options,出现Repeated Measures: Options对话框;14. 将treatment、time和treatment*time选入Display Means for:中,下方Compare main effects为勾选状态,在Confidence interval adjustment:下选择Bonferroni,在Display下方勾选Descriptive statistics 和Estimates of effect size,点击Continue,点击OK。
双因素方差分析

双因素方差分析一、无交互作用下的方差分析设A 与B 是可能对试验结果有影响的两个因素,相互独立,无交互作用。
设在双因素各种水平的组合下进行试验或抽样,得数据结构如下表:表中每行的均值.i X (i=1,2,…r )是在因素A 的各个水平上试验结果的平均数;每列的均值jX .(j=1,2,…,n)是在因素B 的各种水平上试验的平均数。
以上数据的离差平方和分解形式为:SST=SSA+SSB+SSE (6.13) 上式中:∑∑-=2)(X X SST ij(6.14)∑-=∑∑-=2.2.)()(X X n X XSSA i i (6.15)∑-=∑∑-=2.2)()(X Xr X XSSB j j(6.16)∑+-∑-=2..)(X X X X SSE ji ij(6.17)SSA 表示的是因素A 的组间方差总和,SSB 是因素B 的组间方差总和,都是各因素在不同水平下各自均值差异引起的;SSE 仍是组内方差部分,由随机误差产生。
各个方差的自由度是:SST 的自由度为nr-1,SSA 的自由度为r-1,SSB 的自由度为n-1,SSE 的自由度为nr-r-n-1=(r-1)(n-1)。
各个方差对应的均方差是:对因素A 而言: 1-=r SSA MSA (6.18) 对因素B 而言: 1-=n SSB MSB (6.19)对随机误差项而言:1---=n r nr SSEMSE (6.20)我们得到检验因素A 与B 影响是否显著的统计量分别是:)]1)(1(,1[~---=n r r F MSE MSA F A (6.21))]1)(1(,1[~---=n r n F MSE MSBF B (6.22)【例6-2】某企业有三台不同型号的设备,生产同一产品,现有五名工人轮流在此三台设备上操作,记录下他们的日产量如下表。
试根据方差分析说明这三台设备之间和五名工人之间对日产量的影响是否显著?(α=0.05)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,
本科学生实验报告
学号:……………………:******
学院:生命科学学院专业、班级:11级应用生物教育A班
实验课程名称:生物统计学实验
教师:孟丽华(教授)
开课学期:2012至2013学年下学期
填报时间:2013年5月15日
云南师范大学教务处编印
实验序号及名称:实验九:为了选出某物质较为适宜的条件的两因素方差分析检验
实验时间2013-05-10 实验室睿智楼3幢326
(一)、实验目的:
1、能够熟练的使用SPSS进行二因素方差分析;
2、通过本次试验理解二因素方差分析的概念和思想,理解多个因素存在交互效应的统计学含义和实际含义;
3、了解方差分析分解的理论基础和计算原理,能够熟练应用单因素方差分析对具体的实际问题进行有效的分析,通过测量数据研究各个因素对总体的影响效果,判定因素在总变异中的重要程度;
4、进一步熟悉SPSS软件的应用。
(二)、实验设备及材料:
微机、SPSS for Windows V18.0统计软件包及相应的要统计的数据
(三)、实验原理:
1、两因素方差分析主要用来检测两个自变量之间的是否有显著的影响,检测不同
的差异对试验结果是否有显著影响,即为检验如下假设是否成
绘制(T)…
两两比较(H)…
选项(O)…
4、表格绘制出来后,进行检查修改,将其复制到实验报告中,将虚框隐藏等;
5、将所求的描述性统计指标数据表格保存,对其所求得的结果进行分析,书写实验报告。
(五)、实验结果:
UNIANOVA 适宜的条件BY 原料温度
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/POSTHOC=原料温度(SNK)
/PLOT=PROFILE(原料*温度)
/EMMEANS=TABLES(OVERALL)
/EMMEANS=TABLES(原料) COMPARE ADJ(LSD)
/EMMEANS=TABLES(温度) COMPARE ADJ(LSD)
/EMMEANS=TABLES(原料*温度)
/PRINT=OPOWER ETASQ HOMOGENEITY DESCRIPTIVE PARAMETER
/PLOT=SPREADLEVEL
/CRITERIA=ALPHA(.05)
/DESIGN=原料温度原料*温度.
方差的单变量分析
表1
主体间因子
值标签N
原料 1 A1 12
2 A2 12
3 A3 12
温度 1 B1(30℃)12
2 B2(35℃)12
3 B3(40℃)12
表2
误差方差等同性的Levene 检验a
因变量:适宜的条件
F df1 df2 Sig.
1.367 8 27 .255
检验零假设,即在所有组中因变量的误差方差均相
等。
a. 设计: 截距+ 原料+ 温度+ 原料* 温度
表3
描述性统计量
因变量:适宜的条件
原料温度均值标准偏差N
A1 B1(30℃)34.50 12.583 4 B2(35℃)18.25 7.274 4
B3(40℃)18.00 8.641 4
总计23.58 11.958 12
A2 B1(30℃)49.00 7.874 4 B2(35℃)37.50 4.203 4
B3(40℃)15.50 5.972 4
总计34.00 15.562 12
A3 B1(30℃)45.25 8.016 4 B2(35℃)46.00 7.071 4
B3(40℃)27.00 6.055 4
总计39.42 11.196 12
总计B1(30℃)42.92 10.900 12 B2(35℃)33.92 13.413 12
B3(40℃)20.17 8.167 12
总计32.33 14.313 36
表4
主体间效应的检验因变量:适宜的条件
源III 型平方
和df 均方 F Sig.
偏Eta
方非中心参数
观测到的幂
b
校正模型5513.500a8 689.187 11.233 .000 .769 89.867 1.000 截距37636.000 1 37636.000 613.445 .000 .958 613.445 1.000 原料1554.167 2 777.083 12.666 .000 .484 25.332 .993 温度3150.500 2 1575.250 25.676 .000 .655 51.351 1.000 原料* 温
度
808.833 4 202.208 3.296 .025 .328 13.184 .766 误差1656.500 27 61.352
总计44806.000 36
校正的总计7170.000 35
a. R 方= .769(调整R 方= .701)
b. 使用alpha 的计算结果= .05
表5
参数估计
因变量:适宜的条件
参数 B 标准
误差t Sig.
95% 置信区间偏Eta
方
非中心
参数
观测到的幂
a
下限上限
截距27.000 3.916 6.894 .000 18.964 35.036 .638 6.894 1.000 [原料=1] -9.000 5.539 -1.625 .116 -20.364 2.364 .089 1.625 .347 [原料=2] -11.500 5.539 -2.076 .048 -22.864 -.136 .138 2.076 .517 [原料=3] 0b. . . . . . . . [温度=1] 18.250 5.539 3.295 .003 6.886 29.614 .287 3.295 .888 [温度=2] 19.000 5.539 3.430 .002 7.636 30.364 .304 3.430 .911 [温度=3] 0b. . . . . . . . [原料=1] * [温度=1] -1.750 7.833 -.223 .825 -17.821 14.321 .002 .223 .055 [原料=1] * [温度=2] -18.750 7.833 -2.394 .024 -34.821 -2.679 .175 2.394 .636 [原料=1] * [温度=3] 0b. . . . . . . . [原料=2] * [温度=1] 15.250 7.833 1.947 .062 -.821 31.321 .123 1.947 .467 [原料=2] * [温度=2] 3.000 7.833 .383 .705 -13.071 19.071 .005 .383 .066 [原料=2] * [温度=3] 0b. . . . . . . . [原料=3] * [温度=1] 0b. . . . . . . . [原料=3] * [温度=2] 0b. . . . . . . . [原料=3] * [温度=3] 0b. . . . . . . .
a. 使用alpha 的计算结果= .05
b. 此参数为冗余参数,将被设为零。
估算边际均值
表6
1. 总均值
因变量:适宜的条件。
