(完整word)八年级一道几何题的一题多解发散思维
初二几何证明题的解题思路

初二几何证明题的解题思路一、题目11. 题目- 已知:在平行四边形ABCD中,E、F分别是AB、CD的中点,连接DE、BF。
求证:四边形DEBF是平行四边形。
2. 解析- 思路:要证明四边形DEBF是平行四边形,根据平行四边形的判定定理,可以从对边平行且相等入手。
- 证明:因为四边形ABCD是平行四边形,所以AB = CD,AB∥ CD。
- 又因为E、F分别是AB、CD的中点,所以BE=(1)/(2)AB,DF=(1)/(2)CD。
- 所以BE = DF。
- 且BE∥ DF(因为AB∥ CD)。
- 根据平行四边形的判定定理:一组对边平行且相等的四边形是平行四边形,所以四边形DEBF是平行四边形。
二、题目21. 题目- 已知:在 ABC中,AD是BC边上的中线,E是AD的中点,连接BE并延长交AC于F。
求证:AF=(1)/(2)FC。
2. 解析- 思路:过点D作DG∥ BF交AC于G,利用中位线定理和平行线分线段成比例定理来证明。
- 证明:过点D作DG∥ BF交AC于G。
- 因为AD是BC边上的中线,所以D是BC中点。
- 又因为DG∥ BF,根据中位线定理,可得G是FC中点,即FG = GC。
- 因为E是AD的中点,DG∥ BF,根据平行线分线段成比例定理,可得AF = FG。
- 所以AF=(1)/(2)FC。
三、题目31. 题目- 已知:在矩形ABCD中,AC、BD相交于点O,AE平分∠ BAD交BC于E,∠ CAE = 15^∘。
求∠ BOE的度数。
2. 解析- 思路:先求出∠ BAE的度数,进而得出 ABE的形状,再求出∠ ACB的度数,最后根据三角形的内角和求出∠ BOE的度数。
- 证明:- 因为四边形ABCD是矩形,AE平分∠ BAD,所以∠ BAE = 45^∘。
- 又因为∠ CAE=15^∘,所以∠ BAC=∠ BAE +∠ CAE = 45^∘+15^∘=60^∘。
- 在矩形ABCD中,AC = BD,OA=OC=(1)/(2)AC,OB =OD=(1)/(2)BD,所以OA = OB。
一题多解 发展思维——一道中考几何题的解法探究

一题多解发展思维——一道中考几何题的解法探究
刘钦娜
【期刊名称】《中学数学教学参考》
【年(卷),期】2024()6
【摘要】数学是思维的体操,如何通过解题活动培养学生的思维能力是数学教学的中心问题。
针对一道中考几何题,引导学生通过一题多解开阔思路、发散思维,同时借助多解归一加深对数学原理、通性通法的认识,帮助他们在变式中寻找通法、在探究中提升能力。
【总页数】3页(P57-59)
【作者】刘钦娜
【作者单位】河南省驻马店市泌阳县花园中心学校
【正文语种】中文
【中图分类】G63
【相关文献】
1.一题多解拓思维,数形结合来渗透——一道正方形几何证明解法探究
2.一题多解,提高学生思维与逻辑推理能力——2012年安徽省中考第23题的解法探究
3.关注一题多解强化思维训练--对一道中考几何题的探究
4.一题多解阔思路,发散思维形成中——对一道几何题多种解法的探索
5.一题多解,发散思维,多解归一,能力升华——以一道几何探究题为例
因版权原因,仅展示原文概要,查看原文内容请购买。
初中几何多解题

初中几何多解题初中几何多解题是指在解决一个几何问题时,存在多种方法或角度可以得到正确答案的情况。
这些不同的解题方法可以帮助学生培养灵活的思维,深入理解几何概念,并且提高解答问题的能力。
下面我将通过几个具体例子来展示初中几何的多解题方法。
首先,我们来看一个简单的例子。
假设有一个直角三角形ABC,角C为直角,边AB为斜边。
我们要求AC的长度。
传统的解题方法是使用勾股定理:AC^2 = AB^2 + BC^2。
然而,我们也可以运用相似三角形的性质来解答。
由于角C为直角,所以三角形ABC和三角形ACD相似,其中D为直角三角形ABC的斜边AB上的任意一点。
根据相似三角形的性质,我们有AC/AB = AB/AD。
由此可以得到AC^2 = AB*AD。
这是一个全新的解题方法,而且它不需要使用勾股定理。
接下来,我们来看一个更复杂一些的例子。
假设有一个梯形ABCD,AB平行于CD,AD与BC不平行,并且角BAD等于角CDA。
我们要证明角BCD等于角DAB。
这个问题可以使用多种方法来解答。
一种方法是使用平行线之间的性质。
由于AB平行于CD,所以角BAD和角CDA是同位角。
根据同位角定理,我们可以得出角BCD等于角DAB。
另一种方法是利用等腰三角形的性质。
可以观察到三角形BAD和三角形CDA是等腰三角形,因为它们的底边分别与平行于底边的线相交于同一点。
根据等腰三角形的性质,我们可以推导出角DAB等于角BDA,而角CDA等于角BCD。
进而,根据等腰三角形的唯一角性质,我们可以得到角BCD等于角DAB。
最后,我们来看一个涉及面积的几何问题。
假设有一个正方形ABCD,其中AB的长度为10。
我们要找到一个与正方形相似的矩形,使得其周长比正方形的周长小20,并且面积也比正方形的面积小20。
传统的解题方法是运用正方形和矩形的面积和周长公式来进行计算。
我们可以设矩形的长为x,宽为y,则矩形的周长为2(x+y),面积为xy。
根据题目要求,我们可以列出如下方程组:2(x+y) = 4*10 - 20xy = 10*10 - 20通过解这个方程组,我们可以找到矩形的长和宽。
利用一题多解、一题多变来提高初中学生的数学解题能力

利用一题多解、一题多变来提高初中学生的数学解题能力作者:苏淑妮来源:《中学课程辅导·教师教育(中)》2017年第04期(广东省惠州市惠阳区崇雅中学广东惠州 516000)【摘要】数学课程标准中,要求使学生站在不同角度,探索分析和解决问题的方法,此外,教育心理学也指出:问题解决有两种类型:一是常规性问题解决;二是创造性问题解决。
通过一题多解、一题多变训练,使学生能够体验到解决问题的多样性方式,能够掌握分析及解决问题的基本技巧和方法,使所学的知识得到活化,融会贯通,开阔思路,培养学生的发散、创新思维能力。
【关键词】一题多解一题多变初中数学发散思维【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711(2017)04-173-01先观察以下4个例题,是初中数学练习过程经常碰到的,具体的解答过程后文有详细的描述,以此四个例题用以论述本文的观点。
例1:相切两圆半径分别是4和6,求圆心距。
例2:在几何题型中:直角三角形两边长3和4,求第三边。
例3:一道求证题:顺次连接平行四边形各边中点所得的四边形是平行四边形变式1:顺次连接矩形各边中点所得的四边形是菱形变式2:顺次连接菱形各边中点所得的四边形是矩形变式3:顺次连接正方形各边中点所得的四边形变式4:顺次连接什么四边形各边中点可以得到平行四边变式5:顺次连接什么四边形各边中点可以得到矩形变式6:顺次连接什么四边形各边中点可以得到菱形例4:在梯形ABCD中,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.一、一题多解、一题多变帮助学生循坏往复调动所学知识,强化记忆在学习生涯中,知识点是解题的基础和灵魂,千千万万的题目是从知识点出发延伸设计出来问题考察学生的。
由于时间和空间有限,学生不可能做完所有的题目,对于教师也不可能讲解完所有的题目。
而对于数学,单是一道题目中也不可能只有一个知识点的考察,例题1这道题中涉及的知识点有:相切圆、半径、圆心距,最终的问题虽然是求圆心距,但是如果没有正确的对于圆、半径以及相切的概念,那么也就无从下手。
案例3-一题多解,注意学生思维的发散

一题多解,注重学生思维的发散与发展在人教版七年级第三章《多姿多彩的图形》学习过程中,有这样一道题目:已知,如图,∠AOC=∠BOD=90°,∠BOC=52°.求∠AOD的度数.ODAB C对于这道题目的解答方法,备课的时候我仅仅考虑了两种方法:第一种,是把∠AOD看成两个直角叠加之后再减去∠BOC(因为∠BOC被重复叠加了)的度数(即∠AOD=∠AOC﹢∠BOD﹣∠BOC=90°﹢90°﹣52°=128°);第二种,是先求出∠AOB或者∠COD的度数,然后∠AOD就等于一个直角再加上∠AOB或者∠COD的度数(即∠AOD=∠BOD﹣∠BOC﹢∠AOC =90°﹣52°﹢90°=128°).教师在备课的时候,之所以考虑这两种方法,是因为这两种方法浅显易懂,向学习有困难的学生比较好解释,不需要费太多的口舌。
可是等我站到讲台上讲到这道题目的时候,我的学生当堂就提出了其他的解法,其思维之灵活,思维之发散和开阔,都令我大吃一惊。
学生甲的看法:将OD反向延长得到射线OE,则∠AOE=∠BOC=52°.所以∠AOD=180°﹣∠AOE=180°﹣52°=128°.EODAB C学生说到这里的时候,我和其他同学都向他投去了赞许的目光,大家不由自主的鼓起掌来。
这种气氛很快感染了全班同学,大家的热情被调动起来了,我也趁热打铁的追问,“还有没有不一样的方法呢”?我看到班里的同学有的开始低头思考,有的则拿起铅笔开始画图,我就要求大家两个人一组开始讨论,希望得到更多的解法。
这个时候,一个平时不怎么喜欢回答问题的同学举起了手,我就赶快叫起了她。
学生乙的看法:认为根据“同角的余角相等”,∠AOB和∠COD都是∠BOC的余角,所以它们相等,都等于38°.然后可以用上面的方法求出∠AOD的度数。
数学人教版八年级上册专题学习“一题多解”

方法1:延长AD到点E,使 DE=AD,连结CE. 方法2:取AC的中点E,连 结DE.
B
D
.
E C
E
谢谢! 再见!
专题学习
----几何证明中常见 “一题多解”方法
乐加初中 王刚
典例: 如图,四边形ABCD中, ∠A= ∠D =90o, BE、CE均是角平分线, 求证:BC=AB+CD.
证明:在BC上截取BF=AB,连接E,F ∵ BE、CE均是角平分线 ∴ ∠ABE= ∠FBE ∠BCE= ∠DCE 解法 1.在BC上截取BF=AB 在△ABE与△FBE中 AB=BF : 构造了 ∠ABE= ∠FBE 全等的三角形 BE=BE ∴ △ABE ≌ △FBE ∴ ∠A= ∠BFE BF=AB CF=CD 从而证得: ∵ ∠A= ∠D =90o 进而得证: BC=AB+CD. ∴ ∠A= ∠BFE = ∠CFE= ∠D =90o 在△FCE与△DCE中 ∠FCE= ∠DCE ∠CFE= ∠D CE=CE ∴ △FCE ≌ △DCE ∴CF=CD ∵ BC=BF+ CF BF=AB CF=CD ∴ BC=AB+CD
如图,四边形ABCD中, ∠A= ∠D =90o, BE、CE均是角平分线, 求证:BC=AB+CD.
练习:如图,△ABC中, ∠C =90o,AC=BC, AD平分∠BAC,求证:AB=AC+DC. 解法1:在AB上截取AE=AC,连接E,D 构造了: 解法2:过点E作DE⊥AB,垂足为E. 全等的直角三角形 从而证得: DC=DE =BE 构造了 : 解法3:延长AC至E使CE=DC,连接E,D E 进而得证:AB=AC+DC 全等的直角三角形 从而证得: AC=AE DC=BE 构造了: B 进而得证: AB=AC+DC 全等的三角形 从而证得:AB=AE 进而得证:AB=AC+DC
(完整版)八年级一道几何题的一题多解发散思维
题目:如图,四边形ABCD是正方形,点E是边BC上一点,∠AEF=90°,EF交正方形外角的平分线CF于F.求证:AE=EF.【方法一】在AB上取一点G使得AG=CE,易得△BGE为等腰直角三角形,再证明△AGE≌△ECF(ASA)即可.【方法二】过点E作EG⊥BC交FC的延长线于点G,证明△AEC≌△FEG(ASA)即可.【方法三】延长AC至点G使得CG=CF并连接EG,证明△ECF≌△ECG(SAS),再得∠ECA=∠G(提示:外角的性质)即可.【方法四】分别延长AB,FC交于点G,并连接EG,证明△ABE≌△GBE(SAS),再证∠EGC=∠F(提示:外角的性质)即可.【方法五】延长AB至点G,使得BG=BE,并连接EG,CG,证明△ABE≌△CBG (SAS),再证明四边形EGCF为平行四边形即可(两组对边分别平行).【方法六】连接AC,过点E作EG⊥BC,交AC于点G,证明△AEG≌△FEC(ASA)即可.【方法七】如图,分别过点E,F作EG∥CF,FG∥CD和FH∥BC,EG分别与FG,FH 交于点G,H,易得四边形ECFH为平行四边形,再证明△ACE≌△EGF (ASA)即可.【方法八】过点F作FG⊥BC于点G,分别设AB=a,EC=x,FG=CG=y,则BE=a-x,根据△ABE∽△EGF得AB:BE=EG:GF,即a:(a-x)=(x+y):y,得ay=ax+ay-x2-xy,得x(a-x-y)=0,即a=x+y,所以AB=EG,BE=FG所以AE=EF.【总结】本题还有许多其他构造辅助线的方法来证明,有的是同种类型的不同构法,异曲同工。
欢迎大家讨论!当然,除了一题多解之外,大家也可以考虑把条件和结论对调进行证明,要不试试看?题目:如图,四边形ABCD是正方形,点E是边BC上一点,在正方形外角的平分线CF上取一点F使得AE=EF.求证:∠AEF=90°.。
巧用圆中的“一题多解”,培养学生发散性思维

巧用圆中的“一题多解”,培养学生发散性思维摘要:在初中数学教学中,习题解答是重要的组成部分,这不仅是由数学学科能用于解决现实问题的特征决定的,更是为了培养学生的逻辑思维、解题能力。
一题多解指的就是学生在解决数学问题的时候,不再局限一道题目一个解题思路和方法的限制,而是学会从不同的角度寻找切入点,使用多种方法解决问题。
本文从初中数学教学“圆”的一题多解教学入手展开研究,进行有效的一题多解训练,带出多种数学知识与方法,培养学生的发散性思维。
关键词:发散性思维;一题多解;初中数学;圆数学本身具有着一定的抽象性和逻辑性,而且解决问题的方式也是多样的。
教师注重转变教学理念和教学方法,引导学生从多角度和多层面进行问题的分析,学会使用一题多解来找到解决问题的多种方式,对发散学生的思维,培养学生的数学能力至关重要。
一、数学课程中的一题多解数学学科教学本身具有一定的抽象性与综合性内涵,它旨在培养学生的灵活逻辑思维能力。
在新课改背景下,为了实现数学教学实效性的有效提升,教师也希望从多个方面思考,实现多角度数学教学,引入一题多解训练模式,在提炼数学知识内容过程中也希望培养学生良好的变式思维,更多结合数学问题、条件、结论之间的相互转换来彰显学生对于教学内容、方法的不同理解,培养学生思维的广阔性和慎密性。
在该过程中,教师的教学过程不再固定于某一局限性定式思维上思考问题,要鼓励学生充分的发挥出想象力,能针对一个题目从多角度和多方向进行观察和分析,多角度和多变并且多层次的应用学习过的知识,得出不同类型解决问题的方式方法,同时也养成任何问题都去多方面思考的习惯。
二、圆的一题多解问题探析在学完圆的有关知识后,很多学生会发现有些习题常出现一题多解的特点.这是由于图形的位置及圆的对称性等特性而出现的情况。
本文将课本中的例、习题的改编题及近几年来全国各地的中考题有关圆中一题多解的问题归纳起来,作为培养学生发散思维的有效路径并展开分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
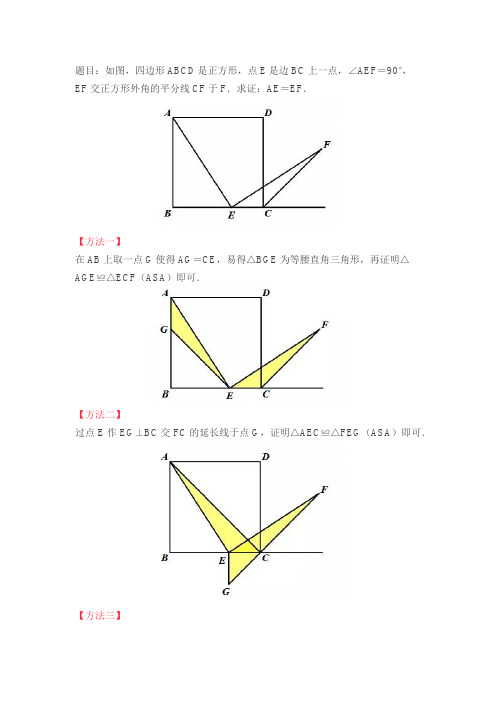
题目:如图,四边形ABCD是正方形,点E是边BC上一点,∠AEF=90°,
EF交正方形外角的平分线CF于F.求证:AE=EF.
【方法一】
在AB上取一点G使得AG=CE,易得△BGE为等腰直角三角形,再证明△AGE≌△ECF(ASA)即可.
【方法二】
过点E作EG⊥BC交FC的延长线于点G,证明△AEC≌△FEG(ASA)即可.
【方法三】
延长AC至点G使得CG=CF并连接EG,证明△ECF≌△ECG(SAS),再得∠ECA=∠G(提示:外角的性质)即可.
【方法四】
分别延长AB,FC交于点G,并连接EG,证明△ABE≌△GBE(SAS),再证∠EGC=∠F(提示:外角的性质)即可.
【方法五】
延长AB至点G,使得BG=BE,并连接EG,CG,证明△ABE≌△CBG (SAS),再证明四边形EGCF为平行四边形即可(两组对边分别平行).
【方法六】
连接AC,过点E作EG⊥BC,交AC于点G,证明△AEG≌△FEC(ASA)即可.
【方法七】
如图,分别过点E,F作EG∥CF,FG∥CD和FH∥BC,EG分别与FG,FH 交于点G,H,易得四边形ECFH为平行四边形,再证明△ACE≌△EGF (ASA)即可.
【方法八】
过点F作FG⊥BC于点G,分别设AB=a,EC=x,FG=CG=y,则BE=a
-x,根据△ABE∽△EGF得AB:BE=EG:GF,即a:(a-x)=(x+y):y,得ay=ax+ay-x2-xy,得x(a-x-y)=0,即a=x+y,所以AB=EG,BE=FG所以AE=EF.
【总结】本题还有许多其他构造辅助线的方法来证明,有的是同种类型的不同
构法,异曲同工。
欢迎大家讨论!
当然,除了一题多解之外,大家也可以考虑把条件和结论对调进行证明,要不
试试看?
题目:如图,四边形ABCD是正方形,点E是边BC上一点,在正方形外角的
平分线CF上取一点F使得AE=EF.
求证:∠AEF=90°.。
