三角函数的最值问题(章节练习)
三角函数精题最值问题及练习题
1三角函数最值问题的几种常见解法一 配方法 例1 函数3sin 3cos 2+--=x x y 的最小值为及y=4cos 5sin 2-+x 的最小值和最大值例2 求函数y=5sinx+cos2x 的最值 二 引入辅助角法 例3已知函数()R x x x x y ∈+⋅+=1cos sin 23cos212当函数y 取得最大值时，求自变量x 的集合。
三 利用三角函数的有界性 例4求函数1cos 21cos 2-+=x x y 的值域 函数 y=3cos 4cos 2++x x例5 （2003年高考题）已知函数())cos (sin sin 2x x x x f +=，求函数f(x)的最小正周期和最大值。
四 引入参数法（换元法）例6 求函数y=sinx+cosx+sinxcosx 的最大值。
练习 求函数的最值。
五 利用基本不等式法 和利用均值不等式求解的最值 例7（1）函数的最值；（2） 求函数的最值。
（3）求函数xxy 22cos4sin1+=的最值。
六 利用函数在区间内的单调性 例8 已知()π,0∈x ，求函数xx y sin 2sin +=的最小值。
七 数形结合 例9 求函数()π<<--=x xx y 0cos 2sin 的最小值。
八 判别式法 例10 求函数xx x x y tan sectan sec 22+-=的最值。
2九 分类讨论法 例 11 设()⎪⎭⎫ ⎝⎛≤≤--+-=20214sin cos 2πx a x a x x f ，用a 表示f(x)的最大值M(a).三角函数 最值1设M 和m 分别表示函数1cos 31-=x y 的最大值和最小值，则M+m等于（ ）（A ）32（B ）32-（C ） 34-（D ）-2（2003北京春季）2、函数f(x)=2sin 1sin 3+-x x 的最大值是，最小值是3 求函数f(θ)=2cos 1--θθSin 的最大值与最小值是什么？（两种方法解答）4求函数278cos 2[,]63sin y x x x ππ=--∈-，的值域5、(2000年高考)已知：212cos 12siny x x x x R =+⋅+∈，，求y 的最大值及此时x 的集合． ．6、（90年高考）求函数sin cos sin cos y x x x x =++的最小值．37：已知[]πθ,0∈,f （θ）=sin(cos θ)的最大值为a,最小值为b ，g(θ)=cos(sin θ)的最大值为c,最小值为d,则a,b,c,d 的大小顺序为 。
三角函数的最值问题
三角函数的最值问题 The Standardization Office was revised on the afternoon of December 13, 2020三角函数的最值问题三角函数最值问题散见于不同的章节，或作为问题的背景、或作为单独的数学问题、或作为解题的工具。
今天，我们就求解最值的方法层面展开讨论！一 化为单名函数的形式例1 函数f(x)=x x x x 44sin cos sin 2cos --① 求f(x)得最小正周期;② ⎥⎦⎤⎢⎣⎡∈2,0πx 时，求f(x)的最小值。
解:(1) x x x x x f cos sin 2sin cos )(22--= x x 2sin 2cos -= )222sin 222(cos 2⋅-=x x )42cos(2π+=x ∴ f(x)最小正周期是π=T（2）20π≤≤x ∴ ⎥⎦⎤⎢⎣⎡∈+45,422πππx ∴ 442ππ=+x 即0=x 时最大值是1 ππ=+42x 即83π=x 时最小值是－2 注意① 辅助角公式)sin(cos sin 22ϕ++=+x b a x b x a 的应用② 注意三角函数区间最值的正确取舍二 单名函数的复合型例2 31sin sin =+y x ，求x y 2cos sin -的最值解：∵ x y sin 31sin -= ∴ 1sin 311≤-≤-x ∴ 34sin 32≤≤-x ∴ 1211)21(sin cos sin 22--=-=x x y u ∴ 21sin =x u 的最小值为1211- ； 32sin -=x u 的最大值为94 注意：隐含条件不可忽视！三 关系代换x x cos sin ±与x x cos sin例3 求函数xx x x y cos sin 1cos sin ++=的最值 解：令x x t cos sin += 则 x x t cos sin 12+=∴ )1(211212-=+-=t t t y ∴ 22≤≤-t 且 1≠t∴ )12(21)12(21-≤≤+-y 且 1-≠y注意① 代换要等效 ；② 原函数中对代换量的现定！四 限量代换例4 求函数21x x y -+=的值域解：函数的定义域[]1,1-∈x令 θcos =x ， πθ≤≤0 )4sin(2sin cos πθθθ+=+=y ∴ 21≤≤-y注意：限量代换要求对代换量进一步分析并“定性”五 建立关系等式整体带入或转化例5 设A y x =+，求y x sin sin 的最值解：∵ y x y x y x sin sin cos cos )cos(+=- y x y x y x sin sin cos cos )cos(-=+∴ )cos(cos )cos()cos(sin sin 2y x A y x y x y x +-=+--=∴21cos sin sin 21cos +≤≤-A y x A ∴ y x sin sin 最大值为21cos +A ， 最小值为21cos -A 注意：找沟通已知与未知的一个或两个函数！练习：1求)3cos(sin 3π++=x x y 的最值 2 Rt ABC ∆中，090=∠C ，求B A sin sin +的最大值 3 求x x y cos sin +=的最大值与最小值4 求x x a x f 2cos sin 42)(--=的最值5已知A y x =+，求y x cos sin 的最值 6 )2sin(5)(ϕ+=x x f 对任意都有)3()3(x f x f +=-ππ （1）求ϕ的最小值；（2）ϕ取最小值时若⎥⎦⎤⎢⎣⎡-∈6,6ππx ，求f(x) 的最小值。
正余弦函数的单调性和最值练习
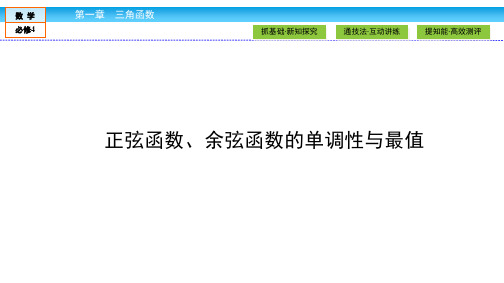
∴sin－π 12＜sin －π 18， ∴g－π 12＜g－π 18， ∴f－π 18＞f－π 12.
抓基础·新知探究
通技法·互动讲练
提知能·高效测评
数学 必修4
第一章 三角函数
抓基础·新知探究
通技法·互动讲练
提知能·高效测评
[规律方法] 求三角函数值域或最值的常用方法
(1)可化为单一函数 y＝Asin(ωx＋φ)＋k 或 y＝Acos(ωx＋φ)＋k 的最大值为|A| ＋k，最小值为－|A|＋k(其中 A，ω，k 为常数，A≠0，ω≠0)．
(2)可化为 y＝Asin2x＋Bsin x＋C 或 y＝Acos2x＋Bcos x＋C(A≠0)的最大、最小 值，利用二次函数在区间[－1,1]上的最大、最小值的求法来求．(换元法)
数学 必修4
第一章 三角函数
抓基础·新知探究
通技法·互动讲练
提知能·高效测评
◎ 变式训练 3.若函数 y＝a－bcos x(b＞0)的最大值为32，最小值为－12，求函数 y＝－4acos bx 的最值和最小正周期.
第一章 三角函数
抓基础·新知探究
通技法·互动讲练
提知能·高效测评
解析： (1)∵函数 f(x)＝sin x－1 与 g(x)＝sin x 的单调区间相同， ∴f(x)＝sin x－1 的增区间为 2kπ－π2 ，2kπ＋π2 (k∈Z). 减区间为2kπ＋π2 ，2kπ＋32π(k∈Z).
数学 必修4
提知能·高效测评
数学 必修4
第一章 三角函数
抓基础·新知探究
通技法·互动讲练
提知能·高效测评
[思想方法] 三角函数相关的恒成立问题 ◎若cos2θ＋2msin θ－2m－2＜0恒成立，求实数m的取值范围. 【分析】 本题主要考查三角函数的性质与一元二次不等式的知识，可将原 不等式化为sin2θ－2msin θ＋2m＋1＞0，令sin θ＝t，由于－1≤sin θ≤1，故－1≤t≤1 ，只要求出使函数f(t)＝t2－2mt＋2m＋1(－1≤t≤1)的最小值大于0的m的取值范围 即可.
三角函数的周期和最值经典练习及答案详解
[基础巩固]1．函数f (x )＝sin x cos x ＋32cos 2x 的最小正周期是( ) A ．πB ．π2C ．2πD ．3π2 解析 由f (x )＝sin x cos x ＋32cos 2x ＝12sin 2x ＋32cos 2x ＝sin ⎝⎛⎭⎫2x ＋π3， 得最小正周期为π.答案 A2．函数f (x )＝sin 4x ＋2sin x cos x －cos 4x 的最小正周期为( )A ．π4B ．π2C ．πD ．2π 解析 f (x )＝sin 4x ＋2sin x cos x －cos 4x＝(sin 2x －cos 2x )(sin 2x ＋cos 2x )＋2sin x cos x＝sin 2x －cos 2x＝2sin ⎝⎛⎭⎫2x －π4. ∴f (x )的最小正周期为2π2＝π.故选C. 答案 C3．(多选)关于函数f (x )＝sin 2x －cos 2x ，下列命题是真命题的是( )A ．函数y ＝f (x )的周期为πB ．直线x ＝π4是y ＝f (x )的一条对称轴 C ．点⎝⎛⎭⎫π8，0是y ＝f (x )的图象的一个对称中心D ．函数y ＝f (x )的最大值为2解析 ∵f (x )＝sin 2x －cos 2x ＝2sin ⎝⎛⎭⎫2x －π4， ∵ω＝2，故T ＝2π2＝π，故A 为真命题； 当x ＝π4时，2x －π4＝π4终边不在y 轴上， 故直线x ＝π4不是y ＝f (x )的一条对称轴，故B 为假命题；当x ＝π8时，2x －π4＝0，终边落在x 轴上， 故点⎝⎛⎭⎫π8，0是y ＝f (x )的图象的一个对称中心，故C 为真命题；函数y ＝f (x )的最大值为2，D 为假命题．故选A 、C.答案 AC4．函数y ＝32sin 2x ＋cos 2x 的最小正周期为________． 解析 y ＝32sin 2x ＋12cos 2x ＋12＝sin ⎝⎛⎭⎫2x ＋π6＋12，所以其最小正周期为2π2＝π. 答案 π5．已知f (x )＝sin x ＋3cos x (x ∈R )，函数y ＝f (x ＋φ) ⎝⎛⎭⎫|φ|≤π2的图象关于直线x ＝0对称，则φ的值为____________ .解析 f (x )＝sin x ＋3cos x ＝2sin ⎝⎛⎭⎫x ＋π3， y ＝f (x ＋φ)＝2sin ⎝⎛⎭⎫x ＋π3＋φ图象关于x ＝0对称， 即f (x ＋φ)为偶函数． ∴π3＋φ＝π2＋k π，k ∈Z ，即φ＝k π＋π6，k ∈Z ， 又∵|φ|≤π2，∴φ＝π6. 答案 π66．已知函数f (x )＝(sin x ＋cos x )2＋2cos 2x －2.(1)求f (x )的单调递增区间；(2)当x ∈⎣⎡⎦⎤π4，3π4时，求函数f (x )的最大值、最小值．解析 (1)f (x )＝sin 2x ＋cos 2x ＝2sin ⎝⎛⎭⎫2x ＋π4， 令2k π－π2≤2x ＋π4≤2k π＋π2，k ∈Z ， 得k π－3π8≤x ≤k π＋π8，k ∈Z . 故f (x )的单调递增区间为⎣⎡⎦⎤k π－3π8，k π＋π8，k ∈Z . (2)∵x ∈⎣⎡⎦⎤π4，3π4，∴3π4≤2x ＋π4≤7π4，∴－1≤sin ⎝⎛⎭⎫2x ＋π4≤22，∴－2≤f (x )≤1， ∴当x ∈⎣⎡⎦⎤π4，3π4时，函数f (x )的最大值为1，最小值为－ 2.[能力提升]7．(2021·全国乙卷)函数f (x )＝sin x 3＋cos x 3的最小正周期和最大值分别是( ) A ．3π和 2 B ．3π和2C ．6π和 2D ．6π和2解析 ∵f (x )＝sin x 3＋cos x 3＝ 2sin ⎝⎛⎭⎫x 3＋π4，∴T ＝2π13＝6π.当sin ⎝⎛⎭⎫x3＋π4＝1时，函数f (x )取得最大值 2；∴函数f (x )的周期为 6π，最大值为 2.故选C.答案 C8．如果α∈⎝⎛⎭⎫π2，π，且sin α＝45，那么sin ⎝⎛⎭⎫α＋π4＋cos ⎝⎛⎭⎫α＋π4等于() A ．425 B ．－425 C.325 D ．－325解析 由已知cos α＝－35，∴sin ⎝⎛⎭⎫α＋π4＋cos ⎝⎛⎭⎫α＋π4＝2sin ⎝⎛⎭⎫α＋π4＋π4＝2cos α＝－35 2.答案 D9．函数f (x )＝3sin x ＋cos ⎝⎛⎭⎫π3＋x 的最大值为________．解析 f (x )＝3sin x ＋cos π3cos x －sin π3sin x＝12cos x ＋32sin x ＝sin ⎝⎛⎭⎫x ＋π6. ∴f (x )max ＝1.答案 110．已知函数f (x )＝4cos ωx ·sin ⎝⎛⎭⎫ωx ＋π4(ω>0)的最小正周期为π. (1)求ω的值；(2)讨论f (x )在区间⎣⎡⎦⎤0，π2上的单调性． 解析 (1)f (x )＝4cos ωx ·sin ⎝⎛⎭⎫ωx ＋π4 ＝22sin ωx ·cos ωx ＋22cos 2ωx＝2(sin2ωx ＋cos2ωx )＋ 2＝2sin ⎝⎛⎭⎫2ωx ＋π4＋ 2. 因为f (x )的最小正周期为π，且ω>0，从而有2π2ω＝π，故ω＝1. (2)由(1)知f (x )＝2sin ⎝⎛⎭⎫2x ＋π4＋ 2. 若0≤x ≤π2，则π4≤2x ＋π4≤5π4. 当π4≤2x ＋π4≤π2， 即0≤x ≤π8时，f (x )单调递增； 当π2≤2x ＋π4≤5π4，即π8≤x ≤π2时，f (x )单调递减． 综上可知，f (x )在区间⎣⎡⎦⎤0，π8上单调递增，在区间⎣⎡⎦⎤π8，π2上单调递减． [探索创新]11．已知角α的顶点在坐标原点，始边与x 轴的正半轴重合，终边经过点P (－3，3)．(1)求sin 2α－tan α的值；(2)若函数f (x )＝cos(x －α)cos α－sin(x －α)sin α，求函数g (x )＝3f ⎝⎛⎭⎫π2－2x －2f 2(x )在区间⎣⎡⎦⎤0，2π3上的取值范围． 解析 (1)∵角α的终边经过点P (－3，3)，∴sin α＝12，cos α＝－32，tan α＝－33.∴sin 2α－tan α＝2sin αcos α－tan α ＝－32＋33＝－36. (2)∵f (x )＝cos(x －α)cos α－sin(x －α)sin α ＝cos x ，x ∈R ，∴g (x )＝3cos ⎝⎛⎭⎫π2－2x －2cos 2x ＝3sin 2x －1－cos 2x ＝2sin ⎝⎛⎭⎫2x －π6－1， ∵0≤x ≤2π3， ∴－π6≤2x －π6≤7π6. ∴－12≤sin ⎝⎛⎭⎫2x －π6≤1， ∴－2≤2sin ⎝⎛⎭⎫2x －π6－1≤1， 故函数g (x )＝3f ⎝⎛⎭⎫π2－2x －2f 2(x )在区间⎣⎡⎦⎤0，2π3上的取值范围是[－2,1]．。
三角函数的最值习题精选精讲
三角函数的值域或最值常见的三角函数最值的基本类型有：（1）y=asinx+b （或y=acosx+b ）型，利用()1cos 1sin ≤≤x x 或，即可求解，此时必须注意字母a 的符号对最值的影响。
（2）y=asinx+bcosx 型，引入辅助角ϕ ，化为y=22b a +sin （x+ϕ）,利用函数()1sin ≤+ϕx 即可求解。
Y=asin 2x+bsinxcosx+mcos 2x+n 型亦可以化为此类。
（3）y=asin 2x+bsinx+c （或y=acos 2x+bcosx+c ），型，可令t=sinx （t=cosx ）,-1≤t ≤1,化归为闭区间上二次函数的最值问题。
（4）Y=d x c b x a ++sin sin （或y=dx bx a ++cos cos ）型，解出sinx （或cosx ）,利用()1cos 1sin ≤≤x x 或去解；或用分离常数的方法去解决。
（5）y=d x c b x a ++cos sin （y=dx c bx a ++sin cos ）型，可化归为sin （x+ϕ）g （y ）去处理；或用万能公式换元后用判别式去处理；当a=c 时，还可利用数形结合的方法去处理上。
（6）对于含有sinx±cosx,sinxcosx 的函数的最值问题，常用的方法是令sinx±cosx=t,2≤t ,将sinxcosx 转化为t 的函数关系式，从而化为二次函数的最值问题。
一、利用三角函数的有界性．求解这类问题，首先利用有关三角函数公式化为sin()y A x k ωϕ=++的形式．在化简过程中常常用到公式：22sin cos sin(),tan ,ba xb x x aab ϕϕϕ+=++=其中由及点(a,b)的位置确定. 例1 、(2000年高考)已知：2123sin cos 12sin y x x x x R =+⋅+∈，，求y 的最大值及此时x 的集合． 解：∵2123sin cos 12sin y x x x =+⋅+1cos 2315sin 21sin(2)44264x x x π+=++=++，∴当sin(2)16x π+=时，max 157244y=+= ．此时，2262x k πππ+=+，即6x k ππ=+． 所以y 的最大值为74，此时x 的集合为{|}6x x k k Z ππ=+∈，．例2、求函数1cos 3cos xy x-=+的值域．解： 1cos 3cos x y x -=+⇒(1)cos 2y x +=-⇒2cos 1x y=-+，由|cos |1x ≤得2||11y -≤+， |1|2y +≥即，解得31y y ≤-≥或，所以函数1cos 3cos xy x-=+的值域是3][1-∞-∞ （，，+）二、利用二次函数最值性质求解这类问题，首先利用有关三角函数公式化为2sin sin y x b x c a =++的形式．例3、求函数278cos 2[,]63sin y x x x ππ=--∈-，的值域． 解：278c o s 2s i n y x x =--＝278cos 2(1)cos x x ---＝223,(cos 2)x --∵[,]63x ππ∈-，∴1cos [1]2x ∈，，∴3[1]2y ∈-，．例4、（90年高考）求函数sin cos sin cos y x x x x =++的最小值． 解：设sin cos x x t +=，[22]t ∈-，，则21sin cos 2x x t -=，所以()y f t =＝211,2(1)t ⋅-+([2,2])t ∈-，当1[22]t =-∈-，时，y 有最小值1-．三、利用均值不等式*利用均值不等式求三角函数时，一定要注意均值不等式中的使用条件：一正、二定、三相等．例6、当0x π<<时，求sin 2cos xy x=+的最大值．解：设2223tan 0,(0),,23233x t t t x y t t π=><<=≤=⋅+则（当且仅当tan 32xt ==时取等号）。
三角函数与解三角形中的最值(范围)问题
sin
2
2
（sin＋cos）
sin
＝
π
4
）
sin
2
1
（1＋
），
2
tan
π
π
因为 B ∈［ ， ），所以tan
6
4
因为函数 y ＝
sin（＋
B ∈［
3
，1），
3
2
1
3
（1＋ ）在［ ，1）上单调递减，
2
3
所以 的取值范围为（
2，
6＋ 2
］.
2
＝
高中总复习·数学
2. （2024·湖北三校联考）记△ ABC 的内角 A ， B ， C 的对边分别为
π
≤ ）的图象离原点最近的对称轴为 x ＝ x 0，若满足｜ x 0｜≤
2
π
，则称 f （ x ）为“近轴函数”.若函数 y ＝2
6
“近轴函数”，则φ的取值范围是（
）
sin （2 x －φ）是
高中总复习·数学
解析： y ＝2 sin
π
（2 x －φ），令2 x －φ＝ ＋ k π， k ∈Z，∴图象
6
6
π
［0， ］上的值域为[－1，2].故选D.
2
高中总复习·数学
2.
4
3
sin+5
函数 y ＝
的最大值是
2−sin
6 ，最小值是
解析：法一
2−5
sin x ＝
，而－1≤
+1
原函数可化为
.
sin x ≤1，所以
2−5
4
－1≤
≤1，所以 ≤ y ≤6，因此原函数的最大值是6，最小值
第40课 三角函数的最值(经典例题练习、附答案)
第40课 三角函数的最值◇考纲解读①理解正弦函数.余弦函数在区间 [0 ， 2π] 的最大和最小值.②三角函数的最值都是在给定区间上取得的，因而特别要注意题设中所给出的区间◇知识梳理1.sin y a x b =+ 型：设sin t x =化为一次函数y at b =+在闭区间[1,1]t ∈-上的最值求之； 2.sin cos y a x b x c =++型：引入辅助角(cos sin ϕϕϕ==，化为)y x c ϕ=++；3.2sin sin y a x b x c =++ 型：设sin t x =，化为二次函数2y at bt c =++在[1,1]t ∈-上的最值求之； 4. sin sin a x b y c x d+=+型根据正弦函数的有界性，即可分析法求最值，还可“不等式”法或“数形结合”． 5. y =dx c b x a ++cos sin 型（1）当x R ∈时，将分母与y 乘转化变形为sin （x +ϕ）＝()f y 型（2）转化为直线的斜率求解（特别是定义域不是R 时，必须这样作） 6．同角的正弦余弦的和差与积的转换：同一问题中出现sin cos ,sin cos ,sin cos x x x x x x +-∙，求它们的范围，一般是令sin cos x x t+=或21sin cos sin cos 2t x x t x x --=⇒∙=或21sin cos 2t x x -∙=-，转化为关于t 的二次函数来解决◇基础训练1.设函数()sin 2(0)f x a x b a =+<，则()f x 的最大值是 .2.函数sin cos 2y x x =++的最小值是 .3.函数2()cos sin f x x x =+在区间[,]44ππ-上的最大值是 ，最小值是 .4.函数sin sin 2x y x =+的最大值是 ，最小值是 .◇典型例题例1. 求函数2sin 2cos x y x-=-的最大值和最小值例2.求sin cos sin cos y x x x x =++的值域◇能力提升1. 函数|sin |2sin y x x =-的值域为（ ）A.[3,1]--B.[－1,3]C.[0, 3]D.[－3, 0] 2.函数sin y x x =-在［2π，π］上的最大值是( )A2π－1 Bπ3+1 Cπ322 D π3.2y sin x(sin x cos x )=+的最大值是 .4.函数3f (x )cos x cos(x )π=++的最小值是 .5.已知函数12)6(,8)0(,cos 2cos sin 2)(2==+=πf f x b x x a x f 且（１）求实数,a b 的值；（２）求函数)(x f 的最大值及取得最大值时x 的值6．(2008华附)如图，四边 形ABCD 是一个边长为100米的正方形地皮，其中A TPS 是一半径为90米的扇形小山，其余部分都是平地，P 是弧TS 上一点，现有一位开发商想在平地上建造一个两边落在BC 与CD 上的长方形停车场PQCR.（Ⅰ）若∠PA T=θ，试写出四边形RPQC 的面积S 关于θ 的函数表达式，并写出定义域； （Ⅱ）试求停车场的面积最大值第40课 三角函数的最值◇基础训练1. b a -2. 2-5412- 4.131-◇典型例题例1. 解法一：去分母，原式化为sin cos 22x y x y -=-，即sin()x ϕ-=故21|22|yy +-≤1，解得374-≤y ∴max y =374+，m in y =解法二：令1sin x x = ，1cos y x =有22111x y +=它表示单位圆，则所给函数y 就是经过定点P （2，2）以及该圆上的动点(cos ,sin )M x x 的直线PM 的斜率k ，故只需求此直线的斜率k 的最值即可由21|22|kk+-=1，得k ∴maxy =374+，m in y =374-例2.求sin cos sin cos y x x x x =++的值域解：设sin cos t x x =+，则t∈［－2，2］由221(sin cos )12sin cos sin cos 2t x x x x x x -+=+⇒=。
三角函数最值问题(典型题型)
三角函数最值问题求解三角函数最值问题不仅需要用到三角函数的定义域、值域、单调性、图象以及三角函数的恒等变形，还经常涉及到函数、不等式、方程以及几何计算等众多知识．这类问题往往概念性较强，具有一定的综合性和灵活性，下面结合例子给出几种求最值的方法，供大家学习时参考。
1、利用三角函数的单调性求最值例1：求函数x x x x x f 44sin cos sin 2cos )(-⋅-= ⎢⎣⎡⎥⎦⎤∈2,0πx 的最值 解:x x x x x x x x f 2sin 2cos 2sin )sin )(cos sin (cos )(2222-=--+=)42cos(2π+=x 45424,20ππππ≤+≤∴≤≤x x ,由余弦函数的单调性及图像知： 当442ππ=+x ， 即0=x 时 ，)42cos(π+x 取最大值22； 当ππ=+42x ，即83π=x 时，)42cos(π+x 取最小值-1； 故2)(,1)(min max -==x f x f方法评析：本题虽然含有的三角函数的项的次数不尽相同，但最终能通过变形变为形如θθcos sin b a +的形式，再用辅助角公式)sin(cos sin 22ϕθθθ++=+b a b a 化为标准形式结合三角函数的单调性加以解决，这是一种最常见的求最值的方法。
2、利用三角函数的有界性或数形结合求最值例2：求1cos 2sin --=x x y 的最小值 解：(方法一)由1cos 2sin --=x x y 得：y x y x -=-2cos sin ，y x y -=-+∴2)sin(12ϕ 即212)sin(y yx +-=-ϕ，故11212≤+-≤-y y ，解之得43≥y ， 故y 的最小值为43 方法评析：通过变形，借助三角函数的有界性求函数最值是一种很常见的方法，一般在分式型且对自变量无特殊限制条件下使用。
(方法二)设),(),sin ,(cos 21M x x P ,则1cos 2sin --=x x y 表示单位圆上的动点P 与平面内定点M 连线的斜率，当斜率存在时，设过P 、M 两点的直线方程为)1(2-=-x k y ，由距离公式得1122=+-k k ，解之得43=k ，结合图形可知函数的最小值为43。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三角函数的最值问题
三角函数最值问题散见于不同的章节，或作为问题的背景、或作为单独的数学问题、或作为解题的工具。
今天，我们就求解最值的方法层面展开讨论！ 一 化为单名函数的形式 例1 函数f(x)=x x x x 44
sin cos sin 2cos
--
①求f(x)得最小正周期;
② ⎥⎦
⎤⎢⎣⎡∈2,0πx 时，求f(x)的最小值。
解: (1) x
x x x x f cos sin 2sin cos
)(22
--= x x 2sin 2cos -=
)2
2
2sin 222(cos 2⋅-=x x
)4
2cos(2π
+=
x ∴ f(x)最小正周期是π=T
（2）2
0π≤≤x ∴ ⎥⎦
⎤
⎢⎣⎡∈+45,42
2πππx
∴ 4
4
2π
π
=
+x 即0=x 时最大值是1
ππ=+4
2x 即8
3π=x 时最小值是－
2
注意
① 辅助角公式)sin(cos sin 22ϕ++=+x b a x b x a 的应用
② 注意三角函数区间最值的正确取舍
二 单名函数的复合型
例2 3
1sin sin =+y x ，求x y 2
cos sin -的最值
解：∵ x y sin 3
1sin -= ∴ 1sin 3
11≤-≤-x
∴ 3
4sin 3
2≤≤-x
∴ 12
11
)21(sin cos
sin 22
--=-=x x y u
∴ 21sin =x u
的最小值为12
11- ；
3
2sin -=x u 的最大值为94
注意：隐含条件不可忽视！ 三 关系代换x x cos sin ±与x x cos sin 例3 求函数x
x x
x y cos sin 1cos sin ++=
的最值
解：令x x t cos sin += 则 x x t
cos sin 12
+=
∴ )1(2
1121
2-=+-=t t t y
∴ 22≤≤-
t 且 1≠t
∴ )
12(2
1
)12(
2
1-≤≤+-y 且 1-≠y
注意① 代换要等效 ；② 原函数中对代换量的现定！ 四 限量代换 例4 求函数2
1x x y -+
=的值域
解：函数的定义域[]1,1-∈x 令 θcos =x ， πθ≤≤0 )4sin(2sin cos π
θθθ+=+=y
∴ 21≤
≤-y
注意：限量代换要求对代换量进一步分析并“定性”
五 建立关系等式整体带入或转化 例5 设A y x =+，求y x sin sin 的最值 解：∵ y x y x y x sin sin cos cos )cos(+=- y x y x y x sin sin cos cos )cos(-=+
∴ )cos(cos )cos()cos(sin sin 2y x A y x y x y x +-=+--= ∴ 2
1cos sin sin 2
1cos +≤≤-A y x A
∴ y x sin sin 最大值为2
1cos +A ，
最小值为2
1cos -A
注意：找沟通已知与未知的一个或两个函数！ 练习： 1求)3
cos(sin 3π
+
+=
x x y 的最值
2 Rt ABC ∆中，0
90=∠C ，求B A sin sin +的最大值 3 求x x y cos sin +=的最大值与最小值 4 求x x a x f 2cos sin 42)(--=的最值 5已知A y x =+，求y x cos sin 的最值 6 )2sin(5)(ϕ+=
x x f
对任意都有)3
()3
(x f x f +=-ππ
（1）求ϕ的最小值；
（2）ϕ取最小值时若⎥⎦
⎤
⎢⎣⎡-∈6,6ππx ，
求f(x) 的最小值。