二次函数abc组合的符号判断解析
二次函数图像与abc符号关系课件

目 录
• 二次函数的基本概念 • 二次函数的图像分析 • 二次函数的abc符号变化对图像的影响 • 实际应用举例 • 总结与思考
01
二次函数的基本概念
二次函数的一般形式
总结词
二次函数的一般形式是$f(x) = ax^2 + bx + c$,其中$a, b, c$是常数,且$a neq 0$。
于负半轴。
对二次函数图像与abc符号关系的深入思考
a符号与开口大小的关系
虽然a决定了开口方向,但a的绝对值大小也会影响开口的大小。当|a|越大,开口越宽; 当|a|越小,开口越窄。
b符号与对称性的关系
b的符号和大小决定了抛物线的对称性。当b=0时,抛物线关于y轴对称;当b≠0时,抛物 线关于x=−b/2a对称。
详细描述
在二次函数的一般形式$f(x) = ax^2 + bx + c$中,$a, b, c$分别被称为二次项系数、一次项系数和常数项。它 们的符号决定了函数的开口方向、顶点位置等性质。例如,当$a > 0$时,函数图像开口向上;当$a < 0$时,函 数图像开口向下。
二次函数的开口方向与abc符号的关系
04
实际应用举例
利用二次函数解决实际问题
总结词
通过理解二次函数的图像和abc符 号关系,可以解决一些实际问题 。
详细描述
二次函数图像的开口方向、顶点 位置和对称轴等特性,可以帮助 我们解决一些实际问题,例如最 值问题、面积问题等。
二次函数在数学建模中的应用
总结词
二次函数是数学建模中常用的函数之 一,可以用来描述一些实际问题中的 数量关系。
05
总结与思考
二次函数a.b.c的判断
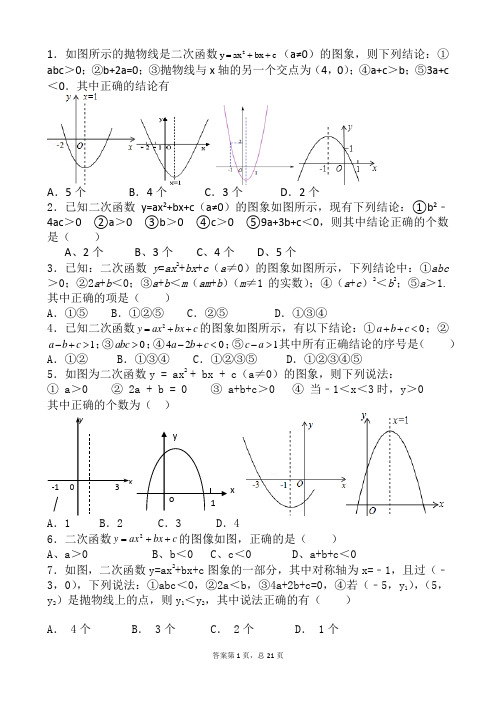
1.如图所示的抛物线是二次函数2y ax bx c =++(a≠0)的图象,则下列结论:①abc >0;②b+2a=0;③抛物线与x 轴的另一个交点为(4,0);④a+c >b ;⑤3a+c<0.其中正确的结论有A .5个B .4个C .3个D .2个2.已知二次函数y=ax 2+bx+c (a≠0)的图象如图所示,现有下列结论:①b 2﹣4ac >0 ②a >0 ③b >0 ④c >0 ⑤9a+3b+c <0,则其中结论正确的个数是( )A 、2个B 、3个C 、4个D 、5个3.已知:二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,下列结论中:①abc >0;②2a +b <0;③a +b <m (am +b )(m ≠1的实数);④(a +c )2<b 2;⑤a >1.其中正确的项是( )A .①⑤B .①②⑤C .②⑤D .①③④4.已知二次函数2y ax bx c =++的图象如图所示,有以下结论:①0a b c ++<;②1a b c -+>;③0abc >;④420a b c -+<;⑤1c a ->其中所有正确结论的序号是( )A .①②B .①③④C .①②③⑤ D.①②③④⑤ 5.如图为二次函数y=ax 2+bx+c (a≠0)的图象,则下列说法:①a >0②2a+b=0③a+b+c >0④当﹣1<x <3时,y >0其中正确的个数为( )A .1B .2C .3D .46.二次函数c bx ax y ++=2的图像如图,正确的是( )A 、a >0B 、b <0C 、c <0D 、a+b+c <07.如图,二次函数y=ax 2+bx+c 图象的一部分,其中对称轴为x=﹣1,且过(﹣3,0),下列说法:①abc <0,②2a <b ,③4a+2b+c=0,④若(﹣5,y 1),(5,y 2)是抛物线上的点,则y 1<y 2,其中说法正确的有()A . 4个B . 3个C . 2个D . 1个x8.二次函数2y ax bx c =++的图象如图所示,对于下列结论:①a <0;②b <0;③c >0;④b+2a=0;⑤a+b+c <0.其中正确的个数是【 】A .1个B .2个C .3个D .4个9.如图,二次函数y=ax 2+bx+c (a≠0)的图象与x 轴交于A 、B 两点,与y 轴交于点C ,点B 坐标(﹣1,0),下面的四个结论:①OA=3;②a+b+c <0;③ac >0;④b 2﹣4ac >0.其中正确的结论是【 】A .①④B .①③C .②④D .①②10的图象如图所示,则下列结论:①abc >0; ②2=++c b a ;④b >1.其中正确的结论是 ( )A. ①② C.③④ D.②④11.小强从如图所示的二次函数2y ax bx c =++的图象中,观察得出了下面五条信息:(1)0a <;(2)1c >;(3)0b >;(4)0a b c ++>;(5)0a b c -+>. 你认为其中正确信息的个数有( )A .2个B .3个C .4个D .5个12.如图所示是二次函数y=ax 2+bx+c 图象的一部分,图象过A 点(3,0),二次函数图象对称轴为直线x=1,给出五个结论:①bc>0;②a+b+c<0;③方程ax 2+bx+c=0的根为x 1= -1,x 2=3;④当x<1时,y 随着x 的增大而增大;⑤4a-2b+c>0其中正确结论是()A.①②③B .①③④C .②③④D.③④⑤ 13.已知二次函数2y ax bx c =++的图象如图所示.下列结论: ①0abc >;②20a b -<;③420a b c -+<;④22()a c b +<,其中正确的个数有( )A .1B .2C .3D .414.如图,二次函数y =ax 2+bx +c (a ≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0),下列结论:①ab<0,②b 2>4a ,③0<a +b +c<2,④0<b<1,⑤当x>-1时,y>0.其中正确结论的个数是( )A .2个B .3个C .4个D .5个15.已知二次函数y =ax 2+bx +c(a≠0)的图像如图,则下列结论中正确的是( )A .a >0B .当x >1时,y 随x 的增大而增大C .c <0D .3是方程ax 2+bx +c =0的一个根160<abc ;②a b 20-<<;③( ) A .1个 B .4个17.如图,二次函数y=ax 2+bx+c 的图象经过点(0,﹣2),与x 轴交点的横坐标分别为x 1,x 2,且﹣1<x 1<0,1<x 2<2,下列结论正确的是( )A .a <0B .a ﹣b+c .4ac ﹣b 2<﹣8a 18x=1,图象经过(3,0),下列结论中,正确的一项是( )A .abc <0B .2a+b <0C .a ﹣b+c <0D .24ac b 0﹣<19.如图所示,二次函数y=ax 2+bx+c 的图象中,王刚同学观察得出了下面四条信息:(1)b 2﹣4ac >0;(2)c >1;(3)2a ﹣b <0;(4)a+b+c <0,其中错误的有A .1个 B .2个 C .3个 D .4个20.如图是二次函数2y ax bx c =++图象的一部分,其对称轴为x=﹣1,3,0).下列说法:①abc <0;②2a ﹣b=0;③4a+2b+c <0;④若(﹣5,y 1),y 2)是抛物线上两点,则y 1>y 2.其中说法正确的是【 】A .①②B .②③C .①②④D .②③④21.二次函数y =ax 2+bx +c (a≠0)的图象如图所示,下列结论:①c <0,②b >0,③4a +2b +c >0,④(a +c )2<b 2,其中正确的有( )A .1个B .2个C .3个D .4个22.已知二次函数)0(2≠++=a c bx ax y 的图象开口向上,与 x 轴的交点坐标是(1,0),对称轴x=-1.下列结论中,错误的是A .abc <0B .b=2aC .a+b+c=0D .20=+b a23.二次函数2(0)y ax bx c a =++≠的图象如下图,以下结论正确的是A.0abc> B.方程ax2+bx+c=0有两个实数根分别为-2和6C.a b c-+< D.当4y=时,x的取值只能为024.已知二次函数2y ax bx c=++(0a≠)的图象如图所示,对称轴为直线12x=-,有下列结论:①abc<0;②2b c+<0;③4a c+<2b.(A)0 (B)1 (C)2 (D)325.已知二次函数2(0)y ax bx c a=++≠的图象如图所示,则下列结论:①方程20ax bx c++=的两根之和大于1;②0<+ba;③y随x的增大而增大;④0<+-cba.其中正确的个数()A.4个B.3个C.2个D.1个26.如图,二次函数2y ax bx c=++(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>2.其中正确的个数是A.1 B.2 C.3 D.427.如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③方程ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.其中正确的命题的个数是A.1个B.2个C.3个D.4个28.小明从如图所示的二次函数2y ax bx c=++的图象中,观察得出了下面五条信息:①0c<;②0<abc;③0a b c-+>;④230a b-=;⑤420a b c++>.你认为其中正确的是()A.①②④B.①③⑤C.②③⑤D.①③④⑤29.二次函数()20y ax bx c a=++≠)图象如图所示,现有下列结论:①b2-4a c>0②a>0 ③b>0 ④c>0 ⑤4a+2b+c<0,则其中结论正确的个数是()A、2个B、3个C、4个D、5个30.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①abc<0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0其中正确结论的有()xyO 1A.①②③ B.①②④ C.①③④ D.②③④31.已知二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,有下列结论:①abc>0,②b2-4ac<0,③a-b+c>0,④4a-2b+c<0,其中正确结论的个数是()A.1B.2C.3D.432.已知抛物线20y ax bx c a=++≠()在平面直角坐标系中的位置如图所示,则下列结论中,正确的是()A.0a< B.b>0 C.0a b c++= D.420a b c+﹣>33.二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:①b2﹣4ac>0;②2a+b<0;③4a﹣2b+c=0;④a:b:c=﹣1:2:3.其中正确的个数是()A.1 B.2 C.3 D.434.二次函数cbxaxy2++=的图像如图所示,则关于此二次函数的下列四个结论①a<0 ②a>0 ③ac4-b2>0 ④ab<0中,正确的结论有()A.1个B.2个C.3个D.4个35.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①b2﹣4ac >0;②abc>0;③8a+c>0;④9a+3b+c<0其中,正确结论的个数是()A.1 B.2 C.336.如图,二次函数2y ax bx c=++的图像与y轴正半轴相交,其顶点坐标为,下列结论:①0ac<;②0a b+=;③244ac b a-=;④0a b c++<.其中正确结论的个数是()A. 1 B. 2 C. 3 D. 437.二次函数cbxaxy++=2(a,b,c是常数,a≠0)图象的对称轴是直线1=x,其图象一部分如图所示,对于下列说法:①0abc >;②0<+-c b a ;③03<+c a ;④当23x -<<时,0>y 其中正确的是( )A ①②B ①④C ②③D ②③④38.如图是二次函数y=ax 2+bx+c 图像的一部分,其对称轴是直线x=-1,且过点(-3,0),下列说法:①abc >0;②2a -b=0;③4a+2b+c <0;④若(-5,y 1),(2.5,y 2)是抛物在线两点,则y 1>y 2,其中正确的是()A .② B.②③ C.②④ D.①②39.二次函数2y ax bx c =++的图象如图所示,给出下列说法:①ac >0;②b a +2=0;③0=++c b a ;④当1x >时,函数y 随x 的增大而增大;⑤当0y >时,13x -<<.其中,正确的说法有 .(请写出所有正确说法的序号)40.如图是二次函数2y ax bx c =++图象的一部分,图象过点A (3,0),且对称轴为1x =,给出下列四个结论:①;②0bc <;③20a b +=;④0a b c ++=,其中正确结论的序号是___________.(把你认为正确的序号都写上)参考答案1.B。
二次函数a.b.c等的符号的确定

-1 o 1 x
(5)△=b2-4ac决定抛物线与x轴交点情况:
① △>0 ② △=0
抛物线与x轴有两个交点; 抛物线与x轴有唯一的公共点;
③ △<0 抛物线与x轴无交点。
y ox
y ox
y ox
勇攀高峰
1. 二次函数y=ax2+bx+c的图象如图所示,下列结论中:
①abc>0;② a+b+c<0 ③ a-b+c>0 ;
o1 特殊值法
x
y aabb cc 0 0
y=ax2+bx+c 当x 1时 y=a-b+c
y aabbcc0 0 y
y aabbcc00
-1 o
x
y aabbcc00
x=-1
比拼速度
二次函数y ax2 bx c的图象如图,用(< , >或 =)填空: a< 0,b < 0,c > 0,a+b+c< 0,a-b+c> 0, Nhomakorabeay
开口向下
a<0
数形结合法
x
⑵c决定抛物线与y轴交点(0,c)的位置:
① 图象与y轴交点在y轴正半轴;
c>0
② 图象过原点
c=0
③ 图象与y轴交点在y轴负半轴
c<0
y
指出下列二次函数与y轴交点的坐标.
(1) y=x2-8x+7 (2) y=-2x2+9x-17
x
⑶a,b决定抛物线对称轴的位置: 对称轴是直线x =
转化 + 特殊值
根据抛物线y=ax2+bx+c图象位置,你 会判断那些字母或代数式的符号?
二次函数的图象中abc式子的正负判断《解析答案》

(2013•遵义)10.二次函数y=ax 2+bx+c (a ≠0)的图象如图如图所示,若M=a+b ﹣c ,N=4a ﹣2b+c ,P=2a ﹣b .则M ,N ,P 中,值小于0的数有( )A . 3个B . 2个C . 1个D . 0个考点:二次函数图象与系数的关系.专题:计算题.分析:根据图象得到x=﹣2时对应的函数值小于0,得到N=4a ﹣2b+c 的值小于0,根据对称轴在直线x=﹣1右边,利用对称轴公式列出不等式,根据开口向下得到a 小于0,变形即可对于P 作出判断,根据a ,b ,c 的符号判断得出a+b ﹣c 的符号.解:∵图象开口向下,∴a <0,∵对称轴在y 轴左侧,∴a ,b 同号,∴a <0,b <0,∵图象经过y 轴正半轴,∴c >0,∴﹣c <0∴M=a+b ﹣c=a+b+(﹣c )<0,当x=﹣2时,y=4a ﹣2b+c点(-2,4a ﹣2b+c )在第二象限∴4a ﹣2b+c <0,∴N=4a ﹣2b+c <0, ∵﹣ab 2>﹣1, ∴ab 2<1, ∴b >2a ,∴2a ﹣b <0,∴P=2a ﹣b <0,则M ,N ,P 中,值小于0的数有M ,N ,P .故选:A .点评: 此题主要考查了二次函数图象与系数的关系,根据图象判断出对称轴以及a ,b ,c 的符号是解题关键.(2016•遵义)12.如图为二次函数y=ax2+bx+c (a ≠0)的图象,则下列说法:①a >0;②2a+b=0;③a+b+c >0;④△>0;⑤4a ﹣2b+c <0,其中正确的个数为( )A .1B .2C .3D .4【考点】二次函数图象与系数的关系.【分析】由抛物线的开口方向判断a 与0的关系,由抛物线与y 轴的交点判断c 与0的关系,然后根据对称轴x=1计算2a+b 与0的关系;再由根的判别式与根的关系,进而对所得结论进行判断.【解答】解:①由抛物线的开口向下知a <0,故本选项错误;②由对称轴为x=231+-=1, ∴﹣a b 2231+-=1, ∴b=﹣2a ,则2a+b=0,故本选项正确;③由图象可知,当x=1时,y=a+b+c点(1,a+b+c )在第一象限y >0,则a+b+c >0,故本选项正确;④从图象知,抛物线与x 轴有两个交点,∴△>0,故本选项错正确;⑤由图象可知,当x=﹣2时,y=4a ﹣2b+c点(-2,4a ﹣2b+c )在第二象限∴4a ﹣2b+c <0,∴4a ﹣2b+c <0,故本选项正确;故选D .【点评】本题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a 与b 的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.(2017•遵义)11.如图,抛物线y=ax 2+bx+c 经过点(﹣1,0),对称轴l 如图所示,则下列结论:①abc >0;②a ﹣b+c=0;③2a+c <0;④a+b <0,其中所有正确的结论是( )A .①③B .②③C .②④D .②③④【考点】:二次函数图象与系数的关系.【分析】①根据开口向下得出a <0,根据对称轴在y 轴右侧,得出b >0,根据图象与y 轴的交点在y 轴的正半轴上,得出c >0,从而得出abc <0,进而判断①错误;②由抛物线y=ax2+bx+c 经过点(﹣1,0),即可判断②正确;③由图可知,x=2时,y <0,即4a+2b+c <0,把b=a+c 代入即可判断③正确;④由图可知,x=2时,y <0,即4a+2b+c <0,把c=b ﹣a 代入即可判断④正确.解:①∵二次函数图象的开口向下,∴a <0,∵二次函数图象的对称轴在y 轴右侧,∴﹣>0,∴b >0,∵二次函数的图象与y 轴的交点在y 轴的正半轴上,∴c >0,∴abc <0,故①错误;②∵抛物线y=ax 2+bx+c 经过点(﹣1,0),∴a ﹣b+c=0,故②正确;③∵a ﹣b+c=0,∴b=a+c .由图可知,x=2时,y <0,即4a+2b+c <0,∴4a+2(a+c )+c <0,∴6a+3c <0,∴2a+c <0,故③正确;④∵a ﹣b+c=0,∴c=b ﹣a .由图可知,x=2时,y <0,即4a+2b+c <0,∴4a+2b+b ﹣a <0,∴3a+3b <0,∴a+b <0,故④正确.故选D .4、二次函数y=ax 2+bx+c (a ≠0)的图象如图,给出下列四个结论:①4ac-b 2<0;②4a+c <2b ;③3b+2c <0;④m (am+b )+b <a (m ≠-1),其中正确结论的个数是( )A .4个B .3个C .2个D .1个∵抛物线和x 轴有两个交点,∴b 2-4ac >0,∴4ac-b 2<0,∴①正确;∵对称轴是直线x=-1,和x 轴的一个交点在点(0,0)和点(1,0)之间,∴抛物线和x 轴的另一个交点在(-3,0)和(-2,0)之间,∴把(-2,0)代入抛物线得:y=4a-2b+c >0,∴4a+c >2b ,∴②错误;∵把(1,0)代入抛物线得:y=a+b+c <0,(第11题图)∴2a+2b+2c<0,∵b=2a,∴3b+2c<0,∴③正确;∵抛物线的对称轴是直线x=-1,∴y=a-b+c的值最大,即把(m,0)(m≠-1)代入得:y=am2+bm+c<a-b+c,∴am2+bm+b<a,即m(am+b)+b<a,∴④正确;即正确的有3个,故选:B.5、二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:①2a+b=0②当-1≤x≤3时,y<0③若。
二次函数与abc的关系总结

二次函数与abc的关系总结在数学中,二次函数是一个具有以下形式的函数:$f(x) = ax^2 + bx + c$。
其中,$a$、$b$和$c$是常数。
二次函数在数学分析、物理学、经济学等领域中都有广泛的应用。
本文将总结二次函数与$a$、$b$和$c$之间的关系。
关系一:二次函数的图像开口方向与$a$的正负有关。
当$a>0$时,二次函数的图像开口向上;当$a<0$时,二次函数的图像开口向下。
这是因为当$a>0$时,$f(x) = ax^2 + bx + c$关于$y$轴对称,所以图像开口向上;当$a<0$时,$f(x) = ax^2 + bx + c$关于$y$轴对称,所以图像开口向下。
关系二:二次函数的图像是否与$x$轴相交与$c$的正负有关。
当$c>0$时,二次函数的图像与$x$轴有两个交点;当$c=0$时,二次函数的图像与$x$轴有一个交点(相切);当$c<0$时,二次函数的图像与$x$轴没有交点。
关系三:二次函数的顶点坐标与$a$和$b$有关。
对于二次函数$f(x) = ax^2 + bx + c$,它的顶点的$x$坐标为$x =\frac{-b}{2a}$,$y$坐标为$y = f(\frac{-b}{2a})$。
根据$a$和$b$的不同取值,顶点可以位于$y$轴的上方或下方,并且根据$a$的正负可以确定顶点的凹凸性质。
当$a>0$时,顶点位于图像的下方(凹);当$a<0$时,顶点位于图像的上方(凸)。
综上所述,二次函数与$a$、$b$和$c$之间存在着紧密的关系。
通过对$a$、$b$和$c$的取值进行分析,可以推断出二次函数的图像特征、对称性以及与$x$轴的交点情况等。
这种关系在数学中具有重要的意义,对于解题和应用中的问题分析都起到了重要的作用。
了解和掌握这些关系,有助于提高对二次函数性质的理解和应用能力。
在实际应用中,二次函数与$a$、$b$和$c$的关系也有着重要的应用。
二次函数中的abc

课题由二次函数y=ax2+bx+c的图像判断a、b、c的符号授课类型微课教材分析二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的系数a,b,c的符号和它的图像之间有着相辅相成的关系.由二次函数的图像位置可以得到a,b,c(或者含有的a,b,c的代数式)的符号;反之,由a,b,c(或者含有的a,b,c的代数式)的符号也可以确定图像的位置.这是一种由形到数、由数到形的转换,是数形结合思想的很好的诠释.也是一种等价、同一的关系。
学情分析学生已经学习了二次函数的概念图像和简单性质,能够简单运用函数知识解决方程和不等式问题。
从中考命题要求和课程标准的角度来看,关于二次函数的a、b、c的试题主要包括:简单结论型、结论综合型、结论组合导出型。
要学好二次函数内容、从容应对二次函数中考题,熟悉二次函数的a、b、c与图像的关系,必须深刻领会数形结合思想,能够用函数的观点看方程与不等式(组)。
教学目标知识与技能1.会根据二次函数的图像判断a,b,c的符号以及与a,b,c有关的代数式的符号;2.能够根据a,b,c的符号,判断二次函数的图像.过程与方法1.利用几何画板演示,让学生感受函数图像与系数a,b,c的关系,体会数形结合的思想方法.情感态度与价值 1.在学习过程中,培养学生的探究精神,合作能力.教学重点探究二次函数的图像与系数a,b,c的关系.教学难点根据二次函数的图像判断与a,b,c有关的代数式的符号.教学方法几何画板演示教学法、引导分析法、合作探究法.教学过程教学环节教师活动学生活动设计意图(一)问题引入教师提出思考问题已知二次函数y=ax2+bx+c的图像如图所示,则a 0 , b 0 , c 0(填>、<、=).学生思考问题.通过问题提出,引发学生思考,进入学习状态.。
二次函数中的符号问题

(2)C的符号: 由抛物线与y轴的交点位置确定:
交点在x轴上方 交点在x轴下方 经过坐标原点
c>0
c<0
c=0
4
归纳知识点:
(3)b的符号:由对称轴的位置确定: 对称轴在y轴左侧 对称轴在y轴右侧 对称轴是y轴 (4)b2-4ac的符号:
a、b同号
a、b异号 b=0 简记为:左同右异
由抛物线与x轴的交点个数确定:
17
仔细想一想:
6.(06.浙江省)如图,二次函数y=ax2+bx+c的图象开口向上, 图象经过点(-1,2)和(1,0),且与y轴相交于负半轴. (以下有(1)、(2)两问,每个考生只须选答一问,若两问都答, 则只以第(2)问计分) 第(1)问:给出四个结论: ①a>0;② b>0;③c>0;④ a+b+c=0.其中正确结论的序号 是 ①④ (答对得3分,少选、错选均不得分). 第(2)问:给出四个结论: ① abc<0;②2a+b>0;③a+c=1;④a>1.其中正确结论的序 号是 ② ③ ④(答对得5分,少选、错选均不得分). y
y
C、4个
D、5个
-1 o
1
x
15
想一想:
4.二次函数y=ax2+bx+c的图象的一部分如图,已知它的顶 点M在第二象限,且经过A(1,0),B(0,1),请判断实数a的范 围,并说明理由.
y M 1 B A x O 1
16
再想一想:
5.(06.芜湖市)如图,在平面直角坐标系中,二次函数 y=ax2+c(a<0)的图象过正方形ABOC的三个顶点A、B、C, 则ac的值是 -2 .
二次函数abc判定

合用标准文案3. 〔 2021? 山东威海,第 11 题 3 分〕二次函数y=ax2+bx+c〔a≠0〕的图象如图,那么以下说法:2①c=0;②该抛物线的对称轴是直线x=﹣1;③当 x=1时, y=2a;④ am+bm+a>0〔 m≠﹣1〕.其中正确的个数是〔〕A.1B.2C.3D.4考点:二次函数图象与系数的关系.解析:由抛物线与y 轴的交点判断 c 与0的关系,尔后依照对称轴及抛物线与x 轴交点情况进行推理,进而对所得结论进行判断.解答:解:抛物线与y 轴交于原点, c=0,故①正确;该抛物线的对称轴是:,直线 x=﹣1,故②正确;当 x=1时, y=2a+b+c,∵对称轴是直线 x=﹣1,∴, b=2a,又∵ c=0,∴y=4a,故③错误;2x=m对应的函数值为y=am+bm+c,∵b=2a,2∴am+bm+a>0〔 m≠﹣1〕.故④正确.应选: C.谈论:此题观察了二次函数图象与系数的关系.二次函数y=ax2+bx+c〔a≠0〕系数符号由抛物线张口方向、对称轴、抛物线与y 轴的交点抛物线与x 轴交点的个数确定.5. 〔 2021? 山东烟台,第 11 题 3 分〕二次函数y=ax2+bx+c〔a≠ 0〕的局部图象如图,图象过点〔﹣ 1, 0〕,对称轴为直线x=2,以下结论:①4a+b=0;② 9a+c>3b;③ 8a+7b+2c> 0;④当x>﹣ 1 时,y的值随x值的增大而增大.其中正确的结论有〔〕A.1 个B.2个C.3个D.4个考点:二次函数的图象与性质.解答:依照抛物线的对称轴为直线x=﹣=2,那么有 4a+b=0;观察函数图象获适合x=﹣3时,函数值小于0,那么 9a﹣ 3b+c< 0,即 9a+c< 3b;由于x=﹣ 1 时,y=0,那么a﹣b+c=0,易得c=﹣5a ,所以 8 +7 +2 =8 ﹣28 ﹣10a=﹣30,再依照抛物线张口向下得< 0,于是有 8 +7 +2a b c a a a a a b c>0;由于对称轴为直线x=2,依照二次函数的性质获适合x>2时, y 随 x 的增大而减小.解答:∵抛物线的对称轴为直线x=﹣=2,∴ b=﹣4a,即4a+b=0,所以①正确;∵当 x=﹣3时, y<0,∴9a﹣3b+c<0,即9a+c<3b,所以②错误;∵抛物线与x 轴的一个交点为〔﹣1, 0〕,∴a﹣b+c=0,而 b=﹣4a,∴ a+4a+c=0,即 c=﹣5a,∴8a+7b+2c=8a﹣28a﹣10a=﹣30a,∵抛物线张口向下,∴ a<0,∴8a+7b+2c>0,所以③正确;∵对称轴为直线x=2,∴当﹣ 1<x< 2 时,y的值随x值的增大而增大,当x>2时, y 随 x 的增大而减小,所以④错误.应选B.谈论:此题观察了二次函数图象与系数的关系:二次函数y=ax2+bx+c〔 a≠0〕,二次项系数a 决定抛物线的张口方向和大小,当a>0时,抛物线向上张口;当a<0时,抛物线向下开口;一次项系数b 和二次项系数 a 共同决定对称轴的地址,当 a 与 b 同号时〔即ab>0〕,对称轴在 y 轴左;当 a 与 b 异号时〔即 ab<0〕,对称轴在 y 轴右;常数项c 决定抛物线与 y 轴交点.抛物线与 y 轴交于〔0,c〕;抛物线与 x 轴交点个数由△决定,△=b2﹣4ac>0 时,抛物线与x 轴有2个交点;△=b2﹣4ac=0时,抛物线与 x 轴有1个交点;△=b2﹣4ac <0 时,抛物线与x 轴没有交点.27. 〔2021? 山东聊城,第 12 题,3 分〕如图是二次函数y=ax +bx+c〔 a≠ 0〕图象的一局部,x=﹣ 1 是对称轴,有以下判断:①b﹣ 2a=0;② 4a﹣ 2b+c< 0;③ a﹣ b+c=﹣ 9a;④假设〔﹣ 3, y1〕,〔, y2〕是抛物线上两点,那么 y1>y2,其中正确的选项是〔〕A.①②③B.①③④C.①②④D.②③④考点:二次函数图象与系数的关系.解析:利用二次函数图象的相关知识与函数系数的联系,需要依照图形,逐一判断.解答:解:∵抛物线的对称轴是直线x=﹣ 1,∴﹣=﹣ 1,b=2a,∴b﹣ 2a=0,∴①正确;∵抛物线的对称轴是直线x=﹣1,和 x 轴的一个交点是〔2, 0〕,∴抛物线和x 轴的另一个交点是〔﹣4, 0〕,∴把 x=﹣ 2 代入得: y=4a﹣ 2b+c> 0,∴②错误;∵图象过点〔 2, 0〕,代入抛物线的解析式得:4a+2b+c=0,又∵ b=2a,∴c= ﹣ 4a﹣2b=﹣ 8a,∴a﹣ b+c=a﹣ 2a﹣ 8a=﹣ 9a,∴③正确;∵抛物线和x 轴的交点坐标是〔2, 0〕和〔﹣ 4, 0〕,抛物线的对称轴是直线x=﹣ 1,∴点〔﹣ 3, y1〕关于对称轴的对称点的坐标是〔〔1,y1〕,∵〔, y2〕, 1<,∴y1> y2,∴④正确;即正确的有①③④,应选 B.谈论:此题主要观察了二次函数图象与系数的关系,在解题时要注意二次函数的系数与其图象的形状,对称轴,特别点的关系,也要掌握在图象上表示一元二次方程2的ax +bx+c=09. (2021年贵州黔东南9.〔 4 分〕 ) 如图,二次函数y=ax2+bx+c〔 a≠ 0〕的图象如图所示,以下 4 个结论:①a bc < 0;② b< a+c;③ 4a+2b+c> 0;④ b2﹣ 4ac > 0其中正确结论的有〔〕A.①②③ B.①②④C.①③④D.②③④考点:二次函数图象与系数的关系.解析:由抛物线的张口方向判断 a 与 0 的关系,由抛物线与 y 轴的交点得出 c 的值,尔后依照抛物线与 x 轴交点的个数及x=﹣ 1 时,x=2 时二次函数的值的情况进行推理,进而对所得结论进行判断.解答:解:由二次函数的图象张口向上可得a>0,依照二次函数的图象与y 轴交于正半轴知: c> 0,由对称轴直线 x=2,可得出 b 与 a 异号,即 b<0,那么 abc< 0,故①正确;把 x=﹣ 1代入 y=ax 2+bx+c 得: y=a﹣ b+c,由函数图象可以看出当x=﹣ 1 时,二次函数的值为正,即 a+b+c> 0,那么 b< a+c,故②选项正确;把 x=2 代入 y=ax 2+bx+c 得:y=4a+2b+c,由函数图象可以看出当x=2 时,二次函数的值为负,即 4a+2b+c< 0,故③选项错误;由抛物线与 x 轴有两个交点可以看出方程ax2+bx+c=0 的根的鉴识式 b2﹣ 4ac >0,故④ D选项正确;应选 B.谈论:此题观察二次函数图象与二次函数系数之间的关系,二次函数与方程之间的变换,根的鉴识式的熟练运用.会利用特别值代入法求得特其他式子,如:y=a+b+c, y=4a+2b+c,尔后依照图象判断其值.16.〔 2021? 四川南充,第10 题, 3 分〕二次函数y=ax2+bx+c〔 a≠0〕图象如图,以下结论:①abc >0;② 2 +=0;③当≠1 时,+ >2+ ;④﹣ + >0;⑤假设ax12+bx1=ax22+2,a b m a b am bm a b c bx且 x1≠ x2, x1+x2=2.其中正确的有〔〕A.①②③B.②④C.②⑤D.②③⑤解析:依照抛物线张口方向得a<0,由抛物线对称轴为直线x=﹣=1,获取b=﹣ 2a> 0,即 2a+b=0,由抛物线与y 轴的交点地址获取c>0,所以 abc<0;依照二次函数的性质适合x=1时,函数有最大值22a+b+c,那么当 m≠1时, a+b+c> am+bm+c,即 a+b> am+bm;依照抛物线的对称性获取抛物线与x 轴的另一个交点在〔﹣1,0〕的右侧,那么当 x=﹣1时, y<0,所以 a﹣ b+c<0;把 ax122+bx1=ax2 +bx2先移项,再分解因式获取〔x1﹣x2〕 [ a〔x1+x2〕 +b]=0 ,而 x≠ x ,那么 a〔 x +x 〕+b]=0,即x+x =﹣,尔后把b=﹣ 2a代入计算获取x+x =2.12121212解:∵抛物线张口向下,∴a<0,∵抛物线对称轴为性质x=﹣=1,∴b=﹣2a>0,即2a+b=0,所以②正确;∵抛物线与y 轴的交点在x 轴上方,∴c>0,∴ abc<0,所以①错误;∵抛物线对称轴为性质x=1,∴函数的最大值为a+b+c,22∴当 m≠1时, a+b+c> am+bm+c,即 a+b> am+bm,所以③正确;∵抛物线与x 轴的一个交点在〔3, 0〕的左侧,而对称轴为性质x=1,∴抛物线与x 轴的另一个交点在〔﹣1, 0〕的右侧∴当 x=﹣1时, y<0,∴ a﹣b+c<0,所以④错误;2222﹣ bx2=0,∵ax1+bx1=ax2+bx2,∴ax1+bx1﹣ax2∴a〔 x1+x2〕〔 x1﹣ x2〕+b〔 x1﹣ x2〕=0,优秀文档谈论:此题观察了二次函数图象与系数的关系:二次函数y=ax2+bx+c〔a≠0〕,二次项系数a 决定抛物线的张口方向和大小,当> 0 时,抛物线向上张口;当a< 0 时,抛物线向下开a口;一次项系数b 和二次项系数a共同决定对称轴的地址,当a与b同号时〔即> 0〕,ab对称轴在y 轴左;当a与b异号时〔即< 0〕,对称轴在y轴右;常数项c决定抛物线与aby 轴交点.抛物线与 y 轴交于〔0, c〕;抛物线与 x 轴交点个数由△决定,△=b2﹣ 4ac> 0时,抛物线与 x 轴有2个交点;△=b2﹣4ac=0时,抛物线与x 轴有1个交点;△=b2﹣4ac<0 时,抛物线与x 轴没有交点.11.〔 2021?莱芜,第212 题 3 分〕二次函数 y=ax +bx+c 的图象以以下图.以下结论:①a bc > 0;② 2a﹣ b< 0;③ 4a﹣2b+c < 0;④〔 a+c〕2<b2其中正确的个数有〔〕A. 1 B. 2 C.3D.4考点:二次函数图象与系数的关系.专题:数形结合.解析:由抛物线张口方向得 a< 0,由抛物线对称轴在y 轴的左侧得 a、 b 同号,即 b< 0,由抛物线与 y 轴的交点在 x 轴上方得 c> 0,所以 abc> 0;依照抛物线对称轴的地址获取﹣1<﹣< 0,那么依照不等式性质即可获取2a﹣ b< 0;由于 x=﹣ 2 时,对应的函数值小于0,那么 4a﹣ 2b+c< 0;同样当 x=﹣1 时, a﹣b+c> 0,x=1 时, a+b+c< 0,那么〔 a﹣b+c〕〔 a+b+c〕<0,利用平方差公式张开获取〔2222.a+c〕﹣ b < 0,即〔 a+c〕< b解答:解:∵抛物线张口向下,∴a< 0,∵抛物线的对称轴在y 轴的左侧,∴x= ﹣< 0,∴b< 0,∵抛物线与y 轴的交点在x 轴上方,∴c> 0,∴a bc > 0,所以①正确;∵﹣ 1<﹣<0,∴2a﹣b<0,所以②正确;∵当 x=﹣ 2 时, y< 0,∴4a﹣2b+c<0,所以③正确;∵当 x=﹣ 1 时, y> 0,∴a﹣ b+c>0,∵当 x=1 时, y< 0,∴a+b+c< 0,∴〔 a﹣ b+c〕〔 a+b+c〕< 0,即〔 a+c﹣b〕〔 a+c+b〕< 0,22应选 D.谈论:此题观察了二次函数的图象与系数的关系:二次函数 y=ax 2+bx+c〔 a≠ 0〕的图象为抛物线,当 a> 0,抛物线张口向上;对称轴为直线x=﹣;抛物线与 y 轴的交点坐标为〔 0,c〕;当 b2﹣ 4ac> 0,抛物线与 x 轴有两个交点;当b2﹣ 4ac=0,抛物线与 x 轴有一个交点;当 b2﹣4ac< 0,抛物线与 x 轴没有交点.3. (2021 年四川资阳,第 10 题 3 分 ) 二次函数=ax 2++ 〔≠ 0〕的图象如图,给出以下y bx c a四个结论:①4ac﹣b2< 0;② 4a+c< 2b;③ 3b+2c< 0;④m〔am+b〕 +b<a〔m≠﹣ 1〕,其中正确结论的个数是〔〕A.4个B.3个C.2个D.1个考点:二次函数图象与系数的关系.解析:利用二次函数图象的相关知识与函数系数的联系,需要依照图形,逐一判断.解答:解:∵抛物线和x 轴有两个交点,∴b2﹣4ac>0,∴4ac﹣b2< 0,∴①正确;∵对称轴是直线x﹣1,和 x 轴的一个交点在点〔0, 0〕和点〔 1,0〕之间,∴抛物线和x 轴的另一个交点在〔﹣3, 0〕和〔﹣ 2, 0〕之间,∴把〔﹣ 2, 0〕代入抛物线得:y=4a﹣2b+c>0,∴4a+c> 2b,∴②错误;∵把〔 1, 0〕代入抛物线得:y=a+b+c<0,∴2a+2b+2c< 0,∵b=2a,∴3b, 2c<0,∴③正确;∵抛物线的对称轴是直线 x=﹣1,∴y=a﹣ b+c 的值最大,2即把〔 m,0〕〔 m≠0〕代入得: y=am+bm+c< a﹣ b+c,2∴am+bm+b<a,即 m〔 am+b〕+b< a,∴④正确;即正确的有 3 个,应选 B.谈论:此题主要观察了二次函数图象与系数的关系,在解题时要注意二次函数的系数与其图象的形状,对称轴,特别点的关系,也要掌握在图象上表示一元二次方程2的ax +bx+c=0解的方法.同时注意特别点的运用.4. (2021 年天津市,第 12 题 3 分 ) 二次函数y=ax2+bx+c〔a≠ 0〕的图象如图,且关于x 的一元二次方程 ax2+bx+c﹣ m=0没有实数根,有以下结论:①b2﹣4ac>0;② abc<0;③ m>2.其中,正确结论的个数是〔〕A.0B.1C.2D.3考点:二次函数图象与系数的关系.解析:由图象可知二次函数y=ax2+bx+c 与 x 轴有两个交点,进而判断①;先依照抛物线的张口向下可知a<0,由抛物线与y 轴的交点判断 c 与0的关系,依照对称轴在 y 轴右侧得出 b 与0的关系,尔后依据有理数乘法法那么判断②;222一元二次方程ax +bx+c﹣m=0没有实数根,那么可转变成ax +bx+c=m,即可以理解为y=ax +bx+c 和 y=m没有交点,即可求出m的取值范围,判断③即可.解答:解:①∵二次函数=2++ 与x 轴有两个交点,y ax bx c ∴b2﹣4ac>0,故①正确;②∵抛物线的张口向下,∴a<0,∵抛物线与y 轴交于正半轴,∴c>0,∵对称轴 x=﹣>0,∴a b<0,∵a<0,∴b>0,∴a bc<0,故②正确;③∵一元二次方程ax2+bx+c﹣ m=0没有实数根,∴y=ax2+bx+c 和y=m没有交点,由图可得, m>2,故③正确.应选 D.谈论:此题主要观察图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的变换,根的鉴识式的熟练运用.8.〔 2021? 孝感,第 12 题 3 分〕抛物线y=ax2+bx+c的极点为D〔﹣ 1,2〕,与x轴的一个交点 A 在点〔﹣3,0〕和〔﹣2,0〕之间,其局部图象如图,那么以下结论:①b2﹣4ac<0;② a+b+c<0;③ c﹣ a=2;④方程 ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论的个数为〔〕A.1个B.2个C.3个D.4个考点:二次函数图象与系数的关系;抛物线与x 轴的交点专题:数形结合.解析:由抛物线与x 轴有两个交点获取b2﹣4ac>0;有抛物线极点坐标获取抛物线的对称轴为直线 x=﹣1,那么依照抛物线的对称性得抛物线与x 轴的另一个交点在点〔0, 0〕和〔 1,0〕之间,所以当x=1时, y<0,那么 a+b+c<0;由抛物线的极点为D〔﹣1,2〕得 a﹣b+c=2,由抛物线的对称轴为直线x =﹣=1得 =2,所以﹣ =2;依照二次函数的最大值问题,b ac a当 x=﹣1时,二次函数有最大值为2,即只有x=1 时,ax2+bx+c=2,所以说方程ax2+bx+c﹣2=0 有两个相等的实数根.解答:解:∵抛物线与x 轴有两个交点,∴b2﹣4ac>0,所以①错误;∵极点为 D〔﹣1,2〕,∴抛物线的对称轴为直线x=﹣1,∵抛物线与x 轴的一个交点 A 在点〔﹣3,0〕和〔﹣2,0〕之间,∴抛物线与x 轴的另一个交点在点〔0, 0〕和〔 1, 0〕之间,∴当 x=1时, y<0,∴a+b+c<0,所以②正确;∵抛物线的极点为 D〔﹣1,2〕,∴a﹣ b+c=2,∵抛物线的对称轴为直线 x=﹣=1,∴b=2a,∴a﹣2a+c=2,即 c﹣ a=2,所以③正确;∵当 x=﹣1时,二次函数有最大值为2,即只有 x=1时, ax2+bx+c=2,∴方程 ax2+bx+c﹣2=0有两个相等的实数根,所以④正确.应选 C.谈论:此题观察了二次函数的图象与系数的关系:二次函数 y=ax2+bx+c〔 a≠0〕的图象为抛物线,当 a>0,抛物线张口向上;对称轴为直线x=﹣;抛物线与 y 轴的交点坐标为〔0,c〕;当 b2﹣4ac>0,抛物线与 x 轴有两个交点;当b2﹣4ac=0,抛物线与 x 轴有一个交点;当 b2﹣4ac<0,抛物线与 x 轴没有交点.12.〔 2021? 菏泽第 8 题 3 分〕如图,Rt△ABC中,AC=BC=2,正方形CDEF的极点D、F分别在 AC、 BC边上, C、D两点不重合,设 CD的长度为 x,△ ABC与正方形 CDEF重叠局部的面积为 y,那么以以下图象中能表示y 与 x 之间的函数关系的是〔〕优秀文档A.B.C.D.考点:动点问题的函数图象.专题:数形结合.解析:分类谈论:当0<x≤ 1 时,依照正方形的面积公式获取y=x2;当1< x≤2时, ED交 AB于 M, EF交 AB于 N,利用重叠的面积等于正方形的面积减去等腰直角三角形MNE的面积获取 y=x2﹣2〔 x﹣1〕2,配方获取 y=﹣〔 x﹣2〕2+2,尔后依照二次函数的性质对各选项进行判断.解答:解:当0<x≤ 1时, y=x2,当 1<x ≤2 时,交于,交于,如图,ED AB M EF AB NCD=x,那么 AD=2﹣ x,∵R t △ ABC中, AC=BC=2,∴△ADM为等腰直角三角形,∴DM=2﹣ x,∴EM=x﹣〔2﹣ x〕=2x﹣2,∴S△ ENM=〔2x﹣2〕2=2〔 x﹣1〕2,∴y=x2﹣2〔 x﹣1〕2=﹣ x2+4x﹣2=﹣〔 x﹣2〕2+2,∴y=,应选 A.15. 〔 2021 年山东泰安,第20 题 3 分〕二次函数y=ax2+bx+c〔 a, b,c 为常数,且a≠0〕中的 x 与 y 的局部对应值以下表:X﹣1013y﹣1353以下结论:(1〕ac< 0;(2〕当x> 1 时,y的值随x值的增大而减小.(3〕 3 是方程ax2+〔b﹣ 1〕x+c=0 的一个根;(4〕当﹣ 1<x< 3 时,ax2+〔b﹣1〕x+c> 0.其中正确的个数为〔〕A.4个B.3个C.2个D.1个解析:依照表格数据求出二次函数的对称轴为直线x ,尔后依照二次函数的性质对各小题解析判断即可得解.解:由图表中数据可得出: x=1时,y=5值最大,所以二次函数2y=ax +bx+c 张口向下, a<0;又 x=0时, y=3,所以 c=3>0,所以 ac<0,故〔1〕正确;∵二次函数y=ax2+bx+c 张口向下,且对称轴为x==1.5 ,∴当x>1.5 时,y的值随x值的增大而减小,故〔2〕错误;2∵x=3时, y=3,∴9a+3b+c=3,∵ c=3,∴9a+3b+3=3,∴9a+3b=0,∴3是方程 ax +〔b﹣1〕x+c=0的一个根,故〔3〕正确;∵x=﹣1时,ax2+bx+c=﹣1,∴x=﹣1时,ax2+〔 b﹣1〕x+c=0,∵x=3时,ax2+〔 b﹣1〕x+c=0,且函数有最大值,∴当﹣ 1<x< 3 时,ax2=〔b﹣ 1〕x+c> 0,故〔 4〕正确.应选 B .谈论: 此题观察了二次函数的性质, 二次函数图象与系数的关系,抛物线与 x 轴的交点,二次函数与不等式,有必然难度.熟练掌握二次函数图象的性质是解题的要点.5. 〔 2021? 贵港,第 12 题 3 分〕二次函数 y =ax 2+bx +c 〔 a ≠ 0〕的图象如图,解析以下四个结论:① a bc < 0;② b 2﹣ 4ac >0;③ 3a +c > 0;④〔 a +c 〕 2< b 2,其中正确的结论有〔〕A . 1个B .2个C .3个D .4个考点 : 二次函数图象与系数的关系.解析:①由抛物线的张口方向, 抛物线与 y 轴交点的地址、对称轴即可确定 a 、b 、c 的符号,即得 abc 的符号;②由抛物线与 x 轴有两个交点判断即可;③ 〔﹣ 2〕+2 〔 1〕=6 +3 <0,即 2 + < 0;又由于a <0,所以 3 + < 0.故错误;ff a ca ca c④将 x =1 代入抛物线解析式获取+ + <0,再将x =﹣ 1 代入抛物线解析式获取﹣ +>0,a b ca b c 两个不等式相乘,依照两数相乘异号得负的取符号法那么及平方差公式变形后,获取〔 a +c 〕2<b 2,解答:解:①由张口向下,可得 a <0,又由抛物线与 y 轴交于正半轴,可得 c > 0,尔后由对称轴在 y 轴左侧,获取 b 与 a 同号,那么可得 b < 0, abc >0,故①错误;②由抛物线与 x 轴有两个交点,可得b 2﹣4ac > 0,故②正确;③当 x =﹣ 2 时, y < 0,即 4a ﹣2b +c < 0 〔 1〕当 x =1 时, y < 0,即 a +b +c <0 〔 2〕( 1〕 +〔 2〕× 2 得: 6a +3c <0,即 2a +c < 0又∵ a < 0,∴ a +〔 2a +c 〕 =3a +c < 0.故③错误;④∵ x=1时, y=a+b+c<0, x=﹣1时, y=a﹣ b+c>0,∴〔 a+b+c〕〔 a﹣ b+c〕<0,即[ 〔a+c〕+b][ 〔a+c〕﹣b]= 〔a+c〕2﹣b2< 0,∴〔 a+c〕2<b2,故④正确.综上所述,正确的结论有 2 个.应选: B.谈论:此题观察了二次函数图象与系数的关系.二次函数y=ax2+bx+c〔 a≠0〕系数符号由抛物线张口方向、对称轴、抛物线与y 轴的交点抛物线与x 轴交点的个数确定.11. 〔 2021? 广东深圳,第11 题23 分〕二次函数y=ax +bx+c图象如图,以下正确的个数为〔〕①b c>0;②2a﹣ 3c<0;③2a+b> 0;④a x2+bx+c=0有两个解 x1, x2, x1>0, x2<0;⑤a+b+c>0;⑥当 x>1时, y 随 x 增大而减小.A.2B.3C.4D.5考点:二次函数图象与系数的关系.解析:依照抛物线张口向上可得a>0,结合对称轴在y 轴右侧得出b<0,依照抛物线与y 轴的交点在负半轴可得c<0,再依据有理数乘法法那么判断①;再由不等式的性质判断②;依照对称轴为直线x=1判断③;依照图象与x 轴的两个交点分别在原点的左右两侧判断④;解答:解:①∵抛物线张口向上,∴a>0,∵对称轴在y 轴右侧,∴a, b 异号即 b<0,∵抛物线与y 轴的交点在负半轴,∴c<0,∴b c>0,故①正确;②∵ a>0,c<0,∴2a﹣ 3c>0,故②错误;③∵对称轴 x=﹣<1,a>0,∴﹣ b<2a,∴2a+b> 0,故③正确;④由图形可知二次函数 y=ax2+bx+c 与 x 轴的两个交点分别在原点的左右两侧,即方程 ax2+bx+c=0有两个解 x1,x2,当 x1> x2时, x1>0, x2<0,故④正确;⑤由图形可知x=1时, y=a+b+c<0,故⑤错误;⑥∵ a>0,对称轴 x=1,∴当 x>1时, y 随 x 增大而增大,故⑥错误.综上所述,正确的结论是①③④,共 3 个.应选 B.谈论:主要观察图象与二次函数系数之间的关系,二次函数的性质,会利用对称轴的范围求 2a与b的关系,以及二次函数与方程之间的变换.14.〔 2021? 齐齐哈尔, 9 题 3 分〕如图,二次函y=ax2+bx+c〔 a≠0〕图象的一局部,对称轴为直线 x=,且经过点〔2,0〕,以下说法:① abc<0;② a+b=0;③4a+2b+c<0;④假设〔﹣2,y1〕,〔,y2〕是抛物线上的两点,那么y1< y2,其中说法正确的选项是〔〕A.①②④B.③④C.①③④D.①②考点:二次函数图象与系数的关系.解析:①依照抛物线张口方向、对称轴地址、抛物线与y 轴交点地址求得、、的符号;a b c②依照对称轴求出b=﹣ a;③把 x=2代入函数关系式,结合图象判断符号;④求出点〔﹣ 2,y1〕关于直线x=的对称点的坐标,依照对称轴即可判断y1和 y2的大小.解答:解:①∵二次函数的图象张口向下,∴a<0,∵二次函数的图象交y 轴的正半轴于一点,∴c>0,∵对称轴是直线 x=,∴﹣ =,∴b=﹣ a>0,∴a bc<0.故①正确;②∵ b=﹣ a∴a+b=0.故②正确;③把 x=2代入 y=ax2+bx+c 得: y=4a+2b+c,∵抛物线经过点〔2, 0〕,∴当 x=2时, y=0,即4a+2b+c=0.故③错误;④∵〔﹣ 2,y1〕关于直线x=的对称点的坐标是〔3,y1〕,又∵当 x>时, y 随 x 的增大而减小,<3,∴y1< y2.故④错误;综上所述,正确的结论是①②④.应选: A.谈论:此题观察了二次函数的图象和系数的关系的应用,注意:当a>0时,二次函数的图象张口向上,当a<0时,二次函数的图象张口向下.6.〔 2021? 扬州,第 16 题, 3 分〕如图,抛物线y=ax2+bx+c〔a> 0〕的对称轴是过点〔 1,0〕且平行于y 轴的直线,假设点P〔4,0〕在该抛物线上,那么4a﹣ 2b+c的值为0.〔第 3 题图〕考点:抛物线与 x 轴的交点解析:依照抛物线的对称性求得与x 轴的另一个交点,代入解析式即可.解答:解:设抛物线与x 轴的另一个交点是,Q∵抛物线的对称轴是过点〔1, 0〕,与x轴的一个交点是P〔4,0〕,∴与 x 轴的另一个交点Q〔﹣2,0〕,把〔﹣ 2, 0〕代入解析式得:0=4a﹣ 2b+c,∴4a﹣ 2b+c=0,故答案为: 0.谈论:此题观察了抛物线的对称性,知道与x 轴的一个交点和对称轴,可以表示出与x 轴的另一个交点,求得另一个交点坐标是此题的要点.2.〔 2021? 四川省德阳,第24 题 14 分〕如图,抛物线经过点A〔﹣2,0〕、 B〔4,0〕、C〔0,﹣8〕.〔1〕求抛物线的解析式及其极点D的坐标;〔2〕直线CD交x轴于点E,过抛物线上在对称轴的右侧的点P,作 y 轴的平行线交x 轴于点 F,交直线 CD于 M,使 PM=EF,央求出点P 的坐标;(3〕将抛物线沿对称轴平移,要使抛物线与〔 2〕中的线段EM总有交点,那么抛物线向上最多考点:二次函数综合题;解一元二次方程- 因式分解法;根的鉴识式;待定系数法求一次函数解析式;待定系数法求二次函数解析式.专题:综合题.解析:〔1〕由于抛物线与x 轴的两个交点,抛物线的解析式可设成交点式:y=a〔 x+2〕(x﹣4〕,尔后将点 C的坐标代入即可求出抛物线的解析式,再将该解析式配成极点式,即可获取极点坐标.(2〕先求出直线CD的解析式,再求出点E的坐标,尔后设点P的坐标为〔m,n〕,进而可以用m的代数式表示出 PM、EF,尔后依照 PM=EF建立方程,即可求出 m,进而求出点 P 的坐标.〔3〕先求出点的坐标,尔后设平移后的抛物线的解析式为=x 2﹣ 2 ﹣8+ ,尔后只要考虑M y xc三个临界地址〔①向上平移到与直线EM相切的地址,②向下平移到经过点M的地址,③向下平移到经过点 E 的地址〕所对应的 c 的值,就可以解决问题.解答:解:〔 1〕依照题意可设抛物线的解析式为y=a〔 x+2〕〔 x﹣4〕.∵点 C〔0,﹣8〕在抛物线y=a〔 x+2〕〔x﹣4〕上,∴﹣ 8a=﹣ 8.∴a=1.∴y=〔 x+2〕〔 x﹣4〕=x2﹣2x﹣ 8=〔x﹣ 1〕2﹣9.∴抛物线的解析式为y=x2﹣2x﹣8,极点 D的坐标为〔1,﹣9〕.〔2〕如图,设直线 CD的解析式为y=kx+B.∴解得:.∴直线 CD的解析式为y=﹣ x﹣8.当 y=0时,﹣ x﹣8=0,那么有 x=﹣8.∴点 E 的坐标为〔﹣8,0〕.设点 P 的坐标为〔 m, n〕,22那么 PM=〔 m﹣2m﹣8〕﹣〔﹣ m﹣8〕=m﹣ m,EF=m﹣〔﹣8〕=m+8.∵PM=EF,2∴m﹣ m=〔 m+8〕.2整理得: 5m﹣6m﹣ 8=0.∴〔 5m+4〕〔m﹣ 2〕 =0解得: m1=﹣, m2=2.∵点 P 在对称轴 x=1的右侧,∴m=2.此时, n=22﹣2×2﹣8=﹣8.∴点 P 的坐标为〔2,﹣8〕.(3〕当m=2 时,y=﹣ 2﹣ 8=﹣10.∴点 M的坐标为〔2,﹣10〕.设平移后的抛物线的解析式为y=x2﹣2x﹣8+c,①假设抛物线y=x2﹣2x﹣8+c 与直线 y=﹣ x﹣8相切,那么方程 x2﹣2x﹣8+c=﹣x﹣8即 x2﹣ x+c=0有两个相等的实数根.∴〔﹣ 1〕2﹣4× 1×c=0.∴c=.②假设抛物线y=x2﹣2x﹣8+c 经过点 M,那么有 22﹣ 2× 2﹣ 8+c=﹣10.∴c=﹣2.③假设抛物线y=x2﹣2x﹣8+c 经过点 E,那么有〔﹣ 8〕2﹣ 2×〔﹣ 8〕﹣ 8+c=0.综上所述:要使抛物线与〔 2〕中的线段 EM 总有交点,抛物线向上最多平移个单位长度,向下最多平移 72 个单位长度.谈论: 此题观察了用待定系数法求二次函数的解析式、用待定系数法求一次函数的解析式、解一元二次方程、根的鉴识式、 抛物线与直线的交点问题等知识,而把抛物线与直线相切的问题转变成一元二次方程有两个相等的实数根的问题是解决第三小题的要点,有必然的综合性.8、〔 2021 年内蒙古包头〕 二次函数y ax2bx c的图象与 x 轴交于点 ( 2,0) ( x 1,0),、且 1x 1 2 ,与 y 轴的正半轴的交点在(0,2) 的下方.以下结论:① 4a 2b c 0 ;②a b 0 ;③ 2a c0 ;④ 2a b 10 .其中正确结论的个数是个.【答案】 4【解析】 此题观察二次函数图象的画法、鉴识理解, 方程根与系数的关系筀等知识和数形结合能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数abc组合的符号判断
对于二次函数中abc组合的符号判断套路掌握情况,分为三个层次,首先根据函数图象确定a,b,c符号以及对称轴信息,其次是找特殊点的函数值,获取等式和不等式,最后在判断残缺型符号时,将等式代入不等式。
过程中考查学生读图,数形结合以及逻辑分析能力。
单选题(本大题共7小题,共100分)
1.(本小题12分)如图,二次函数的图象开口向上,对称轴为直线x=1,且图象经过点(3,0),则下列结论正确的是( )
• A.
• B.
• C.
• D.
核心考点: 二次函数图象与系数的关系 abc组合的符号判断
2.(本小题12分)已知二次函数的图象如图所示,下列结论:①
;②;
③;④b+2a=0;⑤.其中正确的有( )
• A. 1个
• B. 2个
• C. 3个
• D. 4个
核心考点: 二次函数图象与系数的关系abc组合的符号判断
3.(本小题12分)已知二次函数的图象如图所示,下列结论:①;
②;③;④.其中正确的是( )
• A. ②③
• B. ③④
• C. ②④
• D. ①④
核心考点: 二次函数图象与系数的关系 abc组合的符号判断
4.(本小题16分)如图所示,二次函数的图象中,王刚同学观察
得出了下面四条结论:①;②;③;④.其中错误的有( )
• A. 1个
• B. 2个
• C. 3个
• D. 4个
核心考点: 二次函数图象与系数的关系abc组合的符号判断
5.(本小题16分)已知二次函数的图象如图所示,其对称轴为直线,则下列结论正确的是( )
• A.
• B. a+b=0
• C.
• D.
核心考点: 二次函数图象与系数的关系 abc组合的符号判断
6.(本小题16分)如图,二次函数图象的顶点在第一象限,且过点(0,1)和(-1,0).下列结论:①;②;③;
④当时,.其中正确的有( )
• A. 1个
• B. 4个
• C. 3个
• D. 2个
核心考点: 二次函数图象与系数的关系abc组合的符号判断
7.(本小题16分)已知二次函数的图象如图所示,下列结论:①;
②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④;⑤.其中正确的是( )
• A. ②③⑤
• B. ①②③⑤
• C. ①②④⑤
• D. ①③④⑤
核心考点: 二次函数图象与系数的关系 abc组合的符号判断
单选题(本大题共6小题,共100分)
1.(本小题15分)二次函数图象的一部分如图所示,其对称轴为直线x=-1,且过点(-3,0).下列说法:①;②2a-b=0;③;④若,
是抛物线上的两点,则.其中正确的是( )
• A. ①②
• B. ②③
• C. ①②④
• D. ②③④
核心考点: 二次函数图象与系数的关系 abc组合的符号判断
2.(本小题15分)二次函数的图象如图所示,下列结论:①;
②;③;④.其中正确的是( )
• A. ①②
• B. ②③
• C. ③④
• D. ①④
核心考点: 二次函数图象与系数的关系abc组合的符号判断
3.(本小题15分)如图所示,二次函数的图象中,小轩同学观察得出了如下四条结论:①;②;③;④.其中正确的是( )
• A. ①②
• B. ②③
• C. ①②③
• D. ①②③④
核心考点: 二次函数图象与系数的关系 abc组合的符号判断
4.(本小题15分)已知二次函数的图象如图所示,有下列结论:①;
②2a+b=0;③;④.其中正确的有( )个.
• A. 1
• B. 2
• C. 3
• D. 4
核心考点: 二次函数图象与系数的关系abc组合的符号判断
5.(本小题20分)已知二次函数的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).下列结论:①;②b-2a=0;③;④
.其中正确的是( )
• A. ③
• B. ②③
• C. ③④
• D. ①②
核心考点: 二次函数图象与系数的关系 abc组合的符号判断
6.(本小题20分)已知二次函数的图象经过,(2,0)
两点,且,图象与y轴正半轴的交点在(0,2)的下方,则下列结论:①;②;
③;④.其中正确的是( )
• A. ①②
• B. ②③
• C. ①②④
• D. ①②③④
核心考点: 二次函数图象与系数的关系abc组合的符号判断。
