工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第12章 动载荷与疲劳强度简述
工程力学课后习题答案（静力学和材料力学）
解：图（a）：θ = arcsin 4 ,
5
∑ Fx = 0 ,
F sin(60° − θ ) − W sinθ = 0 , F = 1672 N
图（b）：θ = 53.13° ,
∑ Fx = 0 , F cos(θ − 30°) − W sinθ = 0 , F = 217N
Fy
x
30D B
Wθ
y
可推出图（b）中 FAB = 10FDB = 100F = 80 kN。
FED αD
FDB FD′ B
FCB
α
B
F 习题 1－12 解 1 图
F AB 习题 1－12 解 2 图
1—13 杆 AB 及其两端滚子的整体重心在 G 点，滚子搁置在倾斜的光滑刚性平面上，如
图所示。对于给定的θ 角，试求平衡时的 β 角。
=
25 kN 6
即
FR
= ( 5 , 10 )kN 23
作用线方程： y = 4 x + 4 3
讨论：本题由于已知数值的特殊性，实际 G 点与 E 点重合。
2－3三个小拖船拖着一条大船，如图所示。每根拖缆的拉力为5kN。试求：(1)作用于大 船上的合力的大小和方向。(2)当A船与大船轴线x的夹角θ为何值时，合力沿大船轴线方向。
投影： Fx1 = F cosα ， Fy1 = F sinα
讨论： ϕ = 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
图（b）：
分力： Fx2 = (F cosα − F sin α tan ϕ )i2 ，
Fy2
=
F sinα sinϕ
j2
投影： Fx2 = F cosα ，
Fy2 = F cos(ϕ − α )
工程力学(静力学和材料力学)第2版课后习题答案 范钦珊主编 第10章 组合受力与变形杆件的强度计算
解：危险截面在 A 处，其上之内力分量为： 弯矩： M y = FP1 a ， M z = FP2 H 扭矩： M x = FP2 a 轴力： FNx = FP1 在截面上垂直与 M 方向的垂直线 ab 与圆环截 求得 M y 与 M z 的矢量和 M 过截面中心， 面边界交于 a、b 两点，这两点分别受最大拉应力和最大压应力。但由于轴向压力的作用，最 大压应力值大于最大拉应力值，故 b 点为危险点，其应力状态如图所示。 10－7 试求图 a 和 b 中所示之二杆横截面上最大正应力及其比值。 解： （a）为拉弯组合
7
y
y
A
O
0.795
B
14.526
+13.73MPa
z
(a)
O O
+14.43MPa
(b)
C
y
A
C
B B
y
A
O O
B
z
12.6mm
14.1mm
zC
−15.32MPa
16.55MPa
zC
z
(c)
(d)
习题 10－9 解图
∴
+ σ max
= 14.526 − 0.795 = 13.73 MPa
− σ max = −14.526 − 0.795 = −15.32 MPa
Ebh
由此得
2 FP 6e
e=
10－9
ε1 − ε 2 h × ε1 + ε 2 6
图中所示为承受纵向荷载的人骨受力简图。试：
1．假定骨骼为实心圆截面，确定横截面 B－B 上的应力分布； 2．假定骨骼中心部分(其直径为骨骼外直径的一半)由海绵状骨质所组成，忽略海绵状承受 应力的能力，确定横截面 B－B 上的应力分布；
范钦珊版材料力学习题全解 第12章 简单的静不定系统
（a）
（b） 习题 12－4 图
（A） FQA = FQB = 0 ， FNA = FNB = 0 ， M A = M B = 3( M / 3) ； （B）需解超静定才能确定； （C） FQA = FQB = 0 ， FNA
= FNB = 0 ，MA 、MB 需解超静定才能确定；
M 。 2
（D） FQA = FQB = FNA = FNB ，但需解超静定才能确定具体数值， M A = M B =
X 1δ11 + X 2δ12 + ∆1FP = 0 ⎫ ⎪ ⎬ X 1δ 21 + X 2δ 22 + ∆2 FP = 0 ⎪ ⎭
（a）
10
(a)
(b) 习题 12－7 (b) 解的图－1
利用图乘法求其中的位移，作用在静定基本系统上的载荷（图 c）以及沿多余约束力 X1 和 X2 方向施加的单位力（图 e 和 g）所产生的弯矩图分别如图 f 和 h 所示。据此，可以求得：
由此解得：
1 5 FP = FP （→） 6 3 10 考虑静定基本系统平衡，得到全部约束力 11 F Ax = FP + FRD = FP （←） 10 FRD =
M A = FP ⋅ l = FP l （逆）
12－7 平面刚架各杆的刚度都相同，所受载荷如图所示。若忽略轴力和剪力影响，试用 图乘法确定其约束力，并画出弯矩图,确定绝对值最大的弯矩值及其所在横截面。
应用卡氏定理，建立变形协调条件 ∆Dx = 0 。
∂M 3 = x3 ∂FRD
∆Dx =
l l ⎤ ∂M 3 ∂M 1 ∂M 2 1 ⎡ l dx1 + ∫ M 2 ( x2 ) dx2 + ∫ M 3 ( x3 ) dx3 ⎥ ⎢ ∫ 0 M 1 ( x1 ) 0 0 ∂FRD ∂FRD ∂FRD EI ⎣ ⎦
工程力学(工程静力学与材料力学)第二版答案(完整资料).doc
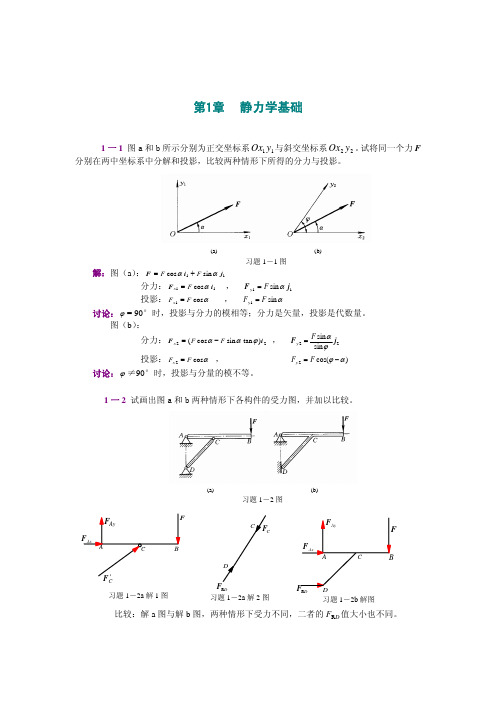
(a) (b)习题1-1图 【最新整理，下载后即可编辑】1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一方F 分别对两坐标系进行分解和投影，并比较分力与力的投影。
解：（a ），图（c ）：11 sin cos j i F ααF F +=分力：11 cos i F αF x = ， 11 sin j F αF y = 投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
（b ），图（d ）：1y F x xF 1y Fα1xF y F（c ）2F2y F2y2x 2x F2y FF（d ）(a) (b)习题1－2图F DR AC BD AxF AyF(a-1)Ay F FB C A AxF 'F C(a-2) C DF DR(a-3)AxFF A C BD AyF (b-1) 分力：22)tan sin cos (i F ϕααF F x -= ，22sin sin j FϕαF y =投影：αcos 2F F x = ， )cos(2αϕ-=F F y 讨论：ϕ≠90°时，投影与分量的模不等。
1－2 试画出图a 、b 两情形下各物体的受力图，并进行比较。
比较：图（a-1）与图（b-1）不同，因两者之F R D 值大小也不同。
1－3 试画出图示各物体的受力图。
习题1－3图F AxFAyF D C BABF或(a-2)FB AF DCA(a-1)BF AxF AAyF C(b-1)WF BD CF FCBBF AACBF(f-1)(e-3)'A(f-2)1O(f-3)c FF AF DF BF AF A习题1－4图1－4 图a所示为三角架结构。
力F1作用在B铰上。
杆AB 不计自重，杆BD杆自重为W。
试画出图b、c、d所示的隔离体的受力图，并加以讨论。
工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩[1]
![工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩[1]](https://img.taocdn.com/s3/m/5939f6a70029bd64783e2cf5.png)
45D 30D
FB
C
FP
习题 5－6 图
习题 5－6 解图
∑ Fx = 0 ， FB = 2 FA
（1） （2） （3）
∑ Fy = 0 ，
2 3 FA + FB − FP = 0 2 2
1+ 3 FB 2 π FB ≤ [σ ] ⋅ d 2 4 FP =
5
FP ≤
1+ 3 π 2 ⋅ d [σ ] 2 4 ` （4） 1+ 3 π = ⋅ × 20 2 × 10 − 4 × 157 × 106 = 67.4k N 2 4
解：1. 受力分析：由图（a）有
5 FP 3 4 4 ∑ Fx = 0 ， F1 = − F3 = − FP 5 3
由图（b）由
2. 强度计算：
3m
F1
F3
F4
C
θ
B
F2
FP
F3
习题 5－7 图
(a)
(b)
∑ F y = 0 ， F3 =
4 4 F3 = FP 5 3 5 ∑ F y = 0 ， F2 = − F3 = − FP 3
（2）
∴
x=
5 b 6
5－11 电线杆由钢缆通过旋紧张紧器螺杆稳固。已知钢缆的横截面面积为 1× 103 mm 2 ， E=200GPa， [σ ] = 300MPa 。欲使电杆有稳固力 FR=100kN，张紧器的螺杆需相对移动多少? 并校核此时钢缆的强度是否安全。
FR
习题 5－11 图
解： （1）设
= 2.947 +
100 ×103 × 2500 × 4 = 5.286 mm 105 ×103 × π × 362
材料力学课后答案范钦珊
材料力学课后答案范钦珊第一篇：材料力学课后答案范钦珊材料力学课后答案范钦珊普通高等院校基础力学系列教材包括“理论力学”、“材料力学”、“结构力学”、“工程力学静力学材料力学”以及“工程流体力学”。
目前出版的是前面的3种“工程力学静力学材料力学”将在以后出版。
这套教材是根据我国高等教育改革的形势和教学第一线的实际需求由清华大学出版社组织编写的。
从2002年秋季学期开始全国普通高等学校新一轮培养计划进入实施阶段新一轮培养计划的特点是加强素质教育、培养创新精神。
根据新一轮培养计划课程的教学总学时数大幅度减少为学生自主学习留出了较大的空间。
相应地课程的教学时数都要压缩基础力学课程也不例外。
怎样在有限的教学时数内使学生既能掌握力学的基本知识又能了解一些力学的最新进展既能培养学生的力学素质又能加强工程概念。
这是很多力学教育工作者所共同关心的问题。
现有的基础教材大部分都是根据在比较多的学时内进行教学而编写的因而篇幅都比较大。
教学第一线迫切需要适用于学时压缩后教学要求的小篇幅的教材。
根据“有所为、有所不为”的原则这套教材更注重基本概念而不追求冗长的理论推导与繁琐的数字运算。
这样做不仅可以满足一些专业对于力学基础知识的要求而且可以切实保证教育部颁布的基础力学课程教学基本要求的教学质量。
为了让学生更快地掌握最基本的知识本套教材在概念、原理的叙述方面作了一些改进。
一方面从提出问题、分析问题和解决问题等方面作了比较详尽的论述与讨论另一方面通过较多的例题分析特别是新增加了关于一些重要概念的例题分析著者相信这将有助于读者加深对于基本内容的了解和掌握。
此外为了帮助学生学习和加深理解以及方便教师备课和授课与每门课材料力学教师用书lⅣ程主教材配套出版了学习指导、教师用书习题详细解答和供课堂教学使用的电子教案。
本套教材内容的选取以教育部颁布的相关课程的“教学基本要求”为依据同时根据各院校的具体情况作了灵活的安排绝大部分为必修内容少部分为选修内容。
工程力学第二版答案
工程力学第二版答案工程力学是工程学的基础学科之一，通过研究物体的力学行为来解决工程问题。
本文档是对工程力学第二版教材的习题答案的整理和总结。
希望能对学习该科目的学生以及工程领域从业者提供帮助。
第一章矢量代数与力学基本原理习题1-11.如何判断两个向量相等？2.什么是矢量的加法和减法？3.如何计算矢量的模和方向？答案：1.两个矢量相等的条件是它们的模和方向完全相同。
2.矢量的加法就是将两个矢量的对应分量相加，矢量的减法是将两个矢量的对应分量相减。
3.矢量的模可以通过计算矢量的分量的平方和的平方根来得到，矢量的方向可以通过计算矢量的分量的比值和反三角函数得到。
习题1-21.什么是力的平衡？2.如何判断一个物体在平衡状态下的受力情况？3.什么是支撑反力？答案：1.力的平衡指的是物体所受的合力为零的情况，物体处于静止或匀速直线运动的状态。
2.在平衡状态下，物体所受的合力为零，因此可以通过将所有作用力相互抵消来判断物体的受力情况。
3.支撑反力是指物体在受到外界作用力时，支持物体的支点对物体施加的反作用力。
第二章刚体力学基础习题2-11.什么是刚体？2.刚体有几个自由度？3.刚体在平面上的运动有哪些约束条件？答案：1.刚体指的是物体在力作用下，保持形状和大小不变的物体。
2.刚体有6个自由度，包括3个平移自由度和3个旋转自由度。
3.刚体在平面上的运动有3个约束条件，包括沿x轴平移、沿y轴平移和绕z轴旋转三个约束。
习题2-21.什么是力矩？2.如何计算力矩？3.力矩的方向规定是怎样的？答案：1.力矩是衡量力对物体旋转影响的物理量，也可以理解为力的偏转能力。
2.力矩可以通过力与力臂的乘积来计算，其中力臂是力对旋转轴的垂直距离。
3.力矩的方向遵循右手定则，即当右手握住力臂并使之指向力的方向时，拇指所指的方向即为力矩的方向。
结论本文档对工程力学第二版教材中的一些重要概念和习题进行了解答。
通过学习这些答案，读者可以更好地理解工程力学的基本原理和刚体力学基础，进一步提升解决工程问题的能力。
工程力学 第2版 第12章 动荷应力和交变应力
影响构件持久极限的主要因素 构件外形的影响 构件截面尺寸的影响 构件表面加工质量的影响
a
Kd 1 g
j max
Kd
12.1.2 构件受冲击时的动荷应力 当具有一定速度的运动物体碰到静止的构件时，物体 和构件间会产生很大的作用力，这种现象称为冲击。如汽 锤锻造工件、落锤打桩、金属冲压加工、铆钉枪铆接、高
速转动的传动轴制动等，都是冲击的一些工程实例。
d max Kd j max [ ]
综合考虑以上三种主要因素，则在对称循环下构件的持久极限表示为
0 1
K
1
或
0 1
K
1
目前在机械设计中，通常将疲劳强度设计准则写成比较安全因数的形式
构件在对称循环弯曲或拉压时
n n
n
0 1
[ 1 ]
n
0 1
max
通 常 把 由 最 大 应 力 max 变 到 最 小 应 力 min ， 再 由 最 小 应 力 min变回到最大应力max的过程，称之为一个应力循环。把 一个应力循环中最小应力与最大应力之比值称为循环特性， 用r表示，即
r min max
常见的交变应力循环有 对称循环，
循环特性r = -1。
第12章 动荷应力与交变应力
12.1 动荷应力 10.2 交变应力
12.1 动荷应力
如果作用在构件上的载荷随时间有显著的变化，或在载荷作
用下构件上各点有显著的加速度，这种载荷即称为动载荷。
理论力学课后答案范钦珊)
AyF FBCAAxF 'F CCDCF FAxF DR F FACBDAyFFDR F A CBD Ax F Ay F(a-1)第1篇 工程静力学基础第1章 受力分析概述1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一力F 分别对两坐标系进行分解和投影，并比较分力与力的投影。
习题1－1图解：（a ）图（c ）：11 sin cos j i F ααF F +=分力：11 cos i F αF x = ， 11 sin j F αF y =投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
（b ）图（d ）： 分力：22)cot sin cos (i F ϕααF F x -= ，22sin sin j F ϕαF y = 投影：αcos 2F F x = ， )cos(2αϕ-=F F y讨论：ϕ≠90°时，投影与分量的模不等。
1－2 试画出图a 和b 两种情形下各物体的受力图，并进行比较。
习题1－2图1y F x1F 1yF α1x F yF （c ） 2x F 2y F 2y 2x 2x F 2y F F（d ）比较：图（a-1）与图（b-1）不同，因两者之F R D 值大小也不同。
1－3 试画出图示各物体的受力图。
习题1－3图F AxF AyF D C B A B F或(a-2)FF AF DCA(a-1)BF AxF AAyF C(b-1)W F BD C AyF F(c-1)F F CB B F A或(b-2) αDAF ABCBFAx F AAyFDF DC αF1－4 图a 所示为三角架结构。
荷载F 1作用在铰B 上。
杆AB 不计自重，杆BC 自重为W 。
试画出b 、c 、d 所示的隔离体的受力图，并加以讨论。
习题1－4图C F CAAF (e-1) BF FCDBOOx F OyF W1O F A(f-1)FF DCABBF(e-3)'F AOOxF OyF AW(f-2)AF 1F A1O(f-3)F AF BF AAF xB 2F'yB 2F'1(c-1)F A B1B F(b-1)Dy F DDx F yB F C2(b-2)xB 2F'1F 1F'yB 2F'B(b-3)B WDxF DCyB F'(c-2)AF A D GF CH F H (a)1－5 图示刚性构件ABC 由销钉A 和拉杆D 支撑，在构件C 点作用有一水平力F 。
工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第5章_轴向拉伸与压缩
解：1. 受力分析：由图（a）有
5 FP 3 4 4 ∑ Fx = 0 ， F1 = − F3 = − FP 5 3
由图（b）由
2. 强度计算：
3m
F1
F3
F4
C
θ
B
F2
FP
F3
习题 5－7 图
(a)
(b)
∑ F y = 0 ， F3 =
4 4 F3 = FP 5 3 5 ∑ F y = 0 ， F2 = − F3 = − FP 3
5－4 螺旋压紧装置如图所示。现已知工件所受的压紧力为 F＝4 kN。装置中旋紧螺栓 螺纹的内径 d1＝13.8 mm；固定螺栓内径 d2＝17.3 mm。两根螺栓材料相同，其许用应力 [σ ] ＝53.0 MPa。试校核各螺栓的强度是否安全。 解： ∑ M B = 0 ，FA = 2kN
∑ F y = 0 ，FB = 6kN
uB = 60 × 10 3 × 1.2 × 10 3 70 × 10 3 × 1.10 × 10 −3 × 10 6 = 0.935 mm
钢杆 C 端的位移为
FPlBC 60 ×103 × 2.1×103 uC = uB + = 0.935 + = 4.50mm π Es As 200 ×103 × ×152 4
解：当小车开到 A 点时，AB 杆的受力最大，此时轴力为 FNAB 。 （1） 受力分析，确定 AB 杆的轴力 FNAB ，受力图如图 5－12 解图所示， 由平衡方程
∑F
解得轴力大小为：
y
= 0，
0.8
FNAB sin α − FP = 0
sin α =
0.82 + 1.9 2
FNAB = 38.7kN
材料力学第2版 课后习题答案 第12章 变形能法要点
− LP ⋅ sin α ⋅ L ⋅ δ CH = EJ L 2L L PL cos α ⋅⋅ 3 2 3 = Pl ( 2 cos α − 3sin α 2+ EJ 6 EJ δ cv δ CH 3 ⎛⎞ 2 ⎜ 4sin α − cos α ⎟ 2 ⎠ = tgα = ⎝ ( 2 cos α − 3sin α 8 − 3ctgα = 2 − 3tgα ctgα − tgα = 2 ，2tgα 1 − tg 2α 2tgα =1 1 − tg 2α ∵ tg 2α =α l T2 T1 B b h ∴ tg 2α = 1 ，α = 22.5� 11-29 图示矩形截面梁 AB，设其底面和顶面的温度分别升高 T1oC 和 T2oC，沿横截面高度按线性规律变化，试用单位载荷法计算 A 端横截面的铅垂位移和水平位移。
解：dθ = a ( T1 − T2 dx h d 2v dx 2 = ∴ d 2 v a (T1 − T2 = dx 2 h M = EJa ( T1 − T2 h ∵ M = EJ l yA = ∫ ' xA =∫ 0 MM y dx 0 EJ al 2 (T1 − T2 2h 0 MM x dx l = a (T1 − T2 0 EJ 2 l求的单位力求水平位移的单位力由于梁轴线因 T1 ， T2 影响将发生平位移xA '' xA = a (T1 + T2 '' l 2 ∴ ' '' xA = xA + xA = a ⋅ L ⋅ T1 11-30 图示三角支架，两杆横截面面积均为 A ，材料相同，材料的应力 - 应变关系是σ = B ε ，其中 B 为常数，这一关系对于拉伸和压缩是相同的。
试用虚功原理求 A 节点的水平位移与铅直位移。
解：L2 = L cos α ， L1 = LN2 = P sin α 2 ，N1 = Pctgα 2 ⎛ σ ⎞⎛ Pctgα ⎞ ε1 = ⎜ 1 ⎟ = ⎜⎟⎝ B ⎠⎝ A⋅B ⎠ P ⎛⎞ ε2 = ⎜⎟⎝ A ⋅ B sin α ⎠ 2 ⎛ Pctgα ⎞ ∆1 = L ⋅ ε1 = l ⋅⎜⎟⎝ A⋅ B ⎠∆2 = 2 l l ⎛ P ⎞⋅ε2 = ⋅⎜⎟ cos α cos α ⎝ A ⋅ B sin α⎠∆1 cos α + ∆ 2 sin α 2 0 δ AV = N10 ⋅ ∆1 + N 2 ⋅ ∆2 = 0 δ AH = N10 ⋅ ∆1 + N 2 ⋅ ∆ 2 = ∆1。
工程力学课后习题答案
6-7空心圆截面轴，外径 ，内径 ，扭矩 ，试计算距轴心 处的扭转切应力，以及横截面上的最大与最小扭转切应力。
2-24平面桁架的支座和载荷如图所示，求杆1，2和3的内力。（提示：先截断AD、3、2杆，用截面法分析；再取C节点）
2-25两根相同的均质杆AB和BC，在端点B用光滑铰链连接，A，C端放在不光滑的水平面上，如图所示。当ABC成等边三角形时，系统在铅直面内处于平衡状态。求杆端与水平面间的摩擦因数。
题2-25图
题5-9图
题5-9图
5-10图示外伸梁，承受集度为 的均布载荷作用。试问当 为何值时梁内的最大弯矩之值（即 ）最小。
题5-10图
为保证梁的最大弯矩值最小，即最大正弯矩等于最大负弯矩
第六章杆件的应力
6-1图示的杆件，若该杆的横截面面积 ，试计算杆内的最大拉应力与最大压应力。
题6-1图
6-2图示阶梯形圆截面杆，承受轴向载荷 与 作用， 与 段的直径分别为 与 ，如欲使 与 段横截面上的正应力相同，试求载荷 之值。
4-3材料力学的基本假设是什么？均匀性假设与各向同性假设有何区别？能否说“均匀性材料一定是各向同性材料”？
4-4杆件的轴线与横截面之间有何关系?
4-5试列举五种以上不是各向同性的固体。
4-6杆件的基本变形形式有几种？请举出相应变形的工程实例。
第五章杆件的内力
5-1试求图示各杆1-1、2-2、3-3截面上的轴力，并作轴力图。
5-5某传动轴，转速 ，轮1为主动轮，输入功率 ，轮2、轮3与轮4为从动轮，输出功率分别为 ， 。
（1）试画轴的扭矩图，并求轴的最大扭矩；
（2）若将轮1和轮3的位置对调，轴的最大扭矩变为何值，对轴的受力是否有利。
工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第3章_静力学平衡问题
第3章 静力学平衡问题3－1 图a 、b 、c 所示结构中的折杆AB 以3种不同的方式支承。
假设3种情形下，作用在折杆AB 上的力偶的位置和方向都相同，力偶矩数值均为M 。
试求3种情形下支承处的约束力。
解：由习题3－1a 解图lM F F B A 2== 由习题3－1b 解图lM F F B A == 将习题3－1c 解1图改画成习题3－1c 解2图，则lM F F BD A ==习题3－1c 解2图)B习题3－1c 解1图B习题3－1b 解图习题3－1图B习题3－1a 解图'B A习题3－2解2图∴ l M F F BD B ==， lMF F BD D 22==3－2 图示的结构中，各构件的自重都略去不计。
在构件AB 上作用一力偶，其力偶矩数值M ＝800 N·m 。
试求支承A 和C 处的约束力。
解：BC 为二力构件，其受力图如习题3－2解1图所示。
考虑AB 平衡，由习题3－2解图，A 、B 二处的形成力偶与外加力偶平衡。
800269.4N 1.81.2A B M F F BD ′====3－3 图示的提升机构中，物体放在小台车C 上，小台车上装有A 、B 轮，可沿垂导轨ED 上下运动。
已知物体重2 kN 。
试求导轨对A 、B 轮的约束力。
解： W = 2kN ，T = W ΣF x = 0， F A = F BΣM i = 0， 0800300=×−×A F W ，kN 75.083==W FA ，FB = 0.75 kN ，方向如图示。
习题3－2图习题3－3图BF C习题3－2解1图 A F BF习题3－3解图MA习题3－4解1图3－4 结构的受力和尺寸如图所示，求：结构中杆1、2、3杆所受的力。
解：1、2、3杆均为为二力杆 由习题3－4解1图ΣM i = 0，03=−⋅M d F ,dMF =3, F = F 3（压） 由习题3－4解2图ΣF x = 0，F 2 = 0, ΣF y = 0，dMF F ==1（拉）3－5 为了测定飞机螺旋桨所受的空气阻力偶，可将飞机水平放置，其一轮搁置在地秤上。
工程力学(静力学与材料力学)习题及答案 - 设计准则
工程力学（静力学与材料力学）习题第12章 失效分析与设计准则12－ 1 对于建立材料在一般应力状态下的失效判据与设计准则，试选择如下合适的论述。
（A ）逐一进行试验，确定极限应力；（B ）无需进行试验，只需关于失效原因的假说；（C ）需要进行某些试验，无需关于失效原因的假说； （D ）假设失效的共同原因，根据简单试验结果。
正确答案是 。
12－2 对于图示的应力状态（y x σσ>）若为脆性材料，试分析失效可能发生在：（A ）平行于x 轴的平面； （B ）平行于z 轴的平面；（C ）平行于Oyz 坐标面的平面； （D ）平行于Oxy 坐标面的平面。
正确答案是 。
12－3 对于图示的应力状态，若x y σσ=，且为韧性材料，试根据最大切应力准则，失效可能发生在：（A ）平行于y 轴、其法线与x 轴的夹角为45°的平面，或平行于x 轴、其法线与y 轴的夹角为45°的平面内；（B ）仅为平行于y 轴、法线与z 轴的夹角为45°的平面； （C ）仅为平行于z 轴、其法线与x 轴的夹角为45°的平面； （D ）仅为平行于x 轴、其法线与y 轴的夹角为45°的平面。
正确答案是 。
12－4 铸铁处于图示应力状态下，试分析最容易失效的是：（A ）仅图c ；（B ）图a 和图b ； （C ）图a 、b 和图c ； （D ）图a 、b 、c 和图d 。
正确答案是 。
12－5低碳钢处于图示应力状态下，若根据最大切应力准则，试分析最容易失效的是： （A ）仅图d ； （B ）仅图c ； （C ）图c 和图d ； （D ）图a 、b 和图d 。
正确答案是 。
12－6 韧性材料所处应力状态如图所示，根据最大切应力准则，试分析二者同时失效的条件是： （A ）τσ>，3/2στ=； （B ）τσ<，3/4στ=； （C ）τσ=；（D ）τσ>，3/2τσ=。
工程力学(静力学和材料力学)第2版课后习题答案_范钦珊主编_第6章_圆轴扭转
该轴的扭转强度是安全的。
上一章
返回总目录
下一章
8
3
习题 6－5 图
解：1． τ 1 max =
Mx T T 3 × 10 3 × 16 = = = = 70.7 MPa WP WP π π× 0.06 3 d3 16
A1
2． M r =
∫
ρ ⋅ τdA =
∫
r
0
ρ⋅
2πM x r 4 Mx ρ ⋅ 2πρ d ρ = ⋅ 4 Ip Ip
Mr r4 r4 1 2π 2π 16r 4 15 = = = = 16 × ( ) 4 = = 6.25% 4 4 Mx 16 4I p 60 d d π 4⋅ 32 Mx T = 3． τ 2 max = =75.4MPa Wp 1 4⎞ π d3 ⎛ ⎜1 − ( ) ⎟ 16 ⎝ 2 ⎠
16 M x
3 π d1
=
16 M x
3 π D2 (1 − α 4 )
即
d1 = (1 − α 4 ) 3 D2
1
（a）
二者重量之比
W1 A1 d2 = = 2 1 2 W2 A2 D2 (1 − α )
（b）
式（a）代入式（b） ，得
W1 (1 − α 4 ) = W2 1−α2
2 3
所以，正确答案是
16 M x 3 16 × 10.53 × 10 6 = = 96.3 π [τ ] π × 60
（3）按刚度条件求轴的直径
θ=
Mx ≤ [θ ] GI P
[θ ] = 1D / 2m =
π
180 × 2 × 10 3
rad/mm
6
D≥4
32M x 32 × 10.53 × 10 6 =4 = 110.6mm Gπ [θ ] 82 × 10 3 π [θ ]
工程力学(工程静力学与材料力学)第二版答案
(a) (b) 习题1-1图 (a) (b) 习题1－2图D R(a-1)C(a-2)D R(a-3)(b-1) 1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2分别为正交与斜交坐标系。
试将同一方F 分别对两坐标系进行分解和投影，并比较分力与力的投影。
解：（a ），图（c ）：11 s i n c o s j i F ααF F += 分力：11 cos i F αF x = ， 11 s i n j F αF y = 投影：αcos 1F F x = ， αs i n 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
（b ），图（d ）：分力：22)tan sin cos (i F ϕααF F x -= ，22sin sin j F ϕαF y =投影：αcos 2F F x = ， )cos(2αϕ-=F F y 讨论：ϕ≠90°时，投影与分量的模不等。
1－2 试画出图a 、b比较：图（a-1）与图（b-1）不同，因两者之F R D 值大小也不同。
1－3 试画出图示各物体的受力图。
（c ）22x （d ）习题1－4图习题1－3图1－4 图a 所示为三角架结构。
力F 1作用在B 铰上。
杆AB 不计自重，杆BD 杆自重为W 。
试画出图b 、c 、d 所示的隔离体的受力图，并加以讨论。
或(a-2) B (a-1) (b-1)F (c-1) 或(b-2)(e-1) (f-1)'A (f-2) 1O (f-3)Ax F'(b-3)E D(a-3)习题1－5图B (b-2)(b-1) Ax F1－5 试画出图示结构中各杆的受力图。
F F'F 1(d-2)y B 21 F (b-2) (b-3) F y B 2F A B1B F习题1－8图F 'CB C(c) F(a) 'F(a)1－6 图示刚性构件ABC 由销钉A 和拉杆GH 支撑，在构件的点C 作用有一水平力F 。
工程力学(静力学与材料力学)范钦珊唐静静课后习题答案解析
= 114°35′
图（a）：A 平衡： ∑ Fy = 0 ， TA = 1⋅ sinϕ1
B 平衡： ∑ Fy = 0 ， TB = 2 ⋅ sin ϕ 2
∵ TA = TB
10
（1）
（2） （3）
∴ sin ϕ1 = 2 sin ϕ 2 sin ϕ1 = 2 sin(114°35′ − ϕ1) ϕ1 = 84°44′
d =3
（2）
y
4 G
C
E
θ2
Dθ d −4.5 F O
FR
3
Ax
2
习题 2－2 解图
∴ F 点的坐标为（-3, 0） 合力方向如图所示，作用线过 B、F 点；
tan θ = 4 3
AG = 6 sinθ = 6 × 4 = 4.8 5
M A = FR × AG = FR × 4.8
FR
=
20 4.8
Fw
习题 1—9 图
FT1
F Fw
T2
FN
习题 1—9 解图
7
1 一 10 图示压路机的碾子可以在推力或拉力作用下滚过 100mm 高的台阶。假定力 F 都是沿着杆 AB 的方向，杆与水平面的夹角为 30°，碾子重量为 250 N。试比较这两种情形 下，碾子越过台阶所需力 F 的大小。
习题 1－10 图
(1) 油缸的受力图； (2) 活塞铆枪的受力图； (3) 铆钳的受力图。
6
习题 1－8 图
p
q FQ
p q'
FQ'
(b)
(c)
习题 1－8 解图
1—9 安置塔器的竖起过程如图所示，下端搁在基础上，C 处系以钢绳，并用绞盘拉住； 上端在 B 处系以钢缆，通过定滑轮 D 连接到卷扬机 E 上。设塔器的重量为 FW，试画出塔器 的受力图。
工程力学习题答案范钦珊蔡新著工程静力学与材
(a) (b) 习题1-1图 (a) (b) 习题1－2图FD R F AC BD Ax F AyF(a-1) Ay F F B C A AxF 'F C (a-2)C D C F D R(a-3)AxF D R F FA C BD Ay F(b-1) 1－1 图a 、b 所示，Ox 1y 1与Ox 2y 2别离为正交与斜交坐标系。
试将同一方F 别离对两坐标系进行分解和投影，并比较分力与力的投影。
解：（a ），图（c ）：11 sin cos j i F ααF F += 分力：11 cos i F αF x = ， 11 sin j F αF y = 投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
（b ），图（d ）：分力：22)tan sin cos (i F ϕααF F x -= ，22sin sin j F ϕαF y =投影：αcos 2F F x = ， )cos(2αϕ-=F F y 讨论：ϕ≠90°时，投影与分量的模不等。
1－2 试画出图a 、b 两情形下各物体的受力图，并进行比较。
比较：图（a-1）与图（b-1）不同，因二者之F R D 值大小也不同。
1－3 试画出图示各物体的受力图。
1y F x 1x F 1y F α1x F y F （c ）2F 2y F 2y 2x 2x F 2y F F （d ）习题1－3图1－4 图a 所示为三角架结构。
力F 1作用在B 铰上。
杆AB 不计自重，杆BD 杆自重为W 。
试画出图b 、c 、d 所示的隔离体的受力图，并加以讨论。
F AxF AyF D C B A B F 或(a-2) F B B AF D C A (a-1) B F AxF A Ay F B C(b-1)W F B DC Ay F AxF (c-1) F A F C BBF A或(b-2) αD A F A B CB FC F C AA F (e-1) Ax F A Ay F D F D C αF或(d-2)B F FCD B OOx F OyF W 1O F A(f-1)FA F D C AB B F (e-3) F AO Ox F OyF AW (f-2) A F 1O F A 1O (f-3) c F F A F D F B F A F AAx F C 'Cx F 'B F B AyF 'F Cy A(b-3)E F D F E D (a-3) CF F CE 'F E(a-2) 习题1－5图E EF B B F (b-2)CxF C CyF W T(b-1) Ay F Ax F 'BF 'C F C 'DF A D ED F EF 'E F E BB F CF C D(c) A F A D G FC HF H(a)B F BC 'C F D'D F Ax F Ay F A (a-1)1－5 试画出图示结构中各杆的受力图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
工程力学
（静力学与材料力学）
习题详细解答
（教师用书） (第 12 章) 范钦珊 唐静静
2006-12-18
1
第 12 章 动载荷与疲劳强度简述
12－1 图示的 No.20a 普通热轧槽钢以等减速度下降，若在 0.2s 时间内速度由 1.8m/s 降至 0.6m/s，已知 l=6m，b=1m。试求槽钢中最大的弯曲正应力。
⎛
⎞ 2F l
12－6
试确定下列各题中轴上点 B 的应力比：
1．图 a 为轴固定不动，滑动绕轴转动，滑轮上作用着不变载荷 FP；
习题 12－6 图
2．图 b 为轴与滑轮固结成一体面转动，滑轮上作用着不变载荷 FP。
解：1．B 点受到是静应力，即
σ max = σ min ， r =
σ min =1 σ max
12－2 钢制圆轴 AB 上装有一开孔的匀质圆盘如图 所示。圆盘厚度为 δ ，孔直径 D=300mm。圆盘和轴一起 以匀角速度 ω 转动。若已知： δ =30mm，a=1000mm， e=300mm；轴直径 d=120mm， ω =40rad/s；圆盘材料密 度 ρ = 7.8 × 103 kg m3 。 试求由于开孔引起的轴内最大弯曲 正应力（提示：可以将圆盘上的孔作为一负质量（-m） ， 计算由这一负质量引起的惯性力） 。 解：因开孔引起的惯性力： π FI = meω 2 = ρ × × D 2 × δ × eω 2 4
3
解： （1）计算静应力
σ=
P 4 × 5 × 10 3 = = 0.071MPa A π × 300 2
（2）计算动荷系数
kd = 1 + 1 + 2H
δj
δj =
5 × 10 3 × 6 × 10 3 = 0.0424 π × 300 2 3 10 × 10 × 4 2 × 1000 kd = 1 + 1 + = 218 0.0424 Pl = EA
12－3 质量为 m 的匀质矩形平板用两根平行且等长的轻杆悬挂着，如图所示。已知平 板的尺寸为 h、l。若将平板在图示位置无初速度释放，试求此瞬时两杆所受的轴向力。
FA
30o 30o
A
B
n
FI
30o
h
aτ O
D
O
C
mg
l
习题 12－3 图 习题 12－3 解图
解：平板作曲线平移，初瞬时 ω = 0 ，只有加速度 aO 惯性力 τ FI = maO g o τ τ ∑ Ft = 0 ， mg sin 30 − maO = 0 ， aO = 2 l o h o l o ∑ M A ( F ) = 0 ， − mg ⋅ + FI cos 30 ⋅ + FI sin 30 ⋅ + FB cos 30 ⋅ l = 0 2 2 2
4
kd = 1 + 1 +
2H
δj
δj =
4 Pl 3 243EI 243EI 2 Pl 3
kd = 1 + 1 +
（2）最大静荷应力与梁中点静挠度
0 σ max =
M C 2 FP l = 9W W 3 23FP l 0 ＝ w中 1296EI
（3）最大动荷应力与梁中点的挠度
243EI 0 ⎟ P σ d max = k d σ max =⎜ ⎜1 + 1 + 2 Pl 3 ⎟ 9W ⎝ ⎠ ⎛ 243EI 0 d + + 1 1 w中 ＝k d w 中 =⎜ ⎜ 2 Pl 3 ⎝ ⎞ 23FP l 3 ⎟ ⎟ 1296EI ⎠
习题 12－7 图
解：
1．偏心质量产生的惯性力，使圆轴有对称循环的弯矩，所以 B 点受对称循环交变应力
σ max = −σ min ，
r=
σ min = −1 σ max
2．旋转轴上 AC 段产生的惯性力，对 B 点始终受不变的拉应力，即
σ max = σ min
r=
σ min =1 σ max
3．当振形为最低部曲线时，B 点有 σ max ，最高部位时有 σ min ，而
τ
（1）
将 FI =
1 mg 代入上式，得 2
FB =
mg ( 3l − h) 4l
（2）
o ∑ Fn = 0 ， FA + FB − mg cos 30 = 0 ，
FA =
mg ( 3l + h) 4l
（3）
12－4 重量=5kN 的物体自由下落在直径为 300mm 的圆木柱上。木材的 E=10GPa。试 求木柱内的最大正应力。若在柱上端垫以直径与木柱相同、厚度为 20mm 的橡皮，假设橡 皮的受力与变形近似满足胡克定律，且其 E=8.0MPa，则木柱内的最大正应力减至多少?
σ max δ + a = σ min δ − a
r=
σ min δ − a = σ max δ + a
4．齿轮上的点受到脉动交变应力，即
σ max ≠ 0 ， σ min ≠ 0
r=
σ min =0 σ max
上一章
返回总目录
6
总的均布载荷集度：
q = q1 + q 2 = ρ ( g + a)
弯矩：
8 M C = M max = −q × 4 × 2 + q × × 3 = q × 4 = 4 ρ ( g + a) 2 =4×22.63(9.8+6)=1430 N·m 槽钢横截面上的最大正应力 M 1430 σ d max = C = = 59.1 MPa Wmin 24.2 × 10 −6
2．B 点受到是对称循环交变应力，即
σ max = −σ min ， r =
σ min = −1 σ max
5
12－7
确定下列各题中构件上指定点 B 的应力比：
1．图 a 为一端固定的圆轴，在自由端处装有一绕轴转动的轮子，轮上有一偏心质量 m。 2．图 b 为旋转轴，其上安装有偏心零件 AC。 3．图 c 为梁上安装有偏心转子电机，引起振动，梁的静载挠度为 δ ，振辐为 a。 4．图 d 为小齿轮（主动轮）驱动大齿轮时，小齿轮上的点 B。
2 习题 12－2 图
由此引起的附加动反力：
FI 2 动载荷引起的附加最大动弯矩发生在 C 截面，其值为： 1 M max = FA a = FI a 2 于是最大附加弯曲动应力： a π 2 2 M dmax 2 ⋅ 4 ρ D ⋅ δ eω σ dmax = = = 22.4 MPa πd 3 W 32 FA = FB =
q 1m A
6m C
B 1m
MA
A
习题 12－1 图
MB
B
a
v
MC
习题 12－1 解图
解：No.20a 槽钢的线密度 ρ = 22.63 kg/m 加速度 0.6 − 1.8 a= = −6 m/s2 0.2 由自重引起的均布载荷集度：
q1 = ρg (↓)
由惯性力引起的均布载荷集度：
q 2 = ρa (↓) (加速度↑)
习题 12－4 图
（3）动应力
σ d max = k d σ = 218 × 0.071 = 15.47 MPa
（4）加橡皮后的动荷系数： 假设橡皮的力和变形近似满足胡克定律，故橡皮变形量为
3 Δ = 5 × 10 × 20 = 0.177 π × 300 2 8× 4
kd = 1 + 1 +
2 × 1000 = 1 + 95.57 = 96.57 0.219
σ d max = k d σ = 96.57 × 0.071 = 6.78MPa
加橡皮后，的重物自由下落在图示梁上。设梁的抗弯刚度 EI 及抗弯截面系数 W 已知。试求梁内的最大正应力及梁跨度中间截面的挠度。
FP
习题 12－5 图
解： （1）计算动荷系数