多种人口预测方法汇总
人口预测的几种方法

人口预测的几种方法附录A 重要技术方法附表A1 土地需求预测的步骤与方法一、人口预测在调查分析规划期间人口数量、构成及动态变化趋势的基础上,测算总人口、城镇人口、农村居民点人口增长变化规模。
(一)总人口预测1、人口变动比较稳定地区的人口预测法在人口变动比较稳定的地区,可采用自然平均增长法预测。
计算公式如下:PN=P0(1+K)n±ΔP式中:PN──规划目标年总人口(人)P0──规划基期年总人口(人)K──规划期间人口自然增长率(%)N ──规划年限(年)ΔP──规划期间人口机械增长数(人)人口自然增长率应根据计划生育指标,分析人口年龄与性别构成状况予以确定。
人口机械增长,宜按平均增长法计算,依公安部门统计的多年人口净迁入(出)量计算平均值,并分析影响机械增长的因素予以确定。
2、人口变动不稳定地区的人口预测法在人口变动不稳定的地区,应分析人口变动因素,采用适当方法测算。
计算公式如下:ΔP=A〔W c(1- W双/2)〕C + W单式中:ΔP──新建项目人口机械增长数A ──新建项目迁入职工总数W c──带眷职工占职工总数的比例(%)W双──双职工占带眷职工的比例(%)C──带眷系数W单──单身职工人数3、受资源、生态条件严重制约地区的人口预测方法应按环境容量法确定适宜的人口规模。
计算公式如下:P MAX=MIN{P1max,P2max,P3max,…,P imax,…}式中:P MAX──城市的极限人口P imax──自然资源、生态条件供给能力和某项基础设施支持能力的最大值(二)城镇与乡村人口预测1、一般预测方法城镇人口是指城市、建制镇建成区范围内常住人口。
常住人口指实际居住在某地区一定时间(指半年以上)的人口,包括:除离开本地半年以上(不包括在国外工作或学习的人)的全部常住本地的户籍人口;户口在外地,但在本地居住半年以上者,或离开户口地半年以上而调查时在本地居住的人口;调查时居住在本地,但在任何地方都没有登记常住户口,如手持户口迁移证、出生证、退伍证、劳改劳教释放证等尚未办理常住户口的人。
人口预测方法

人口预测方法人口预测是指通过各种统计方法和模型来预测未来其中一地区或全球的人口规模及其结构的变化趋势。
人口预测对于制定政府的经济、社会和城市规划等方面具有重要意义。
下面将综述几种常用的人口预测方法。
1.经验法(目测法)经验法是最简单的人口预测方法,通常是通过从过去的数据中观察到的趋势来推测未来的人口变化。
这种方法主要是基于历史数据和经验知识,没有复杂的统计和推理模型。
往往被用于近期短期的人口预测。
2.简单线性回归法简单线性回归法是基于线性回归模型的一种方法。
这种方法认为人口和时间是呈线性关系的,通过拟合历史数据的线性回归方程来进行预测。
然而,这种方法并未考虑到时间序列数据的非线性特征。
3.复杂线性回归法与简单线性回归法类似,复杂线性回归法采用更多的变量来构建回归模型。
这些变量可以是经济指标、社会指标、环境指标等。
通过考虑更多的因素,人口预测的准确性可以得到一定提高。
4.ARIMA模型ARIMA模型是一种基于时间序列分析的方法,其模型包括自回归(AR)、差分(I)和滑动平均(MA)三个部分。
这种方法相对来说更为复杂,但可以更好地处理时间序列数据中的趋势、季节性和随机性。
5.灰色关联度预测模型灰色关联度预测模型是一种非线性、非统计的预测方法。
它通过建立灰色模型,将历史数据和未知因素进行内部关联和外部关联计算,得到一个相对准确的预测结果。
这种方法适用于样本数据不多,变化规律较为复杂的情况。
6.基于机器学习的方法随着机器学习的发展,越来越多的人口预测方法开始采用机器学习的算法。
例如,支持向量机(SVM)、人工神经网络(ANN)和决策树等。
这些方法可以通过更大规模的数据和更多的特征来进行预测,提高预测的准确性。
总结起来,人口预测方法可以分为经验法、线性回归法、ARIMA模型、灰色关联度预测模型和基于机器学习的方法等。
每种方法都有其适用的场景和局限性,需要根据具体情况选择合适的预测方法。
随着数据的增多和技术的发展,人口预测的准确性也将不断提高,这对于社会经济的发展和规划具有重要意义。
人口预测的数学模型与预测方法分析

人口预测的数学模型与预测方法分析人口预测是对未来一定时期内人口数量和结构的变动进行估计和预测的过程。
人口预测在社会经济发展规划、城市规划、教育医疗资源配置等方面具有重要的参考价值。
为了准确预测人口的变动趋势,需要建立合理的数学模型和选择适当的预测方法。
人口预测的数学模型主要包括线性回归模型、指数模型、Logistic模型等。
线性回归模型是一种用来描述两个变量之间线性关系的统计模型,可以用来预测人口随时间的变化。
指数模型假设人口数量按照指数规律增长或减少,适用于人口增长较快的情况。
Logistic模型则适用于人口增长速度放缓后的情况,它是一种描述增长速度逐渐趋近于饱和的模型。
在选择数学模型时,需要综合考虑以下几个因素:人口历史变动趋势、人口自然增长率、人口迁移和流动情况、政策调控等因素。
同时,还需根据实际情况对模型的参数进行合理的设定和修正,以提高预测的准确性。
在预测方法上,常用的有趋势线法、复合增长率法、比较推理法、时间序列分析法和系统动力学方法等。
趋势线法是基于历史数据的发展趋势来进行预测,适用于人口变动趋势比较稳定的情况。
复合增长率法是将历史数据中的增长率按一定规则进行加权平均,再用来推算未来人口的增长率。
比较推理法通过对不同因素的比较和推理,来估计未来人口的变化。
时间序列分析法是根据时间序列数据的历史模式来预测未来的变化趋势。
系统动力学方法则是通过对不同因素的动态关系建立模型,用来探索人口变动的内在机制和规律。
在具体应用时,可以结合不同的数学模型和预测方法,进行多角度的分析和预测。
同时,还需要不断对模型进行修正和优化,以适应不断变化的人口变动趋势和社会经济背景。
此外,还应该注意对预测结果的不确定性进行评估和把握,提供多种可能性的预测结果,为决策者提供科学的参考依据。
人口预测方法范文

人口预测方法范文人口预测是指根据已有的人口数据,运用各种统计方法和模型来估计未来人口的变化趋势和规模。
人口预测对于制定社会经济发展规划、推进公共政策以及资源分配等方面具有重要意义。
以下将介绍几种常见的人口预测方法。
1.线性回归法线性回归法是一种基本的、广泛应用的预测方法,它建立了人口数量与一组解释变量(例如,年份、年龄结构、生育率、死亡率等)之间的线性关系模型。
通过拟合这一模型,可以得到一条直线来预测未来人口的变化趋势。
2.指数平滑法指数平滑法是一种基于历史数据加权的预测方法。
其核心思想是过去的数据对未来的预测具有不同的影响力,越近期的数据权重越大。
指数平滑法通过对历史数据按照一定的权重进行加权平均,得到一个平滑的趋势线,进而预测未来的人口变化。
3.ARIMA模型ARIMA(AutoRegressive Integrated Moving Average)模型是一种时间序列预测方法,它考虑到人口数量可能受到前期数据的影响,并结合时间序列的平稳性来建立预测模型。
ARIMA模型包括自回归(AR)、差分(I)和滑动平均(MA)三个阶段。
通过这三个阶段的组合,可以较准确地预测未来人口的变化。
4. Gompertz模型Gompertz模型是一种常用的人口增长模型,它是基于生物学定律的人口模型,认为人口增长率与人口的大小成正比。
Gompertz模型假设人口增长率在恒定的出生率和死亡率条件下呈指数衰减的趋势。
通过拟合Gompertz模型,可以预测未来人口的增长速度和规模。
5.人口脉冲响应模型人口脉冲响应模型是一种基于协方差函数的人口预测方法,它通过分析人口数量与其他社会经济因素之间的关系,利用协方差函数来描述它们之间的时滞效应。
通过测量不同因素对人口的影响,可以预测未来人口的变化情况。
除了上述方法,还有许多其他的人口预测方法,如人口动态模型、时间序列分析、人口合理预测模型等。
每种方法都有其适用的场景和条件,可以根据具体情况选择合适的方法进行人口预测。
城市人口预测方法

城市人口预测方法人口预测是指以人口现状为基础,对未来人口的发展趋势提出合理的控制要求和假定条件,即参数条件来获得对未来人口数据提出预报的技术或方法。
城市人口预测是城市总体规划的首要工作,它既是城市规划的目标,又是确定总体规划中的具体技术指标与城市合理布局的前提和依据,因此合理预测城市人口对城市的总体规划和城市的可持续发展有着十分重要的意义。
1、含义城市人口预测(urban population forecast)是对未来一定时期内城市人口数量和人口构成的发展趋势所进行的测算。
2、传统人口预测方法传统的人口预测方法包括平均增长率法、带眷系数法、剩余劳动力转化法和劳动平衡法等。
1)平均增长率法在城市进行总体规划时,对人口规模预测的常见方法之一为平均增长率法,计算时应分析近年来人口的变化情况,确定每年的人口增长率。
人口规模预测公式为:P = P0 (1 + K1 + K2)n。
式中,P为规划期末城市人口规模,P0 为城市现状人口规模,K1 为城市年平均自然增长率,K2 为城市年平均机械增长率,n 为规划年限。
这种方法适合初步经济发展稳定的城市,人口增长会逐步增加,人口增长率变化不大。
但是随着人口基数的增大,人口结构逐步趋于老龄化,人口增长的速度将会越来越慢,不可能都以平均的速度增长。
若要考虑到未来社会经济发展等因素对人口变动的影响,则可按预见的趋势改变人口增长率进行测算。
该方法具有普遍的适用性,但它对人口增长率的精度要求较高。
2)带眷系数法带眷系数法是根据新建工业项目的职工数及带眷情况计算的。
当建设项目已经落实,规划期内人口机械增长稳定的情况下,宜按带眷系数法计算人口发展规模。
计算时应分析从业人员的来源、婚育、落户等状况以及城镇的生活环境和建设条件等因素,确定增加的从业人员及其带眷系数。
具体预测公式为:P =P1 (1 + a) + P2 + P3。
式中,P为规划期末城镇人口规模,P1 为带眷职工人数,a 为带眷系数,P2 为单身职工人数,P3 为规划期末城镇其他人口数。
人口预测方法(总结)
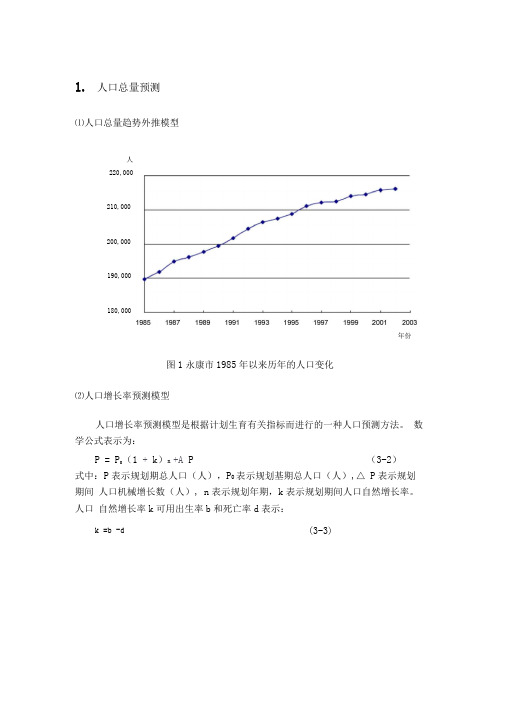
1. 人口总量预测⑴人口总量趋势外推模型图1永康市1985年以来历年的人口变化⑵人口增长率预测模型人口增长率预测模型是根据计划生育有关指标而进行的一种人口预测方法。
数学公式表示为:P = P 0(1 + k )n +A P (3-2)式中:P 表示规划期总人口(人),P 0表示规划基期总人口(人),△ P 表示规划期间 人口机械增长数(人), n 表示规划年期,k 表示规划期间人口自然增长率。
人口 自然增长率k 可用出生率b 和死亡率d 表示:(3-3)人 220,000k =b -d210,000200,000190,000180,000年份年份永康市1989年以来历年的人口出生率、死亡率和自然增长率%图3永康市1989年以来历年的户籍人口迁移数量(3)人口离散预测模型人口离散预测模型也即人口差分方程预测模型,又称“宋健模型”,是我国自行提出的比较成功的人口发展预测模型,能较好的运用人口普查资料对未来人口进行预测。
该模型是根据分年龄的人口结构递推公式进行预测,模型的数学表达如下:r2X o(t)=[1-4oo(t)] ^(t)送h i(t) k i(t) X(t) (3_6)XF(t +1)=[1-B(t)] "Xe + fe i =0,12..,m—1式中:X o(t)为t年代O岁出生婴儿数,X i(t)为t年代之年龄组人口数,卩oo(t)为t 年出生婴儿当年死亡率,P(t)为妇女总和生育率,即社会人中平均意义下一个妇女在整个育龄时期的生育总数(「2, r1即为生育年龄的上下限),h i(t)为生育模式,反映某一地区某一个育龄妇女生育状态分布,k i(t)为t年代之年龄组女性性别比,M(t)为t年代之年龄组人口死亡率,f i(t)为t年代之年龄组净迁移数。
在模型的具体应用中,课题组工作的重点是如何确定公式3-6中的各种参数。
①第五次人口普查资料中的数据是2000年11月1日的数据,而规划所需的数据是年末的数据,课题组将普查的户籍人口分龄人口数按比例修正到2000年底的统计人口总数作为X i(t);②从普查资料来看45岁以下的性别比比较稳定,为了简化模型,t年代之年龄组女性性别比k i(t)用常量k表示,即采用普查资料中的45岁以下的男女性别比=104.85(女性=100)推算,故k= 0.488326;③根据普查资料,妇女总和生育率取2000年的数据P(t)= 0.8795;④模型中出生婴儿当年死亡率Moo(t)假定与2000年出生婴儿当年死亡率的80%,即采用4OO=3.88%O。
规划人口预测方法

规划人口预测方法
人口预测是基于现有的人口数据和一定的假设条件来预测未来人口数量和结构的变化。
以下是一些常见的人口预测方法:
1.基于趋势分析:根据历史人口数据的变化趋势,通过统计分析和数学模型来预测未来的人口走势。
2.基于复发方法:根据人口出生率、死亡率和迁移率等指标,结合历史数据和概率模型,来预测未来的人口变化。
3.基于整体模型:根据国民经济、社会发展和政策变化等因素,构建数学模型,通过模拟和推演预测未来的人口变化。
4.基于区域模型:考虑到不同地区的人口变化趋势可能存在差异,根据区域特定的经济、社会和环境因素,建立区域性的人口模型来预测未来的人口走势。
5.基于专家判断:借助专家的经验和知识,结合相关指标和数据,通过专家评估和判断来预测未来的人口情况。
需要注意的是,人口预测方法的选择取决于可用的数据、研究目的和预测的时间范围等因素。
同时,人口预测结果也受到多个外部因素的影响,如经济发展、社
会政策、自然灾害等。
因此,在进行人口预测时,需要综合考虑各种因素和不确定性,并持续更新和修正预测模型。
人口预测方法(情况总结)
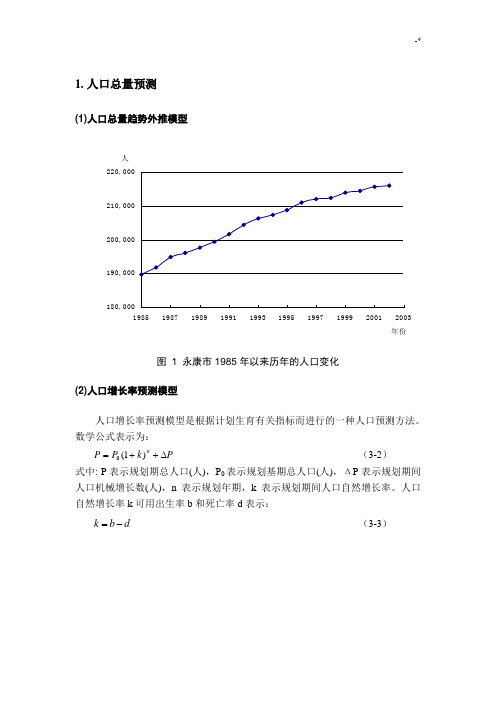
1. 人口总量预测(1)人口总量趋势外推模型图 1 永康市1985年以来历年的人口变化(2)人口增长率预测模型人口增长率预测模型是根据计划生育有关指标而进行的一种人口预测方法。
数学公式表示为:+1(=)+PP n∆kP(3-2)0式中: P表示规划期总人口(人),P0表示规划基期总人口(人),ΔP表示规划期间人口机械增长数(人),n表示规划年期,k表示规划期间人口自然增长率。
人口自然增长率k可用出生率b和死亡率d表示:=(3-3)k-db图 2 永康市1989年以来历年的人口出生率、死亡率和自然增长率图3 永康市1989年以来历年的户籍人口迁移数量(3)人口离散预测模型人口离散预测模型也即人口差分方程预测模型,又称“宋健模型”,是我国自行提出的比较成功的人口发展预测模型,能较好的运用人口普查资料对未来人口进行预测。
该模型是根据分年龄的人口结构递推公式进行预测,模型的数学表达如下:1,...,2,1,0)()()](1[)1()()()()()](1[)(100021-=+⋅-=+⋅⋅⋅⋅-=+∑m i t f t X t t X t X t k t h t t t X i i i i r r i i i μβμ (3-6)式中:X 0(t)为t 年代0岁出生婴儿数,X i (t)为t 年代之年龄组人口数,μ00(t)为t 年出生婴儿当年死亡率,β(t)为妇女总和生育率,即社会人中平均意义下一个妇女在整个育龄时期的生育总数(r 2,r 1即为生育年龄的上下限),h i (t)为生育模式,反映某一地区某一个育龄妇女生育状态分布,k i (t)为t 年代之年龄组女性性别比,μi (t)为t 年代之年龄组人口死亡率,f i (t)为t 年代之年龄组净迁移数。
在模型的具体应用中,课题组工作的重点是如何确定公式3-6中的各种参数。
①第五次人口普查资料中的数据是2000年11月1日的数据,而规划所需的数据是年末的数据,课题组将普查的户籍人口分龄人口数按比例修正到2000年底的统计人口总数作为X i (t);②从普查资料来看45岁以下的性别比比较稳定,为了简化模型,t 年代之年龄组女性性别比k i (t)用常量 k 表示,即采用普查资料中的45岁以下的男女性别比=104.85(女性=100)推算,故k= 0.488326;③根据普查资料,妇女总和生育率取2000年的数据β(t)= 0.8795;④模型中出生婴儿当年死亡率μ00(t)假定与2000年出生婴儿当年死亡率的80%,即采用μ00=3.88‰。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人口预测方法
人口预测模型的适用性,是决定预测结果的科学性和是否符合人口发展的趋势的先决条件。
人口预测作为人口研究中的重要方面,近年来其预测方法的发展很快,主要的预测方法分为用微分方程方法预测的Logistic 模型,用数理统计方法预测的线性回归模型,用矩阵方法预测的Leslie 模型,具体又包括了人口增长率法、Logistic 模型、Leslie 模型、一元线性回归预测、多元回归预测、自回归法、指数函数法、幂函数法、系统动力学以及适用更为广泛的灰色系统GM(1,1)模型预测等主要方法。
(1) 人口增长率法
人口增长率法是利用所选定的人口增长数学公式,根据基数人口总数,按照一定的人口增长速度推算未来时期人口总数的方法。
该法要求人口增长符合算数增长规律,还要求未来人口净增长量或增长速度大小方向均不变(至少相对稳定),其常用的推算公式为:00(1)n p p r n =+或0n p p mn =+。
(2) Logistic 模型
Logistic 模型增长公式为:(1)a bt t m p p e +=+,其中t p 为时刻的人口总数,m p 为人口极限规模,e 为自然对数的底,t 为时刻长度,a 、b 为待定参数。
Logistic 模型考虑到人口总数增长的有限性,提出了人口总数增长的规律即随着人口总数的增长,人口增长率逐渐下降,但对于在短期内如30-50年内人口增长可能呈上升趋势如人口生育率上升、死亡率下降等原因而导致人口呈上升趋势。
Logistic 模型在应用中对时间长,人口数据变化大,因此误差较大且不稳定。
而小城镇人口的变化就存在人口数据变化较大的特点,所以Logistic 模型对小城镇人口的预测并不适合。
(3) Leslie 模型
Leslie 模型不受短期外界因素的影响,对于中长期预测中具有很大的优势,尤其对人口转折时期的预测具有较高的精度,其模型为:()(1)k k P LP -=。
(4) 一元线性回归法
人口发展过程中线上任一点的切线斜率基本保持不变,即各时期人口发展速度较一致,这里将时间作为控制变量,人口数量作为状态变量,确定它们之间的数学模型y a bx =+,其中a y b x =-,22[()()(/)
()/]i i i i i i b x y x y n x x n =--∑∑∑∑∑,一元线性回归法所预测的结果往往与实际结果相
比较低。
(6) (5) 幂函数法 幂函数法主要是适用于人口发展前期较快,后期逐渐减少的情况。
其预测方程为:b y ax =。
(6) 指数函数法
有些地区的人口发展前一段时期较慢,越往后发展速度越快,如城市人口的发展,这种情况下一般选用指数函数模型:0()rt p t p e = ,其中()p t 为时刻的人口总数,0p 为起始时刻的人口总数,r 为人口增长率,t 为时间长度。
(7) 灰色系统GM (1,1)模型
部分信息已知、部分信息未知的系统,称为“灰色系统”。
灰色系统GM (1,1)模型预测的特点是单数列预测,它把受众多因素影响,而又无法确定那些复杂关系的量,称为灰色量,其预测模型为:()(1)[(1)/]/ak x k x u a e u a -+=-+ 。
各种人口预测的方法都具有自身的优点和适用范围,对于不同变化规律的人口发展预测都可以准确的预测出结果,但是每一种方法都有自身的适用范围,在具体方法的选择上必须结合所预测地区的特点,占有数据量的多少,预测时段的长短来选择最合适的方法,以求预测的准确性和实用性。
