计量经济学 实验一 一元线性回归 完成版
计量经济学实验一 一元回归模型
实验二一元回归模型【实验目的】掌握一元线性、非线性回归模型的建模方法【实验内容】建立我国税收预测模型【实验步骤】【例1】建立我国税收预测模型。
表1列出了我国1985-1998年间税收收入Y和国内生产总值(GDP)x的时间序列数据,请利用统计软件Eviews建立一元线性回归模型。
一、建立工作文件⒈菜单方式在录入和分析数据之前,应先创建一个工作文件(Workfile)。
启动Eviews软件之后,在主菜单上依次点击File\New\Workfile(菜单选择方式如图1所示),将弹出一个对话框(如图2所示)。
用户可以选择数据的时间频率(Frequency)、起始期和终止期。
图1 Eviews菜单方式创建工作文件示意图图2 工作文件定义对话框本例中选择时间频率为Annual(年度数据),在起始栏和终止栏分别输入相应的日期85和98。
然后点击OK,在Eviews软件的主显示窗口将显示相应的工作文件窗口(如图3所示)。
图3 Eviews工作文件窗口一个新建的工作文件窗口内只有2个对象(Object),分别为c(系数向量)和resid(残差)。
它们当前的取值分别是0和NA(空值)。
可以通过鼠标左键双击对象名打开该对象查看其数据,也可以用相同的方法查看工作文件窗口中其它对象的数值。
⒉命令方式还可以用输入命令的方式建立工作文件。
在Eviews软件的命令窗口中直接键入CREATE命令,其格式为:CREATE 时间频率类型起始期终止期本例应为:CREATE A 85 98二、输入数据在Eviews软件的命令窗口中键入数据输入/编辑命令:DA TA Y X此时将显示一个数组窗口(如图4所示),即可以输入每个变量的数值图4 Eviews数组窗口三、图形分析借助图形分析可以直观地观察经济变量的变动规律和相关关系,以便合理地确定模型的数学形式。
⒈趋势图分析命令格式:PLOT 变量1 变量2 ……变量K作用:⑴分析经济变量的发展变化趋势⑵观察是否存在异常值本例为:PLOT Y X⒉相关图分析命令格式:SCAT 变量1 变量2作用:⑴观察变量之间的相关程度⑵观察变量之间的相关类型,即为线性相关还是曲线相关,曲线相关时大致是哪种类型的曲线说明:⑴SCAT命令中,第一个变量为横轴变量,一般取为解释变量;第二个变量为纵轴变量,一般取为被解释变量⑵SCAT命令每次只能显示两个变量之间的相关图,若模型中含有多个解释变量,可以逐个进行分析⑶通过改变图形的类型,可以将趋势图转变为相关图本例为:SCA T Y X图5 税收与GDP趋势图图5、图6分别是我国税收与GDP时间序列趋势图和相关图分析结果。
计量经济学上机实验

计量经济学上机实验上机实验一:一元线性回归模型实验目的:EViews软件的基本操作实验内容:对线性回归模型进行参数估计并进行检验上机步骤:中国内地2011年中国各地区城镇居民每百户计算机拥有量和人均总收入一.建立工作文件:1.在主菜单上点击File\New\Workfile;2.选择时间频率,A3.键入起始期和终止期,然后点击OK;二.输入数据:1.键入命令:DATA Y X2.输入每个变量的统计数据;3.关闭数组窗口(回答Yes);三.图形分析:1.趋势图:键入命令PLOT Y X2.相关图:键入命令 SCAT Y X 散点图:趋势图:上机结果:Yˆ11.958+0.003X=s (βˆ) 5.6228 0.0002t (βˆ) 2.1267 11.9826prob 0.0421 0.00002=0.831 R2=0.826 FR=143.584 prob(F)=0.0000上机实验二:多元线性回归模型实验目的:多元回归模型的建立、比较与筛选,掌握基本的操作要求并能根据理论对分析结果进行解释实验内容:对线性回归模型进行参数估计并进行检验上机步骤:商品的需求量与商品价格和消费者平均收入趋势图:散点图:上机结果:i Yˆ=132.5802-8.878007X1-0.038888X2s (βˆ) 57.118 4.291 0.419t (βˆ) 2.321 -2.069 -0.093prob 0.0533 0.0773 0.9286 R2=0.79 R2=0.73 F =13.14 prob(F)=0.00427三:非线性回归模型实验目的:EViews软件的基本操作实验内容:对线性回归模型进行参上机步骤:我国国有独立核算工业企业统计资料一.建立工作文件:1.在主菜单上点击File\New\Workfile;2.选择时间频率,A3.键入起始期和终止期,然后点击OK;二.输入数据:1.键入命令:DATA Y L K2.输入每个变量的统计数据;3.关闭数组窗口(回答Yes);三.图形分析:1.趋势图:键入命令PLOT Y K L2.相关图:键入命令 SCAT Y K L四.估计回归模型:键入命令LS Y C K L上机结果:Y =4047.866K1.262204L-1.227157s (βˆ) 17694.18 0232593 0.759696t (βˆ) 0.228768 5.426669 -1.615325prob 0.8242 0.0004 0.1407R2=0.989758 R2=0.987482 F=434.8689 prob(F)=0.0000上机实验四:异方差实验目的::掌握异方差的检验与调整方法的上机实现实验内容:我国制造工业利润函数行业销售销售行业销售销售实验步骤:一.检验异方差性1.图形分析检验:1) 观察Y、X相关图:SCAT Y X2) 残差分析:观察回归方程的残差图LS Y C X在方程窗口上点击Residual按钮;2. Goldfeld-Quant检验:SORT XSMPL 1 10LS Y C X(计算第一组残差平方和)SMPL 19 28LS Y C X(计算第二组残差平方和)计算F统计量,判断异方差性3.White检验:SMPL 1 28LS Y C X在方程窗口上点击:View\Residual\Test\White Heteroskedastcity 由概率值判断异方差性。
计量经济学实验报告

一、实验目的及要求:1、目的利用EVIEWS 实验软件,使学生在实验过程中全面了解和熟悉计量经济学的基本概念,熟悉一元线性回归模型估计的基本程序和基本方法。
2、内容及要求(1) 熟悉EVIEWS实验软件的基本操作程序和方法; (2) 掌握一元线性回归模型基本概念,了解其估计和检验原理 (3) 提交实验报告二、仪器用具:三、实验结果与数据处理:1下面是利用1970-1980年美国数据得到的回归结果。
其中Y 表示美国咖啡消费(杯/日.人),X 表示平均零售价格(美元/磅)。
注:262.2)9(2/=αt ,228.2)10(2/=αt6628.006.42)()1216.0(4795.06911.2ˆ2===-=R t se X Y tt)(值1. 写空白处的数值。
12. 对模型中的参数进行显著性检验。
3. 解释斜率系数1β的含义,并给出其95%的置信区间。
解:(1)1308.221216.06911.2)(00===ββse t0114.006.424795.0)(11-=-==tse ββ(2)用t 检验法分别对模型中的参数0β1β进行显著性水平检验: 在5%的显著性水平下,模型的自由度为11-2=9,且262.2)9(025.0=t 由于262.21308.220>=βt ,故该模型的截距项在统计上是显著的; 同理 262.206.421>=βt ,即斜率系数在统计上也是显著的。
(3)斜率系数4795.01-=β,小于0,在其他条件不变的情况下,咖啡的平均零售价格每增加一个单位,美国咖啡的日消费将平均减少0.4795个单位,说明咖啡的消费量与其平均零售价格呈负相关关系。
1β的95%的置信区间为:]4537.0,5053.0[)]ˆ(ˆ),ˆ(ˆ[12/112/1--+-即ββββααse t se t2美国各航空公司业绩的统计数据公布在《华尔街日报1999年年鉴》(The Wall Street Journal Almanac 1999)上。
计量经济学一元线性回归作业

计量经济学实验报告姓名孙晓晗学号0842226 班级经济管理学院上机时间:2010-10-19 上机地点:实验楼A105上机目的:熟悉EVIEWS的基本操作,以及学习一元线形回归模型的简单建立标题一、研究的问题研究随着GDP的变化国家财政收入会如何变化,从而研究GDP 与国家财政收入的关系。
二、对问题的经济理论分析、所涉及的经济变量财政收入是政府部门的公共收入,是国民收入分配中用于保证政府行使其公共职能、实施公共政策及提供公共服务的资金需求。
其主要有资源配置、收入再分配和宏观经济调控三大职能。
财政收入的增长情况关系着一个国家经济的发展和社会的进步。
因此,研究财政收入的增长就显得尤为必要。
财政收入的增长受到多方面因素的影响,但最根本的原因是经济的总体发展态势,即GDP的增长。
因此,此次分析涉及到GDP和国家财政收入两个经济变量。
三、理论模型的建立以财政收入(CZSR)为被解释释变量,GDP为解释变量,构造回归模型:Y i=b0+b1X i+u i四、相关变量的数据收集及数据来源说明数据来源于中华人民共和国国家统计局,网址为:/五、数据的计算机输入及运行过程、模型的结果1.数据输入,给变量赋值2.获得X与Y的散点图3.建立一元线性回归方程六、模型检验、对结果的解释及说明1.检验(1)经济模型意义检验由建立一元线性回归方程结果可得:Y i=389.5147+0.116157Xa.正负号由建立回归方程结果可得b1=0.116157,为正值,说明国家财政收入按照小于1的正比例随GDP增长,因此此值在经济学上有意义。
b.斜率大小由建立回归方程结果可得b0=389.5147,有较好的经济学含义。
(2)统计学检验a.拟合优度检验R2=1.94,说明回归方程与样本观察值拟合优度很好。
b.T检验Prob(t-Statistic)=0.45〉5%,不通过检验c.F检验Prob(F-Statistic)=0.00001〈5%,通过检验七、用模型就现实问题进行分析(一)财政收入占GDP的比重低且比重总体呈下降的趋势从世界各国的情况分析,财政收入占GDP的比重随经济发展而渐渐提高。
计量经济学 第二章 一元线性回归模型
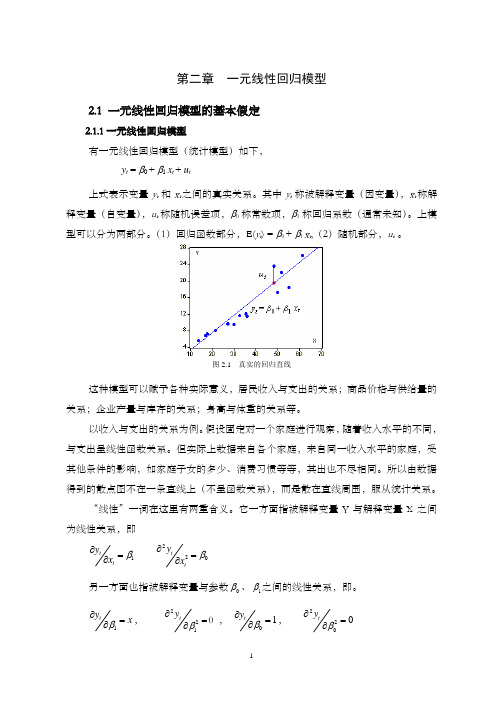
第二章 一元线性回归模型2.1 一元线性回归模型的基本假定2.1.1一元线性回归模型有一元线性回归模型(统计模型)如下, y t = β0 + β1 x t + u t上式表示变量y t 和x t 之间的真实关系。
其中y t 称被解释变量(因变量),x t 称解释变量(自变量),u t 称随机误差项,β0称常数项,β1称回归系数(通常未知)。
上模型可以分为两部分。
(1)回归函数部分,E(y t ) = β0 + β1 x t ,(2)随机部分,u t 。
图2.1 真实的回归直线这种模型可以赋予各种实际意义,居民收入与支出的关系;商品价格与供给量的关系;企业产量与库存的关系;身高与体重的关系等。
以收入与支出的关系为例。
假设固定对一个家庭进行观察,随着收入水平的不同,与支出呈线性函数关系。
但实际上数据来自各个家庭,来自同一收入水平的家庭,受其他条件的影响,如家庭子女的多少、消费习惯等等,其出也不尽相同。
所以由数据得到的散点图不在一条直线上(不呈函数关系),而是散在直线周围,服从统计关系。
“线性”一词在这里有两重含义。
它一方面指被解释变量Y 与解释变量X 之间为线性关系,即1tty x β∂=∂220tt y x β∂=∂另一方面也指被解释变量与参数0β、1β之间的线性关系,即。
1ty x β∂=∂,221ty β∂=∂0 ,1ty β∂=∂,2200ty β∂=∂2.1.2 随机误差项的性质随机误差项u t 中可能包括家庭人口数不同,消费习惯不同,不同地域的消费指数不同,不同家庭的外来收入不同等因素。
所以在经济问题上“控制其他因素不变”是不可能的。
随机误差项u t 正是计量模型与其它模型的区别所在,也是其优势所在,今后咱们的很多内容,都是围绕随机误差项u t 进行了。
回归模型的随机误差项中一般包括如下几项内容: (1)非重要解释变量的省略, (2)数学模型形式欠妥, (3)测量误差等,(4)随机误差(自然灾害、经济危机、人的偶然行为等)。
3 计量经济学上机实验报告-简单线性回归

实验一 简单线性回归一、 实验名称:简单线性回归 二、实验目的掌握一元线性回归模型的估计与应用,熟悉EViews 的基本操作,并且给案例做一元回归并做预测。
三、实验中所需要掌握的知识点掌握一元回归及其预测四、实验前预备的情况说明(包括上机步骤、实验所涉及的基本原理知识的复习理解、 对实验结果的预期解释等)(1)最小二乘法估计的原理 (2) t 检验 (3)拟合优度检验(4)点预测和区间预测五、上机实验内容(填写本次上机的情况)1.上机步骤⑴统计结果,如图1所示,Y ,X 的均值分别为3081.158和22225.13,Y,X 的标准差为2212.591,和22024.6图1(2) 设定模型为 12i i i Y X u ββ=++,经运算的 Equation 界面如图2图3由图2的数据得:;2.上机结果(1)回归估计结果为:Dependent Variable: Y Method: Least SquaresDate: 04/09/14 Time: 18:53 Sample (adjusted): 1978 1997Included observations: 20 after adjustmentsVariable CoefficientStd. Errort-Statistic Prob. X 0.100036 0.002172 46.04910 0.0000 C857.837567.1257812.77955 0.0000R-squared 0.991583 Mean dependent var 3081.158 Adjusted R-squared 0.991115 S.D. dependent var 2212.591 S.E. of regression 208.5553 Akaike info criterion 13.61293 Sum squared resid 782915.7 Schwarz criterion 13.71250 Log likelihood -134.1293 F-statistic2120.520 Durbin-Watson stat0.864032 Prob(F-statistic)0.000000因此得到回归模型为: Y=857.8375+0.100036X斜率系数的经济意义为:GDP 增加1亿元,财政收入增加0.1亿元。
计量经济学EIVEWS实验步骤和案例
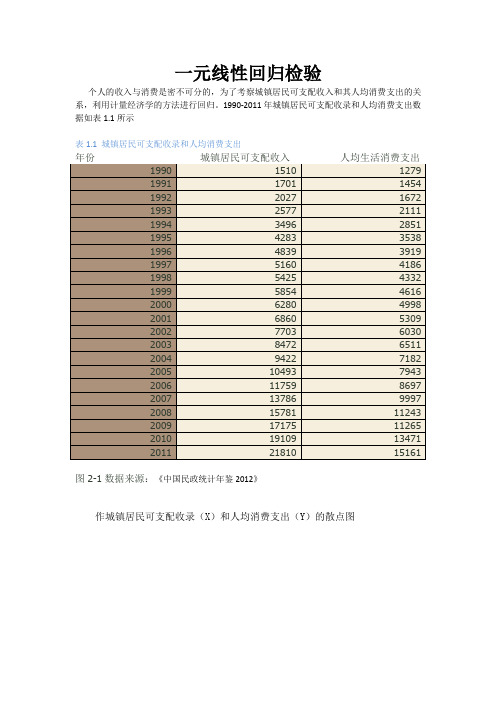
一元线性回归检验个人的收入与消费是密不可分的,为了考察城镇居民可支配收入和其人均消费支出的关系,利用计量经济学的方法进行回归。
1990-2011年城镇居民可支配收录和人均消费支出数据如表1.1所示表1.1 城镇居民可支配收录和人均消费支出图2-1数据来源:《中国民政统计年鉴2012》作城镇居民可支配收录(X)和人均消费支出(Y)的散点图图2. 2从散点图可以看出居民家庭平均每人每年消费支出(Y)和城市居民人均年可支配收入(X)大体呈现为线性关系,所以建立的计量经济模型为如下线性模型:12i i i Y X u ββ=++三、估计参数假定所建模型及随机扰动项i u 满足古典假定,可以用OLS 法估计其参数。
运用计算机软件EViews 作计量经济分析十分方便。
利用EViews 作简单线性回归分析的步骤如下:1、建立工作文件首先,双击EViews 图标,进入EViews 主页。
在菜单一次点击File\New\Workfile图2-3选择数据类型和起止日期。
时间序列提供起止日期(年、季度、月度、周、日),非时间序列提供最大观察个数。
本例中在Start Data 里输入1990,在End data 里输入2011,见图2-3。
单击OK 后屏幕出现Workfile 工作框,如图2-4所示。
图2-4二、输入和编辑数据建立或调入工作文件以后,可以输入和编辑数据。
在主菜单上单击Quick→Empty Group(见图2-5)图2-5再用方向键将光标移到每一列的顶部之后,输入各个变量名,回车后输入数据(见图2-7)。
另外数据还可以从Excel中直接复制到空组。
然后为每个时间序列取序列名。
单击数据表中的SER01,在数据组对话框中的命令窗口输入该序列名称,如本例中输入X,回车后Yes。
采用同样的步骤修改序列名Y(见图2-8)。
数据输入操作完成。
图2-8数据输入完毕,单击工作文件窗口工具条的Save或单击菜单兰的File→Save将数据存入磁盘。
计量经济学一元线性回归模型总结

计量经济学⼀元线性回归模型总结第⼀节两变量线性回归模型⼀.模型的建⽴1.数理模型的基本形式y x αβ=+ (2.1)这⾥y 称为被解释变量(dependent variable),x 称为解释变量(independent variable)注意:(1)x 、y 选择的⽅法:主要是从所研究的问题的经济关系出发,根据已有的经济理论进⾏合理选择。
(2)变量之间是否是线性关系可先通过散点图来观察。
2.例如果在研究上海消费规律时,已经得到上海城市居民1981-1998年期间的⼈均可⽀配收⼊和⼈均消费性⽀出数据(见表1),能否⽤两变量线性函数进⾏分析?表1.上海居民收⼊消费情况年份可⽀配收⼊消费性⽀出年份可⽀配收⼊消费性⽀出 1981 636.82 585 1990 2181.65 1936 1982 659.25 576 1991 2485.46 2167 1983 685.92 615 1992 3008.97 2509 1984 834.15 726 1993 4277.38 3530 1985 1075.26 992 1994 5868.48 4669 19861293.24117019957171.91586819871437.09128219968158.746763 19881723.44164819978438.896820 19891975.64181219988773.168662.⼀些⾮线性模型向线性模型的转化⼀些双变量之间虽然不存在线性关系,但通过变量代换可化为线性形式,这些双变量关系包括对数关系、双曲线关系等。
例3-2 如果认为⼀个国家或地区总产出具有规模报酬不变的特征,那么采⽤⼈均产出y与⼈均资本k的形式,该国家或者说地区的总产出规律可以表⽰为下列C-D⽣产函数形式y Akα=(2.2)也就是⼈均产出是⼈均资本的函数。
能不能⽤两变量线性回归模型分析这种总量⽣产规律?3.计量模型的设定(1)基本形式:y x αβε=++ (2.3)这⾥ε是⼀个随机变量,它的数学期望为0,即(2.3)中的变量y 、x 之间的关系已经是不确定的了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一一元线性回归方程1.下表是中国2007年各地区税收Y和国内生产总值GDP的统计资料。
单位:亿元地区Y GDP 地区Y GDP北京1435.7 9353.3 湖北434.0 9230.7 天津438.4 5050.4 湖南410.7 9200.0 河北618.3 13709.5 广东2415.5 31084.4 山西430.5 5733.4 广西282.7 5955.7 内蒙古347.9 6091.1 海南88.0 1223.3 辽宁815.7 11023.5 重庆294.5 4122.5 吉林237.4 5284.7 四川629.0 10505.3 黑龙江335.0 7065.0 贵州211.9 2741.9 上海1975.5 12188.9 云南378.6 4741.3 江苏1894.8 25741.2 西藏11.7 342.2 浙江1535.4 18780.4 陕西355.5 5465.8 安徽401.9 7364.2 甘肃142.1 2702.4 福建594.0 9249.1 青海43.3 783.6 江西281.9 5500.3 宁夏58.8 889.2 山东1308.4 25965.9 新疆220.6 3523.2 河南625.0 15012.5要求,运用Eviews软件:(1)作出散点图,建立税收随国内生产总值GDP变化的一元线性回归方程,并解释斜率的经济意义;解:散点图如下:得到估计方程为:ˆ0.07104710.62963=-y x这个估计结果表明,GDP 每增长1亿元,各地区税收将增加0.071047亿元。
(2) 对所建立的回归方程进行检验;解:从回归的估计的结果来看,模型拟合得较好。
可决系数20.7603R =,表明各地区税收变化的76.03%可由GDP 的变化来解释。
从斜率项的t 检验值看,大于5%显著性水平下自由度为229n -=的临界值0.025(29) 2.05t =,且该斜率满足0<0.071047<1,表明2007年,GDP 每增长1亿元,各地区税收将增加0.071047亿元。
(3) 若2008年某地区国内生产总值为8500亿元,求该地区税收收入的预测值及预测区间。
解:由上述回归方程可得地区税收收入的预测值:ˆ0.0710********.62963593.3Y =⨯-= 下面给出税收收入95%置信度的预测区间:由于国内生产总值X 的样本均值与样本房差为()8891.126()57823134E X Var X ==于是,在95%的置信度下,0()E Y 的预测区间为593.3 2.045±593.3113.4761=±或(479.8239,706.7761)当GDP 为8500亿元时地区的税收收入的个值预测值仍为593.3。
同样的,在95%的置信度下,该地区的税收收入的预测区间为593.3 2.045593.3641.0421±=±或(-47.7,1234.3)。
1992 42.9599 317.3194 1993 67.2507 449.2889 1994 74.3992 615.1933 1995 88.0174 795.6950 1996 131.7490 950.0446 1997 144.7709 1130.0133 1998 164.9067 1289.0190 1999 184.7908 1436.0267 2000 225.0212 1665.4652 2001265.65321954.6539资料来源:《深圳统计年鉴2002》,中国统计出版社解:(1)建立深圳地方预算内财政收入对GDP 的回归模型;得到回归方程:ˆ0.134582 3.611151yx =-(2)估计所建立模型的参数,解释斜率系数的经济意义;X 的系数为0.314582,常数项为-3.611151。
说明深圳市国内生产总值每增加1亿元,地区税收增加0.134582亿元。
(3)对回归结果进行检验;从回归估计的结果看,模型拟合得较好。
可决系数R 2=0.991810,表明地方预算内财政收入变化的99.18%可由国内生产总值的变化来解释。
从斜率项的t 检验看,大于5%显著性水平下自由度为n-2=10的临界值0.025(10) 2.228t =,且斜率值满足0<0.135<1,表明在深圳,国内生产总值每增加1亿元,地方预算内财政收入增加0.134582亿元。
(4)若是2005年的国内生产总值为3600亿元,确定2005年财政收入的预测值和预 测区间(0.05α=)。
由上述回归方程可得财政收入的预测值为:ˆ0.134582 3.611151480.884Y X =-= 下面给出财政收入的95%的置信区间。
由国内生产总值GDP 的样本均值与样本方差为:()917.5874E X = ()344884.4Var X =于是在95%的置信区间下,E (Y 0)的预测区间为:()()23600917.5874567.38311480.9 2.22812212121344884.4⎛⎫-±⨯⨯+ ⎪ ⎪--⨯⎝⎭480.924.7199=±或(456.1801,505.6199)当国内生产总值为3600亿元时财政收入的个值预测值仍为480.884。
同样的,在95%的置信度下,该地区的税收收入的预测区间为()()23600917.5874567.38311480.9 2.228112212121344884.4⎛⎫-±⨯⨯++ ⎪ ⎪--⨯⎝⎭或(451.0215,510.7785)。
3. 表中是16支公益股票某年的每股帐面价值和当年红利: 公司序号帐面价值(元) 红利(元) 公司序号帐面价值(元) 红利(元)1 22.44 2.4 9 12.14 0.802 20.89 2.98 10 23.31 1.943 22.09 2.06 11 16.23 3.004 14.48 1.09 12 0.56 0.285 20.73 1.96 13 0.84 0.84 67 819.25 20.37 26.431.552.16 1.6014 15 1618.05 12.45 11.33 1.80 1.21 1.07根据上表资料:解:(1)建立每股帐面价值和当年红利的回归方程;得到回归方程:ˆ0.0728760.479775yx =+(2)解释回归系数的经济意义;从回归方程得知,当当年红利每增加1元时,账面价值增加0.072876元。
(3)若序号为6的公司的股票每股帐面价值增加1元,估计当年红利可能为多少?由上述回归方程可得该区的税收的预测值为:ˆ0.072876(19.251)0.479775 1.94Y =⨯++= 下面给出当年红利的95%的置信区间。
由账面价值的样本均值与样本方差为:() 1.67125E X = ()0.592612Var X =于是在95%的置信区间下,E (Y 0)的预测区间为:1.942.12±1.940.4014=±或(1.5386,2.3414)当账面价值为1元时当年红利的个值预测值仍为1.94。
同样的,在95%的置信度下,该地区的税收收入的预测区间为1.942.12±或 (0.6812,3.1988)。
4. 美国各航空公司业绩的统计数据公布在《华尔街日报1999年年鉴》(The Wall Street Journal1。
1资料来源:(美)David R.Anderson等《商务与经济统计》,第405页,机械工业出版社美国(US Airways)航空公司 75.7 0.68 联合(United)航空公司 73.8 0.74 美洲(American)航空公司 72.2 0.93 德尔塔(Delta )航空公司 71.2 0.72 美国西部(Americawest)航空公司70.8 1.22 环球(TW A)航空公司 68.51.25解:(1)画出这些数据的散点图(2)根据散点图。
表明二变量之间存在什么关系?根据散点图,表明二变量之间存在线性关系(3)求出描述投诉率是如何依赖航班按时到达正点率的估计的回归方程。
得方程ˆ0.070414 6.017832yx =-+(4)对估计的回归方程的斜率作出解释。
X 的系数为-0.070414,常数项为 6.017832。
正点率每增加1%,投诉率就减少0.070414次、10万乘客。
(5)如果航班按时到达的正点率为80%,估计每10万名乘客投诉的次数是多少?如果航班按时到达的正点率为80%,由上述回归方程可得每10万名乘客投诉的预测次数是:ˆ0.070414 6.0178320.3847Y X =-+= 下面给出投诉率的95%的置信区间。
由正点率的样本均值与样本方差为:()74.13E X = ()16.0875Var X =于是在95%的置信区间下,E (Y 0)的预测区间为:0.3847 2.365±0.38470.2341=±或(0.1506,0.6188)同样的,在95%的置信度下,投诉率的个值预测区间为0.3847 2.365±或(-0.0619,0.8313)。
试建立曲线回归方程yˆ=a bx e (Y ˆ= a ln +b x )并进行计量分析。
解:由题意可知建立单对数模型 ls log(y) c x由图可知:x所对应得P值小于0.05,故y x=-+ln0.313960 5.7304886. 为研究美国软饮料公司的广告费用X与销售数量Y的关系,分析七种主要品牌软饮料公司的有关数据2(见下表)美国软饮料公司广告费用与销售数量品牌名称广告费用X(百万美元) 销售数量Y(百万箱) Coca-Cola Classic 131.3 1929.2Pepsi-Cola 92.4 1384.6Diet-Coke 60.4 811.4Sprite 55.7 541.5Dr.Pepper 40.2 546.9Moutain Dew 29.0 535.67-Up 11.6 219.5 分析广告费用对美国软饮料工销售影响的数量关系。
解:画出销售销量Y对广告费用X的散点图如下:2资料来源:(美)David R.Anderson等《商务与经济统计》,第405页,机械工业出版社由图可得出结论:销售销量Y与广告费用X存在明显的线性关系,即当广告费用增加时,销售销量也增加,考虑建立两者之间的线性回归方程来描述广告费用对美国软饮料工销售影响的数量关系。
从回归估计的结果看,模型拟合得较好。
可决系数R2=0.56774,表明销售销量变化的95.68%可由广告费用的变化来解释。
