混合效应线性模型与单因素方差分析在重复测量数据中的应用比较
JAMA:应用混合模型分析重复测量资料

JAMA:应用混合模型分析重复测量资料医学数据挖掘出品,戴云鹤译。
本篇内容翻译自Michelle A. Detry 和Yan Ma于2016年1月26日发表在JAMA的文章《Analyzing Repeated Measurements Using Mixed Models》,查看英文原文请点击“原文链接”。
纵向研究通常会包括有关病人状态或结局的多元重复测量资料,这些资料可用于评估结局的差异,或不同时间点上治愈率或死亡率的差异。
与来自不同病人的测量资料相比,来自于同一病人的重复测量资料相似度更高,分析结果时还需要考虑数据的关联性。
许多常见的统计方法(例如线性回归模型)都假定测量资料之间彼此独立,因此不适用于这种情况。
在比较不同治疗方法结局的差异时,我们可以只对最后一次测量进行分析,以判断研究结束时两组之间的结局是否存在差异。
但是,这种方法会忽略掉重复测量中的许多信息,也不能反映出每个病人的病情变化过程。
当对不同时间点的结局进行重复测量时,很多重要的临床问题就能得到解决。
JAMA最近发表的一篇研究中,Moseley等[1]对踝关节骨折病人的活动限制和生活质量(QOL)进行了测量,以判断监督锻炼计划与康复建议相结合的方式是否比单独建议更有效。
有关病人活动限制和生活质量的数据,该研究组分别在基线水平以及随访1个月、3个月和6个月时进行了测量。
作者使用混合模型2对两干预组病人不同时间点的结局进行了比较。
混合模型的使用为什么混合模型用于分析重复测量数据?当所有研究对象都即受某些相同因素的影响(例如,干预效果),又都具有某些不同的特征时(例如,踝关节骨折的程度、功能的基线水平以及生活质量),混合模型就很适合于分析研究对象不同时间点上结局的变化轨迹。
混合模型可以明确地解释同一研究对象的重复测量资料之间的关联。
对许多研究对象都产生相同效应的因素称为固定效应,而在不同研究对象之间存在差异的因素就称为随机效应。
例如,假定某种新疗法对所有病人的疗效相同,并将模型设为固定效应;但是病人的基线功能或恢复速度存在差异,因此应当选择随机效应模型。
第十讲 重复测量数据的方差分析

重复测量设计资料的方差分析(四)一、重复测量资料的特征:重复测量资料系指同一受试对象的某项观测指标进行多次测量所得的数据。
如对病人治疗(或手术)后1天、3天、1周、2周等多个时间点连续观察;又如在眼睛视觉研究中,让同一受试者戴上效率分别为6/6,6/18,6/36/,6/60的镜片;观察其大脑皮质在佩戴不同镜片时的电反延迟时间等。
在重复测量中,由于同一个观察单位具有多个观察值,而这些观察值来自同一受试对象的不同时间(部位等),因此这类数据间往往有相关性存在,违背了方差分析要求数据满足独立性的基本条件。
此时若用一般方差分析方法,将会增大犯I 类错误的概率。
例如:为比较某一降压新药与上市的标准药品降低舒张压的效果,将24名病人随机分配到新药组和标准药物组,每组12名病人,给药前先测定基础血压(3次测定的均数)。
给药后每隔2周测量一次血压,共连续测量4次。
在此期间有3名病人退出(标准药物组1名、新药组2名),试分析新药的降压效果是否不同于标准药。
两组舒张压变化量(服药后-服药前)(mmHg)基础标准药物组基础标准药物组编号血压2w 4w 6w 8w M i编号血压2w 4w 6w 8w M i1 108 -8 -10 -19 -17 -54 3 104 -7 -7 -11 -13 -382 105 -6 -2 -14 -13 -35 5 102 -5 -9 -6 -14 -344 105 -4 -5 -11 -15 -356 98 -3 -10 -9 -13 -357 103 0 -11 -17 -19 -47 9 99 -3 -2 -1 -14 -2012 96 1 -3 -5 -8 -15 10 98 -1 -3 -8 -15 -2714 108 -3 -3 -17 -16 -39 11 100 2 -4 -8 -16 -2615 104 -3 -7 -10 -15 -35 17 106 -5 -8 -15 -20 -4816 97 2 3 -2 -3 0 18 108 -9 -12 -15 -17 -5319 98 1 -5 -7 -11 -22 21 104 0 -6 -7 -24 -3722 104 -1 -1 -11 -10 -23 24 107 -2 -7 -12 -19 -4023 103 -1 -1 -5 -8 -15均数102.8 -2 -4.9 -10.4 -12.3 均数102.6 -3.3 -6.8 -9.2 -16.5标准差 3.15 3.41 5.61 4.76 标准差 3.30 3.16 4.26 3.57 T i-22 -45 -118 -135 A1=-320 T i-33 -68 -92 -165 A2=-358 B1=-55 B2=-113 B3=-210 B4=-300由于重复测量结果即使不施加任何干预,也常会随时间的推移产生自然变化,因此重复测量试验常常需要设立平行对照.试验设计阶段需考虑以下三个因素:1、处理因素各组给以不同的干预2、重复测量因素时间(可根据专业的要求确定,其间隔可以不等或相等。
医学统计学(高级篇)文字题

第一章单选题(4/5 分数)1.统计学中所说的样本是指( )。
.随意抽取的总体中任意部分 .有意识的选择总体中的典型部分 .依照研究者要求选取总体中有意义的一部分 .依照随机原则抽取总体中有代表性的一部分 .依照随机原则抽取总体中有代表性的一部分 - 正确. 有目的的选择总体中的典型部分2.下列资料属等级资料的是( )。
.白细胞计数 .住院天数 .门急诊就诊人数 .病人的病情分级 .病人的病情分级 - 正确 . ABO 血型分类3.为了估计某年华北地区家庭年医疗费用的平均支出,从华北地区的5个城市随机抽样调查了1500户家庭,他们的平均年医疗费用支出是 997元,标准差是 391 元。
该研究中研究者感兴趣的总体是( ).华北地区1500户家庭.华北地区的5个城市 .华北地区1500户家庭的年医疗费用.华北地区所有家庭的年医疗费用 .华北地区所有家庭的年医疗费用 - 正确 . 全国所有家庭的年医疗费用 4.欲了解研究人群中原发性高血压病(EH)的患病情况,某研究者调查了1043人,获得了文化程度(高中及以下、大学及以上)、高血压家族史(有、无)、月人均收入(元)、吸烟(不吸、偶尔吸、经常吸、每天)、饮酒(不饮、偶尔饮、经常饮、每天)、打鼾(不打鼾、打鼾)、脉压差(mmHg)、心率(次/分)等指标信息。
则构成计数资料的指标有( ).文化程度、高血压家族史吸烟、饮酒、打鼾.月人均收入、脉压差、心率 .月人均收入、脉压差、心率 - 不正确.文化程度、高血压家族史、打鼾 .吸烟、饮酒 . 高血压家族史吸烟、饮酒、打鼾5.总体是指().全部研究对象.全部研究对象中抽取的一部分.全部样本.全部研究指标. 全部同质研究对象的某个变量的值第二章单选题(10/10 分数)1.描述一组偏态分布资料的变异度,以()指标较好。
. 全距. 标准差. 变异系数. 四分位数间距 . 四分位数间距 - 正确.方差2.用均数和标准差可以全面描述()资料的特征。
单因素重复实验设计方差分析(GLM

实验设计步骤
1. 确定实验目的和假设。
3. 设定实验处理和测量指标。
5. 进行统计分析,包括数据清 洗、方差齐性检验等。
2. 选择样本和分组。
4. 实施实验并记录数据。
6. 解读和分析结果,得出结论 。
实验设计注意事项
样本代表性
确保样本具有足够的代表性,能够反映总体 的情况。
数据处理规范
遵循数据处理规范,确保数据的准确性和可 靠性。
05
结论
研究成果总结
01
验证了单因素重复实验设计方差分析(GLM)在处理重复测量数 据时的有效性。
02
揭示了不同处理组之间的显著差异,为进一步研究提供了依 据。
03
证明了GLM在处理具有重复测量特点的数据时具有优越性, 能够更准确地估计实验处理效应。
研究不足与展望
需要更多的研究来验证GLM在处理不同类型重复测量数据时的适用性和稳 健性。
背景
在科学实验、社会科学调查和工 业生产等领域中,经常需要进行 单因素重复实验设计,以评估不 同处理或条件下的结果差异。
GLM简介
GLM全称General Linear Model,即一般线性模型,是一种广泛使用的统计分析方 法。
它通过构建线性模型来描述因变量和自变量之间的关系,并使用适当的统计技术来 估计模型参数和检验假设。
对数据进行整理,计算出每个 组的均值和观测值的总数。
5. 检验假设
通过比较组间变异和组内变异 的比例,判断处理方式是否对 实验结果验是方差分析中重要的一步,它通过比较组间变异和组内变异的比例来检验多个总体均值是否 相等。
在进行假设检验时,需要选择合适的统计量来描述组间变异和组内变异的比例,并确定显著性水平。
利用线性混合随机效应模型评价临床疗效

利用线性混合随机效应模型评价临床疗效摘要讨论了线性混合随机效应模型在糖尿病临床试验重复观测数据中的应用,在病人初始入组时,采用不同治疗方案得到重复观测的血糖数据,根据数据的图示以及它们具有相关性的特点,采用线性混合随机效应模型拟合数据,通过参数和标准误差的估计构造检验统计量,对临床疗效进行评价,并给出一种能较客观地评价临床疗效的方法。
关键词测量数据;线性混合随机效应模型;评价1研究背景——临床试验中的问题为了比较方案1和方案2 2种治疗方案对糖尿病人的临床疗效水平,吕梁某医院将171名糖尿病患者分成2组,一组104名患者,另一组67名患者,对这2组病人分别采用方案1和方案2治疗。
对每个患者分别在入组之前、入组之后1周、2周,测量患者的血糖值,3个时间点分别记为0、1、2,可得这2组的观测数据分别为312个和201个,具体见表1。
2种方案病人血糖值分布特点如图1~2所示。
对不同方案的观测数据在不同时间点分别求平均值之后得到2种方案观测平均值图,如图3所示。
从图中可以看出,无论采用哪种治疗方案,病人的平均血糖呈线性降低趋势,采用方案2的病人初始入组的平均血糖水平较高,然而直线的变化斜率大,需要做统计分析,以给出统计意义上2种临床治疗方案的疗效是否显著的结论。
由于研究得到的观测数据为重复观测量数据,其一般不满足独立性的要求,常用的统计方法,如t检验、方差分析、一般线性模型等,不能揭示出其内在特点,勉强用之,甚至会造成许多偏倚。
2线性混合效应模型混合效应模型是研究非独立数据常用的统计学模型之一,根据图3采用线性混合随机效应模型拟合数据。
线性混合效应模型:分别是对应于p维固定效应β和q维随机效应bi的ni×p和ni×q的矩阵。
通常假定bi服从均值为零、方差为Di的正态分布,且对不同个体i,Di相同。
假定εi=(εi1,L,ε■)τ是独立的,服从均值为零、方差为σ2的正态分布,且εi和bi独立。
线性混合效应模型

线性混合效应模型线性混合效应模型(Linear Mixed Effects Model,LME)是一种非常有用的统计模型,它允许将个体差异和时间序列效应集成在一起,以便更好地了解数据中发生的不断变化。
LME模型是一个结构复杂的模型,首先要求对建模进行概括,然后就可以使用概括的参数进行建模。
LME模型由两部分组成:随机效应和固定效应。
随机效应允许将个体差异考虑在内,从而可以更好地量化个体之间的差异。
固定效应是将可测量的变量作为解释变量考虑进来的。
例如,在研究学生成绩时,可以将课程、年级、学习时间等变量作为固定效应加以考虑。
LME模型可以用来分析和预测复杂的数据,例如研究人员从多个独立样本中观察到的实验数据。
它可以帮助弄清实验变量之间的相互作用,并发现不同样本之间的差异。
同时,它还可以用来考察分组效应,以了解样本之间的差异可能是由独立的因素导致的,也可能是由某些群体作用导致的,又或者是由两者共同作用导致的。
另外,LME模型还可以用来研究变量之间的关系,特别是用于分析长期追踪和时间序列数据,这些数据可能会随时间而发生变化。
此外,它还可以用于分析多变量之间的关系,以了解哪些因素会影响另一变量,以及这些变量之间的相互作用。
由于LME模型的复杂性,使用它需要专业统计学知识,以便将模型中的参数准确估计出来,从而能够得到有意义的结果。
同时,模型的参数也有可能会出现过拟合以及其他问题,因此,使用者需要仔细检查模型的参数,以避免出现这些问题。
总的来说,LME模型是一种非常有用的统计模型,能够将个体差异和时间序列效应考虑在内,从而有助于更好地解释和预测复杂的数据。
它可以用来分析和预测变量之间的关系,以及考查多变量之间的相互作用。
然而,由于它的复杂性,使用LME模型可能会出现过拟合或其他问题,因此,使用者需要仔细检查模型的参数,以避免出现这些问题。
混合效应线性模型与单因素方差分析在重复测量数据中的应用比较

混合效应线性模型与单因素方差分析在重复测量数据中的应用比较王超;王汝芬;张淑娴【期刊名称】《数理医药学杂志》【年(卷),期】2006(019)004【摘要】目的:通过混合效应线性模型与单因素方差分析在重复测量资料中的应用比较,旨在说明两方法在处理重复测量资料时的应用特点.方法:用混合效应线性模型和单因素方差分析处理重复测量资料并比较.结果:混合效应线性模型和单因素方差分析都是处理重复测量资料的重要统计方法,前者在选择协方差结构下可对重复测量资料的固定效应和随机效应参数及协方差矩阵进行参数估计和统计检验,后者可对重复测量资料的固定效应做出统计推断.结论:混合效应线性模型是处理重复测量资料的有力方法,它对资料的协方差结构要求宽松,且结论可靠;单因素方差分析对资料的协方差结构有严格的限定.【总页数】3页(P355-357)【作者】王超;王汝芬;张淑娴【作者单位】潍坊医学院,潍坊,261042;潍坊医学院,潍坊,261042;潍坊医学院,潍坊,261042【正文语种】中文【中图分类】R311【相关文献】1.非线性混合效应模型和广义线性模型拟合随机效应logistic回归的应用比较 [J], 杨志雄;袁岱菁2.重复测量数据的混合模型及其MIXED过程实现 --混合线性模型及其SAS软件实现(二) [J], 张岩波;何大卫;刘桂芬;张晋昕;郭静3.用混合线性模型处理重复测量数据的方法分析福建省脑血管病死亡率 [J], 周天枢;洪荣涛;陈崇帼4.重庆地区儿童尿碘重复测量数据混合线性模型研究 [J], 姚宁;曾庆;李革;张婷;窦贵旺5.方差分析和混合线性模型在重复测量数据中的应用探讨 [J], 高萌;张强;邓红;宋魏因版权原因,仅展示原文概要,查看原文内容请购买。
第三讲重复测量资料的方差分析
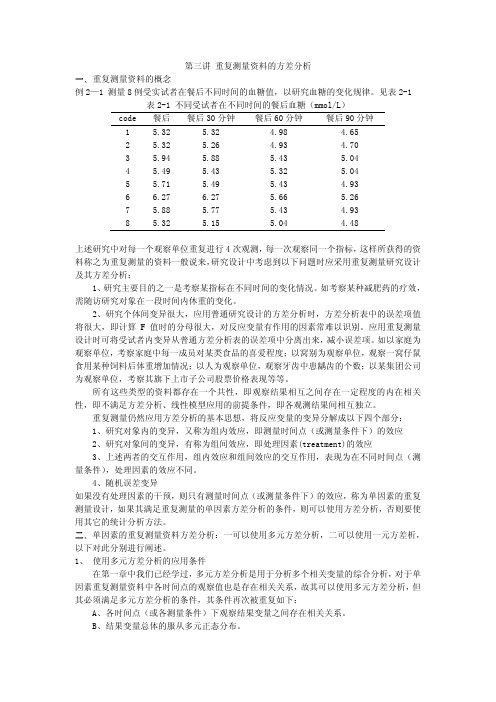
第三讲 重复测量资料的方差分析一、重复测量资料的概念例2—1 测量8例受实试者在餐后不同时间的血糖值,以研究血糖的变化规律。
见表2-1 表2-1 不同受试者在不同时间的餐后血糖(mmol/L)code 餐后 餐后30分钟 餐后60分钟 餐后90分钟1 5.32 5.32 4.98 4.652 5.32 5.26 4.93 4.703 5.94 5.88 5.43 5.044 5.49 5.43 5.32 5.045 5.71 5.49 5.43 4.936 6.27 6.27 5.66 5.267 5.88 5.77 5.43 4.938 5.32 5.15 5.04 4.48上述研究中对每一个观察单位重复进行4次观测,每一次观察同一个指标,这样所获得的资料称之为重复测量的资料一般说来,研究设计中考虑到以下问题时应采用重复测量研究设计及其方差分析:1、研究主要目的之一是考察某指标在不同时间的变化情况。
如考察某种减肥药的疗效,需随访研究对象在一段时间内休重的变化。
2、研究个体间变异很大,应用普通研究设计的方差分析时,方差分析表中的误差项值将很大,即计算F值时的分母很大,对反应变量有作用的因素常难以识别。
应用重复测量设计时可将受试者内变异从普通方差分析表的误差项中分离出来,减小误差项。
如以家庭为观察单位,考察家庭中每一成员对某类食品的喜爱程度;以窝别为观察单位,观察一窝仔鼠食用某种饲料后体重增加情况;以人为观察单位,观察牙齿中患龋齿的个数;以某集团公司为观察单位,考察其旗下上市子公司股票价格表现等等。
所有这些类型的资料都存在一个共性,即观察结果相互之间存在一定程度的内在相关性,即不满足方差分析、线性模型应用的前提条件,即各观测结果间相互独立。
重复测量仍然应用方差分析的基本思想,将反应变量的变异分解成以下四个部分:1、研究对象内的变异,又称为组内效应,即测量时间点(或测量条件下)的效应2、研究对象间的变异,有称为组间效应,即处理因素(treatment)的效应3、上述两者的交互作用,组内效应和组间效应的交互作用,表现为在不同时间点(测量条件),处理因素的效应不同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
混合效应线性模型与单因素方差分析在重复测量数据中的应用比较
【关键词】重复测量;混合效应线性模型;单因素方差分析;
摘要:目的:通过混合效应线性模型与单因素方差分析在重复测量资料中的应用比较,旨在说明两方法在处理重复测量资料时的应用特点。
方法:用混合效应线性模型和单因素方差分析处理重复测量资料并比较。
结果:混合效应线性模型和单因素方差分析都是处理重复测量资料的重要统计方法,前者在选择协方差结构下可对重复测量资料的固定效应和随机效应参数及协方差矩阵进行参数估计和统计检验,后者可对重复测量资料的固定效应做出统计推断。
结论:混合效应线性模型是处理重复测量资料的有力方法,它对资料的协方差结构要求宽松,且结论可靠;单因素方差分析对资料的协方差结构有严格的限定。
关键词:重复测量;混合效应线性模型;单因素方差分析;
统计方法特点重复测量数据(repeated measures data)是医学领域中常见的一种数据资料。
所谓重复测量是指对同一个观察对象在不同时间点上进行的多次测量[1]。
由于重复测量资料是对同一受试对象的某一观察指标进行的重复观察所得的数据,同一受试者的观察数据间可能存在相关性,一些传统的统计学方法如t检验等就不能充分揭示这一内在特点,有时甚至会导致错误的结论。
对重复测量资料的分析方法大致可分为两类,即单变量统计分析方法和多变量统计分析方法[2]。
本研究通过选用多变量统计分析方法中的混合线性效应模型对一例题的分析,并与单因素方差分析进行比较,来说明两种方法在处理重复测量资料中的应用特点。
1方法简介
简单说,混合效应线性模型就是所拟和的模型中既包含固定效应又包含随机效应,特别是个体内的数据结构的选择将对各因素的评价产生直接影响[3]。
混合效应线性模型是一般线性模型的扩展,其表达式为:
Y=Xβ+Zγ+ε(1)
X为已知设计矩阵,β为固定效应参数构成的未知向量,ε是未知的随机误差向量,其元素不必为同独立分布了。
在式(1)中Y,γ都是正态随机向量,其均值为0,方差阵分别为G与R,二者之间不相关,因此Y的方差表达式为:
V=ZGZ+R(2)
当R=σ2I,Z=0时,混合线性模型退化为一般线性模型。
对G和R 必须选择其协方差结构,常用的结构有无结构(一般为协方差)、自
回归(常用一阶)、复合对称(共同协方差加一对角元)等[4]。
选择协方差矩阵的方法是在相同的结构模型下,选择几个不同结构的协方差矩阵,从中选取似然比统计量(-2Log Likelihood)、Akaikes 信息量标准(Akaikes Information Criterion,AIC)及Schwarts Bayesian标准(Schwarts Bayesian Criterion ,BIC)较小的一个,当这些统计量较接近时,则选取含参数个数最少的一个。
通常以AIC 为主要判断指标。
2实例分析
下面用一实例比较两种方法对处理重复测量资料时的特点:某药有新旧两种剂型,为了比较这两种剂型的代谢情况,对16例病人服药后分别在0、4、8、12小时测得血药浓度(表1),问该药新旧剂型的血药浓度随时间变化的趋势是否一致。
表1四个时间点某药新旧剂型血药浓度1用SAS软件的MIXED过程对固定效应和随机效应参数β、γ及协方差矩阵G、R进行估计和统计检验。
在本例中因变量为血药浓度,药物剂型、测量时间为固定效应,受试者为随机效应,同时选择合适的协方差结构以便在控制随机误差的基础上分析处理因素(药物剂型)对反应变量(血药浓度)的关系。
本例指定为常用的无结构协方差(UN)和复合对称性协方差(CS)。
模型拟合情况见表2。
表2模型配合统计量由表2可见,在UN结构下协方差配合的似然比统计量-2Log Likelihood=398.0(表2),对无效模型的似然比检验,χ2=134.43,ν=9,P<0.0001,说明模型拟合效果显著,模型较好地拟和了资料。
在CS结构下,似然比统计量-2Log Likelihood=506.4,AIC、AICC、BIC三个值都是UN模型小于CS模型,故本例选用UN结构作模型拟合。
在UN结构下的固定效应参数估计值及假设检验结果见表3、4。
由表4可知,在UN结构下,不同处理组之间的差别无统计学意义(P=0.07551),不同测量时间点的血药浓度及处理组×时间点的交互作用的差别有统计学意义(P<0.0001),且这种交互作用主要体现在新剂型组。
22应用SAS 软件的GLM过程,对表1的资料处理结果见表5。
由表5可见,各处理组间时间因素间无差别,服从精确F分布,本例F处理组=0.09,P=0.77可见其处理组主效应与时间因素无关。
主效应F时间点受协方差矩阵类型分布影响,球形检验的近似χ2=27.0284,ν=5,对应P=0.0001,不符合球形假定,故须对分子分母的自由度进行校正,用H-F=0.8469作为校正因子,得:
分子的校正自由度为:
ν1=(p-1)=0.8469(4-1)=0.8469×3=2.54073
分母的校正自由度为:
ν2=(p-1)(∑m g=1(ng-1))=0.8469×3(14)=35.569836
查表得F0.05(3,36)=2.87<74.97,P<0.0001,可认为不同时间点的血药浓度是不同的。
交互效应F处理组*F时间点也涉及时间点这一重复测量因子,故也要对其分子分母的自由度进行校正:
分子的校正自由度为:
ν1=(m-1)(p-1)=0.8469(2-1)(3-1)=1.69382
分母自由度校正同上,ν236
F0.05(2,36)=3.26<46.90,P<0.0001,可认为不同组在不同时间点的血药浓度是不同的。
表3固定效应的参数估计与比较表5单因素方差分析结果
3讨论
由两种方法对同一资料的处理可见,两种方法的结论一致,但混合效应线性模型既考虑了观察对象在不同观察时点间的内在联系,又考虑了观察值间的内部相关性,结论更为可靠。
单因素方差分析和混合效应线性模型都可用来处理重复测量资料,单因素方差分析是应用最小二乘法进行配合的一般线性模型,此模型对协方差矩阵有着极端的假定,如果协方差阵的球形性得不到满足,就必须进行多元方差分析或对F统计量进行校正,获得校正概率;混合效应线性模型是基于似然函数法的原理,它对协方差矩阵的要求比单因素方差分析宽松,它允许资料存在某种相关性及协方差矩阵的多样性,无须对自由度进行校正,能较好的适合重复资料的特点。
单因素方差分析很难估计参数,混合效应线性模型可以在所选择的协方差结构下,估计固定效应及随机效应参数,还可以估计随机参数及随机误差的协方差阵G和R,所以应用范围广,即使常规分析模型,亦可作为其特例来应用[6]。
在配合混合效应线性模型时要根据研究目的和资料特点选择一种模型,然后在此模型下选择合适的协方差结构,只有选择合适的协方差结构对固定效应参数的估计和推论才有意义。
