方位角与象限角关系及5800程序
标准方向_方位角_象限角

2
因标准方向有真子午线方向、磁子午线方向和
坐标纵轴方向之分,对应的方位角分别称为真方位
角(用A表示)、磁方位角(用Am表示)和坐标方 位角(用α表示)。
三、三种方位角之间的关系 *
过一点的真北方向与磁北方向之间的夹角称为 磁偏角,用δ ['deltə]表*示。
过一点的真北方向与坐标纵轴北方向之间的夹
x(N)
4
Ⅳ (W)
Ⅲ 3
RO4 RO1 O
RO3 RO2
(S)
1 Ⅰ Ⅱ 2
y(E)
2.坐标方位角与象限角的换算关系
x(N)
αO1 RO1
O
1 Ⅰ
y(E)
x(N)
αO2 y(E)
O
Ⅱ
RO2 2
(S)
x(N)
4
(W)
Ⅲ
3
O
αO3
Ⅳ
y
(W)
RO3
(S)
x(N)
RO4
Oy
αO4
在第Ⅰ象限 R 在第Ⅱ象限 R 180
推算坐标方位角的一般公式为:
180 L
180 R
式中 α——前一条边的坐标方位角;
α′——后一条边的坐标方位角。
如果α>360˚,应自动减去360°;如果α<0˚,则自
动加上360˚。
五、象限角
1.象限角
由坐标纵轴的北端或南端起,沿顺时针或逆时针方向 量至直线的锐角,称为该直线的象限角,用R表示,其角 值范围为0˚~90˚。
在第Ⅲ象限 R 180 在第Ⅳ象限 R 360
返回
在高斯平面直角坐标系中,坐标纵轴线方向就是地面 点所在投影带的中央子午线方向。
在同一投影带内,各点的坐标纵轴线方向是彼此平行 的。
方位角计算公式
辅助 计算
点名 2 BM1 1
2
3
BM2
测站数 3 8 3 4 5
20
表 2-2 附合水准路线计算
观测高差 /m
改正数 /m
改正后高差 /m
4
5
6
+8.364
- 0.014
+8.350
- 1.433
- 0.005
- 1.438
- 2.745
- 0.007
- 2.752
+4.661
- 0.008
+4.653
+ 8.847
- 0.034
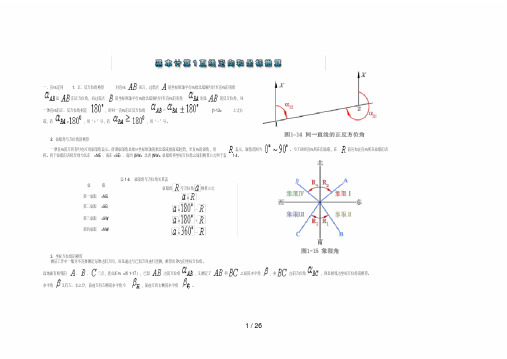
一、直线定向
1、正、反方位角换算
对直线
而言,过始点
的坐标纵轴平行线指北端顺时针至直线的夹角
是
的正方位角,而过端点
的坐标纵轴平行线指北端顺时针至直线的夹角
则是
的反方位角,同
一条直线的正、反方位角相差
,即同一直线的正反方位角
=
(1-13>
上式右
端,若
<
,用“+”号,若
,用“-”号。
2、象限角与方位角的换算
算
各
待
定
点
的
高
程
。
如上 所述,闭 合水准 路线的 计算方法除高差 闭合差 的计算有 所区别 而外,其余与附 合路线 的计算 完全相 同。
二
、
举
例
1.
附
合
水
准
路
线
算
例
5 / 26
下图 2-18 所示附合水准路线为例,已知水准点 A 、 B 和待定点 1、2、3 将整个路线分为四个测段。
测段号 1 1 2 3
方位角计算公式

一、直线定向1、正、反方位角换算对直线而言,过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角,而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角,同一条直线的正、反方位角相差,即同一直线的正反方位角= (1-13) 上式右端,若<,用“+”号,若,用“-”号。
2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。
所谓象限角是指从坐标纵轴的指北端或指南端起始,至直线的锐角,用表示,取值范围为。
为了说明直线所在的象限,在前应加注直线所在象限的名称。
四个象限的名称分别为北东(NE)、南东(SE)、南西(SW)、北西(NW)。
象限角和坐标方位角之间的换算公式列于表1-4。
表1-4 象限角与方位角关系表象限象限角与方位角换算公式第一象限(NE)=第二象限(SE)=-第三象限(SW)=+第四象限(NW)=-3、坐标方位角的推算1 / 32测量工作中一般并不直接测定每条边的方向,而是通过与已知方向进行连测,推算出各边的坐标方位角。
设地面有相邻的、、三点,连成折线(图1-17),已知边的方位角,又测定了和之间的水平角,求边的方位角,即是相邻边坐标方位角的推算。
水平角又有左、右之分,前进方向左侧的水平角为,前进方向右侧的水平角。
设三点相关位置如图1-17()所示,应有=++ (1-14)设三点相关位置如图1-17()所示,应有=++-=+- (1-15)若按折线前进方向将视为后边,视为前边,综合上二式即得相邻边坐标方位角推算的通式:=+(1-16)显然,如果测定的是和之间的前进方向右侧水平角,因为有=-,代入上式即得通式2 / 32=- (1-17)上二式右端,若前两项计算结果<,前面用“+”号,否则前面用“-”号。
二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。
坐标正算,就是根据直线的边长、坐标方位角和一个端点的坐标,计算直线另一个端点的坐标的工作。
如图1所示,设直线AB的边长DAB和一个端点A的坐标XA、YA为已知,则直线另一个端点B的坐标为:XB=XA+ΔXABYB=YA+ΔYAB式中,ΔXAB、ΔYAB称为坐标增量,也就是直线两端点A、B的坐标值之差。
CASIOfx-5800P边长方位角反算计算程序编制及使用说明

I n v e s t i g a t e o f ir f e s a f e t y ha z a r d s a n d p r e v e n t i o n c o u n t e r me a s u r e s o n c o mb i n e d wo r k p l a c e
C A S I O f x 一 5 8 0 0 P边 长 方 位 角 反 算 计 算 程 序 编 制 及 使 用 说 明
曾 பைடு நூலகம் 忠
( 江西荡坪钨业有限公司 , 江西 大余 3 4 1 5 1 4 )
摘
要: 针对在 已知两个控制点坐标 , 反算两点的距离和方位角 时 , 要考 虑象 限角 ±1 8 0 。 的问题 , 容 易 出现错 误 的情况 , 提 出利 用
2 ) 象限角是从标准方 向的北端 或南端起 , 顺 时针或逆 时针至
某 一直线所夹 的锐角 , 称 为该直 线 的象 限角 , 角值 均在 0 。 一9 0 。 ,
、 / ( ( C—A) +( D— B) ) I f ( C— A) > 0 A n d ( D— B) > 0: T h e n( t a n ~ ( ( D— B)÷( C~A) ) 。 )
人人重 视安全 、 人人关 心安 全 、 人人参 与安 全工作的浓厚氛 围。 民族 大学学报 (自然科 学版 ) , 2 0 0 6 ( 9 ) : 1 7 5 - 1 7 6 . [ 4 ] 吴地 球. “ 三 合一 ” 的危 害及 治理 [ J ] . 劳动保护 科 学技 术 ,
火器使用 、 安全用火用 电、 初起火灾扑 救 、 如何 报警 和组织逃 生 自
5800坐标计算程序+方位角计算方法

1.主程序TYQXJSDefm10:Lbl 0: “1.LC=>XY”: “2.XY=>LC”: {V}:V=1=>GOTO 1: ≠> GOTO 2 △Lbl 1: {DZG}:D:Z”JL=”:G”J=”:Z=0=>G=0:△Prog “QXYS”: Prog “ZSZB” : ”X=”:X ◢”Y=”:Y◢J>360=>J=J-360:△J<0=>J=J+360:△"FWJ=":J→DMS◢{HU}:H“XC”:U“YC”:I=0:J=0:Pol(X-H,Y-U):J<0=>J=J+360:△“FW=”:J→DMS◢“S=”:I◢Prog “SQX”←┘GOTO 0←┘Lbl 2: D=***:Z=0:G=0:{MI}:M”XO”:I”YO”: Prog “FSZB”:”D=”:D ◢”JL=”:Z◢Prog “SQX”←┘GOTO 0←┘D=有效里程即线路起点里程2. 正算坐标ZSZBN=5:P=(1\E-1\R)÷Abs(K-F):Q=Abs(D-F)÷N:S=90Q÷π:J=C+(NPQ+2\R)NS:L=1←┘X=A+Q÷6×(Cos C+Cos J +4∑(Cos (C+((L+0.5)PQ+2\R)×(L+.5)S),L,0,(N-1))+2∑(Cos (C+((LPQ+2\R)LS,L,1,(N-1)))+ZCos(J+G):←┘Y=B+Q÷6×(Sin C+Sin J +4∑(Sin (C+((L+0.5)PQ+2\R)×(L+.5)S),L,0,(N-1))+2∑(Sin (C+((LPQ+2\R)LS,L,1,(N-1)))+Z Sin(J+G):←┘3. 反算坐标:FSZBLbl 0:Prog “QXYS” :Prog “ZSZB”:O=J-90:←┘P= (I-Y)cosO-(M-X) sinO :D=D+P:←┘AbsP≥0.001=> GOTO 0 :≠> GOTO 1 △←┘Lbl 1: Z= (I-Y)cosJ-(M-X) sinJ: ←┘4. 《SQX》高程计算子程序Prog“SB”:W=Z[1]-Z[2]:W>0=>Z[6]=-1:≠>Z[6]=1△Z[3]:T“T”=Abs(Z[3]W/2) :E“E”=T^2÷2Z[3]:C=D-Z[4]:D≦Z[4]=>Z[7]=Z[1]:≠>Z[7]=Z[2]△Z[5]:AbsC≦T=> “H0”: Z[8]=Z[5]+CZ[7]+Z[6](T- Abs C)^2÷2Z[3] ◢≠> “H0”: Z[8]=Z[5]+CZ[7]5、曲线元要素数据库:QXYS◢D≥F=>D<K=> F=**:A=**:B=**:C=**:R=**:K=**E=**△△←┘D≥F=>D<K=> F=**:A=**:B=**:C=**:R=**:K=**E=**△△←┘D≥F=>D<K=> F=**:A=**:B=**:C=**:R=**:K=**E=**△△←┘D≥F=>D<K=> F=**:A=**:B=**:C=**:R=**:K=**E=**△△←┘D≥F=>D<K=> F=**:A=**:B=**:C=**:R=**:K=**E=**△△┘……………………………D≥F=>D<K=> F=**:A=**:B=**:C=**:R=**:K=**E=**△△←┘(注:如有多个曲线元要素继续添加入数据库QXYS中)6、《SB》竖曲线数据库D≥竖曲线起点里程=>Z[1]=?:Z[2]=?:Z[3]=?:Z[4]=?:Z[5]=?△D≥?=>Z[1]=?:Z[2]=?:Z[3]=?:…………△TYQXJS(主程序名)LbI 0:4→Dimz:Cls"1.SZ→XY""2.XY→SZ"?→N:Cls"XO"?U: "YO"?V: "SO"?O:"FO"?G: "LS"?H: "RO"?P:"RN"?R:?Q1÷P→C:(P-R)÷(2HPR) →D:180÷π→EN=2=>Goto 2LbI 1:Cls:?SS=0=>Goto 0 (注:當S輸入0時,程序會由LbI 0開始重新運行)Z:Abs(S-O)→WProg"SUB1":Cls"XS=":X◢"YS=":Y◢"FS=":F-90 ?DMS◢Goto 1LbI 2:Cls:?XX=0=>Goto 0 (注:當X輸入0時,程序由會LbI 0開始重新運行)Y:X→I:Y→JProg"SUB2":O+W→S:Cls"S=":S◢"Z=":Z◢Goto 2注:紅色部可以不要,亦可以要,它的作用是將S或X輸入0時,程序會重新由頭開始運行,(即是可以計算下段線元)SUB1(子程序名)0.1739274226→A:0.3260725774→B0.0694318442→K:0.330009482→L1-L→F:1-K→MG+QEKW(C+KWD)→Z[1]G+QELW(C+LWD)→Z[2]G+QEFW(C+FWD)→Z[3]G+QEMW(C+MWD)→Z[4]A×cos(Z[1])→X (剩號可省略)X+Bcos(Z[2])→XX+Bcos(Z[3])→XX+Acos(Z[4])→XU+WX→XAsin(Z[1])→YY+Bsin(Z[2])→YY+Bsin(Z[3])→YY+Asin(Z[4])→YV+WY→YG+QEW(C+WD)+90→FX+Zcos(F)→XY+Zsin(F)→YSUB2(子程序名)G-90→T(Y-V)cos(T)-(X-U)sin(T)→WAbs(W)→W:0→ZLbI 4:Prog"SUB1"T+QEW(C+WD)→L(J-Y)cos(L)-(I-X)sin(L)→ZIf Abs(Z)<1E-6:Then 0→Z Prog"SUB1" (J-Y)÷sin(F)→ZElse W+Z→W:Goto 4:IfEnd计算器主程序:ZHU-CHENG-XULbi0:“1,ZS=FS,2ZS,3FS,4XY=>SG,5。
坐标方位角连续计算 fx-5800计算器编程

坐标方位角连续计算fx-5800计算器编程摘要:利用fx-5800计算器可编程的特点,编写坐标方位角连续计算程序,使计算方位角的工作变得简单易行,并且工作量大幅度降低。
关键词:方位角;左侧转角;导线Abstract: using fx-5800 calculator programmable characteristics, write coordinates continuous calculation program azimuth, make millionsCalculate azimuth of work has become simple and feasible, and greatly reduce the workload.Keywords: azimuth; The left corner; wire一、基本原理如上图,沿A B1 2 3 4 5方向测得左侧转角分别为、、、、;AB方向的坐标方位角为。
则:B1方向坐标方位角为①当时,②当时,③当时,12方向坐标方位角为①当时,②当时,③当时,2 3方向坐标方位角为①当时,②当时,③当时,3 4方向坐标方位角为①当时,②当时,③当时,4 5方向坐标方位角为①当时,②当时,③当时,二、源程序FWJJS 程序名0J:0 B:”N=“?JLbl1“ =“?BJ+B JIfJ<1800:Then J+1800J:N=J: “N=“:J►DMS◢Goto 1Else If J≥5400:Then J-5400 J:N=J: “N=“:J►DMS◢Else J-1800 J:N=J:”N=“:J►DMS◢IfEnd:Goto 1三、程序运行【例】已知AB边的坐标方位角,由B点起始向前分别实测了1、2、3、4导线点,已知数据如下,计算B1、12、23、34边的坐标方位角。
已知边实测水平角NAB=操作步骤按MODE 5 2 按▲▼键,当文件名为TLX—FWJJS高亮度显示时,按EXE 。
Fx-5800计算器程序(含定向及放样方位角、距离计算)
Fx-5800计算器程序一、道路放样(含定向及放样方位角、距离计算)1、主程序:1JDZB(利用第一交点坐标,第二交点坐标,第三交点坐标及里程,偏角,半径,缓和曲线长度计算)20→DimZ“JD1X=”:?X:X→Z[1]:“JD1Y=”:?Y:Y→Z[2]: 输入JD1坐标“JD2X=”:?X:X→U:“JD2Y=”:?Y:Y→V: 输入JD2坐标“JD3X=”:?X:X→Z[3]:“JD3Y=”:?Y:Y→Z[4]: 输入JD3坐标I=PoI(U-Z[1],V-Z[2]):If J<0:Then J+360→J:EIse J→J:IfEnd:J→F:"F12=":F►DMS▲显示起始边方位角I=PoI(Z[3]-U,Z[4]-V):If J<0:Then J+360→J:EIse J→J:IfEnd:J→Z[5]:"F23=":Z[5]►DMS▲显示结束边方位角F-Z[5]→A:If A<-180:Then A+360→A:EIse A→A:If End:"A=":A►DMS▲显示偏角Prog“2FJDA”2、次主程序:2FJDA(利用起始方位角,交点坐标及里程,偏角,半径,缓和曲线长度计算)"HX="?X:"HY="?Y: 输入定向(后视点)坐标"ZX="?H:"ZY="?K: 输入测站点坐标Prog“J”显示定向(后视点)距离和方位角“A=”?A:输入偏角(左“-”右“+”),当利用1JDZB程序时,不用再次输入“R=”?R:输入平曲线半径“LS=”?L:输入缓和曲线长度“JDL=”?N:输入平曲线交点里程“JDX=”?U:输入交点X坐标,当利用1JDZB程序时,不用再次输入“JDY=”?V:输入交点Y坐标,当利用1JDZB程序时,不用再次输入“F=”?F:输入起边方位角,当利用1JDZB程序时,不用再次输入180/R/π→Z:ZL/2→B: “B=”:B►DMS▲缓和曲线角“P=”:L^(2)/(24R)-L^(4)/(2688R^(3))→P▲内移距“Q=”:L/2-L^(3)/(240R^(2))+L^(5)/(34560R^(4))→Q▲切线增长“T=”:(R+P)tan(Abs(A/2))+Q→T▲显示平曲线切线长度“E=”:(R+P)/Cos(Abs(A/2))-R→E▲显示平曲线外距值“L=”:(Abs(A)-2B)/Z+2L→o▲显示平曲线曲线长度“D=”:2T-o→D▲显示球曲差30→DimZ“ZH=”:N-T→Z[1]▲显示直缓点里程“HY=”:Z[1]+L→Z[2]▲显示缓圆点里程“QZ=”:Z[1]+o/2→Z[3]▲显示曲中点里程“YH=”:Z[1]+o-L→Z[4]▲显示圆缓点里程“HZ=”:Z[1]+o→Z[5]▲显示缓直点里程“ZHX=”:U+Tcos(F+180)→Z[7]▲显示直缓点X坐标“ZHY=”:V+Tsin(F+180)→Z[8]▲显示直缓点Y坐标“HZX=”:U+Tcos(F+A)→Z[15]▲显示缓直点X坐标“HZY=”:V+Tsin(F+A)→Z[16]▲显示缓直点Y坐标0→C:0→W:L-L^(3)/(90R^(2))→C:ZL/6→W:If A<0:Then -W→W: EIse W→W: If End:“HYX=”:Z[7]+Ccos(F+W)→Z[9]▲显示缓圆点X坐标“HYY=”:Z[8]+Csin(F+W)→Z[10]▲显示缓圆点Y坐标“YHX=”:Z[15]+Ccos(F+A+180-W)→Z[13]▲显示圆缓点X坐标“YHY=”:Z[16]+Csin(F+A+180-W)→Z[14]▲显示圆缓点Y坐标If A<0:Then -B→B:EIse B→B:If End:0→S:0→C:0→W:o/2-L→S:SZ/2→W:2Rsin(W)→C:If A<0:Then -W→W: EIse W→W:If End:“QZX=”:Z[9]+Ccos(F+B+W)→Z[11]▲显示曲中点X坐标“QZY=”:Z[10]+Csin(F+B+W)→Z[12]▲显示曲中点Y坐标LbI8:“LP=”?→M:Prog“3ZBJS”:Goto8 输入放样点P里程3、子程序:3ZBJS20→DimZ0→S:0→W:0→D:0→G:If M≤Z[1]:Then F+180→W:F+90→G:N-M→S:U→P:V→Q:Goto5: Else If M≤Z[2]:Then M-Z[1]→S:Z[7]→P:Z[8]→Q:Goto1:Else If M<Z[4]:Then M-Z[2]→S:Z[9]→P:Z[10]→Q:Goto2:Else If M<Z[5]:Then Z[5]-M→S:Z[15]→P:Z[16]→Q:Goto1: Else F+A→W:W+90→G:T+M-Z[5]→S:U→P:V→Q:Goto5:If End:LbI 1:ZS^(2)/(6L)→W:3W→G:S-S^(5)/(90R^(2)L^(2))→S:If A<0:Then -W→W:-G→G:EIse W→W:G→G:If End:If M<Z[2]:Then F+W→W:F+G+90→G:EIse F+A+180-W→W:F+A+180-G-90→G:If End:Goto5:LbI 2:SZ/2→W:2W→G:2Rsin(W)→S:If A<0:Then -W→W:-G→G:EIse W→W:G→G:If End:F+B+W→W:F+B+G+90→G:Goto5:LbI 5:“X=”:P+Scos(W)→Z[13]▲“Y=”:Q+Ssin(W)→Z[14]▲Z[13]→X:Z[14]→Y:Prog“J”:显示放样点(前视点)距离和方位角Goto6:LbI 6:“BZ=”?D: 输入偏距(左“-”右“+”)“X=”:Z[13]+Dcos(G)→Z[17]▲“Y=”:Z[14]+Dsin(G)→Z[18]▲Z[17]→X:Z[18]→Y:Prog“J”显示放样点(前视点)距离和方位角4、子程序:JI=PoI(X-H,Y-K):If J<0:Then J+360→J:EIse J→J:IfEnd:"S=":I▲"F=":J►DMS▲。
方位角计算公式.
一、直线定向1、正、反方位角换算对直线而言,过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角,而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角,同一条直线的正、反方位角相差,即同一直线的正反方位角= (1-13)上式右端,若<,用“+”号,若,用“-”号。
2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。
所谓象限角是指从坐标纵轴的指北端或指南端起始,至直线的锐角,用表示,取值范围为。
为了说明直线所在的象限,在前应加注直线所在象限的名称。
四个象限的名称分别为北东(NE)、南东(SE)、南西(SW)、北西(NW)。
象限角和坐标方位角之间的换算公式列于表1-4。
表1-4 象限角与方位角关系表象限象限角与方位角换算公式第一象限(NE)=第二象限(SE)=-第三象限(SW)=+第四象限(NW)=-3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向,而是通过与已知方向进行连测,推算出各边的坐标方位角。
设地面有相邻的、、三点,连成折线(图1-17),已知边的方位角,又测定了和之间的水平角,求边的方位角,即是相邻边坐标方位角的推算。
水平角又有左、右之分,前进方向左侧的水平角为,前进方向右侧的水平角。
设三点相关位置如图1-17()所示,应有=++ (1-14)设三点相关位置如图1-17()所示,应有=++-=+- (1-15)若按折线前进方向将视为后边,视为前边,综合上二式即得相邻边坐标方位角推算的通式:=+(1-16)显然,如果测定的是和之间的前进方向右侧水平角,因为有=-,代入上式即得通式=- (1-17)上二式右端,若前两项计算结果<,前面用“+”号,否则前面用“-”号。
二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。
坐标正算,就是根据直线的边长、坐标方位角和一个端点的坐标,计算直线另一个端点的坐标的工作。
如图1所示,设直线AB的边长DAB和一个端点A的坐标XA、YA为已知,则直线另一个端点B的坐标为:XB=XA+ΔXABYB=YA+ΔYAB式中,ΔXAB、ΔYAB称为坐标增量,也就是直线两端点A、B的坐标值之差。
方位角计算
三、三种方位角之间的关系因标准方向选择的不同,使得一条直线有不同的方位角,如图4-19所示。
过1点的真北方向与磁北方向之间的夹角称为磁偏角,用δ表示。
过1点的真北方向与坐标纵轴北方向之间的夹角称为子午线收敛角,用γ表示。
δ和γ的符号规定相同:当磁北方向或坐标纵轴北方向在真北方向东侧时,δ和γ的符号为“+”;当磁北方向或坐标纵轴北方向在真北方向西侧时,δ和γ的符号为“-”。
同一直线的三种方位角之间的关系为:δ+=m A A (4-14); γα+=A (4-15);2图4-19 三种方位角之间的关系γδα-+=M A (4-16)四、坐标方位角的推算 1.正、反坐标方位角如图4-20所示,以A 为起点、B 为终点的直线AB 的坐标方位角αΑB ,称为直线AB 的坐标方位角。
而直线BA 的坐标方位角αBA ,称为直线AB 的反坐标方位角。
由图4-20中可以看出正、反坐标方位角间的关系为:︒±=180BA AB αα(4-17)2.坐标方位角的推算y图4-20 正、反坐标方位角在实际工作中并不需要测定每条直线的坐标方位角,而是通过与已知坐标方位角的直线连测后,推算出各直线的坐标方位角。
如图4-21所示,已知直线12的坐标方位角α12,观测了水平角β2和β3,要求推算直线23和直线34的坐标方位角。
由图4-21可以看出:21222123180βαβαα-︒+=-= 32333234180βαβαα+︒+=+=因β2在推算路线前进方向的右侧,该转折角称为右角;β3在左侧,称为左角。
从而可归纳出推算坐标方位角的一般公式为:134图4-21 坐标方位角的推算左后前βαα+︒+=180(4-18)右后前βαα-︒+=180(4-19)计算中,如果α前>360˚,应自动减去360°;如果α前<0˚,则自动加上360˚。
五、象限角 1.象限角(E)图4-22 象限角由坐标纵轴的北端或南端起,沿顺时针或逆时针方向量至直线的锐角,称为该直线的象限角,用R表示,其角值范围为0˚~90˚。
方位角计算公式
一、直线定向1、正、反方位角换算对直线而言,过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角,而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角,同一条直线的正、反方位角相差,即同一直线的正反方位角= (1-13> 上式右端,若<,用“+”号,若,用“-”号。
2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。
所谓象限角是指从坐标纵轴的指北端或指南端起始,至直线的锐角,用表示,取值范围为。
为了说明直线所在的象限,在前应加注直线所在象限的名称。
四个象限的名称分别为北东<NE)、南东<SE)、南西(SW>、北西(NW>。
象限角和坐标方位角之间的换算公式列于表1-4。
象限角与方位角换算公式==-=+=-3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向,而是通过与已知方向进行连测,推算出各边的坐标方位角。
设地面有相邻的、、三点,连成折线<图1-17),已知边的方位角,又测定了和之间的水平角,求边的方位角,即是相邻边坐标方位角的推算。
水平角又有左、右之分,前进方向左侧的水平角为,前进方向右侧的水平角。
设三点相关位置如图1-17(>所示,应有=++ (1-14>设三点相关位置如图1-17(>所示,应有=++-=+- (1-15>若按折线前进方向将视为后边,视为前边,综合上二式即得相邻边坐标方位角推算的通式:=+(1-16>显然,如果测定的是和之间的前进方向右侧水平角,因为有=-,代入上式即得通式=- (1-17>上二式右端,若前两项计算结果<,前面用“+”号,否则前面用“-”号。
二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。
坐标正算,就是根据直线的边长、坐标方位角和一个端点的坐标,计算直线另一个端点的坐标的工作。
如图1所示,设直线AB的边长DAB和一个端点A的坐标XA、YA为已知,则直线另一个端点B的坐标为:XB=XA+ΔXABYB=YA+ΔYAB式中,ΔXAB、ΔYAB称为坐标增量,也就是直线两端点A、B的坐标值之差。
