高二数学选修2-2第二章推理与证明
_高中数学第二章推理与证明2

跟踪练习
(2014~2015·合肥一六八中高二期中)观察下题的解答过
程:
已知正实数 a、b 满足 a+b=1,求 2a+1+ 2b+1的最
大值.
解:∵
2a+1· 2≤
2a+12+ 2
22=a+32,
2b+1· 2
≤
2b+12+ 2
22=b+32,
相 加 得 2a+1 · 2 + 2b+1 · 2 = 2 ( 2a+1 + 2b+1)≤a+b+3=4.
综合法: ∵a、b、c∈R+,∴(a-b)2+(b-c)2+(c-a)2≥0, ∴2(a2+b2+c2)≥(ab+bc+ac), ∴3(a2+b2+c2)≥a2+b2+c2+2ab+2bc+2ac, ∴3(a2+b2+c2)≥(a+b+c)2, ∴ a2+b32+c2≥a+3b+c.
人教版 选修2-2
第二章 推理与证明
2.2 直接证明与间接证明
2.2.1 综合法和分析法
目标导航
• 了解综合法与分析法的特点,熟练应用分析法与综合法证明 命题.
重点难点
• 重点:综合法和分析法的概念及思考过程、特点. • 难点:综合法和分析法的应用.
新知导学
1.综合法证明不等式
• 1.定义 • 利用___已__知__条__件___和某些数学__定__义____、__定__理____、
、已知的重要不等式和逻辑推理的基本理论;
• (2)适用范围:对于一些条件复杂,结构简单的不等式的证明 ,经常用综合法.而对于一些条件简单、结论复杂的不等式 的证明,常用分析法;
• (3)思路方法:分析法证明不等式的思路是从要证的不等式出 发,逐步寻求使它成立的充分条件,最后得到的充分条件是 已知(或已证)的不等式;
高中数学选修2-2(人教A版)第二章推理与证明2.2知识点总结含同步练习及答案

4. 当 q ≠ 1 时, S n =
−a1 n a q + 1 = aq n + b ,这里 a + b = 0 ,且 a ≠ 0, b ≠ 0 ,这是等比数 1−q 1−q 列前 n 项和公式的一个特征,据此很容易根据 S n ,判断数列 {an } 是否为等比数列.如若 {an } 是
等比数列,且 S n = 3 n + r ,则 r =
)
C.2 D.3
B.1
2. 从任何一个正整数 n 出发,若 n 是偶数就除以 2 ,若 n 是奇数就乘 3 再加 1 ,如此继续下去
⋯ ⋯,现在你从正整数 3 出发,按以上的操作,你最终得到的数不可能是 (
A.1
答案: C 解析: 按照题中给出的规则:
)
B.2
C.3
D.4
10 = 5 ;得到的第三个数是 2 16 8 5 × 3 + 1 = 16 ;得到的第四个数是 = 8 ;得到的第五个数为 = 4 ; 2 2 4 2 得到的第六个数为 = 2 ;得到第七个数为 = 1 ;得到第八个数为 1 × 3 + 1 = 4. 2 2 所以后面的数是以 4、2、1 为一个周期的数.
高中数学选修2-2(人教A版)知识点总结含同步练习题及答案
第二章 推理与证明 2.1 合情推理与演绎推理
一、学习任务 1. 能用归纳和类比等进行简单的推理,体会并了解合情推理在数学发现中的作用. 2. 理解演绎推理的基本方法,并能运用它们进行一些简单推理. 3. 了解合情推据已知中的点
E, F 的位置,如图,可知入射角的正切值为 2 ,第一次碰撞点为 F ,在反射 的过程中,直线是平行的,利用平行关系及三角形的相似可得第二次碰撞点 G 在 DA 上 ,且 1 1 DG = , 第三次碰撞点 H 在 DC 上,且 DH = ,第四次碰撞点 M 在 CB 上,且 6 3 1 1 1 CM = ,第五次碰撞点为 N ,在 DA 上,且 AN = ,第六次回到 E 点, AE = . 3 6 3
高二数学选修2-2第二章推理与证明课时练习一合情推理

高二数学选修2-2第二章推理与证明课时练习一合情推理一、选择题1、数列2,5,11,20,x ,47…中的x 等于( )A 28B 32C 33D 27 2、对“c b a 、、是不全相等的正数”,给出以下判断:① 0)()()(222≠-+-+-a c c b b a ;② b a b a b a =<>及与中至少有一个成立; ③ c a c b c a ≠≠≠,,不能同时成立,其中判断准确的个数是( )A 0B 1C 2D 33、数列1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,…的第1000项是( ) A 42 B 45 C 48 D 514、与函数x y =为相同函数的是( )A 2x y = B xx y 2= C xe y ln = D x y 22log =二、填空题5、从222576543,3432,11=++++=++=中,克的一般性结论是_________________ 6、设221)(+=xx f ,利用课本中推导等差数列前n 项和公式的方法,可求得)6()5()0()4()5(f f f f f ++⋅⋅⋅++⋅⋅⋅+-+-的值是________________.三、解答题7、若数列{}n a 为等差数列,且),,(,+∈≠==N n m n m b a a a n m ,则mn ambn a n m --=+,现已知数列{}),0(+∈>N n b b nn 为等比数列,且),,(,+∈≠==N n m n m b b a b n m ,类比以上结论,可得到什么命题?并证明你的结论.8、若数列{}n a 满足1,2211+-==+n n n na a a a ,试猜测这个数列的通项公式。
选做题9、若数列{}n a 的前8项的值各异,且n n a a =+8对任意的+∈N n 都成立,则以下数列中,可取遍{}n a 的前8项值的数列是( )A {}12+k aB {}13+k aC {}14+k aD {}16+k a 10、观察(1)15tan 75tan 75tan 10tan 10tan 5tan )2(;110tan 60tan 60tan 20tan 20tan 10tan 000000000000=++=++由以上两式成立,推广到一般结论,写出你的推论。
高二数学选修2-2第二章 推理与证明

§2.1.1 合情推理学习目标1. 结合已学过的数学实例,了解归纳推理的含义;2. 能利用归纳进行简单的推理,体会并认识归纳推理在数学发现中的作用.学习过程一、课前准备(预习教材P 70~ P77,找出疑惑之处) 在日常生活中我们常常遇到这样的现象:(1)看到天空乌云密布,燕子低飞,蚂蚁搬家,推断天要下雨; (2)八月十五云遮月,来年正月十五雪打灯.以上例子可以得出推理是 的思维过程.二、新课导学探究任务一:考察下列示例中的推理问题:因为三角形的内角和是180(32)︒⨯-,四边形的内角和是180(42)︒⨯-,五边形的内角和是180(52)︒⨯-……所以n 边形的内角和是新知1:从以上事例可一发现: 叫做合情推理。
归纳推理和类比推理是数学中常用的合情推理。
探究任务二:问题1:在学习等差数列时,我们是怎么样推导首项为1a ,公差为d 的等差数列{a n }的通项公式的?新知 2 归纳推理就是根据一些事物的 ,推出该类事物的 的推理归纳是 的过程 例子:哥德巴赫猜想:观察 6=3+3, 8=5+3, 10=5+5, 12=5+7, 14=7+7, 16=13+3, 18=11+7, 20=13+7, ……,50=13+37, ……, 100=3+97,猜想: .归纳推理的一般步骤1 。
2 。
※ 典型例题例1用推理的形式表示等差数列1,3,5,7……2n-1,……的前n 项和S n 的归纳过程。
例2设2()41,f n n n n N +=++∈计算(1),(2),(3,)...(10)f f f f 的值,同时作出归纳推理,并用n=40验证猜想是否正确。
练1. 观察圆周上n 个点之间所连的弦,发现两个点可以连一条弦,3个点可以连3条弦,4个点可以连6条弦,5个点可以连10条弦,由此可以归纳出什么规律?三、总结提升※ 学习小结 1.归纳推理的定义. 2. 归纳推理的一般步骤:①通过观察个别情况发现某些相同的性质; ②从已知的相同性质中推出一个明确表述的一般性命题(猜想). ※ 当堂检测(时量:5分钟 满分:10分)计分: 1.下列关于归纳推理的说法错误的是( ). A.归纳推理是由一般到一般的一种推理过程 B.归纳推理是一种由特殊到一般的推理过程 C.归纳推理得出的结论具有或然性,不一定正确 D.归纳推理具有由具体到抽象的认识功能2. 已知2()(1),(1)1()2f x f x f f x +==+ *x N ∈(),猜想(f x )的表达式为( ).A.4()22x f x =+B.2()1f x x =+C.1()1f x x =+D.2()21f x x =+3.111()1()23f n n N n +=+++⋅⋅⋅+∈,经计算得357(2),(4)2,(8),(16)3,(32)222f f f f f =>>>>猜测当2n ≥时,有__________________________.4 已知1+2=3,1+2+3=6,1+2+3+4=10,……1+2+3+……+n=(1)2n n +,观察下列立方和: 13,13+23,13+23+33,13+23+33+43,…… 试归纳出上述求和的一般公式。
高中数学选修2-2(人教B版)第二章推理与证明2.1知识点总结含同步练习题及答案

第二章 推理与证明 2.1 合情推理与演绎推理
一、学习任务 1. 能用归纳和类比等进行简单的推理,体会并了解合情推理在数学发现中的作用. 2. 理解演绎推理的基本方法,并能运用它们进行一些简单推理. 3. 了解合情推理和演绎推理的联系和区别.
二、课后作业
(查看更多本章节同步练习题,请到快乐学)
1. 下面说法正确的有 (
)
①演绎推理是由一般到特殊的推理; ②演绎推理得到的结论一定是正确的; ③演绎推理一般模式是"三段论"形式; ④演绎推理的结论的正误与大前提、小前提和推理形式有关. A.1 个
答案: D
B.2 个
答案: B
)
B.4 或 6 或 7 或 8 个部分D.6 或 7 或 8 个部分
C.4 或 7 或 8 个部分
4. 已知 √2 +
− − − − − − − − − − − − − − − − − − − − −− − 2 2 3 3 4 4 = 2 ⋅ √ ,√3 + = 3 ⋅ √ ,√4 + = 4 ⋅ √ ,….若 3 3 8 8 15 15 − − − − − − − a a √8 + = 8 ⋅ √ (a, t 均为正实数),类比以上等式,可推测 a, t 的值,则 a + t = t t
答案: 解析: 根据已知归纳推理有根号下的分子和根号前面的数字一样,即
.
71
数相乘减一,所以 t = 64 − 1 = 63 .
a = 8,分母等于分子与根式外的
高考不提分,赔付1万元,关注快乐学了解详情。
C.3 个
D.4 个
2. "因为对数函数 y = loga x 是增函数,而 y = log 1 x 是对数函数,所以 y = log 1 x 是增函数".这个推 理是错误的,是因为 ( A.大前提错误
最新人教版高中数学选修2-2第二章《推理与证明》本章小结
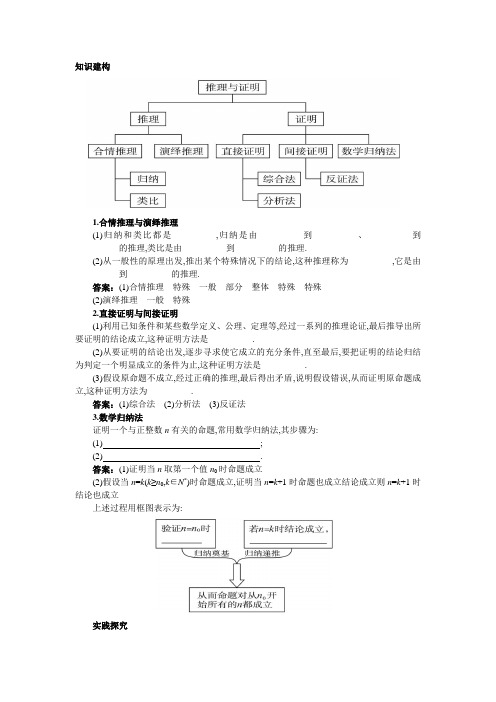
知识建构1.合情推理与演绎推理(1)归纳和类比都是__________,归纳是由__________到__________、__________到__________的推理,类比是由__________到__________的推理.(2)从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为__________,它是由__________到__________的推理.答案:(1)合情推理特殊一般部分整体特殊 特殊(2)演绎推理一般特殊2.直接证明与间接证明(1)利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法是__________.(2)从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,要把证明的结论归结为判定一个明显成立的条件为止,这种证明方法是__________.(3)假设原命题不成立,经过正确的推理,最后得出矛盾,说明假设错误,从而证明原命题成立,这种证明方法为__________.答案:(1)综合法(2)分析法(3)反证法3.数学归纳法证明一个与正整数n有关的命题,常用数学归纳法,其步骤为:(1);(2).答案:(1)证明当n取第一个值n0时命题成立(2)假设当n=k(k≥n0,k∈N*)时命题成立,证明当n=k+1时命题也成立结论成立则n=k+1时结论也成立上述过程用框图表示为:实践探究1.下图中的三角形称为希尔宾斯基(S ierpi n s k i)三角形,在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式__________.思路分析:如题图,这4个三角形中着色三角形的个数依次为1,3,9,27.则所求数列的前4项都是3的指数幂,指数为序号减1.猜想这个数列的一个通项公式是a n =3n -1.答案:a n =3n -1温馨提示:(1)上面数列的递推关系为a n +1=3a n .(2)通项公式可用数学归纳法证明.2.若数列{a n }是一个等差数列,则{na a a n 21+++ }是一个等差数列.类比这条性质,若数列{b n }是一个等比数列,则有__________是一个等比数列.思路分析:在等差数列{a n }与等比数列{b n } 中,有{a n } {b n }和 a 1+a 2+…+a n积 b 1b 2…b n算术平均数{n a a a n 21+++ }等差几何平均数{n n 21b b b }等比证明:设数列{b n }的首项为b 1,公比为q, 则n 1)-(n 2111n n 211n 1n n211n 1n 21q b q b b b b b b b ++++++++++= =2121n 12n 1n 21)n(n n 11n 21)n (n 1n 1q q b q b q b q b --+++=(常数),∴数列{n n 21b b b }为等比数列. 答案:{ n n 21b b b }3.已知O 是△A B C 内任意一点,连结A O 、BO 、C O 并延长交对边于A′、B ′、C′,则1C C C O B B B O A A A O =''+''+''.这是平面几何中的一道题,其证明常采用“面积法”: C C C O B B B O A A A O ''+''+''=ABCABC ABC OAB ABC OCA ABC OBC S S S S S S S S ∆∆∆∆∆∆∆∆+++=1. 运用类比,猜想对于空间中的四面体A —B CD,存在什么类似的结论?并用“体积法”证明. 猜想:已知点O 为四面体A —B CD 内任意一点,连结A O 、BO 、C O 、D O 并延长交相对面于A′、B ′、C′、D′,则有OD D O OC C O OB B O OA A O '+'+'+'=1. 证明:设点A 、O 到平面B CD 的距离分别为h 、h′,则OA A O h h '=', ∴OA A O h h h S 31h S 31V V BCD BCD BCD A BCDO '='=⋅'⋅=∆∆--. 同理,ACDB ACD O V V OB B O --=', ABDC ABD O V V OC C O --=', ,V V OD D O ABCD ABC O --=' ∴OD D O OC C O OB B O OA A O '+'+'+'=BCDA BCD A V V --=1.。
人教新课标版数学高二-选修2-2第二章《推理与证明》小结

数学·选修2-2(人教A版)推理是人们思维活动的过程,本章主要介绍人们在日常生活和科学研究中经常使用的两种推理——合情推理和演绎推理.合情推理包括归纳推理和类比推理,演绎推理部分主要学习直接证明、间接证明和数学归纳法.1.归纳和类比都是合情推理,前者是由特殊到一般、部分到整体的推理,后者是由特殊到特殊的推理,但两者都能由已知推测未知,都能用于猜想,推理的结论不一定为真,有待进一步证明.2.演绎推理与合情推理不同,是由一般到特殊的推理,是数学中证明的基本形式,也是公理化体系所采用的推理形式;另一方面,合情推理与演绎推理又是相辅相成的,前者是后者的前提,后者论证前者的可靠性.3.直接证明和间接证明是数学证明的两类基本证明方法.直接证明的两类基本方法是综合法和分析法:综合法是从已知条件推出结论的证明方法,分析法是从结论追溯到条件的证明方法.在解决数学问题时,常把它们结合起来使用.间接证明的一种方法是反证法.反证法是从结论反面成立出发,推出矛盾的方法.4.数学归纳法主要用于解决与正整数有关的数学命题.证明时,它的两个步骤缺一不可,它的第一步(归纳奠基)是证n=n0时结论成立;第二步(归纳递推)是假设n=k时结论成立,推得n=k+1时结论也成立.数学归纳法原理建立在归纳推理的基础上,它可用有限的步骤(两步)证明出无限的命题成立.题型一合情推理与演绎推理(1)对奇数列1,3,5,7,9,…,进行如下分组:第一组含一个数{1};第二组含两个数{3,5};第三组含三个数{7,9,11};第四组含四个数{13,15,17,19};…试观察猜想每组内各数之和f(n)(n∈N*)与组的编号数n的关系式为____________.(2)在平面几何中,对于Rt△ABC,设AB=c,AC=b,BC=a,则:①a2+b2=c2;②cos2A+cos2B=1;③Rt△ABC的外接圆半径为r=a2+b2 2.把上面的结论类比到空间写出相类似的结论解析:(1)由于1=13,3+5=8=23,7+9+11=27=33,13+15+17+19=64=43,…,猜想第n组内各数之和f(n)与组的编号数n的关系式为f (n)=n3.(2)选取3个侧面两两垂直的四面体作为直角三角形的类比对象.①设3个两两垂直的侧面的面积分别为S1,S2,S3,底面面积为S,则S21+S22+S23=S2.②设3个两两垂直的侧面与底面所成的角分别为α,β,γ,则cos2α+cos2β+cos2γ=1.③设3个两两垂直的侧面形成的侧棱长分别为a,b,c,则这个四面体的外接球的半径为R=a2+b2+c22.点评:(1)归纳推理的难点是由部分结果得到一般结论,破解的方法是充分考虑这部分结果提供的信息,从中发现一般规律,解题的一般步骤是:①对有限的资料进行观察、分析、归纳整理;②提出带有规律性的结论,即猜想;③检验猜想.(2)类比是从已经掌握了的事物的属性,推测正在研究的事物的属性,是以旧有的认识为基础,类比出新的结果;类比是从一种事物的特殊属性推测另一种事物的特殊属性;类比的结果是猜测性的,不一定可靠,但它却有发现的功能.题型二综合法与分析法(1)若实数a,b满足a+b=3,证明:2a+2b≥42;(2)设a >b >0,证明:a 2-b 2a 2+b 2>a -b a +b.证明:(1)因为2a +2b ≥22a ·2b =2v 2a +b ,又a +b =3,所以2a +2b ≥223=4 2.当且仅当a =b =32时等号成立. 故2a +2b ≥42成立.(2)要证明a 2-b 2a 2+b 2>a -b a +b(由a >b >0,得a -b >0),只需证(a 2-b 2)(a +b )>(a 2+b 2)(a -b ),只需证(a +b )2>a 2+b 2,即2ab >0,因为a >b >0,所以2ab >0显然成立.因此当a >b >0时,a 2-b 2a 2+b 2>a -b a +b成立. 点评:分析法和综合法是对立统一的两种方法,在使用这两种方法解题是,一般步骤是:①分析条件和结论之间的联系和区别,选择解题方向.②确定恰当的解题方法,若能够结合题设条件,通过相关的公理、定理、公式、结论推得所求结果,则用综合法,若从条件出发,应用相关的公理、定理、公式、结论难以推得所求结果,则可以考虑使用分析法.③解题反思,回顾解题过程,对所得结果和解题步骤进行检查,确保解题的严谨性和完备性.题型三 反证法已知直线ax -y =1与曲线x 2-2y 2=1相交于P ,Q 两点,证明:不存在实数a ,使得以PQ 为直径的圆经过坐标原点O .证明:假设存在实数a ,使得以PQ 为直径的圆经过坐标原点O ,则OP ⊥OQ .设P (x 1,y 1),Q (x 2,y 2),则y 1x 1·y 2x 2=-1, 所以(ax 1-1)(ax 2-1)=-x 1·x 2,即(1+a 2)x 1·x 2-a (x 1+x 2)+1=0.由题意得(1-2a 2)x 2+4ax -3=0,所以x 1+x 2=-4a 1-2a 2,x 1·x 2=-31-2a 2. 所以(1+a 2)·-31-2a 2-a ·-4a 1-2a 2+1=0, 即a 2=-2,这是不可能的.所以假设不成立.故不存在实数a ,使得以PQ 为直径的圆经过坐标原点O .点评:一般以下题型用反证法:①当“结论”的反面比“结论”本身更简单、更具体、更明确; ②否定性命题、唯一性命题,存在性命题、“至多”“至少”型命题; ③有的肯定形式命题,由于已知或结论涉及无限个元素,用直接证明比较困难,往往用反证法.用反证法证明不等式要把握三点:①必须先否定结论,即肯定结论的反面;②必须从否定结论进行推理,即应把结论的反面作为条件,且必须依据这一条件进行推证;③推导出的矛盾可能多种多样,有的与已知矛盾,有的与假设矛盾,有的与已知事实矛盾等,但是推导出的矛盾必须是明显的.题型四 数学归纳法用数学归纳法证明122+132+142+ (1)2<1-1n (n ≥2,n ∈N *).证明:当n =2时,左式=122=14,右式=1-12=12,因为14<12,所以不等式成立.假设n =k (k ≥2,k ∈N *)时,不等式成立,即122+132+142+…+1k 2<1-1k ,则当n =k +1时,122+132+142+…+1k 2+1(k +1)2<1-1k +1(k +1)2=1-(k +1)2-k k (k +1)2=1-k 2+k +1k (k +1)2<1-k (k +1)k (k +1)2=1-1k +1,所以当n =k +1时,不等式也成立.综上所述,对任意n ≥2的正整数,不等式都成立.点评:(1)用数学归纳法证明与n 有关的不等式一般有两种具体形式:一是直接给出不等式,按要求进行证明;二是给出两个式子,按要求比较它们的大小.对第二种形式往往要先对n 取前几个值的情况分别验证比较,以免出现判断失误,最后猜出从某个n 值开始都成立的结论,再用数学归纳法证明.(2)用数学归纳法证明不等式的关键是由n =k 时成立得n =k +1时成立,主要方法有:①放缩法;②利用基本不等式法;③作差比较法等.一、选择题1.“因为指数函数y =a x是增函数(大前提),而y =⎝ ⎛⎭⎪⎫13x 是指数函数(小前提),所以函数y =⎝ ⎛⎭⎪⎫13x 是增函数(结论)”,以上推理的错误的原因是( )A .大前提错误导致结论错B .小前提错误导致结论错C .推理形式错误导致结论错D .大前提和小前提错误导致结论错解析:推理形式没有错误,而大前提“y =a x 是增函数”是不正确的,当0<a <1时,y =a x 是减函数;当a >1时,y =a x 是增函数.故选A.答案:A2.锐角三角形的面积等于底乘高的一半;直角三角形的面积等于底乘高的一半;钝角三角形的面积等于底乘高的一半.所以,凡是三角形的面积都等于底乘高的一半.以上推理运用的推理规则是( )A .三段论推理B .假言推理C .关系推理D .完全归纳推理解析:所有三角形按角分,只有锐角三角形、直角三角形和钝角三角形三种情形,上述推理穷尽了所有的可能情形,故为完全归纳推理.答案:D3.用数学归纳法证明等式1+2+3+…+(n+3)=(n+3)(n+4)2(n∈N*)时,验证n=1,左边应取的项是()A.1 B.1+2C.1+2+3 D.1+2+3+4解析:当n=1时,左=1+2+…+(1+3)=1+2+…+4,故应选D.答案:D4.由“正三角形的内切圆切于三边的中点”可类比:正四面体的内切球切于四个面()A.各正三角形内一点B.各正三角形的某高线上的点C.各正三角形的中心D.各正三角形外的某点解析:正三角形的边对应正四面体的面,即正三角形所在的正四面体的侧面,所以边的中点对应的就是正四面体各正三角形的中心.故选C.答案:C5.已知a+b+c=0,则ab+bc+ca的值() A.大于0 B.小于0C.不小于0 D.不大于0解析:解法一因为a+b+c=0,所以a2+b2+c2+2ab+2ac+2bc=0,所以ab+bc+ca=-a2+b2+c22≤0.解法二令c=0,若b=0,则ab+bc+ca=0,否则a、b异号,所以ab+bc+ca=ab<0,排除A、B、C,故选D.答案:D6.若凸k边形的内角和为f(k),则凸(k+1)边形的内角和f(k+1)(k≥3且k∈N*)等于()A.f(k)+π2B.f(k)+πC.f(k)+32π D.f(k)+2π解析:由凸k边形到凸(k+1)边形,增加了一个三角形,故f(k+1)=f(k)+π.故选B.答案:B7.公差不为零的等差数列{a n}的前n项和为S n.若a4是a3与a7的等比中项,S8=32,则S10=()A.18 B.24 C.60 D.90解析:由a24=a3a7得(a1+3d)2=(a1+2d)(a1+6d),2a1+3d=0.再由S8=8a1+562d=32,得2a1+7d=8,则d=2,a1=-3.所以S10=10a1+902d=60,选C.答案:C8.设函数f (x)定义如下表,数列{x n}满足x0=5,且对任意的自=f(x n),则x2 011=()然数均有x n+1A.1 B.2 C.4 D.5解析:x1=f(x0)=f(5)=2,x2=f(2)=1,x3=f(1)=4,x4=f(4)=5,x5=f(5)=2,…,数列{x n}是周期为4的数列,所以x2 011=x3=4,故应选C.答案:C二、填空题9.命题“在△ABC 中,A >B ,则a >b ”,用反证法证明时,假设是________.解析:命题的结论是a >b ,假设应是“a ≤b ”. 答案: a ≤b10.若数列{a n }满足:a 1=1,a n +1=2a n (n ∈N *),则a 5=________;前8项的和S 8=________(用数字作答).解析:a 1=1,a 2=2a 1=2,a 3=2a 2=4,a 4=2a 3=8,a 5=2a 4=16,易知S 8=28-12-1=255,∴应填255.答案:16 25511.(2013·济南高二检测)如果x >0,y >0,x +y +xy =2,则x +y 的最小值__________.解析:由x >0,y >0,x +y +xy =2,得2-(x +y )=xy ≤⎝ ⎛⎭⎪⎪⎫x +y 22,所以(x +y )2+4(x +y )-8≥0,所以x +y ≥23-2或x +y ≤-2-23, 因为x >0,y >0,所以x +y 的最小值为23-2. 答案:23-212.已知数列{a n }满足:a 4n -3=1,a 4n -1=0,a 2n =a n ,n ∈N *,则a 2 009=________,a 2 014=________.解析:依题意,得a 2 009=a 4×503-3=1,a 2 014=a 2×1 007=a 1 007=a 4×252-1=0.∴应填1,0. 答案:1 0三、解答题13.证明不等式:12×34×…×2n -12n <12n +1(n ∈N *).证明:(1)当n =1时,左边=12,右边=13,显然12 < 13,不等式成立.(2)假设n=k时,不等式成立,即1 2×34×…×2k-12k<12k+1,则n=k+1时,12×34×…×2k-12k×2k+12k+2<12k+1×2k+12k+2=2k+12k+2,要证n=k+1时,不等式成立,只要2k+1 2k+2<12k+3成立.即证(2k+1)(2k+3)<(2k+2)2,即证4k2+8k+3<4k2+8k+4.该不等式显然成立.即n=k+1时,不等式成立.由(1)(2)知,对任意的正整数n,不等式成立.14.如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.(1)若CD=2,平面ABCD⊥平面DCEF,求MN的长;解析:如下图,取CD的中点G,连接MG,NG,因为ABCD,DCEF为正方形,且边长为2,所以MG⊥CD,MG=2,NG= 2.因为平面ABCD⊥平面DCEF,所以MG⊥平面DCEF.所以MG⊥GN.所以MN=MG2+GN2= 6.(2)用反证法证明:直线ME与BN是两条异面直线.证明:假设直线ME与BN共面,则AB⊂平面MBEN,且平面MBEN ∩平面DCEF =EN .由已知,两正方形ABCD 和DCEF 不共面,故AB ⊄平面DCEF . 又AB ∥CD ,所以AB ∥平面DCEF . 所以EN ∥AB ,又AB ∥CD ∥EF , 所以EF ∥NE ,这与EF ∩EN =E 矛盾, 故假设不成立.所以ME 与BN 不共面,它们是异面直线.15.某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:①sin 213°+cos 217°-sin 13°cos 17°; ②sin 215°+cos 215°-sin 15°cos 15°; ③sin 218°+cos 212°-sin 18°cos 12°; ④sin 2(-18°)+cos 248°-sin(-18°)cos 48°; ⑤sin 2(-25°)+cos 255°-sin(-25°)cos 55°.(1)试从上述五个式子中选择一个,求出这个常数;解析:选择②式,计算如下:sin 215°+cos 215°-sin 15°cos 15°=1-12sin 30°=1-14=34.(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.解析:三角恒等式为sin 2α+cos 2(30°-α)-sin αcos(30°-α)=34.证明如下:证法一 sin 2α+cos 2(30°-α)-sin αcos(30°-α) =sin 2α+(cos 30°cos α+sin 30°sin α)2- sin α(cos 30°cos α+sin 30°sin α)=sin 2α+34cos 2α+32sin αcos α+14sin 2α-32sin αcos α-12sin 2α=34sin 2α+34cos 2α=34.证法二 sin 2α+cos 2(30°-α)-sin αcos(30°-α)=1-cos 2α2+1+cos (60°-2α)2-sin α(cos 30°cos α+sin 30°sin α) =12-12cos 2α+12+12(cos 60°cos 2α+sin 60°sin 2α)-32sin αcos α-12sin 2α=1-12cos 2α+14cos 2α+34sin 2α-34sin 2α-14(1-cos 2α)=1-14cos 2α-14+14cos 2α=34.16.已知{a n }是等差数列,其前n 项和为S n ,{b n }是等比数列,且a 1=b 1=2,a 4+b 4=27,S 4-b 4=10.(1)求数列{a n }与{b n }的通项公式;解析:设等差数列{a n }的公差为d ,等比数列{b n }的公比为q .由a 1=b 1=2,得a 4=2+3d ,b 4=2q 3,S 4=8+6d .由条件得方程组⎩⎨⎧2+3d +3q 3=27,8+6d -2q 3=10⇒⎩⎨⎧d =3,q =2.故a n =3n -1,b n =2n ,n ∈N *.(2)记T n =a n b 1+a n -1b 2+…+a 1b n ,n ∈N *,证明:T n +12=-2a n+10b n (n ∈N *).证明:证法一 T n =a n b 1+a n -1b 2+a n -2b 3+…+a 1b n =2n a 1+2n -1a 2+…+2a n =2n ⎝⎛ a 1+a 22+…+⎭⎪⎪⎫a n 2n -1. 令a n 2n -1=3n -12n -1=3n +22n -2-3n +52n -1=c n -c n +1, ∴T n =2n [(c 1-c 2)+(c 2-c 3)+…+(c n -c n +1)]=10×2n -2(3n +5)=10b n -2a n -12⇔T n +12=10b n -2a n .证法二(数学归纳法)①当n=1时,T1+12=a1b1+12=16,-2a1+10b1=16,故等式成立.②假设当n=k时等式成立,即T k+12=-2a k+10b k,则当n=k+1时,有:T k+1=a k+1b1+a k b2+a k-1b3+…+a1b k+1=a k+1b1+q(a k b1+a k-1b2+…+a1b k)=a k+1b1+qT k=a k+1b1+q(-2a k+10b k-12)=2a k+1-4(a k+1-3)+10b k+1-24=-2a k+1+10b k+1-12,即T k+1+12=-2a k+1+10b k+1,因此n=k+1时等式也成立.由①②可知,对任意n∈N*,T n+12=-2a n+10b n成立.。
人教版高中数学选修2-2第二章推理与证明复习小结优质课件

现命题等,著名哲学家康德说:“每当理智缺乏可靠论证思
路时,类比法往往能指明前进的方向.”
工具
人教A版数学选修2-2 第二章 推理与证明
栏目导引
特别提醒: (1) 归纳推理是由部分到整体,个体到一般
的推理,其结论正确与否,有待于严格证明.
(2) 进行类比推理时,要合理确定类比对象,不能乱 比,要对两类对象的共同特点进行对比.
[ 思维点击 ] 归纳猜想 ――→ fn推理与证明
栏目导引
1 [规范解答] 因为 an= 2, n+1 f(n)=(1-a1)(1-a2)„(1-an) 1 3 所以 f(1)=1-a1=1-4=4,
1 1- f(2)=(1-a1)(1-a2)=f(1)· 9
推理与证明章末小结
工具
人教A版数学选修2-2 第二章 推理与证明
栏目导引
一、合情推理和演绎推理
1.归纳和类比是常用的合情推理,都是根据已有的事
实,经过观察、分析、比较、联想,再进行归纳类比,然后 提出猜想的推理.从推理形式上看,归纳是由部分到整体, 个别到一般的推理,类比是由特殊到特殊的推理,演绎推理 是由一般到特殊的推理.
推出结论的线索不够清晰; (2) 如果从正面证明,需要分成多种情形进行分类讨 论,而从反面进行证明,只要研究一种或很少的几种情形.
工具
人教A版数学选修2-2 第二章 推理与证明
栏目导引
三、数学归纳法
数学归纳法是推理逻辑,它的第一步称为归纳奠基,是
论证的基础保证,即通过验证落实传递的起点,这个基础必 须真实可靠;它的第二步称为归纳递推,是命题具有后继传 递性的保证,两步合在一起为完全归纳步骤,这两步缺一不 可,第二步中证明“当n =k +1 时结论正确”的过程中,必
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2) 6 + 7 >2 2 + 5 。
15、设 a,b,x,y∈R,且
16、若 a,b,c 均为实数,且
,
,
,
求证:a,b,c 中至少有一个大于 0。
17、数学归纳法证明:
能被
整除,
.
18、观察以下各等式:
① tan100 tan 200 tan 200 tan 600 tan 600 tan100 1 ② tan 50 tan100 tan100 tan 750 tan 750 tan 50 1
1 4
, 1 1 1 1 ≥ 4 3 5
1 1 1 1 ,…,由此猜测第 n 个不等式为
3 2 4 6
.( nN*)
1 (1 1 1 … 1 ) ≥ 1 (1 1 1 … 1 )
n1 3 5
2n 1 n 2 4 6
2n
7. 在 RtABC 中 , 若 C 90 0 , AC b, BC a, 则 三 角 形 ABC 的 外 接 圆 半 径
16、可以用综合法与分析法---略
17、可以用反证法---略
18、(1)可以用数学归纳法---略
(2)当 n k 1时,左边 (1 1 1 ) ( 1 1 ) k
2
2k 1 2k
2k1 1
( 1 1 1 ) k 2k 1 k 1=右边,命题正确
2k 2k
2k
(A)假设三内角都不大于 60 度; (C) 假设三内角至多有一个大于 60 度;
(B) 假设三内角都大于 60 度; (D) 假设三内角至多有两个大于 60 度。
5、在十进制中 2004 4100 0101 0102 2103 ,那么在 5 进制中数码 2004 折合成
十进制为 ( )
B. 254 C. 602
将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等
式的特例,则推广的不等式可以是 a mn bmn a mbn a nbm a, b 0, a b, m, n 0
6. 观 察 下 列 不 等 式 :
1 2
1 ≥
1 1 12
,
1 1 3
1 3
≥
1 1 2 2
17、用数学归纳法证明:
(Ⅰ) 12 22
n2
n(n 1) ;
13 35
(2n 1)(2n 1) 2(2n 1)
20、已知数列{an}满足 Sn+an=2n+1, (1) 写出 a1, a2, a3,并推测 an 的表达式; (2) 用数学归纳法证明所得的结论。(12 分)
第四十一中学高二数学选修 2-2《推理与证明测试题》答案
cos 2 cos 2 1。若把它推广到空间长方体中,试写出相应的命题形式:_____________ (长方体 ABCD A1B1C1D1 中,对角线 A1C 与棱 A1A 、A1B1 、A1D1 所成的角分别为 、 、 ,则 cos2 cos2 cos2 1 , sin2 sin2 sin2 2 。或是:长方体 ABCD A1B1C1D1 中,对角线 A1C 与 平 面 A1B 、A1C1 、A1D 所 成 的 角 分 别 为 、 、 , 则 cos2 cos2 cos2 2 , sin2 sin2 sin2 1 。或是:长方体 A1C 中,对角面 A1ACC1 与平面 A1ABB1 、A1ADD1所成的 二面角分别为 、 ,则 cos2 cos2 1 。)
一、 选择题:本大题共 10 小题,每小题 3 分,共 30 分. DCABB CABBB
二、 填空题:本大题共 4 小题,每小题 3 分,共 12 分. 11、14
12、
13
、
14、 5 ;
三、解答题:本大题共 6 题,共 58 分。 15、证明:(1) ∵ a2 b2 2ab ,
a2 3 2 3a ,
2
2
通过观察上述两等式的规律,请你写出一般性的命题:
sin 2 sin 2 ( 60 ) sin 2 ( 120 ) 3 2
5.考察下列一组不等式: 23 53 22 5 2 52 ,
24 54 23 5 2 53, 24 54 23 5 2 53, 25 55 23 52 22 53 , .
(2)三个直角面面积的平方和等于斜面面积的平方;
(3)斜面与三个直角面所成二面角的余弦平方和等于 1.
11.通过圆与球的类比,由“半径为 R 的圆的内接矩形中,以正方形的面积为最大,最大值
为 2R2 .”猜想关于球的相应命题为
.(半径为 R 的球的内接六面体中以正方体的体积
为最大,最大值为 8 3 R3 ) 9
分析上述各式的共同特点,写出能反映一般规律的等式,并对你的结论进行证明。
19、 已知数列 an 的前 n 项和为 S n ,且 a1 1, Sn n2an (n N ) ,
(1)试计算 S1, S2 , S3, S4 ,并猜想 S n 的表达式;
(2) 证明你的猜想,并求出 an 的表达式。
9.若 AB 是过二次曲线中心的任一条弦,M 是二次曲线上异于 A、B 的任一点,且 AM、BM 均与
坐标轴不平行,则对于椭圆 x2 a2
y2 b2
1有 K AM
K BM
b2 a2
。类似地,对于双曲线 x2 a2
y2 b2
1有
b2
K AM K BM =
a2
10.将侧棱相互垂直的三棱锥称为“直角三棱锥”,三棱锥的侧面和底面分别叫为直角三棱锥 的“直角面和斜面”;过三棱锥顶点及斜面任两边中点的截面均称为斜面的“中面”.请仿照 直角三角形以下性质:(1)斜边的中线长等于斜边边长的一半;(2)两条直角边边长的平方 和等于斜边边长的平方;(3)斜边与两条直角边所成角的余弦平方和等于 1.写出直角三棱 锥相应性质(至少一条):_____________. 答案:(1) 斜面的中面面积等于斜面面积的四分之一;
“ n k到n k 1”时,左边应增添的式子是
()
A. 2k 1
B. 2(2k 1)
9、已知 n 为正偶数,用数学归纳法证明
C. 2k 1 k 1
D. 2k 2 k 1
1 1 1 1 1 2( 1 1 1 ) 时,若已假设 n k(k 2 为偶
234
n 1 n 2 n 4
2k
2k 项
19、可以用数学归纳法---略
20、解:
(1) a1= 3 , a2= 7 , a3= 15 ,
2
4
8
猜测
an=2-
1 2n
(2) ①由(1)已得当 n=1 时,命题成立;
②假设 n=k 时,命题成立,即
ak=2-
1 2k
,
当 n=k+1 时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,
且 a1+a2+……+ak=2k+1-ak
∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2-
1 2k
,
ak+1=2-
1 2k 1
,
即当 n=k+1 时,命题成立.
根据①②得 n∈N+
,
an=2-
1 2n
都成立
例 2.设在 R 上定义的函数 f (x) ,对任意实数 x 都 有 f (x 2) f (x 1) f (x), 且f (1) lg 3 lg 2, f (2) lg 3 lg 5 ,试求归纳出 f (2001)
b2 3 2 3b ; 将此三式相加得 2 (a2 b2 3) 2ab 2 3a 2 3b , ∴ a2 b2 3 ab 3(a b) .
(2)要证原不等式成立,
只需证( 6 + 7 ) 2 >(2 2 + 5 ) 2 , 即证 2 42 2 40成立. 现已知当 n 7 时该命题不成立,那么可推得
A.当 n=6 时该命题不成立
B.当 n=6 时该命题成立
C.当 n=8 时该命题不成立
D.当 n=8 时该命题成立
()
8、用数学归纳法证明“ (n 1)(n 2)(n n) 2n 1 2 (2n 1) ”( n N )时,从
r a 2 b 2 ,把此结论类比到空间,写出类似的结论 2
。(取空间三条侧棱互
相 垂 直 的 四 面 体 , 三 条 侧 棱 长 分 别 为 a, b, c , 则 此 三 棱 锥 外 接 球 的 半 径 是
r a 2 b 2 c 2 。) 2
8.已知命题:平面上一矩形 ABCD的对角线 AC 与边 AB 和 AD 所成角分别为 、 ,则
).
A.“若 a3 b3 ,则 a b ”类推出“若 a 0 b 0,则 a b ”
B.“若 (a b)c ac bc ”类推出“ (a b)c ac bc ”
C.“若 (a b)c ac bc ” 类推出“ a b a b (c≠0)” c cc
D.“(ab)n anbn ” 类推出“(a b)n an bn ”
_________________________.
13、设平面内有n条直线 (n 3) ,其中有且仅有两条直线互相平行,任意三条直线不过同一
点.若用 f (n) 表示这n条直线交点的个数,则 f (4) =
;
当n>4时, f (n) =
(用含 n 的数学表达式表示)。
14、求证:(1) a2 b2 3 ab 3(a b) ;
D. 2004
6、利用数学归纳法证明“1+a+a2+…+an+1= 1 a n2 , (a≠1,n∈N)”时,在验证 n=1 1 a
成立时,左边应该是 ( )
(A)1
(B)1+a
(C)1+a+a2
(D)1+a+a2+a3
7、某个命题与正整数 n 有关,如果当 n k(k N ) 时命题成立,那么可推得当 n k 1时
