例谈构造平行六面体解立体几何题
用空间向量法求解立体几何问题典例及解析

用空间向量法求解立体几何问题典例及解析以多面体为载体,以空间向量为工具,来论证和求解空间角、距离、线线关系以及线面关系相关问题,是近年来高考数学的重点和热点,用空间向量解立体几何问题,极大地降低了求解立几的难度,很大程度上呈现出程序化思想。
更易于学生们所接受,故而执教者应高度重视空间向量的工具性。
首先,梳理一下利用空间向量解决立体几何的知识和基本求解方法 一:利用空间向量求空间角 (1)两条异面直线所成的夹角范围:两条异面直线所成的夹角的取值范围是 。
向量求法:设直线,a b 的方向向量为a,b ,其夹角为θ,则有cos ___________.θ= (2)直线与平面所成的角定义:直线与平面所成的角是指直线与它在这个平面内的射影所成的角。
范围:直线和平面所夹角的取值范围是 。
向量求法:设直线l 的方向向量为a ,平面的法向量为n ,直线与法向量所成角的余弦值为|cos |___________.θ=直线与平面所成的角为ϕ,则有sin ___________.ϕ=或在平面内任取一个向量m ,则|cos |___________.θ=.(3)二面角二面角的取值范围是 . 二面角的向量求法:方法一:在两个半平面内任取两个与棱垂直的向量,则这两个向量所成的 即为所求的二面角的大小;方法二:设1n ,2n 分别是两个面的 ,则向量1n 与2n 的夹角(或其补角)即为所求二面角的平面角的大小。
二:利用空间向量求空间距离 (1)点面距离的向量公式平面α的法向量为n ,点P 是平面α外一点,点M 为平面α内任意一点,则点P 到平面α的距离d 就是 ,即d =||||MP ⋅n n . (2)线面、面面距离的向量公式平面α∥直线l ,平面α的法向量为n ,点M ∈α、P ∈l ,平面α与直线l 间的距离d 就是MP 在向量n 方向射影的绝对值,即d = .平面α∥β,平面α的法向量为n ,点M ∈α、P ∈β,平面α与平面β的距离d 就是MP 在向量n 方向射影的绝对值,即d =||||MP ⋅n n . (3)异面直线的距离的向量公式设向量n 与两异面直线a 、b 都垂直,M ∈a 、P ∈b ,则两异面直线a 、b 间的距离d 就是MP 在向量n 方向射影的绝对值,即d =||||MP ⋅n n .三:利用空间向量解证平行、垂直关系1:①所谓直线的方向向量,就是指 的向量,一条直线的方向向量有 个。
探索立体几何多面体练习题汇总

探索立体几何多面体练习题汇总在学习立体几何的过程中,掌握各种多面体的性质和计算方法是非常重要的。
本文将为大家梳理一些立体几何多面体的练习题,帮助大家巩固这一知识点。
一、正方体正方体是具有六个面都是正方形的多面体。
假设正方体的边长为a,则它的表面积为6a^2,体积为a^3。
练习题一:一个正方体的表面积是96平方厘米,求其边长和体积。
解答:设正方体的边长为a,则有6a^2=96。
解得a=4。
所以该正方体的边长为4厘米,体积为4^3=64立方厘米。
二、长方体长方体是具有六个面都是矩形的多面体。
假设长方体的长、宽、高分别为a、b、c,则它的表面积为2(ab+ac+bc),体积为abc。
练习题二:一个长方体的表面积为144平方厘米,其长、宽、高分别为3厘米、4厘米和x厘米,求x的值以及体积。
解答:根据表面积的计算公式2(ab+ac+bc)=144,代入a=3、b=4,得到2(12+3x+4x)=144。
化简得到30x=108,解得x=3.6。
所以该长方体的高为3.6厘米,它的体积为3×4×3.6=43.2立方厘米。
三、正六面体正六面体是具有六个面都是正六边形的多面体。
设正六面体的边长为a,则它的表面积为6a^2,体积为(√2a)^3。
练习题三:一个正六面体的表面积为54√3平方厘米,求其边长和体积。
解答:根据表面积的计算公式6a^2=54√3,化简得到a^2=9√3。
解得a=3√3。
所以该正六面体的边长为3√3厘米,体积为(√2×3√3)^3=54√2立方厘米。
四、正四面体正四面体是具有四个面都是正三角形的多面体。
设正四面体的边长为a,则它的表面积为√3a^2,体积为(a^3)/(6√2)。
练习题四:一个正四面体的表面积为12√3平方厘米,求其边长和体积。
解答:根据表面积的计算公式√3a^2=12√3,化简得到a^2=16。
解得a=4。
所以该正四面体的边长为4厘米,体积为(4^3)/(6√2)=16√2/3立方厘米。
巧用平面向量解立体几何问题

=1+12(2cos60°cos40°)-12(cos40°-cos120°)=1+12cos40°-12cos40°+12cos120°=1-14=34.四、其它转化在求值问题中,除了重组角度转化之外,还应重视三角函数名,结构等方面的转化,如:①切割化弦;②降幂转化来计算.例6 求tan20°+4sin20°的值.分析:对此类问题一般先将切化弦:tan20°+4sin20°=sin20°cos20°+4sin20°=sin20°+4sin20°cos20°cos20°由于题目中出现了20°与40°的角,其和为60°的特殊角,这样就为转化带来了空间,而且方法不是唯一的.变式1 tan20°+4sin20°=sin20°+2sin40°cos20°=sin(60°-40°)+sin40°cos20°=sin60°cos40°-cos60°sin40°+2sin40°cos20°=32cos40°-12sin40°+2sin40°cos20°=32cos40°+32sin40°cos20°=3(12cos40°+32sin40°)cos20°=3sin70°cos20°=3.变式2 tan20°+4sin20°=sin20°+2sin(60°-20°)cos20°=sin20°+3cos20°-sin20°cos20°=3cos20°cos20°=3.以上几种形式的转化求值问题,只是在三角函数教学中比较普遍存在的转化思想的体现,在很多的具体求值中,还有些异于上述的其它方法.但任何问题的解决都是将未知转化为已知的过程,在三角函数求值中体现得更为突出.在教学中应提炼出来,以便于学生共享.黑龙江省农垦总局哈尔滨分局高级中学(150088)●韩晓辉巧用平面向量解立体几何问题 平面向量是解答立体几何问题的一种快速、简捷的运算工具.不少复杂的立体几何问题,引入平面向量后,通过将空间元素的位置关系转化为数量关系,将过去的形式逻辑证明转化为数值运算,即借助平面使解题模式化,用机械性操作把问题转化,因此,平面向量为立体几何代数化带来了极大的便利.下面,介绍平面向量在立体几何中的应用.例1 如图1,AB、CD为异面直线,CD<平面α,AB∥平面α,M、N分别是AC、BD的中点,求证MN∥平面α证明因为D<平面α,B∥平面α且··数理化学习(高中版)©:.:C A12AB 、CD 异面,所以在α内存在�a 、�b 使AB =�a ,CD =�b ,且�a 、�b 不共线,由M 、N 分别是AC 、BD 的中点,得MN =12(MB +MD )=12[(MA +AB )+(MC +CD )]=12[(MA +AB )+(MC +C D )]=12[-M C +AB +MC +CD ]=12[AB +CD ]=12(�a +�b ),即MN 与�a 、�b 共面.又因为�a 、�b 在平面α内,故MN ∥平面α或MN <平面α,而若MN <平面α,则A B 、C D 同在平面α内,与AB 、CD 为异面直线矛盾,所以MN ∥平面α.例2 正四面体V -ABC 的高VD 的中点为O ,AC 的中点为M.求证:A O 、BO 、CO 两两垂直.证明:设V A =�a,V �b =�b ,VC =�c ,正四面体棱长为m,则VD =13(�a +�b +�c ),A O =16(�b +�c -5�a ),BO =16(�a +�c -5�b ),CO =16(�a +�b -5�c ).因为AO ·BO =136(�b +�c -5�a )·(�a +�c -5�b )=0,所以AO ⊥BO,即AO ⊥BO,同理,AO ⊥CO ,BO ⊥C O.例3 如图3,在三棱锥S -A BC 中,∠S AB =∠S AC =∠AC B =90°,AC =2,SA =23,BC =13,S B =29.证明:(1)SC ⊥BC;(2)求异面直线SC 与AB 所成角α的余弦值.解:(1)证明:由题意,S ·B =,·B =,所以S ·B =(S +)·B =S A ·CB +AC ·C B =0,即SC ⊥BC .(2)因为SC ·AB =(S A +AC)·(AC +C B )=S A ·AC +SA ·C B +AC ·AC +AC ·CB =0+0+|AC |2+0=|AC |2=4,|SC |=(23)2+22=4,|A B |=(13)2+22=17,所以cosα=SC ·AB |SC |·|AB |=4417=1717.例4 如图3,已知平行六面体ABC D -A 1B 1C 1D 1的底面是菱形,且∠C 1CB =∠C 1C D=∠BC D =60°.(1)证明:C 1C ⊥BD ;(2)当CDCC 1的值为多少时,能使A 1C ⊥平面C 1BD 请给予证明.证明:(1)取C D 、CB 、CC 1为空间的一个基.因为∠C 1CB =∠BC D =60°,ABCD 是棱形,所以|C D |=|CB |,又因为BD =C D -CB,所以CC 1·BD =CC 1·(C D -CB )=CC 1·CD -CC 1·C B =0.所以C 1C ⊥BD.(2)设CDCC 1=λ(λ>0),即|C D |=λ|CC 1|时,能使A 1C ⊥平面C 1BD.因为C 1D ∩BD =D ,所以A 1C ⊥平面C 1BD ΖA 1C ⊥C 1D 且A 1C ⊥BD ΖA 1C ·C 1D =0且A 1C ·BD =0.因为=(D +B +),D =D ,<B,D >=6°,<B ,>=6°,··数理化学习(高中版)©A C 0AC C 0C C A AC C A 1C -C C CC 1C 1C -CC 1C C 0C CC 1022|CD|=|CB|,所以A1C·C1D=-(|C D|2-CD·CC1+ CB·CD-CB·CC1+CC1·CD-|CC1|2)=-(λ2|CC1|2+12λ2|CC1|2-12λ|CC1|2-|CC1|2)=-(32λ2-12λ-1)|CC1|2.所以A1C·C1D=0Ζ32λ2-12λ-1=0Ζ(λ-1)(3λ+2)=0,因为λ>0,所以λ=1.经验证,当λ=1时,A1C·C1D=0.即当C DCC1=1时,能使A1C⊥平面C1BD.前面这些题目若采用传统的立体几何方法证明,大多数不可避免地需要添加“辅助线”,然后再分别证明线线平行(垂直)或面面平行(垂直),而这些证法与用平面向量法相比,显然难度是大的.因此,平面向量确实是处理立体几何问题的重要而又简便的方法.作为平面向量的主要技巧,是将相关量表示为基向量的形式,把问题转化为平面向量的运算,这与把空间图形关系转化为平面图形关系的传统解法相比,显然是更高的思维方式,它抓住了空间的主要特征和其内在规律,使“纷繁复杂的现象变得井然有序.”河北省乐亭县第一中学(063600)●张云飞线段定比分点的向量公式及应用例举(一) 线段的定比分点公式是同学们所熟悉的重要公式,它在中学数学中有较为广泛的应用,近几年的高考也时有涉及,如2000年全国高考文理科倒数第一大题都直接考查了定比分点公式的运用.同学们所熟悉的是定比分点的坐标公式,其实,除此以外,定比分点公式还有其向量形式.运用定比分点的向量形式解题有时显得更为简洁明快.一、线段的定比分点向量公式设P1、P2是直线l上的两点,点P是l上不同于、的任意一点,O 是平面内任意一点,设O P1=�a,O P2=�b,P分有向线段P1P2所成的比为λ,则有O P=�a+λ�b1+λ.证明:如图1,因为P1P=O P-�a,.PP2=�b-O P,P1P=λPP2,所以O P-�a=λ(�b-O P)所以O P=�a+λ�b1+λ①公式①就是线段的定比分点向量公式.二、应用例1 在△ABC中,已知D是BC的中点, E是AD的中点,直线B E交AC于F,求证:CF =2FA.证明如图,在△B中,设BD=�,B=�,·3·数理化学习(高中版)©P1P2:2A Ca A b2。
空间几何体的表面积和体积讲解及经典例题

空间几何体的表面积和体积一.课标要求:了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式)。
二.命题走向近些年来在高考中不仅有直接求多面体、旋转体的面积和体积问题,也有已知面积或体积求某些元素的量或元素间的位置关系问题。
即使考查空间线面的位置关系问题,也常以几何体为依托.因而要熟练掌握多面体与旋转体的概念、性质以及它们的求积公式.同时也要学会运用等价转化思想,会把组合体求积问题转化为基本几何体的求积问题,会等体积转化求解问题,会把立体问题转化为平面问题求解,会运用“割补法”等求解。
由于本讲公式多反映在考题上,预测2009年高考有以下特色:(1)用选择、填空题考查本章的基本性质和求积公式;(2)考题可能为:与多面体和旋转体的面积、体积有关的计算问题;与多面体和旋转体中某些元素有关的计算问题;三.要点精讲1.多面体的面积和体积公式表中S表示面积,c′、c分别表示上、下底面周长,h表斜高,h′表示斜高,l表示侧棱长。
2.旋转体的面积和体积公式表中l、h分别表示母线、高,r表示圆柱、圆锥与球冠的底半径,r1、r2分别表示圆台上、下底面半径,R表示半径。
四.典例解析题型1:柱体的体积和表面积例1.一个长方体全面积是20cm 2,所有棱长的和是24cm ,求长方体的对角线长. 解:设长方体的长、宽、高、对角线长分别为xcm 、ycm 、zcm 、lcm 依题意得:⎩⎨⎧=++=++24)(420)(2z y x zx yz xy )2()1(由(2)2得:x 2+y 2+z 2+2xy+2yz+2xz=36(3)由(3)-(1)得x 2+y 2+z 2=16 即l 2=16所以l =4(cm)。
点评:涉及棱柱面积问题的题目多以直棱柱为主,而直棱柱中又以正方体、长方体的表面积多被考察。
我们平常的学习中要多建立一些重要的几何要素(对角线、内切)与面积、体积之间的关系。
例2.如图1所示,在平行六面体ABCD —A 1B 1C 1D 1中,已知AB=5,AD=4,AA 1=3,AB ⊥AD ,∠A 1AB=∠A 1AD=3π。
立体几何知识点和例题(含有答案)

【考点梳理】一、考试内容1.平面。
平面的基本性质。
平面图形直观图的画法。
2.两条直线的位置关系。
平行于同一条直线的两条直线互相平行。
对应边分别平行的角。
异面直线所成的角。
两条异面直线互相垂直的概念。
异面直线的公垂线及距离。
3.直线和平面的位置关系。
直线和平面平行的判定与性质。
直线和平面垂直的判定与性质。
点到平面的距离。
斜线在平面上的射影。
直线和平面所成的角。
三垂线定理及其逆定理。
4.两个平面的位置关系。
平面平行的判定与性质。
平行平面间的距离。
二面角及其平面角。
两个平面垂直的判定与性质。
二、考试要求1.掌握平面的基本性质,空间两条直线、直线与平面、平面与平面的位置关系(特别是平行和垂直关系)以及它们所成的角与距离的概念。
对于异面直线的距离,只要求会计算已给出公垂线时的距离。
2.能运用上述概念以及有关两条直线、直线和平面、两个平面的平行和垂直关系的性质与判定,进行论证和解决有关问题。
对于异面直线上两点的距离公式不要求记忆。
3.会用斜二测画法画水平放置的平面图形(特别是正三角形、正四边形、正五边形、正六边形)的直观图。
能够画出空间两条直线、两个平面、直线和平面的各种位置关系的图形,能够根据图形想象它们的位置关系。
4.理解用反证法证明命题的思路,会用反证法证明一些简单的问题。
三、考点简析1.空间元素的位置关系2.平行、垂直位置关系的转化3.空间元素间的数量关系(1)角①相交直线所成的角;②异面直线所成的角——转化为相交直线所成的角;③直线与平面所成的角——斜线与斜线在平面内射影所成的角;④二面角——用二面角的平面角来度量。
(2)距离①两点之间的距离——连接两点的线段长;②点线距离——点到垂足的距离;③点面距离——点到垂足的距离;④平行线间的距离——平行线上一点到另一直线的距离;⑤异面直线间的距离——公垂线在两条异面直线间的线段长;⑥线面距离——平行线上一点到平面的距离;⑦面面距离——平面上一点到另一平面的距离;⑧球面上两点距离——球面上经过两点的大圆中的劣弧的长度。
第二十一章平行六面体的性质及应用

第二十一章平行六面体的性质及应用【基础知识】平行六面体是平行四边形的一个三维类比模型,平行四边形的一系列有趣性质可推证到平行六面体中去.平行四边形与三角形有着极为密切的关系,因而平行六面体与四面体也有着极为密切的关系,这些构成了平行六面体一系列既有趣又有重要应用的性质.性质1平行六面体的四条对角线相交于一点,且在这一点互相平分,并称该点为中心.推论称侧面对角线的交点为侧面中心,则相对侧面中心的连线也交于平行六面体的中心,且在这一点互相平分.(见例5)性质2平行六面体所有对角线的平方和等于所有棱的平方和.推论1平行六面体所有侧面对角线的平方和等于其所有(体)对角线平方和的两倍.推论2平行六面体每一侧棱的平方等于与这侧棱共面的两侧面四条面对角线的平方和减去与这侧棱不共面而共端点的两条侧面对角线平方和所得差的四分之一.推论3平行六面体的每一对角线长的平方等于过这条对角线一端点的三条侧面对角线的平方和减去过另一端点的三条棱的平方和.性质3平行六面体的每一对角线长的平方等于共一端点的三条棱长的平方和减去这三条棱中每两条棱长及其所夹角余弦之积的两倍.性质4平行六面体的每一对角线通过与该对角线共端点的三条棱的另一端点构成的三角形截面的重心,且被这三角形截面分成三等分.性质5平行六面体的每个由三条侧面对角线构成的三角形截面面积平方的4倍,等于这截面所截三个侧面面积的平方和减去这三个侧面中每两个侧面面积及其所夹二面角余弦之积的两倍.推论平行六面体的八个由三条侧面对角线构成的三角形截面面积的平方和等于六个侧面面积的平方和.性质6设平行六面体的全面积为S ,四条对角线长为1AC l 、1A C l 、1BD l 、1BD l 、1B D l ,则111122222AC A C BD B DS l l l l +++≤. 性质7通过平行六面体中心的任何平面,将平行六面体分成体积相等的两部分.推论1以平行六面体任一顶点及这顶点出发的三条棱的端点构成的四面体体积是平行六面体体积的六分之一.推论2以平行六面体任一顶点及这顶点出发的三条侧面对角线端点构成的四面体体积是平行六面体体积的三分之一.性质8平行六面体的体积等于底面积与高的乘积,或任一侧面面积与相对面距离之积. 推论设共一顶点的三条棱长为a 、b 、c ,每两条棱的夹角为α、β、γ,则体积V 为V abc ==若记()12θαβγ=++,则2V =. 性质9()11113/22222124AC A C BD BDV l l l l +++≤;3/26S V ⎛⎫ ⎪⎝⎭≤.推论l 表面积一定的平行六面体中,以正方体之体积为最大.推论2在各个侧面面积为定值的平行六面体中,以长方体之体积为最大.性质11由平行六面体的各顶点,至不截此体的一平面所引诸垂线段之和,等于由其对角线之交点至同平面所引垂线段之和的8倍.性质10在平行六面体1111ABCD A B C D -中,截面分别与AB 、AD 、1AA 、1AC 交于0B 、0C 、0A 、0D 各点,则11000AC AA AB AD AC AB AD AA =++. 下面介绍平行六面体与四面体的密切关系. 1.对应关系作四面体的外接平行六面体,且使四面体的六条棱均成为平行六面体的侧面对角线.此时,四面体与其外接平行六面体是一一对应的.特别地,一个正四面体对应着一个正方体,一个等腰四面体(三对对棱分别相等的四面体)对应着一个长方体,一个两对对棱分别相等的四面体对应着一个直平行六面体,一个对棱均互相垂直的四面体(直角四面体或正三棱锥四面体)对应着一个菱形六面体等等.当四面体的共一顶点的三棱成为平行六面体的共顶点的三棱时,一个四面体对应着四个外接平行六面体,特别地,一个正四面体对应着一个一顶点面角均为60︒的菱形六面体,一个等腰四面体对应着两个一顶点面角之和为180︒的平行六面体等等. 2.隐显关系从本世纪初开始,人们试图将三角形的许多性质引申到四面体——最简单的多面体,事实证明发展四面体的几何学比三角形几何学困难得多,有些提法并不复杂的问题解答起来非常费劲,甚至未能解决.下面的例题将启示我们:四面体某些数量关系的发现及几何特征的显露,借助于其外接平行六面体的性质的运用是一种方便的重要途径.因此,可以说四面体的一些性质可以利其外接平行六面体来显现,平行六面体隐含了四面体的一些重要性质. 【典型例题与基本方法】例1在四面体ABCD 中,AB m =,CD n =,AD p =,BC q =,AC u =,BD u =.若AB 与CD 所成的角为θ,则()()2222cos 2p q u v mn+--=.证明如图211-,作四面体ABCD 的外接平行六面体A DB C AD BC ''''-,使四面体的棱都成为平行六面体的侧面对角线.A'B'C 'D '图21-1DA C显然,AB 与CD 所成的角θ就是A B ''与CD 所成的角,于是 ()()2222221/21/24cos 112222m n B D m n B D mn m n θ'+-⎡⎤⎡⎤'+-⎣⎦⎣⎦==⎛⎫⎛⎫⋅⋅ ⎪ ⎪⎝⎭⎝⎭ 222222242222A D B D B D A D B D mn mn'''''+--==()()22222222222222p q u v A D D D D D B D mn mn+--''''---==. 例2若四面体的六条棱长分别为a 、b 、c 、d 、e 、f ,体积为V ,则有333333a b c d e f +++++≥(Weisenbock 不等式的一种三维推广).证明如图211-,将四面体ABCD 补成平行六面体,则3ABCD V V =平行六面体.设平行六面体共顶点A 的三条棱长为l 、m 、n ,由前面的性质2的推论1,即有()2222222224a b c d e f l m n +++++=++.又由V l m n ⋅⋅平行六面体≤及幂平均值不等式,有113333332222223266a b c d e f a b c d e f ⎛⎫⎛⎫++++++++++ ⎪ ⎪⎝⎭⎝⎭≥.于是()322224212ABCD l m nV ⎡⎤++⎢⎥⎢⎥⎣⎦①()32222222112a b c d e f ⎡⎤=+++++⎢⎥⎣⎦()312233333331612a b c d e f ⎧⎫⎪⎪⎡⎤+++++⎨⎬⎢⎥⎣⎦⎪⎪⎩⎭≤②)333333a b c d e f =+++++.故333333a b c d e f +++++≥.其中等号当且仅当①、②中满足l 、m 、n 互相垂直且l m n ==,即平行六面体为正方体,亦即a b c d e f =====时成立.类似上例,并运用前面的性质5的推论,可证明Weisenbock 不等式的另一种三维推广:若四面体各顶点A 、B 、C 、D 所对的面的面积分别为A S 、B S 、C S 、D S ,体积为V ,则33332A B C D S S S S +++ 例3空间四平面互相平行,相邻两面间距离都是h .今有一正四面体,它的四个顶点分别在这四个面上.求正四面体的棱长.解设正四面体ABCD 的外接正方体为'AC BD A CB D '''-.又设过棱D D '及B C '中点F 的截面为3α,过棱C C '及A D '中点E 的截面为2α,过棱A A ',过棱B B '且与3α、2α平行的平面分别为1α、4α,这样这四个平面即为两相邻距离都相等的互相平行的四平面.又设过A B ''的中点O '与CE 垂直的直线为l ,l 与4α、3α、2α、1α的交点分别为B ''、D ''、C ''、A '',如图21-2(b),则4α、3α、2α、1α两相邻平面间距离为B D ''''、D C ''''、C A ''''.DEGO 'B"A"C "D "A'B'C 'D (b)(a)D图21-2CF当A C h ''''=时,可求得A E '=,从而A B ''=.这就是我们所要求的正四面体的棱长. 例4四面体ABCD 中,若AB CD ⊥,AC BD ⊥,则AD BC ⊥.(1957年天津市、1979年上海市中学竞赛题)证明如图211-,作四面体ABCD 的外接平行六面体A DB C AD BC ''''-.由平行六面体每一侧面两对角线所夹的角(锐角)的余弦值等于这侧面两相邻棱的平方差的绝对值除以这两条侧面对角线长的乘积,即()22cos A D DB A B CD A B CD''-'=''⋅.由AB CD ⊥,则()cos cos()0AB CD A B CD ''==,从而A D DB ''=,即侧面A DB C ''为菱形,同理,由AC BD ⊥.有侧面A CC A ''为菱形,从而侧面A DD A ''也为菱形,故AD BC ⊥. 例5求证四面体的三双对棱中点连线必交于一点,且互相平分.证明如图213-,设E 、F 、G 、H 、M 、N 分别是四面体ABCD 的六条棱的中点.作四面体的外接平行六面体1A C ,则E 、F 、G 、H 、M 、N 分别是其六侧面对角线的交点.图21-3G N EH OCDBAC 1A 1D 1B 1MF在11AAC C 中,连EF ,则11EF AA CC ∥∥,且过六面体对角线1A C 的中点O ,同时被O 平分.因六面体的四条对角线共点O ,于是同理可证GH 、MN 过O ,且被O 平分.例6立方体八个顶点中有四个恰是正四面体的顶点.求出立方体的表面积与四面体的表面积之比.(1980年美国中学生竞赛AHSME 第16题) 解设立方体表面积为S ,四面体表面积为0S ,由平行六面体所有三角形截面(三角形的边由六面体侧面对角线组成)面积的平方和等于所有侧面面积的平方和,有2206/4264S S ⎛⎫⎛⎫⋅⋅= ⎪ ⎪⎝⎭⎝⎭,故0/S S =【解题思维策略分析】1.善于将四面体问题转化为平行六面体问题例7若A 、B 、C 、D 表示空间四点,AB 表示A 、B 两点间的距离,AC 表示A 、C 两点间的距离,⋯.证明:222222AC BD AD BC AB CD ++++≥.(第4届美国中学生竞赛题) 证明以空间四边形的边为侧面对角线构造平行六面体,由平行六面体所有侧面对角线的平方和等于所有棱的平方和的两倍及图213-,有222222222111444AC BD AD BC AB CD AD AA A B +++++=++()22242AD AB CD =++故222222AC BD AD BC AB CD ++++≥.当A 、B 、C 、D 共面时,10AD =,上式取等号.此时,可看作是压扁了的四面体.例8在四面体ABCD 中,BDC ∠是直角,由D 到ABC △所在的平面的垂线的垂足H 是ABC △的垂心,证明:()()22226AB BC CA AD BD CD ++++≤.(IMO 12-试题)证明如图214-,平行六面体1111AC BD B D AC -为四面体ABCD 的外接平行六面体.由题设,D 到ABC △所在的平面的垂线的垂足是ABC △的垂心,知这个四面体的对棱互相垂直,又BDC ∠是直角,即知四面体ABCD 的三面角D ABC -是直三面角,故此平行六面体为长方体.CDBAC 1A 1D 1B 1图21-4H由()2222AD BD CD ++()()()222222AD BD BD CD CD AD =+++++222AB BC AC =++.故()()22222263AD BD CD AB BC AC ++=++222222AB BC CA AB BC BC CA AB CA +++⋅+⋅+⋅≥ ()2AB BC CA =++.例9若a 、b 、c 是四面体共顶点的三条棱的长,α、β、γ,是这三条棱组成的面角,ω是这三个面角和的一半,则四面体的体积为:13V abc =四面体证明如图21-4,设DA a =,DB b =,DC c =,BDC α∠=,ADC β∠=, ADB γ∠=.由平行六面体的体积公式()V abc S A =⋅平行六面体,其中()S A= 有16V V =四面体平行六面体1=3abc 2.善于构造平行六面体解答有关问题例10已知a 、b 、c +∈R ,且2221a b c ++=3a b c ++>.证明由2221a b c ++=3a b c ++>.参见图212- (a),构作长方体AB '.设对角线1AB '=,AD a '=,AC b '=,AA c '=,则A B ''B C ''=,B D ''.在A AB ''△中,A A A B B A ''''+>,即1c >.同理,1b >1a >.以上三式相加,即证.例11锐角α.β、γ满足222sin sin sin 1αβγ++=,求证:π3π24αβγ<++<. 证明构造长方体D AC B DA CB ''''-,参见图212- (a),使其长、宽、高分别为sin D A α'=,sin AC β'=,sin C C γ'=,则1AB D C ''===,D B A α''∠=,C B A β''∠=,C D C γ''∠=,且AB BA '>.sin sin sin D A D AD B A D BA B A BA α'''''∴=∠=<=∠', sin sin sin AC AC C B A C BA B A BAβ'''''=∠=<=∠'.从而D BA α'<∠,C BA β'<∠. 1π2D BA C BA αβ''∴+<∠+∠=.同理,π2βγ+<,π2αγ+<,即3π4αβγ++<. 设B A '与D C '相交于O ,则知2D OA α'∠=,2AOC β'∠=,2C OC γ'∠=. 由于三面角的任意两个面角的和大于第三个面角,则 22D OA AOC D OC αβ'''+=∠+∠>∠. ()2πD OC C OC αβγ''∴++=∠+∠=.故π3π24αβγ<++<. 3.注意特殊平面体的性质的运用例12正方体1111ABCD A B C D -的棱长为1,求正方体底面ABCD 内切圆周上的点与过顶点1A 、C 和1B 的圆周上的点之间的最小距离.(第19届全苏奥林匹克题)图21-5C1A B解如图215-,考察两个圆周分别在以正方体的对称中心为球心的两个同心球面上,即与正方体各棱都)上,这两个球面上的点之间的最小距离是它们的半径之差12d =.如果两圆周上各有一点恰好在球心O 发出的同一射线上,那么d 即为最小值.考察在以O 为位似比的变换下,小球面变为大球面,而小球面上的圆周的象集为大球面上的圆周.注意到ABCD 的内切圆1O 与线段BD 的交点E 和F 在该位似变换下的象在平面1AB C 的两侧(因11145O OF BB O ∠=︒>∠,故射线OF 不与平面1AB C 相交),因此,1O 的象集(圆周)将与过顶点A ,C 和1B 的圆周相交.设一交点为N ,而N 的原象为M,那么M ,N 之间的距离就是考察的两圆周上的点之间的距离的最小值,其值为12d =.【模拟实战】习题A1.在正方体1111ABCD A B C D -中,O 是面ABCD 的中心,1O 是面11ADD A 的中心.求异面直线1D O 与1BO 所成角的余弦值.2.已知空间一个平面与一个正方体的12条棱的夹角都等于口α,求α的值.3.能否用一个平面去截一个正方体,使得截面为五边形?进一步,截面是否为正五边形?4.设一个平面截棱长为1的正方体1111ABCD A B C D -,过顶点1C ,交1A D 1中点于E ,1A A 距A 较近的一个三等分点于F ,AB 于G ,BC于H .求截面1C EFGH 的周长.5.已知一个平面截棱长为1的正方体所得截面是—个六边形.证明:此六边形周长≥. 6.正三棱锥S ABC -的侧棱与底面边长相等,如果E ,F 分别为SC ,AB 的中点,那么异面直线EF 与SA 所成的角等于多少?7.已知111ABC A B C -是直三棱柱,90BAC ∠=︒,点1D ,1F 分别是11A B ,11B C 的中点.若1AB CA AA ==,求1BD 与1CF 所夹角的余弦值.8.已知ABCD 是边长为4的正方形,E ,F 分别是AB ,AD 的中点,GC ⊥面ABCD ,且2GC =.求点B 到面EFG 的距离.9.在四面体SABC 中,已知SA BC a ==,SC AB b ==,SB AC c ==,求此四面体的体积. 10.在四面体1234A A A A 中,相应对棱中点的三条连线分别为1m ,2m ,3m ,顶点i A 所对侧面的重心为i G ,其四面体体积记为V ,则 (Ⅰ)1233m m m V ⋅⋅≥;(Ⅱ)421412716i j i i i j i A A AG =-∑∑≤≤≤≥(Ⅲ)421i i i AG =∑ 11.已知α,β,γ是锐角,且222cos cos cos 1αβγ++=.求证:(Ⅰ)tan tan tan αβγ⋅⋅≥ (Ⅱ)3ππ4αβγ<++<. 12.已知0a >,0b >,0c >,且1a b c ++=.习题B1.有一立方体,中心和边长为a b c <<的长方体的对称中心重合,诸界面与长方体各界面平行,求立方体的棱长,使得它与长方体的并的体积减去它与长方体的交的体积的差最小.(1979年捷克竞赛题) 2.证明:在棱长为a 的立方体内部可以作两个棱长为a 的正四面体,使得它们没有公共点.(1983年民主德国竞赛题)。
空间向量立体几何(绝对经典)
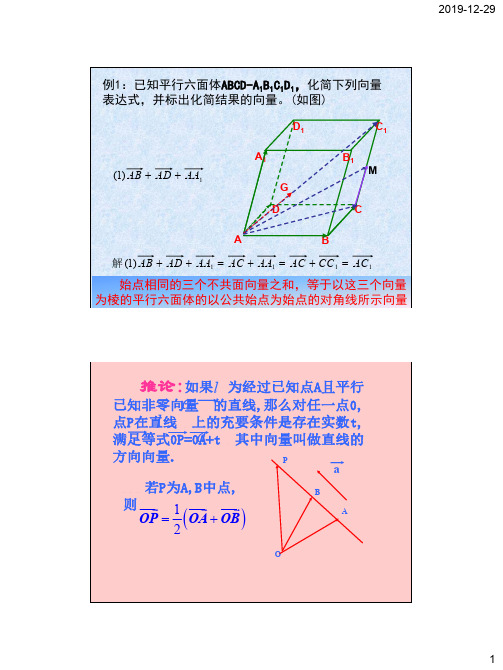
例1:已知平行六面体ABCD-A 1B 1C 1D 1,化简下列向量表达式,并标出化简结果的向量。
(如图)A BCD A 1B 1C 1D 1G1)1(AA AD AB ++1111)1(AC CC AC AA AC AA AD AB =+=+=++解M 始点相同的三个不共面向量之和,等于以这三个向量为棱的平行六面体的以公共始点为始点的对角线所示向量推论:如果 为经过已知点A且平行已知非零向量 的直线,那么对任一点O,点P在直线 上的充要条件是存在实数t,满足等式OP=OA+t 其中向量叫做直线的方向向量.ll aaOABP a若P为A,B中点,则()12=+ OP OA OB2.共面向量定理:如果两个向量 不共线,则向量 与向量 共面的充要条件是存在实数对 使, a b yx , p ,a b OM a b A B A 'Pp p xa yb =+ 推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y使或对空间任一点O,有=+MP xMA yMB =++ OP OM xMA yMB 注意:空间四点P 、M 、A 、B 共面⇔存在唯一实数对,,x y MP xMA yMB =+ ()使得(1)OP xOM yOA zOB x y z ⇔=++++= 其中,例1:已知m,n 是平面α内的两条相交直线,直线l 与α的交点为B ,且l ⊥m ,l ⊥n ,求证:l ⊥α。
n mg g m n αl l 证明:在α内作不与m、n重合的任一条直线g,在l、m、n、g上取非零向量l、m、n、g ,因m与n相交,得向量m、n 不平行,由共面向量定理可知,存在唯一的有序实数对(x,y),使g =x m +y n ,l ·g =x l ·m +y l ·n∵ l ·m =0,l ·n =0∴ l ·g =0∴ l⊥g∴ l⊥g这就证明了直线l垂直于平面α内的任一条直线,所以l⊥α巩固练习:利用向量知识证明三垂线定理αa A O P ().,0,,,,0,0,PA a PA a a OA a PO a PA OAy PO x PA y x OA PO OA PO a OA a OA a PO a PO PO aa ⊥⊥∴=⋅+⋅=⋅∴+==⋅∴⊥=⋅∴⊥∴⊥即使有序实数对定理可知,存在唯一的不平行,由共面向量相交,得又又而上取非零向量证明:在αPA a OAa a PA OA PA PO ⊥⊥⊂求证:且内的射影,在是的垂线,斜线,分别是平面已知:,,ααα复习:2. 向量的夹角:a bO ABabθ0a b π≤≤ ,a b ,向量 的夹角记作:a b 与a b = ||||cos ,a b a b 1.空间向量的数量积:111222(,,),(,,)a x y z b x y z == 设121212x x y y z z =++cos ||||a ba b a b =,121212222222111222++=++⋅++x x y y z z x y z x y z 5.向量的模长:2222||a a x y z ==++ (,,)a x y z = 设4.有关性质:(1)两非零向量111222(,,),(,,)a x y zb x y z == 1212120x x y y z z ++=0a b a b ⊥⇔=⇔ (2)||||||a b a b ≤ ||||,a b a b a b =⇒ 同方向||||,a b a b a b =-⇒ 反方向注意:此公式的几何意义是表示长方体的对角线的长度。
在平行六面体中巧解四面体问题

OA B C D E C BA SFz 四面体问题求解中的“嵌”与“补”江苏省姜堰中学 张圣官(225500)四面体(即三棱锥)是立体几何中最基本的一个几何体,而它又是与平行六面体密切相关的。
有些四面体问题,若将之放到平行六面体背景中,则往往能显现其中隐含的线面关系,从而使问题获得优解。
本文通过事例重点说明在正方体或长方体中如何巧解相关的四面体问题。
1. 将四面体“嵌入”到平行六面体中我们知道,任何一个四面体都可以“嵌入”到一个平行六面体中,而使四面体的六条棱分别是平行六面体六个面的一条面对角线。
例如,在证明“四面体顶点到对面三角形重心的四条连线交于一点”(此即为四面体重心)时,实施这种“嵌入”后,问题就转化为论证“平行六面体四条体对角线交于一点”,这就容易多了,而且易得四面体重心把四条连线都分成3:1的两部分。
下面看几例这种“嵌入”的应用。
例1(2000年全国高中数学联赛题)一个球与正四面体的六条棱都相切,若正四面体的棱长为a ,则这个球的体积是____________________。
分析:将正四面体ABCD “嵌入”到正方体中,使正四面体的六条棱分别是正方体六个面的面对角线(如图1),则球O 与正四面体的六条棱都相切等价于球O 与正方体的六个 面都相切。
易知正方体棱长为a 22,所以球半径为a 42,故 (图1)球的体积为363334a R ππ=。
例2(1990年全国高考题)正三棱锥S-ABC 的侧棱与底面边长相等,如果E 、F 分别为SC 、AB 的中点,那么异面直线EF 与SA 所成的角等于 ( ) A 900 B 600 C 450 D 300分析:本题的正三棱锥S-ABC 即为正四面体,将正 四面体SABC “嵌入”到正方体中,使正四面体的六条棱分别是正方体六个面的面对角线(如图2),易知EF 在正方体的两底面中心连线上,与正方体的一条侧棱平行。
而 SA 与该侧棱所成角是450,故异面直线EF 与SA 所成的 角等于450,选(C )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例谈构造平行六面体解立体几何题立体几何题的题设中若有“垂直”(包括线线垂直、线面垂直及面面垂直)可以试着构造长方体来求解,若没有“垂直”也可尝试构造平行六面体来求解.本文以普通高中课程标准实验教科书《数学·选修2-1·A 版》(人民教育出版社,2007年第2版)(下简称教科书)中的题目及几道高考题来谈谈这种解题方法.题1 (教科书第106页例2)如图1,甲站在水库底面上的点A 处,乙站在水坝斜面上的点B 处.从,A B 到直线l (库底与水坝的交线)的距离AC 和BD 分别为a 和b ,CD 的长为c ,AB 的长为d .求库底与水坝所成二面角的余弦值.图1 图2 解 可在如图2所示的平行六面体中求解:因为,//CD AC AC A D '⊥,所以CD A D '⊥.又CD BD ⊥,所以CD ⊥面A DB ',得AA A B ''⊥,所以222A B d c '=-.在A BD '∆中,由余弦定理可求得2222cos 2a b c d A DB ab++-'∠=,此即所求二面角的余弦值.题 2 (教科书第107页练习第2题)如图3,60︒的二面角棱上有,A B 两点,直线,AC BD 分别在这个二面角的两个半平面内,且都垂直于AB .已知4,6,8AB AC BD ===,求CD 的长.图3 图4 解 可在如图4所示的平行六面体中求解:在ACE ∆中,6,6,60AC AE BD CAE ===∠=︒,由余弦定理可求得252CE =.可证BA ⊥面ACE ,所以有DE CE ⊥,在CDE ∆中可求得217CD =.题3 (教科书第113页第12题)一条线段夹在一个直二面角的两个半平面内,它与两个半平面所成的角都是30︒,求这条线段与这个二面角的棱所成角的大小.解 可在如图5所示的长方体中求解:30ADB DAE ∠=∠=︒,可不妨设2AD =,得1,3,2DE CB AB AE BD BE CD =======,所以在Rt ACD ∆中可求得45ADC ∠=︒,即夹在直二面角A BE D --的线段AD 与棱BE 所成角的大小是45︒.图5题 4 已知两平行平面,αβ的距离为23,点,A B α∈,点,C D β∈,且3,2AB CD ==,异面直线,AB CD 成60︒角,求四面体ABCD 的体积.解 可在如图6所示的平行六面体中求解:图6 在图6所示的平行六面体中,60A CD '∠=︒或120︒,133,23sin 322A CD A C AB S A CD '∆''===⋅⋅∠=,所以13323332A BCD A BCD V V '--===. 题 5 (2012·安徽·文·15) 若四面体ABCD 的三组对棱分别相等,即,,AB CD AC BD AD BC ===,则下列命题正确的是 (写出所有正确命题的编号)。
①四面体ABCD 每组对棱相互垂直②四面体ABCD 每个面的面积相等③从四面体ABCD 每个顶点出发的三条棱两两夹角之和大于90°而小于180° ④连接四面体ABCD 每组对棱中点的线段相互垂直平分⑤从四面体ABCD 每个顶点出发的三条棱可作为一个三角形的三边长解 ②④⑤.如图7,可把四面体ABCD 放置在如图所示的平行六面体中,由该四面体的三组对棱分别相等,可得该平行六面体是长方体(在图7,由AD BC =可得图7中的平行六面体左面的平行四边形的对角线相等,所以它是矩形.同理得该平行六面体的表面均是矩形,所以该平行六面体是长方体).①错误:因为长方体不一定是正方体.②正确:可证ABC CDA BAD DCB ∆≅∆≅∆≅∆.③错误:可得从四面体ABCD 每个顶点出发的三条棱两两夹角之和为180°,比如180BAC CAD BAD ABD BDA BAD ∠+∠+∠=∠+∠+∠=︒.④错误:如图8,易证顺次连接四面体ABCD 的棱,,,AB BC CD DA 的中点,,,E F G H 得到的四边形是菱形.⑤正确:比如,从四面体ABCD 的顶点A 出发的三条棱可组成BCD ∆.图7 图8 题6 (2012·大纲全国·理·16)三棱柱111ABC A BC -中,底面边长和侧棱长都相等,1160BAA CAA ∠=∠=︒,则异面直线1AB 与1BC 所成角的余弦值为 .解法1 66.如图9,作1AO '⊥面ABC 于O ',由1160BAA CAA ∠=∠=︒可得AO '是BAC ∠的平分线.设直线AO BC O '⋂=,则点O 是BC 的中点.图9由11cos cos cos A AO O AB A AB ''∠⋅∠=∠,得11cos cos30cos 60,cos 3A AO A AO ''∠⋅︒=︒∠= 可不妨设123AB AA ==12,22,3AO AO AD ''===.可如图1建立空间直角坐标系O xyz -,得1(0,3,0),(3,0,0),(3,0,0),(0,0,0),(0,1,0),(0,1,22)A B C O O A'-,再由111(0,2,22)AA BB CC ===-,得11(3,2,22),(3,2,22)B C ---,所以11(3,5,22),(23,2,22)AB BC =--=- 设异面直线1AB 与1BC 所成角的大小为α,则11116cos 626AB BC AB BC α⋅===⋅⋅ 解法2 6.如图10,可把三棱柱111ABC A BC -补成平行六面体1111ABCD A BC D -.图10作1AO '⊥面ABC 于O ',由1160BAA CAA ∠=∠=︒可得AO '是BAC ∠的平分线.设直线AO BC O '⋂=,则点O 是BC 的中点.由BC AO ⊥得1BC AA ⊥,所以1BC CC ⊥.可不妨设11BC CC ==,得112AD BC ==菱形11A ABB 的边长为1,160BAA ∠=︒,所以13AB=;菱形ABCD 的边长为1,2120BAD BAC ∠=∠=︒,所以113B D BD ==在等腰11AB D ∆中,11113,2B A B D AD =,易求得116cos 6B AD ∠=,所以异面直线1AB 与1BC 所成角的余弦值为66. 题7 如图11所示,在三棱锥A -BCD 中,AB =AC =BD =CD =3,AD =BC =2,点M ,N 分别为AD ,BC 的中点,则异面直线AN ,CM 所成的角的余弦值是________.解 78.所有的四面体(即三棱锥)都可以放置在平行六面体中,且四面体的四个顶点是平行六面体的八个顶点中的四个.进一步,还可得:对棱长相等的四面体都可以放置在长方体中,且四面体的四个顶点是长方体的八个顶点中的四个.所以本题也可利用长方体建立坐标系简洁求解.可把三棱锥A -BCD 放置在如图12所示的长方体中.图12如图12所示,设长方体的长、宽、高分别是z y x ,,,由勾股定理得⎪⎩⎪⎨⎧=+=+=+222222222323x z z y y x解得2,7===z y x .可如图12所示建立空间直角坐标系xyz C -来求解. 得)2,7,0(),0,7,2(),2,0,2(),0,0,0(A D B C ,所以⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛22,0,22,22,7,22N M ,再得⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛--=22,7,22,22,7,22.得87887,cos -=⋅-=⋅>=<CM AN CM AN ,所以异面直线AN ,CM 所成的角的余弦值是87. 题8 (2010年同济大学自主招生数学试题)如图13所示,在四面体ABCD 中,b CD a AB ==,,异面直线CD AB ,的距离为d ,夹角为θ.图13(1)若⊥=AB ,2πθ面BCD ,求四面体ABCD 的体积;(2)若2πθ=,求证:四面体ABCD 的体积为定值;(3)求四面体ABCD 的体积.解 我们先解第(3)问:(3)如图14所示,将四面体ABCD 补成一个平行六面体D C C A D B AB ''-'',得θ='∠A DC ,上下两底面C A B A ''',的距离为d ,所以θθsin 2sin 21abd d ab V D C C A D B AB =⋅⎪⎭⎫ ⎝⎛⋅=''-''平行六面体 θsin 6161abd V V D C C A D B AB BCD A ==''-''-平行六面体图14由第(3)问的结论,立得头两问的解法: (1)abd V BCD A 61=-;(2)abd V BCD A 61=-(定值).题9 求证:若四面体ABCD 的六条棱长满足d CD c AB b AC BD a BC AD ======,,,,则(1)可把该四面体放置在如图15所示的直平行六面体D B C A D B C A ''-''中:图15(2)对棱AD 和BC ,BD 和AC ,AB 和CD 之间的距离分别为z l y S l x S l ===321,,,其中 2222222222222221,2221,2221d c b a z d c a b y d c b a x --+=++-=++-= ))((212222a b cd a b cd S +--+= 证明 (1)略.(2)在图15的直平行六面体D B C A D B C A ''-''中,设z A A y C A x D A ='='=',,. 由勾股定理,可得222222,b z y a z x =+=+.如图16所示,在平行四边形D B C A ''中,可得222222y x d c +=+.可解得结论(2)中关于z y x ,,的结论成立.图16又平行四边形D B C A ''的面积是D AO cd S '∠=sin 21,在D AO '∆中由余弦定理可求得cd b a D AO 22cos -='∠,所以可得结论(2)中关于S 的结论也成立.因为对棱AD 和BC 的距离就是如图16所示的直平行六面体D B C A D B C A ''-''中左、右两个侧面的距离,也即平行四边形D B C A ''的对边B C D A '',的距离,所以对棱AD 和BC 的距离是xS l =1. 同理可得BD 和AC ,AB 和CD 之间的距离分别为z l y S l ==32,.证毕.题10 求证:若四面体ABCD 有两组对棱互相垂直(则可证得其三组对棱均互相垂直),且d AD c AB b AC a BC ====,,,,则(1)可把该四面体放置在如图17所示的所有棱长均相等的平行六面体D B C A D B C A ''-''中:图17 (2)222222,d c a CD d b a BD +-=+-=;(3)对棱AD 和BC ,BD 和AC ,AB 和CD 之间的距离分别为2223222212,2,2dc a c Sh ld b a b Sh l ad Sh l +-=+-==,其中 aSc b a c b a S l c b a s c s b s a s s S ld h a a 8))((16,2,))()((,222222222+--+-=++=---=-= 证明 (1)略.(2)由平行四边形两条对角线的平方和等于各边的平方和,可得222222BD b d a CD c +=+=+进而可得欲证结论成立.(3)设ABC ∆的垂心为点H .如图18所示,分别以边BC 和BC 上的高所在的直线为x 轴和y 轴建立平面直角坐标系xOy .图18可设)0,(),0,(),,0(000z C y B x A ,得220202202000,,c y x b z x a y z =+=+=-,解得a a c b z a a c b y a S x 2,2,2222022200+-=--==,其中2,))()((c b a s c s b s a s s S ++=---=. 得直线⎪⎪⎭⎫ ⎝⎛+--+--=a a c b x a c b S y AC 24:222222. 又直线AC BH ⊥,所以直线⎪⎪⎭⎫ ⎝⎛---+-=a a c b x S a c b y BH 24:222222. 可得⎪⎪⎭⎫ ⎝⎛+--+aS c b a c b a H 8))((,0222222. 进而可得垂心H 到顶点A 的距离为aSc b a c b a S l a 8))((162222222+--+-=. 如图19所示,设侧棱C C '与底面D B C A ''所成角的大小为θ.图19得平行六面体的体积θsin sin ⋅'∠⋅'⋅'⋅'=B C A C C B C A C V ,又θsin sin 61⋅'∠⋅'⋅'⋅'='-B C A C C B C A C V C AB C 三棱锥,进而可得V V ABCD 31=四面体,即Sh l ad =12,得adSh l 21=. 进而可得欲证结论成立.本文介绍的技巧“构造平行六面体解立几题”实际上就是一种补形法,在立体几何中还有很多用补形法简洁解题的例子,比如把正四面体放置在正方体中的补形法解题技巧.。
