2017年全国高考理科数学试题分类汇编7:立体几何 Word版含答案
2017的年的高考立体几何大题(理科).doc

2017年高考立体几何大题(理科)1、(2017新课标Ⅰ理数)(12分)如图,在四棱锥P-ABCD中,AB//CD,且90BAP CDP o.(1)证明:平面PAB⊥平面PAD;APD o,求二面角A-PB-C的余弦值.(2)若PA=PD=AB=DC,902、(2017新课标Ⅱ理)(12分)如图,四棱锥P -ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,o1,90,2ABBC AD BAD ABC E 是PD 的中点.(1)证明:直线CE ∥平面PAB ;(2)点M 在棱PC 上,且直线BM 与底面ABCD 所成角为o 45,求二面角M AB D 的余弦值.如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD//平面MAC,PA=PD=,AB=4.6(I)求证:M为PB的中点;(II)求二面角B-PD-A的大小;(III)求直线MC与平面BDP所成角的正弦值.5、(2017山东理)如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120得到的,G是?DF的中点.(Ⅰ)设P是?CE上的一点,且AP BE,求CBP的大小;AD,求二面角E AG C的大小.AB,2(Ⅱ)当36、(2017江苏)(本小题满分14分)如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E 与A,D不重合)分别在棱AD,BD上,且EF⊥AD.求证:(1)EF∥平面ABC;(2)AD⊥AC.7、如图,在三棱锥P-ABC 中,PA ⊥底面ABC ,∠BAC =90°,点D 、E 、N 分别为棱PA 、PC 、BC 的中点,M 是线段AD 的中点,PA =AC =4,AB =2(1)求证:MN ∥平面BDE ;(2)求二面角C-EM-N 的正弦值;(3)已知点H 在棱PA 上,且直线NH 与直线BE 所成角的余弦值为217,求线段AH 的长。
高考立体几何大题及答案(理)

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载高考立体几何大题及答案(理)地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容1.如图,四棱锥中,底面为矩形,底面,,,点在侧棱上,。
(I)证明:是侧棱的中点;求二面角的大小。
2.如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1(Ⅰ)证明:AB=AC (Ⅱ)设二面角A-BACBA1B1C1DED-C为60°,求B1C与平面BCD所成的角的大小3.如图,平面,,,,分别为的中点.(I)证明:平面;(II)求与平面所成角的正弦值.4.如图,四棱锥的底面是正方形,,点E在棱PB上.(Ⅰ)求证:平面;(Ⅱ)当且E为PB的中点时,求AE与平面PDB所成的角的大小.5.如图,在四棱锥中,底面是矩形,平面,,.以的中点为球心、为直径的球面交于点.(1)求证:平面⊥平面;(2)求直线与平面所成的角;(3)求点到平面的距离.6.如图,正方形所在平面与平面四边形所在平面互相垂直,△是等腰直角三角形,(I)求证:;(II)设线段、的中点分别为、,求证:∥(III)求二面角的大小。
7.如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD =AD=a,点E是SD上的点,且DE=a(0<≦1). (Ⅰ)求证:对任意的(0、1),都有AC⊥BE:(Ⅱ)若二面角C-AE-D的大小为600C,求的值。
8.如图3,在正三棱柱中,AB=4, ,点D是BC的中点,点E 在AC上,且DEE.(Ⅰ)证明:平面平面; (Ⅱ)求直线AD 和平面所成角的正弦值。
9.如图,正方形所在平面与平面四边形所在平面互相垂直,△是等腰直角三角形,(I)求证:;(II)设线段、的中点分别为、,求证:∥(III)求二面角的大小。
2017-2018年高考数学立体几何汇编及答案解析

2017—2018年高考数学试题立体几何汇编及答案解析类型一 空间几何体的结构特征与三视图1.【2017浙江,3】某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是A .12+πB .32+πC .123+πD .323+π【答案】A 【解析】2π1211π3(21)1322V ⨯=⨯⨯+⨯⨯=+,选A. 2.【2017北京,理7】某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为(A ) (B )(C ) (D )2 【答案】B 【解析】几何体是四棱锥,如图红色线为三视图还原后的几何体,最长的棱长为正方体的对角线,l == B.3.【2017山东,理13】由一个长方体和两个14圆柱体构成的几何体的三视图如右图,则该几何体的体积为 .【答案】22π+【解析】该几何体的体积为21112211242V π=π⨯⨯⨯+⨯⨯=+. 4.(2018年高考北京卷理科)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )A.1 B.2 C.3 D.4【解答】解:四棱锥的三视图对应的直观图为:PA⊥底面ABCD,AC=,CD=,PC=3,PD=2,可得三角形PCD不是直角三角形.所以侧面中有3个直角三角形,分别为:△PAB,△PBC,△PAD.故选:C.5.(2018年高考数学全国卷1理科)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()A.2B.2C.3 D.2【解答】解:由题意可知几何体是圆柱,底面周长16,高为:2,直观图以及侧面展开图如图:圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度:=2.故选:B.6.(2018年高考数学全国卷3理科)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()A. B . C . D .【解答】解:由题意可知,如图摆放的木构件与某一带卯眼的木构件咬合成长方体,小的长方体,是榫头,从图形看出,轮廓是长方形,内含一个长方形,并且一条边重合,另外3边是虚线,所以木构件的俯视图是A .故选:A .7.(2018年高考浙江卷)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是( ) A .2B .4C .6D .8【解答】解:根据三视图:该几何体为底面为直角梯形的四棱柱.如图所示:故该几何体的体积为:V=.故选:C .8.某多面体的三视图如图所示,则该几何体的体积与其 外接球的体积之比为( )A .π186B .π96 C .π36 D .π26选A类型二 空间几何体与空间旋转体的面积、体积问题1、如图,半径为4的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是______.解:如图,2、设球的一条半径与圆柱相应的母线的夹角为α,圆柱侧面积S =2π×4sin α×2×4cos α=32πsin2α,当α=π4时,S 取最大值32π,此时球的表面积与该圆柱的侧面积之差为32π.3、(2018年高考数学天津卷理科)已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E ,F ,G ,H ,M (如图),则四棱锥M ﹣EFGH 的体积为 .【解答】解:正方体的棱长为1,M ﹣EFGH 的底面是正方形的边长为:,四棱锥是正四棱锥,棱锥的高为, 四棱锥M ﹣EFGH 的体积:=.故答案为:.4、(2014·课标Ⅱ)如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.13解:原来毛坯体积为:π·32·6=54π(cm 3),由三视图知该零件由左侧底面半径为2cm ,高为4cm 的圆柱和右侧底面半径为3cm ,高为2cm 的圆柱构成,故该零件的体积为:π·22·4+π·32·2=34π(cm 3),切削掉部分的体积为54π-34π=20π(cm 3),故切削掉部分的体积与原来毛坯体积的比值为20π54π=1027 .故选C.6.【2017课标3,理8】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A .πB .3π4C .π2D .π4【答案】B【解析】由题可知球心在圆柱体中心,圆柱体上下底面圆半径r =则圆柱体体积23ππ4V r h ==,故选B.7.【2017天津,理10】已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为 . 【答案】92π 【解析】设正方体边长为a ,则226183a a =⇒= ,外接球直径为34427923,πππ3382R V R ====⨯=. 8.【2017江苏,6】 如图,在圆柱12,O O 内有一个球O ,该球与圆柱的上、下面及母线均相切.记圆柱12,O O 的体积为1V ,球O 的体积为2V ,则12V V 的值是 ▲ .【答案】32 【解析】设球半径为r ,则2132π2342π3V r r V r ⨯==.故答案为32. 9、(2018年高考数学全国卷3理科)10.(5分)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且面积为9,则三棱锥D ﹣ABC 体积的最大值为( ) A .12B .18C .24D .54【解答】解:△ABC 为等边三角形且面积为9,可得,解得AB=6,球心为O ,三角形ABC 的外心为O′,显然D 在O′O 的延长线与球的交点如图:O′C==,OO′==2,则三棱锥D ﹣ABC 高的最大值为:6, 则三棱锥D ﹣ABC 体积的最大值为:=18.故选:B .10、(2018年高考数学全国卷2理科)16.(5分)已知圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为,SA 与圆锥底面所成角为45°,若△SAB 的面积为5,则该圆锥的侧面积为40π .【解答】解:圆锥的顶点为S ,母线SA ,SB 所成角的余弦值为,可得sin ∠AMB==.△SAB 的面积为5,可得sin ∠AMB=5,即×=5,即SA=4.SA 与圆锥底面所成角为45°,可得圆锥的底面半径为:=2.则该圆锥的侧面积:π=40π.故答案为:40π.11、(2018年高考数学全国卷1理科)12.(5分)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )A .B .C .D .【解答】解:正方体的所有棱中,实际上是3组平行的棱,每条棱所在直线与平面α所成的角都相等,如图:所示的正六边形平行的平面,并且正六边形时,α截此正方体所得截面面积的最大,此时正六边形的边长明明就的最大值为:6×=.故选:A.12、(2018年江苏省高考数学试卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.【解答】解:正方体的棱长为2,中间四边形的边长为:,八面体看做两个正四棱锥,棱锥的高为1,多面体的中心为顶点的多面体的体积为:2×=.故答案为:.类型三点共线、线共点问题1、如图,E,F,G,H分别是空间四边形内AB,BC,CD,DA上的点,且EH与FG交于点O.求证:B,D,O三点共线.证明:∵点E∈平面ABD,点H∈平面ABD,∴EH⊂平面AB D.∵EH∩FG=O,∴点O∈平面AB D.同理可证点O∈平面BC D.∴点O∈平面ABD∩平面BCD=B D.即B,D,O三点共线.类型四共面问题1、下列如图所示的正方体和正四面体,P、Q、R、S分别是所在棱的中点,则四个点共面的图形是____________.(填所有满足条件图形的序号)解:易知①③中PS ∥Q R ,∴四点共面.在②中构造如图所示的含点P ,S ,R ,Q 的正六边形,易知四点共面.在④中,由点P ,R ,Q 确定平面α,由图象观察知点S 在平面α外,因此四点不共面.综上知,故填①②③.类型五 异面直线问题1.【2017课标II ,理10】已知直三棱柱111C C AB -A B 中,C 120∠AB =,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为( )A ..5 C .5D 【答案】C【解析】如图所示,补成四棱柱1111ABCD A B C D - ,则所求角为1111,BC D BC BD C D AB ∠=====因此1cos 5BC D ∠== ,故选C 。
湖北省各地2017届高三最新考试数学理试题分类汇编:立体几何 含答案 精品

湖北省各地2017届高三最新考试数学理试题分类汇编立体几何2017.02一、选择、填空题 1、(黄冈市2017届高三上学期期末)如图,网格纸上正方形小格的边长为1,图中粗线画的是某几何体的三视图,则该几何体的表面积为S 为()S R r l π=+(注:圆台侧面积公式为)A. 17π+B. 20π+C.22πD. 17π+2、(荆、荆、襄、宜四地七校考试联盟2017届高三2月联考)某几何体的三视图如图所示,图中的四边形都是边长为4的正方形,两条虚线互相垂直,则该几何体的体积是A.1763 B.1603 C.1283D.323、(荆门市2017届高三元月调考)如上图,某几何体的三视图中,正视图和侧视图都是半则它的表面积是A .6πB .8πC .10πD .11π4、(荆州市五县市区2017届高三上学期期末)某三棱锥的三视图如上图所示,其侧(左)视图为直角三角形,则该三棱锥最长的棱长等于A .B CD .5、(天门、仙桃、潜江市2017届高三上学期期末联合考试)一只蚂蚁从正方体1111ABCD A B C D -的顶点A 处出发,经过正方体的表面,按最短路线爬行到达顶点1C 的位置,则下列图中可以表示正方体及蚂蚁最短爬行路线的正视图是A .①②B .①③C .②④D .③④6、(武汉市2017届高三毕业生二月调研考)如图是某个几何体的三视图,其中正视图为正方形,俯视图是腰长为2的等腰直角三角形,则该几何体外接球的直径为A. 2B.7、(武汉市武昌区2017届高三1月调研)中国古代数学名著《九章算术》中记载了公元前344年商鞅监制的一种标准量器——商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为12.6(立方寸),则图中的x 为( )A .1.2B .1.6 C. 1.8 D .2.48、(襄阳市2017届高三1月调研)某空间几何体的三视图如图所示,则该几何体的体积为 A.73 B. 83π- C. 83 D. 73π-9、(襄阳市优质高中2017届高三1月联考)已知某几何体的三视图如图所示(正视图的弧线是半圆),根据图中标出的数据,这个几何体的表面积是A. 36288π+B. 36216π+C. 33288π+D. 33216π+10、(孝感市七校教学联盟2017届高三上学期期末)已知四棱锥P -ABCD 的三视图如图,则四棱锥P -ABCD 的全面积为( ) A .3+ 5 B .2+ 5C .5D .4第4题图11、(湖北省部分重点中学2017届高三上学期第二次联考)如图所示,在四边形ABCD 中,//,,45,90AD BC AD AB BCD BAD =∠=∠=,将ABD ∆沿BD 折起,使得平面ABD ⊥平面BCD ,构成四面体A BCD -,则在四面体中,下列说法正确的是 A.平面ABD ⊥平面ABC B.平面ACD ⊥平面BCD C. 平面ABC ⊥平面BCD D.平面ACD ⊥平面ABC12、(荆州中学2017届高三1月质量检测)已知两条不同的直线,m n 和两个不同的平面,αβ,以下四个命题中正确命题的个数是( )①若//,//m n αβ,且//αβ,则//m n ②若,//m n αβ⊥,且//αβ,则m n ⊥ ③若//,m n αβ⊥,且αβ⊥,则//m n ④若,m n αβ⊥⊥,且αβ⊥,则m n ⊥ A .4 B .3 C. 2 D .113、(荆州市五县市区2017届高三上学期期末)在三棱锥A BCD -中,ABC ∆与BCD ∆都是边长为6的正三角形,平面ABC ⊥平面BCD ,则该三棱锥的外接球的面积为________.二、解答题1、(黄冈市2017届高三上学期期末)如图,在各棱长均为2的三棱柱111ABC A B C -中,侧面11A ACC ⊥底面ABC ,160.A AC ∠=(1)求侧棱1AA 与平面1ABC 所成角的正弦值的大小;(2)已知点D 满足BD BA BC =+,在直线1AA 上是否存在点P ,使DP//平面1ABC ?若存在,请确定点P 的位置,若不存在,请说明理由.2、(荆、荆、襄、宜四地七校考试联盟2017届高三2月联考)如图,在四棱锥P ABCD-中,底面A B C D是平行四边形,135∠=,BAP∠=,侧面PAB⊥底面A B C D,90BCDBC AD的中点,点M在线段PD上.===,,E F分别为,AB AC PA2(Ⅰ)求证:EF⊥平面PAC;(Ⅱ)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求PM的值.PD3、(荆门市2017届高三元月调考)如图,在五面体ABCDEF中,底面ABCD是正方形,△,△都是等边三角形, EF∥AB,且EF>AB,M,O分别为,ADE BCFEF BD的中点,连接MO.(Ⅰ)求证:MO⊥底面ABCD;--的余弦值.(Ⅱ)若EF=2AB,求二面角E BD F4、(荆州市五县市区2017届高三上学期期末)在三棱柱ABC A 1B 1C 1中,侧面ABB 1A 1为矩形,AB =3,AA 1=32,D 为AA 1的中点,BD 与AB 1交于点O ,CO ⊥侧面ABB 1A 1.(Ⅰ)证明:BC ⊥AB 1;(Ⅱ)若OC =OA ,求二面角A 1-AC -B 的余弦值.5、(天门、仙桃、潜江市2017届高三上学期期末联合考试)如图,在三棱柱111ABC A B C -中,90BAC ∠=︒,2AB AC ==,14A A =,1A 在底面ABC 的射影为BC 的中点,D 是11B C 的中点.(Ⅰ)证明:11A D A BC ⊥平面;(Ⅱ)求二面角11A BD B --的平面角的余弦值.6、(武汉市2017届高三毕业生二月调研考) 如图,在三棱柱111ABC A B C -中,AB ⊥平面11BCC B ,11,2,1,3BCC AB BB BC D π∠====为1CC 的中点.(1)求证:1DB ⊥平面ABD ; (2)求二面角11A B D A --的余弦值.7、(武汉市武昌区2017届高三1月调研)如图,四棱锥中,//AB CD ,BC CD ⊥,侧面为等边三角形,2AB BC == ,1CD SD == . (Ⅰ)证明:SD ⊥平面SAB ;(Ⅱ)求AB 与平面SBC 所成角的正弦值.8、(襄阳市2017届高三1月调研)在长方体1111ABCD A BC D -中,E,F 分别是1,AB CD 的中点,11, 2.AA AD AB ===. (1)求证:EF//平面11BCC B ; (2))求证:平面1CD E ⊥平面1D DE ;在线段1CD 上是否存在一点Q,使得二面角1Q DE D --为45,若存在,求11D Q D C的值,不存在,说明理由.9、(襄阳市优质高中2017届高三1月联考)如图,在四棱锥P ABCD -中,1//,90,.2A DBC AD C P A B B C C D A D ∠=∠===E 为棱AD 的中点,异面直线PA 与CD 所成的角为90.(1)在平面PAB 内找一点M ,使得直线//CM 平面PBE ,并说明理由; (2)若二面角P CD A --的大小为45,求二面角P CE B --的余弦值.10、(孝感市七校教学联盟2017届高三上学期期末)图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,AD ∥BC ,90ADC ∠=︒,平面PAD ⊥底面ABCD ,Q 为AD 的中点,M是棱PC 上的点,2PA PD ==,112BC AD ==,CD =. (1)求证:平面MQB ⊥平面PAD ;(2)若二面角M BQ C --大小的为60 ,求QM 的长11、(湖北省部分重点中学2017届高三上学期第二次联考)如图,在直三棱柱111ABC A B C -中,平面1A BC ⊥侧面11ABB A ,且1 2.AA AB == (1)求证:AB BC ⊥;(2)若直线AC 与平面1A BC 所成的角为6π,请问在线段1AC 上是否存在点E ,使得二面角A BE C --的大小为23π,请说明理由.12、(荆州中学2017届高三1月质量检测)如图,在四棱锥P ABCD -中,侧面PCD ⊥底面ABCD ,PD CD ⊥,E 为PC 的中点,底面ABCD 是直角梯形,//AB CD ,90ADC ∠=,2AB AD PD ===,4CD =.(Ⅰ)求证://BE 平面PAD ;(Ⅱ)设Q 为棱PC 上一点,CQ CP λ=,试确定λ的值使得二面角Q BD P --为45.参考答案一、选择、填空题1、D2、B3、C4、C5、C6、D7、B8、B9、D10、A 11、D 12、C13、60π二、解答题1、解:(1)∵侧面底面,作于点,∴平面.又,且各棱长都相等,∴,,.…2分故以为坐标原点,建立如图所示的空间直角坐标系,则,,,,∴,,.……4分设平面的法向量为,则,解得.由.而侧棱与平面所成角,即是向量与平面的法向量所成锐角的余角,∴侧棱与平面所成角的正弦值的大小为…………………6分(2)∵,而∴又∵,∴点的坐标为.假设存在点符合题意,则点的坐标可设为,∴.∵,为平面的法向量,∴由,得. ……………10分又平面,故存在点,使,其坐标为,即恰好为点.………12分2、(Ⅰ)证明:在平行四边形ABCD 中,因为AB AC =,135BCD ∠=, 所以AB AC ⊥.由,E F 分别为,BC AD 的中点,得//EF AB ,所以EF AC ⊥. …………2分因为侧面PAB ⊥底面ABCD ,且90BAP ∠=,所以PA ⊥底面ABCD . 又因为EF ⊂底面ABCD ,所以PA EF ⊥. …………4分又因为PAAC A =,PA ⊂平面PAC ,AC ⊂平面PAC ,所以EF ⊥平面PAC . ………………6分 (Ⅱ)解:因为PA ⊥底面ABCD ,AB AC ⊥,所以,,AP AB AC 两两垂直,以,,AB AC AP分别为x 、y 、z ,建立空间直角坐标系,则(0,0,0),(2,0,0),(0,2,0),(0,0,2),(2,2,0),(1,1,0)A B C P D E -,所以(2,0,2)PB =-,(2,2,2)PD =--,(2,2,0)BC =-,设([0,1])PMPDλλ=∈,则(2,2,2)PM λλλ=--,所以(2,2,22)M λλλ--,(12,12,22)ME λλλ=+--,易得平面ABCD 的法向量(0,0,1)=m .设平面PBC 的法向量为(,,)x y z =n ,由0BC ⋅=n ,0PB ⋅=n ,得220,220,x y x z -+=⎧⎨-=⎩令1x =, 得(1,1,1)=n .因为直线ME 与平面PBC 所成的角和此直线与平面ABCD 所成的角相等,所以|c o s ,||c o sM E M E <>=<>m n ,即||||||||||||M E M E M E M E ⋅⋅=⋅⋅m n m n ,所以|22||λ-=,解得λ=λ=. 综上所得:PM PD =分 3、(Ⅰ)证法一:取BC 、AD 中点G 、H ,连接EH 、FG 、HG ,又因为EF ∥AB ,所以EF ∥平面ABCD ,则EF ∥HG ,由EH =FG ,可知EFGH 是等腰梯形, …………………………………2分 M 和O 分别为EF 和HG 的中点,则MO ⊥HG .因为,ADE BCF △△均为正三角形,所以EH ⊥AD 、FG ⊥BC 、HG ⊥BC ,则 BC ⊥平面EFGH , …………………………………4分MO 在平面EFGH 内,所以BC ⊥MO ;又MO ⊥HG ,HG 和BC 是底面ABCD 上的两条相交直线, 故MO ⊥底面ABCD . …………………………………6分证法二:连接AC 、AM 、CM ,则O 为AC 中点,因为EF ∥AB ,所以EF ∥平面ABCD ,则EF ∥CD , 因为,ADE BCF △△均为正三角形,则EA=ED =FB=FC ,可知EFBA 和EFCD 是全等的等腰梯形, …………………………………2分因为M 为EF 中点,则MA=MB=MC=MD .所以∆MAC 和∆MBD 是全等的等腰三角形, …………………………………4分所以MO ⊥AC ,MO ⊥BD ,又AC 和BD 是底面ABCD 上的两条相交直线,故MO ⊥底面ABCD . …………………………………6分(Ⅱ)方法一:过F 作OG 延长线的垂线交于N 点,连接BN , 因为EF =2AB ,所以MF =ON =AB ,12OG GN BG AB ===,则BO ⊥BN , 又FN ∥MO ,所以FN ⊥底面ABCD ,则FN ⊥BO ,所以BO ⊥平面BFN ,则BO⊥BF ,因此∠FBN 为二面角F —BD —N 的平面角,………………………………9分设AB a 2=,则EM =MF =ON a 2=,,3,a GF a GN ==则FN ,又BN ,所以∠FBN 45=,即二面角F —BD —N 为45,同样二面角E —BD —A 为45, 因此二面角E B D --为90,则所求余弦值为0. (12)分方法二:以O 为坐标原点,直线HG 、OM 分别为y 轴、z 轴,建立空间直角坐标系, 过F 作OG延长线的垂线交于N 点,连接BN ,因为EF =2AB ,设AB a 2=,则EM =MF =ON a 2=,,3,a GF a GN ==则FN OM ==,则B )0,,(a a ,D )0,,(a a --,F )2,20(a a ,E )2,2,0(a a -,设平面BDE 的法向量为),,(z y x m =,则(2,2,0)DB a a =,(,3,)BE a a =--,(,)BF a a =-,220,30m DB ax ay m BE ax ay ⎧⋅=+=⎪⎨⋅=--+=⎪⎩,取)2,1,1(--=m,…………9分设平面BDF 的法向量为),,(z y x n = ,则220n DB ax ay n BF ax ay ⎧⋅=+=⎪⎨⋅=-++=⎪⎩,取)2,1,1(-=n, 因为0)2,1,1()2,1,1(=-⋅--=⋅n m,即n m⊥,所以平面BDE ⊥平面BDF ,因此二面角E BD F --为90,则所求余弦值为0. …12分4、解:(Ⅰ)证明:由题意tan∠ABD =ADAB =22,tan ∠AB 1B =AB BB 1=22, 0<∠ABD 2π<,0<∠AB 1B <π2,∴∠ABD =∠AB 1B ,∴∠ABD +∠BAB 1=∠AB 1B +∠BAB 1=π2,∴AB 1⊥BD …………………2分又CO ⊥侧面ABB 1A 1,∴AB 1⊥CO . …………………3分 又BD 与CO 交于点O ,∴AB 1⊥平面CBD , …………………4分 又BC ⊂平面CBD ,∴BC ⊥AB 1. …………………5分(Ⅱ)如图,以O 为原点,分别以OD ,OB 1,OC 所在的直线为x ,y ,z 轴,建立空间直角坐标系Oxyz,则(0,A,(B,C,1B .∴(AB =-,AC =,11(6,2AA BB ==. (7)分设平面ABC 的法向量为n =(x ,y ,z ), 则=0=0AB AC ì×ïíï×în n,即=0=0ì-ïíïî, 令x =1,可得n =(1,2,-2)是平面ABC 的 一个法向量. …………………9分 设平面A 1AC 的法向量为m =(x ,y ,z ), 则1=0=0AA AC ì×ïíï×îm m,即=0=0ìïíïî, 令x =2,可得m =(2,-2,2)是平面A 1AC 的一个法向量.…………………10分 设二面角A 1-AC -B 的平面角为α,则cos cos ,a ×==m n m n m n ∴二面角A 1-AC-B . …………………12分5、【解析】(Ⅰ)设E 为BC 的中点,连接1,,,A E AE DE 由题意得1A E ABC ⊥平面 所以1A E AE ⊥因为AB AC =,所以AE BC ⊥故1AE A BC ⊥平面………………………………………………3分 由D ,E 分别为11B C ,BC 的中点,得11//DE B B DE B B =且,从而11//DE A A DE A A =,,所以四边形1A AED 为平行四边形故1//A D AE ,又因为1AE A BC ⊥平面所以11A D A BC ⊥平面………………………………6分 (Ⅱ)(解法一)作11A F BD A F BD F ⊥=且,连接1B F由1190AE EB A EA A EB =∠=∠=︒,得114A B A A == 由1111,A D B D A B B B ==,得11A DB B DB ∆∆与全等 由1A F BD ⊥,得1B F BD ⊥,因此11A FB ∠为二面角11A BD B --的平面角……9分由1114,90A D A B DA B =∠=︒,得1143BD A F B F ===由余弦定理得111cos 8A FB ∠=-………………………………12分(解法二)以CB 的中点E 为原点,分别以射线EA ,EB 为x ,y 轴的正半轴,建立空间直角坐标系Exyz , 如图所示……………………………………7分由题意知各点坐标如下:1(0,14)0,2,0),A B1((D B所以1A B =(BD =1DB =……9分 设平面1A BD 的法向量为111(,,)x y z =m ,平面1B BD 的法向量为222(,,)x y z =n 由10A B BD ⎧=⎪⎨=⎪⎩m m,即1111100=+=⎪⎩可取=m由10DB BD ⎧=⎪⎨=⎪⎩n N,即222200=-+=⎪⎩可取=n于是||1|cos ,|||||8〈〉==m n m n m n由题意可知,所求二面角的平面角是钝角,故二面角11A BD B --的平面角的余弦值为18-……………………12分6、7、解:方法一:空间向量法(Ⅰ)以C 为坐标原点,射线CD 为x 轴正半轴,建立如图所示的空间直角坐标系C xyz -,则()1,0,0D ,()2,2,0A ,()0,2,0B , 设(),,S x y z ,则0,0,0x y z >>> ,且()2,2,AS x y z =--,(),2,BS x y z =- ,()1,,DS x y z =- ,由AS BS =,=,解得:1x = ,由1DS =,得221y z += ① 由2BS =,得22410y z y +-+= ②解①②,得1,22y z ==,11,,22S ⎛∴ ⎝⎭ ,31,,22AS ⎛=-- ⎝⎭ ,31,,22BS ⎛⎫=- ⎪ ⎪⎝⎭ ,10,,22DS ⎛= ⎝⎭ , 0DS AS ∴⋅=,0DS BS ⋅= ,,DS AS DS BS ∴⊥⊥ ,SD ∴⊥平面SAB …………………6分(Ⅱ)设平面SBC 的法向量()111,,n x y z =, 则n BS ⊥,n CB ⊥,0,0n BS n CB ∴⋅=⋅= ,又31,,22BS ⎛⎫=- ⎪ ⎪⎝⎭,()0,2,0CB =, 1111302220x y z y ⎧-+=⎪∴⎨⎪=⎩ ,取12z = ,得()3,0,2n =-, ()2,0,0AB =-,2cos ,77AB n AB n AB n-⨯⋅∴<>===⨯ ,故AB 与平面SBC . 方法二:综合法(Ⅰ) 解:如下图,取AB 的中点E ,连结DE ,SE ,则四边形BCDE 为矩形,2DE CB ∴==AD ∴=侧面SAB 为等边三角形,2AB =,2SA SB AB ∴===,且SE =又1SD = ,222SA SD AD ∴+=,222SE SD ED += ,,SD SA SD SE ∴⊥⊥, SD ∴⊥平面SAB .(Ⅱ)过点S 作SG DE ⊥于G ,因为AB SE ⊥,AB DE ⊥,所以平面AB ⊥平面SDE 所以平面SDE ⊥平面ABCD ,由平面与平面垂直的性质,知SG ⊥平面ABCD ,在Rt DSE ∆中,由SD SE DE SG ⋅=⋅,得12SG =⨯,所以SG =. 过点A 作AH ⊥平面SBC 于H ,连结BH ,则ABH ∠为AB 与平面SBC 所成角的角, 因为//CD AB ,AB ⊥平面SDE , 所以CD ⊥平面SDE ,所以CD SD ⊥,在Rt CDS ∆中,由1CD SD ==,求得SC =在SBC 中,2,SB BC SC ==所以122SBCS == , 由A SBC S ABC V V --=,得1133SBCABC S AH S SG ⋅=⋅ ,即11122332AH =⨯⨯⨯,解得AH =所以sin AH ABH AB ∠==故AB 与平面SBC 所成角的正弦值为7. 8、(Ⅰ)证:过F 作FM ∥C 1D 1交CC 1于M ,连结BM∵F 是CD 1的中点,∴FM ∥C 1D 1,错误!未找到引用源。
(精校版)2017年新课标Ⅰ理数高考真题文档版(含答案)

更多优质资料请关注公众号:诗酒叙华年绝密★启用前2017年普通高等学校招生全国统一考试理科数学本试卷5页,23小题,满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必将自己的姓名、考生号、考场号和座位号填写在答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.作答选择题时,选出每小题答案后,用2B 铅笔在答题卡上对应题目选项的答案信息点涂黑;如需要改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A ={x |x <1},B ={x |31x <},则 A .{|0}A B x x =<I B .A B =R U C .{|1}A B x x =>UD .A B =∅I2.如图,正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是A .14B .π8C .12D .π43.设有下面四个命题1p :若复数z 满足1z∈R ,则z ∈R ;更多优质资料请关注公众号:诗酒叙华年2p :若复数z 满足2z ∈R ,则z ∈R ;3p :若复数12,z z 满足12z z ∈R ,则12z z =; 4p :若复数z ∈R ,则z ∈R .其中的真命题为 A .13,p pB .14,p pC .23,p pD .24,p p4.记n S 为等差数列{}n a 的前n 项和.若4524a a +=,648S =,则{}n a 的公差为A .1B .2C .4D .85.函数()f x 在(,)-∞+∞单调递减,且为奇函数.若(11)f =-,则满足21()1x f --≤≤的x 的取值范围是 A .[2,2]-B .[1,1]-C .[0,4]D .[1,3]6.621(1)(1)x x++展开式中2x 的系数为 A .15B .20C .30D .357.某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为A .10B .12C .14D .168.右面程序框图是为了求出满足3n −2n >1000的最小偶数n ,那么在和两个空白框中,可以分别填入A .A >1 000和n =n +1更多优质资料请关注公众号:诗酒叙华年B .A >1 000和n =n +2C .A ≤1 000和n =n +1D .A ≤1 000和n =n +29.已知曲线C 1:y =cos x ,C 2:y =sin (2x +2π3),则下面结论正确的是 A .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2B .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2C .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2D .把C 1上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 210.已知F 为抛物线C :y 2=4x 的焦点,过F 作两条互相垂直的直线l 1,l 2,直线l 1与C 交于A 、B 两点,直线l 2与C 交于D 、E 两点,则|AB |+|DE |的最小值为 A .16B .14C .12D .1011.设xyz 为正数,且235x y z ==,则A .2x <3y <5zB .5z <2x <3yC .3y <5z <2xD .3y <2x <5z12.几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一项是20,接下来的两项是20,21,再接下来的三项是20,21,22,依此类推.求满足如下条件的学科网&最小整数N :N >100且该数列的前N 项和为2的整数幂.那么该款软件的激活码是 A .440B .330C .220D .110二、填空题:本题共4小题,每小题5分,共20分。
2017年普通高等学校招生全国统一考试理科数学试卷与答案

绝密★启用前2017年普通高等学校招生全国统一考试理科数学注意事项:.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共 小题,每小题 分,共 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
已知集合 31x< 则 {|0}AB x x =< A B =R {|1}A B x x => A B =∅如图,正方形 内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称 在正方形内随机取一点,则此点取自黑色部分的概率是14 π8 12 π4设有下面四个命题1:p 若复数z 满足1z ∈R ,则z ∈R ;2:p 若复数z 满足2z ∈R ,则z ∈R ;3:p 若复数12,z z 满足12z z ∈R ,则12z z =; 4:p 若复数z ∈R ,则z ∈R其中的真命题为13,p p 14,p p 23,p p 24,p p.记n S 为等差数列{}n a 的前n 项和.若4524a a +=,48S =,则{}n a 的公差为 .....函数()f x 在(,)-∞+∞单调递减,且为奇函数.若(11)f =-,则满足21()1x f --≤≤的x 的取值范围是.[2,2]-. [1,1]-. [0,4]. [1,3]621(1)(1)x x++展开式中2x 的系数为某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为 ,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为右面程序框图是为了求出满足 的最小偶数 ,那么在和两个空白框中,可以分别填入和 和 ≤ 和 ≤ 和已知曲线 : , :2π3,则下面结正确的是 把 上各点的横坐标伸长到原来的 倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线把 上各点的横坐标伸长到原来的 倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线把 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线把 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π12个单位长度,得到曲线已知 为抛物线 : 的焦点,过 作两条互相垂直的直线 , ,直线 与 交于 、两点,直线 与 交于 、 两点,则 的最小值为. . . . 设 为正数,且235xyz==,则. . . .几位大学生响应国家的创业号召,开发了一款应用软件 为激发大家学习数学的兴趣,他们退出了 解数学题获取软件激活码 的活动 这款软件的激活码为下面数学问题的答案:已知数列 , , , , , , , , , , , , , , , ,其中第一项是 ,接下来的两项是 , ,再接下来的三项是 , , ,依此类推 求满足如下条件的最小整数 :且该数列的前 项和为 的整数幂 那么该款软件的激活码是二、填空题:本题共 小题,每小题 分,共 分。
2017年普通高等学校招生全国统一考试理科数学试卷与答案

绝密★启用前2017年普通高等学校招生全国统一考试理科数学注意事项:1. 答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3. 考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合A={x|x<1}, B={x| 3x1},则AI B {x|x 0} AU B R AU B {x|x 1} AI B 如图,正方形ABCD内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是n丄n设有下面四个命题14 8 2 4P1 :若复数z满足丄R,则z R ;zP2 :若复数z满足z2R,则z R ;P3:若复数Z1,Z2 满足Z1Z2 R,则Z1 Z2 ;P4:若复数z R,则Z R.其中的真命题为P1, P3 P1, P4 P2, P3 P2, P44•记S n为等差数列{a n}的前n项和.若a4 24 , S4 8,则{a.}的公差为A . 1 B. 2G. 4D. 85 .函数f(x)在( ,)单调递减,且为奇函数.若 f(1)1,则满足 1 f(x 2) 1 的的取值范围是A . [ 2,2]B. [ 1,1] G. [0,4] D. [1,3]6. (1 —)(1 X )6展开式中x 2的系数为X某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组 成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是 梯形,这些梯形的面积之和为右面程序框图是为了求出满足 3n -2n >1000的最小偶数n,那么在禾两个空 白框中,可以分别填入>1000 和 n =n +1 >1000 和 n =n +2 禾口 n =n +1和 n =n +2x +2n),则下面结正确的是32倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线G个单位长度,得到曲线G9.已知曲线 C : y =cos x ,G: y =sin(2 A.把G 上B.把G 上各点的横坐标伸长到原来的 2倍,纵坐n12G.把G 上各点的横坐标缩短到原来的 2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线G个单位长度,得到曲线GD.把G 上各点的横坐标缩短到原来的 2倍,纵坐标不变,再把得到的曲线向右平移 n1210. 已知F为抛物线C: y2=4x的焦点,过F作两条互相垂直的直线11, 12,直线I i与C交于A B两点,直线I 2与C交于D E两点,则|AB+| DE的最小值为A. 16B. 14C. 12D 1011. 设xyz为正数,且2x3y5z,贝yA. 2x<3y<5zB. 5z<2x<3yC. 3y<5z<2xD. 3y<2x<5z12. 几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们退出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:已知数列1, 1, 2, 1, 2, 4, 1, 2, 4, 8, 1, 2, 4, 8, 16,…,其中第一项是2°,接下来的两项是20, 21,再接下来的三项是26, 21, 22,依此类推. 求满足如下条件的最小整数N: N>100且该数列的前N项和为2的整数幕.那么该款软件的激活码是二、填空题:本题共4小题,每小题5分,共20分。
2017年高考数学—立体几何(选择+填空+答案)
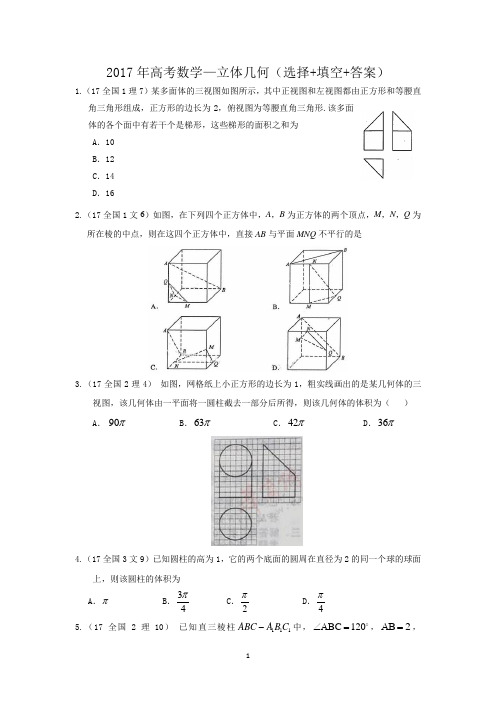
2017年高考数学—立体几何(选择+填空+答案)1.(17全国1理7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为A .10B .12C .14D .162.(17全国1文6)如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直接AB 与平面MNQ 不平行的是3.(17全国2理4) 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A . 90πB .63πC .42πD .36π4.(17全国3文9)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A .πB .34πC .2πD .4π 5.(17全国2理10) 已知直三棱柱111ABC A B C -中,C 120∠AB =o ,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为( )A .32B .155C .105D .33 6.(17全国3文10)在正方体1111ABCD A B C D -中,E 为棱CD 的中点,则A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥7.(17北京理(7))某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为(A )32 (B )23 (C )22 (D )28.(17北京文(6))某三棱锥的三视图如图所示,则该三棱锥的体积为(A )60(B )30(C )20(D )109.(17浙江3)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是A .12π+B .32π+C .312π+ D .332π+ 10.(17浙江9)如图,已知正四面体D –ABC (所有棱长均相等的三棱锥),PQR 分别为AB ,BC ,CA 上的点,AP=PB ,2BQ CR QC RA ==,分别记二面角D –PR –Q ,D –PQ –R ,D –QR –P 的平面较为,,αβγ,则A .γ<α<βB .α<γ<βC .α<β<γD .β<γ<α11.(17全国1文16)已知三棱锥S-ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年全国高考理科数学试题分类汇编7:立体几何一、选择题1 .(2017年高考新课标1(理))如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为( )A .35003cm πB .38663cm πC .313723cm πD .320483cm π【答案】A2 .(2017年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是( )A .若αβ⊥,m α⊂,n β⊂,则m n ⊥B .若//αβ,m α⊂,n β⊂,则//m nC .若m n ⊥,m α⊂,n β⊂,则αβ⊥D .若m α⊥,//m n ,//n β,则αβ⊥【答案】D3 .(2017年上海市春季高考数学试卷(含答案))若两个球的表面积之比为1:4,则这两个球的体积之比为( )A .1:2B .1:4C .1:8D .1:16【答案】C4 .(2017年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))已知正四棱柱1111ABCD A BC D -中12AA AB =,则CD 与平面1BDC 所成角的正弦值等于( )A .23B C D .13【答案】A5 .(2017年高考新课标1(理))某几何体的三视图如图所示,则该几何体的体积为( )A .168π+B .88π+C .1616π+D .816π+【答案】A6 .(2017年高考湖北卷(理))一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为1V ,2V ,3V ,4V ,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则有 ( )A .1243V V V V <<<B .1324V V V V <<<C .213V V V <<<【答案】C7 .(2017年高考湖南卷(理))已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能...等于 ( )A .1B C .2D .2【答案】C8 .(2017年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))某四棱台的三视图如图所示,则该四棱台的体积是( )A .4B .143C .163D .6【答案】B 9 .(2017年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))已知nm ,为异面直线,⊥m 平面α,⊥n 平面β.直线l 满足,,,l m l n l l αβ⊥⊥⊄⊄,则 ( )A .βα//,且α//lB .βα⊥,且β⊥lC .α与β相交,且交线垂直于lD .α与β相交,且交线平行于l【答案】D10.(2017年普通高等学校招生统一考试山东数学(理)试题(含答案))已知三棱柱111ABC A B C -的侧棱与底面垂直,体积为94,.若P 为底面111A B C 的中心,则PA 与平面ABC 所成角的大小为( )A .512πB .3πC .4πD .6π【答案】B11.(2017年普通高等学校招生统一考试重庆数学(理)试题(含答案))某几何体的三视图如题()5图所示,则该几何体的体积为 ( )A .5603B .5803C .200D .240正视图俯视图侧视图第5题图【答案】C12.(2017年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))已知三棱柱111ABC A B C -的6个顶点都在球O的球面上,若34AB AC ==,,AB AC ⊥,112AA =,则球O 的半径为( )A B .C .132D .【答案】C13.(2017年高考江西卷(理))如图,正方体的底面与正四面体的底面在同一平面α上,且AB CD ,正方体的六个面所在的平面与直线CE,EF 相交的平面个数分别记为,m n ,那么m n +=( )A .8B .9C .10D .11【答案】A14.(2017年普通高等学校招生统一考试新课标Ⅱ卷数学(理)(纯WORD 版含答案))一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到正视图可以为( )A .B .C .D .【答案】A15.(2017年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))在下列命题中,不是公理..的是 ( )A .平行于同一个平面的两个平面相互平行B .过不在同一条直线上的三点,有且只有一个平面C .如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D .如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线 【答案】A 16.(2017年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))在空间中,过点A作平面π的垂线,垂足为B ,记)(A f B π=.设βα,是两个不同的平面,对空间任意一点P ,)]([)],([21P f f Q P f f Q βααβ==,恒有21PQ PQ =,则( )A .平面α与平面β垂直B .平面α与平面β所成的(锐)二面角为045C .平面α与平面β平行D .平面α与平面β所成的(锐)二面角为060【答案】A 17.(2017年高考四川卷(理))一个几何体的三视图如图所示,则该几何体的直观图可以是【答案】D 二、填空题18.(2017年高考上海卷(理))在xOy 平面上,将两个半圆弧22(1)1(1)x y x -+=≥和22(3)1(3)x y x -+=≥、两条直线1y = 和1y =-围成的封闭图形记为D,如图中阴影部分.记D 绕y 轴旋转一周而成的几何体为Ω,过(0,)(||1)y y ≤作Ω的水平截面,所得截面面积为48ππ,试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为__________【答案】2216ππ+.19.(2017年高考陕西卷(理))某几何体的三视图如图所示, 则其体积为___3π_____.【答案】3π 20.(2017年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))已知圆O和圆K 是球O 的大圆和小圆,其公共弦长等于球O 的半径,32OK =,且圆O 与圆K 所在的平面所成的一个二面角为60,则球O 的表面积等于______.【答案】16π21.(2017年高考北京卷(理))如图,在棱长为2的正方体ABCD -A1B 1C 1D 1中,E 为BC 的中点,点P 在线段D 1E 上,点P 到直线CC 1的距离的最小值为__________.【答案】 1B22.(2017年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))如图,在三棱柱ABC C B A -111中,F E D ,,分别是1AA AC AB ,,的中点,设三棱锥ADE F -的体积为1V ,三棱柱ABC C B A -111的体积为2V ,则=21:V V ____________.【答案】1:2423.(2017年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于________2cm .【答案】2424.(2017年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))如图,正方体1111ABCD A BC D -的棱长为1,P 为BC 的中点,Q 为线段1CC 上的动点,过点A,P,Q 的平面截该正方体所得的截面记为S.则下列命题正确的是__①②③⑤___(写出所有正确命题的编号).①当102CQ <<时,S 为四边形;②当12CQ =时,S 为等腰梯形;③当34CQ =时,S 与A BCADEF BC11C D 的交点R 满足1113C R =;④当314CQ <<时,S 为六边形;⑤当1CQ =时,S 的面积【答案】①②③⑤25.(2017年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))某几何体的三视图如图所示,则该几何体的体积是____________.【答案】1616π-26.(2017年普通高等学校招生统一考试福建数学(理)试题(纯WORD 版))已知某一多面体内接于一个简单组合体,如果该组合体的正视图.测试图.俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是_______________【答案】12π27.(2017年上海市春季高考数学试卷(含答案))在如图所示的正方体1111ABCD A BC D -中,异面直线1A B 与1B C 所成角的大小为_______【答案】3πD 1 C 1 B 1A 1D C AB三、解答题28.(2017年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))如图,AB 是圆的直径,PA垂直圆所在的平面,C 是圆上的点. (I)求证:PAC PBC ⊥平面平面;(II)2.AB AC PA C PB A ===--若,1,1,求证:二面角的余弦值【答案】29.(2017年普通高等学校招生统一考试重庆数学(理)试题(含答案))如图,四棱锥P ABCD-中,PA ABCD ⊥底面,2,4,3BC CD AC ACB ACD π===∠=∠=,F 为PC 的中点,AF PB ⊥.(1)求PA 的长; (2)求二面角B AF D --的正弦值.【答案】1.(2017年普通高等学校招生统一考试安徽数学(理)试题(纯WORD版))如图,圆锥顶点为p.底面圆心为o ,其母线与底面所成的角为22.5°.AB 和CD 是底面圆O 上的两条平行的弦,轴OP 与平面PCD 所成的角为60°.(Ⅰ)证明:平面PAB 与平面PCD 的交线平行于底面; (Ⅱ)求cos COD ∠. 【答案】解:(Ⅰ)PAB P D ,////C m AB CD CD PCD AB PCD ⋂=⊂⇒设面面直线且面面//AB m ⇒直线 ABCD m ABCD AB 面直线面//⇒⊂ . 所以,ABCD D P PAB的公共交线平行底面与面面C . (Ⅱ)rPOOPF F CD r =︒︒=∠5.22tan .60,由题知,则的中点为线段设底面半径为. ︒-︒=︒∠==︒⋅︒⇒=︒5.22tan 15.22tan 245tan ,2cos 5.22tan 60tan 60tan ,2COD r OF PO OF .)223(3)],1-2(3[21cos ,1-25.22tan 12cos 2cos 22-==+∠=︒⇒-∠=∠COD COD COD 212-17cos .212-17cos =∠=∠COD COD 所以.法二:1.(2017年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))如图,在四面体BCD A -中,⊥AD 平面BCD ,22,2,==⊥BD AD CD BC .M 是AD 的中点,P是BM 的中点,点Q 在线段AC 上,且QC AQ 3=.(1)证明://PQ 平面BCD ;(2)若二面角D BM C --的大小为060,求BDC ∠的大小.【答案】解:证明(Ⅰ)方法一:如图6,取MD 的中点F ,且M 是AD 中点,所以3AF FD =.因为P 是BM 中点,所以//PF BD ;又因为(Ⅰ)3AQ QC =且3AF FD =,所以//QF BD ,所以面//PQF 面BDC ,且PQ ⊂面BDC ,所以ABCDPQM(第20题图)//PQ 面BDC;方法二:如图7所示,取BD 中点O ,且P 是BM 中点,所以1//2PO MD ;取CD 的三等分点H ,使3DH CH =,且3AQ QC =,所以11////42QH AD MD ,所以////P O Q H P Q OH ∴,且OH BCD ⊂,所以//PQ 面BDC ; (Ⅱ)如图8所示,由已知得到面ADB ⊥面BDC ,过C 作CG BD ⊥于G ,所以CG BMD ⊥,过G 作GH BM ⊥于H ,连接CH ,所以CHG ∠就是C BM D --的二面角;由已知得到3BM ==,设BDC α∠=,所以cos ,sin ,sin ,,CD CG CBCD CG BC BD CD BDαααααα===⇒===,在RT BCG ∆中,2sin BGBCG BG BCααα∠=∴=∴=,所以在RT BHG ∆中2133HG α=∴=,所以在RT CHG ∆中tan tan 6033CG CHG HG ∠====tan (0,90)6060BDC ααα∴=∈∴=∴∠=;2.(2017年上海市春季高考数学试卷(含答案))如图,在正三棱锥111ABC A B C -中,16AA =,异面直线1BC 与1AA 所成角的大小为6π,求该三棱柱的体积.【答案】[解]因为1CC 1AA .所以1BC C ∠为异面直线1BC 与1AA .所成的角,即1BC C ∠=6π. 在Rt 1BC C ∆中,11tan 6BC CC BC C =⋅∠==从而24ABC S BC ∆==因此该三棱柱的体积为16ABC V S AA ∆=⋅==3.(2017年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分14分.如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,BC AB ⊥,AB AS =,过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点. 求证:(1)平面//EFG 平面ABC ; (2)SA BC ⊥.【答案】证明:(1)∵AB AS =,SB AF ⊥∴F 分别是SB 的中点∵E.F 分别是SA.SB 的中点 ∴EF∥AB又∵EF ⊄平面ABC, AB ⊆平面ABC ∴EF∥平面ABC 同理:FG∥平面ABC又∵EF FG=F, EF.FG ⊆平面ABC∴平面//EFG 平面ABC (2)∵平面⊥SAB 平面SBCABCS GFEB 1A 1C 1ACB平面SAB 平面SBC =BC AF ⊆平面SABAF⊥SB∴AF⊥平面SBC 又∵BC ⊆平面SBC ∴AF⊥BC又∵BC AB ⊥, AB AF=A, AB.AF ⊆平面SAB ∴BC⊥平面SAB 又∵SA ⊆平面SAB∴BC⊥SA4.(2017年高考上海卷(理))如图,在长方体ABCD-A 1B 1C 1D 1中,AB=2,AD=1,A 1A=1,证明直线BC 1平行于平面DA 1C,并求直线BC 1到平面D 1AC 的距离.C 11A【答案】因为ABCD-A 1B 1C 1D 1为长方体,故1111//,AB C D AB C D =,故ABC 1D 1为平行四边形,故11//BC AD ,显然B 不在平面D 1AC 上,于是直线BC 1平行于平面DA 1C;直线BC 1到平面D 1AC 的距离即为点B 到平面D 1AC 的距离设为h考虑三棱锥ABCD 1的体积,以ABC 为底面,可得111(12)1323V =⨯⨯⨯⨯= 而1ADC ∆中,11AC DC AD ==故132AD C S ∆= 所以,13123233V h h =⨯⨯=⇒=,即直线BC 1到平面D 1AC 的距离为23.5.(2017年高考湖北卷(理))如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,直线PC ⊥平面ABC ,E ,F 分别是PA ,PC 的中点.(I)记平面BEF 与平面ABC 的交线为l ,试判断直线l 与平面PAC 的位置关系,并加以证明;(II)设(I)中的直线l 与圆O 的另一个交点为D ,且点Q 满足12DQ CP =.记直线PQ 与平面ABC 所成的角为θ,异面直线PQ 与EF 所成的角为α,二面角E l C --的大小为β,求证:sin sin sin θαβ=.【答案】解:(I)EF AC ,AC ABC ⊆平面,EF ABC ⊆平面EF ABC ∴平面又EF BEF ⊆平面EF l ∴ l PAC ∴平面(II)连接DF,用几何方法很快就可以得到求证.(这一题用几何方法较快,向量的方法很麻烦,特别是用向量不能方便的表示角的正弦.个人认为此题与新课程中对立体几何的处理方向有很大的偏差.)第19题图6.(2017年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))如图1,在等腰直角三角形ABC 中,90A ∠=︒,6BC =,,D E 分别是,AC AB 上的点,CD BE ==O 为BC 的中点.将ADE ∆沿DE 折起,得到如图2所示的四棱锥A BCDE '-,其中A O '=(Ⅰ) 证明:A O '⊥平面BCDE ; (Ⅱ) 求二面角A CDB '--的平面角的余弦值.【答案】(Ⅰ) 在图1中,易得3,OC AC AD ===.CO BDEA CDOBE'A图1图2连结,OD OE ,在OCD ∆中,由余弦定理可得OD==由翻折不变性可知A D '=,所以222A O OD A D ''+=,所以A O OD '⊥, 理可证A O OE '⊥, 又ODOE O =,所以A O '⊥平面BCDE .(Ⅱ) 传统法:过O 作OH CD ⊥交CD 的延长线于H ,连结A H ', 因为A O '⊥平面BCDE ,所以A H CD '⊥, 所以A HO '∠为二面角A CD B '--的平面角.结合图1可知,H 为AC 中点,故2OH =,从而2A H '==所以cos 5OH A HO A H '∠==',所以二面角A CD B '--向量法:以O 点为原点,建立空间直角坐标系O xyz -则(A ',()0,3,0C -,()1,2,0D -所以(CA '=,(1,DA '=- 设(),,n x y z =为平面A CD '的法向量,则00n CA n DA ⎧'⋅=⎪⎨'⋅=⎪⎩,即3020y x y⎧=⎪⎨-+=⎪⎩,解得y x z =-⎧⎪⎨=⎪⎩,令1x =,得(1,n =- 由(Ⅰ) 知,(OA '=为平面CDB 的一个法向量,所以cos ,3n OA n OA n OA '⋅'===',即二面角A CD B '--的平面角的余弦C D OBE'AH(2017年普通高等学校招生统一考试天津数学(理)试题(含答案))如图, 四棱柱ABCD-A1B1C1D1 7.中, 侧棱A1A⊥底面ABCD, AB//DC, AB⊥AD, AD = CD = 1, AA1 = AB = 2, E为棱AA1的中点.(Ⅰ) 证明B1C1⊥CE;(Ⅱ) 求二面角B1-CE-C1的正弦值.(Ⅲ) 设点M在线段C1E上, 且直线AM与平面ADD1A1, 求线段AM 的长.【答案】8.(2017年高考新课标1(理))如图,三棱柱ABC-A1B1C1中,CA=CB,AB=A A1,∠BA A1=60°.(Ⅰ)证明AB⊥A1C;(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB=2,求直线A1C 与平面BB1C1C所成角的正弦值.【答案】(Ⅰ)取AB 中点E,连结CE,1A B ,1A E,∵AB=1AA ,1BAA ∠=060,∴1BAA ∆是正三角形,∴1A E ⊥AB, ∵CA=CB, ∴CE⊥AB, ∵1CE A E ⋂=E,∴AB⊥面1CEA,∴AB⊥1AC ;(Ⅱ)由(Ⅰ)知EC⊥AB,1EA ⊥AB,又∵面ABC⊥面11ABB A ,面ABC∩面11ABB A =AB,∴EC⊥面11ABB A ,∴EC⊥1EA , ∴EA,EC,1EA 两两相互垂直,以E 为坐标原点,EA 的方向为x 轴正方向,|EA |为单位长度,建立如图所示空间直角坐标系O xyz -, 有题设知A(1,0,0),1A(0,,0),C(0,0,),B(-1,0,0),则BC),1BB =1AA),1AC设n =(,,)x y z 是平面11CBB C 的法向量,则100BC BB ⎧∙=⎪⎨∙=⎪⎩n n ,即0x x ⎧=⎪⎨=⎪⎩,可取n,1,-1), ∴1cos ,A C n =11|A C A C∙n |n ||∴直线A 1C 与平面BB 1C 1C9.(2017年高考陕西卷(理))如图, 四棱柱ABCD -A 1B 1C 1D 1的底面ABCD 是正方形, O 为底面中心, A 1O ⊥平面ABCD, 1AB AA =(Ⅰ) 证明: A 1C ⊥平面BB 1D 1D ;(Ⅱ) 求平面OCB 1与平面BB 1D 1D 的夹角θ的大小.1A【答案】解:(Ⅰ) BD O A ABCD BD ABCD O A ⊥∴⊂⊥11,,面且面 ;又因为,在正方形ABCD 中,BDC A AC A C A AC A BD A AC O A BD AC ⊥⊂⊥=⋂⊥11111,,故面且面所以;且.在正方形AB CD 中,AO = 1 . .111=∆O A OA A RT 中,在O E C A OCE A E D B 1111111⊥为正方形,所以,则四边形的中点为设.,所以由以上三点得且,面面又O O BD D D BB O D D BB BD =⋂⊂⊂111111E .E ,D D BB C A 111面⊥.(证毕)(Ⅱ) 建立直角坐标系统,使用向量解题.以O 为原点,以OC 为X 轴正方向,以OB 为Y 轴正方向.则)1,0,1()1,1,1(),100(),001(,0,1,0111-=⇒C A B A C B ,,,,)(.由(Ⅰ)知, 平面BB 1D 1D 的一个法向量.0,0,1),1,1,1(),1,0,1(111)(==-==OC OB C A n 设平面OCB 1的法向量为,则0,0,2122=⋅=⋅OC n OB n n ).1-,1,0(法向量2=n 为解得其中一个21221|||||,cos |cos 212111=⋅=⋅=><=n n n n θ.1A所以,平面OCB 1与平面BB 1D 1D 的夹角θ为3π 10.(2017年高考江西卷(理))如图,四棱锥P A B C-中,PA ,ABCD E BD ⊥平面为的中点,G PD 为的中点,3,12DAB DCB EA EB AB PA ∆≅∆====,,连接CE 并延长交AD 于F . (1) 求证:AD CFG ⊥平面;(2) 求平面BCP 与平面DCP 的夹角的余弦值.【答案】解:(1)在ABD ∆中,因为E 是BD 的中点,所以1EA EB ED AB ====,故,23BAD ABE AEB ππ∠=∠=∠=,因为DAB DCB ∆≅∆,所以EAB ECB ∆≅∆, 从而有FED FEA ∠=∠,故,EF AD AF FD ⊥=,又因为,PG GD =所以FG ∥PA . 又PA ⊥平面ABCD ,所以,GF AD ⊥故AD ⊥平面CFG . (3) 以点A 为坐标原点建立如图所示的坐标系,则3(0,0,0),(1,0,0),(2A B C D ,(4)3(0,0,)2P ,故133333(0),(,),(2222BC CP CD ==--=-,,,设平面BCP 的法向量111(1,,)n y z =,则111102233022y y z ⎧+=⎪⎪⎨⎪--+=⎪⎩ ,解得1123y z ⎧=⎪⎪⎨⎪=⎪⎩,即12(1,)33n =-.设平面DCP 的法向量222(1,,)n y z =,则22232233022y y z ⎧-+=⎪⎪⎨⎪--+=⎪⎩,解得222y z ⎧=⎪⎨=⎪⎩, 即2(1n =.从而平面B C P 与平面D C P 的夹角的余弦值为12124cos 416n n n n θ⋅=== 11.(2017年高考四川卷(理))如图,在三棱柱11ABC A B C -中,侧棱1AA ⊥底面ABC ,12AB AC AA ==,120BAC ∠=,1,D D 分别是线段11,BC B C 的中点,P 是线段AD 的中点.(Ⅰ)在平面ABC 内,试作出过点P 与平面1A BC 平行的直线l ,说明理由,并证明直线l ⊥平面11ADD A ;(Ⅱ)设(Ⅰ)中的直线l 交AB 于点M ,交AC 于点N ,求二面角1A A M N --的余弦值.1C【答案】解:()I如图,在平面ABC 内,过点P 做直线l //BC ,因为l 在平面1ABC 外,BC 在平面1ABC 内,由直线与平面平行的判定定理可知, l //平面1ABC . 由已知,AB AC =,D 是BC 的中点,所以,BC AD ⊥,则直线l AD ⊥.因为1AA ⊥平面ABC ,所以1AA ⊥直线l .又因为1,AD AA 在平面11ADDA 内,且AD 与1AA 相交,所以直线平面11ADD A()II 解法一:连接1A P ,过A 作1AE A P ⊥于E ,过E 作1EF AM ⊥于F ,连接AF . 由()I 知,MN ⊥平面1AEA ,所以平面1AEA ⊥平面1A MN . 所以AE ⊥平面1A MN ,则1AM AE ⊥. 所以1A M ⊥平面AEF ,则1A M ⊥AF .故AFE ∠为二面角1A AM N --的平面角(设为θ). 设11AA =,则由12A B AC AA ==,120BAC ∠=,有60BAD ∠=,2,1AB AD ==.又P 为AD 的中点,所以M 为AB 的中点,且1,12AP AM ==, 在1Rt AAP 中, 1AP =;在1Rt A AM 中, 1AM从而,11AA AP AE A P ∙==11AA AM AF A M ∙==所以sin AE AF θ==所以cos θ===. 故二面角1A AM N --解法二:设11AA =.如图,过1A 作1A E 平行于11B C ,以1A 为坐标原点,分别以111,AE AD ,1AA 的方向为x 轴,y 轴,z 轴的正方向,建立空间直角坐标系Oxyz (点O 与点1A 重合).则()10,0,0A ,()0,0,1A .因为P 为AD 的中点,所以,M N 分别为,AB AC 的中点,故11,1,,122M N ⎫⎛⎫⎪ ⎪⎪ ⎪⎝⎭⎝⎭,所以131,122A M ⎛⎫= ⎪⎪⎝⎭,()10,0,1A A =,()3,0,0NM =.设平面1AA M 的一个法向量为()1111,,n x y z =,则1111,,n A M n A A ⎧⊥⎪⎨⊥⎪⎩即11110,0,n A M n A A ⎧∙=⎪⎨∙=⎪⎩故有()()()1111111,,,10,2,,0,0,10,x y z x y z ⎧⎫∙=⎪⎪⎪⎨⎝⎭⎪∙=⎩从而111110,220.x y z z ++=⎪⎨⎪=⎩取11x =,则1y =,所以()11,n =. 设平面1A MN 的一个法向量为()2222,,n x y z =,则212,,n A M n NM ⎧⊥⎪⎨⊥⎪⎩即2120,0,n A M n NM ⎧∙=⎪⎨∙=⎪⎩故有()())2222221,,,10,22,,0,x y z x y z ⎧⎛⎫∙=⎪⎪ ⎪⎪⎝⎭⎨⎪∙=⎪⎩从而222210,20.x y z ++=⎨⎪=⎩取22y =,则21z =-,所以()20,2,1n =-. 设二面角1A AM N --的平面角为θ,又θ为锐角, 则1212cos n n n n θ∙===∙故二面角1A AM N -- 12.(2017年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))本小题满分10分.如图,在直三棱柱111A B C ABC -中,AC AB ⊥,2==AC AB ,41=AA ,点D 是BC 的中点(1)求异面直线B A 1与D C 1所成角的余弦值 (2)求平面1ADC 与1ABA 所成二面角的正弦值.【答案】本题主要考察异面直线.二面角.空间向量等基础知识以及基本运算,考察运用空间向量解决问题的能力.解:(1)以{}1,,AA 为为单位正交基底建立空间直角坐标系xyz A -,则)0,0,0(A )0,0,2(B ,)0,2,0(C ,)4,0,0(1A ,)0,1,1(D ,)4,2,0(1C ∴)4,0,2(1-=A ,)4,1,1(1--=A∴10103182018,cos 11==>=<C A ∴异面直线B A 1与D C 1所成角的余弦值为10103 (2))0,2,0(= 是平面1ABA 的的一个法向量设平面1ADC 的法向量为),,(z y x =,∵)0,1,1(=,)4,2,0(1=AC 由1,AC ⊥⊥ ∴⎩⎨⎧=+=+0420z y y x 取1=z ,得2,2=-=x y ,∴平面1ADC 的法向量为)1,2,2(-=m设平面1ADC 与1ABA 所成二面角为θ∴32324,cos cos =⨯-==><=θ, 得35sin =θ ∴平面1ADC 与1ABA 所成二面角的正弦值为3513.(2017年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))如图,四棱锥P ABCD -中,902,ABC BAD BC AD PAB ∠=∠==∆,与PAD ∆都是等边三角形.(I)证明:;PB CD ⊥ (II)求二面角A PD C --的大小.【答案】14.(2017年普通高等学校招生统一考试山东数学(理)试题(含答案))如图所示,在三棱锥P ABQ -中,PB ⊥平面ABQ ,BA BP BQ ==,,,,D C E F 分别是,,,A Q B Q A P B P 的中点, 2AQ BD =,PD 与EQ 交于点G ,PC 与FQ 交于点H ,连接GH .(Ⅰ)求证:AB GH ; (Ⅱ)求二面角D GH E --的余弦值.【答案】解:(Ⅰ)证明:因为,,,D C E F 分别是,,,AQ BQ AP BP 的中点,所以EF ∥AB ,DC ∥AB ,所以EF ∥DC , 又EF ⊂平面PCD ,DC ⊂平面PCD , 所以EF ∥平面PCD , 又EF ⊂平面EFQ ,平面EFQ 平面PCD GH =,所以EF ∥GH , 又EF ∥AB , 所以AB ∥GH .(Ⅱ)解法一:在△ABQ 中, 2AQ BD =,AD DQ =,所以=90ABQ ∠,即AB BQ ⊥,因为PB ⊥平面ABQ ,所以AB PB ⊥, 又BPBQ B =,所以AB ⊥平面PBQ ,由(Ⅰ)知AB ∥GH ,所以GH ⊥平面PBQ ,又FH ⊂平面PBQ ,所以GH FH ⊥,同理可得GH HC ⊥, 所以FHC ∠为二面角D GH E --的平面角,设2BA BQ BP ===,连接PC , 在t R △FBC 中,由勾股定理得,FC , 在t R △PBC 中,由勾股定理得,PC ,又H 为△PBQ 的重心,所以13HC PC ==同理3FH =,在△FHC 中,由余弦定理得552499cos 5529FHC +-∠==-⨯,即二面角D GH E --的余弦值为45-.解法二:在△ABQ 中,2AQ BD =,AD DQ =,所以90ABQ ∠=,又PB ⊥平面ABQ ,所以,,BA BQ BP 两两垂直, 以B 为坐标原点,分别以,,BA BQ BP 所在直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,设2BA BQ BP ===,则(1,0,1)E ,(0,0,1)F ,(0,2,0)Q ,(1,1,0)D ,(0,1,0)C (0,0,2)P ,,所以(1,2,EQ =--,(0,2,1)FQ =-,(1,1,2)DP =--,(0,1,2)CP =-,设平面EFQ 的一个法向量为111(,,)m x y z =,由0m EQ ⋅=,0m FQ ⋅=,得111112020x y z y z -+-=⎧⎨-=⎩取11y =,得(0,1,2)m =.设平面PDC 的一个法向量为222(,,)n x y z =由0n DP ⋅=,0n CP ⋅=,得222222020x y z y z --+=⎧⎨-+=⎩取21z =,得(0,2,1)n =.所以4cos ,5m n m n m n⋅==因为二面角D GH E --为钝角,所以二面角D GH E --的余弦值为45-.15.(2017年高考湖南卷(理))如图5,在直棱柱1111//ABCD A BC D AD BC -中,,90,,1BAD AC BD BC ∠=⊥=,13AD AA==.(I)证明:1AC B D ⊥; (II)求直线111B C ACD 与平面所成角的正弦值.【答案】解: (Ⅰ)AC BB ABCD BD ABCD BB D C B A ABCD ⊥⇒⊂⊥∴-111111,面且面是直棱柱 D B AC BDB D B BDB AC B BB BD BD AC 11111,,⊥∴⊂⊥∴=⋂⊥,面。
