广州市高二下学期期末数学试卷(理科)(II)卷
2022-2023学年广东省广州市高二下学期期末数学试题【含答案】

2022-2023学年广东省广州市高二下学期期末数学试题一、单选题1.设集合{}03M x x =<<,163N x x ⎧⎫=≤≤⎨⎬⎩⎭,则()R M N ⋂=ð()A .{}06x x <≤B .133x x ⎧⎫≤<⎨⎬⎩⎭C .{}36x x <≤D .{}36x x ≤≤【答案】D【分析】先求集合M 的补集R M ð,再取R M ð与集合N 的交集即可.【详解】由{}03M x x =<<,可得{}R 03M x x x =≤≥或ð则(){}{}R 1036363M N x x x x x x x ⎧⎫⋂=≤≥⋂≤≤=≤≤⎨⎬⎩⎭或ð故选:D 2.复数4i1iz =+,则z =()A .22i --B .22i-+C .22i+D .22i-【答案】D【分析】先计算z ,再根据共轭复数的概念即可求解.【详解】根据复数除法的运算法则可得41i z i =+()()()414422112i i i i i i -+===+-+,所以可得其共轭复数22z i =-.故选:D.3.函数(sin sin 2)y x x x =-的部分图象大致为()A .B .C .D .【答案】C【分析】判断函数的奇偶性,再用赋值法,排除ABD ,即可.【详解】由()(sin sin 2)y f x x x x ==-,得()()()()()sin sin 2sin sin 2f x x x x x x x f x -=----=--+=⎡⎤⎣⎦,所以()f x 为偶函数,故排除BD.当π2x =时,ππππ(sin sin π)02222y f ⎛⎫==-=> ⎪⎝⎭,排除A.故选:C.4.用一个平行于圆锥底面的平面去截圆锥,截得的圆台上底面半径为1,下底面半径为2,且该圆台侧面积为35π,则原圆锥的母线长为()A .2B .5C .4D .25【答案】D【分析】设圆台的母线长为l ,根据圆台的侧面积公式求出圆台的母线长,利用圆台的性质以及相似三角形即可求解.【详解】设圆台的母线长为l ,因为该圆台侧面积为35π,则由圆台侧面积公式可得π(12)3π35πl l +==,所以5l =,设截去的圆锥的母线长为l ',由三角形相似可得12l l l '='+,则25l l ''=+,解得5l '=,所以原圆锥的母线长5525l l '+=+=,故选:D .5.某兴趣小组研究光照时长x (h )和向日葵种子发芽数量y (颗)之间的关系,采集5组数据,作如图所示的散点图.若去掉()10,2D 后,下列说法正确的是()A .相关系数r 变小B .决定系数2R 变小C .残差平方和变大D .解释变量x 与预报变量y 的相关性变强【答案】D【分析】从图中分析得到去掉()10,2D 后,回归效果更好,再由相关系数,决定系数,残差平方和和相关性的概念和性质作出判断即可.【详解】从图中可以看出()10,2D 较其他点,偏离直线远,故去掉()10,2D 后,回归效果更好,对于A ,相关系数r 越接近于1,模型的拟合效果越好,若去掉()10,2D 后,相关系数r 变大,故A 错误;对于B ,决定系数2R 越接近于1,模型的拟合效果越好,若去掉()10,2D 后,决定系数2R 变大,故B 错误;对于C ,残差平方和越小,模型的拟合效果越好,若去掉()10,2D 后,残差平方和变小,故C 错误;对于D ,若去掉()10,2D 后,解释变量x 与预报变量y 的相关性变强,且是正相关,故D 正确.故选:D .6.已知函数()()e e 2x xx f x --=,则21log3a f ⎛⎫= ⎪⎝⎭,342b f -⎛⎫= ⎪⎝⎭,432c f ⎛⎫=- ⎪⎝⎭的大小关系为()A .b a c <<B .a b c <<C .c<a<bD .a c b<<【答案】A【分析】先判断函数的奇偶性,再判断函数的单调性,然后再比较43342log 3,2,2-的大小,再根据函数的单调性可得结果【详解】()f x 的定义域为R ,因为()()()e e ee ()22x xxx x x f x f x ------===,所以()f x 为偶函数,所以()()2221log log 3log 33a f f f ⎛⎫==-= ⎪⎝⎭,443322c f f ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,当0x >时,()()()e e e e 2xx x xx f x ---++'=,因为0x >,所以e 1,0e 1x x -><<,所以e e 0x x -->,(e e )0x x x -+>,所以()0f x '>,所以()f x 在(0,)+∞上单调递增,因为2x y =在R 上单调递增,且340143-<<<,所以43013402222-<<<<,即433402122-<<<<,因为2log y x =在(0,)+∞上为增函数,且234<<,所以222log 2log 3log 4<<,即21log 32<<,所以4334202log 32-<<<,所以()433422log 32f f f -⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭,即b a c <<,故选:A7.已知抛物线21:4C y x =的焦点为F ,过F 且斜率大于零的直线l 与1C 及抛物线22:4C y x =-的所有公共点从左到右分别为点A B C 、、,则BC =()A .4B .6C .8D .10【答案】C【分析】设直线l 的方程为1(0)x my m =+>,代入22:4C y x =-,化简后由Δ0=求出m 的值,从而可得直线方程,再代入21:4C y x =化简,结合弦长公式可得答案.【详解】由题意可得()1,0F ,设直线l 的方程为1(0)x my m =+>,由题意可得直线l 与抛物线1C 必有2个交点,与抛物线2C 相切,联立方程组214x my y x=+⎧⎨=-⎩,可得2440y my ++=,所以2Δ16160m =-=,解得1m =,故直线l 的方程为1x y =+,与抛物线1C 方程联立214x y y x=+⎧⎨=⎩,得2610x x -+=,设()()1122,,,B x y C x y ,则126x x +=,所以1228BC x x =++=.故选:C.8.互相垂直且有公共原点的两条数轴构成平面直角坐标系,但如果平面坐标系中两条坐标轴不垂直,则这样的坐标系称为“斜坐标系”.如图,在斜坐标系中,过点P 作两坐标轴的平行线,其在x 轴和y 轴上的截距,a b 分别作为点P 的x 坐标和y 坐标,记(),P a b .若斜坐标系中,x 轴正方向和y 轴正方向的夹角为θ,则该坐标系中()11,M x y 和()22,N x y 两点间的距离为()A .()()()()22121212122cos x x y y x x y y θ-+-+--B .()()()()22121212122cos x x y y x x y y θ-+----C .()()()()22121212122cos x x y y x x y y θ-+-+--D .()()()()22121212122cos x x y y x x y y θ-+----【答案】A【分析】建立直角坐标系,求出直角坐标,即可得解.【详解】以O 为坐标原点,原x 轴正方向为x 轴,垂直于x 轴的方向为y 轴建立平面直角坐标系,则在直角坐标系下,()111cos s n ,i M x y y θθ+,()222cos s n ,i N x y y θθ+,则()()22211221cos cos sin sin MN x y x y y y θθθθ+---=+()()()()22121212122cos x x y y x x y y θ=-+-+--.故选:A.二、多选题9.下列结论正确的是()A .若随机变量X 服从两点分布,1(1)2P X ==,则()12E X =B .若随机变量Y 的方差()2D Y =,则(32)8D Y +=C .若随机变量ξ服从二项分布14,2B ⎛⎫⎪⎝⎭,则1(3)4P ξ==D .若随机变量η服从正态分布()25,N σ,(2)0.1P η<=,则(28)0.8P η<<=【答案】ACD【分析】根据二点分布的期望公式,可判定A 正确;根据方差的性质,可判定B 错误;根据二项分布的概率计算公式,可判定C 正确;根据正态分布曲线的对称性,可判定D 正确.【详解】对于A 中,由随机变量X 服从两点分布且1(1)2P X ==,则()11122E X =⨯=,故A 正确;对于B 中,由随机变量Y 的方差()2D Y =,可得()2(32)318D Y D X +==,故B 错误;对于C 中,由变量ξ服从二项分布14,2B ⎛⎫ ⎪⎝⎭,则334111(3)C ()(1)224P ξ==-=,所以C 正确;对于D 中,由随机变量η服从正态分布()25,N σ,(2)0.1P η<=,根据正态分布曲线的对称性,可得(28)1(2)0.8P P ηη<<=-<=,所以D 正确.故选:ACD.10.已知函数21()3sin cos cos 2f x x x x =-+,则下列说法正确的是()A .()sin 26πf x x ⎛⎫=- ⎪⎝⎭B .函数()f x 的最小正周期为πC .函数()f x 的图象的对称轴方程为()ππZ 12x k k =+∈D .函数()f x 的图象可由cos 2y x =的图象向左平移π12个单位长度得到【答案】AB【分析】利用二倍角公式及辅助角公式化简函数()f x ,再结合正弦函数的性质逐项判断作答.【详解】2131cos 21()3sin cos cos sin 22222x f x x x x x +=-+=-+31πsin 2cos 2sin 2226x x x ⎛⎫=-=- ⎪⎝⎭,故A 正确;函数()f x 的最小正周期为2ππ2T ==,故B 正确;由ππ2π()62x k k Z -=+∈,得ππ(Z)32k x k =+∈,故C 错误;由cos 2y x =的图象向左平移π12个单位长度,得ππcos 2cos 2cos 212623ππy x x x ⎡⎤⎛⎫⎛⎫⎛⎫=+=+=-- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦2πsin sin π2π2π223sin 33x x x ⎡⎤⎛⎫⎛⎫⎛⎫==-+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝+⎭⎝⎦-⎭⎣,故D 错误.故选:AB11.一口袋中有除颜色外完全相同的3个红球和2个白球,从中无放回的随机取两次,每次取1个球,记事件A 1:第一次取出的是红球;事件A 2:第一次取出的是白球;事件B :取出的两球同色;事件C :取出的两球中至少有一个红球,则()A .事件1A ,2A 为互斥事件B .事件B ,C 为独立事件C .()25P B =D .()234P C A =【答案】ACD【分析】根据互斥事件、独立事件的定义判断AB ,由组合知识求得()P B 判断C ,根据条件概率的定义求得2(|)P C A 判断D .【详解】第一次取出的球是红球还是白球两个事件不可能同时发生,它们是互斥的,A 正确;由于是红球有3个,白球有2个,事件B 发生时,两球同为白色或同为红色,2325223225C C ()3()C C ()4C P BC P C P B ===+,事件B 不发生,则两球一白一红,()1P C =,,B C 不独立,B 错;223225C C 2()C 5P B +==,C 正确;事件2A 发生后,口袋中有3个红球1个白球,只有从中取出一个红球,事件C 才发生,所以23(|)4P C A =,D 正确.故选:ACD .12.已知函数()sin ln f x x x =+,将()f x 的所有极值点按照由小到大的顺序排列,得到数列{}n x ,对于正整数n ,则下列说法中正确的有()A .()1ππn n x n-<<B .1πn n x x +-<C .(21)π2n n x ⎧-⎫-⎨⎬⎩⎭为递减数列D .()2(41)π1ln2n n f x ->-+【答案】AC【分析】()f x 的极值点为()f x '的变号零点,即为函数cos y x =与函数1y x=-图像在()0,∞+交点的横坐标.将两函数图像画在同一坐标系下.A 选项,利用零点存在性定理及图像可判断选项;BC 选项,由图像可判断选项;D 选项,注意到(41)π(41)π1ln22n n f --⎛⎫=-+ ⎪⎝⎭,由图像可得()f x 单调性,后可判断选项.【详解】()f x 的极值点为()1cos f x x x'=+在()0,∞+上的变号零点.即为函数cos y x =与函数1y x=-图像在()0,∞+交点的横坐标.又注意到()0,x ∈+∞时,10x -<,N k ∈时,()1212cos π+ππ+πk k =-<-,N k *∈,022222πππ,∪π,πx k k ⎛⎫⎛⎫∈-++ ⎪ ⎪⎝⎭⎝⎭时,cos 0x >.据此可将两函数图像画在同一坐标系中,如下图所示.A 选项,注意到N k ∈时,120222ππππf k k ⎛⎫'+=> ⎪⎝⎭+,()12102ππππf k k '+=-+<+,31203222ππππf k k ⎛⎫'+=> ⎪⎝⎭+.结合图像可知当21,N n k k *=-∈,()()112π,ππ,πn x n n n n ⎛⎫⎛⎫∈-⊆- ⎪ ⎪⎝⎭⎝⎭.当2,N n k k *=∈,()()()1112π,ππ,πn x n n n n ⎛⎫⎛⎫∈--⊆- ⎪ ⎪⎝⎭⎝⎭.故A 正确;B 选项,由图像可知325322π,πx x ><,则32πx x ->,故B 错误;C 选项,(21)π2n n x --表示两点(),0n x 与12π,0n ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭间距离,由图像可知,随着n 的增大,两点间距离越来越近,即(21)π2n n x ⎧-⎫-⎨⎬⎩⎭为递减数列.故C 正确;D 选项,由A 选项分析可知,()241212π,π,N n n x n n *⎛⎫-∈-∈ ⎪⎝⎭,又结合图像可知,当()2412,πn n x x ⎛⎫-∈ ⎪ ⎪⎝⎭时,1cos x x >-,即此时()0f x ¢>,得()f x 在()2412,πn n x ⎛⎫- ⎪ ⎪⎝⎭上单调递增,则()2(41)π(41)π1ln 22n n n f x f --⎛⎫<=-+ ⎪⎝⎭,故D 错误.故选:AC【点睛】关键点点睛:本题涉及函数的极值点,因函数本身通过求导难以求得单调性,故将两相关函数画在同一坐标系下,利用图像解决问题.三、填空题13.函数()ln f x x x =⋅在e x =处的切线方程为.【答案】2ey x =-【分析】求出函数的导函数,即可求出切线的斜率,再由点斜式求出切线方程.【详解】因为()ln f x x x =⋅,则()e e ln e e f =⋅=,又()ln 1f x x '=+,则()e ln e 12f '=+=,所以函数()ln f x x x =⋅在e x =处的切线方程为()e 2e y x -=-,即2e y x =-.故答案为:2ey x =-14.若12nx x ⎛⎫- ⎪⎝⎭展开式的二项式系数之和为64,则展开式中的常数项是.【答案】60【分析】先根据二项式系数之和求出n ,然楼根据展开式的通式,令x 的次数为零即可得常数项.【详解】由12nx x ⎛⎫- ⎪⎝⎭展开式的二项式系数之和为64得264n=,解得6n =,即612x x ⎛⎫- ⎪⎝⎭,其展开式的通式为()()366621661C 212C rr r r r r rr T x xx ---+⎛⎫=-=- ⎪⎝⎭令3602r-=得4r =,()42441612C 60T +∴=-=故答案为:60.15.某高中学校在新学期增设了“传统文化”、“数学文化”、“综合实践”、“科学技术”和“劳动技术”5门校本课程.小明和小华两位同学商量每人选报2门校本课程.若两人所选的课程至多有一门相同,且小明必须选报“数学文化”课程,则两位同学不同的选课方案有种.(用数字作答)【答案】36【分析】分两类:所选课程恰有一门相同和没有相同,利用排列、组合分别求出每类的种数,再利用分类计数原理即可求出结果.【详解】当小明和小华两位同学所选的课程恰有一门相同时:相同的课程为“数学文化”时,有24A 12=种,相同的课程不是“数学文化”时,有1134C C 12=种,所以小明和小华两位同学所选的课程恰有一门相同时,共有24种,当小明和小华两位同学所选的课程没有相同时,有1243C C 12=,所以,两位同学不同的选课方案有241236+=,故答案为:3616.费马定理是几何光学中的一条重要原理,在数学中可以推导出圆锥曲线的一些光学性质.例如,点P 为双曲线(1F ,2F 为焦点)上一点,点P 处的切线平分12F PF ∠.已知双曲线C :22142x y -=,O 为坐标原点,l 是点103,2P ⎛⎫ ⎪ ⎪⎝⎭处的切线,过左焦点1F 作l 的垂线,垂足为M ,则OM =.【答案】2【分析】延长2PF 交1F M 延长线于点N ,结合题意得点M 为1F N 的中点,1PN PF =,从而得到212OM F N =,再结合双曲线的定义即可求解.【详解】如图,延长2PF 交1F M 延长线于点N ,因为点M 是12F PF ∠的角平分线上的一点,且1F M MP ⊥,所以点M 为1F N 的中点,所以1PN PF =,又点O 为12F F 的中点,且1224PF PF a -==,所以()()22111142222OM F N PN PF PN PF ==-=-+=.故答案为:2.四、解答题17.已知等差数列{}n a 的前n 项和为n S ,数列{}n b 为等比数列,满足12542,30,2a b S b ===+是3b 与5b 的等差中项.(1)求数列{}{},n n a b 的通项公式;(2)设()(1)n n n n c a b =-+,求数列{}n c 的前20项和20T .【答案】(1)2n a n =,12n n b -=;(2)202+593【分析】(1)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q ,利用12a =,515452S a d ⨯=+求出d 值即可得到{}n a 的通项公式;再由题意得4352(2)b b b +=+,结合12b =可求出q 值,进一步可得{}n b 的通项公式;(2)由()392021(246840)12222T =-+-+-++-+-+-+ ,利用等比数列求和公式,结合分组求和即可求出20T .【详解】(1)设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q ,因为12a =,所以55410302S d ⨯=+=,解得2d =,所以22(1)2n a n n =+-=,由题意知:()43522b b b +=+,因为22b =,所以()2322222q q q +=+,解得2q =,所以12n n b -=;(2)由(1)得()11(1)22(1)2(1)2n n n n n n c n n --=-+=-⋅+-⋅,()392021(246840)12222T =-+-+-++-+-+-+ ()220200112212+59210201(2)33⎡⎤-⨯---⎣⎦=⨯+=+=--.18.近年来,绿色环保和可持续设计受到社会的广泛关注,成为了一种日益普及的生活理念和方式.可持续和绿色能源,是我们这个时代的呼唤,也是我们每一个人的责任.某环保可持续性食用产品做到了真正的“零浪费”设计,其外包装材质是蜂蜡.食用完之后,蜂蜡罐可回收用于蜂房的再建造.为了研究蜜蜂进入不同颜色的蜂蜡罐与蜜蜂种类的关系,研究团队收集了黄、褐两种颜色的蜂蜡罐,对,M N 两个品种的蜜蜂各60只进行研究,得到如下数据:黄色蜂蜡罐褐色蜂蜡罐M 品种蜜蜂4020N 品种蜜蜂5010(1)依据小概率值0.05α=的独立性检验,分析蜜蜂进入不同颜色的蜂蜡罐是否与蜜蜂种类有关联?(2)假设要计算某事件的概率()P B ,常用的一个方法就是找一个与B 事件有关的事件A ,利用公式:()()()()()()()P B P AB P AB P A P B A P A P B A =+=⋅+⋅求解,现从装有a 只M 品种蜜蜂和b 只N 品种蜜蜂的蜂蜡蠸中不放回地任意抽取两只,令第一次抽到M 品种蜜蜂为事件A ,第二次抽到M 品种蜜蜂为事件B ,求()P B (用,a b 表示()P B )附:()()()()22()n ad bc a b c d a c b d χ-=++++,其中n a b c d =+++.临界值表:α0.10.050.010.0050.001x α 2.706 3.841 6.6357.87910.828【答案】(1)蜜蜂进入不同颜色的蜂蜡罐与蜜蜂种类有关联;(2)()a P B a b =+【分析】(1)由已知数据结合公式求2χ,比较其与临界值的大小,由此确定蜜蜂进入不同颜色的蜂蜡罐与蜜蜂种类有关联,进一步求频率判断;(2)由古典概型概率公式和条件概率公式求()()()(),,,P A P B A P A P B A ,再代入所给公式求解.【详解】(1)根据列表得2212060040 4.444 3.841609309χ⨯==≈>⨯⨯,所以依据0.05α=的独立性检验,蜜蜂进入不同颜色的蜂蜡罐与蜜蜂种类有关联,M 品种进入黄色蜂蜡罐的频率为23,M 品种进入褐色蜂蜡罐的频率为13,N 品种进入黄色蜂蜡罐的频率为56,N 品种进入褐色蜂蜡罐的频率为16,依据频率分析,M 品种的蜜蜂选择褐色蜂蜡罐的频率是N 品种的蜜蜂的两倍,所以品种M N 、的蜜蜂选择进入黄色蜂蜡罐与褐色蜂蜡罐有显著差异;(2)由已知上式知,()()()()1,,,11a a b a P A P B A P A P B A a b a b a b a b -====++-++-则()()()()()()()P B P AB P AB P A P B A P A P B A=+=⋅+⋅,所以1()11a a b a P B a b a b a b a b -=⋅+⋅++-++-,所以()()()()11a a b a P B a b a b a b +-==++-+,所以()a P B a b =+.19.如图,在平面四边形ABCD 中,4AC =,BC CD ⊥.(1)若2AB =,3BC =,15CD =,求△ACD 的面积;(2)若2π3B ∠=,π6D ∠=,求3162AD BC ⎛⎫+- ⎪ ⎪⎝⎭的最大值.【答案】(1)7154(2)463【分析】(1)先用余弦定理求出cos ACB ∠,再利用面积公式求解;(2)设BCA θ∠=,运用正弦定理分别表示出,BC AD ,再利用恒等变换以及三角函数的性质求解.【详解】(1)在ABC 中,22216947cos 22438AC BC AB ACB AC BC +-+-∠===⋅⨯⨯,因为BC CD ⊥,所以7sin cos 8ACD ACB ∠=∠=,所以ACD 的面积117715sin 4152284S AC CD ACD =⋅⋅∠=⨯⨯⨯=;(2)设BCA θ∠=,π03θ<<,则π2ACD θ∠=-,π3BAC θ∠=-.在ABC 中,2ππsin sin 33BC AC θ=⎛⎫- ⎪⎝⎭,则8πsin 33BC θ⎛⎫=- ⎪⎝⎭,在ACD 中,ππsin sin 62AD AC θ=⎛⎫- ⎪⎝⎭,则8cos AD θ=,所以31438π4cos sin 62333AD BC θθ⎛⎫⎛⎫⎛⎫+-=+-- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭434346πcos sin sin 3334θθθ⎛⎫=+=+ ⎪⎝⎭,当π4θ=时,3162AD BC ⎛⎫+- ⎪ ⎪⎝⎭取得最大值463;综上,ACD 的面积为7154,3162AD BC ⎛⎫+- ⎪ ⎪⎝⎭的最大值463.20.如图,四棱锥P ABCD -的底面为正方形,2AB AP ==,PA ⊥平面ABCD ,E ,F 分别是线段PB,PD的中点,G是线段PC上的一点.(1)求证:平面EFG⊥平面PAC;(2)若直线AG与平面AEF所成角的正弦值为13,且G点不是线段PC的中点,求三棱锥E ABG-体积.【答案】(1)证明见解析(2)1 9【分析】(1)由面面垂直的判定定理证明即可;(2)建立空间直角坐标系,用坐标法求出G点坐标,然后求解即可.【详解】(1)证明:如图:连接BD,在正方形ABCD中BD AC⊥,又PA⊥平面ABCD,故PA BD⊥.而PA,AC是平面PAC上的两条相交直线,所以BD⊥平面PAC.在PBD△中,EF为中位线,故EF BD∥.所以EF⊥平面PAC.又EF⊂平面EFG,所以平面EFG⊥平面PAC.(2)如图:以AB ,AD ,AP 所在直线为x ,y ,z 轴建立如图空间直角坐标系A xyz -,则()0,0,0A ,()2,0,0B ,()2,2,0C ,()002P ,,,()0,2,0D ,()1,0,1E ,()0,1,1F ,()1,0,1AE =uuu r ,()0,1,1AF = ,设平面AEF 的一个法向量为()111,,m x y z = ,则00AE m AF m ⎧⋅=⎪⎨⋅=⎪⎩,即111100x z y z +=⎧⎨+=⎩,取()1,1,1m =- ,设101,2PG PC λλλ⎛⎫=<<≠ ⎪⎝⎭ ,则(0,0,2)(2,2,2)(2,2,22)AG AP PG AP PC λλλλλ=+=+=+-=- .则222621sin cos ,3344(22)m AG λθλλλ-===⨯++- ,整理得212810λλ-+=,解得16λ=或12λ=(舍去),故16PG PC = ,故G 到平面PAB 的距离1163h BC ==,故1226EBG S BE h =⋅=△.因为()()1,0,10,1,00AE BC ⋅=⋅= ,所以AE BC ⊥,又()()1,0,12,0,20AE BP ⋅=⋅-= ,所以AE BP ⊥,又BP BC P = ,所以EA ⊥平面PBC ,故A 到平面BEG 的距离为2EA =.三棱锥E ABG -体积为112123369E ABG A EBG EBG V V S EA --==⋅=⨯⨯=△.21.已知函数()()2ln 21f x a x x a x =+-+,其中0a >.(1)求函数()f x 的单调区间;(2)当102a <<时,判断函数()f x 零点的个数.【答案】(1)答案见解析(2)一个零点,理由见解析【分析】(1)求出()f x ',分12a =、102a <<、12a >讨论可得答案;(2)由(1)当102a <<时,函数()f x 的单调递增区间为()0,a ,1,2⎛⎫+∞ ⎪⎝⎭,单调递减区间为1,2a ⎛⎫ ⎪⎝⎭可得函数()f x 的极大值()f a ,再利用导数证明()0f a <可得答案.【详解】(1)()()()()()212210x x a a f x x a x x x --'=+-+=>,令()0f x '=得21,2x x a ==,当12a =时,()0f x '≥,则函数()f x 在()0,∞+上单调递增,当102a <<时,0x a <<或12x >时,()0f x ¢>,12a x <<时,()0f x '<,所以函数()f x 在()0,a ,1,2⎛⎫+∞ ⎪⎝⎭上单调递增,在1,2a ⎛⎫ ⎪⎝⎭上单调递减,当12a >时,102x <<或x a >时,()0f x ¢>,12x a <<时,()0f x '<,所以函数()f x 在10,2⎛⎫ ⎪⎝⎭,(),a +∞上单调递增,在1,2a ⎛⎫ ⎪⎝⎭上单调递减.综上所述,当12a =时,函数()f x 的单调递增区间为()0,∞+,无单调递减区间;当102a <<时,函数()f x 的单调递增区间为()0,a ,1,2⎛⎫+∞ ⎪⎝⎭,单调递减区间为1,2a ⎛⎫ ⎪⎝⎭;当12a >时,函数()f x 的单调递增区间为在10,2⎛⎫ ⎪⎝⎭,(),a +∞,单调递减区间为1,2a ⎛⎫ ⎪⎝⎭.(2)当102a <<时,函数()f x 仅有一个零点的个数,理由如下,由(1)得当10,2a ⎛⎫∈ ⎪⎝⎭时,函数()f x 在()0,a ,1,2⎛⎫+∞ ⎪⎝⎭单调递增,在1,2a ⎛⎫ ⎪⎝⎭单调递减;则函数()f x 的极大值为()()()2ln 21ln 1f a a a a a a a a a =+-+=--,且极小值为()12f f a ⎛⎫< ⎪⎝⎭,令()ln 1g x x x =--,10,2x ⎛⎫∈ ⎪⎝⎭,则()1110x g x x x -'=-=>,10,2x ⎛⎫∈ ⎪⎝⎭,所以()g x 在10,2x ⎛⎫∈ ⎪⎝⎭上单调递增,所以()13ln 2022g x g ⎛⎫<=--< ⎪⎝⎭,所以当10,2a ⎛⎫∈ ⎪⎝⎭时,()()ln 10f a a a a =--<,()()()()224222e ln e e 21e e 1e 2f a a a =+-+=--,因为10,2a ⎛⎫∈ ⎪⎝⎭,所以()20,1a ∈,22e 10,e 20a ->->,可得()2e 0f >,如下图,作出函数()f x 的大致图象,由图象可得当102a <<时,函数()f x 仅有一个零点的个数.【点睛】关键点点睛:解题的关键点是利用导数研究函数的单调性与极值,考查数形结合思想与运算求解能力.22.已知中心在坐标原点,焦点在x 轴上的椭圆过点()23P ,,且它的离心率12e =(I )求椭圆的标准方程;(II )与圆()2211x y -+=相切的直线:l y kx t =+交椭圆于M 、N 两点,若椭圆上一点C 满足OM ON OC λ+= ,求实数λ的取值范围【答案】(1)22186x y +=;(2)()()2,00,2-⋃【分析】(1)根据题意先设出椭圆的标准方程,然后根据椭圆上的点及离心率可求出方程中的待定系数,进而可得所求的方程;(2)由直线和圆相切可得212t k t-=(t≠0),然后将直线方程代入椭圆方程后得到关于x 的一元二次方程,根据根据系数的关系可得点C 的坐标,代入椭圆方程后整理得到2222222234111t k t t λ==+⎛⎫++ ⎪⎝⎭,根据t 的范围可得202λ<<,进而得到所求范围.【详解】(1)设椭圆的标准方程为22221(0)x y a b a b+=>>,由已知得2222243112a b c a c a b ⎧+=⎪⎪⎪=⎨⎪=-⎪⎪⎩,,,解得2286a b ⎧=⎨=⎩,,所以椭圆的标准方程为22186x y +=.(2)因为直线l :y =kx +t 与圆(x -1)2+y 2=1相切,所以21t kk ++=1,整理得212t k t-=(t≠0).由22186y kx t x y =+⎧⎪⎨+=⎪⎩消去y 整理得(3+4k 2)x 2+8ktx +4t 2-24=0,因为直线l 与椭圆交于M ,N 两点,所以()()()2222226443442416243180k t k t k t ∆=-=-+>+-,将212t k t-=代入上式可得0∆>恒成立.设M(x 1,y 1),N(x 2,y 2),则有x 1+x 2=-2834kt k +,所以y 1+y 2=kx 1+t +kx 2+t =k(x 1+x 2)+2t =2634t k +,因为OC λ= ()1212,x x y y ++2286,3434kt t k k ⎛⎫=- ⎪++⎝⎭),所以可得C ()()2286,3434kt t k k λλ⎛⎫-- ⎪ ⎪++⎝⎭,又因为点C 在椭圆上,所以()22222834k t k λ++()2222634t k λ+=1,所以2222222234111t k t t λ==+⎛⎫++ ⎪⎝⎭,因为t 2>0,所以221t ⎛⎫ ⎪⎝⎭+21t +1>1,所以202λ<<,所以λ的取值范围为()()2,00,2-⋃.【点睛】解决圆锥曲线中的范围或最值问题时,若题目的条件和结论能体现出明确的函数关系,则可先建立目标函数,再求这个函数的最值.在利用代数法解决最值与范围问题时常从以下几个方面考虑:①利用判别式构造不等关系,从而确定参数的取值范围;②利用已知参数的范围,求出新参数的范围,解题的关键是建立两个参数之间的等量关系;③利用基本不等式求出参数的取值范围;④利用函数值域的求法,确定参数的取值范围.。
广东省广州市第二中学2023-2024学年高二下学期期末考试数学试题

广东省广州市第二中学2023-2024学年高二下学期期末考试数学试题一、单选题1.已知{}(){}42,lg 10A x x B x x =-≤≤=-<,则A B =I ( ) A .{}42x x -≤< B .{}42x x -≤≤ C .{}12x x <<D .{}12x x <≤2.已知复数1i z =+(i 是虚数单位),则izzz =+( ) A .31i 55+B .11i 55+C .31i 55-+D .11i 55-+3.已知向量(3,1)a =-r ,(2,1)b m =--r ,若(2)a a b ⊥+r r r ,则m =( ) A .1-B .2-C .1D .04.若nx ⎛⎫ ⎝的展开式中各项系数之和为128-,则展开式中2x 的系数为( ) A .2835- B .945 C .2835 D .945-5.若π(0,)2α∈,2cos tan 232sin ααα=-,则tan α等于( )A B .18C D 6.已知球与某圆台的上、下底面及侧面均相切,若球与圆台的表面积之比为12,则球与圆台的体积之比为( )A .14B .12C .23D .347.当a<0时,函数()()2e xf x x ax =+的图象大致是( )A .B .C .D .8.已知函数()f x ,()g x 的定义域均为R ,()1f x +为奇函数,()2g x -为偶函数,()()121f x g x -=-+,()11f -=,则()()20232024f g =( )A .1-B .1C .2023D .2024二、多选题9.下列说法中,正确的是( )A .设随机变量X 服从正态分布()0,1N ,若()1P X p ≥=,则(10)12P X p -<<=-B .某人在10次答题中,答对题数为X ,()10,0.7X B :,则答对7题的概率最大C .基于小概率值α的检验规则是:当2x αχ≥时,我们就推断0H 不成立,即认为X 和Y不独立,该推断犯错误的概率不超过α;当2x αχ<时,我们没有充分证据推断0H 不成立,可以认为X 和Y 独立D .将4名老师分派到两个学校支教,每个学校至少派1人,则共有14种不同的分派方法10.已知()f x 是定义在R 上的奇函数,当()0,x ∈+∞时,()332f x x x =--,则( )A .()f x 的极大值点为1-B .函数()y f x = 3C .函数()()y f f x =的零点个数为7D .()()0f f x >的解集为()()2,02,-+∞U11.费马原理是几何光学中的一条重要原理,可以推导出双曲线具有如下光学性质:从双曲线的一个焦点发出的光线,经双曲线反射后,反射光线的反向延长线经过双曲线的另一个焦点.由此可得,过双曲线上任意一点的切线平分该点与两焦点连线的夹角.已知1F 、2F 分别是以34y x =?为渐近线且过点()A 的双曲线C 的左、右焦点,在双曲线C 右支上一点()()0000,4,0P x y x y >>处的切线l 交x 轴于点Q ,则( )A .双曲线CB .双曲线C 的方程为221169x y -=C .过点1F 作1F K PQ ⊥,垂足为K ,则8OK =D .点Q 的坐标为016,0x ⎛⎫⎪⎝⎭三、填空题12.等差数列{}n a 中,148121520a a a a a ++++=,则15S =.13.已知函数()32f x x x =+,若0m >,0n >,且()()()210f m f n f +-=,则12m n+的最小值是14.某校高三年级有(2,N )n n n *>∈个班,每个班均有(30)n +人,第k (1,2,3,,k n =⋅⋅⋅)个班中有(10)k +个女生,余下的为男生.在这n 个班中任取一个班,再从该班中依次取出三人,若第三次取出的人恰为男生的概率是813,则n =.四、解答题15.已知a ,b ,c 分别为ABC V 三个内角A ,B ,C 的对边,且2cos 2a cC b-=. (1)求角B 的大小; (2)若3b =,sin C ABC V 的面积. 16.已知函数()2e ,R xf x x a x =-+∈,曲线()y f x =在()()0,0f 处的切线方程为y bx =.(1)求()f x 的解析式;(2)当x ∈R 时,求证:()2f x x x ≥-+;(3)若()f x kx ≥对任意的()0,x ∈+∞恒成立,求实数k 的取值范围.17.如图,在三棱柱111ABC A B C -中,AB AC ⊥,3AB ==,2AD DB =,O 为BC 的中点,1AO ⊥平面ABC .(1)求证:1AA OD ⊥;(2)若1AA =1BAA 和平面1AAO 夹角的余弦值. 18.已知点()2,3在双曲线2222:12x y C a a -=+上. (1)求双曲线C 的方程;(2)设点Q 为双曲线右支上除右顶点外的任意点,证明:点Q 到C 的两条渐近线的距离之积为定值;(3)过点1,12P ⎛⎫⎪⎝⎭作斜率为k 的动直线l 与双曲线右支交于不同的两点M ,N ,在线段MN 上取异于点M ,N 的点H ,满足PM MH PNHN=.(ⅰ)求斜率k 的取值范围;(ⅱ)证明:点H 恒在一条定直线上.19.对于数列{}n a ,如果存在等差数列{}n b 和等比数列{}n c ,使得()n n n a b c n *=+∈N ,则称数列{}n a 是“优分解”的.(1)证明:如果{}n a 是等差数列,则{}n a 是“优分解”的.(2)记()2*11ΔΔΔΔn n n n n n a a a a a a n ++=-=-∈N ,,证明:如果数列{}n a 是“优分解”的,则()2*Δ0n a n =∈N 或数列{}2Δn a 是等比数列.(3)设数列{}n a 的前n 项和为n S ,如果{}n a 和{}n S 都是“优分解”的,并且123346a a a ===,,,求{}n a 的通项公式.。
广东省高二下学期期末考试数学(理科)试题(含参考答案)
)
A. ? m∈ A,都有 f ( m+ 3)>0 B . ? m∈ A,都有 f ( m+3)<0
C. ? m0∈ A,使得 f ( m0 +3) = 0 D . ? m0∈ A,使得 f ( m0+ 3)<0
k=k+1 否
k≥3 是
输出 (x, y)
结束
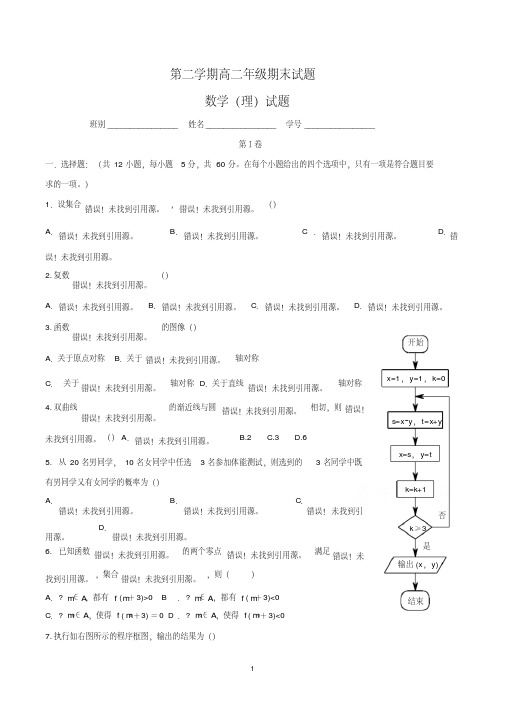
7. 执行如右图所示的程序框图,输出的结果为()
(Ⅰ)求直方图中 错误!未找到引用源。 的值;
(Ⅱ)由频率分布直方图可以认为,这种产品的质量指
标值 错误!未找到引用源。 服从正态分布 错误!未找到
引用源。,试计算数据落在 错误! 未找到引用源。 上的概 率.
3
参考数据:若 错误!未找到引用源。 ,则 错误!未找到引用源。 , 错误!未找到引用源。 .
③所有的二面角中恰有 3 个是 错误!未找到引用源。 的二面角
P4
P3
D
其中 正确 的有( ) A. ①②③ B. ②
C.③
D. ①②
2
第Ⅱ卷 本卷包括必考题和选考题两个部分。第( 13)题 - 第( 21)题为必考题,每个考生都必须作答。第( 题- 第( 23)题为选考题,考生根据要求作答。 二.填空题:(本大题共 4小题,每小题 5分)。
(换数列,已经有了)数列的前项和为,满足 ,. (Ⅰ)求证: ; (Ⅱ)是否存在常数,使得数列为等比数列?若存在求出;若不存在则说明理由。
18. (本小题满分 12 分) 某食品公司研发生产一种新的零售食品,从产品中抽取 由测量结果得到如图频率分布直方图:
100 件作为样本,测量这些产品的一项质量指标值,
进行如下折叠操作:先将矩形沿折痕 错误!未找到引用源。 折起一定角度;再
广东省2021年数学高二下学期理数期末考试试卷(II)卷

广东省2021年数学高二下学期理数期末考试试卷(II)卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2020高二下·宿迁期末) 若复数 ( 为虚数单位)为纯虚数,则实数的值为()A . 1B . 0C .D . -12. (2分) (2016高一下·福建期中) 已知x与y之间的一组数据:x0123y m3 5.57已求得关于y与x的线性回归方程为 =2.1x+0.85,则m的值为()A . 1B . 0.85C . 0.7D . 0.53. (2分) (2018高二下·黑龙江期中) “中国梦”的英文翻译为“ ”,其中又可以简写为,从“ ”中取6个不同的字母排成一排,含有“ ” 字母组合(顺序不变)的不同排列共有()A . 360种B . 480种C . 600种D . 720种4. (2分)(2020·温岭模拟) 已知,随机变量,n的分布列如表所示,则()A . ,B . ,C . ,D . ,5. (2分)下列试验能构成事件的是()A . 掷一次硬币B . 标准大气压下,水烧至100℃C . 从100件产品中任取3件D . 某人投篮5次,恰有3次投中6. (2分)(2017·鹰潭模拟) 用三段论推理:“任何实数的绝对值大于0,因为a是实数,所以a的绝对值大于0”,你认为这个推理()A . 大前提错误B . 小前提错误C . 推理形式错误D . 是正确的7. (2分)在建立两个变量的回归模型中,分别选择了4个不同的模型,他们的相关指数R2如下,其中拟合得最好的模型为()A . R2=0.75的模型1B . R2=0.90的模型2C . R2=0.45的模型3D . R2=0.65的模型48. (2分)设函数的导函数为,且,,则下列不等式成立的是()A .B .C .D .9. (2分)从边长为1的正方形的中心和顶点这五点中,随机(等可能)取两点,则该两点间的距离为的概率是()A .B .C .D .10. (2分) (2018高二下·沈阳期中) 下列函数求导运算正确的个数为()① ;② ;③ ;④ ;⑤ .A . 1B . 2C . 3D . 411. (2分)(2020·江西模拟) 的展开式的各项系数之和为5,则该展开式中x项的系数为()A . -66B . -18C . 18D . 6612. (2分) (2016高二下·肇庆期末) 若定义在R上的函数f(x)满足f(0)=﹣1,其导函数f′(x)满足f′(x)>k>1,则下列结论中一定错误的是()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2016高二上·枣阳期中) 高二年级某班共有60名学生,在一次考试中,其数学成绩满足正态分布,数学平均分为100分,若P(x≤80)=0.1(x表示本班学生数学分数),求分数在[100,120]的人数________14. (1分)若在散点图中,所有的样本点都落在一条斜率为非0实数的直线上,则相关指数R2=________ .15. (1分)(2017·邵阳模拟) (x+3)(1﹣)5的展开式中常数项为________.16. (1分)(2014·陕西理) 观察分析下表中的数据:多面体面数(F)顶点数(V)棱数(E)三棱柱569五棱锥6610立方体6812猜想一般凸多面体中F,V,E所满足的等式是________.三、解答题 (共7题;共70分)17. (10分)已知复数z满足 i(z+1)=-2+2i( i 是虚数单位)(1)求z的虚部;(2)若求.18. (10分) (2017高二下·黑龙江期末) 为了了解青少年的肥胖是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:常喝不常喝总计肥胖2不肥胖18总计30已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为.(1)请将列联表补充完整;(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?独立性检验临界值表:P(K2≥k0)0.150.100.050.0250.0100.0050.001 k0 2.072 2.706 3.841 5.024 6.6357.87910.828参考公式:,其中n=a+b+c+d .19. (10分) (2018高二下·中山月考) 设数列满足,(1)求,,的值,并猜想数列的通项公式(不需证明);(2)记为数列的前项和,用数学归纳法证明:当时,有成立.20. (10分)(2020·南京模拟) 五个自然数1、2、3、4、5按照一定的顺序排成一列.(1)求2和3不相邻的概率;(2)定义:若两个数的和为6且相邻,称这两个数为一组“友好数”.随机变量表示上述五个自然数组成的一个排列中“友好数”的组数,求的概率分布和数学期望.21. (15分)(2019·浙江模拟) 已知函数 .(1)当时,求的极值;(2)当时,讨论的单调性;(3)若对任意的,,恒有成立,求实数的取值范围.22. (10分) (2016高二下·南城期末) 在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:sinθ=ρcos2θ,过点M(﹣1,2)的直线l:(t为参数)与曲线C相交于A、B两点.求:(1)线段AB的长度;(2)点M(﹣1,2)到A、B两点的距离之积.23. (5分)(2017·常德模拟) 已知函数f(x)=|x﹣1|,x∈R(Ⅰ)求不等式|f(x)﹣3|≤4的解集;(Ⅱ)若f(x)+f(x+3)≥m2﹣2m恒成立,求实数m的取值范围.参考答案一、选择题 (共12题;共24分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共4题;共4分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共7题;共70分)答案:17-1、答案:17-2、考点:解析:答案:18-1、答案:18-2、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、答案:20-2、考点:解析:答案:21-1、答案:21-2、答案:21-3、考点:解析:答案:22-1、答案:22-2、考点:解析:答案:23-1、考点:解析:。
广东省2020-2021年高二数学理科下学期期末考试试题(含解析)

高二数学下学期期末考试试题 理(含解析)一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求的) 1.i 是虚数单位,则12ii-的虚部是( ) A. -2 B. -1C. i -D. 2i -【答案】B 【解析】 【分析】根据复数的除法运算把复数化为代数形式后可得其虚部.【详解】由题意得221222i i i i i i--==--,所以复数12ii-的虚部是1-. 故选B .【点睛】本题考查复数的运算和复数的基本概念,解答本题时容易出现的错误是认为复数z a bi =+的虚部为bi ,对此要强化对基本概念的理解和掌握,属于基础题.2.用反证法证明“方程()200++=≠ax bx c a 至多有两个解”的假设中,正确的是( )A. 至少有两个解B. 有且只有两个解C. 至少有三个解D. 至多有一个解【答案】C 【解析】分析:把要证的结论进行否定,得到要证的结论的反面,即为所求. 详解:由于用反证法证明数学命题时,应先假设命题的否定成立,命题:“方程ax 2+bx+c=0(a≠0)至多有两个解”的否定是:“至少有三个解”, 故选:C .点睛:本题主要考查用命题的否定,反证法证明数学命题的方法和步骤,把要证的结论进行否定,得到要证的结论的反面,是解题的突破口,属于中档题.3.已知函数()f x 导函数为'()f x ,且满足2()'(2)ln f x x f x =+,则'(2)f 的值为( )A. 6B. 7C. 8D. 9【答案】C 【解析】 【分析】求出''1()2(2)f x x f x=+⋅,再把2x =代入式子,得到'(2)8f =. 【详解】因为''1()2(2)f x x f x =+⋅,所以'''1(2)4(2)(2)82f f f =+⋅⇒=.选C.【点睛】本题考查对'(2)f 的理解,它是一个常数,通过构造关于'(2)f 的方程,求得'(2)f 的值.4.甲、乙、丙、丁四位同学各自对A 、B 两变量的线性相关性做试验,并用回归分析方法分别求得相关系数r 与残差平方和m 如表:则哪位同学的试验结果体现A 、B 两变量有更强的线性相关性( ) A. 甲 B. 乙C. 丙D. 丁【答案】D 【解析】试题分析:由题表格;相关系数越大,则相关性越强。
广东省广州三校(广铁一中、广州外国语学校、广州大学附属中学)2023-2024学年高二下学期期末考试

广东省广州三校(广铁一中、广州外国语学校、广州大学附属中学)2023-2024学年高二下学期期末考试数学试题一、单选题1.已知数列{}n a 为等差数列,且1492324a a a ++=,则11S =( ) A .33B .44C .66D .882.已知随机变量X 的分布列为()1,1,2,3,2kP X k k ===L ,则()16P X <≤=( ) A .1732B .1532C .3364D .31643.若()2ln f x a x bx x =++在1x =和2x =处有极值,则函数()f x 的单调递增区间是( )A .(),1-∞B .()2,+∞C .()1,2D .1,12⎛⎤ ⎥⎝⎦4.某学校校医研究温差x (℃)与本校当天新增感冒人数y (人)的关系,该医生记录了5天的数据,且样本中心点为()8,25.由于保管不善,记录的5天数据中有两个数据看不清楚,现用,m n 代替,已知1824m ≤≤,2634n ≤≤,则下列结论正确的是( )A .在,m n 确定的条件下,去掉样本点()8,25,则样本的相关系数r 增大B .在,m n 确定的条件下,经过拟合,发现基本符合线性回归方程ˆˆ2.6yx a =+,则ˆ4a = C .在,m n 确定的条件下,经过拟合,发现基本符合线性回归方程ˆˆ2.6y x a =+,则当12x =时,残差为0.4D .事件“20m =,28n =”发生的概率为155.设双曲线()2222:10,0x y C a b a b-=>>的左焦点为F ,O 为坐标原点,P 为双曲线C 右支上的一点,0PF OP PF OF ⋅+⋅=u u u r u u u r u u u r u u u r ,u u u r FO 在FP u u u r 上的投影向量的模为45OF u u u r ,则双曲线C 的离心率为( ) A .3B .4C .5D .66.在x 的展开式中含3x 项的系数为15,则展开式中二项式系数最大项是( )A .第4项B .第5项C .第6项D .第3项7.对于函数()f x ,当0x >时,()()f x f x '>.锐角ABC V 中,角A ,B ,C 的对边分别为a ,b ,c ,且cos cos cos cos b C c B a C c A +>+,设1a x b=,2sin sin A x B =,3A x B =,则( )A .()()()312123e e e x x x f x f x f x >> B .()()()312123e e e x x x f x f x f x << C .()()()312123e e e x x x f x f x f x => D .()()()312123e e e x x x f x f x f x =< 8.甲、乙两人进行一场游戏比赛,其规则如下:每一轮两人分别投掷一枚质地均匀的骰子,比较两者的点数大小,其中点数大的得3分,点数小的得0分,点数相同时各得1分.经过三轮比赛,在甲至少有一轮比赛得3分的条件下,乙也至少有一轮比赛得3分的概率为( ) A .209277B .210277C .211277D .212277二、多选题9.已知随机变量()2,X B p :,且()23E X =,则下列说法正确的是( ) A .13p =B .()89D X =C .157229P X ⎛⎫≤≤= ⎪⎝⎭D .()7213E X +=10.爆竹声声辞旧岁,银花朵朵贺新春.除夕夜里小光用3D 投影为家人进行虚拟现实表演,表演分为“燃爆竹、放烟花、辞旧岁、迎新春”4个环节.小光按照以上4个环节的先后顺序进行表演,每个环节表演一次.假设各环节是否表演成功互不影响,若每个环节表演成功的概率均为34,则( )A .事件“成功表演燃爆竹环节”与事件“成功表演辞旧岁环节”互斥B .“放烟花”、“迎新春”环节均表演成功的概率为916C .表演成功的环节个数的期望为3D .在表演成功的环节恰为3个的条件下“迎新春”环节表演成功的概率为3411.函数ln ()ln x axf x b x x x=+++(a ,b ∈R ),下列说法正确的是( )A .当0a =,不等式()0f x ≤恒成立,则b 的取值范围是1,e ⎛⎫-∞ ⎪⎝⎭B .当0a =,函数()f x 有两个零点,则b 的取值范围是1,0e ⎛⎫- ⎪⎝⎭C .当1a =,函数()f x 有三个不同的零点,则b 的取值范围是211,1e e ⎛⎫--- ⎪+⎝⎭D .当1a =,函数()f x 有三个零点123,,x x x 且123x x x <<,则2312123ln ln ln 111x x x x x x ⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值为1.三、填空题12.在等比数列{}n a 中,123453116a a a a a ++++=,314a =,则1234511111a a a a a ++++=.13.某校数学建模社团对校外一座山的高度h (单位:m )进行测量,方案如下:如图,社团同学朝山沿直线行进,在前后相距a 米两处分别观测山顶的仰角α和β(βα>),多次测量相关数据取平均值后代入数学模型求解山高,这个社团利用到的数学模型h =;多次测量取平均值是中学物理测量中常用的减小误差的方法之一,对物理量进行n 次测量,其误差n ε近似满足20,n N n ε⎛⎫~ ⎪⎝⎭,为使误差n ε在(0.5,0.5)-的概率不小于0.9973,至少要测量次.参考数据:若占()2,N ξμσ:,则(3,3)0.9973P μσξμσ-<+=.14.若12()e ln x x x x f x x x --=+-,设()f x 的零点分别为12,,,n x x x L ,则[]1ni i x ==∑.(其中[]a 表示a 的整数部分,例如:[2.1]2,[π]3==)四、解答题15.记()()23*2,n n S x x x x x x n =++++-∈∈R N L .(1)当2x =时,()2n S 为数列{}n a 的前n 项和,求{}n a 的通项公式;(2)记()2024S x '是()2024S x 的导函数,求()20242S '. 16.已知函数()2e xf x =,()()()21g x m x m =+∈R ,()()()h x f x g x =-.(1)当1m =时,求函数()h x 的最小值;(2)若直线()y g x =是曲线()y f x =的切线,求证:对任意的a b >,都有()()22e 2a h a h b a b-<--.17.已知四棱柱1111ABCD A B C D -如图所示,底面ABCD 为平行四边形,其中点D 在平面1111D C B A 内的投影为点1A ,且1AB AA ==2,120AD ABC ︒∠=.(1)求证:平面1A BD ⊥平面11ADD A ;(2)已知点E 在线段1C D 上(不含端点位置),且平面1A BE 与平面11BCC B的夹角的余弦值为1DE EC 的值.18.四月的武汉被百万株蔷薇花覆盖,形成了全城的花海景观。
广东省2023年高二下学期数学(理)期末试卷

广东省高二下学期数学(理)期末试卷(试卷总分150分、考试时间120分钟)一、选择题(每小题5分共50分) 1.321i i =- ( ) A.1i + B.1i -C.1i -+D. 2、从211=、2231=+、23531=++、247531=+++、…、得到 ++312)12(n n =-+用的是( )(A )归纳推理 (B )演绎推理 (C )类比推理 (D )特殊推理3.抛物线x y 102=的焦点到准线的距离是( ) A .25 B .5 C .215 D .10 4.已知a =(-3,2,5),b =(1,x ,-1),且a ·b =2,则x 的值是( ) A .6 B .5 C .4 D .35.从4台甲型和5台乙型电视机中任意取出3台,其中至少有甲型与乙型电视机各1台,则不同的取法共有( )A .140种 B.84种 C.70种 D.35种6.在8312x x ⎛⎫- ⎪⎝⎭的展开式中的常数项是( ) A.7 B .7- C .28 D .28-7.若椭圆的对称轴为坐标轴,长轴长与短轴长的和为18,焦距为6,则椭圆的方程为( ) A .116922=+y x B .1162522=+y x C .1162522=+y x 或1251622=+y x D .以上都不对 8.现有男、女学生共8人,从男生中选2人,从女生中选1人分别参加数学、物理、化学三科竞赛,共有90种不同方案,那么男、女生人数分别是( )A .男生2人,女生6人B .男生3人,女生5人C .男生5人,女生3人D .男生6人,女生2人.9、直线32+=x y 与抛物线2x y =所围成的图形面积是 ( )A .20B .328 C .332 D . 343 10.已知函数()y xf x '=的图象如右图所示(其中'()f x 是函数()f x 的导函数),下面四个图象中()y f x =的图象大致是 ( )二、填空题(每小题5分共20分)11.双曲线的渐近线方程为20x y ±=,焦距为10,这双曲线的方程为_______________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广州市高二下学期期末数学试卷(理科)(II)卷
姓名:________ 班级:________ 成绩:________
一、选择题 (共12题;共24分)
1. (2分)当<m<1时,复数z=(m﹣1)+(3m﹣2)i在复平面上对应的点位于()
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
2. (2分) (2016高二下·海南期中) 对一批产品的长度(单位:毫米)进行抽样检测,如图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上为一等品,在区间[15,20)和[25,30)上为二等品,在区间[10,15)和[30,35]上为三等品.用频率估计概率,现从该批产品中随机抽取1件,则其为二等品的概率是()
A . 0.09
B . 0.20
C . 0.25
D . 0.45
3. (2分)若P=, Q=, R=,则P,Q,R的大小关系是()
A . P=Q>R
B . P=Q<R
C . P>Q>R
D . P<Q<R
4. (2分) (2016高二下·六安开学考) 已知命题p:<1,q:x2+(a﹣1)x﹣a>0,若p是q的充分不必要条件,则实数a的取值范围是()
A . (﹣2,﹣1]
B . [﹣2,﹣1]
C . [﹣3,﹣1]
D . [﹣2,+∞)
5. (2分) (2016高二下·威海期末) 已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.6826,则P(X<2)=()
A . 0.1588
B . 0.1587
C . 0.1586
D . 0.1585
6. (2分)若函数在点P处取得极值,则P点坐标为()
A . (2,4)
B . (2,4)、(-2,-4)
C . (4,2)
D . (4,2)、(-4,-2)
7. (2分)复数z=(i是虚数单位),则|z|=()
A . 1
B .
C .
D . 2
8. (2分) (2016高二下·宁波期末) 把7个字符1,1,1,A,A,α,β排成一排,要求三个“1”两两不相邻,且两个“A“也不相邻,则这样的排法共有()
A . 12种
B . 30种
C . 96种
D . 144种
9. (2分)为了研究高中学生对乡村音乐的态度(喜欢和不喜欢两种态度)与性别的关系,运用2×2列联表进行独立性检验,经计算K2=8.01,则认为“喜欢乡村音乐与性别有关系”的把握性约为
P(K2≥k0)0.1000.0500.0250.0100.001
k0 2.706 3.841 5.024 6.63510.828
A . 0.1%
B . 1%
C . 99%
D . 99.9%
10. (2分)已知两条不同的直线m、n,两个不同的平面α、β,则下列命题中的真命题是()
A . 若m⊥α,n⊥β,α⊥β,则m⊥n
B . 若m⊥α,n∥β,α⊥β,则m⊥n
C . 若m∥α,n∥β,α∥β,则m∥n
D . 若m∥α,n⊥β,α⊥β,则m∥n
11. (2分) (2016高二下·郑州期末) 设(2﹣x)6=a0+a1x+a2x+…+a6x6则|a1|+|a2|+…+|a6|的值是()
A . 665
B . 729
C . 728
D . 63
12. (2分) (2018高二下·雅安期中) 已知定义在R上的可导函数的导函数为,满足
,且,则不等式的解集为()
A .
B .
C .
D .
二、填空题 (共4题;共4分)
13. (1分)(2018·内江模拟) 的展开式中,的系数是________.(用数字作答)
14. (1分) (2017高一下·滨海期末) 容量为20的样本数据,分组后的频数如表:
分组[10,20)[20,30)[30,40)[40,50)[50,60)[60,70)
频数234542
则样本数据落在区间[10,50)的频率为________.
15. (1分) (2017高三上·福州开学考) 曲线f(x)= +3x在点(1,f(1))处的切线方程为________.
16. (1分) (2016高一下·信阳期末) 某同学在求解某回归方程中,已知x,y的取值结果(y与x呈线性相
关)如表:
x234
y64m
并且求得了线性回归方程为 =﹣ x+ ,则m等于________.
三、解答题 (共6题;共80分)
17. (5分)(2020·茂名模拟) 设为椭圆:上任意一点,以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为,为上任意一点.
(Ⅰ)写出参数方程和普通方程;
(Ⅱ)求最大值和最小值.
18. (15分)(2018·河北模拟) 某葡萄基地的种植专家发现,葡萄每株的收获量(单位:)和与它“相近”葡萄的株数具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过),并分别记录了相近葡萄的株数为1,2,3,4,5,6,7时,该葡萄每株收获量的相关数据如下:
123567
1513121097
(1)求该葡萄每株的收获量关于它“相近”葡萄的株数的线性回归方程及的方差;
(2)某葡萄专业种植户种植了1000株葡萄,每株“相近”的葡萄株数按2株计算,当年的葡萄价格按10元/ 投入市场,利用上述回归方程估算该专业户的经济收入为多少万元;(精确到0.01)
(3)该葡萄基地在如图所示的正方形地块的每个格点(指纵、横直线的交叉点)处都种了一株葡萄,其中每个小正方形的面积都为,现在所种葡萄中随机选取一株,求它的收获量的分布列与数学期望.(注:每株收获
量以线性回归方程计算所得数据四舍五入后取的整数为依据)
19. (15分) (2017高二下·沈阳期末) 近年来,空气质量成为人们越来越关注的话题,空气质量指数(,Air Quality Inder简称)是定量描述空气质量状况的指数,空气质量按照大小分为六级,为优;为良;为轻度污染;为中度污染;为重度污染;大于300为严重污染.环保部门记录了2017年某月哈尔滨市10天的的茎叶图如下:
(1)利用该样本估计该地本月空气质量优良()的天数;(按这个月总共30天计算)
(2)现工作人员从这10天中空气质量为优良的日子里随机抽取2天进行某项研究,求抽取的2天中至少有一天空气质量是优的概率;
(3)将频率视为概率,从本月中随机抽取3天,记空气质量优良的天数为,求的概率分布列和数学期望.
20. (10分) (2017高一上·济南月考) 如图所示,四边形是圆柱的轴截面,是圆柱的一条母线,己知,, .
(1)求证:
(2)求圆柱的侧面积.
21. (20分)(2016·南平模拟) 设函数f(x)=ln(1+x).
(1)若曲线y=f(x)在点(0,f(0))处的切线方程为y=g(x),当x≥0时,f(x)≤ ,求t的最小值;
(2)若曲线y=f(x)在点(0,f(0))处的切线方程为y=g(x),当x≥0时,f(x)≤ ,求t的最小值;
(3)当n∈N*时,证明:.
(4)当n∈N*时,证明:.
22. (15分) (2017高二下·黑龙江期末) 已知函数;
(1)若函数在上为增函数,求正实数的取值范围;
(2)当时,求函数在上的最值;
(3)当时,对大于1的任意正整数,试比较与的大小关系.
参考答案一、选择题 (共12题;共24分)
1-1、答案:略
2-1、答案:略
3-1、
4-1、
5-1、
6-1、
7-1、答案:略
8-1、
9-1、答案:略
10-1、答案:略
11-1、
12-1、
二、填空题 (共4题;共4分)
13-1、答案:略
14-1、
15-1、
16-1、
三、解答题 (共6题;共80分) 17-1、答案:略
18-1、答案:略
18-2、答案:略
18-3、答案:略
19-1、答案:略
19-2、答案:略
19-3、答案:略
20-1、答案:略
20-2、答案:略
21-1、答案:略
21-2、答案:略
21-3、答案:略
21-4、答案:略
22-1、答案:略
22-2、答案:略
22-3、答案:略。
