二年级数学奥数讲义-解应用题一题多解通用版
二年级下册数学试题-奥数习题讲练:第九讲 倍数问题(解析版)全国通用

第九讲倍数问题【精品】数学乐园1、同学们,我们一起来玩一个“鸡生蛋、蛋生鸡”的游戏.请从右上方的“↓”开始,按“蛋—雏鸡一小鸡一大鸡”的顺序,走一条不重复、不交叉的路线,最后从下方箭头走出来.走完后,用符号表示你找到的路线.本节课中我们主要引导学生来掌握“倍”的概念,知道在求相同加数和的运算中,我们常常把相同加数叫做1倍量.已知两个量各是多少,求一个量是另一个量的几倍,通常用除法计算.另外我们还将学习简单的“和倍”问题.在解答这类问题的时候一定要弄清楚题目中的数量关系,结合线段图来进行分析.2、先帮小动物找座位.然后说一说,哪一个数是另一个数的2倍?48是24的2倍36是18的2倍在应用题中,常有两个数有倍数关系的题目.例如:学校有篮球8个,足球的个数是篮球的5倍,篮球和足球共有多少个?这里要把篮球的个数当作1倍数,足球的个数就是5倍数,求足球的个数就是求5倍数是多少,求篮球和足球一共多少个,就是求(1+5)倍数是多少.8×5=40(个)……足球的个数40+8=48(个)……足球和篮球一共的个数或8×(5+1)=48(个)因此,倍数问题实际上就是1倍数和几倍数的问题,明确了这一点,很多有关倍数的问题都可以解答.一个数是另一个数的几倍【例1】如下图,前两排是女孩,合唱队一共有多少人?总人数是女孩人数的几倍?男孩数比女孩数多几倍?【分析】总人数有6排,总人数应是6的6倍,即36人.男孩占4排,女孩占2排,女孩有12人.6×6=36(人)……总人数6÷2=3……总人数是女孩的倍数(4-2)÷2=1……男孩比女孩多的倍数答:合唱队一共有36人,总人数是女孩的3倍,男孩数比女孩数多1倍.【例2】公园里有15棵杏树,4棵柏树,要使杏树棵树是柏树的6倍,应再种上几棵杏树?【分析】从条件“要使杏树棵树是柏树的6倍”可知:杏树应为4×6=24(棵),而公园里只由15棵杏树,所以杏树应再种上:24-15=9(棵).列式:4×6=24(棵)24-15=9(棵)答:应再种上9棵杏树.【例3】粮店里有大米22袋,面粉6袋,要卖出多少袋大米,才能使大米的袋数是面粉的3倍?【分析】从题目中可以看出:要使大米的袋数是面粉的3倍,大米应有6×3=18(袋),而实际上店里大米有22袋,所以应卖出22-18=4(袋),才能使大米的袋数是面粉的3倍.列式:6×3=18(袋)22-18=4(袋)答:大米要卖出4袋后,才能使大米的袋数是面粉的3倍.拓展练习教室里有24个男同学,7个女同学,要使男同学人数是女同学的3倍,应从教室里走出几个男同学?【分析】24-7×3=3(人),应从教室里走出3个男同学.【例4】小方与大强两人打扫一间教室需要6分钟.如果人数增加1倍,一共要用多少分钟才能打扫完毕?【分析】增加1倍人数,即人数由2人变为(2+2=)4人.这样人多了,打扫教室就会快一些.原来小方与大强要打扫一间,现在只要打扫半间教室,所以用的时间是原来的一半.6÷2=3(分).答:一共要用3分钟.和倍问题【例5】学校买来一些乒乓球和羽毛球共40个,乒乓球的个数是羽毛球的4倍.买来的乒乓球和羽毛球各多少个?【分析】根据题意和线段图可知,羽毛球的个数看作1份数,乒乓球的个数就是4份数,40个就相当于(4+1)份数,这样就可求出1份数,也就是羽毛球的个数,把羽毛球的个数乘4就是乒乓球的个数.羽毛球有多少个?40÷(4+1)=40÷5=8(个)乒乓球有多少个?8×4=32(个)答:乒乓球有32个,羽毛球有8个.【例6】果园里有梨树和苹果树共54棵,苹果树的棵数是梨树的5倍,苹果树比梨树多多少棵?【分析】把梨树的棵数看作l份数,苹果树的棵数就是5份数,54棵就相当于(5+1)份数,用例5的方法可分别求出梨树和苹果树的棵数,再把苹果树的棵数减去梨树的棵数,就是苹果树比梨树多的棵数.这道题还可以这样想,先求出1份数,再求苹果树比梨树多几份,就可直接求出苹果树比梨树多多少棵了.解法一:梨树有多少棵?54÷(5+1) =9(棵)苹果树有多少棵?9×5=45(棵)苹果树比梨树多多少棵?45-9=36(棵)解法二:梨树有多少棵?54÷(5+1)=9(棵)苹果树比梨树多多少棵?9×(5-1)=36(棵)答:苹果树比梨树多36棵.拓展练习根据线段图列式:列式:28÷(3+1)=7(米)列式:54÷(1+5)×5=45(棵)【例7】师、徒两人共加工105个零件,师傅加工的个数比徒弟的3倍还多5个,师傅和徒弟各加工零件多少个?【分析】从线段图上可以看出,把徒弟加工的个数看作1份数,师傅加工的个数就比3份数还多5个,如果师傅少加工5个,两人加工的总数就少5个,总数变为(105-5)个,这样这道题就转化为例5类型的题目,就可以求出师傅和徒弟各加工多少个了.列式:如果师傅少做5个,师、徒共做多少个?105-5=100(个)徒弟做了多少个?100÷(3+1)=25(个)师傅做了多少个?25×3+5=80(个)答:师傅做了80个,徒弟做了25个.拓展练习实验小学共有学生956人,男生比女生2倍少4人.问:实验小学男学生和女学生各有多少人?【分析】女生:(956+4)÷3=320(人),男生:956-320=636(人)或320×2-4=636(人)【例8】大红有贺卡54张,小琴有贺卡70张,大红给小琴几张卡片后,小琴的卡片张数就是大红的3倍?【分析】现在大红和小琴共有贺卡(54+70)张,大红拿出几张贺卡给小琴后,他们的贺卡总数还是(54+70)张.根据例1的解题思路,可求出当小琴的贺卡张数是大红的3倍时,大红有多少张贺卡.比大红原来的54张少了几张,就是大红给小琴的张数.大红、小琴共有贺卡多少张?54+70=124(张)小琴贺卡的张数是大红的3倍时大红有多少张?124÷(3+1)=31(张)大红给了小琴多少张?54-31=23(张)答:大红给了小琴23张.【例9】学校买来篮球、足球、排球共49个,其中篮球的个数是足球的3倍.排球比足球多4个.问学校买来的篮球、足球、排球各多少个?【分析】从线段图上可以看出,把足球的个数看作1份数,篮球的个数是3份数,如果排球少买4个,也是l份数,这时三种球一共(49-4)个,总份数是(1+3+1),就可先求出足球的个数,再分别求篮球和排球的个数.如果排球减少4个,三种球一共多少个?49-4=45(个)足球多少个?45÷(1+3+1)=9(个)篮球多少个?9×3=27(个)排球多少个?9+4=13(个)答:学校买来篮球27个,足球9个,排球13个.拓展练习一筐苹果、一筐梨、一筐香蕉共重112千克.已知苹果的重量是梨的3倍,香蕉的重量比梨少3千克.一筐苹果、一筐梨、一筐香蕉各重多少千克?【分析】梨的重量是:(112+3)÷(1+1+3)=23(千克)苹果的重量是:23×3=69(千克)香蕉的重量是:23-3=20(千克)【例10】在一道减法算式中,已知被减数、减数、差的和是240,而减数是差的5倍.求差是多少?【分析】我们先看下面一道简单的减法算式:15 - 10 = 5被减数减数差被减数、减数、差这三个数有下面的关系:被减数=差+减数,如15=5+10 这道题中,被减数、减数、差的和是15+5+10=30,30是被减数的2倍,30÷2=15,就得被减数,也就是减数与差的和,这样题目就转化为:“已知减数与差的和是15,减数是差的2倍”,按照和倍问题的解题方法,就可求出差是:15÷(2+1)=5.小朋友们,你看了上面的分析,上面这道题你会解答吗?列式:减数与差的和是多少?240÷2=120差是多少?120÷(5+1)=20答:差是20.1倍与1半【例11馋嘴和尚吃一堆馒头.第一次吃了一半,觉得不够;第二次又吃了剩下的一半,觉得差不多了;第三次又吃了5个,觉得饱了.他发现还剩下5个,干脆又吃光了.这一堆馒头有多少个?【分析】这类问题可以通过画图倒退来分析.把第三次吃的5个看作1倍,则剩下的也是1倍.共2倍,占第二次吃时的一半,也就是第二次吃时有(2×2=)4倍.这4倍占第一次吃时的一半,也就是第一次吃时有(4×2=)8倍.【解法1】5×(1×2×2×2)=5×8=40(个).【解法2】5+5=10(个),第二次吃的:10+10=20(个),第一次吃的:20+20=40(个).答:这一堆馒头共有40个.【例12在高家庄猪八戒干了很多活,但同时也很能吃.高老太太拿来一篮烧饼,八戒吃了一半又半个,又吃了剩下的一半又半个,再吃了剩下的一半又半个.最后只剩下一个,他连这一个也不放过,也吃了进去.高老太太的这篮烧饼有多少个?你能把猪八戒4次吃的烧饼画出来吗?小结:和倍问题的特点是已知两个数的和与大数是小数的几倍,要求两个数,一般是把较小数看作1倍数,大数就是几倍数,这样就可知总和相当于小数的几倍了,可求出小数,再求大数.和倍问题的数量关系式是:和÷(倍数+1)=小数小数×倍数=大数或和一小数=大数如果要求两个数的差,要先求1份数.l份数×(倍数一1)=两数差.解决和倍问题,关键是学会画线段图,这样可以帮助我们更好的弄清各数量之间的关系.【分析】这道题我们要采用倒推法来分析.最后剩下的1个加半个是第三次吃的一半.即1个半加半个是第三次吃的.吃2个,剩1个,共有3个.第二次吃了一半又半个,这3个半加半个是4个.这是第二次吃的,吃之前共有7个.第一次吃了一半又半个,7个半加半个是8个,这是第一次吃的,所以这篮烧饼有15个.附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)二(1)班的图书角里有故事书和连环画共47本,如果故事书拿走7本后,故事书的本数就是连环画的4倍.原有连环画和故事书各有多少本?【分析】从线段图可以看出,如果故事书拿走7本以后,则正好是连环画的4倍.这时故事书与连环画总数应减少7本,列式成47-7=40(本),正好是连环画本数的(1+4)倍.(1 )如果故事书拿走7本,总本数为:47-7=40(本)(2) 现在连环画与故事书的倍数和为:4+1=5(3) 连环画有:40÷5=8(本)(4) 故事书有:8×4+7=39(本)答:原有连环画8本,故事书39本.小红家养了一些鸡,黄鸡比黑鸡多13只,比白鸡少18只.白鸡的只数是黄鸡的2倍,白鸡、黄鸡、黑鸡一共有多少只?【分析】(1)黄鸡多少只?18÷(2-1)=18(只)(2)白鸡多少只?18×2=36(只) ‘(3)黑鸡多少只?18-13=5(只)(4)白鸡、黄鸡、黑鸡共多少只?18+36+5=59(只)有一包糖,妈妈分给妹妹8颗后,又把一些分给哥哥.哥哥分得的正好是妹妹的一半多2颗,剩下的糖数是哥哥分得的一半.哥哥分得几颗糖?这包糖一共有多少颗?【分析】8÷2=4(颗)……这是妹妹的一半4+2=6(颗)……这是哥哥的糖6÷2=3(颗)……这是剩下的糖8+6+3=17(颗)……一共的糖答:哥哥分得6颗糖,这包糖一共有17颗.练习九1. 动物园里有3只大猴,13只小猴,要添上几只小猴后,才能使小猴只数是大猴只数的6倍?【答案】3×6-13=5(只),要添上5只小猴后,才能使小猴只数是大猴只数的6倍.2. 小华和爷爷今年共72岁,爷爷的岁数是小华的7倍.爷爷比小华大多少岁?【答案】小华:72÷(1+7)=9(岁),爷爷:9×7=63(岁),63-9=54(岁)或9×(7-1)=54(岁)3. 小敏有14元,小花有10元,小花给小敏几元,小敏的钱数就是小花的2倍?【答案】小花现在的邮票:(14+10)÷(1+2)=8(张),10-8=2(张)4. 玩具厂生产红、黄、白气球共125个,其中红气球的个数是黄气球的3倍,白气球比黄气球少25个.问三种气球各生产了多少个?【答案】黄气球:(125+25)÷(3+1+1)=30(个);红气球:30×3=90(个);白气球:30-25=5(个)5. 植树节,老师带两个小组的同学去植树.分给第一小组6棵树苗.剩下的分给第二小组,第一小组分得的正好是第二小组的一半,两个小组一共分得多少棵树?【答案】6×2+6=18(棵),两个小组一共分得18棵树.6. 猪八戒化斋讨来了一篮果子.吃了一半,觉得不够,又吃了剩下的一半,还是觉得不够,再吃了4个果子,觉得饱了.把剩下的给唐僧吃,孙悟空一看发现篮子里只剩下4个果子了.那么猪八戒到底吃了多少个果子呢?【答案】第三次吃了:4个;第二次吃了:4+4=8(个)‘第一次吃了:8×2=16(个)一共吃的:4+8+16=28(个)不要让昨日的沮丧令明天的梦想黯然失色!在一次讨论会上,一位著名的演说家没讲一句开场白,手里却高举着一张20美元的钞票.面对会议室里的200个人,他问:"谁要这20美元?"一只只手举了起来.他接着说:"我打算把这20美元送给你们中的一位,但在这之前,请准许我做一件事."他说着将钞票揉成一团,然后问:"谁还要?"仍有人举起手来.他又说:"那么,假如我这样做又会怎么样呢?"他把钞票扔到地上,又踏上一只脚,并且用脚碾它.尔后他拾起钞票,钞票已变得又脏又皱"现在谁还要?"还是有人举起手来."朋友们,你们已经上了一堂很有意义的课.无论我如何对待那张钞票,你们还是想要它,因为它并没贬值,它依旧值20美元.人生路上,我们会无数次被自己的决定或碰到的逆境击倒、欺凌甚至碾得粉身碎骨.我们觉得自己似乎一文不值.但无论发生什么,或将要发生什么,在上帝的眼中,你们永远不会丧失价值.在他看来,肮脏或洁净,衣着齐整或不齐整,你们依然是无价之宝."温馨提示:生命的价值不依赖我们的所作所为,也不仰仗我们结交的人物,而是取决于我们本身!我们是独特的--永远不要忘记这一点!。
二年级下册数学试题-奥数习题讲练:第四讲 图形剪拼(解析版)全国通用
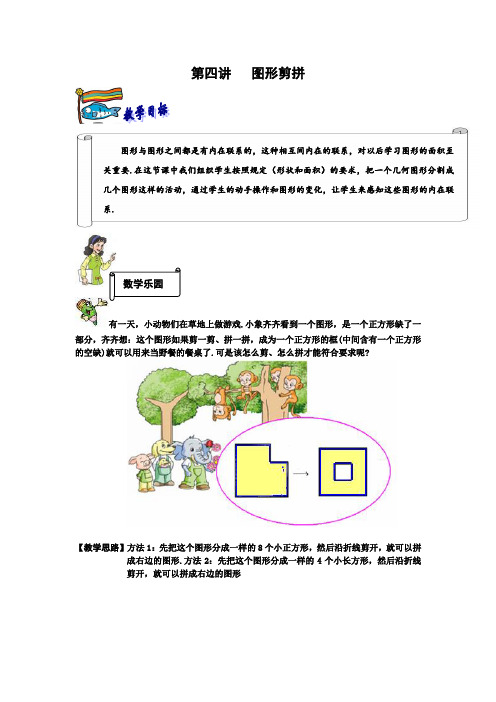
第四讲图形剪拼数学乐园有一天,小动物们在草地上做游戏.小象齐齐看到一个图形,是一个正方形缺了一部分,齐齐想:这个图形如果剪一剪、拼一拼,成为一个正方形的框(中间含有一个正方形的空缺)就可以用来当野餐的餐桌了.可是该怎么剪、怎么拼才能符合要求呢?【教学思路】方法1:先把这个图形分成一样的8个小正方形,然后沿折线剪开,就可以拼成右边的图形.方法2:先把这个图形分成一样的4个小长方形,然后沿折线剪开,就可以拼成右边的图形图形与图形之间都是有内在联系的,这种相互间内在的联系,对以后学习图形的面积至关重要.在这节课中我们组织学生按照规定(形状和面积)的要求,把一个几何图形分割成几个图形这样的活动,通过学生的动手操作和图形的变化,让学生来感知这些图形的内在联系.方法1 方法2同学们,我们已经学过一些简单的基本几何图形,如、□、△、○等,通过折、剪、拼,这些图形之间是可以相互变化的,这不仅可以锻炼我们的动手能力,还能拓展我们的思维,使我们的头脑越来越灵活.今天这节课就用我们灵巧的小手来玩一玩拼图游戏吧!分一分【例1】要把一个正方形剪成形状相同、大小相等的4个图形,该怎样分?【分析】把一个正方形分成形状、大小相等的4个图形,我们可以先让学生把这个正方形分成形状、大小相等的2个图形,然后再把这两个图形继续分成形状、大小相等的4份.有些方法中我们也可以利用对称图形的特点来分.本题有很多种解法,这里只列举最常用的几种:.【例2】你能把下面的图形分成7个长方形吗?动手画一画.【分析】可以分成7块含有2个小方格的长方形,答案如下:(答案不唯一)拓展练习你能把下面的图形分成7个长方形,使每个长方形中包含相连的2个小方格吗?【分析】不能,因为如果可分的话,每块图形中一定是一个黑色、一个白色.那么黑白方格应分别有7个,但图中白色方格只有6个.【例3】你能将下面的图形分割成4个形状相同、大小相等的图形吗?【分析】首先可以把这个图形分成12个小正方形,要把这个图形分成大小相等的4个图形,那么每个小图形必须包含:12÷4=3个小方格,然后我们再来考虑分得的形状相同,通过尝试我们就可以得到答案.在分割不规则图形时,我们可以考虑把这个图形分割成若干个规则图形,然后再来进一步思考.答案如下图:拓展练习1、你能把下面的两个图形分割成4个形状相同、大小相等的图形吗?【分析】答案如下:2、下图是由18个小正方形组成的图形,请你把它分成6个完全相同的图形.【例4】你能把一个正三角形分成形状相同,大小相等的2个、3个、4个、6个、9个三角形吗?【分析】观察:正三角形有几条对称轴?正三角形有3条对称轴,我们把一个正三角形分成若干份,都可以根据它的对称轴来分.答案如下:思考:(1)分成4个、9个的方法与分成2个、3个、6个的方法有什么不同?(2)哪几种分割的结果仍得到正三角形?【例5】你能把一个正方形分成6个、7个、8个、9个小正方形(不要求面积相等)吗?【分析】首先我们来观察:一个正方形分成4个小正方形,每分一次,正方形的个数增加3个.根据这样的规律,我们可以想到怎样把一个正方形分成4个、6个、8个正方形的方法.分成6个分成7个分成8个分成9个【例6】下图是由三个正三角形组成的梯形.你能把它分割成4个形状相同、大小相等的梯形吗?【分析】连接正三角形各边的中点,正好把这个正三角形分割成了4个形状相同,大小相等的梯形.【例7】将下图分割成大小、形状相同的三块,使每块都包含一个小圆圈.【分析】数一数,一共有18个小方格,要分成大小、形状相同的三块,每块里面应该包含6个小方格.然后再来考虑每块里面要含一个小圆圈,通过尝试答案如下:拓展练习在下面的方格中有4个圆圈,请你把方格分成4个完全相同的非正方形,使每部分都有1个圆圈(圆圈的位置相同).动手画出你的方法.答案不唯一拼一拼【例8】晚饭后,平平和妈妈玩拼木板游戏.妈妈拿出5块木板(如下图),要求平平把这5块木板拼成一个正方形.聪明的平平很快就拼好了.小朋友,你知道她是怎样拼的吗?试一试.【分析】如果用2号、3号、4号、5号这四块木板,就可以拼成近似的正方形.现在加上1号这块正方形,拼成的正方形一定比四块拼成的大得多.【例9】用下面的四块图形能拼成右边的正方形吗?怎样拼?【分析】答案不唯一,以下有三种基本的方法,其他方法可改变不同的方位来排列.拓展练习用下面左边的3个图形,拼成右边的大正方形.【分析】答案有以下几种,其实我们可以发现这几种方法基本相同,只是方位发生了变化.【例10】你能把下面的四块图形拼成一个长方形的宣传牌吗?【分析】答案如下:【例11】下面有5组图形,每个各有5个小正方形,请把这5个图形拼成一个大正方形,可以怎样拼?【分析】这道题可以先让学生摆一摆,通过摆就可以找到答案.【例12】国外有一种流行的七巧板,它由20个小正方形组成的纸板分割而成,利用这种七巧板也可拼成许多有趣的图形.仔细观察图(1),然后把图(2)分割成七巧板.图(1)图(2)【分析】观察图(1)中的“箭头”,给组成它的每个图形编号,按面积从大到小逐步进行分割.先分割出面积最大、边最长的图形①;第二步再分割出五边形②;第三步再分割出梯形③;以此类推,整个七块都分割出来了.动动手:把长方形按上面的方式剪成7块,涂上颜色做成七巧板,然后拼一拼.附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)一个长6厘米,宽4厘米的长方形,从中间剪开,如图所示,得到2个大小、形状都相同的长方形,这两个新长方形的周长是多少?【分析】切割开之后,新形成的2个小长方形除了原有长方形的边之外,新产生了两条边,如下图虚线所示,每个新长方形的周长是:(3+4)×2=14(厘米).两个新长方形的周长是14+14=28(厘米)把下面这个长方形沿格线剪成大小相等、形状相同的四块,使每块内都含有“我爱北京”这四个字中的一个字,该怎样剪呢?【答案】沿下面的粗线剪开,就得到了大小相等、形状相同的四块,并且每块内都含有“我爱北京”这四个字中的一个字.妈妈买来了两张同样大小的方桌布,想把这两张方桌布裁剪一下,然后拼成一张大方桌布,该怎样裁剪?怎样拼呢?【教学思路】要想把两块一样大小的正方形,剪拼成一个最大的正方形,我们可以把这两个小正方形对折,然后剪出四个大小一样的三角形,这四个三角形就可以拼成一个最大的正方形.如下图:有一张纸,被分成大小相等的16个方格.请你沿着方格纸的边把这张纸剪成两部分,使得这两部分正好可以拼成一个正方形.该怎样剪拼呢?(中间空白是空的)【教学思路】数一数一共16个方格,要想剪成两部分拼成一个正方形,这个正方形每条边就应该是4个方格.如下图,第一层有7个方格,我们可以剪掉3个;补到第二层上正好是四个;再把第二层上右边多的一个补到第三层也正好是4个,把第三层上剪出4个放到第四层,这样就拼出了一个正方形.沿粗线剪开:变成下面两部分:拼成正方形:练习四1. 把下图分成5个形状相同、大小相等的图形.【答案】方法如下:2. 将下面的正三角形分割成16个形状、大小一样的三角形.【答案】方法如下:3.把下图剪成形状、大小相等的8个小图形,怎么剪?【答案】方法如下:4. 请把下图中长方形分成形状相同、大小相等的两块,然后再拼成一个正方形.【答案】数一数,这个长方形一共有36块小方块,要剪拼成一个正方形,这个正方形每边应该有6个小方块.具体操作如下图:5. 用下面的四块图形能拼成右边的正方形吗?怎样拼?【答案】方法如下:6. 长为16厘米、宽为4厘米的长方形经过剪拼,组成一个正方形,这个正方形的边长为多少厘米.【答案】这个长方形可看成是边长是4厘米的正方形4个排一排.如下图:现在把这4个小正方形,拼成一个大正方形.这个大正方形的边长是8厘米.有一天,著名科学家爱因斯坦先生被邀请作演讲嘉宾.他的司机对他开玩笑说:「我经常听到你在车中预备演讲,听得多了,我也可以一字不漏地背念出来.」爱因斯坦听罢就说:「那就好极了,我昨日整天都在做研究工作,疲倦得很,况且邀请我演讲的机构与我素未谋面,你大可替我演讲,我做你的司机好了.演讲当晚,司机果然一字不漏地念出爱因斯坦惯说的演讲内容,令在场的人佩服不已,连坐在观众席最后排的爱因斯坦,也频频点头称是.可是,演讲完结后,突然有一位年青科学家,追问了一个颇为深入的问题,那当然是司机的演讲以外的资料,全场都等待着这位冒牌科学家的答复.出乎意料之外,他竟然气定神闲地开始回答说:「年青人,请恕我直言,你刚才的问题实在太简单,甚至可以说是个蠢问题,假如你不信的话,我可以证明给你看.这问题简单得连我的司机也懂得如何回答.」跟着,司机便邀请爱因斯坦上台作答,并且在掌声雷鸣之下离开会场.。
小学二年级数学奥数题应用题150道及答案解析

小学二年级数学奥数题应用题150道及答案解析1. 小明有10 个苹果,小红的苹果数是小明的2 倍,小红有多少个苹果?答案:10×2 = 20(个)解析:求一个数的几倍是多少用乘法,小明有10 个苹果,小红的是小明的2 倍,所以小红有10×2 = 20 个苹果。
2. 商店里有30 个书包,卖出了15 个,还剩下多少个书包?答案:30 - 15 = 15(个)解析:用原有的书包数量减去卖出的数量,就是剩下的数量。
3. 一本书有50 页,小明每天看8 页,看了5 天,还剩多少页没看?答案:50 - 8×5 = 10(页)解析:小明 5 天看的页数为8×5 = 40 页,总页数减去已看的页数就是剩下没看的页数。
4. 有25 只兔子,平均装在5 个笼子里,每个笼子装几只?答案:25÷5 = 5(只)解析:把25 只兔子平均分成 5 份,求每份是多少,用除法计算。
5. 一支铅笔5 角钱,买3 支铅笔需要多少钱?答案:5×3 = 15(角)= 1 元 5 角解析:一支铅笔5 角,3 支铅笔就是3 个 5 角,用乘法计算。
6. 一辆公交车上原来有20 人,到站后下车8 人,上车5 人,现在车上有多少人?答案:20 - 8 + 5 = 17(人)解析:用车上原有的人数减去下车的人数,再加上上车的人数,就是现在车上的人数。
7. 妈妈买了15 个梨,小明吃了3 个,爸爸吃了5 个,还剩下几个梨?答案:15 - 3 - 5 = 7(个)解析:用梨的总数依次减去小明和爸爸吃的个数,就是剩下的个数。
8. 每张桌子可以坐4 个人,有18 个人,需要几张桌子?答案:18÷4 = 4(张)......2(人),4 + 1 = 5(张)解析:18 个人,每张桌子坐 4 人,18÷4 = 4 张余2 人,余下的2 人还需要1 张桌子,所以共需要5 张桌子。
二年级下册数学试题-奥数习题讲练:第十讲 数字分组和拆分(解析版)全国通用

把一个自然数(0除外)拆成几个自然数相加的形式,叫自然数的拆分.在这节课中,我们就将来研究关于自然数的拆分问题.希望通过学习,使学生从中学到一些有序和全面思考问题的方法.知识点:掌握自然数拆分的一般方法——枚举.【教学思路】小松鼠把9个松果分成不一样多的三份,6=1+2+3,所以可以分成.小白兔说它把9个蘑菇分成个数不同的4份.这是不对的.因为1+2+3+4=10.9个蘑菇是分不出个数不同的4份的.① 小松鼠和小白兔上学迟到了.熊猫老师问:“你俩今天为什么迟到了?” 小松鼠说:“我在上学的路上遇到三个小弟弟,他们饿(e)得很,我就采了6个松果.分成数量不同的3份,送给他们每人一份.”② 小白兔说:“我在上学的路上遇到四个小妹妹.她们饿得很,我就采了9个蘑菇.分成数量不同的4份,送给她们每人一份.” 熊猫老师说:“松鼠说的是实话.小白兔说的是谎话.”③ 小白兔听后,惭愧地低下头,说:“老师,我错了,今后我一定做个诚实的孩子.” 小朋友.熊猫老师怎么知道小白兔说的是谎话?把一个自然数(0除外)分拆成几个自然数相加的形式,这种方法叫做自然数的分拆.下面让我们一起来学习怎样分拆自然数,从中学到一些有序和全面思考问题的方法.强强和明明两人到游乐园玩射击游戏,如下图他们每人打了两发子弹,均击中了靶子(即无脱靶现象).强强两发共打了12环,明明两发共打了8环.又已知没有哪两发子弹打在同一环中,请你推算一下他俩打中的是哪几环?【教学思路】要求强强和明明各打中的环数,即是把12,8按环数进行拆分的问题.也就是要把12和8拆分成两个数相加.因为靶子中的环数只有2、4、6、8、10环.所以这两个数只能从这些数中选择.因为12=8+4=10+2,8=6+2.根据“没有哪两发子弹打在同一环中’’的条件,可以知道甲打中的是8环和4环,乙打中的是6环和2环.把5拆成几个自然数相加的形式,共有多少种不同的拆分方法?(0除外)【教学思路】要做到拆分得不重、不漏,要注意有序思考,一般我们采用枚举法.例如先拆成两部分,再拆成三部分、四部分,最后拆成五部分.拆分过程是:5=1+4=2+35=1+1+3=1+2+25=1+1+1+25=1+1+1+1+1答:共有6种不同的拆分方法.按下面的要求,把自然数6进行拆分.(1)把6拆成几个自然数相加的形式(0除外),共有多少种不同的拆分方法?(2)把6拆成几个不完全相同的自然数相加的形式(0除外),共有多少种不同的拆分方法?(3)把6拆成几个完全不相同的自然数相加的形式(0除外),共有多少种不同的拆分方法?【教学思路】(1)6=1+5=2+4=3+3 ;6=1+1+4=1+2+3=2+2+2 ;6=1+1+1+3=1+1+2+2 ;6=1+1+1+1+2 ;6=1+1+1+1+1+1 共10种方法.(2)从(1)中,把完全相同的3种方法剔除6=3+3=2+2+2=1+1+1+1+1+1,则还剩7种.(3)“几个完全不相同的自然数”也就是“不同的自然数”,即拆分的数不能相同.那么就只有6=1+5=2+4=1+2+3 ,3种拆分方法.猪妈妈让小猪三兄弟去摘野果,它要求三兄弟一共要摘10个,每只小猪至少摘2个,按照妈妈的要求,现在小猪们要分配任务了,它们有多少种不同的分配方法?【教学思路】要求有几种不同的分配方法,就是求把10拆成3个不完全相同的自然数,因为每个小猪至少要摘2个,所以0,1除外,共有多少种拆分方法呢.拆分过程是:lO=2+2+610=2+3+510=2+4+410=3+3+4答:共有4种不同的分组方法.巩固拓展体育课上,10个小朋友分成三组做游戏,一共有多少种不同的分组方法?【教学思路】10个小朋友分成三组做游戏,那么每组最少要有1个人,这道题和上一题比不同就是,就是多了拆成1的部分.具体拆分过程如下:10=1+1+8=1+2+7=1+3+6=1+4+510=2+2+6=2+3+5=2+4+410=3+3+4答:一共有8种不同的分组方法.兔妈妈拔了12个萝卜,它要把这些萝卜分给三个兔宝宝吃,每个小兔至少要有1个,并且它们分到的萝卜数量都不同.可以怎样分呢?【教学思路】这道题也就是要我们把12拆分成3个不同的自然数,可以做如下考虑:若将12分拆成三个不同的自然数之和,三个数中最小的数应为1,其次是2,那么第三个数就应是9得:12=1+2+9.下面进行变化,如从9中取1加到2上,又得:12=1+3+8.继续按类似方法变化,可得下列各式:12=1+4+7=2+3+7,12=1+5+6=2+4+6,12=3+4+5.共有7种不同的分拆方式.巩固拓展4个小朋友去学校图书室一共借了12本书.图书室规定,每个人最多只能借9本书,现在这四个小朋友手里的书数量都不一样多.想一想,他们手中各有几本书?【教学思路】把12拆分成4个不同的自然数只有唯一一种方法:12=5+4+2+1,所以这几个小朋友手中的书分别是5本、4本、2本、1本。
二年级数学奥数讲义+练习第15讲 植树问题(全国通用版,含答案)

第15讲植树问题奥数是给那些对奥数有兴趣的孩子搭建的一个舞台,正象我们给那些对英语、对绘画、对音乐、对体育等有兴趣的孩子搭建的舞台一样,让他们自由、快乐地享受童年、享受人生。
其一,奥数包涵了发散思维、收敛思维、换元思维、反向思维、逆向思维、逻辑思维、空间思维、立体思维等等二十几种思维方式,众所周知,思维能力是一个孩子的智力的核心,如果一个孩子在小学期间,思维能力得到了充分的锻炼,有什么比这更重要的呢?奥数能够快速有效、全面提高孩子智商的工具。
奥数学习对开拓思路有着重要作用。
奥数学习好的学生整个理科都会比较优秀,因为数学是理科的基础,物理化学都需要数学这个基础。
正因为这个原因,重点中学喜欢招奥数比较好的学生。
其二,奥数题基本上是比书上知识有所提高的内容,当孩子在做题当中遇到困难,想办法战胜它时,那种来自内心深处的喜悦比吃了十斤蜜枣还甜。
在学习、比赛中,有失败、有成功,让孩子从小就明白:不经历风雨怎能见彩虹的道理,一句话:奥数让孩子学会了面对挫折、战胜困难,学会了永不言败的精神,建立起良好的自信。
可以说既提高孩子的智商又能发展孩子的情商。
【专题简析】植树的学问真不少,这里面有许多有趣的问题,做这类题目要多动脑筋,弄清题意,理解树的棵数与间隔数的关系,掌握植树的解题方法,问题就迎刃而解了。
植树的问题,应该注意如果起点和终点都植树,树的棵数比间隔数多1,如果起点和终点不植树,树的棵数比间隔数少1,在解答这类应用题时,应该看清楚题目要求,然后根据棵数与间隔数的关系,结合已知条件,就能找到解决问题的方法了。
【例题1】一条路长72米,在路的一边每隔8米栽1棵松树,从头到尾一共可以栽多少棵松树?思路导航:每隔8米栽一棵树,72里面有9个8,这个9其实就是把72米平均分成了9个间隔,因为从头到尾都要栽树,所以树的棵数比间隔数多1,即9+1=10(棵),也就是棵数比间隔数多1.解:72÷8+1=10(棵)答:一共可以栽10棵松树.练习11.学校门前的一条路长42米,在路的一边从头到尾栽树,每7米栽一棵,一共能栽多少棵?2.教室前面到教室后面长8米,从头到尾每隔2米摆一盆花,一共摆了多少盆花?3.学校门前的一条路长56米,为迎接国庆节,在路的一边从头到尾都插上彩旗,每7米插一面,一共要插多少面彩旗?【例题2】同学们在一条公路的两边从头到尾每隔6米栽一棵树,共栽了22棵,这条公路长多少米?思路导航:在路的两旁栽树,共栽了22棵,那么每边栽了22÷2=11棵,由此可知,就是把这条路的每边分成了11-1=10(段),又因为每段是6米,10×6=60米,这就是这条公路的长了解:22÷2=11(棵)11-1=10(段)6×10=60(米)答:这条公路长60米。
二年级下册数学试题-奥数习题讲练:第五讲 数字谜(解析版)全国通用

第五讲数字谜数学乐园小红在家做计算题,不小心碰倒了墨水瓶,把这两道题弄得残缺不全.认真观察一下,你能将墨迹破坏的数字找回来吗?【说明】开课的时候,可用这道题来做引题,在学完例1后,可做为巩固练习来做.我们经常会看到一些残缺不全的算式,要求我们在方格内填上合适的数字,使算式成立.我们也经常看到在一个算式里面有很多的汉字或字母,要我们猜猜它们代表几,像这样的问题都是数字谜问题.在填数字时,要认真分析数字的特点,充分运在这一节课中,教材内容中主要是通过不同的符号,汉字或字母来组成各种不同的竖式数字谜,让学生根据竖式的结构来计算(求出)这些未知的数字.弄清楚加减法各部分之间的数量关系是我们学习数字谜的基础.解答数字谜的关键是找准突破口.通过这节课的学习,要使学生掌握解答竖式数字谜的一般技巧.先要观察数字的特点,然后找出“关键位置”认真分析,一般可以引导学生从各个不同的数位进行考虑.解答完题目以后,教师还要培养学生验算的好习惯.用加、减法之间的关系,巧妙地安排每一个数,很快就能求出方格里应填的数字.今天这节课我们就一起来解答数字谜问题.巧填方框里面的数【例1】在“庆元旦”晚会上,主持人小丽出了这样两道题目:请大家想一想,被纸片盖住的是什么数字?【分析】1、先填个位,已知6+口的个位为1,所以口=5,且个位向十位进1.再填十位,由于个位向十位进1,十位上数□+7+1的个位数为1,所以十位数□应填3,且十位向百位进1.最后填百位,由十位进1,可知百位□填1.2、我们可以从位数入手.被减数是一个三位数,减数是一个两位数,差是一个一位数,应能推出它的被减数应尽可能的小,减数应尽可能大.再从个位入手,可知,被减数的个位是2,且个位向十位借1,而差的百位、十位上均无数字,说明被减数的百位是1,而减数十位上的数字是9.当然此题也可反着想:□6+6=□0□,也可推出答案.由上面的解题过程可以看到,解这种题应按三个步骤分析思考:(1)审题审题就是找出算式中数字之间的关系和特征,挖掘题目中的隐含条件,它是确定各空格内应该填什么数字的主要依据.(2)选择解题突破口在审题的基础上,认真思考找出算式中容易填出或关键性的空格,做为解题的突破口.这一步是填空格的关键.(3)确定各空格填什么数字从突破口开始,依据竖式的已知条件,逐个填出各空格中的数字.【例2】用0、1、2、3、4、5、6、7、8、9这十个数字组成下面的加法算式,每个数字只许用一次,现已写出3个数字,请把这个算式补齐.【分析】解题关键:由算式知,和的千位数字只能是百位上数字之和向前进的数,因此把确定千位数字做为突破口(1)填千位据上分析,千位上只能填1.(2)确定百位为了能使百位向千位进l,所以第一个加数的百位可能是9或7.(因为8已用过) 试验:若百位上填9,则和的百位只可能是1或2,而1和2都已用过,因此百位上不能填9,只能填7.则和的百位为0,且十位向百位进1,这时竖式为:(3)确定剩下的4个空格现在只剩下四个数字没有用,它们是9、6、5、3.试验:若第二个加数的个位填5,和的个位为9,剩下的数字6、3不能满足十位上的要求. 若第二个加数的个位填9,和的个位为3,剩下的数字5、6正好满足十位上的要求,即第一个加数的十位填6,和的十位填5.此题的答案为【例3】在下面算式的空格内,各填入一个合适的数字,使算式成立.【分析】解题关键:这是一道四位数减去三位数差为两位数的减法,所以选择被减数的千位做为解题突破口.又由于个位上已知两个数字,因此先从个位入手填.①填个位由于个位这一列只有一个待定的数,减数的个位应为9,且个位向十位借1.②填千位四位数减去三位数差为两位数,所以被减数的千位数字是1,且百位向千位借1.③填百位由于差是两位数,所以被减数的百位数字为0,十位也向百位借1.这样百位向千位借1当10,十位又向百位借1,还剩9,9-9=0,因此减数的百位应填9.④填十位由于十位向百位借1,所以被减数的十位数字不得超过减数的十位数字,即被减数的十位数字是0或1,那么差的十位数字为8或9.此题有两个答案.【例4】把数字1~5分别填写在下面算式中的口里.【分析】这题限制了所需要填的五个数字,且个位这一列只有一个空格,因此把确定个位数字做为解题突破口.①填个位显然,差的个位上填1.②填百位由差的十位数字8知,十位上数相减时,要向被减数的百位借1,这样百位上有9-1-口=口知,减数的百位填3或5,相应的差的百位上填5或3.○3填十位现在只剩下2、4两个数,分别填在被减数和减数的十位上,正好满足题目要求.【例5】下面的算式里四个小纸片各盖住一个数字,问被盖住的四个数字的和是多少?【分析】求被盖住的四个数字的和,对于这四个数具体是几并不十分重要.而和149的个位是9,所以个位数相加没有进位,即个位上两个数的和是9.十位上两个数的和是14.因此,被盖住的四个数字的和是14+9=23.拓展练习下面方框可以填什么数?【分析】这道题两个加数都不知道,只知道两个数的和,我们要知道这两个加数是多少,就要先找到解决问题的突破口.两个两位数的和是191,两个加数十位上数字都必须是9,而个位上两个数字的和要进位才能使十位数字的和是9,这样个位上两个数字和应该是11.因为2+9=11,3+8=11,4+7=11,5+6=11,所以答案有:(答案不唯一,两个加数的顺序也可以颠倒写)【例6】在下面算式的空格内,各填入一个合适的数字,使算式成立.【分析】这是一道加减法混合运算的填空格题,我们把加法、减法分开考虑,使问题简化:1.加法①填十位从算式可以看出,第二个加数与和的十位上都是9,所以个位上数字之和一定向十位进了1,十位数字之和也向百位进了1,因此算式中十位上应是□+9+1=19,故第一个加数的十位上填9.②填个位由于个位上1+口的和向十位进1,所以口中只能填9,和的个位就为0.③填百位和千位由于两位数加三位数,和是四位数,所以百位上数相加后必向千位进1.这样第二个加数的百位应填9,和的千位填1,和的百位填0.2.减法①填个位由于被减数的个位是0,差的个位是4,因此减数的个位应填6.②填十位、百位由于被减数是四位数,减数是三位数,差是两位数,所以减数的百位必须是9,同时十位相减时必须向百位借1,这样减数与差的十位也只能填9.拓展练习下面的方框各应该填几?【分析】在这个题目中,我们要从低位开始考虑,而且一定要注意进位和退位的问题,除了方法更考察学生的口算能力.数字、符号代表几?【例7】算下面竖式中的汉字各代表多少?我=( ) 爱=( )数=( ) 学=( )【分析】先看千位数,两个相同数相加,不可能是9,那么一定是百位向千位进了1,所以千位上是4,由于百位向千位进了1,因此,爱+爱=10,则爱=5,十位没有向百位进1.再看十位数,和是5,肯定个位进上了1,所以十位上数=2,个位上的数,学+学=16,则学=8,即:4528+4528=9056.我=(4),爱=(5)数=(2),学=(8)拓展练习下面的符号和汉字各代表几?△=( 8 )迎=( 1 )奥=( 9 )我=( 2 )爱=( 6 )运=( 4 )北=( 3 )京=( 5 )【例8】求当它们各代表什么数字时,能够使算式成立?【分析】被减数是一个四位数,减数是个三位数,所得的差是一个三位数,说明百位要向千位借l,千位借走后无剩余,说明“儿”=1.因为百位上减1需要借位,所以“童”就只能取0,而十位上“节-童”肯定够减,不用向百位借位,这样从百位可得出“节”=9的结论.个位上分析可得出“乐”=8.即如上式所示.【例9】请你猜一猜,每个算式中的汉字各表示几?【分析】首先我们可以确定百位的“数”=1,看个位,“爱”+5=2,所以“爱”=7;再来观察上面的减法算式:“学”4-67=17,可见“学”=8;再来观察下面的加法算式:17+“我”5=112,可得“我”=9.答案如上.拓展练习相同的汉字代表相同的数字,这些汉字各代表几?泰=( 8 )山=( 9 )福=( 1 )永=( 7 )寿=( 0 )【例10】相同的英文字母代表相同的数字,你知道下面A、B、C代表几?【分析】这道题的突破口是要从百位上的B进行思考,一个两位数加两位数,得数是一个三位数.那么这个三位数百位可能是1或者2.假设B=2,那么十位A+2+A=22,这种情况不存在.因此可以肯定B=1,十位上A+1+A=11,如果个位向十位进一,那么2个A=9,也不可能,因此2个A=10,A=5.当A=5时,看个位1+C+C=5,C=2.答案如下:拓展练习下面竖式中的字母和符号各代表多少?A=( 4 ) B=( 5 )□=( 2 )△=( 9 ) C=( 1 )○=( 5 )【例11】已知下面两个算式中,相同的字母代表相同的数字,不同的字母代表不同的数字,那么满足下列算式的A+B+C+D+E=?【分析】从右边的算式中我们马上可以看出C=1,再看左边算式的个位,C+E=1+E=4,可推出E=3.由右边算式的十位上B+E=7,即B+3=7,推出B=4.从左边算式十位上B+D=6,即4+D=6,所以D=2,再推右边算式个位A+D=A+2=8,所以A=6.于是得到两个算式:A=6,B=4,C=1,D=2,E=3,所以,A+B+C+D+E=6+4+1+2+3=16.附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)请你算一算,下面竖式中每个字各代表几?+ 兵炮马卒兵炮车卒车卒马兵卒兵=( 5 ) 炮=( 2 ) 马=( 4 ) 车=( 1 ) 卒=( 0 )【分析】我们从个位开始观察,卒+卒=卒,只有0+0=0,所以卒=0;再看和是一个五位数,所以车=1;再看千位,兵+兵=10,所以兵=5;然后看十位,马+车=兵,也就是马+1=5,所以马=4;最后看百位炮+炮=4,所以炮=2.下面各数字表示几?【分析】从个位看“宵”+“宵”+“宵”= 4,可见“宵”=8,向十位进2.“元”+“元”+“元”= 9-2= 7,可见“元”=9,向百位进2.“度”+“度”=8-2=6,因此“度”=3,“欢”=1.在下面的加法算式中,第—个加数的各位数字之和恰好是和的各位数字之和的2倍.则第一个加数是多少?【分析】第一个加数是:169,和是170,1+6+9=16,1+7+0=8,16是8的2倍.下面的算式里,每个方框代表一个数字,问:这6个方框中数字的总和是多少?【分析】这6个方框中数字的总和是47.练习五1.在下列竖式的空格内,各填入一个合适的数字,使竖式成立.【答案】2.下面的符号各表示几?3.下面的汉字各代表几?4.下面的符号代表几?5.下边的加法算式中,□内这四个数字之和是多少?【答案】□内的数字之和是30.一只新组装好的小钟放在了两只旧钟当中.两只旧钟“滴答”、“滴答”一分一秒地走着.其中一只旧钟对小钟说:“来吧,你也该工作了.但我又有点担心,你走完三千二百万次以后,恐怕就吃不消了.”“天哪!三千二百万次.”小钟吃惊不已.“要我做这么大的事?办不到,办不到.”另一只旧钟说:“别听他胡说八道.不用害怕,你只要每秒滴答摆一下就行了.”“天下哪有这样简单的事情.”小钟将信将疑.“如果这样,我就试试吧.”小钟很轻松地每秒钟“滴答”摆一下,不知不觉中,一年过去了,它摆了三千二百万次.。
(完整版)二年级数学奥数题及解题详解

第一类:简单推理1、下列算式中,△和★各代表什么数?★+★+★+△+△=22 △+△+★+★+★+★+★=30★=()△=()解题思路:下面算式就比上面多了两个★,结果就多了8。
说明两个★就是8,一个★是4,把求出来的结果代到最简单的算式中,★+★+★+△+△=22,一个★是4,三个★是12,12加几等于22,求出两个△是10,一个△是5。
2、下列算式中△和□各代表什么数?□+□+△+△+△=21 □+□+△+△+△+△+△=27△=()□=()解题思路:下面算式就比上面多了2个△,结果就多了6。
一个△就是3,代到最简单的算式中,□+□+△+△+△=21,求□是6。
3、△+□=9 △+△+□+□+□=25△=()□=()解题思路:一个△和一个□加起来是9,代到第2个算式中,求出□=7,再代入第一个算式△=24、□+□+△=16 □+△+△=14□=()△=()解题思路:上面算式和下面算式就有一个不一样,一个是□一个是△,结果多了2。
说明一个□比△2,□=△+2代入到□+△+△=14,△+2+△+△=14。
求出△=4,□=△+2,□=6。
5、○+★+★=10 ○+★+○=8○=()★=()解题思路:一个★比一个○多2,★=○+2代入○+★+○=8,○+○+2+○=8,○=2,★=4.6、△+○=7 △+△+○=10○-△=()○×△=()解题思路:第二个算式就比第一个算式多一个△,结果就多3,所以△=3,○=4。
第二类:分一分1、甜甜将30颗珠子分成数量不等的五堆,每堆的颗数恰好是双数,你知道每堆各有多少颗吗?2+4+6+8+10=30(颗)解题思路:每堆的棵树是双数,就从最小的双数开始想。
2、雯雯小朋友将25颗珠子分成数量不等的五堆,每堆的颗数恰好都是单数,你知道每堆各有多少颗?1+3+5+7+9=25(颗)解题思路:每堆的棵树是单数,就从最小的单数开始想。
3、兔妈妈把12根萝卜分成数量各不相等的4堆,问最多的一堆中有几根胡萝卜?1+2+3+6=12(根)解题思路:要想有一堆最多,那剩下的3堆就要尽量少,4堆数量各不相同,最少就是一堆1个,一堆2个,一堆3个。
二年级奥数教程第12讲画图法解应用题

二年级奥数教程第12讲:画图法解应用题在解应用题时,特别是一些技巧性比较大的题,如果不认真思考,是很容易做错的.这时你不妨先画一画图,用图来表示题目中的条件,能方便我们理解题意,正确思考解答.例1 16 名同学排成一队,在解应用题时,特别是一些技巧性比较大的题,如果不认真思考,是很容易做错的.这时你不妨先画一画图,用图来表示题目中的条件,能方便我们理解题意,正确思考解答.例1 16名同学排成一队,从前往后数,小小排在第7个,从后往前数,他排在第几个?解我们用下图来表示:通过画图,我们可以发现:从前往后数,小小排在第7个,也就是从最前面到小小共有7个人.由于一共有16个人,所以小小后面还有16-7=9(人).从后面往前数的话,数到小小应该是第10人,即16-7+l=10(人).答:从后往前数,小小排在第10个.随堂练习1 18个小朋友排成一队去看电影,从前往后数,胖胖排在第8个.如果从队伍的最后往前数,胖胖排在第几个?例2 朗诵小组的同学排成一排表演诗朗诵,从左边数起,玲玲是第8个,从右边数起,玲玲是第7个,有多少同学参加表演?解我们还是借助图来帮助分析、理解题意.从图中能够很清楚地看到,从左往右数时,把玲玲数了一次,从右往左数时,玲玲又被数了一次.把两次数出的人数相加时,玲玲被多加了一次.因此,把两次数出的人数相加后减去1就是实际的总人数,即8+7-1=14(个).答:共有14个同学参加表演.随堂练习2 排排队,来报数,正着报数我报6,倒着报数我报9.请你算一算,一共有多少小朋友在报数?例3小明有10支铅笔,小红有4支铅笔,要使两人的铅笔同样多,小明要给小红几支铅笔?解我们用图表示:从图中我们可以清楚地看到,小明比小红多6支铅笔,把多出来的6支铅笔平均分成2份,即6÷2=3.答:小明给小红3支铅笔后,两人的铅笔同样多.随堂练习3 王老师有10本练习本,李老师有18本练习本,要使两人的练习本同样多,李老师要给王老师多少本练习本?例4一排有20个座位,其中有些座位已经有人,小明无论坐在哪一个座位上,旁边都有一个人与他相邻,那么原来至少有多少人已经就座?解通过分析,我们可以知道要使小明无论坐在哪一个座位上,旁边都有一个人与他相邻,也就是说两个人之间只允许有两个空位,且要考虑到如第一个座位为空位的话,第二个座位必须有人.依据以上条件,用★表示已经有人就座,用☆表示空位画图☆★☆☆★☆☆★☆☆★☆☆★☆☆★☆☆★通过画图,很快就可以找到答案了.答:原来至少有7个人已经就座.随堂练习4一排10个座位,其中有些座位已经有人,小明无论坐在哪一个座位上,旁边都有一个人与他相邻,那么原来至少有多少人已经就座?例5如图12—5,一条小街上顺次安装有10盏路灯,为了节约用电又不影响路面照明,要关闭除首末两灯以外的8盏灯中的4盎灯,但被关的灯不能相邻.一共有几种不同的关法?○○○○○○○○○○解我们把所有的情况通过画图12—6,全部列举出来:○●○●○●○●○○○●○●○●○○●○○●○●○○●○●○○●○○●○●○●○○○●○●○●○●○答:共有5种不同的关法.随堂练习5把4个一样的球放到两个相同的盒孑里,有多少种不同的方法?练习题1、二(1)班22个小朋友排成一队去操场做操,从最前面数到丁丁是第9个,君君排在丁丁的后面.从队伍的最后往前数,君君排在第几个?2、第一小队的同学排成一排,排在东东前面的有6个同学,排在东东后面的有4个同学,第一小队一共有几个同学?3、小朋友们排成一队参观博物馆,从排头数起牛牛是第10个,从排尾数起妞妞是第18个,排在牛牛前面的就是妞妞,一共有多少小朋友参观博物馆?4、在20米的校园小道一边种杨柳树,每隔4米种一颗,两端都种,想一想,一共要中几颗树?5、小明给小红4支铅笔后,两人的支数相同,问:小明比小红多几支铅笔?6、姐姐有4支铅笔,妹妹给姐姐3支铅笔后,两人的支数相同,妹妹原来有几支铅笔?7、一根16米长的木条,把它锯成4段,要锯几次?8、小丁从一楼走到四楼用了9分钟,照这样的速度,从一楼走到七楼要用多少分钟?9、妈妈到水果店买苹果,她带的钱若买3斤多1元,若买4斤少1元5角,问:妈妈带了多少钱去买苹果?10、体育小组有20个学生,排成两排队伍做早操,每两个学生之间相隔1米,每排队伍又多长?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解应用题(一题多解)
第一题
1.水果店里有30千克苹果、25千克香蕉,卖了13千克香蕉,还有多少千
克香蕉?
【例1】(★★) 王奶奶家喂了2只大公鸡,喂的老母鸡比大公鸡多6只,每个星期 平均一只老母鸡下4个鸡蛋,王奶奶喂的这些鸡一个星期能下多 少个蛋?
第二题 2.乐乐在学校每天上5节课,一个星期要在学校上几节课?
1、审题 2、分析 3、列式 4、计算
5、检查
6、写答语
二、注意事项
1、是否有多余条件
2、是否有隐藏条件
3、是否可以一题多解
三、方法
假设法
线段图法
2
【拓展】(★★★★★) 大明、小荣、豆豆三个小朋友去称体重,大明和小荣一起称是55 千克,大明和豆豆一起称是49千克,小荣和豆豆一起称是 56千克。 三人的体重各是多少千克?
【例6】(★★★★★)
本讲总结
ห้องสมุดไป่ตู้
三棵树上共有36只鸟,有4只鸟从第一棵树上飞到第二棵树上, 一、应用题解答步骤
有8只鸟从第二棵树上飞到第三棵树上,有10只鸟从第三棵树上 飞到第一棵树上,这时,三棵树上的鸟同样多。原来每棵树上各 有几只鸟?
【拓展】(★★★) 小红每分钟剪4朵小红花,小强每分钟比小红多剪2朵,他们两人 一小时一共剪多少朵小红花?
【例4】(★★★) 草地上有黑兔、白兔、灰兔共27只,黑兔比白兔多2只,灰兔比 白免少2只。黑兔、白兔、灰兔各有多少只?
1
【例5】(★★★★) 小强、中强、大强去称体重,大强和小强一起称是50千克,小强 和中强一起称是49千克,三个人一起称是76千克。三人的体重各 是多少千克?
第三题 3.小明有41张邮票,送给华华12张,小林又送给他17张,现在小明有多
少张邮票?
【例2】(★★★) 小华每天写8个大字,比小军每天多写2个。小华和小军一星期一 共写多少个大字?
【例3】(★★★★) 二年级原来女同学比男同学多25人,今年二年级又增加了80个男 同学和65个女同学,请问:现在是男同学多还是女同学多?多几 人?
