四川省成都市青羊区石室联中2019-2020学年九年级(上)月考数学试卷(9月份)(word版含答案)
2019-2020年九年级(上)月考数学试卷(9月份)(解析版)

2019-2020年九年级(上)月考数学试卷(9月份)(解析版)一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分1.已知关于x的一元二次方程(a﹣1)x2﹣2x+1=0有两个不相等的实数根,则a的取值范围是()A.a<2 B.a>2 C.a<2且a≠1 D.a<﹣22.要将抛物线y=x2+2x+3平移后得到抛物线y=x2,下列平移方法正确的是()A.向左平移1个单位,再向上平移2个单位B.向左平移1个单位,再向下平移2个单位C.向右平移1个单位,再向上平移2个单位D.向右平移1个单位,再向下平移2个单位3.在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为()A.(1.4,﹣1)B.(1.5,2)C.(1.6,1)D.(2.4,1)4.若ab<0,则正比例函数y=ax和反比例函数y=在同一坐标系中的大致图象可能是()A. B.C.D.5.函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c﹣3=0的根的情况是()A.有两个不相等的实数根B.有两个异号实数根C.有两个相等实数根D.无实数根6.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P 的个数是()A.1个B.2个C.3个D.4个7.如图,将∠AOB放置在5×5的正方形网格中,则sin∠AOB的值是()A.B.C.D.8.在下列四个命题中:①所有等腰直角三角形都相似;②所有等边三角形都相似;③所有正方形都相似;④所有菱形都相似.其中真命题有()A.4个B.3个C.2个D.1个9.如图,在△ABC中,已知∠C=90°,BC=3,AC=4,⊙O是内切圆,E,F,D分别为切点,则tan∠OBD=()A. B.C.D.10.定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“凤凰”方程.已知ax2+bx+c=0(a≠0)是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是()A.a=c B.a=b C.b=c D.a=b=c11.如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC 的长是()A.B.C.D.712.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:①当x>3时,y<0;②3a+b>0;③﹣1≤a≤﹣;④3≤n≤4中,正确的是()A.①②B.③④C.①④D.①③二、填空题:本大题共6小题,共24分,只要求填写最后结果,每小题填对得4分.13.半径为1的圆内接正三角形的边心距为.14.若a是方程x2﹣x﹣1=0的一个根,则﹣a3+2a+2017的值为.15.张力同学在校运动会上投掷标枪,标枪运行的高度h(m)与水平距离x(m)的关系式为h=﹣x2+x+2,则大力同学投掷标枪的成绩是m.16.如图,一块直角三角板ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是58°,则∠ACD的度数为.17.在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a).如图,若曲线与此正方形的边有交点,则a的取值范围是.18.如图是由6个棱长均为1的正方体组成的几何体,它的主视图的面积为.三、解答题:本大题共7个小题,满分60分.解答时请写出必要的演推过程.19.计算﹣2sin45°+(﹣2)﹣3+()0.20.如图所示,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s 的速度移动,如果点P、Q分别从A、B同时出发.(1)几秒钟后,△PBQ的面积等于8cm2?(2)△PBQ的面积可能等于10cm2吗?为什么?21.在阳光体育活动时间,小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.(1)如果确定小亮打第一场,再从其余三人中随机选取一人打第一场,求恰好选中大刚的概率;(2)如果确定小亮做裁判,用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是:三人同时伸“手心、手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始,这三人伸出“手心”或“手背”都是随机的,请用画树状图的方法求小莹和小芳打第一场的概率.22.如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD.(1)求证:△CDE∽△CAD;(2)若AB=2,AC=2,求AE的长.23.如图,一次函数y=﹣x+4的图象与反比例函数y=(k为常数,且k≠0)的图象交于A(1,a),B两点.(1)求反比例函数的表达式及点B的坐标;(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB 的面积.24.海丰塔是无棣灿烂文化的象征(如图①),喜爱数学实践活动的小伟查资料得知:海丰塔,史称唐塔,原名大觉寺塔,始建于唐贞观十三年(公元639年),碑记为“尉迟敬德监建”,距今已1300多年,被誉为冀鲁三胜之一.小伟决定用自己所学习的知识测量海丰塔的高度.如图②,他利用测角仪站在B处测得海丰塔最高点P的仰角为45°,又前进了18米到达A处,在A处测得P的仰角为60°.请你帮助小伟算算海丰塔的高度.(测角仪高度忽略不计,≈1.7,结果保留整数).25.我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,AB为半圆的直径,点M为圆心,A点坐标为(﹣2,0),B点坐标为(4,0),D点的坐标为(0,﹣4).(1)你能求出经过点C的“蛋圆”切线的解析式吗?试试看;(2)请你求出“蛋圆”抛物线部分的解析式,并写出自变量x的取值范围.(3)你能求出经过点D的“蛋圆”切线的解析式吗?能,请写出过程,不能,请说明理由.2016-2017学年山东省滨州市无棣县小泊头中学九年级(上)月考数学试卷(9月份)参考答案与试题解析一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分1.已知关于x的一元二次方程(a﹣1)x2﹣2x+1=0有两个不相等的实数根,则a的取值范围是()A.a<2 B.a>2 C.a<2且a≠1 D.a<﹣2【考点】根的判别式.【分析】根据一元二次方程的定义结合根的判别式即可得出关于a的一元一次不等式组,解之即可得出结论.【解答】解:∵关于x的一元二次方程(a﹣1)x2﹣2x+1=0有两个不相等的实数根,∴,解得:a<2且a≠1.故选C.2.要将抛物线y=x2+2x+3平移后得到抛物线y=x2,下列平移方法正确的是()A.向左平移1个单位,再向上平移2个单位B.向左平移1个单位,再向下平移2个单位C.向右平移1个单位,再向上平移2个单位D.向右平移1个单位,再向下平移2个单位【考点】二次函数图象与几何变换.【分析】原抛物线顶点坐标为(﹣1,2),平移后抛物线顶点坐标为(0,0),由此确定平移规律.【解答】解:y=x2+2x+3=(x+1)2+2,该抛物线的顶点坐标是(﹣1,2),抛物线y=x2的顶点坐标是(0,0),则平移的方法可以是:将抛物线y=x2+2x+3向右移1个单位,再向下平移2个单位.故选:D.3.在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为()A.(1.4,﹣1)B.(1.5,2)C.(1.6,1)D.(2.4,1)【考点】坐标与图形变化﹣旋转;坐标与图形变化﹣平移.【分析】根据平移的性质得出,△ABC的平移方向以及平移距离,即可得出P1坐标,进而利用中心对称图形的性质得出P2点的坐标.【解答】解:∵A点坐标为:(2,4),A1(﹣2,1),∴点P(2.4,2)平移后的对应点P1为:(﹣1.6,﹣1),∵点P1绕点O逆时针旋转180°,得到对应点P2,∴P2点的坐标为:(1.6,1).故选:C.4.若ab<0,则正比例函数y=ax和反比例函数y=在同一坐标系中的大致图象可能是()A. B.C.D.【考点】反比例函数的图象;正比例函数的图象.【分析】根据ab<0及正比例函数与反比例函数图象的特点,可以从a>0,b<0和a<0,b>0两方面分类讨论得出答案.【解答】解:∵ab<0,∴a、b为异号,分两种情况:(1)当a>0,b<0时,正比例函数y=ax数的图象过原点、第一、三象限,反比例函数图象在第二、四象限,无此选项;(2)当a<0,b>0时,正比例函数的图象过原点、第二、四象限,反比例函数图象在第一、三象限,选项C符合.故选C.5.函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c﹣3=0的根的情况是()A.有两个不相等的实数根B.有两个异号实数根C.有两个相等实数根D.无实数根【考点】抛物线与x轴的交点.【分析】由图可知y=ax2+bx+c﹣3可以看作是函数y=ax2+bx+c的图象向下平移3个单位而得到,再根据函数图象与x轴的交点个数进行解答.【解答】解:∵函数y=ax2+bx+c的图象顶点的纵坐标为3,∴函数y=ax2+bx+c﹣3的图象可以看作是y=ax2+bx+c的图象向下平移3个单位得到,此时顶点在x轴上,∴函数y=ax2+bx+c﹣3的图象与x轴只有1个交点,∴关于x的方程ax2+bx+c﹣3=0有两个相等实数根.故选C.6.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P 的个数是()A.1个B.2个C.3个D.4个【考点】相似三角形的判定;直角梯形.【分析】由于∠PAD=∠PBC=90°,故要使△PAD与△PBC相似,分两种情况讨论:①△APD∽△BPC,②△APD∽△BCP,这两种情况都可以根据相似三角形对应边的比相等求出AP的长,即可得到P点的个数.【解答】解:∵AB⊥BC,∴∠B=90°.∵AD∥BC,∴∠A=180°﹣∠B=90°,∴∠PAD=∠PBC=90°.AB=8,AD=3,BC=4,设AP的长为x,则BP长为8﹣x.若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:①若△APD∽△BPC,则AP:BP=AD:BC,即x:(8﹣x)=3:4,解得x=;②若△APD∽△BCP,则AP:BC=AD:BP,即x:4=3:(8﹣x),解得x=2或x=6.∴满足条件的点P的个数是3个,故选:C.7.如图,将∠AOB放置在5×5的正方形网格中,则sin∠AOB的值是()A.B.C.D.【考点】锐角三角函数的定义;勾股定理.【分析】在直角△OAC中,利用勾股定理求得OA的长,然后根据正弦的定义即可求解.【解答】解:在直角△OAC中,OC=2,AC=3,则OA===,则sin∠AOB===.故选D.8.在下列四个命题中:①所有等腰直角三角形都相似;②所有等边三角形都相似;③所有正方形都相似;④所有菱形都相似.其中真命题有()A.4个B.3个C.2个D.1个【考点】相似多边形的性质;命题与定理.【分析】相似三角形的判定方法:①两个角对应相等;②两组对应边的比相等,且夹角相等;③三组对应边的比相等.相似多边形的判定:对应角相等、对应边的比相等的两个多边形是相似多边形.【解答】解:①中,所有的等腰直角三角形的三角相等,故正确;②中,所有的等边三角形的三角相等,故正确;③中,所有正方形都四角相等,四条边成比例,故正确;④中,所有菱形的四个角不一定相等,因此不都相似,故错误.故选B.9.如图,在△ABC中,已知∠C=90°,BC=3,AC=4,⊙O是内切圆,E,F,D分别为切点,则tan∠OBD=()A. B.C.D.【考点】三角形的内切圆与内心;切线长定理.【分析】首先根据切线的性质和切线长定理证得四边形OECD是正方形,那么AC+BC﹣AB即为2R(⊙O的半径R)的值,由此可得到OD、CD的值,进而可在Rt△OBD中求出∠OBD的正切值.【解答】解:∵BC、AC、AB都是⊙O的切线,∴CD=CE、AE=AF、BF=BD,且OD⊥BC、OE⊥AC;易证得四边形OECD是矩形,由OE=OD可证得四边形OECD是正方形;设OD=OE=CD=R,则:AC+BC﹣AB=AE+R+BD+R﹣AF﹣BF=2R,即R=(AC+BC﹣AB)=1,∴BD=BC﹣CD=3﹣1=2;在Rt△OBD中,tan∠OBD==.故选C.10.定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“凤凰”方程.已知ax2+bx+c=0(a≠0)是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是()A.a=c B.a=b C.b=c D.a=b=c【考点】根的判别式.【分析】因为方程有两个相等的实数根,所以根的判别式△=b2﹣4ac=0,又a+b+c=0,即b=﹣a﹣c,代入b2﹣4ac=0得(﹣a﹣c)2﹣4ac=0,化简即可得到a 与c的关系.【解答】解:∵一元二次方程ax2+bx+c=0(a≠0)有两个相等的实数根,∴△=b2﹣4ac=0,又a+b+c=0,即b=﹣a﹣c,代入b2﹣4ac=0得(﹣a﹣c)2﹣4ac=0,即(a+c)2﹣4ac=a2+2ac+c2﹣4ac=a2﹣2ac+c2=(a﹣c)2=0,∴a=c.故选A11.如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,则AC 的长是()A.B.C.D.7【考点】勾股定理;全等三角形的性质;全等三角形的判定.【分析】过A、C点作l3的垂线构造出直角三角形,根据三角形全等和勾股定理求出BC的长,再利用勾股定理即可求出.【解答】解:作AD⊥l3于D,作CE⊥l3于E,∵∠ABC=90°,∴∠ABD+∠CBE=90°又∠DAB+∠ABD=90°∴∠BAD=∠CBE,,∴△ABD≌△BCE∴BE=AD=3在Rt△BCE中,根据勾股定理,得BC==,在Rt△ABC中,根据勾股定理,得AC=×=2;故选A.12.如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:①当x>3时,y<0;②3a+b>0;③﹣1≤a≤﹣;④3≤n≤4中,正确的是()A.①②B.③④C.①④D.①③【考点】二次函数图象与系数的关系.【分析】①由抛物线的对称轴为直线x=1,一个交点A(﹣1,0),得到另一个交点坐标,利用图象即可对于选项①作出判断;②根据抛物线开口方向判定a的符号,由对称轴方程求得b与a的关系是b=﹣2a,将其代入(3a+b),并判定其符号;③根据两根之积=﹣3,得到a=﹣,然后根据c的取值范围利用不等式的性质来求a的取值范围;④把顶点坐标代入函数解析式得到n=a+b+c=c,利用c的取值范围可以求得n 的取值范围.【解答】解:①∵抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),对称轴直线是x=1,∴该抛物线与x轴的另一个交点的坐标是(3,0),∴根据图示知,当x>3时,y<0.故①正确;②根据图示知,抛物线开口方向向下,则a<0.∵对称轴x=﹣=1,∴b=﹣2a,∴3a+b=3a﹣2a=a<0,即3a+b<0.故②错误;③∵抛物线与x轴的两个交点坐标分别是(﹣1,0),(3,0),∴﹣1×3=﹣3,∴=﹣3,则a=﹣.∵抛物线与y轴的交点在(0,2)、(0,3)之间(包含端点),∴2≤c≤3,∴﹣1≤﹣≤﹣,即﹣1≤a≤﹣.故③正确;④根据题意知,a=﹣,﹣=1,∴b=﹣2a=,∴n=a+b+c=c.∵2≤c≤3,∴≤c≤4,即≤n≤4.故④错误.综上所述,正确的说法有①③.故选D.二、填空题:本大题共6小题,共24分,只要求填写最后结果,每小题填对得4分.13.半径为1的圆内接正三角形的边心距为.【考点】正多边形和圆.【分析】作出几何图形,再由外接圆半径、边心距和边长的一半组成的三角形中,已知外接圆半径和特殊角,可求得边心距.【解答】解:如图,△ABC是⊙O的内接等边三角形,OB=1,OD⊥BC.∵等边三角形的内心和外心重合,∴OB平分∠ABC,则∠OBD=30°;∵OD⊥BC,OB=1,∴OD=.故答案为:.14.若a是方程x2﹣x﹣1=0的一个根,则﹣a3+2a+2017的值为2016.【考点】一元二次方程的解.【分析】根据方程根的定义,得出a2﹣a﹣1=0,把原式降次即可得出答案.【解答】解:∵a是方程x2﹣x﹣1=0的一个根,∴a2﹣a﹣1=0,∴a3﹣a2﹣a=0,∴﹣a3=﹣a2﹣a,∴﹣a3+2a+2017=﹣a2﹣a+2a+2017=﹣a2+a+2017=﹣a﹣1+a+2017=2016,故答案为2016.15.张力同学在校运动会上投掷标枪,标枪运行的高度h(m)与水平距离x(m)的关系式为h=﹣x2+x+2,则大力同学投掷标枪的成绩是48m.【考点】二次函数的应用.【分析】根据题意可知,大力同学投掷标枪的最远距离就是当h=0时,x的值.【解答】解:∵h=﹣x2+x+2,∴当h=0时,0=﹣x2+x+2,解得,x1=﹣2,x2=48,即大力同学投掷标枪的成绩是48m,故答案为:48.16.如图,一块直角三角板ABC的斜边AB与量角器的直径恰好重合,点D对应的刻度是58°,则∠ACD的度数为61°.【考点】圆周角定理.【分析】首先连接OD,由直角三角板ABC的斜边AB与量角器的直径恰好重合,可得点A,B,C,D共圆,又由点D对应的刻度是58°,利用圆周角定理求解即可求得∠BCD的度数,继而求得答案.【解答】解:连接OD,∵直角三角板ABC的斜边AB与量角器的直径恰好重合,∴点A,B,C,D共圆,∵点D对应的刻度是58°,∴∠BOD=58°,∴∠BCD=∠BOD=29°,∴∠ACD=90°﹣∠BCD=61°.故答案为:61°.17.在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a).如图,若曲线与此正方形的边有交点,则a的取值范围是≤a.【考点】反比例函数图象上点的坐标特征.【分析】根据题意得出C点的坐标(a﹣1,a﹣1),然后分别把A、C的坐标代入求得a的值,即可求得a的取值范围.【解答】解:∵A点的坐标为(a,a).根据题意C(a﹣1,a﹣1),当C在曲线时,则a﹣1=,解得a=+1,当A在曲线时,则a=,解得a=,∴a的取值范围是≤a.故答案为≤a.18.如图是由6个棱长均为1的正方体组成的几何体,它的主视图的面积为5.【考点】简单组合体的三视图.【分析】根据立体图形画出它的主视图,再求出面积.【解答】解:主视图如图所示,∵由6个棱长均为1的正方体组成的几何体,∴主视图的面积为5×12=5,故答案为5.三、解答题:本大题共7个小题,满分60分.解答时请写出必要的演推过程.19.计算﹣2sin45°+(﹣2)﹣3+()0.【考点】实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.【分析】原式第一项利用二次根式性质化简,第二项利用特殊角的三角函数值计算,第三项利用负整数指数幂法则计算,最后一项利用零指数幂法则计算即可得到结果.【解答】解:原式=﹣1﹣2×﹣+1=﹣.20.如图所示,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s 的速度移动,如果点P、Q分别从A、B同时出发.(1)几秒钟后,△PBQ的面积等于8cm2?(2)△PBQ的面积可能等于10cm2吗?为什么?【考点】一元二次方程的应用.【分析】(1)根据直角三角形的面积公式和路程=速度×时间进行求解即可.(2)根据(1)中的解题思路列出方程,结合根的判别式进行解答.【解答】解:(1)设x秒钟后,△PBQ的面积等于8cm2,由题意可得:2x(6﹣x)÷2=8,解得x1=2,x2=4.答:2或4秒钟后,△PBQ的面积等于8cm2.(2)设x秒钟后,△PBQ的面积等于10cm2,由题意可得:2x(6﹣x)÷2=10,整理,得x2﹣6x+10=0,因为△=36﹣40=﹣4<0,所以该方程无解,答:△PBQ的面积不可能等于10cm2.21.在阳光体育活动时间,小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.(1)如果确定小亮打第一场,再从其余三人中随机选取一人打第一场,求恰好选中大刚的概率;(2)如果确定小亮做裁判,用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是:三人同时伸“手心、手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始,这三人伸出“手心”或“手背”都是随机的,请用画树状图的方法求小莹和小芳打第一场的概率.【考点】列表法与树状图法;概率公式.【分析】(1)由小亮打第一场,再从其余三人中随机选取一人打第一场,求出恰好选中大刚的概率即可;(2)画树状图得出所有等可能的情况数,找出小莹和小芳伸“手心”或“手背”恰好相同的情况数,即可求出所求的概率.【解答】解:(1)∵确定小亮打第一场,∴再从小莹,小芳和大刚中随机选取一人打第一场,恰好选中大刚的概率为;(2)列表如下:所有等可能的情况有6种(除去三个人相同的情况),其中小莹和小芳伸“手心”或“手背”恰好相同且与大刚不同的结果有2个,则小莹与小芳打第一场的概率为=22.如图,AB是⊙O的直径,过点A作⊙O的切线并在其上取一点C,连接OC交⊙O于点D,BD的延长线交AC于E,连接AD.(1)求证:△CDE∽△CAD;(2)若AB=2,AC=2,求AE的长.【考点】切线的性质;相似三角形的判定与性质.【分析】(1)根据圆周角定理由AB是⊙O的直径得到∠ADB=90°,则∠B+∠BAD=90°,再根据切线的性质,由AC为⊙O的切线得∠BAD+∠CAD=90°,则∠B=∠CAD,由于∠B=∠ODB,∠ODB=∠CDE,所以∠B=∠CDE,则∠CAD=∠CDE,加上∠ECD=∠DCA,根据三角形相似的判定方法即可得到△CDE∽△CAD;(2)在Rt△AOC中,OA=1,AC=2,根据勾股定理可计算出OC=3,则CD=OC ﹣OD=2,然后利用△CDE∽△CAD,根据相似比可计算出CE,再由AE=AC﹣CE可得AE的值.【解答】(1)证明:∵AB是⊙O的直径,∴∠ADB=90°,∴∠B+∠BAD=90°,∵AC为⊙O的切线,∴BA⊥AC,∴∠BAC=90°,即∠BAD+∠CAD=90°,∴∠B=∠CAD,∵OB=OD,∴∠B=∠ODB,而∠ODB=∠CDE,∴∠B=∠CDE,∴∠CAD=∠CDE,而∠ECD=∠DCA,∴△CDE∽△CAD;(2)解:∵AB=2,∴OA=1,在Rt△AOC中,AC=2,∴OC==3,∴CD=OC﹣OD=3﹣1=2,∵△CDE∽△CAD,∴=,即=,∴CE=.∴AE=AC﹣CE=2﹣=.23.如图,一次函数y=﹣x+4的图象与反比例函数y=(k为常数,且k≠0)的图象交于A(1,a),B两点.(1)求反比例函数的表达式及点B的坐标;(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB 的面积.【考点】反比例函数与一次函数的交点问题;待定系数法求一次函数解析式;轴对称﹣最短路线问题.【分析】(1)由点A在一次函数图象上,结合一次函数解析式可求出点A的坐标,再由点A的坐标利用待定系数法即可求出反比例函数解析式,联立两函数解析式成方程组,解方程组即可求出点B坐标;(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,连接PB.由点B、D的对称性结合点B的坐标找出点D的坐标,设直线AD的解析式为y=mx+n,结合点A、D的坐标利用待定系数法求出直线AD的解析式,令直线AD的解析式中y=0求出点P的坐标,再通过分割图形结合三角形的面积公式即可得出结论.【解答】解:(1)把点A(1,a)代入一次函数y=﹣x+4,得:a=﹣1+4,解得:a=3,∴点A的坐标为(1,3).把点A(1,3)代入反比例函数y=,得:3=k,∴反比例函数的表达式y=,联立两个函数关系式成方程组得:,解得:,或,∴点B的坐标为(3,1).(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,连接PB,如图所示.∵点B、D关于x轴对称,点B的坐标为(3,1),∴点D的坐标为(3,﹣1).设直线AD的解析式为y=mx+n,把A,D两点代入得:,解得:,∴直线AD的解析式为y=﹣2x+5.令y=﹣2x+5中y=0,则﹣2x+5=0,解得:x=,∴点P的坐标为(,0).S△PAB=S△ABD﹣S△PBD=BD•(x B﹣x A)﹣BD•(x B﹣x P)=×[1﹣(﹣1)]×(3﹣1)﹣×[1﹣(﹣1)]×(3﹣)=.24.海丰塔是无棣灿烂文化的象征(如图①),喜爱数学实践活动的小伟查资料得知:海丰塔,史称唐塔,原名大觉寺塔,始建于唐贞观十三年(公元639年),碑记为“尉迟敬德监建”,距今已1300多年,被誉为冀鲁三胜之一.小伟决定用自己所学习的知识测量海丰塔的高度.如图②,他利用测角仪站在B处测得海丰塔最高点P的仰角为45°,又前进了18米到达A处,在A处测得P的仰角为60°.请你帮助小伟算算海丰塔的高度.(测角仪高度忽略不计,≈1.7,结果保留整数).【考点】解直角三角形的应用﹣仰角俯角问题.【分析】设海丰塔的高OP=x,在Rt△POB中表示出OB,在Rt△POA中表示出OA,再由AB=18米,可得出方程,解出即可得出答案.【解答】解:设海丰塔的高OP=x,在Rt△POB中,∠OBP=45°,则OB=OP=x,在Rt△POA中,∠OAP=60°,则OA==x,由题意得,AB=OB﹣OA=18m,即x﹣x=18,解得:x=27+9,故海丰塔的高度OP=27+9≈42米.答:海丰塔的高度约为42米.25.我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,AB为半圆的直径,点M为圆心,A点坐标为(﹣2,0),B点坐标为(4,0),D点的坐标为(0,﹣4).(1)你能求出经过点C的“蛋圆”切线的解析式吗?试试看;(2)请你求出“蛋圆”抛物线部分的解析式,并写出自变量x的取值范围.(3)你能求出经过点D的“蛋圆”切线的解析式吗?能,请写出过程,不能,请说明理由.【考点】二次函数综合题.【分析】(1)易得点A、B的坐标,用交点式设出二次函数解析式,把D坐标代入即可.自变量的取值范围是点A、B之间的数.(2)先设出切线与x轴交于点E.利用直角三角形相应的三角函数求得EM的长,进而求得点E坐标,把C、E坐标代入一次函数解析式即可求得所求的解析式.(3)设出所求函数解析式,让它与二次函数组成方程组,消除y,让跟的判别式为0,即可求得一次函数的比例系数k.【解答】解:(1)如图,设经过点C“蛋圆”的切线CE交x轴于点E,连结CM,∴CM⊥CE,又∵A点坐标为(﹣2,0),B点坐标为(4,0),AB为半圆的直径,点M为圆心,∴M点的坐标为(1,0),∴AO=2,BO=4,OM=1.又因为CO⊥x轴,所以CO2=AO•OB,解得:CO=2,又∵CM⊥CE,CO⊥x轴,∴CO2=EO•OM,解之得:EO=8,∴E点的坐标是(﹣8,0),∴切线CE的解析式为:y=x+2;(2)根据题意可得:A(﹣2,0),B(4,0);则设抛物线的解析式为y=a(x+2)(x﹣4)(a≠0),又∵点D(0,﹣4)在抛物线上,∴a=;∴y=x2﹣x﹣4自变量取值范围:﹣2≤x≤4;(3)设过点D(0,﹣4),“蛋圆”切线的解析式为:y=kx﹣4(k≠0),由题意可知方程组只有一组解.即kx﹣4=x2﹣x﹣4有两个相等实根,∴k=﹣1,∴过点D“蛋圆”切线的解析式y=﹣x﹣4;2017年3月21日。
石室中学教育集团2019—2020学年度上期10月月考

石室中学教育集团2019—2020学年度上期10月月考九年级数学A卷一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡)1.下列方程中个,属于一元二次方程式()A. B. C. D.2.下列说法中正确的是()A.对角线相等的四边形是矩形B. 对角线互相垂直的四边形是正方形C. 平行四边形的对角线平分一组对角D. 矩形的对角线相等且互相平分3. 如图,已知一组平行线a∥b∥c,被直线m、n所截,交点分别为A、B、C和D、E、F,且AB=2,BC=3,DE=,则EF=()A. 2.4B.C. D.4. 在一个不透明的布袋中装有60个白球和若干个黑球,除颜色外其他都相同,小红每次摸出一个球并放回,通过多次试验后发现,摸到黑球的频率稳定在左右,则布袋中黑球的个数可能有()A. 24B. 36C. 40D. 905. 已知如图,在△ABC中,点D、点E分别在AB、BC边上,且DE∥AC,BE=2,CE=1,三△BDE的面积为4,则△ABC的面积为()A. 5B. 6C. 8D. 96. 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点E处,且CE与AB交于F,那么为()A. 12B. 15C. 6D. 107. 某种音乐播放器原来每只售价298元,经过连续两次涨价后,现在每只售价为400元,设平均每次涨价的百分率为x,则列方程正确的是()A. B.C. D.8. 如图,菱形ABCD的周长为48cm,对侥幸AC、BD相交于0点,E 是AE的中点,连接OE,则线段OE的长为()A. 5B. 6 D. 89.已知是关于x的一元二次方程的两个实数根,且则a、b的值分别是()A.-3,1B. 3,1C. D.10. 如图,在边长为2的正方形ABCD中,以对角线AC为一边作菱形AEFC,连接AF交BC于点G,则BG的长为()A. B.C.二、填空题(本大题共4各小题,每小题4分,共16分,答案写在答题卡上)11. 若的值是.12. 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AD=5,BC=12,则四边形ABOM的周长为.13. 如图所示在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点,已知FG=2,则线段AE的长度为.14. 若a、b是一元二次方程的两个实数根,则的值为.三、解答题(本大题共6个小题,共54分解答过程写在答题卡上)15.(12分)解下列方程:(1)(2)16.(6分)已知关于x的一元二次方程有两个不相等实数根.(1)求k的取值范围;(2)等腰△ABC中,AB=AC=2,若AB,BC的长是方程的两根,求BC的长.17.(8分)在坐标系中,△ABC的三个顶点坐标分别为A(2,-4),B(3,-2),C(6,-3)(1)画出△ABC关于x轴对称的(2)以M点为位似中心,在第一象限中画出将按照2:1放大后的位似图形;(3)的面积.(直接写出答案)18.(8分)十一黄金周期间,海阳中学决定组织部分优秀老师去北京旅游,天马旅行社推出如下收费标准(1)学校规定,人均旅游费高于700元,但又想低于100元,那么该校所派人数应在什么范围内;(2)已知学校已付旅游费27000元,问该校安排了多少名老师去北京旅游19.(10分)为了解学生对传统节日的喜爱情况,某学校随机抽取了部分学生进行调查,被调查的学生必须从《我是演说家》(记为A)、《中国诗词大会》(记为B)、《朗读者》(记为C)中选择自己最喜爱的一个栏目,根据调查结果绘制成如图所示的两幅不完整的统计图.请根据图中信息解答下列问题:(1)在这项调查中,并调查了多少名学生(2)将统计图补充完整,并求出扇形统计图中“C”所在扇形圆心角的度数;(3)张老师在班上随机抽取了4名学生,其中A类1人,B类2人,C类1人,若再从这4人随机抽取2人,请用画树状图或列表法求出全是B类学生的概率20.(10分)如图,在菱形ABCD中,∠B=120°,E、F分别是是边BC、CD上点,且满足CE=CF,连接EF。
四川省成都市石室联合中学教育集团2023-2024学年九年级上学期期中数学试题
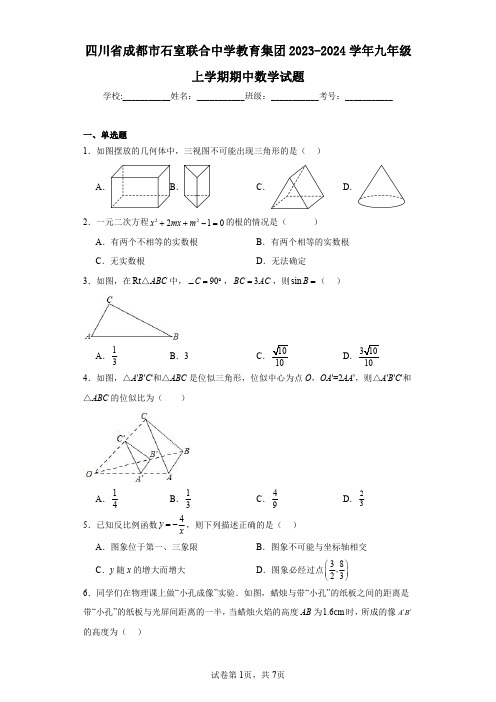
四川省成都市石室联合中学教育集团2023-2024学年九年级上学期期中数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题.B ....一元二次方程2221x m ++-的根的情况是().有两个不相等的实数根.有两个相等的实数根.无实数根.无法确定.如图,在Rt ABC △中,90C ∠=,则sin B =(13.3101031010.如图,△A 'B ′C '和△ABC 是位似三角形,位似中心为点O ,OA ,则△A 'B 'C '和的位似比为()14.134923.已知反比例函数4y =,则下列描述正确的是().图象位于第一、三象限.图象不可能与坐标轴相交y 随x 的增大而增大.图象必经过点.同学们在物理课上做小孔成像实验.如图,蜡烛与带“小孔的纸板之间的距离是小孔”的纸板与光屏间距离的一半,当蜡烛火焰的高度AB 为1.6cm 时,所成的像A B '的高度为()A .0.8cm 7.下列说法正确的是(A .相似图形一定是位似图形C .对角线互相垂直且相等的四边形是正方形矩形8.如图,菱形ABCD OH ,若10OA =,S 菱形A .55B .10二、填空题9.已知0345a b c==≠,则b 10.在双曲线y =2kx-的每一支上,11.已知点P 是线段AB 上的黄金分割点,且是.12.一个几何体的三视图如图所示,则它的体积是留π)三、计算题14.完成下列各题:(1)计算:2cos 3012⎛︒-+- ⎝(2)解方程①2630x x -+=;②四、作图题15.如图,在平面直角坐标系中,把以格点为顶点的三角形称为格点三角形(每个小方格都是边长为1的正方形).图中ABC 是格点三角形,点A 、B 、C 的坐标分别是()3,1--,()2,3--,()0,2-.(1)画出ABC 关于y 轴对称的111A B C △;(2)以O 为位似中心,在第一象限内将ABC 放大为原来的2倍,得到222A B C △,画出222A B C △;(3)ABC 内有一点(),2P a b ,直接写出经过(2)位似变换后P 的对应点1P 的坐标______.五、问答题17.如图,一次函数6y x =-+与反比例函数(ky x=AC 垂直x 轴于点C ,O 为坐标原点,5AC OC =.(1)求反比例函数的解析式和点B 的坐标;(2)点D 在y 轴上,满足ABD △的面积和ABC 的面积相等,求点D 的坐标.18.已知:在ABCD Y 中,60ABC ∠=︒,点E 、点F 分别在边AB 、AD 上且60ECF ∠=︒.图1图2图3(1)如图1,若AB AD =,求证:AE AF BC +=;(2)如图2,若2BC AB =,试探究线段BE 、DF 、BC 的数量关系,并说明理由.(3)如图3,连接EF ,若AE AF =,2BE =,3DF =,求EF 的长.六、填空题21.已知m 、n 、6分别是等腰三角形的三边长,且218800x x k -++=的两根,则23.如图,ABCDY中,则DEAE的最大值是七、应用题24.2023年大运会在成都顺利召开,大运会吉祥物蓉宝公仔爆红.据统计蓉宝公仔在某电商平台8月份的销售量是5万件,10月份的销售量是7.2万件.(1)若该平台8月份到10月份的月平均增长率都相同,求月平均增长率是多少?(2)市场调查发现,某一间店铺蓉宝公仔的进价为每件50元,若售价为每件100元,每天能销售20件,售价每降价1元,每天可多售出2件,为了推广宣传,商家决定降价促销,同时尽量减少库存,若使销售该公仔每天获利1600元,则售价应降低多少元?八、证明题25.对于平面直角坐标系中的两条直线,给出如下定义:若不平行的两条直线与x轴相交所成的锐角相等,则称这两条直线为“等腰三角线”.如图1中,若PQR PRQ∠=∠,则直线PQ与直线PR称为“等腰三角线”;反之,若直线PQ与直线PR为“等腰三角线”,则PQR PRQ∠=∠.(1)如图1,若直线PQ 与直线PR 为“等腰三角线”,且点P 求直线PR 的解析式;(2)如图2,直线14y x =与双曲线1y x =交于点A 、B ,点点A 、C 的横坐标分别为m 、n (0n m <<),直线BC 、①求证:直线AC 与直线BC 为“等腰三角线”;②过点D 作x 轴的垂线l ,在直线l 上存在一点F ,连接出线段DE EF +的值(用含n 的代数式表示).26.点O 为矩形ABCD 的对称中心,4AB =,8AD =,点连接EO 并延长,交BC 于点F .四边形ABFE 与四边形对称,线段B F '交AD 边于点G .(1)求证:GE GF =.(2)当4AE DG =时,求AE 的长.(3)如图2,连接OB '、OD ,分别交AD 、B F '于点H ,K DGK 的面积为2S ,当1AE =时,求12S S 的值.。
2019-2020学年四川省成都市青羊区石室联中西区九年级(上)开学数学试卷

2019-2020学年四川省成都市青羊区石室联中西区九年级(上)开学数学试卷一、选择题:(本大题共有10个小题,每小题3分,共30分)1. −3x<−1的解集是()A.x<13B.x<−13C.x>13D.x>−132. 关于x的方程(a−3)x2+x+2a−1=0是一元二次方程的条件是()A.a≠0B.a≠3C.a≠√3D.a≠−33. 已知mx=ny,则下列各式中不正确的是()A.mn =xyB.my=nxC.yx=mnD.xn=ym4. 下列从左到右的变形是分解因式的是()A.(x−4)(x+4)=x2−16B.x2−y2+2=(x+y)(x−y)+2C.2ab+2ac=2a(b+c)D.(x−1)(x−2)=(x−2)(x−1)5. 关于x的方程xx−3=2+kx−3无解,则k的值为( )A.±3B.3C.−3D.无法确定6. 如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要添加的条件是( )A.AB=CDB.AD=BCC.AB=BCD.AC=BD7.两个相似多边形的一组对应边长分别为3cm和4.5cm,如果它们的面积和为78cm2,则较大多边形的面积为( )A. 42cm2B. 52cm2C. 54cm2D. 64.8cm28. 已知三角形的两边长是4和6,第三边是方程x2−17x+70=0的根,则此三角形的周长是( )A.10B.17C.20D.17或209. 某地区为估计该地区黄羊的只数,先捕捉20只黄羊给它们分别作上标志,然后放回,待有标志的黄羊完全混合于黄羊群后,第二次捕捉40只黄羊,发现其中两只有标志.从而估计该地区有黄羊()A.200只B.400只C.800只D.1000只10. 将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①②两部分,将①展开后得到的平面图形是()A.矩形B.三角形C.梯形D.菱形二、填空题:(本大题共5个小题,每小题3分,共15分)11. 不等式组{2x+13>x24x≤3x+2的解集是________.12. 化简x2+xx2−2x+1÷(2x−1−1x)的结果是________.13. 若a2=b3=c4,则a+2b+3ca=________.14. 已知x1,x2是方程x2−2x−1=0的两个根,则1x1+1x2等于________.15. 已知两个相似三角形对应角平分线的比为4:5,周长和为18cm,那么这两个三角形的周长分别是________.三、解答题(本大题共6个小题,共55分)16. (1)解不等式组,{x−12>−21−1−x3≥x16.(2)解方程:(x−4)(x+8)=13 16.(3)先化简,再求值:2xx+1−2x+6x2−1÷x+3x2−2x+1,其中x=√2−1.17. 已知:如图,∠1=∠2=∠3,求证:AC⋅DE=AE⋅BC.18. 甲、乙两人玩抽扑克牌游戏,游戏规则是:从牌面数字分别为5、6、7的三张扑克牌中.随机抽取一张,放回后,再随机抽取一张,若所抽的两张牌面数字的积为奇数,则甲获胜;若所抽取的两张牌面数字的积为偶数,则乙获胜,这个游戏是否公平?19. 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,但要求每件盈利不低于25元,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件,若商场平均每天要盈利1200元,每件衬衫应降价多少元?20. 如图1,在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作平行四边形APCD,AC与PD相交于点E,已知∠ABC=∠AEP=α(0∘<α<90∘).(1)求证:∠EAP=∠EPA;(2)平行四边形APCD是否为矩形?请说明理由;(3)如图2,F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN (点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.四、填空题:(每小题4分,共12分)21. 若1x +x=3,则x2x4+x2+1=________.22. 在方程组{x+y=a2x−y=6中,已知x>0,y<0,则a的取值范围是________.23. 如图,△ABC中,AB=16,BC=10,AM平分∠BAC,∠BAM=15∘,点D、E分别为AM、AB的动点,则BD+DE的最小值是________.五、解答题:(本题8分)24. 如图,在Rt△ABC中,∠B=90∘,AC=60cm,∠A=60∘,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.(1)求证:AE=DF;(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,请说明理由;(3)当t为何值时,△DEF为直角三角形?请说明理由.。
四川省成都市青羊区成都市石室中学2023-2024学年九年级上学期期末数学试题

四川省成都市青羊区成都市石室中学2023-2024学年九年级上学期期末数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图是一个空心圆柱体,其主视图是()A .B .C .D .2.菱形和矩形都是特殊的平行四边形,那么下列是菱形和矩形都具有的性质是()A .各角都相等B .各边都相等C .有两条对称轴D .对角线相等3.已知方程2240x x -+=,则该方程的根的情况为()A .方程没有实数根B .方程有两个相等的实数根C .方程有两个不相等的实数根D .方程的根无法判定4.如图,D 、E 分别是ABC 的边AB 、AC 上的点,DE BC ∥,1DE =,2AD =,3DB =,则BC 的长为()A .﹣2<x <0或x >1C .x <﹣2或x >18.某人患了流感,经过两轮传染后共有了x 人,则可得到方程()A .()136x x ++=B .(21+二、填空题9.若关于x 的方程:23x x a ++10.如图,在长为9m ,宽为7m 剩余部分进行绿化,则绿化面积共有11.某型号汽车行驶时功率一定,行驶速度是反比例函数关系,其图象如图所示.则所受阻力F 为.12.如图,在平面直角坐标系中,OAB ()()2,1 1.5,0---,.OCD 与OAB 位似,位似中心是原点则点C 的坐标为.13.如图,将菱形纸片ABCD 沿过点折痕CP 交AD 于点P .若30ABC ∠=三、解答题14.解下列方程(1)210x x +-=(2)22530x x -+=(1)求证:△ABE≌△CDF;(2)若AB=32,BE=2,求四边形17.为了培养青少年体育兴趣、体育意识,某校初中开展了篮球、足球、乒乓球、羽毛球、排球这五项球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了一些学生(每名学生必选且只能选择这五项活动中的一种)(1)本次被调查的学生有名,补全条形统计图;(2)扇形统计图中“羽毛球”对应的扇形的圆心角度数(3)学校准备推荐甲、乙、丙、丁四名同学中的2名参加全市中学生篮球比赛,则甲和乙同学同时被选中的概率是多少?18.已知:一次函数210y x =-+的图象与反比例函数k y x=(0k >)的图象相交于B 两点(A 在B 的右侧).(1)当A (4,2)时,求反比例函数的解析式及B 点的坐标;(2)在(1)的条件下,反比例函数图象的另一支上是否存在一点P ,使△为直角边的直角三角形?若存在,求出所有符合条件的点P 的坐标;若不存在,理由.(3)当A (a ,﹣2a +10),B (b ,﹣2b +10)时,直线OA 与此反比例函数图象的另一5BC23.如图,在ABC 中,AB AC =,点连接AE .若DE AB ⊥于点F ,BC =五、解答题24.某商店欲购进A 、B 两种商品,若购进A 种商品5件,B 种商品3件,共需450元;若购进A 种商品10件,B 种商品8件,共需1000元.(1)购进A 、B 两种商品每件各需多少元?(2)该商店购进足够多的A 、B 两种商品,在销售中发现,A 种商品售价为每件80元,每天可销售100件,现在决定对A 种商品在每件80元的基础上降价销售,每件每降价1元,多售出20件,该商店对A 种商品降价销售后每天销量超过200件;B 种商品销售状况良好,每天可获利7000元,为使销售A 、B 两种商品每天总获利为10000元,A 种商品每件降价多少元?25.如图①,在ABC ∆中,AD BC ⊥于点D ,14BC =,8AD =,6BD =,点E 是AD(1)当矩形EFGH 是正方形时,直接写出EF 的长;(2)设ABE 的面积为1S ,矩形EFGH 的面积为2S ,令12S y S =,求(不要求写出自变量x 的取值范围);(3)如图②,点(,)P a b 是(2)中得到的函数图象上的任意一点,过点轴正半轴,y 轴正半轴交于M ,N 两点,求OMN 面积的最小值,并说明理由.26.如图1,点O 为矩形ABCD 的对称中心,4AB =,8AD =,点(03AE <<),连结EO 并延长,交BC 于点F ,四边形ABFE 与线成轴对称,线段B F '交AD 边于点G .GE GF =。
四川省成都实验学校北师大2019学年九年级(上)9月月考数学试卷(有答案)(已纠错)

2019-2020学年四川省成都九年级(上)月考数学试卷(9月份)一、选择题(请在答题卡上将正确答案的序号涂黑,每小题3分,共30分)1.在下列交通标志中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.2.若a>b,则下列式子正确的是()A.﹣4a>﹣4b B.a<b C.4﹣a>4﹣b D.a﹣4>b﹣4 3.如图,用不等式表示数轴上所示的解集,正确的是()A.x<﹣1或x≥3B.x≤﹣1或x>3C.﹣1≤x<3D.﹣1<x≤3 4.若凸n边形的内角和为1260°,则n的值是()A.9B.10C.11D.125.反比例函数的图象位于()A.第一、二象限B.第一、三象限C.第二、四象限D.第三、四象限6.若ax2﹣5x+3=0是一元二次方程,则不等式3a+6>0的解集是()A.a>﹣2B.a>﹣2且a≠0C.a D.a<﹣2 7.方程x2﹣kx﹣1=0根的情况是()A.方程有两个不相等的实数根B.方程有两个相等的实数根C.方程没有实数根D.方程的根的情况与k的取值有关8.下列各式从左到右的变形是分解因式的是()A.2a2﹣b2=(a+b)(a﹣b)+a2B.2a(b+c)=2ab+2acC.x3﹣2x2+x=x(x﹣1)2D.(x﹣1)(y﹣1)=xy﹣x﹣y+19.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①当x<3时,y1>0;②当x<3时,y2>0;③当x>3时,y1<y2中,正确的个数是()A.0B.1C.2D.310.甲、乙两名工人加工某种零件,已知甲每天比乙多加工5个零件,甲加工80个零件和乙加工70个零件所用的天数相同.设甲每天加工x个零件,则根据题意列出的方程是()A.B.C.D.二.填空题(每小题4分,共20分)11.函数y=的自变量x取值范围是12.x2﹣10x+21可以分解为(x+n)(x﹣7),则n=.13.已知点P(2﹣a,﹣3a)在第四象限,那么a的取值范围是.14.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF 的长为.15.在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,AE=4,AF=6,平行四边形ABCD的周长为40,则平行四边形ABCD的面积为.三、解答题:(16题每小题18分,17、18每题6分,19题10分,20题10分)16.(1)解不等式组(2)分解因式(x﹣1)(x﹣3)﹣8(3)解方程:=+17.当+|b+2|+c2=0时,求ax2+bx+c=0的解.18.先化简,后求值,其中x为0、1、2、4中的一个数.19.如图,在直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).(1)先将△ABC沿y轴正方向向上平移3个单位长度,再沿x轴负方向向左平移1个单位长度得到△A1B1C1,画出△A1B1C1,点C1坐标是;(2)将△A1B1C1绕点B1逆时针旋转90°,得到△A2B1C2,画出△A2B1C2,并求出点C2的坐标是;(3)我们发现点C、C2关于某点中心对称,对称中心的坐标是.20.如图1,四边形ABCD是菱形,过点A作BC的垂线交CB的延长线于点E,过点C作AD 的垂线交AD的延长线于点F.(1)说明△AEB≌△CFD的理由;(2)连接AC、BD,AC与DB交于点O(如图2),若BE=1.①当DC=2时,求FC的长度;②当CD是∠ACF的平分线时,求DB的长度与菱形ABCD的边长.一.填空题(每题4分,共20分)21.如果a+b=8,ab=15,则a2b+ab2的值为.22.关于x的方程的解是非正数,则m的取值范围是.23.如图,点D、E分别在△ABC的边AB,AC上,DE∥BC,点G在边BC上,AG交DE于点H,点O是线段AG的中点,若AD:DB=3:1,则AO:OH=.24.已知=k,则k=.25.如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则的值为.二.解答题(26题8分,27题10分,28题12分,共20分)26.某商店如果将进货价为8元的商品按每件10元售出,每天可销售200件,通过一段时间摸索,该店主发现这种商品每涨价0.5元,其销售量就减少10件.(1)将售价定为多少元的时候,使每天利润为700元吗?(2)当售价定为x元时,这天所获利润为y,请写出y与x的关系式.(3)根据(2)问中的关系式,求出这天所获利润y的最大值?27.如图1,在正方形ABCD中,BD是对角线,点E在BD上,△BEG是等腰直角三角形,且∠BEG=90°,点F是DG的中点,连结EF与CF.(1)求证:EF=CF;(2)求证:EF⊥CF;(3)如图2,若等腰直角三角形△BEG绕点B按顺时针旋转45°,其他条件不变,请判断△CEF 的形状,并证明你的结论.28.在矩形OABC中,OA=4,OC=2,以点O为坐标原点,OA所在的直线为x轴,建立直角坐标系.(1)将矩形OABC绕点C逆时针旋转至矩形DEFC,如图1,DE经过点B,求旋转角的大小和点D,F的坐标;(2)将图1中矩形DEFC沿直线BC向左平移,如图2,平移速度是每秒1个单位长度.①经过几秒,直线EF经过点B;②设两矩形重叠部分的面积为S,运动时间为t,写出重叠部分面积S与时间t之间的函数关系式.2019-2020学年四川省成都九年级上月考数学试卷(9月份)参考答案与试题解析一、选择题(请在答题卡上将正确答案的序号涂黑,每小题3分,共30分)1.在下列交通标志中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.【分析】根据轴对称图形与中心对称图形的概念求解.【解答】解:A、是轴对称图形,不是中心对称图形;B、不是轴对称图形,也不是中心对称图形;C、是轴对称图形,也是中心对称图形;D、是轴对称图形,不是中心对称图形.故选:C.【点评】本题主要考查轴对称图形和中心对称图形的概念,以及对轴对称图形和中心对称图形的认识,熟记概念是解题的关键.2.若a>b,则下列式子正确的是()A.﹣4a>﹣4b B.a<b C.4﹣a>4﹣b D.a﹣4>b﹣4【分析】根据不等式的性质(①不等式的两边都加上或减去同一个数或整式,不等号的方向不变,②不等式的两边都乘以或除以同一个正数,不等号的方向不变,③不等式的两边都乘以或除以同一个负数,不等号的方向改变)逐个判断即可.【解答】解:A、∵a>b,∴﹣4a<﹣4b,故本选项错误;B、∵a>b,∴a b,故本选项错误;C、∵a>b,∴﹣a<﹣b,∴4﹣a<4﹣b,故本选项错误;D、∵a>b,∴a﹣4>b﹣4,故本选项正确;故选:D.【点评】本题考查了对不等式的性质的应用,主要考查学生的辨析能力,是一道比较典型的题目,难度适中.3.如图,用不等式表示数轴上所示的解集,正确的是()A.x<﹣1或x≥3B.x≤﹣1或x>3C.﹣1≤x<3D.﹣1<x≤3【分析】不等式的解集表示﹣1与3之间的部分,其中不包含﹣1,而包含3.【解答】解:由图示可看出,从﹣1出发向右画出的折线且表示﹣1的点是空心圆,表示x>﹣1;从3出发向左画出的折线且表示3的点是实心圆,表示x≤3.所以这个不等式组为﹣1<x≤3故选:D.【点评】此题主要考查利用数轴上表示的不等式组的解集来写出不等式组.不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.4.若凸n边形的内角和为1260°,则n的值是()A.9B.10C.11D.12【分析】根据多边形内角和定理列式计算即可.【解答】解:由题意得,(n﹣2)×180°=1260°,解得,n=9,故选:A.【点评】本题考查的是多边形的内角与外角,掌握多边形内角和定理:(n﹣2)•180 (n≥3)且n为整数)是解题的关键.5.反比例函数的图象位于()A.第一、二象限B.第一、三象限C.第二、四象限D.第三、四象限【分析】因为k=2>0,根据反比例函数性质,可知图象在一、三象限.【解答】解:∵k=2>0,∴图象在一、三象限.故选:B.【点评】对于反比例函数(k≠0),(1)k>0,反比例函数图象在一、三象限;(2)k<0,反比例函数图象在第二、四象限内.6.若ax2﹣5x+3=0是一元二次方程,则不等式3a+6>0的解集是()A.a>﹣2B.a>﹣2且a≠0C.a D.a<﹣2【分析】由于ax2﹣5x+3=0是一元二次方程,故a≠0;再解不等式即可求得a的取值范围;这样即可求得不等式的解集.【解答】解:不等式移项,得3a>﹣6,系数化1,得a>﹣2;又∵ax2﹣5x+3=0是一元二次方程,∴且a≠0;所以,a>﹣2且a≠0;故选:B.【点评】一元二次方程必须满足三个条件:(1)只含有一个未知数,未知数的最高次数是2;(2)二次项系数不为0;(3)是整式方程.同时解不等式时,两边同时乘或除一个负数时,不等号的方向要改变.7.方程x2﹣kx﹣1=0根的情况是()A.方程有两个不相等的实数根B.方程有两个相等的实数根C.方程没有实数根D.方程的根的情况与k的取值有关【分析】求出方程的判别式后,根据判别式与0的大小关系来判断根的情况.【解答】解:∵方程的△=k2+4>0,故方程有两个不相等的实数根.故选:A.【点评】总结一元二次方程根的情况与判别式△的关系:(1)△>0⇔方程有两个不相等的实数根;(2)△=0⇔方程有两个相等的实数根;(3)△<0⇔方程没有实数根.8.下列各式从左到右的变形是分解因式的是()A.2a2﹣b2=(a+b)(a﹣b)+a2B.2a(b+c)=2ab+2acC.x3﹣2x2+x=x(x﹣1)2D.(x﹣1)(y﹣1)=xy﹣x﹣y+1【分析】根据把一个多项式转化成几个整式积的形式,可得答案.【解答】解:∵x3﹣2x2+x=x(x﹣1)2,∴C是因式分解,故选:C.【点评】本题考查了因式分解,因式分解的关键是把多项式转化成几个整式积的形式.9.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①当x<3时,y1>0;②当x<3时,y2>0;③当x>3时,y1<y2中,正确的个数是()A.0B.1C.2D.3【分析】根据一次函数图象的位置进行判断,从函数图象来看,就是确定直线y=kx+b是否在在x轴上(或下)方.【解答】解:根据图象可知:①当x<3时,一次函数y1=kx+b的图象在x轴上方,故y1>0;②当x<3时,一次函数y2=x+a的图象一部分在x轴上方,一部分在x轴下方,故y2>0或y2=0或y2<0;③当x>3时,一次函数y1=kx+b的图象在一次函数y2=x+a的图象的下方,故y1<y2,所以正确的有①和③.故选:C.【点评】本题主要考查了一次函数与一元一次不等式的关系,从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围.10.甲、乙两名工人加工某种零件,已知甲每天比乙多加工5个零件,甲加工80个零件和乙加工70个零件所用的天数相同.设甲每天加工x个零件,则根据题意列出的方程是()A.B.C.D.【分析】根据题意列出乙每天加工零件的个数x﹣5,由等量关系式甲加工80个零件和乙加工70个零件所用的天数相同,列出方程即可.【解答】解:据题意列出方程得,,故选:D.【点评】解决此题的关键是:找对等量关系.二.填空题(每小题4分,共20分)11.函数y=的自变量x取值范围是x≤4且x≠3【分析】根据被开方数大于等于0,分母不等于0列式计算即可得解.【解答】解:根据题意得,x﹣3≠0且4﹣x≥0,解得x≠3且x≤4.故函数y=的自变量x取值范围是x≤4且x≠3.故答案为:x≤4且x≠3.【点评】本题考查函数自变量的取值范围,涉及的知识点为:分式有意义,分母不为0;二次根式的被开方数是非负数.12.x2﹣10x+21可以分解为(x+n)(x﹣7),则n=﹣3.【分析】先多项式x2﹣10x+21分解因式可得n的值.【解答】解:x2﹣10x+21=(x﹣3)(x﹣7),∵x2﹣10x+21可以分解为(x+n)(x﹣7),∴n=﹣3,故答案为:﹣3.【点评】本题考查了因式分解与原多项式的关系,解决此类问题,由于多项式因式分解是恒等变形,根据相同项的系数相等,得到方程并求出其解.13.已知点P(2﹣a,﹣3a)在第四象限,那么a的取值范围是0<a<2.【分析】根据点所在的象限,列不等式组,求解即可.【解答】解:∵点P(2﹣a,﹣3a)在第四象限,∴,由①得a<2,由②得a>0,∴a的取值范围是0<a<2,故答案为0<a<2.【点评】本题考查了象限内点的符号特点,以及不等式组的解法,是基础知识比较简单.14.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为.【分析】利用直角三角形斜边上的中线等于斜边的一半,可求出DF的长,再利用三角形的中位线平行于第三边,并且等于第三边的一半,可求出DE的长,进而求出EF的长【解答】解:∵∠AFB=90°,D为AB的中点,∴DF=AB=2.5,∵DE为△ABC的中位线,∴DE=BC=4,∴EF=DE﹣DF=1.5,故答案为:1.5.【点评】本题考查了直角三角形斜边上的中线性质:在直角三角形中,斜边上的中线等于斜边的一半和三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.15.在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,AE=4,AF=6,平行四边形ABCD的周长为40,则平行四边形ABCD的面积为48.【分析】由平行四边形的对边相等可得一组对边的和为20,设BC为未知数,利用两种方法得到的平行四边形的面积相等,可得BC长,乘以4即为平行四边形的面积.【解答】解:∵平行四边形ABCD的周长为40,∴BC+CD=20,=BC•AE=CD•AF,设BC为x,∵S平行四边形ABCD∴4x=(20﹣x)×6,解得x=12,∴平行四边形ABCD的面积为12×4=48.故答案为48.【点评】本题主要考查了平行四边形的性质,平行四边形的对边相等,面积等于底×高.三、解答题:(16题每小题18分,17、18每题6分,19题10分,20题10分)16.(1)解不等式组(2)分解因式(x﹣1)(x﹣3)﹣8(3)解方程:=+【分析】(1)先求出其中各不等式的解集,再求出这些解集的公共部分即可;(2)先化简整理多项式,再根据十字相乘法进行因式分解即可;(3)解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.【解答】解:(1)解不等式①,可得x≥﹣2,解不等式②,可得x<3.5,∴不等式组的解集为:﹣2≤x<3.5;(2)(x﹣1)(x﹣3)﹣8=x2﹣4x+3﹣8=x2﹣4x﹣5=(x﹣5)(x+1);(3)=+方程两边同乘(x+2)(x﹣2),可得(x﹣2)2=(x+2)2+16,解得x=﹣2,检验:当x=﹣2时,(x+2)(x﹣2)=0,∴x=﹣2是原方程的增根,∴原方程无解.【点评】本题主要考查了解一元一次不等式组,因式分解以及解分式方程,解分式方程时,去分母后所得整式方程的解有可能使原方程中的分母为0,所以应检验.17.当+|b+2|+c2=0时,求ax2+bx+c=0的解.【分析】先根据算术平方根、绝对值和平方的非负性可得a、b、c的值,代入方程解出即可.【解答】解;当+|b+2|+c2=0时,则,∴,∴4x2﹣2x=0,2x2﹣x=0,x(2x﹣1)=0,x1=0,x2=【点评】本题考查了算术平方根、绝对值和平方的非负性和利用因式分解解一元二次方程,熟练掌握算术平方根、绝对值和平方的非负性是关键.18.先化简,后求值,其中x为0、1、2、4中的一个数.【分析】原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.【解答】解:原式=﹣•=﹣,当x=0时,原式=1.【点评】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.19.如图,在直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).(1)先将△ABC沿y轴正方向向上平移3个单位长度,再沿x轴负方向向左平移1个单位长度得到△A1B1C1,画出△A1B1C1,点C1坐标是(﹣2,1);(2)将△A1B1C1绕点B1逆时针旋转90°,得到△A2B1C2,画出△A2B1C2,并求出点C2的坐标是(﹣5,0);(3)我们发现点C、C2关于某点中心对称,对称中心的坐标是(﹣3,﹣1).【分析】(1)直接利用平移的性质得出对应点位置进而得出答案;(2)直接利用旋转的性质得出对应点位置进而得出答案;(3)直接利用关于点对称的性质得出对称中心即可.【解答】解:(1)如图所示:△A1B1C1,即为所求,点C1坐标是:(﹣2,1);故答案为:(﹣2,1);(2)如图所示:△A2B1C2,即为所求,点C2坐标是:(﹣5,0);故答案为:(﹣5,0);(3)点C、C2关于某点中心对称,对称中心的坐标是:(﹣3,﹣1).故答案为:(﹣3,﹣1).【点评】此题主要考查了旋转变换和平移变换,根据题意得出对应点位置是解题关键.20.如图1,四边形ABCD是菱形,过点A作BC的垂线交CB的延长线于点E,过点C作AD 的垂线交AD的延长线于点F.(1)说明△AEB≌△CFD的理由;(2)连接AC、BD,AC与DB交于点O(如图2),若BE=1.①当DC=2时,求FC的长度;②当CD是∠ACF的平分线时,求DB的长度与菱形ABCD的边长.【分析】(1)首先这两个三角形是直角三角形,可根据菱形的性质四边相等,对边平行,可得到AB=DC,AE=CF;(2)因为三角形AEB是直角三角形,可根据勾股定理求解;(3)用角平分线上的点到两边的距离相等的性质以及勾股定理可求出DB的长度与菱形ABCD 的边长.【解答】证明:(1)∵四边形ABCD是菱形,∴AB=CD,AD∥BC,又∵AE⊥CE,CF⊥AF,∴AE=CF,∴在直角三角形AEB和直角三角形CFD中,∴△AEB≌△CFD;(2)①∵△AEB≌△CFD,∴DF=BE=1,∴FC==,②当CD是∠ACF的平分线时∵∠DOC=90°,∠CFD=90°,∴DO=DF=1,∴DB=2,∵CD是∠ACF的平分线,∴∠ECA=∠DCA=∠DCF=30°,∴∠BCD=60°,∴△BCD是等边三角形,∴菱形ABCD的边长为2.【点评】本题考查菱形的性质,勾股定理以及角平分线上的点到两边的距离相等,和直角三角形全等的判定,关键是熟记这些性质定理和判定定理.一.填空题(每题4分,共20分)21.如果a+b=8,ab=15,则a2b+ab2的值为120.【分析】把所求的代数式整理为和所给代数式相关的式子,代入求值即可.【解答】解:a2b+ab2=ab(a+b)=15×8=120.【点评】本题考查因式分解的运用,有公因式时,要先考虑提取公因式;注意运用整体代入法求解.22.关于x的方程的解是非正数,则m的取值范围是m≥.【分析】先解方程求得x,然后根据x≤0,求出m的取值范围即可.【解答】解:去分母得,2(x+m)﹣3(2x﹣1)=6m,去括号得,2x+2m﹣6x+3=6m,移项合并得,﹣4x=4m﹣3,系数化为1得,x=,∵关于x的方程的解是非正数,∴≤0,∴m≥.故答案为:m≥.【点评】本题考查了解一元一次方程以及一元一次不等式,是一道综合题,难度不大.23.如图,点D、E分别在△ABC的边AB,AC上,DE∥BC,点G在边BC上,AG交DE于点H,点O是线段AG的中点,若AD:DB=3:1,则AO:OH=2:1.【分析】根据平行线分线段成比例定理求出,,推出AO=AG,OH=OG﹣HG=AG﹣AG,代入求出即可.【解答】解:∵DE∥BC,AD:DB=3:1,∴===,==,∴OH=OG﹣HG=AG﹣AG,∵点O是线段AG的中点,∴OA=OG=AG,∴AO:OH=(AG):(AG﹣AG)=2:1,故答案为:2:1.【点评】本题考查学生对平行线分线段成比例定理的灵活运用,关键是检查学生能否熟练地运用平行线分线段定理进行推理.24.已知=k,则k=2或﹣1..【分析】先根据比例的性质得出bk=a+c,ck=b+a,ak=c+b,再将这三个式子相加,整理得出(a+b+c)k=2(a+b+c).然后分a+b+c≠0与a+b+c=0两种情况,分别求出k的值即可.【解答】解:∵=k,∴bk=a+c,ck=b+a,ak=c+b,∴bk+ck+ak=a+c+b+a+c+b,∴(a+b+c)k=2(a+b+c).①如果a+b+c≠0,那么k=2;②如果a+b+c=0,那么a+c=﹣b,k==﹣1.故答案为2或﹣1.【点评】本题考查了比例的基本性质:两内项之积等于两外项之积.即若a:b=c:d,则ad=bc.分情况讨论是解题的关键.25.如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则的值为.【分析】根据旋转得出∠NCE=75°,求出∠NCO,设OC=a,则CN=2a,根据△CMN也是等腰直角三角形设CM=MN=x,由勾股定理得出x2+x2=(2a)2,求出x=a,得出CD=a,代入求出即可.【解答】解:∵将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,∴∠ECN=75°,∵∠ECD=45°,∴∠NCO=180°﹣75°﹣45°=60°,∵AO⊥OB,∴∠AOB=90°,∴∠ONC=30°,设OC=a,则CN=2a,∵等腰直角三角形DCE旋转到△CMN,∴△CMN也是等腰直角三角形,设CM=MN=x,则由勾股定理得:x2+x2=(2a)2,x=a,即CD=CM=a,∴==,故答案为:.【点评】本题考查了等腰直角三角形性质,勾股定理,含30度角的直角三角形性质,旋转性质,三角形的内角和定理等知识点,主要考查学生综合运用性质进行推理和计算的能力,题目比较好,但有一定的难度.二.解答题(26题8分,27题10分,28题12分,共20分)26.某商店如果将进货价为8元的商品按每件10元售出,每天可销售200件,通过一段时间摸索,该店主发现这种商品每涨价0.5元,其销售量就减少10件.(1)将售价定为多少元的时候,使每天利润为700元吗?(2)当售价定为x元时,这天所获利润为y,请写出y与x的关系式.(3)根据(2)问中的关系式,求出这天所获利润y的最大值?【分析】(1)如果设每件商品提高x元,用x表示出单件的利润以及每天的销售量,然后根据总利润=单价利润×销售量列出关于x的方程,进而求出未知数的值.(2)首先设应将售价提为x元时,才能使得所赚的利润最大为y元,根据题意可得:y=(x﹣8)[200﹣20(x﹣10)];(3)将(2)中关系式化简配方,即可得y=﹣20(x﹣14)2+720,即可求得答案.【解答】解:(1)设每件商品提高x元,则每件利润为(10+x﹣8)=(x+2)元,每天销售量为(200﹣20x)件,依题意,得:(x+2)(200﹣20x)=700.整理得:x2﹣8x+15=0.解得:x1=3,x2=5.∴把售价定为每件13元或15元能使每天利润达到700元;(2)设利润为y:则y=(x﹣8)[200﹣20(x﹣10)]=﹣20x2+560x﹣3200;(3)y=﹣20x2+560x﹣3200,=﹣20(x﹣14)2+720,则当售价定为14元时,获得最大利润;最大利润为720元.【点评】此题考查的是二次函数在实际生活中的应用.此题难度不大,解题的关键是理解题意,找到等量关系,求得二次函数解析式.27.如图1,在正方形ABCD中,BD是对角线,点E在BD上,△BEG是等腰直角三角形,且∠BEG=90°,点F是DG的中点,连结EF与CF.(1)求证:EF=CF;(2)求证:EF⊥CF;(3)如图2,若等腰直角三角形△BEG绕点B按顺时针旋转45°,其他条件不变,请判断△CEF 的形状,并证明你的结论.【分析】(1)根据直角三角形斜边上的中线等于斜边的一半可得EF=DF=DG,CF=DF=DG,从而得证;(2)根据等边对等角可得∠FDE=∠FED,∠FCD=∠FDC,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠EFC=2∠BDC,然后根据正方形的对角线平分一组对角求出∠BDC=45°,求出∠EFC=90°,从而得证;(3)延长EF交CD于H,先求出EG∥CD,再根据两直线平行,内错角相等求出∠EGF=∠HDF,然后利用“角边角”证明△EFG和△HFD全等,根据全等三角形对应边相等可得EG=DH,EF=FH,再求出CE=CH,然后根据等腰三角形三线合一的性质证明即可.【解答】(1)证明:∵∠BEG=90°,点F是DG的中点,∴EF=DF=DG,∵正方形ABCD中,∠BCD=90°,点F是DG的中点,∴CF=DF=DG,∴EF=CF;(2)证明:∵EF=DF,CF=DF,∴∠FDE=∠FED,∠FCD=∠FDC,∴∠EFC=∠EFG+∠CFG=∠FDE+∠FED+∠FCD+∠FDC=2∠FDE+2∠FDC=2∠BDC,在正方形ABCD中,∠BDC=45°,∴∠EFC=2×45°=90°,∴EF⊥CF;(3)解:△CEF是等腰直角三角形.理由如下:如图,延长EF交CD于H,∵∠BEG=90°,∠BCD=90°,∴∠BEG=∠BCD,∴EG∥CD,∴∠EGF=∠HDF,∵点F是DG的中点,∴DF=GF,在△EFG和△HFD中,,∴△EFG≌△HFD(ASA),∴EG=DH,EF=FH,∵BE=EG,BC=CD,∴BC﹣EB=CD﹣DH,即CE=CH,∴EF⊥CF(等腰三角形三线合一),CF=EF=EH,∴△CEF是等腰直角三角形.【点评】本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,等腰直角三角形的判定,熟记各性质是解题的关键,(3)作辅助线构造出等腰直角三角形和全等三角形是解题的关键.28.在矩形OABC中,OA=4,OC=2,以点O为坐标原点,OA所在的直线为x轴,建立直角坐标系.(1)将矩形OABC绕点C逆时针旋转至矩形DEFC,如图1,DE经过点B,求旋转角的大小和点D,F的坐标;(2)将图1中矩形DEFC沿直线BC向左平移,如图2,平移速度是每秒1个单位长度.①经过几秒,直线EF经过点B;②设两矩形重叠部分的面积为S,运动时间为t,写出重叠部分面积S与时间t之间的函数关系式.【分析】(1)根据OA=4,OC=2,BC=OA,因而就可求得BC=2CD,则可以求出∠BCD=60°,则旋转角即可求得;作DM⊥CB于点M,FN⊥CB于点N,根据三角函数即可求得:DM,CM 的长,从而求得D的坐标,在Rt△CFN中,根据三角函数即可求得CN,FN的长,即得F 的坐标;(2)①HB即为直线EF经过点B时移动的距离.在Rt△C′DH中利用三角函数即可求得DH,从而得到HE,再在△HEB中,利用三角函数求得BH,即可求得时间.②重合的部分可能是四边形,也可能是三角形,应分两种情况进行讨论.【解答】解:(1)如图1.在矩形OABC中,OA=4,OC=2,所以在RT△BCD中,BC=2CD,即所以∠BCD=60°.所以旋转角∠OCD=30°作DM⊥CB于点M,FN⊥CB于点N.在RT△CDM中,CM=CD•cos60°=1,DM=CD•sin60°=.所以点D到x轴的距离为.在RT△CFN中,,所以点F到x轴的距离为4.故D(1,),F((2)①如图2,HB即为直线EF经过点B时移动的距离.在RT△C′DH中,,所以.在RT△BEH中,HE=BHcos30°,则.所以直线EF经过点B时所需的时间秒②过点D作DM⊥BC于点M.在RT△DMC′中,C′M=.在RT△DHC′中,C′D=C′Hcos60°=2.当0<t<1时,重叠部分面积为四边形DGCH,如图2,C′C=t,CG=C′Ctan60°=t..当1≤t<4时,重叠部分的面积为△GCH,如图3,.所以重叠部分的面积S=CG•CH=×(4﹣t)(4﹣t)=t2﹣t+.【点评】本题是三角函数与图形的旋转相结合的题目,注意旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.得到相等关系是解决本题的关键.。
四川省成都市青羊实验学校2019-2020学年九年级上学期期中数学试卷 (含答案解析)

四川省成都市青羊实验学校2019-2020学年九年级上学期期中数学试卷一、选择题(本大题共10小题,共30.0分)1.2cos60°的值是()B. √3C. √2D. 1A. 122.函数y=−√x中的自变量x的取值范围是()x−1A. x≥0B. x<0且x≠1C. x<0D. x≥0且x≠13.下列方程中,关于x的一元二次方程的是()=7A. 2x+y=2B. x+y2=0C. 2x−x2=1D. x+1y4.如果(cosA−1)2+|3tanB−3|=0那么△ABC是()2A. 直角三角形B. 锐角三角形C. 钝角三角形D. 等边三角形5.设a是方程x2−x−2016=0的一个实数根,则a2−a+1的值为()A. 2014B. 2015C. 2016D. 20176.某品牌的羽绒服原价980元,连续两次降价x%后售价变成650元,下面所列方程正确的是()A. 650(1+x%)2=980B. 650(1+2x%)=980C. 650(1−2x%)=980D. 980(1−x%)2=6507.某一时刻,身高1.6m的小明在阳光下的影长是0.4m,同一时刻同一地点测得旗杆的影长是5m,则该旗杆的高度是()A. 1.25mB. 10mC. 20mD. 8m8.已知点P是线段MN的黄金分割点,MP>NP,且MP=(√5−1)cm,则NP等于()A. 2cmB. (3−√5)cmC. (√5−1)cmD. (√5+1)cm9.下列命题中是真命题的是()A. 如果a2=b2,那么a=bB. 对角线互相垂直的四边形是菱形C. 旋转前后的两个图形,对应点所连线段相等D. 线段垂直平分线上的点与这条线段两个端点的距离相等10.如图,正方形ABCD的边长为3,将等腰直角三角板的45°角的顶点放在点B处,直角顶点F在CD的延长线上,BF与AD交于点G,斜边与CD交于点E,若CE=1,则DG的长为A. 2√5B. 32C. 2√10D. 3二、填空题(本大题共9小题,共36.0分)11.已知:x2=y3=z4,则x+y−zx+y+z=______ .12.若关于x的一元二次方程ax2+3x−1=0有两个不相等的实数根,则a的取值范围是______.13.如果菱形ABCD的周长为40cm,对角线AC:BD=4:3,那么对角线AC=________cm,BD=________cm.14.如图是一名同学设计的用手电筒来测量某古城墙高度的示意图.在点P处放置一水平的平面镜,光线从点A出发,经平面镜反射后恰好落到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=2m,BP=3m,DP=12m,那么该古城墙的高度CD为________m.15.若α、β是方程x2+2x−2014=0的两个实数根,则α+β的值为________,α2+3α+β的值为________.16.如图,在平行四边形ABCD中,E为边BC上一点,AC与DE相交于点F,若CE=2EB,S△AFD=27,则S△EFC等于______.17.若在△ABC内有一点D,使得∠ADB=∠ADC,AD=a,CD=b,则当BD=________时,△ABD与△ACD相似.18.如图,在锐角△ABC中,AC=6,△ABC的面积是15,∠BAC的平分线交BC于D,M、N分别是AD和AB上的动点,则BM+MN的最小值是________.19.12.如图,在四边形纸片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°.将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平.若铺平后的图形中有一个是面积为2的平行四边形,则CD=_________.三、解答题(本大题共9小题,共84.0分)20.计算:−32+(12)−1−|√48−7|−√6cos45°.21.先化简,再求值:a2−b2a2b+ab2÷(a2+b22ab−1),其中a=3+√5,b=3−√5.22.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(−1,1),B(−3,1),C(−1,4).(1)画出△ABC 绕点C 顺时针旋转90°后得到的△A 1B 1C .(2)画出△ABC 关于原点中心对称的△A 2B 2C 2.23. 如下图,某校教学楼AB 的后面有一建筑物CD ,在距离CD 的正后方30米的观测点P 处,以22°的仰角测得建筑物的顶端C 恰好挡住教学楼的顶端A ,而在建筑物CD 上距离地面3米高的E处,测得教学楼的顶端A 的仰角为45°,求教学楼AB 的高度.(参考数据:sin22∘≈38,cos22∘≈1516,tan22∘≈25)24.如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从点A出发,以每秒1cm的速度沿AC运动;同时点Q从点C出发,以每秒2cm的速度沿CB运动,当Q到达点B时,点P 同时停止运动.(1)求运动几秒时△PCQ的面积为5cm2?(2)△PCQ的面积能否等于10cm2?若能,求出运动时间,若不能,说明理由.25.在锐角三角形ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;(2)如图2,点E为线段AB的中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转的过程中,点P的对应点是点P1,求线段EP1长度的最大值和最小值.26.在国家“一带一路”发展战略等多种因素影响下,某企业的利润逐年提高,据统计,该企业2016年利润为3亿元,2018年利润为4.32亿元,若2019年保持前两年的年平均增长率不变,该企业2019年利润能否超过5亿元?27.如图,在正方形ABCD中,E是AD边上的动点(与A、D不重合),点F在边BC的延长线上,且AE=CF,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H.(1)求证:EF//AC;(2)若BE=EG,求∠BEF大小;−1.(3)求证:tan∠ABE=GFAH28.△ABC中,D,E分别为AB,AC边上的点,DE//BC,连接BE(1)如图1已知AB=6,BC=4,若∠DBE=∠EBC,求DE的长;(2)如图2,F为BC的中点,连结DF交BE于G,连结AG并延长交BC于H,求HF的值;BH(3)如图3,连接DC,若BC=6,AB=9,且△CDE∽△CAD,直接写出AD的长:-------- 答案与解析 --------1.答案:D,解析:解:∵cos60°=12∴2cos60°=1,故选:D.根据cos60°=1,计算即可.2本题考查的是特殊角的三角函数值,熟记特殊角的三角函数值是解题的关键.2.答案:D解析:解:根据二次根式的性质和分式的意义,被开方数大于等于0,可知:x≥0;分母不等于0,可知:x−1≠0,即x≠1.所以自变量x的取值范围是x≥0且x≠1.故选:D.根据二次根式的性质和分式的意义,被开方数大于等于0,分母不等于0,就可以求解.本题考查的是函数自变量取值范围的求法.函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.3.答案:C解析:解:A、不是一元二次方程,故此选项错误;B、不是一元二次方程,故此选项错误;C、是一元二次方程,故此选项正确;D、不是一元二次方程,故此选项错误;故选:C.根据一元二次方程必须同时满足三个条件:①整式方程,即等号两边都是整式;方程中如果有分母,那么分母中无未知数;②只含有一个未知数;③未知数的最高次数是2进行分析即可.此题主要考查了一元二次方程的定义,关键是掌握判断一个方程是否是一元二次方程应注意抓住5个方面:“化简后”;“一个未知数”;“未知数的最高次数是2”;“二次项的系数不等于0”;“整式方程”.4.答案:B解析:本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键.根据非负数的和为零,可得每个非负数同时为零,根据特殊角三角函数值,可得∠A、∠B的度数,由三角形内角和定理可知∠C,从而可判定△ABC的形状.)2+|3tanB−3|=0,得解:由,(cosA−12cosA=1,3tanB=3,即tanB=1.2解得∠A=60°,∠B=45°,因此,∠C=180°−60°−45°=75°,则△ABC一定是锐角三角形,故选B.5.答案:D解析:本题考查的是一元二次方程的根即方程的解的定义.一元二次方程的根就是一元二次方程的解,就是能够使方程左右两边相等的未知数的值.即用这个数代替未知数所得式子仍然成立.根据一元二次方程的解的定义,将a代入已知方程,本题即可得解.解:根据题意,得a2−a−2016=0,解得,a2−a=2016,所以a2−a+1=2016+1=2017.故选:D.6.答案:D解析:本题主要考查增长率问题.可用降价后的价格=降价前的价格×(1−降价率),首先用x表示两次降价后的售价,然后由题意可列出方程.解:依题意得两次降价后的售价为980(1−x%)2,∴980(1−x%)2=650.故选D.7.答案:C解析:本题考查了相似三角形的应用,相似三角形对应边的比相等.设该旗杆的高度为xm,根据三角形相似对应边成比例,得到同一时刻同一地点物体的高度与其影长的比相等,即有1.6:0.4=x:5,然后解方程即可.解:设该旗杆的高度为xm,根据题意得,1.6:0.4=x:5,解得x=20,即该旗杆的高度是20m.故选C.8.答案:B解析:根据黄金比值求出MN的长,结合图形计算即可.本题考查的是黄金分割的概念,把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们叫做黄金比.的比值√5−12解:∵点P是线段MN的黄金分割点,MP>NP,MN,∴MP=√5−12∴MN=2cm,∴NP=MN−MP=(3−√5)cm,故选B.9.答案:D解析:本题主要考查了命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉性质定理.分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.解:A.如果a2=b2,那么a=±b,故本选项错误;B.对角线互相垂直的平行四边形是菱形,故本选项错误;C.平移前后的两个图形,对应点所连线段相等,故本选项错误;D.线段垂直平分线上的点到这条线段的两个端点的距离相等,故本选项正确.故选D.10.答案:B解析:本题考查正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,属于中考常考题型.解:如图将△BCE绕点B逆时针旋转90°得到△BAM.BF与AD交于点G.∵四边形ABCD 是正方形,∴AB =BC =CD =AD =3,∠ABC =90°,∵∠GBE =45°,∴∠CBE +∠GBA =∠ABM +∠GBA =45°=∠GBM ,∵BG =BG ,∠GBM =∠GBE ,BE =BM ,∴△BGM≌△BGE ,∴EG =GM =AM +AG =AG +CE ,设AG =x ,则DG =3−x ,GE =1+x ,在Rt △DGE 中,∵GE 2=DG 2+DE 2,∴(3−x)2+22=(x +1)2,∴x =32, 故选B . 11.答案:19解析:解:设x 2=y 3=z 4=k ,则x =2k ,y =3k ,z =4k ,所以,x+y−z x+y+z =2k+3k−4k 2k+3k+4k =19.故答案为:19.设比值为k ,然后用k 表示出x 、y 、z ,再代入比例式进行计算即可得解.本题考查了比例的性质,利用“设k 法”,用k 表示出x 、y 、z 可以使运算更加简便. 12.答案:a >−94且a ≠0解析:解:∵关于x 的一元二次方程ax 2+3x −1=0有两个不相等的实数根,∴a ≠0且Δ=b 2−4ac =32−4×a ×(−1)=9+4a >0,解得:a >−94且a ≠0.故答案为:a >−94且a ≠0.根据一元二次方程的定义及判别式的意义可得a ≠0且Δ=b 2−4ac =32−4×a ×(−1)=9+4a >0,解不等式组即可求出a 的取值范围.此题考查了根的判别式.一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2−4ac有如下关系:(1)Δ>0⇔方程有两个不相等的实数根;(2)Δ=0⇔方程有两个相等的实数根;(3)Δ<0⇔方程没有实数根.同时考查了一元二次方程的定义.13.答案:16,12解析:本题考查了菱形对角线互相垂直平分的性质,注意菱形各边长相等的性质,勾股定理在直角三角形中的运用,本题中根据勾股定理求AO的值是解题的关键.根据菱形的性质求出AD,AO=OC,BO= DO,AC⊥BD,设AO=4xcm,DO=3xcm,根据勾股定理得出方程,求出方程的解,即可求出答案.【解答】解:如图,∵四边形ABCD是菱形,周长为40cm,∴AB=BC=CD=AD=10cm,AC=2AO=2OC,BO=DO,AC⊥BD,∴∠AOD=90°,∵AC:BD=4:3,∴AO:DO=4:3,设AO=4xcm,DO=3xcm,在△AOD中,由勾股定理得:AO 2+DO 2=AD 2,(3x) 2+(4x) 2=10 2,解得:x=2,∴AO=8cm,DO=6cm∴AC=2AO=16cm,BD=2DO=12cm故答案为16,12.14.答案:8解析:此题主要考查了相似三角形的应用,关键是掌握相似三角形对应边成比例.首先证明△ABP∽△CDP,可得ABBP =CDPD,再代入相应数据可得答案.解:由题意可得:∠APE=∠CPE,∴∠APB=∠CPD,∵AB⊥BD,CD⊥BD,∴∠ABP=∠CDP=90°,∴△ABP∽△CDP,∴ABBP =CDPD,∵AB=2米,BP=3米,PD=12米,∴23=CD12,CD=8米,故答案为8.15.答案:−2;2012解析:本题主要考查了一元二次方程的根与系数的关系,解答此题可根据两根之和等于一次项系数的相反数可得α+β的值,然后再根据α是方程x2+2x−2014=0的根将其代入方程可得α2+2α=2014,再将α2+3α+β变为(α2+2α)+(α+β),最后整体代入计算即可.解:∵α,β是方程x2+2x−2014=0的两个实数根,∴α+β=−2,α2+2α−2014=0,即α2+2α=2014,∴α2+3α+β=(α2+2α)+(α+β),=2014−2,=2012,故答案为−2;2012.16.答案:12解析:根据题意可知△EFC∽△DFA,根据相似比CE:AD即可求出面积比,从而得到△EFC的面积.本题考查的是相似三角形的判定与性质,利用相似三角形面积比是相似比的平方进行解题是关键.解:在平行四边形ABCD中,CE//AD,∴△EFC∽△DFA,,又∵CE=2EB,∴CECB =23,而CB=DA,∴CEDA =23,∴S△EFC27=49,∴S△EFC=12,故答案为12.17.答案:b或a2b解析:本题主要考查了相似三角形,关键是熟练掌握相似三角形的判定方法.根据相似可得比例,从而分情况求解即可.解:若满足相似则有①△ABD∽CAD,则有ADCD =BDAD,∵AD=a,CD=b,∴BD=a2b,②△BAD∽△CAD,∴BDCD =ADAD,∴BD=b.故答案为b或a2.b18.答案:5解析:【分析】本题考查了轴对称确定最短路线问题,垂线段最短的性质,等腰三角形两腰上的高相等的性质,熟练掌握各性质并准确确定出点M的位置是解题的关键.根据AD是∠BAC的平分线确定出点B关于AD的对称点B′在AC上,根据垂线段最短,过点B′作B′N⊥AB于N交AD于M,根据轴对称确定最短路线问题,点M即为使BM+MN最小的点,B′N=BM+MN,过点B作BE⊥AC于E,利用三角形的面积求出BE,再根据等腰三角形两腰上的高相等可得B′N=BE,从而得解.解:如图,∵AD是∠BAC的平分线,∴点B关于AD的对称点B′在AC上,过点B′作B′N⊥AB于N交AD于M,由轴对称确定最短路线问题,点M即为使BM+MN最小的点,B′N=BM+MN,过点B作BE⊥AC于E,∵AC=6,S△ABC=15,×6⋅BE=15,∴12解得BE=5,∵AD是∠BAC的平分线,B′与B关于AD对称,∴AB=AB′,∴△ABB′是等腰三角形,∴B′N=BE=5,即BM+MN的最小值是5.故答案为:5.19.答案:4+2√3或2+√3解析:根据裁开折叠之后平行四边形的面积可得CD的长度为2√3+4或2+√3.【详解】如图①,当四边形ABCE为平行四边形时,作AE//BC,延长AE交CD于点N,过点B作BT⊥EC于点T.∵AB=BC,∴四边形ABCE是菱形.∵∠BAD=∠BCD=90°,∠ABC=150°,∴∠ADC=30°,∠BAN=∠BCE=30°,∴∠NAD=60°,∴∠AND=90°.设BT=x,则CN=x,BC=EC=2x.∵四边形ABCE面积为2,∴EC·BT=2,即2x×x=2,解得x=1,∴AE=EC=2,EN=√22−12=√3,∴AN=AE+EN=2+√3,∴CD=AD=2AN=4+2√3.如图②,当四边形BEDF是平行四边形,∵BE=BF,∴平行四边形BEDF是菱形.∵∠A=∠C=90°,∠ABC=150°,∴∠ADB=∠BDC=15°.∵BE=DE,∴∠EBD=∠ADB=15°,∴∠AEB=30°.设AB= y,则DE=BE=2y,AE=√3y.∵四边形BEDF的面积为2,∴AB·DE=2,即2y2=2,解得y=1,∴AE=√3,DE=2,∴AD=AE+DE=2+√3.综上所述,CD的值为4+2√3或2+√3.考核知识点:平行四边形的性质,菱形判定和性质.20.答案:解:原式=−9+2−(7−4√3)−√6×√22=−14+4√3−√3=−14+3√3.解析:直接利用负指数幂的性质以及绝对值的性质、特殊角的三角函数值分别化简求出答案.此题主要考查了负指数幂的性质以及绝对值的性质、特殊角的三角函数值,正确化简各数是解题关键.21.答案:解:原式=(a+b)(a−b)ab(a+b)÷(a2+b22ab−2ab2ab)=a−bab⋅2ab(a−b)2=2a−b,把a=3+√5,b=3−√5代入,原式=3+√5−3+√5=2 2√5=√55.解析:原式先根据分式混合运算顺序和运算法则化简,再将a、b的值代入计算可得.本题主要考查分式的化简求值,解题的关键是掌握分式混合运算顺序和运算法则.22.答案:解:(1)△A1B1C如图所示;(2)△A2B2C2如图所示..解析:本题考查了旋转作图与中心对称,熟练掌握旋转作图的方法和中心对称的性质是解决此题的关键.(1)分别得出△ABC绕点C顺时针旋转90°后的对应点,进而得到△A1B1C;(2)分别得出点A,B,C关于点O中心对称的对应点,进而得到△A2B2C2即可.23.答案:解:如图作EF⊥AB于F,则四边形EFBD是矩形.∵∠AEF=45°,∠AFE=90°,∴∠AEF=∠EAF=45°,∴EF=AF,设EF=AF=x,则BD=EF=x,在Rt△PAB中,∵AB=x+3,PB=30+x,∴tan22°=APPB,∴25=x+330+x,∴x=15,∴AB=x+3=18m,答:教学楼AB的高度为18m.解析:本题考查解直角三角形−仰角俯角问题、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会构建方程解决问题..如图作EF⊥AB于F,则四边形EFBD是矩形.设EF=AF=x,在Rt△PAB中,AB=x+3,PB=30+x,根据tan22°=APPB ,可得25=x+330+x,解方程即可解决问题.24.答案:解:设运动t秒后△PCQ的面积等于5cm,根据题意得:CP=6−t,QC=2t,0≤t≤82=4,则△PCQ的面积是:1 2CQ⋅CP=12×(6−t)×2t=5,解得t1=1,t2=5(舍去),故经过1秒后,△PCQ的面积等于5cm2;(2)12×(6−t)×2t=−t2+6t=−(t−3)2+9,故△PCQ的面积最大为9,不能等于10cm2.解析:本题考查了一元二次方程的应用,解题的关键是根据题意找到等量关系并列出方程,用到的知识点是三角形的面积公式.(1)设运动t秒后△PCQ的面积等于5cm,分别表示出线段CP和线段CQ的长,再利用三角形的面积公式列出方程求解即可;(2)根据配方法可求△PCQ的面积能否等于10cm2.25.答案:解:(1)由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,∴∠CC1B=∠C1CB=45°,∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°;(2)如图1,过点B作BD⊥AC,D为垂足,∵△ABC为锐角三角形,∴点D在线段AC上,,当P在AC上运动,BP与在Rt△BCD中,BD=BC×sin45°=5√22AC垂直的时候,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值为:EP1=BP1−BE=BD−BE=5√2−2;2当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,如图2,EP1最大,最大值为:EP1=BC+BE=2+5=7.解析:(1)根据旋转的性质得∠A1C1B=∠ACB=45°,BC=BC1,利用等腰三角形的性质得∠CC1B=∠C1CB=45°,于是得到∠CC1A1=∠CC1B+∠A1C1B=90°;(2)如图1,过点B作BD⊥AC,D为垂足,则点D在线段AC上,在Rt△BCD中利用三角函数可计,则当BP与AC垂直的时候,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,算出BD=5√22EP1最小,最小值=EP1=BP1−BE=5√2−2;当P在AC上运动至点C,△ABC绕点B旋转,使点2P的对应点P1在线段AB的延长线上时,如图2,EP1最大,最大值=EP1=BC+BE=7.本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.26.答案:解:设该企业2017、2018年的年平均增长率为x,依题意,得:3(1+x)2=4.32,解得:x1=0.2=20%,x2=−2.2(舍去),∴4.32×(1+20%)=5.184(亿元).答:该企业2019年利润能超过5亿元.解析:设该企业2017、2018年的年平均增长率为x,根据该企业2016年及2018年的利润,即可得出关于x的一元二次方程,解之取其正值,再将其代入2019年的利润=2018年的利润×(1+增长率)中即可求出结论.本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.27.答案:解:(1)∵四边形ABCD是正方形,∴AE//CF,又∵AE=CF,∴四边形AEFC是平行四边形,故EF//AC.(2)连接BG,∵四边形ABCD是正方形,且EF//AC,∴∠DEG=∠DAC=45°,∠DGE=∠DCA=45°;故∠CFG=∠DEG=45°,∠CGF=∠DGE=45°,∴∠CGF=∠CFG,CG=CF;∵AE=CF,∴AE=CG;在△ABE与△CBG中,∵{AB=BC∠EAB=∠GCB AE=CG,∴△ABE≌CBG(SAS),∴BE=BG;又∵BE=EG,∴BE=BG=EG,△BEG是等边三角形,故∠BEF=60°.(3)∵△BAE≌△BCG,∴∠ABE=∠CBG,∵∠BAC=∠F=45°,∴△AHB∽△FGB,∴AHGF =ABBF=1BFAB=1BC+CFAB=1AB+AEAB=11+AEAB=11+tan∠ABE,∴1+tan∠ABE=GFAH ,即tan∠ABE=GFAH−1.解析:(1)根据有一组对边平行且相等的四边形是平行四边形即可判定.(2)先确定△GCF是等腰直角三角形,得出CG=AE,然后通过△BAE≌△BCG,得出BE=BG=EG,即可求得.(3)由△BAE≌△BCG知∠ABE=∠CBG,结合∠BAC=∠F=45°证△AHB∽△FGB得AH GF=AB BF=1BFAB=1 BC+CF AB =1AB+AEAB=11+AEAB=11+tan∠ABE,即可求得.本题考查了平行四边形的判定及性质,全等三角形的判定及性质,正方形的性质,相似三角形的判定及性质,连接BG是本题的关键.28.答案:解:(1)如图1,∵DE//BC,∴∠DEB=∠EBC,∵∠DBE=∠EBC,∴∠DBE=∠DEB,∴DE=DB,设DE=x,则BD=x,AD=AB−BD=6−x,∵DE//BC,∴△ADE∽△ABC,∴DEBC =ADAB,即x4=6−xx,解得x=125,即DE的长为125;(2)设AH交DE于M,如图2,∵DM//BH,∴△ADM∽△ABH,∴DMBH =ADAB①,∵DM//HF,∴△GHF∽△GDM,∴HFDM =FGDG②,①×②得HFBH =ADAB⋅FGDG,∵DE//BC,∴ADAB=DEBC=DE2BF=12⋅DGGF∴HFBH =12⋅DGGF⋅GFDG=12;(3)如图3,∵△CDE∽△CAD,∴∠CDE=∠A,∵DE//BC,∴∠CDE=∠DCB,∴∠DCB=∠A,∴∠B=∠B,∴△ABC∽△CBD,∴BDBC =BCAB,∴BD6=69,∴BD=4,∴AD=AB=BD=5.解析:(1)如图1,根据平行线的性质得到∠DEB=∠EBC,等量代换得到∠DBE=∠DEB,求得DE= DB,设DE=x,则BD=x,AD=AB−BD=6−x,根据相似三角形的性质得到结论;(2)设AH交DE于M,如图2,根据相似三角形的判定和性质定理即可得到结论;(3)根据相似三角形的判定和性质定理即可得到结论.本题考查了相似形的综合题,相似三角形的判定和性质,平行线的性质,正确的识别图形是解题的关键.。
2019-2020学年成都市青羊区树德中学外国语校区九年级(上)9月月考数学试卷(含解析)

2019-2020学年成都市树德中学外国语校区九年级(上)9月月考数学试卷(考试时间:110分钟满分:120分)一.选择题(每小题3分,共36分)四个答案中有且只有一个答案是正确的.1.下列计算正确的是()A.B.C.D.2.方程x(x﹣2)=x的根是()A.x=0 B.x=2 C.x1=0,x2=2 D.x1=0,x2=33.对于二次根式,以下说法不正确的是()A.它是一个正数B.是一个无理数C.是最简二次根式D.它的最小值是34.若a﹣b+c=0,则方程ax2+bx+c=0(a≠0)必有一个根是()A.0 B.1 C.﹣1 D.5.下列式子化为最简二次根式后和是同类二次根式的为()A.B.C.D.6.关于x的一元二次方程(m﹣1)x2+x+m2﹣1=0有一根为0,则m的值为()A.1 B.﹣1 C.1或﹣1 D.7.对于任意实数x,多项式x2﹣6x+10的值是一个()A.负数B.非正数C.正数D.无法确定正负的数8.使分式的值等于零的x是()A.6 B.﹣1或6 C.﹣1 D.﹣69.用配方法解方程x2﹣2x﹣5=0时,原方程应变形为()A.(x+1)2=6 B.(x﹣1)2=6 C.(x+2)2=9 D.(x﹣2)2=910.已知一次函数y=ax+b随x的增大而减小,且与y轴的正半轴相交,则关于x的方程ax2﹣2x+b=0的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.无法确定11.如图所示,某小区规划在一个长为40m、宽为26m的矩形场地ABCD上修建三条同样宽的道路,使其中两条与AB平行,另一条与AD平行,其余部分种草.若使每一块草坪的面积为144m2,求道路的宽度.若设道路的宽度为x m,则x满足的方程为()A.(40﹣x)(26﹣x)=144×6B.40×26﹣40x﹣26x=144×6C.40×26﹣40x﹣2×26x+2x2=144×6D.(40﹣2x)(26﹣2x)=144×612.方程x2﹣9x+18=0的两个根是等腰三角形的底和腰,则这个三角形的周长为()A.12 B.12或15 C.15 D.不能确定二、填空题(每小题3分,共18分)请将最后答案直接填在题中横线上.)13.在二次根式中,x的取值范围是.14.若,则x2012+y2013的值为.15.方程x2﹣2ax+3=0有一个根是1,则另一根为,a的值是.16.若关于x的一元二次方程(m﹣1)x2+5x+m2﹣3m+2=0的常数项为0,则m的值等于.17.将4个数a、b、c、d排成2行、2列,两边各加一条竖直线记成,这个记号叫做2阶行列式.定义,若,则x=.18.已知△ABC的三边a、b、c满足a2+b+=10a+2﹣22,则△ABC的形状是.三、解答题(共66分)19.(18分)计算求值①(3+﹣)÷②③先化简,再求值:,其中x=.20.(12分)解方程①x2+2x﹣3=0(用配方法)②2x2+5x﹣1=0(用公式法)21.(6分)阅读下面例题:请参照例题解方程x2﹣|x﹣1|﹣1=0.例:解方程x2﹣|x|﹣2=0.解:①当x≥0,原方程化为x2﹣x﹣2=0;解得:x1=2,x2=﹣1(不合题意,舍去)②当x<0时,原方程化为x2+x﹣2=0;解得:x1=1(不合题意,舍去),x2=﹣2;∴原方程的根是x1=2,x2=﹣2.22.(6分)已知关于x的一元二次方程(a+1)x2﹣x+a2﹣3a﹣3=0有一根是1.(1)求a的值;(2)求方程的另一根.23.(7分)某商场今年一月份销售额100万元,二月份销售额下降了10%,该商场采取措施,经营管理,使月销售额大幅上升,四月份的销售额达到129.6万元,求三、四月份平均每月销售额增长的百分率.24.(6分)已知x1,x2是一元二次方程4kx2﹣4kx+k+1=0的两个实数根.(1)是否存在实数k,使(2x1﹣x2)(x1﹣2x2)=成立?若存在,求出k的值;若不存在,请说明理由.(2)求使的值为整数的实数k的整数值.25.(11分)西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克,为了促销,该经营户决定降价销售,经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克,另外,每天的房租等固定成本共24元.(1)设销售单价为每千克a元,每天平均获利为y元,请解答下列问题:①每天平均销售量可以表示为;②每天平均销售额可以表示为;③每天平均获利可以表示为y=;(2)该经营户要想每天盈利200元,应将每千克小型西瓜的售价降多少元?参考答案与试题解析一.选择题(每小题3分,共36分)四个答案中有且只有一个答案是正确的.1.【解答】解:A、==×=3,故选项A错误;B、不符合二次根式的运算规则,故选项B错误;C、=×=2×3=6,故选项C错误;D、=×=2×3=6,故选项D正确;故选:D.2.【解答】解:x(x﹣2)=x,x(x﹣2)﹣x=0,x(x﹣3)=0,x﹣3=0或x=0,解得:x1=3,x2=0;故选:D.3.【解答】解:∵x2+9总是正数,∴当x=0时,二次根式==3,是个有理数,∴B错.故选:B.4.【解答】解:由a﹣b+c=0则令x=﹣1,方程ax2+bx+c=0代入方程得:a﹣b+c=0.所以x=﹣1是方程的解.故选:C.5.【解答】解:A、=3,故本选项错误;B、=3,故本选项正确;C、=2,故本选项错误;D、=,故本选项错误.故选:B.6.【解答】解:根据题意得:m2﹣1=0且m﹣1≠0解得m=﹣1故选:B.7.【解答】解:∵x2﹣6x+10=x2﹣6x+9+1=(x﹣3)2+1而(x﹣3)2≥0,∴(x﹣3)2+1>0,故选C.8.【解答】解:∵=0∴x2﹣5x﹣6=0即(x﹣6)(x+1)=0∴x=6或﹣1又x+1≠0∴x=6故选:A.9.【解答】解:方程移项得:x2﹣2x=5,配方得:x2﹣2x+1=6,即(x﹣1)2=6.故选:B.10.【解答】解:∵一次函数y=ax+b随x的增大而减小,∴a<0,∵一次函数与y轴的正半轴相交,∴b>0,∴ab<0,在方程ax2﹣2x+b=0中,△=(﹣2)2﹣4ab=4﹣4ab>0.∴方程有两个不相等的实数根.故选:A.11.【解答】解:设道路的宽度为x m,由题意得:40×26﹣2×26x﹣40x+2x2=144×6.故选:C.12.【解答】解:解方程x2﹣9x+18=0,得x1=6,x2=3∵当底为6,腰为3时,由于3+3=6,不符合三角形三边关系∴等腰三角形的腰为6,底为3∴周长为6+6+3=15故选:C.二、填空题(每小题3分,共18分)请将最后答案直接填在题中横线上.)13.【解答】解:根据题意,得,解得x≥﹣1,且x≠3.14.【解答】解:∵,∴x=1,x+y=0,解得,x=1,y=﹣1,∴x2012+y2013=12012+(﹣1)2013=0.故答案为:0.15.【解答】解:设方程的另一根为x2,根据题意得1•x2=3,则x2=3;∵1+x2=2a,∴1+3=2a,∴a=2;故答案为3,2.16.【解答】解:∵方程(m﹣1)x2+5x+m2﹣3m+2=0是一元二次方程且常数项为0,∴,解得:m=2.故答案为:217.【解答】解:由题意,得:(x+1)(x+1)﹣(x﹣1)(1﹣x)=6,∴x2+2x+1+x2﹣2x+1=6,∴2x2+2=6,∴x=±.18.【解答】解:∵a2+b+|﹣2|=10a+2,∴a2﹣10a+25+b﹣4﹣2+1+|﹣2|=0,即(a﹣5)2+(﹣1)2+|﹣2|=0,根据几个非负数的和为0,则这几个非负数同时为0,得a=5,b=5,c=5.故该三角形是等边三角形.故答案为:等边三角形.三、解答题(共72分)19.【解答】解:(1)原式=(12+2﹣6)÷=8÷=8;(2)原式=3﹣﹣(1+)+1+﹣1=﹣1;(3)原式=﹣===,当x=﹣3时,原式==.20.【解答】解:①方程变形得:x2+2x=3,配方得:x2+2x+1=4,即(x+1)2=4,可得x+1=±2,则x1=1,x2=﹣3;②这里a=2,b=5,c=﹣1,∵△=25+8=33,∴x=,则x1=,x2=.21.【解答】解方程x2﹣|x﹣1|﹣1=0,解:①当x﹣1≥0即x≥1时,原方程化为x2﹣(x﹣1)﹣1=0解得:x1=1,x2=0(不合题意,舍去)②当x﹣1<0即x<1时,原方程化为x2+(x﹣1)﹣1=0解得:x1=1(不合题意,舍去),x2=﹣2故原方程的根是x1=1,x2=﹣2.22.【解答】解:(1)将x=1代入方程(a+1)x2﹣x+a2﹣3a﹣3=0可得(a+1)﹣1+a2﹣3a﹣3=0,解可得:a=﹣1,a=3;a=﹣1时,原方程是一元一次方程,故舍去;则a=3;(2)由(1)得:a=3,则原方程为4x2﹣x﹣3=0,且其中有一根为1,设另一根是m,则m•1=m=﹣,故m=﹣.23.【解答】解:设三、四月份平均每月销售额增长的百分率是x.100(1﹣10%)(1+x)2=129.6,1+x=±x==20%或x=﹣(负值舍去).答:三、四月份平均每月销售额增长的百分率是20%.24.【解答】解:(1)根据题意,得△=(﹣4k)2﹣4×4k(k+1)=﹣16k≥0.解得k≤0.又∵k≠0,∴k<0.由(2x1﹣x2)(x l﹣2x2)=得2(x12+x22)﹣5x1x2=﹣1.5.2(x1+x2)2﹣9x1x2=﹣1.5.2﹣9×=﹣1.518k+18=28k,解得k=1.8.经检验k=1.8是方程2﹣9×=﹣1.5的解.∵k<0,∴不存在实数k.(2)原式=﹣2=﹣2=﹣4=﹣,∴k+1=1或﹣1,或2,或﹣2,或4,或﹣4解得k=0或﹣2,1,﹣3,3,﹣5.∵k<0.∴k=﹣2,﹣3或﹣5.25.【解答】解:(1)由题意,得①(1400﹣400a)千克②(1400﹣400a)a元③y=(a﹣2)(1400﹣400a)﹣24(元)故答案为:(1400﹣400a)千克,(1400﹣400a)a元,(a﹣2)(1400﹣400a)﹣24(元)(2)当y=200时,(a﹣2)(1400﹣400a)﹣24=200整理得:a2+5.5a﹣7.56=0解得:a1=2.7,a2=2.8当a=2.7时,降价为:3﹣a=0.3元当a=2.8时,降价为:3﹣a=0.2元∴应将每千克小型西瓜的售价降低0.2元或0.3元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020 学年四川省成都市青羊区石室联中九年级(上)
月考数学试卷(9 月份)
一、选择题(本大题共 10 个小题,每小题 3 分,共 30 分)
1.(3 分)(2008•沐川县一模)方程02=+x x 的解是(
) A .0=x B .1-=x C .1=x D .01=x ,12-=x
2.(3 分)(2016•兰州模拟)若3:2:=b a ,则下列各式中正确的式子是(
) A .b a 32= B .b a 23= C .32=a b D .3
1=-b b a 3.(3 分)(2019 秋•青羊区校级月考)如图,在ABC ∆ 中,DE / /BC ,9=AB ,3=BD , 4=AE ,则EC 的长为( )
A .1
B .2
C .3
D .4
4.(3 分)(2005•南京)如图,身高为1.6m 的某学生想测量一棵大树的高度,她沿着树影 BA 由B 到A 走去,当走到C 点时,她的影子顶端正好与树的影子顶端重合,测得 m BC 2.3=,m CA 8.0=,则树的高度为( )
A .m 8.4
B .m 4.6
C .m 8
D .m 10 5.(3 分)(2013•成都)一元二次方程022=-+x x 的根的情况是(
) A .有两个不相等的实数根
B .有两个相等的实数根
C .只有一个实数根
D .没有实数根
6.(3 分)(2019 秋•青羊区校级月考)若反比例函数
)0(≠=k x k y 的图象经过点⎪⎭⎫ ⎝⎛-29,4, 则下列点在该图象上的是(
) A .()2,5- B .()6,3- C .()9,2
D .()2,9 7.(3 分)(2011•荆门)如图.位似图形由三角尺与其灯光照射下的中心投影组成,相似 比为 2 : 5 ,且三角尺的一边长为8cm ,则投影三角形的对应边长为( )
A .cm 8
B .cm 20
C .cm 2.3
D .cm 10
8.(3 分)(2018 春•卧龙区期末)函数x
m y
=与)0(≠-=m m mx y 在同一平面直角坐标系 中的大致图象是( )
9.(3 分)(2014•天津)要组织一次排球邀请赛,参赛的每个队之间都要比赛一场,根据 场地和时间等条件,赛程计划安排 7 天,每天安排 4 场比赛.设比赛组织者应邀请x 个队参 赛,则x 满足的关系式为(
)
A .28)1(21=+x x
B .28)1(21=-x x
C .28)1(=+x x
D .28
)1(=-x x 10.(3 分)(2013•黔东南州)如图,直线x y 2=与双曲线x
y 2=在第一象限的交点为A , 过点A 作x AB ⊥轴于B ,将ABO ∆绕点O 旋转90°,得到O B A ''∆,则点'A 的坐标为( )
A .(1,0)
B .(1,0) 或(-1,0)
C .(2,0) 或(0,-2)
D .(-2,1) 或 (2,-1)
二、填空题(本大题共 4 个小题,每小题 4 分,共 16 分)
11.(4 分)(2019 秋•青羊区校级月考)已知 1=a ,2=b ,6=c ,若 a ,b ,c ,d 四条线段成比例,则 =d .
12.(4 分)(2019 秋•青羊区校级月考)已知方程0622
=++kx x 有一个根为2-=x ,则=k ,另一个根为 .
13.(4 分)(2019 秋•青羊区校级月考)已知反比例函数x
m y 21-=的图象上两点()11,y x A ,()22,y x B 当021<<x x 时,有21y y <,则m 的取值范围是 .
14.(4 分)(2019 秋•青羊区校级月考)如图,在 ABCD 中,点E 是边AD 的中点,EC 交对角线BD 于点F ,则=∆∆BCD EFD S S : .
三、解答题(本大题共 6 个小题,共 54 分)
15.(12 分)(2019 秋•青羊区校级月考)(1)解方程:15)3)(1(=++x x
(2)解方程:2232
=-x x
(3)解不等式组⎪⎩⎪⎨⎧->+>+-②①12
2331)1(2x x x x
16.(6 分)(2018 春•安庆期中)先化简,再求值.
221b a b b a a -÷⎪⎭
⎫ ⎝⎛--,其中13+=a ,13-=b .
17.(8 分)(2010 秋•南安市校级期中)如图,直角坐标中,ABC ∆的三个顶点分别为 A (4,4) 、 B (-2,2) 、C (3,0) .
(1)请画出一个以原点O 为位似中心,且把ABC ∆缩小一半的位似图形111C B A ∆,
(2)写出111C B A ∆各顶点的坐标.
18.(8 分)(2019 秋•青羊区校级月考)如图,小李晚上由路灯A 下的B 处走到C 时,测得影子CD 的长为 1 米,继续往前走3米到达E 处时,测得影子EF 的长为2米,已知小李的身高CM 为 1.5 米,求路灯A 的高度AB .
19.(10 分)(2019 秋•青羊区校级月考)如图,已知 A (4,2)、B (n ,-4)是一次函数b kx y +=图象与反比例函数x
m y =图象的两个交点. (1)求此反比例函数和一次函数的解析式;
(2)直接写出AOB ∆的面积;
(3)根据图象直接写出使一次函数的值小于反比例函数的值的x 的取值范围.
20.(10 分)(2019 秋•青羊区校级月考)如图,在平行四边形ABCD 中,CD AC =.点E 、
F 分别为边BC 、CD 上的两点,且CAD EAF ∠=∠
(1)求证:ACB D ∠=∠:
(2)求证:ADF ∆∽ACE ∆:
(3)求证:EF AE =.
一、填空题(本大题共 5 个小题,每小题 4 分,共 20 分)
21.(4 分)(2019 秋•青羊区校级月考)函数
x
k y 2-=的图象与直线1+=x y 没有交点,那么 k 的取值范围是 .
22.(4 分)(2012 春•青州市期中)如图,四边形EFGH 是ABC ∆内接正方形,cm BC 21=, 高 cm AD 15=,则内接正方形边长=EF .
23.(4 分)(2011•锦江区模拟)如图,反比例函数()0>=x x
k y 的图象经过矩形OABC 对 角线的交点M ,分别与AB 、BC 相交于点D 、E .若四边形ODBE 的面积为 6,则k 的值为 .
24.(4 分)(2019 秋•青羊区校级月考)在反比例函数()010>=x x
y 的图象上,有一系列 点1A 、2A 、3A 、...、n A 、1+n A ,若1A 1的横坐标为 2,且以后每点的横坐标与它前一个点的横坐标的差都为 2.现分别过点1A 、2A 、3A 、...、n A 、1+n A 作x 轴与y 轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为1S 、2S 、3S 、...、n S ;则
=3S ,=++++n S S S S ...321 (用n 的代数式表示)
25.(4 分)(2015•高密市一模)已知关于x 的一元二次方程012
=++bx ax 有两个相等的 实数根,那么代数式4
)2(222
-+-b a ab 的值为 . 二、解答题(本大题共 3 个小题,共 30 分)
26.(8 分)(2019•德城区一模)利达经销店为某工厂代销一种建筑材料(这里的代销是 指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售 价为 260 元时,月销售量为 45 吨.该经销店为提高经营利润,准备采取降价的方式进行促 销.经市场调查发现:当每吨售价每下降 10 元时,月销售量就会增加 7.5 吨.综合考虑各 种因素,每售出一吨建筑材料共需支付厂家及其它费用 100 元.
(1)当每吨售价是 240 元时,计算此时的月销售量;
(2)在遵循“薄利多销”的原则下,问每吨材料售价为多少时,该经销店的月利润为 9000 元?
(3)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
27.(10 分)(2019 秋•青羊区校级月考)已知关于 x 的一元二次方程
03)1(222=+++-a x a x 有两个实数根1x ,2x
(1)求实数a 的取值范围
(2)若等腰ABC ∆的三边长分别为 1x ,2x ,6,求ABC ∆的周长
(3)是否存在实数a ,使1x ,2x 恰是一个边长为22的菱形的两条对角线的长?若存在,求出这个菱形的面积;若不存在,说明理由.
28.(12 分)(2015•硚口区模拟)如图,Rt ∆ABC 中,=∠BAC 90°,2=AB ,4=AC ,
D 是BC 边上一动点,G 是BC 边上的一动点,G
E / /AD 分别交AC 、BA 或其延长线于
F 、
E 两点
(1)如图 1,当BD BC 5=时,求证:BC EG ⊥;
(2)如图 2,当CD BD =时,EG FG +是否发生变化?证明你的结论;
(3)当CD BD =,EF FG 2=时,DG 的值= .。
