三角形边角关系专项练习
直角三角形的边角关系单元测试

《直角三角形的边角关系》单元测试班级: 姓名: 学号: 分数:一、选择题(每小题4分,共32分) 1.已知△ABC 中,∠C=90°,tanA=( )A .AB AC B .AB BC C .BC AC D .ACBC2.在△ABC 中,∠C=90,若sinA=31,则cosB= ( )A. 1B. 3C. 31 D 2323.在Rt△ABC中,两直角的比为5:12,则最小角的余弦值( ) A .125 B .123 C .512 D .13124.在Rt△ABC中,如果各边长度都扩大2倍,那么锐角A的正切值( ) A .没有变化 B .扩大2倍 C .缩小2倍 D .不能确定5.如图,Rt △ABC 中,∠ACB=90°,CD ⊥AB 于D,BC=3,AC=4,设∠BCD=α,则 tan α的值为( ) A.34; B.43; C.35; D.456. 若∠A 为锐角,且则∠A 的度数为( )A.30°B.45°C.60°D.90°7.在 Rt △ABC 中,∠C=900, a 、b 、c 分别是∠A 、∠B 、∠C 的对边,下列关系式错误的是( )A. b=c ·cosBB.b=a ·tanBC.a=c ·sinAD. a=b ·tanA 8. 等腰三角形底边长为1Ocm ,周长为36cm ,那么底角的余弦等于( ) A.513 B.1213 C. 1013 D. 512二.填空题:(每小题3分,共15分)1.在△ABC 中,∠C为直角,若3AC=BC 3,则∠A的度数是 ,cosB 的值是_ _ 。
2.已知ABC △中,90C ∠=,A B C ∠∠∠,,所对的边分别是a b c ,,,且3c a =,则cos A =________.3.已知:Rt △ABC 中,∠C=90°,sinA=513,则sinB=________.4.如图,沿倾斜角为30︒的山坡植树,要求相邻两棵树的水平 距离AC 为2m ,那么相邻两棵树的斜坡距离AB 为 m 。
直角三角形的边角关系测试题及答案

AD′直角三角形的边角关系测试题一、选择题(每小题3分,共计30分):1.在△ABC 中,∠C=90°,a 、b 分别是∠A 、∠B 所对的两条直角边,c 是斜边,则有( )A 、sinA=a cB 、cosB=c bC 、cosB=a bD 、tanA=ba 2.在Rt △ABC 中,∠C=90°,sinA=21,则BC ∶AC ∶AB 等于( )A 、1∶2∶5B 、1∶3∶5C 、1∶3∶2D 、1∶2∶33.在△ABC 中,若tanA=1,sinB=22,你认为最确切的判断是( ) A.△ABC 是等腰三角形 B.△ABC 是等腰直角三角形 C.△ABC 是直角三角形 D.△ABC 是一般锐角三角形 4.已知在Rt △ABC 中,∠C=90°.若sinA=22,则sinB 等于( ) A 、21 B 、22 C 、23 D 、1 5.化简2)130(tan - =( )。
A 、331-B 、13-C 、133-D 、13-6.等腰三角形的一腰长为6cm ,底边长为63cm ,则其底角为( )。
A. 120° B. 90° C. 60° D. 30°7如图,已知正方形ABCD 的边长为2,如果将线段BD 绕着点B 旋转后,点D 落在CB 的延长线上的D′处,那么tan ∠BAD′等于( ) A. 22 B.22C. 2D. 18.当锐角A 的cosA >22时,∠A 的值为( )。
A. 小于45° B. 小于30° C. 大于45° D. 大于30°9.小刚在距某电信塔10 m 的地面上(人和塔底在同一水平面上),测得塔顶的仰角是 60°, 则塔高为( )BNACDMA 、103mB 、53mC 、102mD 、20m 10.如图,在△ABC 中,∠C=90°,AC=8cm,AB 的垂直平分线MN交AC 于D ,连结BD ,若cos ∠BDC=53,则BC 的长是( )A 、4cmB 、6cmC 、8cmD 、10cm二、填空题(每小题3分, 共计18分):11.在△ABC 中.∠C=90°,若tanA=1,则∠B= 度. 12.锐角A满足2sin(A-150)=3,则∠A=_____度. 13.如图,若某人沿坡度i =3:4的斜坡前进10米,则他所在 的位置比原来的位置升高________米.14.若︒<<︒900α,︒=60cos sin α,则_____tan =α 15.已知△ABC 中,∠A 、∠B 都是锐角,且(cosA-21)2+|tanB-1|=0,则∠C= 度。
中考数学直角三角形的边角关系综合练习题及答案

中考数学直角三角形的边角关系综合练习题及答案一、直角三角形的边角关系1.图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG =FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为_______分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为_________分米.【答案】553【解析】【分析】如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J.解直角三角形求出MQ,AQ即可求出AM,再分别求出BE,B′E′即可.【详解】解:如图,作OP⊥CD于P,OQ⊥AM于Q,FK⊥OB于K,FJ⊥OC于J.∵AM⊥CD,∴∠QMP=∠MPO=∠OQM=90°,∴四边形OQMP是矩形,∴QM=OP,∵OC=OD=10,∠COD=60°,∴△COD是等边三角形,∵OP⊥CD,∠COD=30°,∴∠COP=12∴QM=OP=OC•cos30°=3∵∠AOC=∠QOP=90°,∴∠AOQ=∠COP=30°,∴AQ=1OA=5(分米),2∴AM=AQ+MQ=5+3∵OB∥CD,∴∠BOD=∠ODC=60°在Rt△OFK中,KO=OF•cos60°=2(分米),FK=OF•sin60°=23(分米),在Rt△PKE中,EK=22-=26(分米),EF FK∴BE=10−2−26=(8−26)(分米),在Rt△OFJ中,OJ=OF•cos60°=2(分米),FJ=23(分米),在Rt△FJE′中,E′J=22-(2)=26,63∴B′E′=10−(26−2)=12−26,∴B′E′−BE=4.故答案为:5+53,4.【点睛】本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.2.下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)【答案】2.5m.【解析】试题分析:设DF=x,在Rt△DFC中,可得CF=DF=x,则BF=4-x,根据线段的和差可得AN=5-x,EN=DM=BF=4-,在Rt△ANE中,∠EAB=,利用∠EAB的正切值解得x的值.试题解析:解:设DF=,在Rt△DFC中,∠CDF=,∴CF=tan·DF=,又∵CB=4,∴BF=4-,∵AB=6,DE=1,BM= DF=,∴AN=5-,EN=DM=BF=4-,在Rt△ANE中,∠EAB=,EN=4-,AN=5-,tan==0.60,解得=2.5,答:DM和BC的水平距离BM为2.5米.考点:解直角三角形.3.如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.(1)求证:△ABC∽△BCD;(2)求x的值;(3)求cos36°-cos72°的值.【答案】(1)证明见解析;(215-+;(3758+【解析】试题分析:(1)由等腰三角形ABC中,顶角的度数求出两底角度数,再由BD为角平分线求出∠DBC的度数,得到∠DBC=∠A,再由∠C为公共角,利用两对角相等的三角形相似得到三角形ABC与三角形BCD相似;(2)根据(1)结论得到AD=BD=BC,根据AD+DC表示出AC,由(1)两三角形相似得比例求出x的值即可;(3)过B作BE垂直于AC,交AC于点E,在直角三角形ABE和直角三角形BCE中,利用锐角三角函数定义求出cos36°与cos72°的值,代入原式计算即可得到结果.试题解析:(1)∵等腰△ABC中,AB=AC,∠BAC=36°,∴∠ABC=∠C=72°,∵BD平分∠ABC,∴∠ABD=∠CBD=36°,∵∠CBD=∠A=36°,∠C=∠C,∴△ABC∽△BCD;(2)∵∠A=∠ABD=36°,∴AD=BD,∵BD=BC,∴AD=BD=CD=1,设CD=x ,则有AB=AC=x+1,∵△ABC ∽△BCD , ∴AB BC BD CD =,即111x x+=, 整理得:x 2+x-1=0, 解得:x 1=15-+,x 2=15--(负值,舍去), 则x=15-+; (3)过B 作BE ⊥AC ,交AC 于点E ,∵BD=CD ,∴E 为CD 中点,即DE=CE=154-+, 在Rt △ABE 中,cosA=cos36°=1515144151AE AB -++==-++, 在Rt △BCE 中,cosC=cos72°=151541EC BC -+-+==, 则cos36°-cos72°=51+=15-+=12. 【考点】1.相似三角形的判定与性质;2.等腰三角形的性质;3.黄金分割;4.解直角三角形.4.问题探究:(一)新知学习:圆内接四边形的判断定理:如果四边形对角互补,那么这个四边形内接于圆(即如果四边形EFGH 的对角互补,那么四边形EFGH 的四个顶点E 、F 、G 、H 都在同个圆上).(二)问题解决:已知⊙O的半径为2,AB,CD是⊙O的直径.P是上任意一点,过点P分别作AB,CD 的垂线,垂足分别为N,M.(1)若直径AB⊥CD,对于上任意一点P(不与B、C重合)(如图一),证明四边形PMON内接于圆,并求此圆直径的长;(2)若直径AB⊥CD,在点P(不与B、C重合)从B运动到C的过程汇总,证明MN的长为定值,并求其定值;(3)若直径AB与CD相交成120°角.①当点P运动到的中点P1时(如图二),求MN的长;②当点P(不与B、C重合)从B运动到C的过程中(如图三),证明MN的长为定值.(4)试问当直径AB与CD相交成多少度角时,MN的长取最大值,并写出其最大值.【答案】(1)证明见解析,直径OP=2;(2)证明见解析,MN的长为定值,该定值为2;(3)①MN=;②证明见解析;(4)MN取得最大值2.【解析】试题分析:(1)如图一,易证∠PMO+∠PNO=180°,从而可得四边形PMON内接于圆,直径OP=2;(2)如图一,易证四边形PMON是矩形,则有MN=OP=2,问题得以解决;(3)①如图二,根据等弧所对的圆心角相等可得∠COP1=∠BOP1=60°,根据圆内接四边形的对角互补可得∠MP1N=60°.根据角平分线的性质可得P1M=P1N,从而得到△P1MN是等边三角形,则有MN=P1M.然后在Rt△P1MO运用三角函数就可解决问题;②设四边形PMON的外接圆为⊙O′,连接NO′并延长,交⊙O′于点Q,连接QM,如图三,根据圆周角定理可得∠QMN=90°,∠MQN=∠MPN=60°,在Rt△QMN中运用三角函数可得:MN=QN•sin∠MQN,从而可得MN=OP•sin∠MQN,由此即可解决问题;(4)由(3)②中已得结论MN=OP•sin∠MQN可知,当∠MQN=90°时,MN最大,问题得以解决.试题解析:(1)如图一,∵PM⊥OC,PN⊥OB,∴∠PMO=∠PNO=90°,∴∠PMO+∠PNO=180°,∴四边形PMON内接于圆,直径OP=2;(2)如图一,∵AB⊥OC,即∠BOC=90°,∴∠BOC=∠PMO=∠PNO=90°,∴四边形PMON是矩形,∴MN=OP=2,∴MN的长为定值,该定值为2;(3)①如图二,∵P1是的中点,∠BOC=120°,∴∠COP1=∠BOP1=60°,∠MP1N=60°,∵P1M⊥OC,P1N⊥OB,∴P1M=P1N,∴△P1MN是等边三角形,∴MN=P1M.∵P1M=OP1•sin∠MOP1=2×sin60°=,∴MN=;②设四边形PMON的外接圆为⊙O′,连接NO′并延长,交⊙O′于点Q,连接QM,如图三,则有∠QMN=90°,∠MQN=∠MPN=60°,在Rt△QMN中,sin∠MQN=,∴MN=QN•sin∠MQN,∴MN=OP•sin∠MQN=2×sin60°=2×=,∴MN是定值.(4)由(3)②得MN=OP•sin∠MQN=2sin∠MQN.当直径AB与CD相交成90°角时,∠MQN=180°﹣90°=90°,MN取得最大值2.考点:圆的综合题.5.如图,抛物线y=﹣x2+3x+4与x轴交于A、B两点,与y轴交于C点,点D在抛物线上且横坐标为3.(1)求tan∠DBC的值;(2)点P为抛物线上一点,且∠DBP=45°,求点P的坐标.【答案】(1)tan∠DBC=;(2)P(﹣,).【解析】试题分析:(1)连接CD,过点D作DE⊥BC于点E.利用抛物线解析式可以求得点A、B、C、D的坐标,则可得CD//AB,OB=OC,所以∠BCO=∠BCD=∠ABC=45°.由直角三角形的性质、勾股定理和图中相关线段间的关系可得BC=4,BE=BC﹣DE=.由此可知tan∠DBC=;(2)过点P作PF⊥x轴于点F.由∠DBP=45°及∠ABC=45°可得∠PBF=∠DBC,利用(1)中的结果得到:tan∠PBF=.设P(x,﹣x2+3x+4),则利用锐角三角函数定义推知=,通过解方程求得点P的坐标为(﹣,).试题解析:(1)令y=0,则﹣x2+3x+4=﹣(x+1)(x﹣4)=0,解得 x1=﹣1,x2=4.∴A(﹣1,0),B(4,0).当x=3时,y=﹣32+3×3+4=4,∴D(3,4).如图,连接CD,过点D作DE⊥BC于点E.∵C(0,4),∴CD//AB,∴∠BCD=∠ABC=45°.在直角△OBC中,∵OC=OB=4,∴BC=4.在直角△CDE中,CD=3.∴CE=ED=,∴BE=BC﹣DE=.∴tan∠DBC=;(2)过点P作PF⊥x轴于点F.∵∠CBF=∠DBP=45°,∴∠PBF=∠DBC,∴tan∠PBF=.设P(x,﹣x2+3x+4),则=,解得 x1=﹣,x2=4(舍去),∴P(﹣,).考点:1、二次函数;2、勾股定理;3、三角函数6.某条道路上通行车辆限速60千米/时,道路的AB段为监测区,监测点P到AB的距离PH为50米(如图).已知点P在点A的北偏东45°方向上,且在点B的北偏西60°方向上,点B在点A的北偏东75°方向上,那么车辆通过AB段的时间在多少秒以内,可认定为32≈1.4).【答案】车辆通过AB段的时间在8.1秒以内,可认定为超速【解析】分析:根据点到直线的距离的性质,构造直角三角形,然后利用解直角三角形的应用,解直角三角形即可.详解:如图,由题意知∠CAB=75°,∠CAP=45°,∠PBD=60°,∴∠PAH=∠CAB–∠CAP=30°,∵∠PHA=∠PHB=90°,PH=50,∴AH=tan PH PAH∠33,∵AC∥BD,∴∠ABD=180°–∠CAB=105°,∴∠PBH=∠ABD–∠PBD=45°,则PH=BH=50,∴3,∵60千米/时=503米/秒,∴时间t=503505033≈8.1(秒),即车辆通过AB段的时间在8.1秒以内,可认定为超速.点睛:该题考查学生通过构建直角三角形,利用某个度数的三角函数值求出具体边长,即实际路程,并进行判断相关的量。
三角形的边角关系(竞赛)

E 图1
3.在⊿ABC中,AB=5,AC=9,则BC
边上的中线AD的长的取值范围是 2<AD<7 _________. 延长AD到E,使DE=AD,连结BE. 证⊿BDE≌⊿CDA,得DE=AC.
B
A
D C
E
在⊿ADE中,4<AE<14.即4<2AD<14.
∴2<AD<7.
4.若三角形的三边长度均为整数,其中两边的差是 7,且三角形的周长是奇数,则第三边长可能是 C( ) A.9 B.8 C.7 D.6 不妨设三角形三边长度为a,b,c,且a-b=7.则a与b一 奇一偶.又a+b+c为奇数, 所以c一定为偶数,可能是8 5.一个三角形的三条边的长分别是a,b,c(a,b,c都是 质数),且a+b+c=16, 则这个三角形是( B ) A.直角三角形 B.等腰三角形 C.等边三角形 D.直角三角形或等腰三角形 不妨设a=2,b<c则b+c=14,又c-b<2,所以c-b=0, ∴b=c=7.选(B)
在⊿ABD中,有AB+AD>BD. 在⊿PDC中,DC+DP>PC.
B
∵∠PDC是⊿ABD的外角, ∴ ∠PDC>∠BAC 又∠BPC是⊿PDC的一个外角,
两式相加:AB+AD+DC+DP>BD+PC=PB+DP+PC ∴∠BPC>∠PDC 即,AB+AC>PB+PC.得证.
∴∠BPC>∠BAC
(3)PA+PB+PC<AB+BC+AC
∴a:b=3:1=3h:h;
∴a:b:c=3h:h:12.
b:c=h:12
可设三边长为3hk,hk,12k(k为正整数)
直角三角形的边角关系专题复习

直角三角形的边角关系测试题1、在Rt △ABC 中,∠A=90º,AB=6,AC=8,则sinB= ,cosC=2、在△ABC 中,∠B=90º,21cos =C ,则∠C=】3、在△ABC 中,∠C=90º,∠A=60º,AC=34,则BC=4、在△ABC 中,∠C=90º,BC=3,AB=32,则∠A=5、在△ABC 中,∠C=90º,若tanA=21,则sinA= 6、在△ABC 中,若∠C=90º,∠A=45º,则tanA+sinB=7、如图1,在△ABC 中,∠C=90º,∠B=30º,AD 是∠BAC 的平分线。
已知AB=34,那么AD=#8、正方形ABCD 中,AM 平分∠BAC 交BC 于M ,AB=2,BM=1,则cos ∠MAC= 9、如果3)20tan(3=︒+α,那么锐角α=10、某校数学课外活动小组的同学测量英雄纪念碑的高,如图2所示,测得的数据为: BC=42m ,倾斜角º︒=30α,测得测角仪高CD=1.5m ,则AB= 。
(结果保留四位 有效数字)11、在△ABC 中,∠C=90º,BC=5,AC=12,则tanA=( ) A 、512 B 、125 C 、513 D 、135 12、在Rt △ABC 中,∠C=90º,53cos =A ,AC=6cm ,则BC=( )cm A 、8B 、C 、D 、 !13、菱形ABCD 的对角线AC=10cm ,BD=6cm ,那么=2tanA ( ) A 、53B 、54C 、34343 D 、3434514、已知:如图3,梯形ABCD 中,AD638642382423231,23-1,23--3253500)3sin 2(3tan 2=-+-A B 5米353103︒+︒+︒-︒45tan 30cos 230tan 330sin ︒-︒+︒-︒-︒60tan 45tan 30sin 160cos 45cos 2226—1为平地上一幢建筑物与铁塔图,题6-2图为其示意图.建筑物AB 与铁塔CD 都垂直于底面,BD=30m ,在A 点测得D 点的俯角为45°,测得C 点的仰角为60°.求铁塔CD 的高度.…图6-1 图6-2图2a CAE B)图1 BCDA图3图4 图524、如图,小明家在A 处,门前有一口池塘,隔着池塘有一条公路l ,AB 是A 到l 的小路。
猜题06直角三角形的边角关系(易错必刷30题8种题型专项训练)(原卷版)
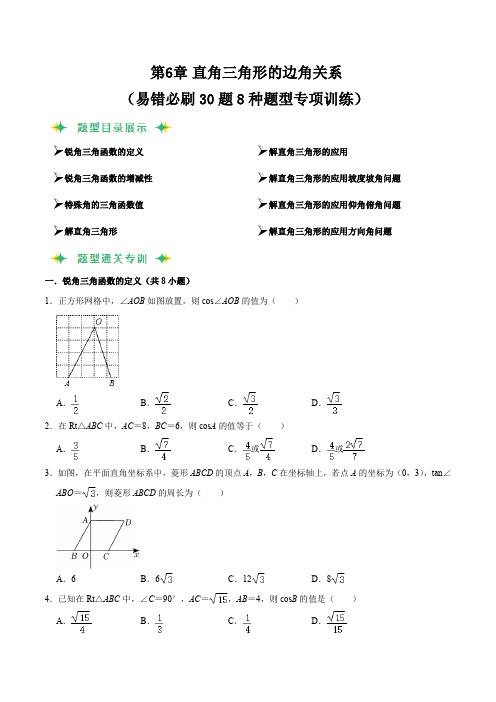
第6章 直角三角形的边角关系(易错必刷30题8种题型专项训练)➢锐角三角函数的定义 ➢锐角三角函数的增减性 ➢特殊角的三角函数值 ➢解直角三角形➢解直角三角形的应用➢解直角三角形的应用坡度坡角问题➢解直角三角形的应用仰角俯角问题➢解直角三角形的应用方向角问题一.锐角三角函数的定义(共8小题)1.正方形网格中,∠AOB 如图放置,则cos ∠AOB 的值为( )A .B .C .D .2.在Rt △ABC 中,AC =8,BC =6,则cos A 的值等于( )A .B .C .或D .或3.如图,在平面直角坐标系中,菱形ABCD 的顶点A ,B ,C 在坐标轴上,若点A 的坐标为(0,3),tan ∠ABO =,则菱形ABCD 的周长为( )A .6B .6C .12D .84.已知在Rt △ABC 中,∠C =90°,AC =,AB =4,则cos B 的值是( ) A . B . C . D .5.如图,在△ABC中,∠C=90°,AC=5,若cos∠A=,则BC的长为()A.8B.12C.13D.186.如图,在网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠OAB的正弦值是.7.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的正弦值是.8.如图,在△ABC中,∠C=90°,AC=6,若cos A=,则BC的长为.二.锐角三角函数的增减性(共1小题)9.若∠A是锐角,且sin A=,则()A.0°<∠A<30°B.30°<∠A<45°C.45°<∠A<60°D.60°<∠A<90°三.特殊角的三角函数值(共2小题)10.在△ABC中,如果∠A、∠B满足|tan A﹣1|+(cos B﹣)2=0,那么∠C=.11.计算:(1)tan45°﹣sin30°cos60°﹣cos245°;(2)3tan30°﹣tan245°+2sin60°.四.解直角三角形(共5小题)12.如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是()A.B.2C.D.13.将一副三角板如图摆放在一起,组成四边形ABCD,∠ABC=∠ACD=90°,∠ADC=60°,∠ACB=45°,连接BD,则tan∠CBD的值等于()A.B.C.D.14.阅读理解:为计算tan15°三角函数值,我们可以构建Rt△ACB(如图),使得∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,可得到∠D=15°,所以tan15°====2﹣.类比这种方法,请你计算tan22.5°的值为()+1B.﹣1C.D.A.15.四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变边长为2的正方形ABCD的内角,变为菱形ABC'D',若∠D'AB=45°,则阴影部分的面积是()A.B.5﹣C.D.5﹣216.我们给出定义:如果两个锐角的和为45°,那么称这两个角互为半余角.如图,在△ABC中,∠A,∠B互为半余角,且,则tan A=.五.解直角三角形的应用(共3小题)17.如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,∠ABC=27°,BC=44cm,则高AD约为()(参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)A.9.90cm B.11.22cm C.19.58cm D.22.44cm18.如图2,有一块四边形的铁板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tan B=tan C =,若要从这块余料中裁出顶点M、N在边BC上且面积最大的矩形PQMN,则该矩形的面为cm2.19.胜利黄河大桥犹如一架巨大的竖琴,凌驾于滔滔黄河之上,使黄河南北“天堑变通途”.已知主塔AB垂直于桥面BC于点B,其中两条斜拉索AD、AC与桥面BC的夹角分别为60°和45°,两固定点D、C 之间的距离约为33m,求主塔AB的高度(结果保留整数,参考数据:≈1.41,≈1.73).六.解直角三角形的应用坡度坡角问题(共2小题)20.如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为()A.5cosαB.C.5sinαD.21.为了防洪需要,某地决定新建一座拦水坝,如图,拦水坝的横断面为梯形ABCD,斜面坡度i=3:4是指坡面的铅直高度AF与水平宽度BF的比.已知斜坡CD长度为20米,∠C=18°,求斜坡AB的长.(结果精确到0.1米)(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)七.解直角三角形的应用仰角俯角问题(共6小题)22.荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为米(≈1.73,结果精确到0.1).23.在一次综合实践活动中,某小组对一建筑物进行测量.如图,在山坡坡脚C处测得该建筑物顶端B的仰角为60°,沿山坡向上走20m到达D处,测得建筑物顶端B的仰角为30°.已知山坡坡度i=3:4,即tanθ=,请你帮助该小组计算建筑物的高度AB.(结果精确到0.1m,参考数据:≈1.732)24.在一次数学课外实践活动中,某小组要测量一幢大楼MN的高度,如图,在山坡的坡脚A处测得大楼顶部M的仰角是58°,沿着山坡向上走75米到达B处,在B处测得大楼顶部M的仰角是22°,已知斜坡AB的坡度i=3:4(坡度是指坡面的铅直高度与水平宽度的比),求大楼MN的高度.(图中的点A,B,M,N,C均在同一平面内,N,A,C在同一水平线上,参考数据:tan22°≈0.4,tan58°≈1.6)25.如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成.如图2,AB是灯杆,CD是灯管支架,灯管支架CD与灯杆间的夹角∠BDC=60°.综合实践小组的同学想知道灯管支架CD的长度,他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得AE=3m,EF=8m(A,E,F在同一条直线上).根据以上数据,解答下列问题:(1)求灯管支架底部距地面高度AD的长(结果保留根号);(2)求灯管支架CD的长度(结果精确到0.1m,参考数据:≈1.73).26.小明为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)(1)求小明此时与地面的垂直距离CD的值;(2)小明的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(sin15°≈0.2588cos15°≈0.9659tan15°≈0.2677)27.《海岛算经》是中国古代测量术的代表作,原名《重差》.这本著作建立起了从直接测量向间接测量的桥梁.直至近代,重差测量法仍有借鉴意义.如图2,为测量海岛上一座山峰AH的高度,直立两根高2米的标杆BC和DE,两杆间距BD相距6米,D、B、H三点共线.从点B处退行到点F,观察山顶A,发现A、C、F三点共线,且仰角为45°;从点D处退行到点G,观察山顶A,发现A、E、G三点共线,且仰角为30°.(点F、G都在直线HB上)(1)求FG的长(结果保留根号);(2)山峰高度AH的长(结果精确到0.1米).(参考数据:≈1.41,≈1.73)八.解直角三角形的应用方向角问题(共3小题)28.如图,湖心岛上有一凉亭B,在凉亭B的正东湖边有一棵大树A,在湖边的C处测得B在北偏西45°方向上,测得A在北偏东30°方向上,又测得A、C之间的距离为100米,则A、B之间的距离是米(结果保留根号形式).29.如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:≈1.732)30.如图,B地在A地的北偏东56°方向上,C地在B地的北偏西19°方向上,原来从A地到C地的路线为A→B→C,现在沿A地北偏东26°方向新修了一条直达C地的分路,路程比原来少了20千米.求从A地直达C地的路程(结果保留整数.参考数据:≈1.41,≈1.73)。
直角三角形的边角关系测试题(含A组答案)

直角三角形的边角关系测试题一、选择题(每小题2分,共计24分):1.在△ABC 中,∠C =90°,下列式子一定能成立的是( ) A .sin a c B = B .cos a b B = C .tan c a B = D .tan a b A =2. 已知△ABC 中,∠A 、∠B 都是锐角,且(cosA-12 )2+|tanB-3 |=0,你认为最确切的判断是( )A.△ABC 是等腰三角形B.△ABC 是等腰直角三角形C.△ABC 是直角三角形D.△ABC 是等边三角形 3.已知在Rt △ABC 中,∠C=90°,若tanA=12,则sinB 等于( ) A 、15 B 、15 5 C 、25 5 D 、24. 当锐角A 的cosA >22时,∠A 的值为( )。
A. 小于45° B. 小于30° C. 大于45° D. 大于30°5.如图,已知正方形ABCD 的边长为2,如果将线段BD 绕着点B 旋转后,点D 落在CB 的延长线上的D′处,那么tan ∠BAD′等于( ) A. 22 B.22C. 2D. 16.如图所示,在△ABC 中,AB =AC =5,BC =8,则tan C =( )A .53B .54C .34D .437.如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB ,D 为垂足.若AC =4,BC =3,则sin ∠ACD的值为( )A .34 B .43 C .54 D .538.如图,从山顶A 望到地面C ,D 两点,测得它们的俯角分别是45°和30°,已知CD =100m ,点C 在BD 上,则山高AB 等于 ( )A .100 mB .350mC .250mD .50(13+)m9.如图,沿AC 方向开山修路,为了加快施工进度,要在小山的另一边同时施工.从AC 上的一点B ,取∠ABD =145°,BD =500米,∠D =55°,要使A ,C ,E 成一直线,那么开挖点E 离点D 的距离是( )5题 6题7题 8题A .500sin55°米B .500cos55°米C .500tan55°米D .500tan35°米10.如图,两条宽度均为40 m 的公路相交成α角,那么这两条公路在相交处的公共部分(图中阴影部分)的路面面积是( )。
边角关系测试题及答案

边角关系测试题及答案一、选择题1. 在三角形ABC中,如果∠A = 50°,∠B = 70°,那么∠C的度数是多少?A. 40°B. 50°C. 60°D. 70°2. 如果一个三角形的内角和为180°,那么在三角形ABC中,如果∠A = 90°,∠B = 45°,∠C的度数是多少?A. 45°B. 90°C. 135°D. 180°3. 在一个直角三角形中,如果一个锐角是30°,那么另一个锐角的度数是多少?A. 30°B. 45°C. 60°D. 90°二、填空题4. 如果三角形的一个角是直角,那么这个三角形的另外两个角的和是______。
5. 在一个三角形中,如果两个内角的度数之和为90°,那么这个三角形被称为______三角形。
三、简答题6. 解释什么是补角,并给出一个补角的例子。
7. 解释什么是邻补角,并给出一个邻补角的例子。
四、计算题8. 在一个三角形中,已知∠A = 120°,求∠B和∠C的度数。
9. 如果一个三角形的三个内角的度数之和为180°,且已知∠A = 60°,∠B = 50°,求∠C的度数。
五、解答题10. 证明在一个三角形中,任意两个内角的和小于180°。
答案:一、选择题1. C2. A3. C二、填空题4. 90°5. 直角三、简答题6. 补角是指两个角的度数之和等于90°,例如,如果一个角是60°,那么它的补角是30°。
7. 邻补角是指两个角共享一条边,且它们的另一条边互为反向延长线,例如,在一个直角三角形中,两个锐角互为邻补角。
四、计算题8. ∠B = ∠C = (180° - 120°) / 2 =30°9. ∠C = 180° - 60° - 50° = 70°五、解答题10. 证明:设三角形ABC中,∠A和∠B为任意两个内角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形边角关系及三线练习题
典型例题
【例1】 已知三角形的三边长分别为4、5、x ,则x 不可能是( )
A. 3
B. 5
C. 7
D. 9
1. 【例2】 一个三角形的三条边中有两条边相等,且一边长为4,还有一边长为9,则它
的周长为( )
A. 17
B. 22
C. 17或22
D. 13
相关变形:一等腰三角形两边长分别为3,5,试求该三角形的周长。
等腰三角形中,一个角为50°,则这个等腰三角形的顶角的度数为( )
A.150°
B.80°
C.50°或80°
D.70°
【例3】 如图SX —02,AD ⊥BC ,则图中以AD 为高的三角形有___________个。
【例4】 如图SX —03,已知线段AD 、AE 分别是△ABC 的中线和高线,且AB=5cm ,AC=3cm ,
(1) △ABD 与△ACD 的周长之差为_________;(2) △ABD 与△ACD 的面积关系为__________。
【例5】 已知△ABC 中,给出下列四个条件:(1) ∠A+∠B=∠C; (2) ∠A=90°-∠B; (3) ∠A :∠B :∠C=1:1:2; (4) ∠A :∠B :∠C=1:2:3. 其中能够判定△ABC 是直角三角形的有( )个。
A. 1
B. 2
C. 3
D. 4
【例6】 如图SX —04,Rt △ABC 中,∠ACB=90°,CD 是AB 边上的高,AB=13cm ,BC=12cm ,AC=5cm ,求:(1) △ABC 的面积; (2) CD 的长。
【例7】 如图SX —05,△ABC 中,∠B 、∠C 的平分线交于点P ,且∠BPC=130°,求∠
BAC
SX —
02 SX —03 SX —
04
的度数。
相关变形:一个零件的形状如图SX—05-1所示,按规定∠BAC=90°,∠B=21°,∠C=20°,检验工人量得∠BDC=130°,于是断定这个零件不合格。
运用所学知识说明零件不合格的理由。
【例8】如图SX—06,AD是△ABC的边BC上的高,AE是△BAC的平分线,若∠B=53°,∠C=77°,求∠DAE的度数。
学习自评
一、选择题
1.有下列长度的三条线段,能构成三角形的是()
A. 1cm 、2cm 、3cm
B. 1cm 、4cm 、2cm
C. 2cm 、3cm 、4cm
D. 6cm 、2cm 、3cm
2.一个三角形的两边长为3和7,且第三边为整数,这样的三角形的周长的最小值是()
A. 14
B. 15
C. 16
D. 17
3.如图SX—07,△ABC的边BA延长得∠1 ,若∠2 >∠l,则△ABC
的形状为()
A. 钝角三角形
B. 直角三角形
C. 锐角三角形
D. 无法确定
SX—07
4.一个三角形的三个内角互不相等,则它的最大角不小于()
A. 45°
B. 60°
C. 90°
D. 120°
5.△ABC中,如果∠A-∠B =90°,那么△ABC是()
A.直角三角形
B. 锐角三角形
C. 钝角三角形
D. 锐角三角形或钝角三角形
二、填空题
6.在△ABC中,AB=4,BC=9,则AC的取值范围是________________。
7.如图SX—08,求下列各图中的∠α。
(1) ∠α=________;(2) ∠α=________;(3) ∠α=________。
8. 已知∠A 、∠B 、∠C 是△ABC 的三个内角。
(1)如果∠A=90°,∠C = 55°,那么∠B =
______;(2)如果∠C=4∠A ,∠A +∠B =100°,那么∠A =______ ,∠B=______。
9. 如图SX —10,将等边三角形剪去一个角后,∠1+∠2=________。
10. 如图SX —11,在Rt △ABC 中,CD 是斜边AB 上的高,∠BCD = 35°,则∠A=_______。
三、解答题
11. 如图SX —12,在△ABC 中,两边长AB=12, AC=2,且周长为奇数,求第三边BC 的长。
12. 如图SX —13,AC ∥DE ,若∠ABC = 70°,∠E = 50°,∠D = 75°,求∠A ,∠A BD 的
度数。
13. 如图SX —14,在△ABC 中,∠A = 60°,∠B = 70°,∠ACB
的平分线交AB 于D ,DE ∥BC ,交AC 于E ,求∠BDC 和
∠EDC 的度数。
14. 在等腰三角形中,一腰上的中线把它的周长分成15cm 和
18cm 的两部分,求
三角形的各边长。
15. 如图SX —15,
∠B+∠C=100°,
∠D=70°,求∠A
SX —
14
SX —
12 SX —13
SX —11 SX —
08 SX —10
的度数。
16.(1) 如图SX—16甲,∠A+∠B+∠C+∠D+∠E =___________。
(2) 如图SX—16乙,∠A+∠B+∠C+∠D+∠E+∠F=___________.17.求一个多边形的内角和,一般可将其转化为三角形,如图SX—17所示。
请你试用含n的代数式表示出n
边形的内角和。
SX—17。
