浙江高考历年真题之三角函数大题(理科)
高考十(理科)分项版 专题04 三角函数与解三角形(浙江专版)(解析版)

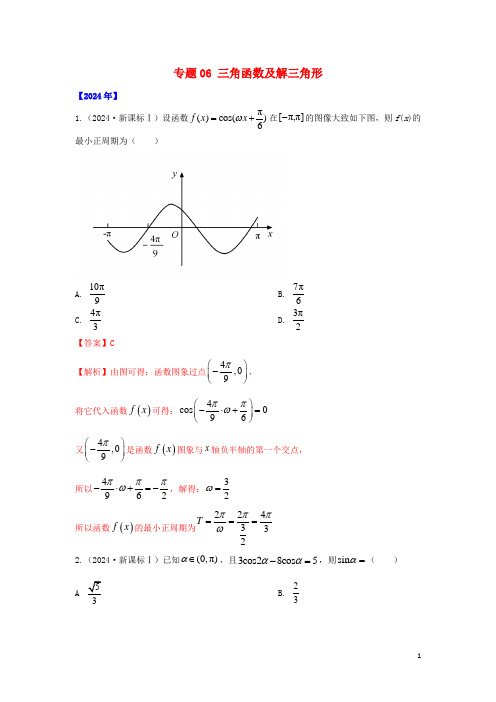
一.基础题组1. 【2014年.浙江卷.理4】为了得到函数x x y 3cos 3sin +=的图像,可以将函数x y 3sin 2=的图像( )A.向右平移4π个单位B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位答案:D解析:sin 3cos3234y x x x π⎛⎫=+=+ ⎪⎝⎭,故只需将23y x =向左平移4π个单位.考点:三角函数化简,图像平移.2. 【2013年.浙江卷.理4】已知函数f (x )=A cos(ωx +φ)(A >0,ω>0,φ∈R ),则“f (x )是奇函数”是“π2ϕ=”的( ). A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件3. 【2013年.浙江卷.理6】已知α∈R ,sin α+2cos α10tan 2α=( ). A .43 B .34 C .34- D .43- 【答案】:C【解析】:由sin α+2cos α=102得,sin α=102-2cos α.① 把①式代入sin 2α+cos 2α=1中可解出cos α=1010或31010,当cos α=1010时,sin α=31010; 当cos α=310时,sin α=10-. ∴tan α=3或tan α=13-,∴tan 2α=34-. 4. 【2012年.浙江卷.理4】把函数y =cos2x +1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图象是( )5. 【2011年.浙江卷.理6】若02πα<<,02πβ-<<,1cos()43πα+=,3cos()423πβ-=,则cos()2βα+=(A )33 (B )33- (C )539 (D )69-02<<-βπ,∴36)24sin(=-βπ,∴)]24()4cos[()2cos(βπαπβα--+=+=)24sin()4sin()24cos()4cos(βπαπβπαπ-++-+=363323331⨯+⨯=935. 6. 【2010年.浙江卷.理9】设函数()4sin(21)f x x x =+-,则在下列区间中函数()f x 不.存在零点的是(A )[]4,2-- (B )[]2,0- (C )[]0,2 (D )[]2,4 【答案】A【解析】:根据函数零点的概念知,()x f 在某个区间上无零点,即方程转()4sin(21)f x x x =+-=0在这个区间上无解,设()g x =()4sin 21x +,()h x =x ,即这两个函数图像在这个区间上无交点,作出()g x =()4sin 21x +,()h x =x 图像,由图像知,选A.7. 【2010年.浙江卷.理11】函数2()sin(2)22sin 4f x x x π=--的最小正周期是__________________ .8. 【2009年.浙江卷.理8】已知a 是实数,则函数()1sin f x a ax =+的图象不可能...是 ( )答案:D【解析】对于振幅大于1时,三角函数的周期为2,1,2T a T aππ=>∴<,而D 不符合要求,它的振幅大于1,但周期反而大于了2π.9. 【2008年.浙江卷.理5】在同一平面直角坐标系中,函数])20[)(232cos(ππ,∈+=x x y 的图象和直线21=y 的交点个数是 (A )0 (B )1 (C )2 (D )410. 【2008年.浙江卷.理13】在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若()C a A c b cos cos 3=-,则=A cos3【解析】:本小题主要考查三角形中正弦定理的应用。
高考真题——理科数学(浙江卷)解析版(1) Word版含答案

数学理试题(浙江卷)一.选择题1、已知i 是虚数单位,则=-+-)2)(1(i iA. i +-3B. i 31+-C. i 33+-D.i +-12、设集合}043|{},2|{2≤-+=->=x x x T x x S ,则=⋃T S C R )( A. ]1,2(- B. ]4,(--∞ C. ]1,(-∞ D.),1[+∞ 答案:C 解析:如图1所示,由已知得到考点定位:此题考查集合的使用之补集和并集体,考查一元二次不等式的解法,利用数轴即可解决此题,体现数形结合思想的应用,此考点是历年来高考必考考点之一,属于简单题; 3、已知y x ,为正实数,则 A.y x yx lg lg lg lg 222+=+ B.y x y x lg lg )lg(222•=+ C.y x yx lg lg lg lg 222+=• D.y x xy lg lg )lg(222•=答案:D解析:此题中,由考点定位:此题考查对数的运算法则和同底数幂的乘法的运算法则;4、已知函数),0,0)(cos()(R A x A x f ∈>>+=ϕωϕω,则“)(x f 是奇函数”是2πϕ=的A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D.既不充分也不必要条件 答案:B 解析:考点定位:充分条件的判断和三角函数的奇偶性性质知识点;5、某程序框图如图所示,若该程序运行后输出的值是59,则 A.4=a B.5=a C. 6=a D.7=a 答案:A解析:由图可知考点定位:此题考查算法及数列的列项相消求和的方法;6、已知210cos 2sin ,=+∈αααR ,则=α2tan A.34 B. 43 C.43- D.34- 答案:C解析:由已知得到:考点定位:此题考查同角三角函数商数关系和平方关系的灵活应用,考查二倍角正切公式的应用,考查学生的运算求解水平;7、设0,P ABC ∆是边AB 上一定点,满足AB B P 410=,且对于边AB 上任一点P ,恒有C P B P PC PB 00•≥•。
高考第二轮复习数学浙江理科专题三 三角函数及解三角形第2讲 三角恒等变换及解三角形

专题三 三角函数及解三角形第2讲 三角恒等变换及解三角形真题试做1.(2012·重庆高考,理5)设tan α,tan β是方程x 2-3x +2=0的两根,则tan(α+β)的值为( ).A .-3B .-1C .1D .32.(2012·山东高考,理7)若θ∈⎣⎡⎦⎤π4,π2,sin 2θ=378,则sin θ=( ). A .35 B .45 C .74 D .343.(2012·天津高考,理6)在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .已知8b=5c ,C =2B ,则cos C =( ).A .725B .-725C .±725D .24254.(2012·湖北高考,理11)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .若(a +b -c )(a +b +c )=ab ,则角C =________.5.(2012·课标全国高考,理17)已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,a cos C +3a sin C -b -c =0. (1)求A ;(2)若a =2,△ABC 的面积为3,求b ,c .6.(2012·浙江高考,理18)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A =23,sin B =5cos C . (1)求tan C 的值;(2)若a =2,求△ABC 的面积. 考向分析本部分主要考查三角函数的基本公式,三角恒等变形及解三角形等基本知识.近几年高考题目中每年有1~2个小题,一个大题,解答题以中低档题为主,很多情况下与平面向量综合考查,有时也与不等式、函数最值结合在一起,但难度不大,而三角函数与解三角形相结合,更是考向的主要趋势.三角恒等变换是高考的热点内容,主要考查利用各种三角函数进行求值与化简,其中降幂公式、辅助角公式是考查的重点,切化弦、角的变换是常考的三角变换思想.正弦定理、余弦定理以及解三角形问题是高考的必考内容,主要考查:①边和角的计算;②三角形形状的判断;③面积的计算;④有关的范围问题.由于此内容应用性较强,与实际问题结合起来命题将是今后高考的一个关注点,不可小视.热点例析热点一 三角恒等变换及求值【例1】(2012·山东淄博一模,17)已知函数f (x )=2cos 2x2-3sin x .(1)求函数f (x )的最小正周期和值域;(2)若α为第二象限角,且f ⎝⎛⎭⎫α-π3=13,求cos 2α1+cos 2α-sin 2α的值. 规律方法 明确“待求和已知三角函数间的差异”是解决三角函数化简、求值、证明问题的关键.三角恒等变换的常用策略有:(1)常值代换:特别是“1”的代换,1=sin 2θ+cos 2θ=tan 45°等. (2)项的分拆与角的配凑:①二倍角只是个相对概念,如α3是α6的二倍角,α+β是α+β2的二倍角等;②α+β2=⎝⎛⎭⎫α-β2-⎝⎛⎭⎫α2-β,α=(α-β)+β等; ③熟悉公式的特点,正用或逆用都要灵活,特别对以下几种变形更要牢记并会灵活运用:1±sin 2α=sin 2α+cos 2α±2sin αcos α=(sin α±cos α)2,cos α=sin 2α2sin α等.(3)降幂与升幂:正用二倍角公式升幂,逆用二倍角公式降幂. (4)角的合成及三角函数名的统一:a sin α+b cos α=a 2+b 2sin(α+φ)⎝⎛⎭⎫tan φ=ba . 变式训练1 (2012·山东济宁模拟,17)已知函数f (x )=3sin ωx -cos ωx (x ∈R ,ω>0)的最小正周期为6π.(1)求f ⎝⎛⎭⎫3π2的值;(2)设α,β∈⎣⎡⎦⎤-π2,0,f ⎝⎛⎭⎫3α+π2=-1013,f (3β+2π)=65,求cos(α+β)的值. 热点二 三角函数、三角形与向量等知识的交会 【例2】(2012·山东烟台适用性测试,理17)在锐角三角形ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,m =(2b -c ,cos C ),n =(a ,cos A ),且m ∥n .(1)求角A 的大小;(2)求函数y =2sin 2B +cos ⎝⎛⎭⎫π3-2B 的值域. 规律方法 以解三角形为命题形式考查三角函数是“众望所归”:正、余弦定理的应用,难度适中,运算量适度,方向明确(化角或化边).(1)利用正弦定理将角化为边时,实际上是把角的正弦替换为所对边与外接圆直径的比值.(2)求角的大小一定要有两个条件:①是角的范围;②是角的某一三角函数值.用三角函数值判断角的大小时,一定要注意角的范围及三角函数的单调性的应用.(3)三角形的内角和为π,这是三角形中三角函数问题的特殊性.在三角形中,任意两角和与第三个角总互补,任意两半角和与第三个角的半角总互余.锐角三角形⇔三内角都是锐角⇔三内角的余弦值均为正值⇔任意两角的和都是钝角⇔任意两边的平方和大于第三边的平方.变式训练2 (2012·湖北武汉4月调研,18)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知B =60°,cos(B +C )=-1114.(1)求cos C 的值;(2)若a =5,求△ABC 的面积. 热点三 正、余弦定理的实际应用 【例3】某城市有一条公路,自西向东经过A 点到市中心O 点后转向东北方向OB .现要修建一条铁路L ,L 在OA 上设一站A ,在OB 上设一站B ,铁路在AB 部分为直线段.现要求市中心O 与AB 的距离为10 km ,问把A ,B 分别设在公路上离市中心O 多远处才能使A ,B 之间的距离最短?并求最短距离.(结果保留根号)规律方法 (1)三角形应用题主要是解决三类问题:测高度、测距离和测角度.(2)在解三角形时,要根据具体的已知条件合理选择解法,同时,不可将正弦定理与余弦定理割裂开来,有时需综合运用.(3)在解决与三角形有关的实际问题时,首先要明确题意,正确画出平面图形或空间图形,然后根据条件和图形特点将问题归纳到三角形中解决.要明确先用哪个公式或定理,先求哪些量,确定解三角形的方法.在演算过程中,要算法简练、算式工整、计算正确,还要注意近似计算的要求.(4)在画图和识图过程中要准确理解题目中所涉及的几种角,如仰角、俯角、方位角,以防出错.(5)有些时候也必须注意到三角形的特殊性,如直角三角形、等腰三角形、锐角三角形等. 变式训练3 如图,一船在海上自西向东航行,在A 处测得某岛M 的方位角为北偏东α,前进m km 后在B 处测得该岛的方位角为北偏东β,已知该岛周围n km 范围内(包括边界)有暗礁,现该船继续东行.当α与β满足条件__________时,该船没有触礁危险.思想渗透化归转化思想——解答三角恒等变换问题求解恒等变换问题的思路:一角二名三结构,即用化归转化的思想“去异求同”的过程,具体分析如下:(1)变角:首先观察角与角之间的关系,注意角的一些常用变换形式,角的变换是三角函数变换的核心;(2)变名:其次看函数名称之间的关系,通常“切化弦”,诱导公式的运用; (3)结构:再次观察代数式的结构特点,降幂与升幂,巧用“1”的代换等. 【典型例题】(2012·福建高考,文20)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:①sin 213°+cos 217°-sin 13°cos 17°;②sin 215°+cos 215°-sin 15°cos 15°;③sin 218°+cos 212°-sin 18°cos 12°;④sin 2(-18°)+cos 248°-sin(-18°)cos 48°;⑤sin 2(-25°)+cos 255°-sin(-25°)cos 55°.(1)试从上述五个式子中选择一个,求出这个常数;(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.解法一:(1)选择②式,计算如下:sin 215°+cos 215°-sin 15°cos 15°=1-12sin 30°=1-14=34.(2)三角恒等式为sin 2α+cos 2(30°-α)-sin αcos(30°-α)=34.证明如下:sin 2α+cos 2(30°-α)-sin αcos(30°-α)=sin 2α+(cos 30°cos α+sin 30°sin α)2-sin α(cos 30°cos α+sin 30°sin α)=sin 2α+34cos 2α+32sin αcos α+14sin 2α-32sin αcos α-12sin 2α=34sin 2α+34cos 2α=34.解法二:(1)同解法一.(2)三角恒等式为sin 2α+cos 2(30°-α)-sin αcos(30°-α)=34.证明如下:sin 2α+cos 2(30°-α)-sin αcos(30°-α)=1-cos 2α2+1+cos(60°-2α)2-sin α(cos 30°cos α+sin 30°sin α)=12-12cos 2α+12+12(cos 60°cos 2α+sin 60°sin 2α)-32sin αcos α-12sin 2α =12-12cos 2α+12+14cos 2α+34sin 2α-34sin 2α-14(1-cos 2α) =1-14cos 2α-14+14cos 2α=34.1.已知3cos x -sin x =-65,则sin ⎝⎛⎭⎫π3-x =( ). A .35 B .-35 C .65 D .-652.在△ABC 中,如果0<tan A tan B <1,那么△ABC 是( ). A .锐角三角形 B .直角三角形 C .钝角三角形 D .不能确定3.(2012·浙江台州中学二模,理2)若sin 2α=2425,0<α<π2,则2cos ⎝⎛⎭⎫π4-α的值为( ). A .15 B .-15C .75D .±154.(2012·江西南昌二模,5)已知cos ⎝⎛⎭⎫x -π6=-33,则cos x +cos ⎝⎛⎭⎫x -π3的值是( ). A .-233 B .±233 C .-1 D .±15.(2012·山东淄博一模,10)在△ABC 中,已知b cos C +c cos B =3a cos B ,其中a ,b ,c分别为角A ,B ,C 的对边,则cos B 的值为( ).A .13B .-13C .223D .-2236.已知sin x =5-12,则sin 2⎝⎛⎭⎫x -π4=______. 7.(2012·浙江部分重点中学联考,理18)在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,向量p =⎝⎛⎭⎫1-sin A ,127,q =(cos 2A,2sin A ),且p ∥q . (1)求sin A 的值;(2)若b =2,△ABC 的面积为3,求a .8.(2012·广东广州二模,16)已知函数f (x )=A sin ⎝⎛⎭⎫ωx -π3(A >0,ω>0)在某一个周期内的图象的最高点和最低点的坐标分别为⎝⎛⎭⎫5π12,2,⎝⎛⎭⎫11π12,-2. (1)求A 和ω的值;(2)已知α∈⎝⎛⎭⎫0,π2,且sin α=45,求f (α)的值. 参考答案命题调研·明晰考向真题试做1.A 解析:因为tan α,tan β是方程x 2-3x +2=0的两根,所以tan α+tan β=3,tan α·tan β=2,而tan(α+β)=tan α+tan β1-tan α·tan β=31-2=-3,故选A.2.D 解析:由θ∈⎣⎡⎦⎤π4,π2,得2θ∈⎣⎡⎦⎤π2,π. 又sin 2θ=378,故cos 2θ=-18.故sin θ=1-cos 2θ2=34. 3.A 解析:在△ABC 中,由正弦定理:b sin B =csin C,∴sin C sin B =c b , ∴sin 2B sin B =85,∴cos B =45. ∴cos C =cos 2B =2cos 2B -1=725.4.2π3 解析:∵由(a +b -c )(a +b +c )=ab ,整理可得,a 2+b 2-c 2=-ab ,∴cos C =a 2+b 2-c 22ab=-ab 2ab =-12,∴C =2π3. 5.解:(1)由a cos C +3a sin C -b -c =0及正弦定理得 sin A cos C +3sin A sin C -sin B -sin C =0. 因为B =π-A -C ,所以3sin A sin C -cos A sin C -sin C =0.由于sin C ≠0,所以sin ⎝⎛⎭⎫A -π6=12. 又0<A <π,故A =π3.(2)△ABC 的面积S =12bc sin A =3,故bc =4.而a 2=b 2+c 2-2bc cos A ,故b 2+c 2=8. 解得b =c =2.6.解:(1)因为0<A <π,cos A =23,得sin A =1-cos 2A =53,又5cos C =sin B =sin(A +C )=sin A cos C +cos A sin C =53cos C +23sin C . 所以tan C = 5.(2)由tan C =5,得sin C =56,cos C =16. 于是sin B =5cos C =56. 由a =2及正弦定理a sin A =csin C ,得c = 3.设△ABC 的面积为S , 则S =12ac sin B =52.精要例析·聚焦热点 热点例析【例1】解:(1)∵f (x )=1+cos x -3sin x=1+2cos ⎝⎛⎭⎫x +π3, ∴函数f (x )的最小正周期为2π.又∵-1≤cos ⎝⎛⎭⎫x +π3≤1, ∴函数f (x )的值域为[-1,3]. (2)∵f ⎝⎛⎭⎫α-π3=13, ∴1+2cos α=13,即cos α=-13.∵cos 2α1+cos 2α-sin 2α=cos 2α-sin 2α2cos 2α-2sin αcos α=(cos α+sin α)(cos α-sin α)2cos α(cos α-sin α)=cos α+sin α2cos α,又∵α为第二象限角,且cos α=-13,∴sin α=223.∴原式=cos α+sin α2cos α=-13+223-23=1-222.【变式训练1】解:(1)f (x )=3sin ωx -cos ωx =2⎝⎛⎭⎫32sin ωx -12cos ωx=2sin ⎝⎛⎭⎫ωx -π6. ∵函数f (x )的最小正周期为6π,∴T =2πω=6π,即ω=13.∴f (x )=2sin ⎝⎛⎭⎫13x -π6. ∴f ⎝⎛⎭⎫32π=2sin ⎝⎛⎭⎫13×32π-π6=2sin π3= 3. (2)f ⎝⎛⎭⎫3α+π2 =2sin ⎣⎡⎦⎤13⎝⎛⎭⎫3α+π2-π6 =2sin α=-1013,∴sin α=-513.f (3β+2π)=2sin ⎣⎡⎤13(3β+2π)-π6 =2sin ⎝⎛⎭⎫β+π2=2cos β=65, ∴cos β=35.∵α,β∈⎣⎡⎦⎤-π2,0, ∴cos α=1-sin 2α=1213,sin β=-1-cos 2β=-45.∴cos(α+β)=cos αcos β-sin αsin β=1213×35-513×45=1665.【例2】解:(1)由m ∥n ,得(2b -c )cos A -a cos C =0, ∴(2sin B -sin C )cos A -sin A cos C =0, 2sin B cos A =sin C cos A +sin A cos C =sin(A +C )=sin(π-B )=sin B .在锐角三角形ABC 中,sin B >0,∴cos A =12,故A =π3.(2)在锐角三角形ABC 中,A =π3,故π6<B <π2. ∴y =2sin 2B +cos ⎝⎛⎭⎫π3-2B =1-cos 2B +12cos 2B +32sin 2B =1+32sin 2B -12cos 2B=1+sin ⎝⎛⎭⎫2B -π6. ∵π6<B <π2,∴π6<2B -π6<5π6. ∴12<sin ⎝⎛⎭⎫2B -π6≤1,32<y ≤2. ∴函数y =2sin 2B +cos ⎝⎛⎭⎫π3-2B 的值域为⎝⎛⎦⎤32,2. 【变式训练2】解:(1)在△ABC 中,由cos(B +C )=-1114,得sin(B +C )=1-cos 2(B +C )=1-⎝⎛⎭⎫-11142=5314,∴cos C =cos [(B +C )-B ]=cos(B +C )cos B +sin(B +C )sin B =-1114×12+5314×32=17.(2)由(1),得sin C =1-cos 2C =1-⎝⎛⎭⎫172=437,sin A =sin(B +C )=5314.在△ABC 中,由正弦定理a sin A =c sin C,得 55314=c 437,∴c =8.故△ABC 的面积为S =12ac sin B =12×5×8×32=10 3.【例3】解:在△AOB 中,设OA =a ,OB =b . 因为OA 为正西方向,OB 为东北方向, 所以∠AOB =135°. 又O 到AB 的距离为10,所以S △ABO =12ab sin 135°=12|AB |·10,得|AB |=220ab .设∠OAB =α,则∠OBA =45°-α. 因为a =10sin α,b =10sin(45°-α),所以ab =10sin α·10sin(45°-α)=100sin α·sin(45°-α)=100sin α⎝⎛⎭⎫22cos α-22sin α=10024sin 2α-24(1-cos 2α)=4002sin(2α+45°)-2≥4002-2. 当且仅当α=22°30′时,“=”成立. 所以|AB |≥220×4002-2=20(2+1). 当且仅当α=22°30′时,“=”成立.所以,当a =b =10sin 22°30′=102(2+2)时,A ,B 之间的距离最短,且最短距离为20(2+1) km.即当A ,B 分别在OA ,OB 上离市中心O 102(2+2) km 处时,能使A ,B 之间的距离最短,最短距离为20(2+1) km.【变式训练3】m cos αcos β>n sin(α-β)解析:∠MAB =90°-α,∠MBC =90°-β=∠MAB +∠AMB =90°-α+∠AMB , 所以∠AMB =α-β.由题可知,在△ABM 中,根据正弦定理得BM sin(90°-α)=m sin(α-β),解得BM =m cos αsin(α-β).要使船没有触礁危险,需要BM sin(90°-β)=m cos αcos βsin(α-β)>n ,所以α与β满足m cos αcos β>n sin(α-β)时,该船没有触礁危险.创新模拟·预测演练1.B 解析:由3cos x -sin x =2⎝⎛⎭⎫32cos x -12sin x=2⎝⎛⎭⎫sin π3cos x -cos π3sin x =2sin ⎝⎛⎭⎫π3-x , 可得sin ⎝⎛⎭⎫π3-x =-35. 2.C 解析:由题意0<A <π,0<B <π,tan A tan B >0,则A ,B 两角为锐角, 又tan(A +B )=tan A +tan B1-tan A tan B>0,则A +B 为锐角,则角C 为钝角,故选C.3.C 解析:因为0<α<π2,则2cos ⎝⎛⎭⎫π4-α=cos α+sin α=(cos α+sin α)2=1+sin 2α=75. 4.C 解析:cos x +cos ⎝⎛⎭⎫x -π3=cos x +cos x cos π3+sin x sin π3=32cos x +32sin x =3cos ⎝⎛⎭⎫x -π6=3×⎝⎛⎭⎫-33=-1. 5.A 解析:因为b cos C +c cos B =3a cos B , 所以sin B cos C +cos B sin C =3sin A cos B ,即sin(B +C )=3sin A cos B ,即cos B =13.6.2-5 解析:sin 2⎝⎛⎭⎫x -π4 =sin ⎝⎛⎭⎫2x -π2=-cos 2x =-(1-2sin 2x )=2sin 2x -1 =2×⎝⎛⎭⎪⎫5-122-1=3-5-1=2- 5. 7.解:(1)∵p ∥q ,∴127cos 2A =(1-sin A )·2sin A , ∴6(1-2sin 2A )=7sin A (1-sin A ),5sin 2A +7sin A -6=0.∴sin A =35(sin A =-2舍).(2)由S △ABC =12bc sin A =3,b =2,得c =5,又cos A =±1-sin 2A =±45,∴a 2=b 2+c 2-2bc cos A =4+25-2×2×5cos A =29-20cos A ,当cos A =45时,a 2=13,a =13;当cos A =-45时,a 2=45,a =3 5.8.解:(1)∵函数f (x )的图象的最高点坐标为⎝⎛⎭⎫5π12,2, ∴A =2.依题意,得函数f (x )的周期T =2⎝⎛⎭⎫11π12-5π12=π,∴ω=2πT=2.(2)由(1)得f (x )=2sin ⎝⎛⎭⎫2x -π3. ∵α∈⎝⎛⎭⎫0,π2,且sin α=45, ∴cos α=1-sin 2α=35.∴sin 2α=2sin αcos α=2425,cos 2α=1-2sin 2α=-725.∴f (α)=2sin ⎝⎛⎭⎫2α-π3 =2⎝⎛⎭⎫sin 2αcos π3-cos 2αsin π3 =24+7325.。
(完整版)近五年浙江三角函数高考真题

近五年浙江三角函数高考真题一、(2013理)4.已知函数()cos()(0,0,R)f x A x A ωφωφ=+>>∈,则“()f x 是奇函数”是“2πφ=”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件6.已知R,sin 2cos ααα∈+=tan2α= A .43B .34 C .34-D .43-16.在△ABC 中,90C ∠=,M 是BC 的中点.若1sin 3BAM ∠=,则sin BAC ∠= .(2013文)3.(与理4姐妹题)若R α∈,则“0α=”是“sin cos αα<”的 A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件6.函数()sin cos f x x x x =+的最小正周期和振幅分别是 A .π,1 B .π,2 C .2π,1 D .2π,218.在锐角△ABC 中,内角,,A B C 的对边分别为,,a b c ,且2sin a B =. (Ⅰ)求角A 的大小;(Ⅱ) 若6,8a b c =+=,求△ABC 的面积.二、(2012理)4.把函数cos21y x =+的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移 1个单位长度,得到的图像是18.(14分)在△ABC 中,内角,,A B C 的对边分别为,,a b c .已知C B A cos 5sin ,32cos ==. (1)求tan C 的值;(2)若2a =ABC 的面积.(2012文) 6.(同理4)18.( 14分)在△ABC 中,内角,,A B C 的对边分别为,,a b c ,且sin 3cos b A a B =. (Ⅰ)求角B 的大小;(Ⅱ)若3,sin 2sin b C A ==,求,a c 的值.三、(2011理) 6.若0,022ππαβ<<-<<,1cos()43πα+=,3cos()42πβ-=,则cos()2βα+= A 3B .3C 53D .618.(14分)在△ABC 中,角,,A B C 所对的边分别为,,a b c .已知sin sin sin (R)A C pB p +=∈,且214ac b =.(Ⅰ)当5,14p b ==时,求,a c 的值;(Ⅱ)若角B 为锐角,求p 的取值范围.(2011文)5.在ABC ∆中,角C B A ,,所对的边分别是c b a ,,,若B b A a sin cos =,则=+B A A 2cos cos sin(A )21-(B )21 (C )1- (D )118.(14分)已知函数()sin ()3f x A x πϕ=+,x R ∈,0A >,02πϕ<<.()y f x =的部分图像如图所示,P 、Q 分别为该图像的最高点和最低点,点P 的坐标为(1,)A .(Ⅰ)求()f x 的最小正周期及ϕ的值; (Ⅱ)若点R 的坐标为(1,0),23PRQ π∠=,求A 的值.三、(2010理) 4.设02x π<<,则“2sin 1x x <”是“sin 1x x <”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件9.设函数()4sin(21)f x x x =+-,则在下列区间中函数()f x 不.存在零点的是 (A )[]4,2-- (B )[]2,0- (C )[]0,2 (D )[]2,4 11.函数2()sin(2)224f x x x π=--的最小正周期是__________________ .18. (l4分)在△ABC 中,角,,A B C 所对的边分别为,,a b c ,已知1cos24C =-.(I)求sin C 的值;(Ⅱ)当2,2sin sin a A C ==时,求b 及c 的长. (2010文) 6.(同理4)12.(与理11姐妹题)函数2()sin (2)4f x x π=-的最小正周期是18.(本题满分)在△ABC ,角,,A B C 所对的边分别为,,a b c ,设S 为△ABC 的面积,满足2223()4S a b c =+-. (Ⅰ)求角C 的大小; (Ⅱ)求sin sin A B +的最大值.三、(2009理)8.已知a 是实数,则函数()1sin f x a ax =+的图象不可能...是D 【命题意图】此题是一个考查三角函数图象的问题,但考查的知识点因含有参数而丰富,结合图形考查使得所考查的问题形象而富有深度.18.(14分)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,且满足25cos25A =,3=⋅AC AB .(I )求ABC ∆的面积; (II )若6b c +=,求a 的值. (2009文) 10.(同理8) 18.(同理18)。
2005-2019年浙江高考理科数学历年真题之三角函数大题(学生版)

2005-2019年浙江高考理科数学历年真题之三角函数大题(学生版)1、(2005年)已知函数f (x )=-3sin 2x +sin x cos x .(Ⅰ)求f (256π)的值;(Ⅱ)设α∈(0,π),f (2α)=41-32,求sin α的值.2、(2006年)如图,函数R x x y ∈+=),sin(2ϕπ,(其中0≤ϕ≤2π)的图象与y 轴交于点(0,1)。
(Ⅰ)求ϕ的值;(Ⅱ)设P 是图象上的最高点,M 、N 是图象与x 轴的交点,求的夹角与PN PM 。
3、(2007年)已知ABC △21+,且sin sin 2A B C +=.(I )求边AB 的长;(II )若ABC △的面积为1sin 6C ,求角C 的度数.4、(2009年)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,且满足25cos 25A =,3AB AC ⋅= .(I )求ABC ∆的面积;(II )若6b c +=,求a 的值.5、(2010年)在ABC ∆中,角A 、B 、C 所对的边分别为a ,b ,c ,已知.412cos -=C (I )求C sin 的值;(II )当a=2,C A sin sin 2=时,求b 及c 的长.6、(2011年)在ABC ∆中,角,,A B C 所对的边分别为a ,b ,c ,已知()sin sin sin ,A C p B p R +=∈且214ac b =.(Ⅰ)当5,14p b ==时,求,a c 的值;(Ⅱ)若角B 为锐角,求p 的取值范围。
7、(2012年)在△ABC 中,内角,,A B C 的对边分别为,,a b c 。
已知cosA=23,sin 5B C =。
(Ⅰ)求tan C 的值;(Ⅱ)若2a =,求△ABC 的面积。
8、(2014年)在ABC ∆中,内角,,A B C 所对的边分别为,,a b c .已知,3a b c ≠=,22cos -cos 3sin cos -3sin cos .A B A A B B =(I )求角C 的大小;(II )若4sin 5A =,求ABC ∆的面积.9、(2015年)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知A =4π,b 2-a 2=21c 2(I )求tan C 的值;(II )若△ABC 的面积为3,求b 的值10、(2016年)在ABC △中,内角,,A B C 所对的边分别为,,.a b c 已知2cos .b c a B +=(1)证明:2;A B =(2)若ABC △的面积2,4a S =求出角A 的大小.11、(2017年)已知函数f (x )=sin 2x –cos 2x –23sin x cos x (x ∈R ).(1)求f (2π3)的值.(2)求f (x )的最小正周期及单调递增区间.12、(2018年)已知角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,它的终边过点P (3455,-).(Ⅰ)求sin (α+π)的值;(Ⅱ)若角β满足sin (α+β)=513,求cos β的值13、(2019年)设函数()sin ,f x x x =∈R .(1)已知[0,2),θ∈π函数()f x θ+是偶函数,求θ的值;(2)求函数22[()][()]124y f x f x ππ=+++的值域.。
最新-2018年高考数学试题分项版解析专题2018 三角函数

2018年高考试题分项版解析数学(理科)专题18 三角函数(教师版)一、选择题:1.(2018年高考浙江卷理科4)把函数y =cos2x +1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图像是2. (2018年高考山东卷理科7)若42ππθ⎡⎤∈⎢⎥⎣⎦,, sin 2=8θ,则sin θ=(A )35(B )45(C (D )34 【答案】D【解析】由42ππθ⎡⎤∈⎢⎥⎣⎦,可得],2[2ππθ∈,812sin 12cos 2-=--=θθ,4322cos 1sin =-=θθ,答案应选D.另解:由42ππθ⎡⎤∈⎢⎥⎣⎦,及sin 2θ可得434716776916761687312sin 1cos sin +=++=+=+=+=+θθθ, 而当42ππθ⎡⎤∈⎢⎥⎣⎦,时θθcos sin >,结合选项即可得47cos ,43sin ==θθ.答案应选D.3.(2018年高考辽宁卷理科7)已知sin cos αα-=,α∈(0,π),则tan α=(A) -1 (B) 2-(C) 2(D) 14.(2018年高考天津卷理科2)设R ϕ∈,则“=0ϕ”是“()=c os(+)f x xϕ()x R ∈为偶函数”的(A )充分而不必要条件 (B)必要而不充分条件 (C)充分必要条件 (D)既不充分也不必要条件5.(2018年高考天津卷理科6)在△ABC 中,内角A ,B ,C 所对的边分别是,,a b c ,已知8=5b c ,=2C B ,则cosC=(A )725(B)725- (C)725± (D)24256.(2018年高考上海卷理科16)在ABC ∆中,若C B A 222sin sin sin <+,则ABC ∆的形状是( )A .锐角三角形B .直角三角形C .钝角三角形D .不能确定 【答案】C【解析】由正弦定理,得,sin 2,sin 2,sin 2C Rc B R b A R a ===代入得到222a b c +<, 由余弦定理的推理得222cos 02a b c C ab+-=<,所以C 为钝角,所以该三角形为钝角三角形.故选择A.【考点定位】本题主要考查正弦定理及其推理、余弦定理的运用.主要抓住所给式子的结构来选择定理,如果出现了角度的正弦值就选择正弦定理,如果出现角度的余弦值就选择余弦定理.本题属于中档题.7.(2018年高考新课标全国卷理科9)已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减。
通用版五年高考2024_2025高考数学真题专题归纳专题06三角函数及解三角形含解析理
1 1
tan tan
2 2
1 1
22 22
3, 5
tan( ) tan 1 2 1 1 , 4 1 tan 1 2 3
11.(2024·江苏卷)已知 sin2 ( ) = 2 ,则 sin 2 的值是____.
4
3
【答案】 1 3
【解析】 sin2 ( ) ( 2 cos 2 sin )2 1 (1 sin 2 )
图1
9
图2
图3
4.【2024·全国Ⅱ卷】已知 α∈(0, ),2sin2α=cos2α+1,则 sinα= 2
A. 1 5
B. 5 5
C. 3 3
【答案】B
D. 2 5 5
【解析】
2sin 2α cos 2α 1,4sin α cos α 2 cos2 α .
α
0,
2
,
cos
α
0
,
sin α 0, 2sin α cos α ,又 sin2 cos2 1,5sin2 α 1,sin2 α 1 ,又 5
f
x
可得:
cos
4 9
6
0
.又
4 9
,
0
是函数
f
x 图象与
x
轴负半轴的第一个交点,
所以 4 ,解得: 3
9
62
2
所以函数
f
x 的最小正周期为T
2
2 3
4 3
2
2.(2024·新课标Ⅰ)已知 (0, π) ,且 3cos2 8cos 5 ,则 sin (
A5 3
B. 2 3
7.(2024·山东卷)下图是函数 y= sin(ωx+φ)的部分图像,则 sin(ωx+φ)= ( )
《三角函数》高考真题理科大题总结和答案解析

《三角函数》大题总结1.【2015高考新课标2,理17】ABC ∆中,D 是BC 上的点,AD 平分BAC ∠,ABD ∆面积是ADC ∆面积的2倍.(Ⅰ) 求sin sin BC∠∠;(Ⅱ)若1AD =,DC =BD 和AC 的长. 2.【2015江苏高考,15】在ABC ∆中,已知 60,3,2===A AC AB .(1)求BC 的长; (2)求C 2sin 的值.3.【2015高考福建,理19】已知函数f()x 的图像是由函数()cos g x x =的图像经如下变换得到:先将()g x 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移2p 个单位长度. (Ⅰ)求函数f()x 的解析式,并求其图像的对称轴方程;(Ⅱ)已知关于x 的方程f()g()x x m +=在[0,2)p 内有两个不同的解,a b . (1)求实数m 的取值范围;(2)证明:22cos ) 1.5m a b -=-( 4.【2015高考浙江,理16】在ABC ∆中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知4A π=,22b a -=122c .(1)求tan C 的值;(2)若ABC ∆的面积为7,求b 的值.5.【2015高考山东,理16】设()2sin cos cos 4f x x x x π⎛⎫=-+ ⎪⎝⎭.(Ⅰ)求()f x 的单调区间;(Ⅱ)在锐角ABC ∆中,角,,A B C 的对边分别为,,a b c ,若0,12A f a ⎛⎫== ⎪⎝⎭,求ABC ∆面积的最大值.6.【2015高考天津,理15】已知函数()22sin sin 6f x x x π⎛⎫=-- ⎪⎝⎭,R x ∈(I)求()f x 最小正周期; (II)求()f x 在区间[,]34p p-上的最大值和最小值.7.【2015高考安徽,理16】在ABC ∆中,3,6,4A AB AC π===,点D 在BC 边上,AD BD =,求AD 的长.8.【2015高考重庆,理18】 已知函数()2sin sin 2f x x x x π⎛⎫=-- ⎪⎝⎭(1)求()f x 的最小正周期和最大值; (2)讨论()f x 在2,63ππ⎡⎤⎢⎥⎣⎦上的单调性.9.【2015高考四川,理19】 如图,A ,B ,C ,D 为平面四边形ABCD 的四个内角. (1)证明:1cos tan ;2sin A A A-= (2)若180,6,3,4,5,A C AB BC CD AD +=====o 求tantan tan tan 2222A B C D+++的值.10.【2015高考湖北,理17】某同学用“五点法”画函数π()sin()(0,||)2f x A x ωϕωϕ=+><在某一个周期内的图象 时,列表并填入了部分数据,如下表:(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置...........,并直接写出函数()f x 的解 析式; (Ⅱ)将()y f x =图象上所有点向左平行移动θ(0)θ>个单位长度,得到()y g x =的图象. 若()y g x =图象的一个对称中心为5π(,0)12,求θ的最小值.11.【2015高考陕西,理17】(本小题满分12分)C ∆AB 的内角A ,B ,C 所对的边分别为a ,b ,c .向量(),3m a b =与()cos ,sin n =A B 平行.(I )求A ;(II )若a =2b =求C ∆AB 的面积.12.【2015高考北京,理15】已知函数2()cos 222x x xf x =-.(Ⅰ) 求()f x 的最小正周期;(Ⅱ) 求()f x 在区间[π0]-,上的最小值.13.【2015高考广东,理16】在平面直角坐标系xoy 中,已知向量2m ⎛= ,()sin ,cos n x x =,0,2x π⎛⎫∈ ⎪⎝⎭. (1)若m n ⊥,求tan x 的值; (2)若m 与n 的夹角为3π,求x 的值.14.【2015高考湖南,理17】设ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,tan a b A =,且B 为钝角.(1)证明:2B A π-=;(2)求sin sin A C +的取值范围.《三角函数》大题答案1.【答案】(Ⅰ)12;(Ⅱ)1. 【解析】(Ⅰ)1sin 2ABD S AB AD BAD ∆=⋅∠,1sin 2ADC S AC AD CAD ∆=⋅∠,因为2ABD ADC S S ∆∆=,BAD CAD ∠=∠,所以2AB AC =.由正弦定理可得sin 1sin 2B AC C AB ∠==∠.(Ⅱ)因为::ABD ADC S S BD DC ∆∆=,所以BD =ABD ∆和ADC ∆中,由余弦定理得2222cos AB AD BD AD BD ADB =+-⋅∠,2222cos AC AD DC AD DC ADC =+-⋅∠.222222326AB AC AD BD DC +=++=.由(Ⅰ)知2AB AC =,所以1AC =.2.【答案】(1(23.【答案】(Ⅰ) f()2sin x x =,(k Z).2x k pp =+?;(Ⅱ)(1)(-;(2)详见解析.【解析】解法一:(1)将()cos g x x =的图像上所有点的纵坐标伸长到原来的2倍(横坐标不变)得到y 2cos x =的图像,再将y 2cos x =的图像向右平移2p个单位长度后得到y 2cos()2x p=-的图像,故f()2sin x x =,从而函数f()2sin x x =图像的对称轴方程为(k Z).2x k pp =+?(2)1) f()g()2sin cos )x x x x x x +=+=)x j +(其中sinj j ==) 依题意,sin(x j +在区间[0,2)p 内有两个不同的解,a b 当且仅当|1<,故m 的取值范围是(-.2)因为,a b )=m x j +在区间[0,2)p 内有两个不同的解, 所以sin()=a j +sin(b j +.当1£+=2(),2();2pa b j a b p b j --=-+当-时, 3+=2(),32();2pa b j a b p b j --=-+所以2222cos )cos 2()2sin ()11 1.5m a b b j b j -=-+=+-=-=-( 解法二:(1)同解法一. (2)1) 同解法一.2) 因为,a b )=m x j +在区间[0,2)p 内有两个不同的解, 所以sin()=a j +sin(b j +.当1£+=2(),+();2pa b j a j p b j -=-+即当-时, 3+=2(),+3();2pa b j a j p b j -=-+即 所以cos +)cos()a j b j =-+(于是cos )cos[()()]cos()cos()sin()sin()a b a j b j a j b j a j b j -=+-+=+++++(22222cos()sin()sin()[1] 1.5mb j a j b j=-++++=--+=-4.【答案】(1)2;(2)3b=.又∵4Aπ=,1sin32bc A=,∴bc=,故3b=.5.【答案】(I)单调递增区间是(),44k k k Zππππ⎡⎤-++∈⎢⎥⎣⎦;单调递减区间是()3,44k k k Zππππ⎡⎤++∈⎢⎥⎣⎦(II)ABC∆【解析】(I)由题意知()1cos2sin2222xxf xπ⎛⎫++⎪⎝⎭=-sin21sin21sin2222x xx-=-=-由222,22k x k k Zππππ-+≤≤+∈可得,44k x k k Zππππ-+≤≤+∈由3222,22k x k k Zππππ+≤≤+∈可得3,44k x k k Zππππ+≤≤+∈所以函数()f x的单调递增区间是(),44k k k Zππππ⎡⎤-++∈⎢⎥⎣⎦;单调递减区间是()3,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦6.【答案】(I)π; (II) max ()f x =,min 1()2f x =-.【解析】(I) 由已知,有1cos 21cos21113()cos22cos222222x x f x x x x π⎛⎫-- ⎪⎛⎫-⎝⎭=-=+- ⎪⎝⎭112cos2sin 2426x x x π⎛⎫-=- ⎪⎝⎭. 所以()f x 的最小正周期22T ππ==. (II)因为()f x 在区间[,]36p p --上是减函数,在区间[,]64p p-上是增函数,11(),(),()34624f f f πππ-=--=-=,所以()f x 在区间[,]34p p -,最小值为12-. 7.【解析】如图,设ABC ∆的内角,,A B C 所对边的长分别是,,a b c ,由余弦定理得2222232cos 626cos1836(36)904a b c bc BAC π=+-∠=+-⨯⨯=+--=,所以a =又由正弦定理得sin sinb BAC B a ∠===.由题设知04B π<<,所以cos B ===在ABD ∆中,由正弦定理得sin 6sin 3sin(2)2sin cos cos AB B B AD B B B Bπ⋅====-8.【答案】(1)最小正周期为p ,(2)()f x 在5[,]612ππ上单调递增;()f x 在52[,]123ππ上单调递减.当223x πππ≤-≤时,即52123x ππ≤≤时,()f x 单调递减, 综上可知,()f x 在5[,]612ππ上单调递增;()f x 在52[,]123ππ上单调递减.9.【答案】(1)详见解析;(2.【解析】(1)2sin2sin 1cos 22tan 2sin cos 2sin cos 222A AA A A A A A-===. (2)由180A C +=,得180,180C A D B =-=-. 由(1),有tantan tan tan 2222A B C D +++ 1cos 1cos 1cos(180)1cos(180)sin sin sin(180)sin(180)A B A B A B A B ------=+++--22sin sin A B=+ 连结BD ,在ABD ∆中,有2222cos BD AB AD AB AD A =+-⋅, 在BCD ∆中,有2222cos BD BC CD BC CD C =+-⋅,所以 222cos AB AD AB AD A +-⋅222cos BC CD BC CD A =++⋅,则2222222265343cos 2()2(6534)7AB AD BC CD A AB AD BC CD +--+--===⋅+⋅⨯+⨯,于是sin A ===. 连结AC ,同理可得2222222263541cos 2()2(6354)19AB BC AD CD B AB BC AD CD +--+--===⋅+⋅⨯+⨯,于是sin B ===所以tan tan tan tan 2222A B C D+++ 22sin sin A B=+=10.【答案】(Ⅰ)π()5sin(2)6f x x =-;(Ⅱ)π6.【解析】(Ⅰ)根据表中已知数据,解得π5,2,6A ωϕ===-. 数据补全如下表:且函数表达式为()5sin(2)6f x x =-.(Ⅱ)由(Ⅰ)知 π()5sin(2)6f x x =-,得π()5sin(22)6g x x θ=+-.因为sin y x =的对称中心为(π,0)k ,k ∈Z . 令π22π6x k θ+-=,解得ππ212k x θ=+-,k ∈Z . 由于函数()y g x =的图象关于点5π(,0)12成中心对称,令ππ5π21212k θ+-=, 解得ππ23k θ=-,k ∈Z . 由0θ>可知,当1k =时,θ取得最小值π6.11.【答案】(I )3π;(II【解析】(I )因为//m n ,所以sin cos 0a B A -=,由正弦定理,得sinAsinB A 0-=又sin 0B ≠,从而tan A =,从而sin B ,又由a b >,知A B >,所以cos B故()sinC sin A B sin sin cos cos sin 333B B πππ⎛⎫=+=B +=+= ⎪⎝⎭所以C ∆AB 的面积为1bcsinA 212.【答案】(1)2π,(2)1-- 【解析】 :211cos ()sincossin sin 22222xxxxf x x -=-=⋅-⋅=sin cos x x =+-sin()4x π=+- (1)()f x 的最小正周期为221T ππ==; (2)30,444x x ππππ-≤≤∴-≤+≤,当3,424x x πππ+=-=-时,()f x取得最小值为:1--13.【答案】(1)1;(2)512x π=. 【解析】(1)∵2m ⎛=,()sin ,cos n x x =且m n⊥, ∴()2sin ,cos sin 04m n x x x x x π⎛⎛⎫⋅=⋅==-= ⎪⎝⎭,又0,2x π⎛⎫∈ ⎪⎝⎭,∴ ,444x πππ⎛⎫-∈- ⎪⎝⎭,∴ 04x π-=即4x π=,∴ tan tan 14x π==; (2)由(1)依题知 sin 4cos sin 34x m n x m nπππ⎛⎫-⋅⎛⎫===- ⎪⎝⎭⋅⎛,∴ 1sin 42x π⎛⎫-= ⎪⎝⎭又,444x πππ⎛⎫-∈- ⎪⎝⎭, ∴ 46x ππ-=即512x π=. 14.【答案】(1)详见解析;(2)9]8.(2)2022A A πππ-+=->,∴(0,)4A π∈,于是sin sin sin sin(2)2A C A A π+=+-2219sin cos 22sin sin 12(sin )48A A A A A =+=-++=--+,∵04A π<<,∴0sin A <<,因此21992(sin )488A <--+≤,由此可知sin sin A C +的取值范围是9]8.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江历年理科高考题之三角函数大题
(教师版)
1、(2005年)已知函数f (x )=-3sin 2x +sin x cos x .
(Ⅰ) 求f (
256π)的值; (Ⅱ) 设α∈(0,π),f (2α
)=413,求sin α的值.
解:(Ⅰ)
251253
sin
,cos 6262
ππ==,2252525253sin cos 6
666f π
πππ⎛⎫∴=-+= ⎪
⎝⎭
(Ⅱ) ()331
2sin 22
f x x x =
-, 31313sin 22
2242f ααα⎛⎫
∴=+-=-
⎪⎝⎭ 216sin 4sin 110αα--=,解得15
sin 8
α±=
()0,,sin 0απα∈∴>,故135
sin α+=
2、(2006年)如图,函数R x x y ∈+=),sin(2ϕπ,(其中0≤ϕ≤2
π
)的图象与y 轴交于点(0,1)。
(Ⅰ)求ϕ的值;
(Ⅱ)设P 是图象上的最高点,M 、N 是图象与x 轴的交点,求的夹角与PN PM 。
解:(I )因为函数图像过点(0,1),所以1sin 2=ϕ,即2
1
sin =
ϕ
因为2
0π
ϕ≤
≤,所以6
π
ϕ=。
(II )由函数)6π+π=x 2sin(y
及其图象,得)0,61(-M ,)2,31(P ,)0,6
5
(N
所以)2,21(--=PM
,)2,2
1
(-=PN ,从而
PN PM PN PM >=
<,cos =
17
15
,故1715arccos ,>=<PN PM 。
3、(2007年)已知ABC △
1
,且sin sin A B C +=
.
(I )求边AB 的长; (II )若ABC △的面积为1
sin 6
C ,求角C 的度数. 解:(I
)由题意及正弦定理,得1AB BC AC ++=
,
BC AC +=,两式相减,得1AB =.
(II )由ABC △的面积
11sin sin 26BC AC C C =,得13
BC AC =, 由余弦定理,得222cos 2AC BC AB C AC BC +-=
22()21
22
AC BC AC BC AB AC BC +--==,所以60C =. 4、(2009年)在ABC
∆中,角,,A B C 所对的边分别为,,a b c ,且满足cos 25
A =,3A
B A
C ⋅=. (I )求ABC ∆的面积;
(II )若6b c +=,求a 的值. 解:(Ⅰ)因为cos
22A =,所以23cos 2cos 125A A =-=,4sin 5
A =.
又由3AB
AC =·,得cos 3bc A =,所以5bc =. 因此1
sin 22
ABC S bc A =
=△. (Ⅱ)由(Ⅰ)知5bc =.又6b c +=, 所以51b c ==,或15b c ==,.
由余弦定理,得2
22
2cos 20a b c bc A =+-=,所以a =
5、(2010年)在ABC ∆中,角A 、B 、C 所对的边分别为a ,b ,c ,已知.4
1
2cos -=C (I )求C sin 的值; (II )当a=2,C A sin sin 2=时,求b 及c 的长. 解:(Ⅰ)因为2
1
cos 212sin 4
C C =-=-
,及0C π<<,所以sin C = (Ⅱ)当2,2sin sin a A C ==时,由正弦定理
sin sin a c
A C
=,得 4.c =
由2
1cos 22cos 1,
4
C C =-=-及0C π<<得cos C =
由余弦定理222
2cos c a b ab C =+-,得2
6120b b ±
-=
解得626b =
或,所以6,26
4 4.
b b
c c ⎧⎧==⎪⎪⎨⎨==⎪⎪⎩⎩或
6、(2011年)在ABC ∆中,角,,A B C 所对的边分别为a ,b ,c ,已知()sin sin sin ,A C p B p R +=∈ 且2
14
ac b =
. (Ⅰ)当5
,14
p b =
=时,求,a c 的值; (Ⅱ) 若角B 为锐角,求p 的取值范围。
7、(2012年)在△ABC 中,内角,,A B C 的对边分别为,,a b c 。
已知cosA=2
3
,sin 5cos B C =。
(1)求tan C 的值; (2)若2a =
,求△ABC 的面积。
浙江历年理科高考题之三角函数大题
1、(2005年)已知函数f (x )=-3sin 2x +sin x cos x .
(Ⅰ) 求f (
256π)的值; (Ⅱ) 设α∈(0,π),f (2
α
)=413,求sin α的值.
2、(2006年)如图,函数R x x y ∈+=),sin(2ϕπ,(其中0≤ϕ≤2
π
)的图象与y 轴交于点(0,1)。
(Ⅰ)求ϕ的值;
(Ⅱ)设P 是图象上的最高点,M 、N 是图象与x 轴的交点,求的夹角与PN PM 。
3、(2007年)已知ABC △1,且sin sin A B C +=.
(I )求边AB 的长; (II )若ABC △的面积为1
sin 6
C ,求角C 的度数.
4、(2009年)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,且满足cos 25
A =,3A
B A
C ⋅=. (I )求ABC ∆的面积; (II )若6b c +=,求a 的值.
5、(2010年)在ABC ∆中,角A 、B 、C 所对的边分别为a ,b ,c ,已知.4
1
2cos -=C (I )求C sin 的值; (II )当a=2,C A sin sin 2=时,求b 及c 的长.
6、(2011年)在ABC ∆中,角,,A B C 所对的边分别为a ,b ,c ,已知()sin sin sin ,A C p B p R +=∈ 且214
ac b =
. (Ⅰ)当5
,14
p b ==时,求,a c 的值; (Ⅱ) 若角B 为锐角,求p 的取值范围。
7、(2012年)在△ABC 中,内角,,A B C 的对边分别为,,a b c 。
已知cosA=2
3
,sin B C =。
(Ⅰ)求tan C 的值;
(Ⅱ)若a =ABC 的面积。
