反比例函数难题拓展(含答案)
反比例函数(含答案)

例1 已知一次函数2y x k =-的图象与反比例函数5k y x+=的图象相交,其中有一个交点的纵坐标为-4,求这两个函数的解析式. 解: 依题意,由两个函数解析式得所以一次函数和反比例函数的解析式分别为例注意: 解本题的关键是正确理解什么叫y 1与x+1成正比例,y 2与x 2成反比例,即把x+1与x 2看成两个新的变量.典型例题四例 (上海试题,2002)如图,直线221+=x y 分别交x 、y 轴于点A 、C ,P 是该直线上在第一象限内的一点,x PB ⊥轴,B 为垂足,9=ABP S ∆(1)求点P 的坐标;(2)设点R 与点P 在同一个反比例函数的图象上,且点R 在直线PB 的右侧.作x RT ⊥轴,T 为垂足,当BRT ∆与AOC ∆相似时,求点R 的坐标.那么2-=b BT ,b RT 6=. ①当RTB ∆∽AOC ∆时,CO BT AO RT =,即2==COAOBT RT , ∴226=-b b ,解得3=b 或1-=b (舍去). ∴ 点R 的坐标为()2,3.②RTB ∆∽ COA ∆时,AO BT CO RT =,即21==AO CO BT RT , ∴2126=-b b ,解得131+=b 或131-=b (舍去). ∴点R 的坐标为⎪⎪⎭⎫ ⎝⎛-+2113,131. 综上所述,点R 的坐标为()2,3或⎪⎫⎛-+113,131.y例 B.((解 :(1)设点A 的坐标为(m,n),那么n AB m OB =-=,.∵ AB OB S ABO ⋅=∆21,∴.4,2)(21-==⋅-mn n m 又mk n =,∴4-==mn k .∴ 双曲线:x y 4-=,直线:4+-=x y .(2)解由xy 4-=,4+-=x y 组成的方程组,得2221+=x ,2221-=y ;例 A 、B 求B 两点的抛物线在x 轴上截得的线段长能否等于3.如果能,求此时抛物线的解析式;如果不能,请说明理由. 解:(1)过点B 作x BH ⊥轴于点H . 在OHB ∆Rt 中,.3,31tan BH HO HO BH HOB =∴==∠由勾股定理,得222OB HO BH =+. 又10=OB ,.3,1,0.)10()3(222==∴>=+∴HO BH BH BH BH ∴ 点B (-3,-1).∵ ∴ ∴ (∵ ∴ ∴ 令 ).31(321)(2122m m GA BH DO GA DO BH DO S +-=+=⋅+⋅=由已知,直线经过第一、二、三象限, ∴ 0>b ,即03>-mm..03,0>-∴>m m由此得 .30<<m ∴ ).31)(3(21mm S +-=即 ).30(292<<-=m mm S (3)过A 、B 两点的抛物线在x 轴上截得的线段长不能等于3.证明如下:S ∆由得 ∵ ∴ ∴ ∴ 即 则 aa 2121令 .321=-x x 则 .9324)21(2=-⋅-+-aa a a 整理,得 01472=+-a a . ∵ ,012174)4(2<-=⨯⨯--=∆∴ 方程01472=+-a a 无实数根.因此过A 、B 两点的抛物线在x 轴上截得的线段长不能等于3.典型例题八例 在以下各小题后面的括号里填写正确的记号.若这个小题成正比例关系,填(正);若成反比例关系,填(反);若既不成正比例关系又不成反比例关系,填(非).(1)周长为定值的长方形的长与宽的关系 [ ]; (2)面积为定值时长方形的长与宽的关系 [ ]; (3)圆面积与半径的关系 [ ]; (4)圆面积与半径平方的关系 [ ];(5)三角形底边一定时,面积与高的关系 [ ]; (6)三角形面积一定时,底边与高的关系 [ ];(7)三角形面积一定且一条边长一定,另两边的关系 [ ]; (8)在圆中弦长与弦心距的关系 [ ];(9)x 越来越大时,y 越来越小,y 与x 的关系 [ ]; (10)在圆中弧长与此弧所对的圆心角的关系 [ ].说明:本题考查了正比例函数和反比例函数的定义,关键是一定要弄清出二者的定义。
反比例函数经典例题(有答案)

反比例函数专题复习一、反比例函数的对称性1、直线y=ax(a>0)与双曲线y= 3/x交于A(x1,y1)、B(x2,y2)两点,则4x1y2-3x2y1=2、如图1,直线y=kx(k>0)与双曲线y= 2/x交于A,B两点,若A,B两点的坐标分别为A(x1,y1),B(x2,y2),则x1y2+x2y1的值为()A、-8B、4C、-4D、0解析:直线Y=KX和双曲线Y=2/X图象都关于原点对称因此两交点A、B也关于原点对称X2=-X1,Y2=-Y1双曲线形式可变化为XY=2,即双曲线上点的横纵坐标乘积为2因此X1Y1=2X1Y2+X2Y1=X1(-Y1)+(-X1)Y1=-X1Y1-X1Y1=-4图1 图2 图3 图4二、反比例函数中“K”的求法1、如图2,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数 y=k/x的图象上.那么k的值是()A、3B、6C、12D、 15/4解析:∵BC在直线X=1上,设B(1,M),则C(1,M-3),∴A(5,M-3),又A、B都在双曲线上,∴1*M=5*(M-3),M=15/4 即K=15/42、如图3,已知点A、B在双曲线y= k/x(x>0)上,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点,若△ABP的面积为3,则k=解析:A(x1,k/x1),B(x2,k/x2)AC:x=x1 BD:y=k/x2P(x1,k/x2)k/x2=k/2x1 2x1=x2BP=x2-x1=x1AP=k/x1-k/x2=k/2x1S=x1*k/(2x1)*1/2)=k/4=3 k=123、如图4,双曲线y= k/x(k>0)经过矩形OABC的边BC的中点E,交AB于点D.若梯形ODBC的面积为3,则双曲线的解析式为()A、y=1/xB、y=2/xC、y=3/xD、y=6/x三、反比例函数“K”与面积的关系1、如图5,已知双曲线 y1=1/x(x>0), y2=4/x(x>0),点P为双曲线y2=4/x上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA、PB分别次双曲线y1=1/x于D、C两点,则△PCD的面积为()图5 图6 图7解析:假设P的坐标为(a,b),则C(a/4,b), D(a,b/4),PC=3/4*a PD=3/4*bS=1/2*3/4*a*3/4*b因为点P为双曲线y2=4/x上的一点所以a*b=4所以S=9/82、如图6,直线l和双曲线 y=k/x(k>0)交于A、B两点,P是线段AB上的点(不与A、B重合),过点A、B、P分别向x轴作垂线,垂足分别为C、D、E,连接OA、OB、0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3,则()A、S1<S2<S3B、S1>S2>S3C、S1=S2>S3D、S1=S2<S3解析:结合题意可得:AB都在双曲线y=kx上,则有S1=S2;而AB之间,直线在双曲线上方;故S1=S2<S3.3、如图7,已知直线y=-x+3与坐标轴交于A、B两点,与双曲线 y=k/x交于C、D两点,且S△AOC=S△COD=S△BOD,则k= 。
反比例函数难题汇编及答案解析

反比例函数难题汇编及答案解析一、选择题1 .下列函数:①y=-x ; @y=2x ; (3) y = ~— ; (4)y=x 2.当x<0时,y 随x 的增大而减小x的函数有()A. 1个B. 2个C. 3个D. 4个【答案】B 【解析】 【分析】分别根据一次函数、反比例函数及二次函数的性质进行逐一判断即可. 【详解】一次函数y=-x 中k<0,随x 的增大而减小,故本选项正确;・ ・,正比例函数y=2x 中,k=2,・,•当xVO 时,y 随x 的增大而增大,故本选项错误; ・ ・•反比例函数丁二一^1■中,k= -1V0,・♦.当xVO 时函数的图像在第二象限,此时y 随x 的 增大而增大,故本选项错误;・ ・,二次函数y=x2,中o=1>0,・,•此抛物线开口向上,当xVO 时,y 随x 的增大而减小, 故本选项正确. 故选B. 【点睛】本题考查的是一次函数、反比例函数及二次函数的性质,解题关键是根据题意判断出各函 数的增减性.2.如图,o/WOC 的顶点的坐标分别是4(0,-3),8 (1, 0),顶点C,。
在双曲线k y 二一上,边8D 交V 轴于点£,且四边形ACO 石的面积是A45石面积的3倍,则Z 的值x为:()【答案】A 【解析】A. -6c. -3 D. -12B. -4过D作DF〃>'轴,过C作CE〃x轴,交点为厂,利用平行四边形的性质证明△DCF = AA80,利用平移写好C, D的坐标,由四边形ACDE的面积是AA8E面积的3倍,得到DB = 2BE,利用中点坐标公式求横坐标,再利用反比例函数写。
的坐标,列方程求解女.【详解】解:过D作DF〃y轴,过c作b//x轴,交点为尸,则CF ± DF,:D ABDC,・•・/CDF, /BAO的两边互相平行,AB = DC,.・.ZCDF = NBAO,・・/DFC = 404 = 90。
反比例函数难题汇编及答案解析

错误;
B、y=x 是一次函数 k=1>0,y 随 x 的增大而增大,错误;
C、y=x+1 是一次函数 k=1>0,y 随 x 的增大而减小,错误;
D、 y 1 是反比例函数,图象无语一三象限,在每个象限 y 随 x 的增大而减小,正确; x
故选 D.
【点睛】
本题综合考查了二次函数、一次函数、反比例函数的性质,熟练掌握函数的性质是解题的
7.下列函数中,当 x>0 时,函数值 y 随自变量 x 的增大而减小的是( )
A.y=x2 【答案】D
B.y=x
C.y=x+1
D. y 1 x
【解析】
【分析】
需根据函数的性质得出函数的增减性,即可求出当 x>0 时,y 随 x 的增大而减小的函数.
【详解】
解:A、y=x2 是二次函数,开口向上,对称轴是 y 轴,当 x>0 时,y 随 x 的增大而增大,
图象过第一、三
试题分析:分别根据题意确定 k 的值,然后相加即可.∵关于 x 的分式方程 =2 的解为
非负数,∴x= ≥0,解得:k≥-1,∵反比例函数 y= 图象过第一、三象限,∴3﹣k> 0,解得:k<3,∴-1≤k<3,整数为-1,0,1,2,∵x≠0 或 1,∴和为-1+2=1,故选,B. 考点:反比例函数的性质.
解:依题意得方程 x3 2x 1 0 的实根是函数 y x2 2 与 y 1 的图象交点的横坐标,
x 这两个函数的图象如图所示,它们的交点在第一象限.
当
1
x=
时, y
x2
22
1
,y
1
4 ,此时抛物线的图象在反比例函数下方;
4
16
x
当 x= 1 时, y x2 2 2 1 , y 1 3 ,此时抛物线的图象在反比例函数下方;
反比例函数解析含答案

反比例函数解析含答案一、选择题1.如图,一次函数1y ax b =+和反比例函数2k y x=的图象相交于A ,B 两点,则使12y y >成立的x 取值范围是( )A .20x -<<或04x <<B .2x <-或04x <<C .2x <-或4x >D .20x -<<或4x >【答案】B【解析】【分析】 根据图象找出一次函数图象在反比例函数图象上方时对应的自变量的取值范围即可.【详解】观察函数图象可发现:2x <-或04x <<时,一次函数图象在反比例函数图象上方, ∴使12y y >成立的x 取值范围是2x <-或04x <<,故选B .【点睛】本题考查了反比例函数与一次函数综合,函数与不等式,利用数形结合思想是解题的关键.2.如图,ABDC Y 的顶点,A B 的坐标分别是()(), 0,3 1, 0A B -,顶点,C D 在双曲线k y x=上,边BD 交y 轴于点E ,且四边形ACDE 的面积是ABE ∆面积的3倍,则k 的值为:( )A .6-B .4-C .3-D .12-【答案】A【解析】【分析】 过D 作DF//y 轴,过C 作//CF x 轴,交点为F ,利用平行四边形的性质证明,DCF ABO ∆≅∆利用平移写好,C D 的坐标,由四边形ACDE 的面积是ABE ∆面积的3倍,得到2,DB BE =利用中点坐标公式求横坐标,再利用反比例函数写D 的坐标,列方程求解k .【详解】解:过D 作DF//y 轴,过C 作//CF x 轴,交点为F ,则,CF DF ⊥ABDC QY ,,CDF BAO ∴∠∠的两边互相平行,,AB DC =CDF BAO ∴∠=∠,90,DFC BOA ∠=∠=︒Q,DCF ABO ∴∆≅∆,,CF BO DF AO ∴== 设(,),k C m m由()(), 0,3 1, 0A B -结合平移可得:(1,3)k D m m ++, Q 四边形ACDE 的面积是ABE ∆面积的3倍,11()322BD BE DE CA h h BE ∴+=⨯⨯, ,,BD BE h h AC BD ==Q3DE AC BE ∴+=,4,DE BD BE BE ∴++=2,DB BE ∴=(1,3),(1,0),0,E k D m B x m++=Q ∴ 由中点坐标公式知:110,2m ++= 2m ∴=- ,(1,)1k D m m ++Q , 3212k k ∴=+-+-, 6.k ∴=-故选A .【点睛】本题考查的是反比例函数的图像与性质,平行四边形的性质,平移性质,中点坐标公式,掌握以上知识点是解题关键.3.如图,菱形OABC 的顶点C 的坐标为(3,4),顶点A 在x 轴的正半轴上.反比例函数k y x=(x>0)的图象经过顶点B ,则k 的值为A .12B .20C .24D .32【答案】D【解析】【分析】【详解】如图,过点C 作CD ⊥x 轴于点D ,∵点C 的坐标为(3,4),∴OD=3,CD=4.∴根据勾股定理,得:OC=5.∵四边形OABC 是菱形,∴点B 的坐标为(8,4).∵点B 在反比例函数(x>0)的图象上, ∴. 故选D.4.如图,反比例函数y =2x的图象经过矩形OABC 的边AB 的中点D ,则矩形OABC 的面积为( )A .1B .2C .4D .8【答案】C【解析】【分析】 由反比例函数的系数k 的几何意义可知:2OA AD g ,然后可求得OA AB g 的值,从而可求得矩形OABC 的面积.【详解】解:Q 反比例函数2y x =, 2OA AD ∴=g . D Q 是AB 的中点,2AB AD ∴=.∴矩形的面积2224OA AB AD OA ===⨯=g g .故选:C .【点睛】本题主要考查的是反比例函数k 的几何意义,掌握反比例函数系数k 的几何意义是解题的关键.5.在同一直角坐标系中,函数y=k(x -1)与y=(0)k k x<的大致图象是 A . B . C . D .【答案】B【解析】【分析】【详解】解:k<0时,y=(0)k k x<的图象位于二、四象限, y=k(x -1)的图象经过第一、二、四象限,观察可知B 选项符合题意,故选B.6.如图直线y =mx 与双曲线y=k x交于点A 、B ,过A 作AM ⊥x 轴于M 点,连接BM ,若S △AMB =2,则k 的值是( )A .1B .2C .3D .4【答案】B【解析】【分析】此题可根据反比例函数图象的对称性得到A、B两点关于原点对称,再由S△ABM=2S△AOM并结合反比例函数系数k的几何意义得到k的值.【详解】根据双曲线的对称性可得:OA=OB,则S△ABM=2S△AOM=2,S△AOM=12|k|=1,则k=±2.又由于反比例函数图象位于一三象限,k>0,所以k=2.故选B.【点睛】本题主要考查了反比例函数y=kx中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点.7.在反比例函数y=93mx+图象上有两点A(x1,y1)、B(x2,y2),y1<0<y2,x1>x2,则有()A.m>﹣13B.m<﹣13C.m≥﹣13D.m≤﹣13【答案】B【解析】【分析】先根据y1<0<y2,有x1>x2,判断出反比例函数的比例系数的正负,求出m的取值范围即可.【详解】∵在反比例函数y=93mx+图象上有两点A(x1,y1)、B(x2,y2),y1<0<y2,x1>x2,∴反比例函数的图象在二、四象限,∴9m+3<0,解得m<﹣13.故选:B.【点睛】此题主要考查了反比例函数的性质,以及反比例函数图象上点的坐标特点,关键是掌握反比例函数的性质8.函数kyx=与y kx k=-(0k≠)在同一平面直角坐标系中的大致图象是()A.B.C.D.【答案】C【解析】【分析】分k>0和k<0两种情况确定正确的选项即可.【详解】当k:>0时,反比例函数的图象位于第一、三象限,一次函数的图象交 y轴于负半轴,y 随着x的增大而增大,A选项错误,C选项符合;当k<0时,反比例函数的图象位于第二、四象限,一次函数的图象交y轴于正半轴,y 随着x的增大而增减小,B. D均错误,故选:C.【点睛】此题考查反比例函数的图象,一次函数的图象,熟记函数的性质是解题的关键.9.如图,点P是反比例函数y=kx(x<0)图象上一点,过P向x轴作垂线,垂足为M,连接OP.若Rt△POM的面积为2,则k的值为()A.4 B.2 C.-4 D.-2【答案】C【解析】【分析】根据反比例函数的比例系数k的几何意义得到S△POD=12|k|=2,然后去绝对值确定满足条件的k的值.【详解】解:根据题意得S△POD=12|k|,所以12|k||=2,而k<0,所以k=-4.故选:C.【点睛】本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=kx图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.10.如图,四边形OABF中,∠OAB=∠B=90°,点A在x轴上,双曲线kyx=过点F,交AB于点E,连接EF.若BF2OA3=,S△BEF=4,则k的值为()A.6 B.8 C.12 D.16【答案】A【解析】【分析】由于23BFOA=,可以设F(m,n)则OA=3m,BF=2m,由于S△BEF=4,则BE=4m,然后即可求出E(3m,n-4m),依据mn=3m(n-4m)可求mn=6,即求出k的值.【详解】如图,过F作FC⊥OA于C,∵23BF OA =, ∴OA=3OC ,BF=2OC∴若设F (m ,n )则OA=3m ,BF=2m∵S △BEF =4∴BE=4m则E (3m ,n-4m) ∵E 在双曲线y=k x 上 ∴mn=3m (n-4m) ∴mn=6即k=6.故选A .【点睛】 此题主要考查了反比例函数的图象和性质、用坐标表示线段长和三角形面积,表示出E 点坐标是解题关键.11.如图,矩形ABCD 的顶点A ,B 在x 轴的正半轴上,反比例函数k y x =在第一象限内的图象经过点D ,交BC 于点E .若4AB =,2CE BE =,34AD OA =,则线段BC 的长度为( )A .1B .32C .2D .23【答案】B【解析】【分析】 设OA 为4a ,则根据题干中的比例关系,可得AD=3a ,CE=2a ,BE=a ,从而得出点D 和点E 的坐标(用a 表示),代入反比例函数可求得a 的值,进而得出BC 长.【详解】设OA=4a根据2CE BE =,34AD OA =得:AD=3a ,CE=2a ,BE=a ∴D(4a ,3a),E(4a+4,a)将这两点代入解析得; 3444k a a k a a ⎧=⎪⎪⎨⎪=⎪+⎩解得:a=12∴BC=AD=32 故选:B【点睛】本题考查反比例函数和矩形的性质,解题关键是用含有字母的式子表示出点D 、E 的坐标,然后代入解析式求解.12.对于反比例函数2y x=-,下列说法不正确的是( ) A .图象分布在第二、四象限B .当0x >时,y 随x 的增大而增大C .图象经过点(1,-2)D .若点()11,A x y ,()22,B x y 都在图象上,且12x x <,则12y y <【答案】D【解析】【分析】根据反比例函数图象的性质对各选项分析判断后利用排除法求解.【详解】A. k=−2<0,∴它的图象在第二、四象限,故本选项正确;B. k=−2<0,当x>0时,y 随x 的增大而增大,故本选项正确;C.∵221-=-,∴点(1,−2)在它的图象上,故本选项正确; D. 若点A (x 1,y 1),B (x 2,y 2)都在图象上,,若x 1<0< x 2,则y 2<y 1,故本选项错误. 故选:D.【点睛】本题考查了反比例函数的图象与性质,掌握反比例函数的性质是解题的关键.13.如图,在平面直角坐标系中,菱形ABCD 在第一象限内,边BC 与x 轴平行,A ,B 两点的纵坐标分别为4,2,反比例函数y k x =(x >0)的图象经过A ,B 两点,若菱形ABCD 的面积为25,则k 的值为( )A .2B .3C .4D .6【答案】C【解析】【分析】 过点A 作x 轴的垂线,交CB 的延长线于点E ,根据A ,B 两点的纵坐标分别为4,2,可得出横坐标,即可求得AE ,BE 的长,根据菱形的面积为25,求得AE 的长,在Rt △AEB 中,即可得出k 的值.【详解】过点A 作x 轴的垂线,交CB 的延长线于点E ,∵A ,B 两点在反比例函数y k x =(x >0)的图象,且纵坐标分别为4,2, ∴A (4k ,4),B (2k ,2), ∴AE =2,BE 12=k 14-k 14=k , ∵菱形ABCD 的面积为5∴BC×AE =5BC 5=∴AB =BC 5=在Rt △AEB 中,BE 22AB AE =-=1 ∴14k =1,∴k=4.故选:C.【点睛】本题考查了菱形的性质以及反比例函数图象上点的坐标特征,熟记菱形的面积公式是解题的关键.14.如图,在平面直角坐标系中,函数y =kx 与y =-2x的图象交于 A、B 两点,过 A 作 y轴的垂线,交函数4yx=的图象于点 C,连接 BC,则△ABC 的面积为()A.2 B.4 C.6 D.8【答案】C【解析】【分析】连接OC,根据图象先证明△AOC与△COB的面积相等,再根据题意分别计算出△AOD与△ODC的面积即可得△ABC的面积.【详解】连接OC,设AC⊥y轴交y轴为点D,如图,∵反比例函数y=-2x为对称图形,∴O为AB 的中点,∴S△AOC=S△COB,∵由题意得A点在y=-2x上,B点在y=4x上,∴S △AOD =12×OD×AD=12xy=1; S △COD =12×OC×OD=12xy=2; S △AOC = S △AOD + S △COD =3,∴S △ABC = S △AOC +S △COB =6.故答案选C.【点睛】本题考查了一次函数与反比例函数的交点问题与三角形面积公式,解题的关键是熟练的掌握一次函数与反比例函数的交点问题与三角形面积运算.15.若A (-3,y 1)、B (-1,y 2)、C (1,y 3)三点都在反比例函数y=k x (k >0)的图象上,则y 1、y 2、y 3的大小关系是( )A . y 1>y 2>y 3B . y 3>y 1>y 2C . y 3>y 2>y 1D . y 2>y 1>y 3 【答案】B【解析】【分析】反比例函数y=k x(k >0)的图象在一、三象限,根据反比例函数的性质,在每个象限内y 随x 的增大而减小,而A (-3,y 1)、B (-1,y 2)在第三象限双曲线上的点,可得y 2<y 1<0,C (1,y 3)在第一象限双曲线上的点y 3>0,于是对y 1、y 2、y 3的大小关系做出判断.【详解】∵反比例函数y=k x(k >0)的图象在一、三象限, ∴在每个象限内y 随x 的增大而减小,∵A (-3,y 1)、B (-1,y 2)在第三象限双曲线上,∴y 2<y 1<0,∵C (1,y 3)在第一象限双曲线上,∴y 3>0,∴y 3>y 1>y 2,故选:B .【点睛】此题考查反比例函数的图象和性质,解题关键在于当k >0,时,在每个象限内y 随x 的增大而减小;当k <0时,y 随x 的增大而增大,注意“在每个象限内”的意义,这种类型题目用图象法比较直观得出答案.16.如图,若直线2y x n =-+与y 轴交于点B ,与双曲线()20y x x=-<交于点(),1A m ,则AOB V 的面积为( )A .6B .5C .3D .1.5【答案】C【解析】【分析】 先根据题意求出A 点坐标,再求出一次函数解析式,从而求出B 点坐标,则问题可解.【详解】解:由已知直线2y x n =-+与y 轴交于点B ,与双曲线()20y x x =-<交于点(),1A m ∴21m=-则m=-2 把A (-2,1)代入到2y x n =-+,得()122n =-⨯-+∴n=-3∴23y x =--则点B (0,-3)∴AOB V 的面积为132=32⨯⨯ 故应选:C【点睛】本题考查的是反比例函数与一次函数的综合问题,解题关键是根据题意应用数形结合思想.17.如图,点A ,B 是双曲线18y x=图象上的两点,连接AB ,线段AB 经过点O ,点C 为双曲线k y x=在第二象限的分支上一点,当ABC V 满足AC BC =且:13:24AC AB =时,k 的值为( ).A.2516-B.258-C.254-D.25-【答案】B【解析】【分析】如图作AE⊥x轴于E,CF⊥x轴于F.连接OC.首先证明△CFO∽△OEA,推出2()COFAOES OCS OA∆∆=,因为CA:AB=13:24,AO=OB,推出CA:OA=13:12,推出CO:OA=5:12,可得出2()COFAOES OCS OA∆∆==25144,因为S△AOE=9,可得S△COF=2516,再根据反比例函数的几何意义即可解决问题.【详解】解:如图作AE⊥x轴于E,CF⊥x轴于F.连接OC.∵A、B关于原点对称,∴OA=OB,∵AC=BC,OA=OB,∴OC⊥AB,∴∠CFO=∠COA=∠AEO=90°,∴∠COF+∠AOE=90°,∠AOE+∠EAO=90°,∴∠COF=∠OAE,∴△CFO∽△OEA,∴2()COFAOES OCS OA∆∆=,∵CA:AB=13:24,AO=OB,∴CA:OA=13:12,∴CO:OA=5:12,∴2()COF AOE S OC S OA ∆∆==25144, ∵S △AOE =9,∴S △COF =2516, ∴||25216k =, ∵k <0, ∴258k =- 故选:B .【点睛】本题主要考查反比例函数图象上的点的特征、等腰三角形的性质、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,根据相似三角形解决问题,属于中考选择题中的压轴题.18.当0x <时,反比例函数2y x=-的图象( ) A .在第一象限,y 随x 的增大而减小 B .在第二象限,y 随x 的增大而增大C .在第三象限,y 随x 的增大而减小D .在第四象限,y 随x 的增大而减小 【答案】B【解析】【分析】 反比例函数2y x =-中的20k =-<,图像分布在第二、四象限;利用0x <判断即可. 【详解】解:Q 反比例函数2y x=-中的20k =-<, ∴该反比例函数的图像分布在第二、四象限;又0x <Q ,∴图象在第二象限且y 随x 的增大而增大.故选:B .【点睛】 本题主要考查的是反比例函数的性质,对于反比例函数()0k y k x=≠,(1)0k >,反比例函数图像分布在一、三象限;(2)k 0< ,反比例函数图像分布在第二、四象限内.19.在函数()0k y k x=<的图象上有()11,A y ,()21,B y -,()32,B y -三个点,则下列各式中正确的是( )A .123y y y <<B .132y y y <<C .321y y y <<D .231y y y <<【答案】B【解析】【分析】 根据反比例函数图象上点的坐标特征得到11y k ⨯=,21y k -⨯=,32y k -⨯=,然后计算出1y 、2y 、3y 的值再比较大小即可.【详解】 解:(0)k y k x=<Q 的图象上有1(1,)A y 、2(1,)B y -、3(2,)C y -三个点, 11y k ∴⨯=,21y k -⨯=,32y k -⨯=,1y k ∴=,2y k =-,312y k =-, 而k 0<,132y y y ∴<<.故选:B .【点睛】 本题考查了反比例函数图象上点的坐标特征:反比例函数k y x=(k 为常数,且0k ≠)的图象是双曲线,图象上的点(),x y 的横纵坐标的积是定值k ,即xy k =.20.已知点()1,3M -在双曲线k y x =上,则下列各点一定在该双曲线上的是( ) A .()3,1-B .()1,3--C .()1,3D .()3,1 【答案】A【解析】【分析】先求出k=-3,再依次判断各点的横纵坐标乘积,等于-3即是在该双曲线上,否则不在.【详解】∵点()1,3M -在双曲线k y x=上, ∴133k =-⨯=-,∵3(1)3⨯-=-,∴点(3,-1)在该双曲线上,∵(1)(3)13313-⨯-=⨯=⨯=,∴点()1,3--、()1,3、()3,1均不在该双曲线上,故选:A.【点睛】此题考查反比例函数解析式,正确计算k值是解题的关键.。
反比例函数经典大题(有详细答案)
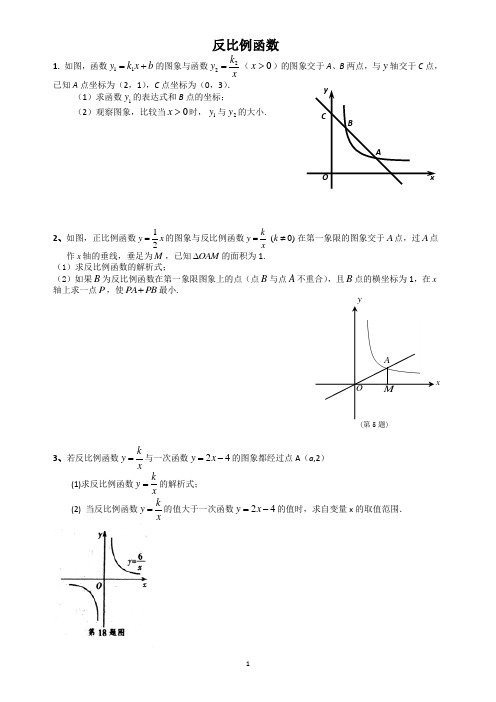
反比例函数1. 如图,函数b x k y +=11的图象与函数xk y 22=(0>x )的图象交于A 、B 两点,与y 轴交于C 点,已知A 点坐标为(2,1),C 点坐标为(0,3).(1)求函数1y 的表达式和B 点的坐标;(2)观察图象,比较当0>x 时,1y 与2y 的大小.2、如图,正比例函数12y x =的图象与反比例函数ky x=(0)k ≠在第一象限的图象交于A 点,过A 点作x 轴的垂线,垂足为M ,已知OAM ∆的面积为1.(1)求反比例函数的解析式;(2)如果B 为反比例函数在第一象限图象上的点(点B 与点A 不重合),且B 点的横坐标为1,在x 轴上求一点P ,使PA PB +最小.3、若反比例函数x ky =与一次函数42-=x y 的图象都经过点A (a ,2) (1)求反比例函数x ky =的解析式;(2) 当反比例函数xky =的值大于一次函数42-=x y 的值时,求自变量x 的取值范围.ABOCxyO Mx A(第5题)4、如图,在直角坐标系中,O 为坐标原点. 已知反比例函数y= (k>0)的图象经过点A (2,m ),过点A 作AB ⊥x 轴于点B ,且△AOB 的面积为 .(1)求k 和m 的值;(2)点C (x ,y )在反比例函数y= 的图象上,求当1≤x ≤3时函数值y 的取值范围;5、如图,四边形ABCD 为菱形,已知A (0,4),B (-3,0)。
⑴求点D 的坐标;⑵求经过点C 的反比例函数解析式.6、如图,一次函数3y kx =+的图象与反比例函数my x=(x>0)的图象交于点P ,PA ⊥x 轴于点A ,PB ⊥y 轴于点B ,一次函数的图象分别交x 轴、y 轴于点C 、点D ,且S △DBP =27,12OC CA =。
(1)求点D 的坐标;(2)求一次函数与反比例函数的表达式;(3)根据图象写出当x 取何值时,一次函数的值小于反比例函数的值?xkxk B O A21xyA O PBC D7、已知一次函数y =kx +b 的图象交反比例函数42my x-=(x>0)图象于点A 、B ,交x 轴于点C . (1)求m 的取值范围;(2)若点A 的坐标是(2,-4),且13BC AB =,求m 的值和一次函数的解析式; (3)写出当x 取何值时,一次函数的值小于反比例函数的值?8、如图,正比例函数11y k x =与反比例函数22k y x=相交于A 、B 点,已知点A 的坐标为(4,n ),BD ⊥x 轴于点D ,且S △BDO =4。
反比例函数压轴题精选(含标准答案)

中考反比率函数经典结论:y如图,反比率函数 k 的几何意义:CA(I )S AOB S1 k ;oBAOC2(II )S矩形 OBACk 。
x下边两个结论是上述结论的拓展 .yy(1)如图①,PBP CCEoAxS OPA S OCD , S OPCS梯形 PADC。
E(2 ) 如图②,o A DxS梯形 OAPBS梯形 OBCA,SBPESACE。
图②图①y经典例题例 1.(1)( 兰州 ) 如图,已知双曲线yk (x 0) 经过矩形 CEBFxOABC 边 AB 的中点 F 且交 BC 于点 E ,四边形 OEBF 的面积oAx为 2,则 k;(2) 如图,点 A 、B 为直线 y x 上的两点,过 A 、B两点分别作 y 轴的平行线交双曲线 y1 于 C 、D 两点,若 BD 2AC ,( x 0)x则 4OC 2 OD 2yBACDox例 2.假如一个正比率函数的图象与一个反比率函数6 1 1 2 2 21 )( y2 1y的图象交 A( x , y ), B( x , y ) ,那么 ( xxy ) 值为.x例 3.如图,一次函数 ykx b 的图象与反比率函数 ym的图象交于点 A ﹙- 2,-5﹚,xC ﹙5,n ﹚,交 y 轴于点 B ,交 x 轴于点D .(1) 求反比率函数 ym和一次函数 y kx b 的表达式;xy(2) 连结 OA ,OC .求△ AOC 的面积.CODxBA例 4.如图,已知直线 y1x 与双曲线 y k(k0) 交于A,B两点,且点A的横坐标为4.2x(1)求k的值;(2)若双曲线y k(k0)上一点 C 的纵坐标为,求△ AOC 的面积;x8(3)过原点O的另一条直线l交双曲线k(k0)于,Q两点(P点在第一象限),y Px若由点 A, B, P, Q 为极点构成的四边形面积为24 ,求点 P 的坐标.yC yNAC DAOO E F x M x B图 1图 2yyPA AEF xPB QO F E xQ图 3B图 4例 5. ( 山东淄博 ) 如图,正方形AOCB的边长为 4,反比率函数的图象过点E(3,4).(1)求反比率函数的解读式;(2)反比率函数的图象与线段BC交于点 D,直线y = -1x + b过点 D,与线段 AB 相2交于点 F,求点 F 的坐标;(3)连结OF,OE,研究∠AOF与∠EOC的数目关系,并证明.。
反比例函数压轴题精选(含标准答案)

中考反比例函数经典结论:如图,反比例函数k 的几何意义: (I ) 12AOB AOC S S k ∆∆==; (II ) OBAC S k =矩形。
下面两个结论是上述结论的拓展.(1) 如图①,OPA OCD S S ∆∆=,OPC PADC S S ∆=梯形(2)如图②,OAPB OBCA S S =梯形梯形,BPE S S ∆∆=经典例题例1.(1)(兰州)如图,已知双曲线(0)ky x x=>经过矩形OABC边AB 的中点F 且交BC 于点E ,四边形OEBF 的面积为2,则k = ;(2) 如图,点A B 、为直线y x =上的两点,过A B 、两点分别作y 轴的平行线交双曲线1(0)y x x=>于C D 、两点,若2BD AC =,则224OC OD -=例2.如果一个正比例函数的图象与一个反比例函数xy 6=的图象交),(),,(2211y x B y x A ,那么))((1212y y x x --值为 .例3.如图,一次函数b kx y +=的图象与反比例函数xm y =的图象交于点A ﹙-2,-5﹚,C ﹙5,n ﹚,交y 轴于点B ,交x 轴于点D .(1) 求反比例函数xm y =和一次函数b kx y +=(2) 连接OA ,OC .求△AOC 的面积.例4.如图,已知直线12y x =与双曲线(0)k y k x=>交于A B ,两点,且点A 的横坐标为4. (1)求k 的值;(2)若双曲线(0)k y k x=>上一点C 的纵坐标为8,求AOC △的面积;(3)过原点O 的另一条直线l 交双曲线(0)k y k x=>于P Q ,两点(P 点在第一象限),若由点A B P Q ,,,为顶点组成的四边形面积为24,求点P 的坐标.图2图4y例5.(山东淄博) 如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).(1)求反比例函数的解读式;过点D,与线段AB (2)反比例函数的图象与线段BC交于点D,直线1y x b2相交于点F,求点F的坐标;(3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
反比例函数经典专题
知识点回顾
由于反比例函数解析式及图象的特殊性,很多中考试题都将反比例函数与面积结合起来进行考察。
这种考察方式既能考查函数、反比例函数本身的基础知识内容,又能充分体现数形结合的思想方法,考查的题型广泛,考查方法灵活,可以较好地将知识与能力融合在一起。
下面就反比例函数中与面积有关的问题的四种类型归纳如下:
一、利用反比例函数中|k|的几何意义求解与面积有关的问题
设P为双曲线上任意一点,过点P作x轴、y轴的垂线PM、PN,垂足分别为M、N,则两垂线段与坐标轴所围成的的矩形PMON的面积为S=|PM|×|PN|=|y|×|x|=|xy|
∴xy=k 故S=|k| 从而得
结论1:过双曲线上任意一点作x轴、y轴的垂线,所得矩形的面积S为定值|k| 对于下列三个图形中的情形,利用三角形面积的计算方法和图形的对称性以及上述结论,可得出对应的面积的结论为:
结论2:在直角三角形ABO中,面积S=
结论3:在直角三角形ACB中,面积为S=2|k|
结论4:在三角形AMB中,面积为S=|k|
例题讲解
【例1】如右图,已知△P10A1,△P2A1A2都是等腰直角三角形,点P1、P2
都在函数y=4
x(x>0)
的图象上,斜边OA1、A1A2都在x轴上.则点A2的坐
标为 .
1、如例1图,已知△P1OA1,△P2A1A2,△P3A2A3…△P n A n-1A n都是等腰直角三角形,点P1、
P2、P3…P n都在函数y=4
x
(x>0)的图象上,斜边OA1、A1A2、A2A3…A n-1A n都在x轴上.则
点A10的坐标为
2、已知点A(0,2)和点B(0,-2),点P在函数y=
1
x
的图像上,如果△PAB的面积为6,
求P点的坐标。
【例2】如右图,已知点(1,3)在函数y=k
x
(x>0)的图像上,矩形ABCD的边BC在x轴
上,E是对角线BD的中点,函数y=k
x
(k>0)的图象又经过A,E两点,点E的横坐标
为m,解答下列各题
1.求k的值
2.求点C的横坐标(用m表示)
3.当∠ABD=45°时,求m的值112
1、已知:如图,矩形ABCD的边BC在x轴上,E是对角线AC、BD的交点,反比例函数y=2 x
(x>0)的图象经过A,E两点,点E的纵坐标为m.
(1)求点A坐标(用m表示)
(2)是否存在实数m,使四边形ABCD为正方形,若存在,请求出m的值;若不存在,请说明理由
2、如图1,矩形ABCD的边BC在x轴的正半轴上,点E(m,1)是对角线BD的中点,点A、
E在反比例函数y=k
x
的图象上.
(1)求AB的长;
(2)当矩形ABCD是正方形时,将反比例函数y=k
x
的图象沿y轴翻折,得到反比例函数y=
1
k
x
的图象(如图2),求k1的值;
(3)直线y=-x上有一长为2动线段MN,作MH、NP都平行y轴交在条件(2)下,第一
象限内的双曲线y=k
x
于点H、P,问四边形MHPN能否为平行四边形(如图3)?若能,请求
出点M的坐标;若不能,请说明理由.
【例3】在平面直角坐标系中,已知A(1,0),B(0,1),矩形OMPN的相邻两边OM,ON分别在x,y轴的正半轴上,O为原点,线段AB与矩形OMPN的两边MP,NP的交点分别为E,F,△AOF∽△BOE(顶点依次对应)
(1)求∠FOE;
(2)求证:矩形OPMN的顶点P必在某个反比例函数图像上,并写出该函数的解析式。
如图,在平面直角坐标系中,直线y=-x+1分别交x轴、y轴于A,B两点,点P(a,b)是
反比例函数y=1
2x
在第一象限内的任意一点,过点P分别作PM⊥x轴于点M,PN⊥y 轴于
点N,PM,PN分别交直线AB于E,F,有下列结论:①AF=BE;②图中的等腰直角三角形有4
个;③S△OEF=1
2
(a+b-1);④∠EOF=45°.其中结论正确的序号是②③④
【例4】已知:如右图,已知反比例函数y=
2k
x
和一次函数y=2x-1,其中一次函数的图像经过(a ,b ),(a+1,b+k ).
(1)求反比例函数的解析式;
(2)如图,已知点A 在第一象限,且同时在上述两个函数的图象上,求点A 的坐标; (3)利用(2)的结果,请问:在x 轴上是否存在点P ,使△AOP 为等腰三角形?若存在,把符合条件的P 点坐标都求出来;若不存在,请说明理由.
已知反比例函数y=2k
x
和一次函数y=2x-1,其中一次函数的图象经过(a ,b ),(a+k ,b+k+2)两点.
(1)求反比例函数的解析式;
(2)求反比例函数与一次函数两个交点A 、B 的坐标: (3)根据函数图象,求不等式
2k
x
>2x-1的解集; (4)在(2)的条件下,x 轴上是否存在点P ,使△AOP 为等腰三角形?若存在,把符合条件的P 点坐标都求出来;若不存在,请说明理由。
一、巩固练习:解答题
1、已知反比例函数y=k
x
图象过第二象限内的点A(-2,m),作AB⊥x轴于B,Rt△AOB面积为3;若直
线y=ax+b经过点A,并且经过反比例函数y=k
x
的图象上另一点C(n,-1).
(1)反比例函数的解析式为y=-6
x
,m=3,n=6;
(2)求直线y=ax+b的解析式;
(3)设直线y=ax+b与x轴交于M,求AM的长;
(4)根据图象写出使反比例函数y=k
x
值大于一次函数y=ax+b的值的x的取值范围。
2、已知如图:矩形ABCD的边BC在x轴上,E为对角线BD的中点,点B、D的坐标分别为B(1,0),D
(3,3),反比例函数y=k
x
的图象经过A点,
(1)写出点A和点E的坐标;(2)求反比例函数的解析式;
3、如右图已知反比例函数y=k
x
(k<0)的图像经过点A(-3,m),过A点作AB⊥x轴于
点B,且△AOB的面积为3。
123
(1)求k和m的值
(2)若一次函数y=ax+1的图像经过点A,并且与x轴相交于点M,求∠AMO和|AO|:|AM|的值
二、 拓展训练 4、已知反比例函数y=2k x
和一次函数y=2x-1,其中一次函数的图象经过(a ,b )、(a+1,b+k )两点. (1)求反比例函数的解析式;
(2)若两个函数图象在第一象限内的交点为A (1,m ),请问:在x 轴上是否存在点B ,使△AOB 为直角三角形?若存在,求出所有符合条件的点B 的坐标;
(3)若直线y=-x+12交x 轴于C ,交y 轴于D ,点P 为反比例函数y=2k x
(x >0)的图象上一点,过P 作y 轴的平行线交直线CD 于E ,过P 作x 轴的平行线交直线CD 于F ,求证:DE •CF 为定值.
过手练习
1、已知:如右图已知反比例函数y=12
x
的图像与一次函数y=kx-7的图像都经过P(m,2)
(1)求这个一次函数的解析式;
(2)如果等腰梯形ABCD的顶点A、B在这个一次函数的图象上,顶点C、D在这个反比例函数的图象上,两底AD、BC与y轴平行,且A和B的横坐标分别为a和a+2,求a的值.118。
