旋转的证明与计算(等边三角形)
数学中考压轴题旋转问题(经典)

数学中考压轴题旋转问题(经典)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN旋转一、选择题1. (广东)如图,把一个斜边长为2且含有300角的直角三角板ABC 绕直角顶点C 顺时针旋转900到△A 1B 1C ,则在旋转过程中这个三角板扫过的图形的面积是【 】A .πB .3C .33+42π D .113+124π 2. (湖北)如图,O 是正△ABC 内一点,OA=3,OB=4,OC=5,将线段BO 以点B 为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A 可以由△BOC 绕点B 逆时针旋转60°得到;②点O 与O′的距离为4;③∠AOB=150°;④AOBO S =6+33四形边;⑤AOC AOB 93SS6+4+=.其中正确的结论是【 】 A .①②③⑤ B .①②③④ C .①②③④⑤ D .①②③ 3. (四川)如图,P 是等腰直角△ABC 外一点,把BP 绕点B 顺时针旋转90°到BP′,已知∠AP′B=135°,P′A :P′C=1:3,则P′A :PB=【 】。
A .1:2 B .1:2 C .3:2 D .1:34. (贵州)点P 是正方形ABCD 边AB 上一点(不与A 、B 重合),连接PD 并将线段PD 绕点P 顺时针旋转90°,得线段PE ,连接BE ,则∠CBE 等于【 】 A .75° B .60° C .45° D .30°5. (广西)如图,等边△ABC 的周长为6π,半径是1的⊙O 从与AB 相切于点D 的位置出发,在△ABC 外部按顺时针方向沿三角形滚动,又回到与AB 相切于点D 的位置,则⊙O 自转了:【 】A .2周B .3周C .4周D .5周二、填空题6. (四川)如图,四边形ABCD 中,∠BAD=∠BCD=900,AB=AD,若四边形ABCD 的面积是24cm 2.则AC 长是 ▲ cm.7. (江西南昌)如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是▲ .8. (吉林省)如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,则△AED的周长是_ ▲____.三、解答题9. (北京市)在ABC△中,BA=BC BAC,,M是AC的中点,P是线段BM上的动点,将线段∠=αPA绕点P顺时针旋转2α得到线段PQ。
中考数学压轴题之旋转(中考题型整理,突破提升)含答案解析

一、旋转 真题与模拟题分类汇编(难题易错题)1.在△ABC 中,AB=AC ,∠BAC=α(︒<<︒600α),将线段BC 绕点B 逆时针旋转60°得到线段BD 。
(1)如图1,直接写出∠ABD 的大小(用含α的式子表示); (2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE 的形状并加以证明; (3)在(2)的条件下,连结DE ,若∠DEC=45°,求α的值。
【答案】(1)1302α︒-(2)见解析(3)30α=︒【解析】解:(1)1302α︒-。
(2)△ABE 为等边三角形。
证明如下:连接AD ,CD ,ED ,∵线段BC 绕点B 逆时针旋转60︒得到线段BD , ∴BC=BD ,∠DBC=60°。
又∵∠ABE=60°,∴1ABD 60DBE EBC 302α∠=︒-∠=∠=︒-且△BCD 为等边三角形。
在△ABD 与△ACD 中,∵AB=AC ,AD=AD ,BD=CD ,∴△ABD ≌△ACD (SSS )。
∴11BAD CAD BAC 22α∠=∠=∠=。
∵∠BCE=150°,∴11BEC 180(30)15022αα∠=︒-︒--︒=。
∴BEC BAD ∠=∠。
在△ABD 和△EBC 中,∵BEC BAD ∠=∠,EBC ABD ∠=∠,BC=BD , ∴△ABD ≌△EBC (AAS )。
∴AB=BE 。
∴△ABE 为等边三角形。
(3)∵∠BCD=60°,∠BCE=150°,∴DCE 1506090∠=︒-︒=︒。
又∵∠DEC=45°,∴△DCE 为等腰直角三角形。
∴DC=CE=BC 。
∵∠BCE=150°,∴(180150)EBC 152︒-︒∠==︒。
而1EBC 30152α∠=︒-=︒。
∴30α=︒。
(1)∵AB=AC ,∠BAC=α,∴180ABC 2α︒-∠=。
专题07 等边三角形的判定与性质(解析版)

1专题07 等边三角形的判定与性质知识对接考点一、等边三角形的判定与性质 1、性质: (1)三边相等.(2)三个内角相等,每一个内角都等于60°. (3)是轴对称图形,有三条对称轴. (4)面积:S=43a 2(a 为等边三角形的边长). 2、判定:(1)三边相等的三角形是等边三角形. (2)三个角都相等的三角形是等边三角形. (3)有一个角是60°的等腰三角形是等边三角形.专项训练一、单选题1.(2021·陕西西安·交大附中分校九年级)如图,点A ,B ,C ,D 在⊙O 上,其中四边形OBCD 为平行四边形,连接AB ,AC ,则⊙A 的度数为( )A .20°B .25°C .30°D .35°【答案】A 【分析】连接OC ,先证明⊙OBC 是等边三角形,得到⊙BOC =60°,然后利用圆周角定理求解即可. 【详解】 解:连接OC .⊙四边形OBCD为平行四边形,⊙OD=BC,⊙OB=OC=OD,⊙OB=OC=BC,⊙⊙OBC是等边三角形,⊙⊙BOC=60°,⊙BOC=30°,⊙⊙BAC=12故选A.【点睛】本题主要考查了平行四边形的性质,等边三角形的性质与判定,圆周角定理,解题的关键在于能够熟练掌握相关知识进行求解.2.(2021·绍兴市柯桥区杨汛桥镇中学九年级二模)如图,正方形ABCD的顶点A、B在⊙O 上,顶点C、D在⊙O内,将正方形ABCD绕点B顺时针旋转α度,使点C落在⊙O上.若正方形ABCD的边长和⊙O的半径相等,则旋转角度α等于()A.36°B.30°C.25°D.22.5°【答案】B【分析】连接OA,OB,OG,由旋转的性质可得,AB=BG,⊙ABE=⊙CBG=α,先证明⊙OAB和⊙OBG 都是等边三角形,得到⊙OBA=⊙OBG=60°,再由⊙ABO+⊙OBG=⊙ABC+⊙CBG=120°,求解即可.【详解】解:如图所示,连接OA,OB,OG,由旋转的性质可得,AB=BG,⊙ABE=⊙CBG=α⊙正方形ABCD的边长和⊙O的半径相等,⊙OA=OB=OG=BG=AB,⊙⊙OAB和⊙OBG都是等边三角形,3⊙⊙OBA =⊙OBG =60°,⊙⊙ABO +⊙OBG =⊙ABC +⊙CBG =120°,⊙ABC =90°(正方形的性质), ⊙⊙CBG =30°, ⊙α=30°, 故选B .【点睛】本题主要考查了旋转的性质,等边三角形的性质与判定,正方形的性质,解题的关键在于能够熟练掌握相关知识进行求解.3.(2021·西安市铁一中学)如图,在矩形ABCD 中,DAB ∠的平分线交BD 于点F ,CD 于点E ,15EAC ∠=︒,AB =EF 的长为( )A.2 BC.2 D1【答案】B 【分析】过点F 作FG AD ⊥于点G ,根据矩形性质证明OAD ∆是等边三角形,利用tan60=︒GF DG ,求出GF 的长,再根据勾股定理即可求出结果. 【详解】解:如图,过点F 作FG AD ⊥于点G ,在矩形ABCD 中,EA 是DAB ∠的平分线, ⊙45DAE EAB AED ∠=∠=∠=︒, ⊙AD DE =,AG GF =, ⊙15EAC ∠=︒,⊙60=︒∠DAC ,⊙OAD ∆是等边三角形, ⊙60ADB ∠=︒, ⊙AB = ⊙2AD =,4BD =, ⊙2AD DE ==, ⊙AE =⊙60GDF ∠=︒,2=-=-DG AD AG GF , ⊙tan60=︒GF DG ,⊙()2=-GF GF解得3=GF⊙==AF⊙(=-=EF AE AF . 故选B . 【点睛】本题主要考查了矩形的性质,角平分线的性质,勾股定理,等边三角形的性质与判定,解直角三角形,解题的关键在于能够熟练掌握相关知识进行求解.4.(2021·海南三亚·九年级一模)如图,在Rt ABC △中,90ABC ∠=︒,AB BC ==ABC 绕点C 逆时针转60︒,得到MNC ,则BM 的长是( )A .1B .1C D .2+【答案】B 【分析】连接AM ,BM 交AC 于D ,如图,利用等腰直角三角形的性质得到AC ==2,再根据旋转的性质得CM =CA =2,⊙ACM =60°,则可判断⊙ACM 为等边三角形,直接证BM 垂直平分AC ,然后利用等腰直角三角形和等边三角形的性质计算出BD 和MD ,从而得到BM 的长. 【详解】5解:连接AM ,BM 交AC 于D ,如图,⊙⊙ABC =90°,AB =BC = ⊙AC ===2,⊙⊙ABC 绕点C 逆时针转60°,得到⊙MNC , ⊙CM =CA =2,⊙ACM =60°, ⊙⊙ACM 为等边三角形, ⊙MA =MC , 而BA =BC , ⊙BM 垂直平分AC , ⊙BD 12=AC =1,MD ==2 ⊙BM =1 故选:B . 【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形和等边三角形的性质. 5.(2021·河北九年级)如图,直线AB 、CD 交于点O ,若AB 、CD 是等边MNP △的两条对称轴,且点P 在直线CD 上(不与点O 重合),则点M 、N 中必有一个在( )A .AOD ∠的内部B .BOD ∠的内部PC .BOC ∠的内部D .直线AB 上【答案】D 【分析】根据等边三角形是轴对称图形,利用轴对称图形的性质解决问题即可. 【详解】 解:如图,⊙⊙PMN是等边三角形,⊙⊙PMN的对称轴经过三角形的顶点,⊙直线CD,AB是⊙PMN的对称轴,又⊙直线CD经过点P,⊙直线AB一定经过点M或N,故选:D.【点睛】本题考查轴对称,等边三角形的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.6.(2021·四川绵阳·)如图,圆锥的左视图是边长为2的等边三角形,则此圆锥的高是()A.2B.3C D【答案】D【分析】如图所示,等边三角形ABC,BC边上的高AD即为所求.【详解】解:如图所示等边三角形ABC,AD是BC边上的高,由题意可知AD的长即为所求,AB=2,⊙B=60°,⊙sinAD AB B==故选D.7【点睛】本题主要考查了等边三角形的性质,三视图,解直角三角形,解题的关键在于能够熟练掌握相关知识进行求解.7.(2021·四川雅安·)如图,四边形ABCD 为⊙O 的内接四边形,若四边形OBCD 为菱形,A ∠为( ).A .45°B .60°C .72°D .36°【答案】B 【分析】根据菱形性质,得OB OD BC CD ===;连接OC ,根据圆的对称性,得OB OC OD ==;根据等边三角形的性质,得BOD ∠,再根据圆周角和圆心角的性质计算,即可得到答案. 【详解】⊙四边形OBCD 为菱形 ⊙OB OD BC CD === 连接OC⊙四边形ABCD 为⊙O 的内接四边形 ⊙OB OC OD ==⊙OBC ,OCD 为等边三角形 ⊙60BOC COD ∠=∠=︒⊙120BOD BOC COD ∠=∠+∠=︒⊙1602A BOD ︒∠=∠=故选:B . 【点睛】本题考查了圆内接多边形、等边三角形、菱形的知识;解题的关键是熟练掌握圆的对称性、等边三角形、菱形、圆周角、圆心角的知识;从而完成求解.8.(2021·山东枣庄·中考真题)如图,四边形ABCD 是菱形,对角线AC ,BD 相交于点O ,=AC 6BD =,点P 是AC 上一动点,点E 是AB 的中点,则PD PE +的最小值为( )A .B .C .3D .【答案】A 【分析】连接DE ,先根据两点之间线段最短可得当点,,D P E 共线时,PD PE +取得最小值DE ,再根据菱形的性质、勾股定理可得6AB =,然后根据等边三角形的判定与性质求出DE 的长即可得. 【详解】解:如图,连接DE ,由两点之间线段最短得:当点,,D P E 共线时,PD PE +取最小值,最小值为DE ,四边形ABCD 是菱形,=AC 6BD =, 11,3,22AB AD OB BD OA AC AC BD ∴=====⊥,6AB ∴=, 6AB AD BD ∴===,ABD ∴是等边三角形,9点E 是AB 的中点, 13,2AE AB DE AB ∴==⊥,DE ∴即PD PE +的最小值为 故选:A . 【点睛】本题考查了菱形的性质、等边三角形的判定与性质等知识点,熟练掌握菱形的性质是解题关键.9.(2021·天津)如图,在ABC 中,120BAC ∠=︒,将ABC 绕点C 逆时针旋转得到DEC ,点A ,B 的对应点分别为D ,E ,连接AD .当点A ,D ,E 在同一条直线上时,下列结论一定正确的是( )A .ABC ADC ∠=∠B .CB CD =C .DE DC BC +=D .AB CD ∥【答案】D 【分析】由旋转可知120EDC BAC ∠=∠=︒,即可求出60ADC ∠=︒,由于60ABC ∠<︒,则可判断ABC ADC ∠≠∠,即A 选项错误;由旋转可知CB CE =,由于CE CD >,即推出CB CD >,即B 选项错误;由三角形三边关系可知DE DC CE +>,即可推出DE DC CB +>,即C 选项错误;由旋转可知DC AC =,再由60ADC ∠=︒,即可证明ADC 为等边三角形,即推出60ACD ∠=︒.即可求出180ACD BAC ∠+∠=︒,即证明//AB CD ,即D 选项正确;【详解】由旋转可知120EDC BAC ∠=∠=︒, ⊙点A ,D ,E 在同一条直线上, ⊙18060ADC EDC ∠=︒-∠=︒, ⊙60ABC ∠<︒,⊙ABC ADC ∠≠∠,故A 选项错误,不符合题意; 由旋转可知CB CE =,⊙120EDC ∠=︒为钝角, ⊙CE CD >,⊙CB CD >,故B 选项错误,不符合题意; ⊙DE DC CE +>,⊙DE DC CB +>,故C 选项错误,不符合题意; 由旋转可知DC AC =, ⊙60ADC ∠=︒, ⊙ADC 为等边三角形, ⊙60ACD ∠=︒. ⊙180ACD BAC ∠+∠=︒,⊙//AB CD ,故D 选项正确,符合题意; 故选D . 【点睛】本题考查旋转的性质,三角形三边关系,等边三角形的判定和性质以及平行线的判定.利用数形结合的思想是解答本题的关键.10.(2021·安徽)如图,在ABC 中,AB =BC =3,⊙ABC =30°,点P 为ABC 内一点,连接P A 、PB 、PC ,求P A +PB +PC 的最小值( )A .B .C .D .【答案】A 【分析】将⊙ABP 绕点B 逆时针旋转60°得到⊙BFE ,连接PF ,E C .易证P A +PB +PC =PC +PF +EF ,因为PC +PF +EF ≥EC ,推出当P ,F 在直线EC 上时,P A +PB +PC 的值最小,求出EC 的长即可解决问题. 【详解】解:将⊙ABP 绕点B 逆时针旋转60°得到⊙BFE ,连接PF ,E C .11由旋转的性质可知:⊙PBF 是等边三角形, ⊙PB =PF , ⊙P A =EF ,⊙P A +PB +PC =PC +PF +EF , ⊙PC +PF +EF ≥EC ,⊙当P ,F 在直线EC 上时,P A +PB +PC 的值最小, 由旋转可知:BC =BE =BA =3,⊙CBE =⊙ABC +⊙ABE =90°, ⊙EB ⊙BC , ⊙ECBC=⊙P A +PB +PC的最小值为 故选A . 【点睛】本题旋转变换,等边三角形的判定和性质,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考压轴题. 二、填空题11.(2021·杭州市十三中教育集团(总校))如图,点D 是等边⊙ABC 边BC 上一点,将等边⊙ABC 折叠,使点A 与点D 重合,折痕为EF (点E 在边AB 上). (1)当点D 为BC 的中点时,AE :EB =________; (2)当点D 为BC 的三等分点时,AE :EB =________.【答案】1:1 7:5或7:8 【分析】(1)连接AD ,然后根据折叠的性质和等边三角形的性质求解即可;(2)分当DC :BD =1:2时,当DC :BD =2:1时两种情况,利用相似三角形进行求解即可. 【详解】解:(1)如图,连接AD ,⊙D 为BC 的中点,⊙ABC 为等边三角形,折叠, ⊙AD ⊙BC ,⊙DAB =⊙DAC =1=2BAC ∠30°,⊙B =60°,⊙⊙EDB =90°﹣30°=60°=⊙B , ⊙⊙BED 为等边三角形,⊙AE =ED =BE ,即AE :EB =1:1, 故答案为:1:1;(2)当DC :BD =1:2时, 设CD =k ,BD =2k , ⊙AB =AC =3k , ⊙⊙ABC 为等边三角形, ⊙⊙EDF =⊙A =60°,⊙⊙EDB +⊙FDC =⊙BED +⊙EDB =120°, ⊙⊙BED =⊙FDC , ⊙⊙B =⊙C =60°, ⊙⊙BED ⊙⊙CDF , ⊙=BE BED DC CDF 的周长的周长, ⊙54BE kk k, ⊙BE =54k ,⊙AE =74k , ⊙AE :BE =7:5,13当DC :BD =2:1时, 设CD =2k ,BD =k , 同上一种情况得:=BE BED DC CDF 的周长的周长, ⊙425BE kk k⊙BE =85k , ⊙AE =75k, ⊙AE :BE =7:8, 故答案为:7:5或7:8.【点睛】本题主要考查了等边三角形的性质与判定,相似三角形的性质与判定,折叠的性质,解题的关键在于能够熟练掌握相关知识进行求解.12.(2021·陕西西安·交大附中分校)如图,在边长为6cm 的正六边形中,点P 在边AB 上,连接PD 、PE .则PDE 的面积为______cm 2.【答案】【分析】首先求得正六边形的边心距,从而求得⊙PDE 边DE 上的高,利用三角形的面积公式求得答案即可.【详解】解:如图所示,连接OD 、OE ,此正六边形中DE=6,则⊙DOE=60°;⊙OD=OE,⊙⊙ODE是等边三角形,⊙OG⊙DE,⊙⊙DOG=30°,⊙OG=OD•cos30°=cm),⊙⊙PDE边DE上的高为2OG=cm),cm2),⊙S⊙PDE=12故答案为【点睛】此题考查了正六边形的性质,三角形面积的求法,解题的关键是根据题意作出辅助线.13.(2021·江苏九年级二模)若线段DE是等边⊙ABC的中位线,且DE=2,则⊙ABC的周长为____.【答案】12.【分析】根据三角形中位线定理求出BC,根据等边三角形的概念计算即可.【详解】解:如图,⊙DE是⊙ABC的中位线,⊙BC=2DE=4,⊙⊙ABC为等边三角形,15⊙AB =AC =BC =4, ⊙⊙ABC 的周长为12, 故答案为:12. 【点睛】本题考查的是三角形中位线定理、等边三角形的概念,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.14.(2021·山东滨州·)如图,在ABC 中,90ACB ∠=︒,30BAC ∠=︒,2AB =.若点P 是ABC 内一点,则PA PB PC ++的最小值为____________.【分析】根据题意,首先以点A 为旋转中心,顺时针旋转⊙APB 到⊙AP ′B ′,旋转角是60°,作出图形,然后根据旋转的性质和全等三角形的性质、等边三角形的性质,可以得到P A +PB +PC =PP ′+P ′B ′+PC ,再根据两点之间线段最短,可以得到P A +PB +PC 的最小值就是CB ′的值,然后根据勾股定理可以求得CB ′的值,从而可以解答本题. 【详解】解:以点A 为旋转中心,顺时针旋转⊙APB 到⊙AP ′B ′,旋转角是60°,连接BB ′、PP ′,CB ',如图所示,则⊙P AP ′=60°,AP =AP ′,PB =P ′B ′, ⊙⊙APP ′是等边三角形, ⊙AP =PP ′,⊙P A +PB +PC =PP ′+P ′B ′+PC ,⊙PP ′+P ′B ′+PC ≥CB ′,⊙PP ′+P ′B ′+PC 的最小值就是CB ′的值, 即P A +PB +PC 的最小值就是CB ′的值, ⊙⊙BAC =30°,⊙BAB ′=60°,AB =AB '=2,⊙⊙CAB ′=90°,AB ′=2,AC =AB •cos ⊙BAC =2×cos 30°=2= ⊙CB=【点睛】本题考查旋转的性质、等边三角形的性质、最短路径问题、勾股定理,解答本题的关键是作出合适的辅助线,得出P A +PB +PC 的最小值就是CB ′的值,其中用到的数学思想是数形结合的思想.15.(2021·四川达州·中考真题)如图,在边长为6的等边ABC ∆中,点E ,F 分别是边AC ,BC 上的动点,且AE CF =,连接BE ,AF 交于点P ,连接CP ,则CP 的最小值为___________.【答案】 【分析】首先证明120APB ∠=︒,推出点P 的运动轨迹是以O 为圆心,OA 为半径的弧.连接CO 交⊙O 于P',当点P 运动到P'时,CP 取到最小值. 【详解】如图所示,⊙边长为6的等边ABC ∆,17⊙6AC AB ==,60ACB CAB ∠=∠=︒ 又⊙AE CF = ⊙()ACF BAE SAS ≅ ⊙CAP PBA ∠=∠⊙60EPA PBA PAB CAP PAB CAB ∠=∠+∠=∠+∠=∠=︒ ⊙120APB ∠=︒⊙点P 的运动轨迹是以O 为圆心,OA 为半径的弧 此时120AOB ∠=︒连接CO 交⊙O 于P',当点P 运动到P'时,CP 取到最小值 ⊙CA CB =,CO CO =,OA OB = ⊙()ACO BCO SSS ≅⊙30ACO BCO ∠=∠=︒,60AOC BOC ∠=∠=︒ ⊙90CAO CBO ∠=∠=︒ 又⊙6AC =⊙'tan 306OP OA AB ==⋅︒==cos30AB OC =⋅==︒⊙''CP OC OP =-==即min CP =故答案为:【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、圆、特殊角的三角函数等相关知识.关键是学会添加辅助线,该题综合性较强. 三、解答题16.(2021·广东广州·中考真题)如图,在四边形ABCD 中,90ABC ∠=︒,点E 是AC 的中点,且AC AD =(1)尺规作图:作CAD ∠的平分线AF ,交CD 于点F ,连结EF 、BF (保留作图痕迹,不写作法);(2)在(1)所作的图中,若45BAD ∠=︒,且2CAD BAC ∠=∠,证明:BEF 为等边三角形.【答案】(1)图见解析;(2)证明见解析. 【分析】(1)根据基本作图—角平分线作法,作出CAD ∠的平分线AF 即可解答;(2)根据直角三角形斜边中线性质得到12BE AC =并求出30BEC BAC ABE ∠=∠+∠=︒,再根据等腰三角形三线合一性质得出CF DF =,从而得到EF 为中位线,进而可证BE EF =,60BEF ∠=︒,从而由有一个角是60°的等腰三角形是等边三角形得出结论.【详解】解:(1)如图,AF 平分CAD ∠,(2)⊙45BAD ∠=︒,且2CAD BAC ∠=∠, ⊙30CAD ∠=︒,15BAC ∠=︒, ⊙AE EC =,90ABC ∠=︒, ⊙12BE AE AC ==, ⊙15ABE BAC ∠=∠=︒, ⊙30BEC BAC ABE ∠=∠+∠=︒, 又⊙AF 平分CAD ∠,AC AD =, ⊙CF DF =, 又⊙AE EC =, ⊙1122EF AD AC ==,//EF AD ,19⊙30CEF CAD ∠=∠=︒, ⊙60BEF BEC CEF ∠=∠+∠=︒ 又⊙12BE EF AC ==⊙BEF 为等边三角形. 【点睛】本题主要考查了基本作图和等腰三角形性质以及与三角形中点有关的两个定理,解题关键是掌握等腰三角形三线合一定理、直角三角形斜边中线等于斜边一半以及三角形中位线定理. 17.(2021·南山实验教育集团南海中学九年级三模)如图,BC 是O 的直径,点A 是O 上一点,点D 是BC 延长线上一点,AB AD =,AE 是O 的弦,30AEC ∠=.(1)求证:直线AD 是O 的切线; (2)若3CD =,求O 的半径;(3)若AE BC ⊥于点F ,点P 为ABE 上一点,连接AP ,CP ,EP ,请找出AP ,CP ,EP 之间的关系,并证明.【答案】(1)见解析;(2)3;(3)EP AP +=,理由见解析 【分析】(1)先求出⊙BAD =120°,再求出⊙OAB ,进而得出⊙OAD =90°,即可得出结论; (2)先判断出⊙AOC 是等边三角形,得出AC =OC ,再判断出AC =CD ,即可得出结论; (3)先判断出⊙CAP =⊙CEM ,进而得出⊙ACP ⊙⊙ECM (SAS ),进而得出CM =CP ,⊙APC =⊙M =30°,再判断出MN =,即可得出结论. 【详解】(1)证明:如图,连接AC OA ,,30AEC ∠=︒, 30ABC AEC ∴∠∠︒==,AB AD =,30D ABC ∴∠∠︒==,120BAD ∴∠=︒,OA OB =,,30OAB ABC ∴∠=∠=︒,90OAD BAD OAB ∴∠∠∠︒=-=,点A 在O 上, ⊙直线AD 是的切线; (2)解:如图1,连接AC ,由(1)知,30D ∠=︒,90OAD ∠=︒,9060AOC D ∴∠︒∠︒=-=,∴AOC △是等边三角形,OC AC ∴=,60OAC ∠=︒,30CAD OAD OAC D ∴∠∠-∠︒∠===, 3AC CD ∴==,3OC ∴=,即O 的半径为3;(3)EP AP +=, 理由:如图, 30AEC ︒∠=, 30APC AEC ︒∴∠=∠=,连接AC ,延长PE 至M ,使EM AP =,连接CM ,AE BC ⊥,BC 为O 的直径,AC EC ∴=,四边形APEC 是O 的内接四边形,CAP CEM ∴∠=∠,∴()ACP ECM SAS ≅,21CM CP ∴=,30APC M ︒∠=∠=,过点C 作CN PM ⊥于N ,2PM MN ∴=,在Rt CNM △中,MNcos CMM =,MN cos30CM ∴︒=MN ∴=,2PM MN ∴===,PM PE EM PE AP =+=+,PE AP ∴+=,即EP AP +=. 【点睛】此题是圆的综合题,主要考查了切线的判定和性质,等边三角形的判定和勾股定理,构造出直角三角形是解本题的关键.18.(2021·广州市八一实验学校九年级)如图,在⊙P AB 中,点C 、D 在AB 上,PC =PD =CD ,⊙A =⊙BPD ,求证:⊙APC ⊙⊙BPD .【答案】见解析 【分析】根据PC =PD =CD ,可得出PCD 为等边三角形,即可得出PCD PDC ∠=∠,进而得出ACP PDB ∠=∠,再根据相似三角形的判定推出即可.【详解】证明:⊙PC =PD =CD , ⊙PCD 为等边三角形, ⊙⊙PCD =⊙PDC 60=︒, ⊙120ACP PDC ∠=∠=︒, ⊙⊙A =⊙BPD , ⊙⊙APC ⊙⊙PBD . 【点睛】本题考查了等边三角形的判定与性质,相似三角形的判定等知识点,注意:如果两个三角形的两个角分别对应相等,那么这两个三角形相似.19.(2021·黄石市有色中学九年级)如图,在ABC 中,AB AC =,120BAC ∠=︒,AD BC ⊥,垂足为G ,且AD AB =,60EDF ∠=︒,其两边分别交AB ,AC 于点E ,F .(1)若2DG =,求AC 的长; (2)求证:AB AE AF =+. 【答案】(1)4;(2)见解析 【分析】(1)连接BD 由等腰三角形的性质和已知条件得出⊙BAD =⊙DAC =12×120°=60°,再由AD =AB ,可得⊙ABD 是等边三角形,由等边三角形的性质得出DG =AG =12AD =2,,即可求解; (2)由⊙ABD 是等边三角形,得出BD =AD ,⊙ABD =⊙ADB =60°,证出⊙BDE =⊙ADF ,由ASA 证明⊙BDE ⊙⊙ADF ,得出AF =BE ,即可求解. 【详解】解:(1)证明:⊙AB =AC ,AD BC ⊥, ⊙⊙BAD =⊙DAC =12⊙BAC , ⊙⊙BAC =120°,⊙⊙BAD =⊙DAC =12×120°=60°,⊙AD =AB ,⊙⊙ABD 是等边三角形, ⊙AD =AB =BD , ⊙AD BC ⊥, ⊙DG =AG =12AD =2, ⊙AD =AB =AC =4, 即AC =4;(2)⊙⊙ABD 是等边三角形, ⊙⊙ABD =⊙ADB =60°,BD =AD , ⊙AB AC =,120BAC ∠=︒,AD BC ⊥,⊙⊙BAD=⊙DAC=12×120°=60°,⊙⊙ABD=⊙DAC,⊙⊙EDF=60°,⊙⊙ADB-⊙ADE=⊙EDF-⊙ADE,即⊙BDE=⊙ADF,⊙⊙BDE⊙⊙ADF(ASA),⊙BE=AF,⊙AB=AE+BE,⊙AB=AE+AF.【点睛】本题主要考查了三角形综合题,考查了全等三角形的判定与性质,等腰三角形的性质,等边三角形的判定与性质;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.20.(2021·合肥市五十中学东校九年级三模)如图1,已知等腰直角ΔABC,⊙ACB=90°,在直角边BC上取一点D,使⊙DAC=15°,以AD为一边作等边ΔADE,且AB与DE相交.(1)求证:AB垂直平分DE;(2)连接BE,判断EB与AC的位置关系,并说明理由;(3)如图2,若F为线段AE上一点,且FC=AC,求EFAF的值.【答案】(1)见解析;(2)互相平行;见解析;(3)1【分析】(1)根据⊙DAC=15°及等腰直角三角形的性质,可得⊙DAB=30°,根据等边三角形的性质可得⊙EAB=30°,由等腰三角形的性质可得结论;(2)由(1)的结论易得BD=BE,⊙EBA=⊙CBA=45°,即BE⊙BC,从而可得BE与AC的位置关系;(3)延长CF,与BE的延长线交于点G.易得CF=BF;其次由(2)的结论易得⊙G=30°,从而CG=2BC=2FC,即CF=GF,然后可证明⊙CAF⊙⊙GEF,从而得AF=EF,即可得结果.【详解】(1)⊙⊙ABC是等腰直角三角形,⊙ACB=90°⊙AC=BC,⊙CAB=⊙CBA=45°⊙⊙DAC=15°⊙⊙DAB=⊙CAB-⊙DAC=30°23⊙⊙ADE 是等边三角形 ⊙⊙DAE =60°⊙⊙EAB =⊙DAE -⊙DAB =30° ⊙⊙DAB =⊙EAB ⊙⊙ADE 是等边三角形 ⊙AB 垂直平分DE (2)互相平行 理由如下: ⊙AB 垂直平分DE ⊙BD =BE⊙⊙EBA =⊙CBA =45° ⊙⊙EBC =⊙EBA +⊙CBA =90° 即⊙EBC +⊙ACB =180° ⊙BE ⊙AC(3)延长CF ,与BE 的延长线交于点G ,如图所示⊙⊙F AC =⊙DAE +⊙DAC =75°,FC =AC ⊙⊙CF A =⊙F AC =75° ⊙⊙FCA =180°-2×75°=30° ⊙AC =BC ,AC =FC ⊙BC =FC由(2)知:BE ⊙AC ⊙⊙G =⊙FCA =30° ⊙⊙EBC =90° ⊙CG =2BC =2FC ⊙CF =GF在⊙CAF 和⊙GEF 中 FCA G CF GFCFA GFE ∠=∠⎧⎪=⎨⎪∠=∠⎩⊙⊙CAF ⊙⊙GEF (ASA ) ⊙AF =EF ⊙1EFAF=25【点睛】本题考查了等腰直角三角形的性质、等边三角形的性质、直角三角形的性质、全等三角形的判定与性质等知识,第(3)问的关键是作辅助线,构造三角形全等.21.(2021·广西柳州市·)如图,已知ABC 中,AC BC =,以BC 为直径的O 交AB 于E ,过点E 作EG AC ⊥于G ,交BC 的延长线于点F .(1)求证:FE 是O 的切线;(2)若30F ∠=︒,求证:24FG FC FB =⋅; (3)当6BC =,4EF =时,求AG 的长. 【答案】(1)见解析;(2)见解析;(3)245【分析】(1)连接EC ,OE ,由BC 为O 的直径,可得90BEC ∠=︒,由AC BC =,可得E 为AB 中点,由O 为BC 中点,利用中位线性质可得OE∥AC ,由EG AC ⊥,可得OE EG ⊥即可; (2)由OE OC =,可得OEC OCE ∠=∠,由EF 为圆的切线,可得90FEC OEC ∠+∠=︒,由90BEC ∠=︒,可得90B BCE ∠+∠=︒,可证FEC FBE △∽△,可得2FE FC FB =⋅,当30F ∠=︒时,可求60FOE ∠=︒,可证OEC △为等边三角形,可得30FEC F ∠=︒=∠,可证2FE FG =即可;(3)由(2)得2FE FC FB =⋅,可得()246FC FC =⋅+,解得2FC =或FC =-8舍去,可证FCG FOE △∽△,可得253CG=,可求65CG =即可. 【详解】解:(1)证明:连接EC ,OE , ⊙BC 为O 的直径, ⊙90BEC ∠=︒, ⊙CE AB ⊥, 又⊙AC BC =, ⊙E 为AB 中点, 又⊙O 为BC 中点, ⊙OE∥AC ,又⊙EG AC ⊥, ⊙OE EG ⊥, 又OE 为O 的半径, ⊙FE 是O 的切线.(2)⊙OE OC =, ⊙OEC OCE ∠=∠, ⊙EF 为圆的切线, ⊙90FEC OEC ∠+∠=︒, ⊙90BEC ∠=︒ ⊙90B BCE ∠+∠=︒, ⊙FEC B ∠=∠, 又⊙F F ∠=∠, ⊙FEC FBE △∽△, ⊙FE FCFB FE=, ⊙2FE FC FB =⋅,当30F ∠=︒时,60FOE ∠=︒, 又OE OC =,⊙OEC △为等边三角形, ⊙60OEC ∠=︒, ⊙30FEC F ∠=︒=∠, ⊙CE CF =, 又CG FE ⊥, ⊙2FE FG =, ⊙()22FG FC FB =⋅, 即24FG FC FB =⋅.(3)由(2)得2FE FC FB =⋅, 又6BC =,4FE =,FB=BC +FC =6+FC ,27⊙()246FC FC =⋅+,因式分解得(FC +8)(FC -2)=0, 解得2FC =或FC =-8舍去, ⊙6BC =, ⊙132OE OC BC ===,6AC BC ==, ⊙235FO FC CO =+=+=, ⊙CG∥OE ,⊙⊙GCF =⊙EOF ,⊙FGC =⊙FEO , ⊙FCG FOE △∽△, ⊙FC CG FO OE =,即253CG=, ⊙65CG =, ⊙624655AG AC CG =-=-=. 【点睛】本题考查圆的切线判定,直径所对圆周角性质,等腰三角形性质,中位线性质,三角形相似判定与性质,等边三角形判定与性质,掌握圆的切线判断,直径所对圆周角性质,等腰三角形性质,中位线性质,三角形相似判定与性质,等边三角形判定与性质是解题关键. 22.(2021·江苏九年级)如图,⊙ABC 为等边三角形,AB =6,将边AB 绕点A 顺时针旋转θ(0°<θ<120°)得到线段AD ,连接CD ,CD 与AB 交于点G ,⊙BAD 的平分线交CD 于点E ,F 为CD 上一点,且DF =2CF . (1)当⊙EAB =30°时,求⊙AEC 的度数;(2)当线段BF 的长取最小值时,求线段AG 的长; (3)请直接写出⊙ADE 的周长的最大值.【答案】(1)60°;(2)AG =12;(3)6+【分析】(1)用角平分线的性质和旋转性质即可;(2)作FM ⊙AD ,连接BM ,FM =2,点F 的运动轨迹是以M 为圆心、2为半径的圆,当B、F 、M 共线时,BF 取最小值; 由⊙ADG ⊙⊙BFG 可求AG ;(3)连接BE ,设BAE α∠=,AE 平分BAD ∠,可得,DAE ED EB α==∠,得到A E B C 、、、四点共圆,作ABC 的外接圆O ,CAB △是等边三角形,可将CAB △绕点C 顺时针旋转60︒得到CAN △,得E 、A 、N 三点共线,求出AE DE +的最大值,即可求出ADE 的周长. 【详解】(1)⊙AD 由AB 旋转得到AD =AB ⊙AE 平分BAD ∠ ⊙30DAE EAB ∠=∠=︒ ⊙120DAC ∠=︒ ⊙30D ∠=︒⊙=AEC D DAE ∠+∠∠ ⊙⊙AEC =60°; (2)如图,⊙CA =AB =6 ⊙2163CM CD ==,⊙13CM CA =,13FM AD =, 又DF 2CF = ⊙13CF CD = ⊙13CF CM CD CA == 又MCF ACD =∠∠ ⊙MCF ACD ∽∠∠ ⊙12,3MF AD CFM D ====∠∠ ⊙FM =2,⊙点F 的运动轨迹是以M 为圆心、2为半径的圆, ⊙当B 、F 、M 共线时,BF 取最小值 即min 2BM BM MF BM =-=- ⊙2,6,60CM BC ACB ===︒∠⊙BM =29⊙min 22BM BM MF BM -=-== ⊙CFM D =∠∠ ⊙FH ⊙AD又BF 取最小值点F 在BM 上, ⊙BFAD⊙⊙ADG ⊙⊙BFG ⊙AD AGBF BG=,6AGAG=-,⊙12AG =;⊙当BF取最小值时,12AG = (3)如图,连接BE ,设BAE α∠= ⊙AE 平分BAD ∠ ⊙,DAE ED EB α==∠ ⊙602DAC α=︒+∠ 又60ABC ∠=︒ ⊙A E B C 、、、四点共圆作ABC 的外接圆O ,则点F 在O 上, 180CBE CAE +=︒∠∠又CAB △是等边三角形,⊙可将CBF 绕点C 顺时针旋转60︒得到CAN △ 由旋转的性质得:,,60CN CE AN EB ECN ===︒∠,CAN CBE =∠∠ ⊙180CAN CAE +=︒∠∠ ⊙E 、A 、N 三点共线 ⊙ECN 为等边三角形,⊙,AE ED AE EB AE AN EN CE +=+=+== ⊙6AB =⊙ABC 的外接圆O 的半径R ==R⊙CE 的最大值为2R =即AE DE +的最大值为⊙ADE 的周长是AD AE DE ++⊙ADE 的周长是6+ 【点睛】本题考查了三角形相似的性质和判定,等边三角形的性质等知识,解题的关键是学会构建辅助圆来确定线段的最值问题.23.(2021·甘肃庆阳·九年级二模)如图,等边三角形ABC 的外部有一点P ,且30BPA ∠=︒,将AP 绕点B 逆时针旋转60°得到CQ ,连接BQ .(1)求证:ABP CBQ ≌△△.(2)若4AP =,3BP =,求P ,C 两点之间的距离. 【答案】(1)见解析(2)5 【分析】(1)由旋转的性质可知,对应边相等,旋转角相等,用“边角边”证明三角形全等即可 (2)连接,PQ PC ,根据已知条件构造直角三角形,用勾股定理求得P C ,的距离 【详解】(1)由旋转的性质可知,,,60AB CB PB QB PBQ ABC ==∠=∠=︒PBA PBQ QBA ABC QBA QBC ∴∠=∠+∠=∠+∠=∠ABP CBQ ∴≌(SAS )(2)连接,PQ PC,60PB BQ PBQ=∠=︒PBQ∴为等边三角形60PQB∴∠=︒,3PQ BQ==ABP CBQ≌△△∴30BPA BQC∠=∠=︒,4QC AP==603090PQB PQB BQC∴∠=∠+∠=︒+︒=︒222PC PQ QC∴=+5PC∴==【点睛】本题考查了旋转的性质,勾股定理,全等三角形的性质与判定,找到旋转角是解题的关键.31。
中考数学总复习图形的旋转1及答案解析 (51)

图形的变化——图形的旋转1一.选择题(共9小题)1.如图,把图中的△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为()A.(a﹣2,b)B.(a+2,b)C.(﹣a﹣2,﹣b)D.(a+2,﹣b)2.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是()A.70° B.65° C.60° D.55°3.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为()A.B.C.D.π4.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为()A.6 B.4 C.3 D.35.如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是()A. B.C.D.6.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为()A.30° B.60° C.90° D.150°7.如图,已知△ABC中,∠C=90°,AC=BC=,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为()A.2﹣B.C.﹣1 D.18如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则的长为()A.πB.6πC.3πD.1.5π9.如图,△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于()A.30° B.40° C.50° D.60°二.填空题(共8小题)10.如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A=_________ .11如图,将等边△ABC绕顶点A顺时针方向旋转,使边AB与AC重合得△ACD,BC的中点E 的对应点为F,则∠EAF的度数是_________ .12.如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形.若∠BAD=60°,AB=2,则图中阴影部分的面积为_________ .13.如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=,则图中阴影部分的面积等于_________ .14.如图,在△A BC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为_________ .15如图,AB是⊙O的直径,分别以OA,OB为直径作半圆.若AB=4,则阴影部分的面积是_________ .16.如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,则DE的长度为_________ .17如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A 顺时针旋转到位置①可得到点P1,此时AP1=;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+;…,按此规律继续旋转,直至得到点P2014为止.则AP2014=_________ .三.解答题(共7小题)18.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.(1)求n的值;(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.19.如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.(1)判断线段DE、FG的位置关系,并说明理由;(2)连结CG,求证:四边形CBEG是正方形.20.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).(1)画出△ABC关于y轴对称的△A1B1C1;(2)画出△ABC关于原点O成中心对称的△A2B2C2.21.如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F 点.若AB=6cm.(1)AE的长为_________ cm;(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;(3)求点D′到BC的距离.22.正方形ABCD中,E是CD边上一点,(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是_________ ,∠AFB=∠_________(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2.23.(1)如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A与点C重合,点P的对应点是Q.若PA=3,PB=2,PC=5,求∠BQC的度数.(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.24.如图,在等腰△ABC中,AB=BC,∠A=30°将△ABC绕点B顺时针旋转30°,得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.(1)证明:△ABE≌△C1BF;(2)证明:EA1=FC;(3)试判断四边形ABC1D的形状,并说明理由.图形的变化——图形的旋转1参考答案与试题解析一.选择题(共9小题)1.如图,把图中的△ABC经过一定的变换得到△A′B′C′,如果图中△ABC上的点P的坐标为(a,b),那么它的对应点P′的坐标为()A.(a﹣2,b)B.(a+2,b)C.(﹣a﹣2,﹣b)D.(a+2,﹣b)考点:坐标与图形变化-旋转.专题:压轴题.分析:先根据图形确定出对称中心,然后根据中点公式列式计算即可得解.解答:解:由图可知,△ABC与△A′B′C′关于点(﹣1,0)成中心对称,设点P′的坐标为(x,y),所以,=﹣1,=0,解得x=﹣a﹣2,y=﹣b,所以,P′(﹣a﹣2,﹣b).故选C.点评:本题考查了坐标与图形变化﹣旋转,准确识图,观察出两三角形成中心对称,对称中心是(﹣1,0)是解题的关键.2如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是()A.70°B.65°C.60°D.55°考点:旋转的性质.专题:几何图形问题.分析:根据旋转的性质可得AC=A′C,然后判断出△ACA′是等腰直角三角形,根据等腰直角三角形的性质可得∠CAA′=45°,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠A′B′C,然后根据旋转的性质可得∠B=∠A′B′C.解答:解:∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,∴AC=A′C,∴△ACA′是等腰直角三角形,∴∠CAA′=45°,∴∠A′B′C=∠1+∠CAA′=20°+45°=65°,由旋转的性质得∠B=∠A′B′C=65°.故选:B.点评:本题考查了旋转的性质,等腰直角三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.3.如图,在△ABC中,∠ACB=90°,∠ABC=30°,AB=2.将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,则点B转过的路径长为()A.B C.D.π考点:旋转的性质;弧长的计算.专题:几何图形问题.分析:利用锐角三角函数关系得出BC的长,进而利用旋转的性质得出∠BCB′=60°,再利用弧长公式求出即可.解答:解:∵在△ABC中,∠ACB=90°,∠ABC=30°,AB=2,∴cos30°=,∴BC=ABcos30°=2×=,∵将△ABC绕直角顶点C逆时针旋转60°得△A′B′C,∴∠BCB′=60°,∴点B转过的路径长为:=π.故选:B.点评:此题主要考查了旋转的性质以及弧长公式应用,得出点B转过的路径形状是解题关键.4.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为()A. 6 B4C3D.3考点:旋转的性质.专题:几何图形问题.分析:利用直角三角形的性质得出AB=4,再利用旋转的性质以及三角形外角的性质得出AB′=2,进而得出答案.解答:解:∵在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∴∠CAB=30°,故AB=4,∵△A′B′C由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,∴AB=A′B′=4,AC=A′C,∴∠CAA′=∠A′=30°,∴∠ACB′=∠B′AC=30°,∴AB′=B′C=2,∴AA′=2+4=6.故选:A.点评:此题主要考查了旋转的性质以及直角三角形的性质等知识,得出AB′=B′C=2是解题关键.5.如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是()A.B C D.考点:旋转的性质;正方形的性质.专题:几何图形问题.分析:连接AC1,AO,根据四边形AB1C1D1是正方形,得出∠C1AB1=∠AC1B1=45°,求出∠DAB1=45°,推出A、D、C1三点共线,在Rt△C1D1A中,由勾股定理求出AC1,进而求出DC1=OD,根据三角形的面积计算即可.解答:解:连接AC1,∵四边形AB1C1D1是正方形,∴∠C1AB1=×90°=45°=∠AC1B1,∵边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,∴∠B1AB=45°,∴∠DAB1=90°﹣45°=45°,∴AC1过D点,即A、D、C1三点共线,∵正方形ABCD的边长是1,∴四边形AB1C1D1的边长是1,在Rt△C1D1A中,由勾股定理得:AC1==,则DC1=﹣1,∵∠AC1B1=45°,∠C1DO=90°,∴∠C1OD=45°=∠DC1O,∴DC1=OD=﹣1,∴S△ADO=×OD•AD=,∴四边形AB1OD的面积是=2×=﹣1,故选:C.点评:本题考查了正方形性质,勾股定理等知识点,主要考查学生运用性质进行计算的能力,题目比较好,但有一定的难度.6.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为()A.30°B60°C.90°D.150°考点:旋转的性质.专题:几何图形问题.分析:根据直角三角形两锐角互余求出∠A=60°,根据旋转的性质可得AC=A′C,然后判断出△A′AC是等边三角形,根据等边三角形的性质求出∠ACA′=60°,然后根据旋转角的定义解答即可.解答:解:∵∠ACB=90°,∠ABC=30°,∴∠A=90°﹣30°=60°,∵△ABC绕点C顺时针旋转至△A′B′C时点A′恰好落在AB上,∴AC=A′C,∴△A′AC是等边三角形,∴∠ACA′=60°,∴旋转角为60°.故选:B.点评:本题考查了旋转的性质,直角三角形两锐角互余,等边三角形的判定与性质,熟记各性质并准确识图是解题的关键.7.如图,已知△ABC中,∠C=90°,AC=BC=,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为()A.2﹣B.C.﹣1 D.1考点:旋转的性质.分析:连接BB′,根据旋转的性质可得AB=AB′,判断出△ABB′是等边三角形,根据等边三角形的三条边都相等可得AB=BB′,然后利用“边边边”证明△ABC′和△B′BC′全等,根据全等三角形对应角相等可得∠ABC′=∠B′BC′,延长BC′交AB′于D,根据等边三角形的性质可得BD⊥AB′,利用勾股定理列式求出AB,然后根据等边三角形的性质和等腰直角三角形的性质求出BD、C′D,然后根据BC′=BD﹣C′D计算即可得解.解答:解:如图,连接BB′,∵△ABC绕点A顺时针方向旋转60°得到△AB′C′,∴AB=AB′,∠BAB′=60°,∴△ABB′是等边三角形,∴AB=BB′,在△ABC′和△B′BC′中,,∴△ABC′≌△B′BC′(SSS),∴∠ABC′=∠B′BC′,延长BC′交AB′于D,则BD⊥AB′,∵∠C=90°,AC=BC=,∴AB==2,∴BD=2×=,C′D=×2=1,∴BC′=BD﹣C′D=﹣1.故选:C.点评:本题考查了旋转的性质,全等三角形的判定与性质,等边三角形的判定与性质,等腰直角三角形的性质,作辅助线构造出全等三角形并求出BC′在等边三角形的高上是解题的关键,也是本题的难点.8.如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则的长为()A.πB6πC.3πD.1.5π考点:旋转的性质;弧长的计算.专题:计算题.分析:根据弧长公式列式计算即可得解.解答:解:的长==1.5π.故选:D.点评:本题考查了旋转的性质,弧长的计算,熟记弧长公式是解题的关键.9.如图,△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于()A.30°B.40°C.50°D.60°考点:旋转的性质.专题:计算题.分析:先根据平行线的性质得∠DCA=∠CAB=65°,再根据旋转的性质得∠BAE=∠CAD,AC=AD,则根据等腰三角形的性质得∠ADC=∠DCA=65°,然后根据三角形内角和定理计算出∠CAD=180°﹣∠ADC﹣∠DCA=50°,于是有∠BAE=50°.解答:解:∵DC∥AB,∴∠DCA=∠CAB=65°,∵△ABC绕点A旋转到△AED的位置,∴∠BAE=∠CAD,AC=AD,∴∠ADC=∠DCA=65°,∴∠CAD=180°﹣∠ADC﹣∠DCA=50°,∴∠BAE=50°.故选:C.点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.二.填空题(共8小题)10.如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A=55°.考点:旋转的性质.分析:根据题意得出∠ACA′=35°,则∠A′=90°﹣35°=55°,即可得出∠A的度数.解答:解:∵把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D,∠A′DC=90°,∴∠ACA′=35°,则∠A′=90°﹣35°=55°,则∠A=∠A′=55°.故答案为:55°.点评:此题主要考查了旋转的性质以及三角形内角和定理等知识,得出∠A′的度数是解题关键.11.如图,将等边△ABC绕顶点A顺时针方向旋转,使边AB与AC重合得△ACD,BC的中点E的对应点为F,则∠EAF的度数是60°.考点:旋转的性质;等边三角形的性质.专题:计算题.分析:根据等边三角形的性质以及旋转的性质得出旋转角,进而得出∠EAF的度数.解答:解:∵将等边△ABC绕顶点A顺时针方向旋转,使边AB与AC重合得△ACD,BC的中点E的对应点为F,∴旋转角为60°,E,F是对应点,则∠EAF的度数为:60°.故答案为:60°.点评:此题主要考查了等边三角形的性质以及旋转的性质,得出旋转角的度数是解题关键.12如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形.若∠BAD=60°,AB=2,则图中阴影部分的面积为12﹣4.考点:旋转的性质;菱形的性质.分析:根据菱形的性质得出DO的长,进而求出S正方形DNMF,进而得出S△ADF即可得出答案.解答:解:如图所示:连接AC,BD交于点E,连接DF,FM,MN,DN,∵将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形,∠BAD=60°,AB=2,∴AC⊥BD,四边形DNMF是正方形,∠AOC=90°,BD=2,AE=EC=,∴∠AOE=45°,ED=1,∴AE=EO=,DO=﹣1,∴S正方形DNMF=2(﹣1)×2(﹣1)×=8﹣4,S△ADF=×AD×AFsin30°=1,∴则图中阴影部分的面积为:4S△ADF+S正方形DNMF=4+8﹣4=12﹣4.故答案为:12﹣4.点评:此题主要考查了菱形的性质以及旋转的性质,得出正确分割图形得出DO的长是解题关键.13.如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=,则图中阴影部分的面积等于﹣1 .考点:旋转的性质;等腰直角三角形.专题:压轴题.分析:根据题意结合旋转的性质以及等腰直角三角形的性质得出AD=BC=1,AF=FC′=AC′=1,进而求出阴影部分的面积.解答:解:∵△ABC绕点A顺时针旋转45°得到△A′B′C′,∠BAC=90°,AB=AC=,∴BC=2,∠C=∠B=∠CAC′=∠C′=45°,∴AD⊥BC,B′C′⊥AB,∴AD=BC=1,AF=FC′=AC′=1,∴图中阴影部分的面积等于:S△AFC′﹣S△DEC′=×1×1﹣×(﹣1)2=﹣1.故答案为:﹣1.点评:此题主要考查了旋转的性质以及等腰直角三角形的性质等知识,得出AD,AF,DC′的长是解题关键.14.如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB、CA′相交于点D,则线段BD的长为 6 .考点:旋转的性质;相似三角形的判定与性质.专题:几何图形问题.分析:利用平行线的性质以及旋转的性质得出△CAD∽△B′A′C,再利用相似三角形的性质得出AD的长,进而得出BD的长.解答:解:∵将△ABC绕点C按逆时针方向旋转得到△A′B′C,∴AC=CA′=4,AB=B′A′=2,∠A=∠CA′B′,∵CB′∥AB,∴∠B′CA′=∠D,∴△CAD∽△B′A′C,∴=,∴=,解得AD=8,∴BD=AD﹣AB=8﹣2=6.故答案为:6.点评:此题主要考查了旋转的性质以及相似三角形的判定与性质等知识,得出△CAD∽△B′A′C是解题关键.15.如图,AB是⊙O的直径,分别以OA,OB为直径作半圆.若AB=4,则阴影部分的面积是2π.考点:旋转的性质.分析:首先计算出圆的面积,根据图示可得阴影部分面积为半圆的面积,进而可得答案.解答:解:∵AB=4,∴BO=2,∴圆的面积为:π×22=4π,∴阴影部分的面积是:×4π=2π,故答案为:2π.点评:此题主要考查了旋转的性质,关键是掌握圆的面积公式.16.如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,则DE的长度为2﹣.考点:旋转的性质.专题:几何图形问题.分析:利用正方形和旋转的性质得出A′D=A′E,进而利用勾股定理得出BD的长,进而利用锐角三角函数关系得出DE的长即可.解答:解:由题意可得出:∠BDC=45°,∠DA′E=90°,∴∠DEA′=45°,∴A′D=A′E,∵在正方形ABCD中,AD=1,∴AB=A′B=1,∴BD=,∴A′D=﹣1,∴在Rt△DA′E中,DE==2﹣.故答案为:2﹣.点评:此题主要考查了正方形和旋转的性质以及勾股定理、锐角三角函数关系等知识,得出A′D的长是解题关键.17.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A 顺时针旋转到位置①可得到点P1,此时AP1=;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+;…,按此规律继续旋转,直至得到点P2014为止.则AP2014=1342+672.考点:旋转的性质.专题:规律型.分析:由已知得AP1=,AP2=1+,AP3=2+;再根据图形可得到AP4=2+2;AP5=3+2;AP6=4+2;AP7=4+3;AP8=5+3;AP9=6+3;每三个一组,由于2013=3×671,则AP2013=(2013﹣671)+671,然后把AP2013加上即可.解答:解:AP1=,AP2=1+,AP3=2+;AP4=2+2;AP5=3+2;AP6=4+2;AP7=4+3;AP8=5+3;AP9=6+3;∵2013=3×671,∴AP2013=(2013﹣671)+671=1342+671,∴AP2014=1342+671+=1342+672.故答案为:1342+672.点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.三.解答题(共7小题)18.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.(1)求n的值;(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.考点:旋转的性质;含30度角的直角三角形;直角三角形斜边上的中线;菱形的判定.专题:几何图形问题.分析:(1)利用旋转的性质得出AC=CD,进而得出△ADC是等边三角形,即可得出∠ACD的度数;(2)利用直角三角形的性质得出FC=DF,进而得出AD=AC=FC=DF,即可得出答案.解答:解:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,∴AC=DC,∠A=60°,∴△ADC是等边三角形,∴∠ACD=60°,∴n的值是60;(2)四边形ACFD是菱形;理由:∵∠DCE=∠ACB=90°,F是DE的中点,∴FC=DF=FE,∵∠CDF=∠A=60°,∴△DFC是等边三角形,∴DF=DC=FC,∵△ADC是等边三角形,∴AD=AC=DC,∴AD=AC=FC=DF,∴四边形ACFD是菱形.点评:此题主要考查了菱形的判定以及旋转的性质和直角三角形斜边上的中线等于斜边的一半等知识,得出△DFC是等边三角形是解题关键.19如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.(1)判断线段DE、FG的位置关系,并说明理由;(2)连结CG,求证:四边形CBEG是正方形.考点:旋转的性质;正方形的判定;平移的性质.专题:几何图形问题.分析:(1)根据旋转和平移可得∠DEB=∠AC B,∠GFE=∠A,再根据∠ABC=90°可得∠A+∠ACB=90°,进而得到∠DEB+∠GFE=90°,从而得到DE、FG的位置关系是垂直;(2)根据旋转和平移找出对应线段和角,然后再证明是矩形,后根据邻边相等可得四边形CBEG是正方形.解答:(1)解:FG⊥ED.理由如下:∵△ABC绕点B顺时针旋转90°至△DBE后,∴∠DEB=∠ACB,∵把△ABC沿射线平移至△FEG,∴∠GFE=∠A,∵∠ABC=90°,∴∠A+∠ACB=90°,∴∠DEB+∠GFE=90°,∴∠FHE=90°,∴FG⊥ED;(2)证明:根据旋转和平移可得∠GEF=90°,∠CBE=90°,CG∥EB,CB=BE,∵CG∥EB,∴∠BCG=∠CBE=90°,∴∠BCG=90°,∴四边形BCGE是矩形,∵CB=BE,∴四边形CBEG是正方形.点评:此题主要考查了图形的旋转和平移,关键是掌握新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.20在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).(1)画出△ABC关于y轴对称的△A1B1C1;(2)画出△ABC关于原点O成中心对称的△A2B2C2.考点:作图-旋转变换;作图-轴对称变换.专题:作图题.分析:(1)根据网格结构找出点A、B、C关于y轴对称的点A1、B1、C1的位置,然后顺次连接即可;(2)根据网格结构找出点A、B、C关于原点对称的点A2、B2、C2的位置,然后顺次连接即可.解答:解:(1)△A1B1C1如图所示;(2)△A2B2C2如图所示.点评:本题考查了利用旋转变换作图,利用轴对称变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.21.如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F 点.若AB=6cm.(1)AE的长为4cm;(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;(3)求点D′到BC的距离.考点:几何变换综合题.专题:几何综合题.分析:(1)首先利用勾股定理得出AC的长,进而求出CD的长,利用直角三角形斜边上的中线等于斜边的一半进而得出答案;(2)首先得出△ADE为等边三角形,进而求出点E,D′关于直线AC对称,连接DD′交AC 于点P,此时DP+EP值为最小,进而得出答案;(3)连接CD′,BD′,过点D′作D′G⊥BC于点G,进而得出△ABD′≌△CBD′(SSS),则∠D′BG=45°,D′G=GB,进而利用勾股定理求出点D′到BC边的距离.解答:解:(1)∵∠BAC=45°,∠B=90°,∴AB=BC=6cm,∴AC=12cm,∵∠ACD=30°,∠DAC=90°,AC=12cm,∴CD=AC÷cos30°=12÷=12×=8(cm),∵点E为CD边上的中点,∴AE=DC=4cm.故答案为:4;(2)∵Rt△ADC中,∠ACD=30°,∴∠ADC=60°,∵E为CD边上的中点,∴DE=AE,∴△ADE为等边三角形,∵将△ADE沿AE所在直线翻折得△AD′E,∴△AD′E为等边三角形,∠AED′=60°,∵∠EAC=∠DAC﹣∠EAD=30°,∴∠EFA=90°,即AC所在的直线垂直平分线段ED′,∴点E,D′关于直线AC对称,连接DD′交AC于点P,∴此时DP+EP值为最小,且DP+EP=DD′,∵△ADE是等边三角形,AD=AE=4,∴DD′=2×AD×=2×6=12,即DP+EP最小值为12cm;(3)连接CD′,BD′,过点D′作D′G⊥BC于点G,∵AC垂直平分线ED′,∴AE=AD′,CE=CD′,∵AE=EC,∴AD′=CD′=4,在△ABD′和△CBD′中,,∴△ABD′≌△CBD′(SSS),∴∠D′BG=45°,∴D′G=GB,设D′G长为xcm,则CG长为(6﹣x)cm,在Rt△GD′C中x2+(6﹣x)2=(4)2,解得:x1=3﹣,x2=3+(不合题意舍去),∴点D′到BC边的距离为(3﹣)cm.点评:此题主要考查了全等三角形的判定与性质和锐角三角函数关系以及等边三角形的判定与性质等知识,利用垂直平分线的性质得出点E,D′关于直线AC对称是解题关键.22.正方形ABCD中,E是CD边上一点,(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是BF ,∠AFB=∠AED(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2.考点:旋转的性质;全等三角形的判定与性质;勾股定理;正方形的性质.分析:(1)直接根据旋转的性质得到DE=BF,∠AFB=∠AED;(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,根据旋转的性质得∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,而∠PAQ=45°,则∠PAE=45°,再根据全等三角形的判定方法得到△APE≌△APQ,则PE=PQ,于是PE=PB+BE=PB+DQ,即可得到DQ+BP=PQ;(3)根据正方形的性质有∠ABD=∠ADB=45°,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,根据旋转的性质得∠ABK=∠ADN=45°,BK=DN,AK=AN,与(2)一样可证明△AMN≌△AMK得到MN=MK,由于∠MBA+∠KBA=45°+45°=90°,得到△BMK为直角三角形,根据勾股定理得BK2+BM2=MK2,然后利用等相等代换即可得到BM2+DN2=MN2.解答:解:(1)∵△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,∵DE=BF,∠AFB=∠AED.故答案为BF,AED;(2)将△ADQ绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABE,如图2,则∠D=∠ABE=90°,即点E、B、P共线,∠EAQ=∠BAD=90°,AE=AQ,BE=DQ,∵∠PAQ=45°,∴∠PAE=45°,∴∠PAQ=∠PAE,在△APE和△APQ中∵,∴△APE≌△APQ,∴PE=PQ,而PE=PB+BE=PB+DQ,∴DQ+BP=PQ;(3)∵四边形ABCD为正方形,∴∠ABD=∠ADB=45°,如图,将△ADN绕点A按顺时针方向旋转90°,则AD与AB重合,得到△ABK,则∠ABK=∠ADN=45°,BK=DN,AK=AN,与(2)一样可证明△AMN≌△AMK得到MN=MK,∵∠MBA+∠KBA=45°+45°=90°,∴△BMK为直角三角形,∴BK2+BM2=MK2,∴BM2+DN2=MN2.点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了三角形全等的判定与性质、正方形的性质以及勾股定理.23.(1)如图1,点P是正方形ABCD内的一点,把△ABP绕点B顺时针方向旋转,使点A 与点C重合,点P的对应点是Q.若PA=3,PB=2,PC=5,求∠BQC的度数.(2)点P是等边三角形ABC内的一点,若PA=12,PB=5,PC=13,求∠BPA的度数.考点:旋转的性质;等边三角形的性质;勾股定理的逆定理;正方形的性质.分析:(1)根据题意得出△ABP绕点B顺时针方向旋转了90°,才使点A与C重合,进而得出∠PBQ=90°,再利用勾股定理得出∠PQC的度数,进而求出∠BQC的度数;(2)由题意可得出:△ABP绕点B顺时针方向旋转60°,才使点A与C重合,进而得出∠PP'C=90°,即可得出∠BPA的度数.解答:解:(1)连接PQ.由旋转可知:,QC=PA=3.又∵ABCD是正方形,∴△ABP绕点B顺时针方向旋转了90°,才使点A与C重合,即∠PBQ=90°,∴∠PQB=45°,PQ=4.则在△P QC中,PQ=4,QC=3,PC=5,∴PC2=PQ2+QC2.即∠PQC=90°.故∠BQC=90°+45°=135°.(2)将此时点P的对应点是点P′.由旋转知,△APB≌△CP′B,即∠BPA=∠BP′C,P′B=PB=5,P′C=PA=12.又∵△ABC是正三角形,∴△ABP绕点B顺时针方向旋转60°,才使点A与C重合,得∠PBP′=60°,又∵P′B=PB=5,∴△PBP′也是正三角形,即∠PP′B=60°,PP′=5.因此,在△PP′C中,PC=13,PP′=5,P′C=12,∴PC2=PP′2+P′C2.即∠PP′C=90°.故∠BPA=∠BP′C=60°+90°=150°.点评:此题主要考查了旋转的性质以及勾股定理逆定理和正方形的性质等知识,熟练利用勾股定理逆定理得出是解题关键.24.如图,在等腰△ABC中,AB=BC,∠A=30°将△ABC绕点B顺时针旋转30°,得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.(1)证明:△ABE≌△C1BF;(2)证明:EA1=FC;(3)试判断四边形ABC1D的形状,并说明理由.考点:旋转的性质;全等三角形的判定与性质;等腰三角形的性质;菱形的判定.分析:(1)利用全等三角形的判定结合ASA得出答案;(2)利用全等三角形的性质对边相等得出答案;(3)首先得出四边形ABC1D是平行四边形,进而利用菱形的判定得出即可.解答:(1)证明:∵等腰△ABC中,AB=BC,∠A=30°将△ABC绕点B顺时针旋转30°,得△A1BC1,∴AB=BC1=A1B=BC,∠ABE=∠C1BF,∠A=∠C1=∠A1=∠C,在△ABE和△C1BF中,,∴△ABE≌△C1BF(ASA);(2)证明:∵△ABE≌△C1BF,∴EB=BF.又∵A1B=CB,∴A1B﹣EB=CB﹣BF,∴EA1=FC;(3)答:四边形ABC1D是菱形.证明:∵∠A1=∠C=30°,∠ABA1=∠CBC1=30°,∠A1=∠C=∠ABA1=∠CBC1.∴AB∥C1D,AD∥BC1,∴四边形ABC1D是平行四边形∵AB=BC1,∴四边形ABC1D是菱形.点评:此题主要考查了旋转的性质、全等三角形的判定与性质以及菱形的判定等知识,利用旋转的性质得出对应边关系是解题关键.。
学案巧用旋转进行证明与计算.doc
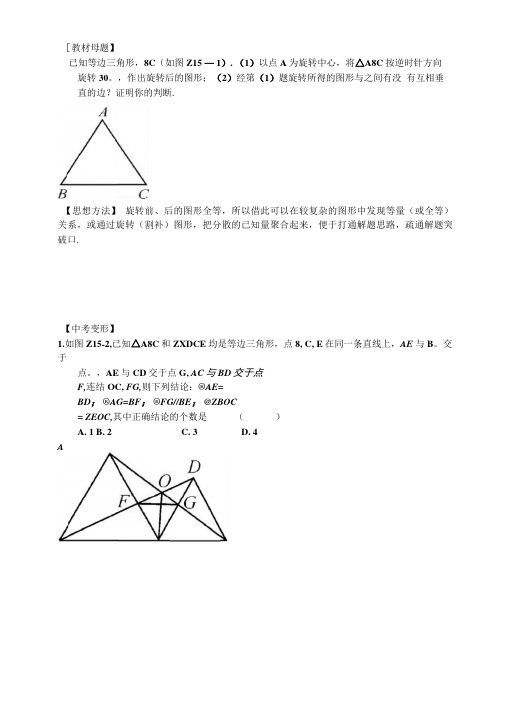
[教材母题】已知等边三角形,8C(如图Z15 — 1). (1)以点A为旋转中心,将△A8C按逆时针方向旋转30。
,作出旋转后的图形;(2)经第(1)题旋转所得的图形与之间有没有互相垂直的边?证明你的判断.【思想方法】旋转前、后的图形全等,所以借此可以在较复杂的图形中发现等量(或全等)关系,或通过旋转(割补)图形,把分散的已知量聚合起来,便于打通解题思路,疏通解题突破口.【中考变形】1.如图Z15-2,已知△A8C和ZXDCE均是等边三角形,点8, C, E在同一条直线上,AE 与B。
交于点。
,AE与CD交于点G, AC与BD交于点F,连结OC, FG,则下列结论:®AE=BD; ®AG=BF; ®FG//BE; @ZBOC= ZEOC,其中正确结论的个数是()A. 1B. 2C. 3D. 4A2.如图Z15-3, P是等腰直角ZkABC外一点,把8P绕点8顺时针旋转90。
到BP',已知ZAP1 8=135°, P‘ A : P' C=1: 3,贝l)P f A : PB= (B. 1 : 2D. 1 :3.如图Z15-4, △ACD和都是等腰直角三角形,ZACD=ZBCE=9Q°f虹交DC于点F, BD分别交CE, AE于点G, H.试猜想线段AE和BD的位置及数量关系,并说明理由.4.如图Z15-5,在RtA4BC中,ZACB=90°t匕8=30。
,将△A8C绕点C按顺时针方向旋转。
度后,得到点D刚好落在A8边上.(1)求"的值;(2)若F是DE的中点,判断四边形ACFD 的形状,并说明理由.5.[2015-南充]如图Z15-6,点P是正方形ABC。
内一点,点P到点4, 8和D的距离分别为1, 2皿,何,AADP 沿点A旋转至△ ABP\连结PP,并延长AP与8C相交于点Q.在数学活动课中,小辉将边长为皿和3的两个正方形放置在直线/上,如图Z15-7,他连结AO, CF,经测量发现AD=CF.①②③(1)他将正方形ODEF绕。
2020届中考数学总复习课件:微专题十五 巧用旋转进行证明与计算 (共29张PPT)

(2)MN2=ND2+DH2.理由如下: 由旋转可知,∠BAM=∠DAH, ∵∠BAM+∠DAN=45°, ∴∠HAN=∠DAH+∠DAN=45°. ∴∠HAN=∠MAN. 在△AMN 与△AHN 中,A∠MM=AANH=,∠HAN,
AN=AN,
∴△AMN≌△AHN(SAS),∴MN=HN. ∵∠BAD=90°,AB=AD, ∴∠B=∠ADB=45°, ∴∠HDN=∠HDA+∠ADB=90°, ∴NH2=ND2+DH2,∴MN2=ND2+DH2;
(3)如答图①,∵∠AEB=∠ACB=90°, ∴A,B,C,E 四点共圆, ∴∠CEB=∠CAB=30°,∠ABD=∠ACE, ∵∠DAE=∠BAC=30°,∴∠BAD=∠CAE, ∴△BAD∽△CAE,∴BEDC=AACB=cos30°= 23, ∴EC= 23BD, 在 Rt△ABE 中,∵AB=5,AE=3,
∴PP′2+P′D2=PD2,∴∠PP′D=90°,
中考变形4答图
∴∠AP′D=∠AP′P+∠PP′D=45°+90°=135°,
∴∠APB=∠AP′D=135°. ∵∠APB+∠AP′P=135°+45°=180°, ∴P′,P,B 三点共线. 过点 A 作 AE⊥PP′于点 E,则 AE=PE=12PP′=2, ∴BE=PE+PB=2+1=3, 在 Rt△ABE 中,AB= AE2+BE2= 22+32= 13.
3.如图 Z15-4,已知 AC⊥BC,垂足为 C,AC=4,BC=3 3,将线段 AC 绕点 A 按 逆时针方向旋转 60°,得到线段 AD,连结 DC,DB. (1)线段 DC=__4__; (2)求线段 DB 的长度.
图 Z15-4
解:(1)∵AC=AD,∠CAD=60°, ∴△ACD 是等边三角形,∴DC=AC=4; (2)如答图,作 DE⊥BC 于点 E. ∵△ACD 是等边三角形, ∴∠ACD=60°,又∵AC⊥BC, ∴∠DCE=∠ACB-∠ACD=90°-60°=30°. 在 Rt△CDE 中,DE=12DC=2,CE= 23DC=2 3, ∴BE=BC-CE=3 3-2 3= 3. 在 Rt△BDE 中,BD= DE2+BE2= 22+( 3)2= 7.
旋转的证明与计算(等边三角形)

旋转的证明与计算模块一:旋转应用之等边旋转类型二:正方形中的旋转 例题1.正方形ABCD 内一点到三顶点距离分别是1,2,3,则正方形的面积等于考点:旋转的性质;正方形的性质分析:把△PAB 绕A 点逆时针旋转90°得△EAD ,把△CPB 绕C 点顺时针旋转90°得△CFD ,连PE ,PF ,则∠1=∠2,∠3=∠4,得到∠2+∠4=90°,∠EDF=180°,即E ,D ,F 共线,且ED=PB=2,DF=PB=2,△APE ,△CPF 均为等腰直角三角形,所以211121=⨯⨯=∆APE S ;293321=⨯⨯=∆CPF S ,再在△PEF 中,PE=2,PF=23,EF=4,利用勾股定理的逆定理得到△PEF 为直角三角形,∠PEF=90°,则22422121=⨯⨯=⨯⨯=∆EF EP S PEF 最后利用S 正方形A B C D =S 五边形A P C F E =S △P E F +S △A P E +S △C P F ,即可得到答案.跟踪训练:2,PC=4,则∠APC的大小是多1、如图点P是等边三角形ABC内部一点,且PA=2,PB=3少度?考点:旋转的性质;勾股定理的逆定理分析:由于△ABC为等边三角形,所以将△ABP绕A点逆时针旋转60°得△ACP′,根据旋转的性质得到AB与AC重合,∠PAP′=60°,2AP′=AP=2,P′C=PB=3,则△APP′是等边三角形,得到PP′=2;在△PPC中,利用勾股定理的逆定理可得到∠PP′C=90°,同时得到∠P′CP=30°,因此∠P′PC=60°,即可得APC=∠APP′+∠P′PC.2、把两块边长为4的等边三角板ABC和DEF先如图1放置,使三角板DEF的顶点D与三角板ABC的AC边的中点重合,DF经过点B,射线DE与射线AB相交于点M,接着把三角形板ABC 固定不动,将三角形板DEF由图11-1所示的位置绕点D按逆时针方向旋转,设旋转角为α.其中0°<α<90°,射线DF与线段BC相交于点N(如图2示).(1)当0°<α<60°时,求AM•CN的值;(2)当0°<α<60°时,设AM=x,两块三角形板重叠部分的面积为y,求y与x的函数解析式并求定义域;(3)当BM=2时,求两块三角形板重叠部分的面积.考点:相似三角形的判定与性质;三角形的面积;等边三角形的性质;旋转的性质分析:(1)根据等边三角形的性质得到∠A=∠C=∠EDF=60°,则∠AMD+∠ADM=120°,∠ADM+∠NDC=120°,可得∠AMD=∠NDC ,根据相似三角形的判定定理得到△AMD ∽△CDN ,有相似的性质得到AM :DC=AD :CN ,即AM •CN=DC •AD ,然后把DC=AD=2代入计算即可;(2)分别过D 点作DP ⊥AB 于P ,DQ ⊥BC 于Q ,连DB ,根据等边三角形的性质得∠A=∠C=60°,而DA=DC=2,根据含30°的直角三角形三边的关系得到AP=CQ=1,DP=DQ=3,由AM=x ,得CN=x 4,MB=4-x ,BN=x44 ,两块三角形板重叠部分为四边形DMBN ,则y=S △D B M +S △D B N ,然后根据三角形的面积公式计算即可,易得到当0°<α<60°时,x 的取值范围为1<x <4;(3)当M 在线段AB 上,BM=2时,x=4-2=2,把x=2代入(2)的关系式中计算即可.当M 点在线段AB 的延长线上,过D 作DH ∥BC 交AB 于H ,BP=21DH=1,由△AMD ∽△CDN ,则AM :DC=AD :CN ,即AM •CN=DC •AD ,可计算出CN ,然后根据三角形的面积公式可计算出S △D P N ,即两块三角形板重叠部分的面积.3、如图,已知△ABC为等边三角形,M为三角形外任意一点.(1)请你借助旋转知识说明AM≤BM+CM;(2)线段AM是否存在最大值?若存在,请指出存在的条件;若不存在,请说明理由.考点:旋转的性质;三角形三边关系;等边三角形的性质.分析:(1)应把AM和BM所在的三角形旋转,与AM组成三角形,将△BMC绕B点逆时针方向旋转,使C点与A点重合,得△BM′A,易得△BMM′为正三角形,根据三角形三边关系即可证明.(2)由(1)得线段AM存在最大值,M′在AM上时4、如图,P是正△ABC内一点,PA=3,PB=4,PC=5,将线段PA以点A为旋转中心逆时针旋转60°得到线段AP1,连结P1C.(1)判断△APB与△AP1C是否全等,请说明理由;(2)求∠APB的度数;(3)求△APB 与△APC的面积之和;(4)直接写出△BPC的面积,不需要说理.考点:旋转的性质;全等三角形的判定与性质;等边三角形的性质;勾股定理.分析:(1)根据正三角形的性质求出AB=AC,∠BAC=60°,再根据旋转的性质可得AP1=AP,然后求出∠CAP1=∠BAP,再利用“边角边”证明△APB与△AP1C全等即可;(2)连结PP1,求出△PAP1是等边三角形,根据等边三角形的性质可得PP1=AP=3,∠AP1P=60°,再利用勾股定理逆定理求出∠CP1P=90°,然后计算即可得解;(3)根据全等三角形的面积相等求出△APB与△APC的面积之和等于四边形APCP1的面积,然后根据等边三角形的面积与直角三角形的面积列式计算即可得解;(4)同理求出△ABP和△BPC的面积的和,△APC和△BPC的面积的和,从而求出△ABC的面积,然后根据△BPC的面积=△ABC的面积-△APB与△APC的面积的和计算即可得解.参考答案:1、解:四边形ABCD为正方形,PA=1,PB=2,PC=3,把△PAB绕A点逆时针旋转90°得△EAD,把△CPB绕C点顺时针旋转90°得△CFD,连PE,PF,如图,∴∠1=∠2,∠3=∠4,而∠1+∠3=90°,∴∠2+∠4=90°,而∠ADC=90°,∴∠EDF=180°,即E,D,F共线;由旋转的性质得到△APE,△CPF均为等腰直角三角形,并且ED=PB=2,DF=PB=2,2、3、解答:(1)∵△ABC和△DEF都是边长为4的等边三角形,∴∠A=∠C=∠EDF=60°,∴∠AMD+∠ADM=120°,∠ADM+∠NDC=120°,∴∠AMD=∠NDC,∴△AMD∽△CDN,∴AM:DC=AD:CN,即AM•CN=DC•AD,而D点为AC的中点,∴DC=AD=2,∴AM•CN=4;(2)分别过D点作DP⊥AB于P,DQ⊥BC于Q,连DB,如图∵∠A=∠C=60°,DA=DC=2,∴AP=CQ=1,∴DP=DQ=3,∵BD为等边三角形的高,∴点D到EF的距离为DB,∴两块三角形板重叠部分为四边形DMBN,在图(1)中,AM=1,∴当0°<α<60°时,x的取值范围为1<x<4;(3)当M 在线段AB 上,BM=2时,x=4-2=2,当M 点在线段AB 的延长线上,如图(备用图),过D 作DH ∥BC 交AB 于H ,∴DH=21BC=2,BH=2, ∵BM=2,∴BP=21DH=1,与①一样可证得△AMD ∽△CDN , ∴AM :DC=AD :CN ,即AM •CN=DC •AD ,4、解答:(1)将△BMC 绕B 点逆时针方向旋转,使C 点与A 点重合,得△BM ′A , ∵∠MBM ′=60°,BM=BM ′,AM ′=MC .∴△BMM ′为正三角形.∴MM ′=BM .①若M ′在AM 上,则AM=AM ′+MM ′=BM+MC ,②若M ′不在AM 上,连接AM ′、MM ′,在△AMM ′中,根据三角形三边关系可知:AM <AM ′+MM ′,∴AM <BM+MC ,综上所述:AM ≤BM+CM ;(2)线段AM 有最大值.当且仅当M ′在AM 上时,AM=BM+MC ;存在的条件是:∠BMC=120°.5、解答:解:(1)∵△ABC 是正三角形,∴AB=AC ,∠BAC=60°,∵线段AP 以点A 为旋转中心逆时针旋转60°得到线段AP 1,∴AP=AP 1,∠PAP 1=60°,∵∠BAP+∠PAC=∠BAC=60°,∠CAP 1+∠PAC=∠PAP 1=60°,∴∠BAP=∠CAP 1,∵在△APB 与△AP 1C 中,∴△APB≌△AP1C(SAS);(2)连结PP1,∴AP=AP1,∠PAP1=60°,∴△PAP1是等边三角形,∴PP1=AP=3,∠AP1P=60°,∵△APB≌△AP1C,∴CP1=BP=4,∵CP=5,∴PP12+CP12=CP2,∴△CP1P是直角三角形,∠CP1P=90°,∴∠APB=∠AP1P+∠CP1P=60°+90°=150°;。
等边三角形的性质与判定(3种题型)-2023年新八年级数学(苏科版)(解析版)

等边三角形的性质与判定(3种题型)了解等边三角形的有关概念,探索并掌握性质及判定方法。
一.等边三角形的性质(1)等边三角形的定义:三条边都相等的三角形叫做等边三角形,等边三角形是特殊的等腰三角形.①它可以作为判定一个三角形是否为等边三角形的方法;②可以得到它与等腰三角形的关系:等边三角形是等腰三角形的特殊情况.在等边三角形中,腰和底、顶角和底角是相对而言的.(2)等边三角形的性质:等边三角形的三个内角都相等,且都等于60°.等边三角形是轴对称图形,它有三条对称轴;它的任意一角的平分线都垂直平分对边,三边的垂直平分线是对称轴.二.等边三角形的判定(1)由定义判定:三条边都相等的三角形是等边三角形.(2)判定定理1:三个角都相等的三角形是等边三角形.(3)判定定理2:有一个角是60°的等腰三角形是等边三角形.说明:在证明一个三角形是等边三角形时,若已知或能求得三边相等则用定义来判定;若已知或能求得三个角相等则用判定定理1来证明;若已知等腰三角形且有一个角为60°,则用判定定理2来证明.三.等边三角形的判定与性质(1)等边三角形是一个非常特殊的几何图形,它的角的特殊性给有关角的计算奠定了基础,它的边角性质为证明线段、角相等提供了便利条件.同是等边三角形又是特殊的等腰三角形,同样具备三线合一的性质,解题时要善于挖掘图形中的隐含条件广泛应用.(2)等边三角形的特性如:三边相等、有三条对称轴、一边上的高可以把等边三角形分成含有30°角的直角三角形、连接三边中点可以把等边三角形分成四个全等的小等边三角形等.(3)等边三角形判定最复杂,在应用时要抓住已知条件的特点,选取恰当的判定方法,一般地,若从一般三角形出发可以通过三条边相等判定、通过三个角相等判定;若从等腰三角形出发,则想法获取一个60°的角判定.一.等边三角形的性质(共9小题)1.(2022秋•崇川区校级月考)如图,在等边△ABC中,BD平分∠ABC交AC于点D,过点D作DE⊥BC 于点E,且CE=1.5,则AB的长为()A.3B.4.5C.6D.7.5【分析】由在等边三角形ABC中,DE⊥BC,可求得∠CDE=30°,则可求得CD的长,又由BD平分∠ABC 交AC于点D,由三线合一的知识,即可求得答案.【解答】解:∵△ABC是等边三角形,∴∠ABC=∠C=60°,AB=BC=AC,∵DE⊥BC,∴∠CDE=30°,∵EC=1.5,∴CD=2EC=3,∵BD平分∠ABC交AC于点D,∴AD=CD=3,∴AB=AC=AD+CD=6.故选:C.【点评】此题考查了等边三角形的性质以及含30°角的直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.2.(2022秋•姜堰区月考)如图,在等边△ABC中,AB=4cm,BD平分∠ABC,点E在BC的延长线上,且∠E=30°,则CE的长是()A.1cm B.2cm C.3cm D.4cm【分析】根据等边三角形的性质解答即可.【解答】解:∵等边△ABC的边长AB=4cm,BD平分∠ABC,∴∠ACB=60°,DC=AD=2cm,∵∠E=30°,∠E+∠EDC=∠ACB,∴∠EDC=60°﹣30°=30°=∠E,∴CD=CE=2cm,故选:B.【点评】此题考查等边三角形的性质,关键是根据等边三角形的三线合一解答.3.(2022秋•常州期中)如图,△ABC是等边三角形,P为BC上一点,在AC上取一点D,使AD=AP,且∠APD=70°,则∠PAB的度数是()A.10°B.15°C.20°D.25°【分析】由已知条件AD=AP可知∠ADP=∠APD,结合∠APD=70°可得∠ADP的度数,从而得到∠P AD 的度数;根据等边三角形的性质,可以得到∠BAC=60°,结合∠PAB=∠BAC﹣∠PAD即可解答此题.【解答】解:∵AD=AP,∴∠ADP=∠APD.∵∠ADP=∠APD,∠APD=70°,∴∠ADP=70°,∠PAD=40°.∵△ABC是等边三角形,∴∠BAC=60°,∴∠PAB=60°﹣40°=20°.故选:C.【点评】本题主要考查等边三角形与等腰三角形的性质,可以结合等边三角形的性质进行解答.4.(2022秋•海门市期末)如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD,DF⊥BE,垂足为点F.(1)求证:CE=2CF;(2)若CF=2,求△ABC的周长.【分析】(1)根据等边三角形的性质可知∠ACB=60°,再由DF⊥BE可知∠DFC=90°,∠FDC=90°﹣∠C=30°,由直角三角形的性质即可得出结论;(2)由CF=2可得出CD=4,故可得出AC的长,进而可得出结论.【解答】(1)证明:∵△ABC为等边三角形,∴∠ACB=60°,∵DF⊥BE,∴∠DFC=90°,∠FDC=90°﹣∠C=30°,∴DC=2CF.∵CE=CD∴CE=2CF;(2)解:∵CF=2,由(1)知CE=2CF,∴DC=2CF=4.∵△ABC为等边三角形,BD是中线,∴AB=BC=AC=2DC=8,∴△ABC的周长=AB+AC+BC=8+8+8=24.【点评】本题考查的是等边三角形的性质,熟知边三角形的三个内角都相等,且都等于60°是解题的关键.5.(2022秋•启东市期末)如图,△ABC是等边三角形,AD是BC边上的中线,点E在AD上,且DE=BC,则∠AFE=()A.100°B.105°C.110°D.115°【分析】根据等边三角形的性质得到∠BAC=60°,∠BAD=BAC=30°,AD⊥BC,BD=CD=BC,根据等腰直角三角形的性质得到∠DEC=∠DCE=45°,根据三角形的内角和定理即可得到答案.【解答】解:∵△ABC是等边三角形,∴∠BAC=60°,∵AD是BC边上的中线,∴∠BAD=BAC=30°,AD⊥BC,BD=CD=BC,∴∠CDE=90°,∵DE=BC,∴DE=DC,∴∠DEC=∠DCE=45°,∴∠AEF=∠DEC=45°,∴∠AFE=180°﹣∠BAD﹣∠AEF=180°﹣30°﹣45°=105°,故选:B.【点评】本题考查了等边三角形的性质,三角形的内角和定理,熟练掌握等边三角形的性质是解题的关键.6.(2022秋•大丰区期中)如图,在等边△ABC中,D为BC边上的中点,以A为圆心,AD为半径画弧,与AC边交点为E,则∠ADE的度数为()A.60°B.105°C.75°D.15°【分析】根据等边三角形三线合一的性质可求出∠DAC=30°,结合AD等于AE求出∠ADE的度数即可.【解答】解:在等边△ABC中,D为BC边上的中点,∴∠DAC=30°(三线合一),在△ADE中,AD=AE,∴∠AED=∠ADE=(180°﹣30°)=75°,故选:C.【点评】本题考查了等边三角形的性质,等腰三角形的性质,解题关键在于能够熟练掌握该知识并进行合理运用.7.(2022秋•如皋市期中)如图,在△ABC中,BC的垂直平分线分别交BC,AB于点E,F,连接CF,若△AFC是等边三角形,则∠B的度数是()A.60°B.45°C.30°D.15°【分析】根据垂直平分线的性质得到∠B=∠BCF,再利用等边三角形的性质得到∠AFC=60°,从而可得∠B的度数.【解答】解:∵EF垂直平分BC,∴BF=CF,∴∠B=∠BCF,∵△ACF为等边三角形,∴∠AFC=60°,∴∠B=∠BCF=30°.故选:C.【点评】本题考查了垂直平分线的性质,等边三角形的性质,三角形外角的性质,解题的关键是利用垂直平分线的性质得到∠B=∠BCF.8.(2022秋•秦淮区校级月考)如图,△ABC是等边三角形,D,E分别是AC,BC上的点,若AE=AD,∠CED=25°,则∠BAE=°.【分析】利用等边三角形的性质可得∠C=∠BAC=60°,从而利用三角形的外角性质可得∠ADE=85°,然后利用等腰三角形的性质可得∠AED=∠ADE=85°,从而利用三角形的内角和定理可得∠DAE=10°,最后利用角的和差关系进行计算即可解答.【解答】解:∵△ABC是等边三角形,∴∠C=∠BAC=60°,∵∠CED=25°,∴∠ADE=∠CED+∠C=85°,∵AE=AD,∴∠AED=∠ADE=85°,∴∠DAE=180°﹣∠AED﹣∠ADE=10°,∴∠BAE=∠BAC﹣∠DAE=60°﹣10°=50°,故答案为:50.9.(2022秋•工业园区校级月考)阅读材料:如图,△ABC中,AB=AC,P为底边BC上任意一点,点P到两腰的距离分别为r1,r2,腰上的高为h,连接AP,则S△ABP+S△ACP=S△ABC,即:,∴r1+r2=h(定值).(1)类比与推理如果把“等腰三角形”改成“等边三角形”,那么P的位置可以由“在底边上任一点”放宽为“在三角形内任一点”,即:已知等边△ABC内任意一点P到各边的距离分别为r1,r2,r3,等边△ABC的高为h,试证明r1+r2+r3=h(定值).(2)理解与应用△ABC中,∠C=90°,AB=10,AC=8,BC=6,△ABC内部是否存在一点O,点O到各边的距离相等?(填“存在”或“不存在”),若存在,请直接写出这个距离r的值,r=.若不存在,请说明理由.【分析】(1)连接AP,BP,CP.根据三角形ABC的面积的两种计算方法进行证明;(2)根据角平分线上的点到角两边的距离相等进行求作.【解答】证明:(1)连接AP,BP,CP.则S△ABP+S△BCP+S△ACP=S△ABC,即,∵△ABC是等边三角形,∴AB=BC=AC,∴r1+r2+r3=h(定值);(2)存在.r=2.【点评】此题主要是考查了等边三角形的性质、角平分线的性质以及三角形的面积公式.注意:直角三角形斜边上的高等于两条直角边的乘积除以斜边.二.等边三角形的判定(共6小题)10.(2022秋•吴江区校级月考)若一个三角形有两条边相等,且有一内角为60°,那么这个三角形一定为()A.钝角三角形B.等腰三角形C.直角三角形D.正三角形【分析】根据有一个角是60°的等腰三角形是等边三角形求解.【解答】解:根据有一个角是60°的等腰三角形是等边三角形可得到该三角形一定为正三角形.【点评】此题考查学生对有一个角是60°的等腰三角形是等边三角形的运用.11.(2022秋•梁溪区期中)如图所示,在等腰△ABC中,AB=AC,AF为BC的中线,D为AF上的一点,且BD的垂直平分线过点C并交BD于E.求证:△BCD是等边三角形.【分析】根据等腰三角形的性质得出AF⊥BC,根据线段垂直平分线性质求出BD=DC,BC=CD,推出BD =DC=BC,根据等边三角形的判定得出即可.【解答】证明:∵AB=AC,AF为BC的中线,∴AF⊥BC,∴BD=DC,∵CE是BD的垂直平分线,∴BC=CD,∴BD=DC=BC,∴△BCD是等边三角形.【点评】本题考查了等边三角形的判定,等腰三角形的性质,线段垂直平分线性质的应用,能正确运用定理进行推理是解此题的关键.12.(2021秋•淮安期末)三角形的三边长a,b,c满足(a﹣b)4+(b﹣c)2+|c﹣a|=0,那么这个三角形一定是()A.直角三角形B.等边三角形C.等腰非等边三角形D.钝角三角形【分析】利用偶次方及绝对值的非负性可得出a﹣b=0,b﹣c=0,c﹣a=0,进而可得出a=b=c,再结合a,b,c是三角形的三边长,即可得出这个三角形是等边三角形.【解答】解:∵(a﹣b)4+(b﹣c)2+|c﹣a|=0,∴a﹣b=0,b﹣c=0,c﹣a=0,又∵a,b,c是三角形的三边长,∴这个三角形是等边三角形.故选:B.【点评】本题考查了等边三角形的判定、偶次方及绝对值的非负性,牢记三条边都相等的三角形是等边三角形是解题的关键.13.(2022秋•吴江区校级月考)在边长为9的等边三角形ABC中,点Q是BC上一点,点P是AB上一动点,以每秒1个单位的速度从点A向点B移动,设运动时间为t秒.(1)如图1,若BQ=6,PQ∥AC,求t的值;(2)如图2,若点P从点A向点B运动,同时点Q以每秒2个单位的速度从点B经点C向点A运动,当t为何值时,△APQ为等边三角形?【分析】(1)由平行线的性质得∠BQP=∠C=60°,∠BPQ=∠A=60°,从而得出△BPQ是等边三角形,列方程求解即可;(2 )根据点Q所在的位置不同,分类讨论△APQ是否为等边三角形,再根据等边三角形的性质得到等量关系,列方程求解即可.【解答】解:(1)如图1,∵△ABC是等边三角形,PQ∥AC,∴∠BQP=∠C=60°,∠BPQ=∠A=60°,又∠B=60°,∴∠B=∠BQP=∠BPQ,∴△BPQ是等边三角形,∴BP=BQ,由题意可知:AP=t,则BP=9﹣t,∴9﹣t=6,解得:t=3,∴当t的值为3时,PQ∥AC;(2)如图2,①当点Q在边BC上时,此时△APQ不可能为等边三角形;②当点Q在边AC上时,若△APQ为等边三角形,则AP=AQ,由题意可知,AP=t,BC+CQ=2t,∴AQ=BC+AC﹣(BC+CQ)=9+9﹣2t=18﹣2t,即:18﹣2t=t,解得:t=6,∴当t=6时,△APQ为等边三角形.题为背景,根据等边三角形、等腰三角形以及全等三角形的性质寻找等量关系,再列方程求解,能根据题目要求进行分类讨论是解题的关键.14.(2022秋•常州期中)如图,AB=AC,∠BAC=120°,AD⊥AC,AE⊥AB.(1)求∠C的度数;(2)求证:△ADE是等边三角形.【分析】(1)因为AB=AC,根据等腰三角形的性质,等腰三角形的两个底角相等,又∠BAC=120°,根据三角形内角和,可求出∠C的度数为30°.(2)AD⊥AC,AE⊥AB,∠ADE=∠AED=60°,三个角是60°的三角形是等边三角形.【解答】(1)解:∵AB=AC,∠BAC=120°,∴∠B=∠C=30°,故答案为:30°.(2)证明:∵∠B=∠C=30°,AD⊥AC,AE⊥AB.∴∠ADC=∠AEB=60°,∴∠ADC=∠AEB=∠EAD=60°,∴△ADE是等边三角形.【点评】本题考查等腰三角形的性质,等腰三角形的底角相等,以及等边三角形的判定定理,三个角是60°的三角形,是等边三角形.15.(2022秋•江都区校级月考)等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.【分析】先证△ABP≌△ACQ得AP=AQ,再证∠P AQ=60°,从而得出△APQ是等边三角形.【解答】解:△APQ证明:∵△ABC为等边三角形,∴AB=AC.在△ABP与△ACQ中,∵,∴△ABP≌△ACQ(SAS).∴AP=AQ,∠BAP=∠CAQ.∵∠BAC=∠BAP+∠PAC=60°,∴∠PAQ=∠CAQ+∠PAC=60°,∴△APQ是等边三角形.【点评】考查了等边三角形的判定及全等三角形的判定方法.三.等边三角形的判定与性质(共9小题)16.(2022秋•梁溪区期中)一艘轮船由海平面上A地出发向南偏西40°的方向行驶100海里到达B地,再由B地向北偏西20°的方向行驶100海里到达C地,则A,C两地相距()A.100海里B.80海里C.60海里D.40海里【分析】先求得∠CBA=60°,然后可判断△ABC为等边三角形,从而可求得AC的长.【解答】解:如图所示:连接AC.∵点B在点A的南偏西40°方向,点C在点B的北偏西20°方向,∴∠ABD=40°,∠CBD=20°,∴∠CBA=∠ABD+∠CBD=60°.又∵BC=BA,∴△ABC为等边三角形.∴AC=BC=AB=100海里.故选:A.【点评】本题主要考查的是方向角、等边三角形的性质和判定,证得△ABC为等边三角形是解题的关键.17.(2022秋•玄武区期中)如图,△ABC为等边三角形,BD⊥AC交AC于点D,DE∥BC交AB于点E.(1)求证:△ADE是等边三角形.(2)求证:AE=AB.【分析】(1)根据等边三角形的性质和平行线的性质证明即可.(2)根据等边三角形的性质解答即可.【解答】证明:(1)∵△ABC为等边三角形,∴∠A=∠ABC=∠C=60°.∵DE∥BC,∴∠AED=∠ABC=60°,∠ADE=∠C=60°.∴△ADE是等边三角形.(2)∵△ABC为等边三角形,∴AB=BC=AC.∵BD平分∠ABC,∴AD=AC.∵△ADE是等边三角形,∴AE=AD.∴AE=AB.【点评】此题考查等边三角形的判定和性质,关键是根据等边三角形的性质和平行线的性质解答.18.(2022秋•姑苏区期中)如图,在四边形ABCD中,AB=AD,CB=CD,∠A=60°,点E为AD上一点,连接BD,CE交于点F,CE∥AB.(1)判断△DEF的形状,并说明理由;(2)若AD=12,CE=8,求CF的长.【分析】(1)先证明△ABD是等边三角形,可得∠ABD=∠ADB=60°,由平行线的性质可得∠CED=∠ADB=∠DFE=60°,可得结论;(2)由等边三角形的性质和平行线的性质可求AE=CE=8,即可求解.【解答】解:(1)△DEF是等边三角形,理由如下:∵AB=AD,∠A=60°,∴△ABD是等边三角形,∴∠ABD=∠ADB=60°,∵CE∥AB,∴∠CED=∠A=60°,∠DFE=∠ABD=60°,∴∠CED=∠ADB=∠DFE,∴△DEF是等边三角形;(2)连接AC交BD于点O,∵AB=AD,CB=CD,∴AC是BD的垂直平分线,即AC⊥BD,∵AB=AD,∠BAD=60°,∴∠BAC=∠DAC=30°,∵CE∥AB,∴∠BAC=∠ACE=∠CAD=30°,∴AE=CE=8,∴DE=AD﹣AE=12﹣8=4,∵△DEF是等边三角形,∴EF=DE=4,∴CF=CE﹣EF=8﹣4=4.【点评】本题考查了等边三角形的判定和性质,平行线的性质,证明AE=CE是解题的关键.19.(2022秋•南通期末)已知等边△ABC的边长为5,点D为直线BC上一点,BD=1,DE∥AB交直线AC于点E,则DE的长为.【分析】分D在线段BC上,和D在线段CB的延长线上,两种情况,讨论求解即可.【解答】解:①当D在线段BC上,如图:∵等边△ABC的边长为5,∴∠A=∠B=∠C=60°,AB=AC=BC=5,∵BD=1,∴CD=BC﹣BD=4,∵DE∥AB,∴∠EDC=∠B=60°,∠DEA=∠A=60°,∴△DEC为等边三角形,∴DE=CD=4;②当D在线段CB的延长线上,如图:同法可得:△DEC为等边三角形,∴DE=CD=BC+BD=6;综上:DE的长为:4或6;故答案为:4或6.【点评】本题考查等边三角形的判定和性质.熟练掌握,两直线平行,同位角相等,证明三角形是等边三角形,是解题的关键.注意,分类讨论.20.(2022秋•鼓楼区校级月考)如图所示,在等边△ABC中,AB=9cm,点P从点C出发沿CB边向点B 以2cm/s的速度移动,点Q从点B出发沿BA边向点A以5cm/s的速度移动.P,Q两点同时出发,它们移动的时间为ts.(1)你能用含的式子表示BP和BQ的长度吗?请你表示出来.(2)请问几秒后,△PBQ第一次为等边三角形?(3)若P,Q两点分别从C,B两点同时出发,并且按顺时针方向沿△ABC三边运动,请问经过几秒后点P与点Q第一次在△ABC的哪条边上相遇?【分析】(1)由等边三角形的性质可求得BC的长,用t可表示出BP和BQ的长;(2)由等边三角形的性质可知BQ=BP,可得到关于t的方程,可求得t的值;(3)设经过t秒后第一次相遇,由条件可得到关于t的方程,可求得t的值,可求得点P走过的路程,可确定出P点的位置.【解答】解:(1)∵△ABC为等边三角形,∴BC=AB=9cm,∵点P的运动速度为2cm/s,运动时间为ts,∴BP=BC﹣CP=(9﹣2t)cm,∵点Q的运动速度为5cm/s,运动时间为ts,∴BQ=5t(cm);(2)若△PBQ为等边三角形,则有BQ=BP,即9﹣2t=5t,解得t=,∴s时,△PBQ第一次为等边三角形;(3)设ts时,Q与P第一次相遇,根据题意得5t﹣2t=18,解得t=6,即6s时,两点第一次相遇.当t=6s时,P走过的路程为2×6=12cm,而9<12<18,即此时P在AB边上,∴经过6秒后点P与点Q在AB上第一次相遇.【点评】本题考查了等边三角形的性质和判定、方程思想等知识.该题为运动型题目,解决这类问题的关键是化“动”为“静”,即用时间和速度表示出线段的长.21.(2022秋•泰州月考)如图,已知点D、E在△ABC的边BC上,AB=AC,AD=AE.(1)求证:BD=CE;(2)若AD=BD=DE=CE,求∠BAE的度数.【分析】(1)作AF⊥BC于点F,利用等腰三角形三线合一的性质得到BF=CF,DF=EF,相减后即可得到正确的结论.(2)根据等边三角形的判定得到△ADE是等边三角形,根据等边三角形的性质、等腰三角形的性质以及角的和差关系即可求解.【解答】(1)证明:如图,过点A作AF⊥BC于F.∵AB=AC,AD=AE.∴BF=CF,DF=EF,∴BD=CE.(2)∵AD=DE=AE,∴△ADE是等边三角形,∴∠DAE=∠ADE=60°.∵AD=BD,∴∠DAB=∠DBA.∴∠DAB=∠ADE=30°.∴∠BAE=∠BAD+∠DAE=90°.【点评】本题考查了等边三角形的判定与性质,熟练运用等边三角形的判定是本题的关键.22.(2022秋•沭阳县期中)已知:如图,点C为线段AB上一点,△ACM,△CBN都是等边三角形,AN 交MC于点E,BM交CN于点F.(1)求证:AN=BM;(2)求证:△CEF为等边三角形.【分析】(1)由等边三角形可得其对应线段相等,对应角相等,进而可由SAS得到△ACN≌△MCB,结论得证;(2)由(1)中的全等可得∠CAN=∠CMB,进而得出∠MCF=∠ACE,由ASA得出△CAE≌△CMF,即CE=CF,又ECF=60°,所以△CEF为等边三角形.【解答】证明:(1)∵△ACM,△CBN是等边三角形,∴AC=MC,BC=NC,∠ACM=∠NCB=60°,∴∠ACM+∠MCN=∠NCB+∠MCN,即∠ACN=∠MCB,在△ACN和△MCB中,∵,∴△ACN≌△MCB(SAS),∴AN=BM.(2)∵△CAN≌△CMB,∴∠CAN=∠CMB,又∵∠MCF=180°﹣∠ACM﹣∠NCB=180°﹣60°﹣60°=60°,∴∠MCF=∠ACE,在△CAE和△CMF中,∵,∴△CAE≌△CMF(ASA),∴CE=CF,∴△CEF为等腰三角形,又∵∠ECF=60°,∴△CEF为等边三角形.【点评】本题主要考查了全等三角形的判定及性质以及等边三角形的判定问题,能够掌握并熟练运用.23.(2022秋•启东市校级月考)数学课上,张老师举了下面的例题:例1:等腰三角形ABC中,∠A=110°,求∠B的度数.(答案:35°)例2:等腰三角形ABC中,∠A=40°,求∠B的度数.(答案:40°或70°或100°)张老师启发同学们进行变式,小敏编的题目如下:变式题:等腰三角形ABC中,∠A=80°,求∠B的度数.(1)请你解答上面的变式题.(2)请继续探索,完成下面问题:等腰三角形ABC中,∠A=60°,则∠B的度数为.(3)根据以上探索,我们发现,∠A的度数不同,得到的∠B度数的个数也可能不同.请你直接写出当∠A 满足什么条件时,∠B能得到三个不同的度数.【分析】(1)∠A是顶角,则∠B是底角,根据等腰三角形的两个底角相等即可求解;∠B是顶角,则∠A 是底角,则根据等腰三角形的两个底角相等,以及三角形的内角和定理即可求解;∠C是顶角,则∠B与∠A都是底角,根据等腰三角形的两个底角相等即可求解;(2)分两种情况:①90≤x<180;0<x<90,结合三角形内角和定理求解即可.【解答】解:(1)当∠A=80°为顶角时,∠B==50°;当∠B是顶角,则∠A是底角,则∠B=180°﹣80°﹣80°=20°;当∠C是顶角,则∠B与∠A都是底角,则∠B=∠A=80°,综上所述,∠B的度数为50°或20°或80°;(2)因为有一个角为60°的等腰三角形为等边三角形,所以∠B=60°,故答案为:60°.(3)分两种情况:设∠A=x°,①当90≤x<180时,∠A只能为顶角,∴∠B的度数只有一个;②当0<x<90时,若∠A为顶角,则∠B=()°;若∠A为底角,∠B为顶角,则∠B=(180﹣2x)°;若∠A为底角,∠B为底角,则∠B=x°.当≠180﹣2x且180﹣2x≠x且≠x,即x≠60时,∠B有三个不同的度数.综上所述,可知当0°<∠A<90°且x≠60°时,∠B有三个不同的度数.【点评】本题考查了等腰三角形的性质及三角形内角和定理,进行分类讨论是解题的关键.24.(2022秋•铜山区校级月考)已知:如图,△DAC、△EBC均是等边三角形,点A、C、B在同一条直线上,且AE、BD分别与CD、CE交于点M、N.求证:(1)AE=DB;(2)△CMN为等边三角形.【分析】(1)根据△DAC、△EBC均是等边三角形,求证△ACE≌△DCB(SAS)即可得出结论.(2)由(1)可知:△ACE≌△DCB,和△DAC、△EBC均是等边三角形,求证△ACM≌△DCN(ASA)即可得出结论.【解答】证明:(1)∵△DAC、△EBC均是等边三角形,∴AC=DC,EC=BC,∠ACD=∠BCE=60°,∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠DCB.在△ACE和△DCB中,∴△ACE≌△DCB(SAS).∴AE=DB.(2)由(1)可知:△ACE≌△DCB,∴∠CAE=∠CDB,即∠CAM=∠CDN.∵△DAC、△EBC均是等边三角形,∴AC=DC,∠ACM=∠BCE=60°.又点A、C、B在同一条直线上,∴∠DCE=180°﹣∠ACD﹣∠BCE=180°﹣60°﹣60°=60°,即∠DCN=60°.∴∠ACM=∠DCN.在△ACM和△DCN中,∴△ACM≌△DCN(ASA).∴CM=CN.又∠DCN=60°,∴△CMN为等边三角形.【点评】此题主要考查学生对等边三角形的性质与判定、全等三角形的判定与性质、三角形内角和定理等知识点的理解和掌握,此题难度不大,但是步骤繁琐,属于中档题.一.选择题(共5小题)1.(2022秋•梁溪区期中)下列命题不正确的是()A.等腰三角形的底角不能是钝角B.等腰三角形不能是直角三角形C.若一个三角形有三条对称轴,那么它一定是等边三角形D.两个全等的且有一个锐角为30°的直角三角形可以拼成一个等边三角形【分析】利用等腰三角形的性质和等边三角形的判定的知识,对各选项逐项分析,即可得出结果.【解答】解:本题可采用排除法;A、利用等腰三角形的性质,等腰三角形的两底角相等,若两底角均为钝角,不能构成三角形,故这种说法错误,故不选A;B、举反例:等腰直角三角形,故B不正确.即答案选B.【点评】本题主要考查了等腰三角形的性质和等边三角形的判定,要求学生在学习过程中要对所学过的知识进行总结和复习,以便灵活的运用所学的知识.2.(2022秋•鼓楼区校级月考)如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是()A.平行B.相交C.垂直D.平行、相交或垂直【分析】先判断出OA=OB,∠OAB=∠ABO,分两种情况判断出∠ABD=∠AOB=60°,进而判断出△AOC ≌△ABD,即可得出结论.【解答】解:∵∠AOB=60°,OA=OB,∴△OAB是等边三角形,∴OA=AB,∠OAB=∠ABO=60°①当点C在线段OB上时,如图1,∵△ACD是等边三角形,∴AC=AD,∠CAD=60°,∴∠OAC=∠BAD,在△AOC和△ABD中,,∴△AOC≌△ABD(SAS),∴∠ABD=∠AOC=60°,∴∠DBE=180°﹣∠ABO﹣∠ABD=60°=∠AOB,∴BD∥OA,②当点C在OB的延长线上时,如图2,同①的方法得出OA∥BD,∵△ACD是等边三角形,∴AC=AD,∠CAD=60°,∴∠OAC=∠BAD,在△AOC和△ABD中,,∴△AOC≌△ABD(SAS),∴∠ABD=∠AOC=60°,∴∠DBE=180°﹣∠ABO﹣∠ABD=60°=∠AOB,∴BD∥OA,故选:A.【点评】此题主要考查了等边三角形的判定和性质,全等三角形的判定和性质,求出∠ABD=60°是解本题的关键.3.(2022秋•射阳县校级月考)如图,将一等边三角形的三条边各8等分,按顺时针方向(图中箭头方向)标注各等分点的序号0、1、2、3、4、5、6、7、8,将不同边上的序号和为8的两点依次连接起来,这样就建立了“三角形”坐标系.在建立的“三角形”坐标系内,每一点的坐标用过这一点且平行(或重合)于原三角形三条边的直线与三边交点的序号来表示(水平方向开始、按顺时针方向、取与三角形外箭头方向一致的一侧序号),如点A的坐标可表示为(1,2,5),点B的坐标可表示为(4,3,1),按此方法,若点C的坐标为(2,m,m﹣2),则m=()A.2B.3C.4D.6【分析】根据点A的坐标可表示为(1,2,5),点B的坐标可表示为(4,3,1),得到经过该点的三条直线对应着等边三角形三边上的三个数,依次为左,上,下,即可解答.【解答】解:由题意得:点C的坐标为(2,4,2),∴m=4,故选:C.【点评】本题考查了等边三角形的性质,规律型:数字的变化类,找出题中的规律是解题的关键.4.(2022秋•扬州期中)在下列结论中:(1)有一个外角是120°的等腰三角形是等边三角形(2)有两个外角相等的等腰三角形是等边三角形(3)有一边上的高也是这边上的中线的等腰三角形是等边三角形(4)三个外角都相等的三角形是等边三角形其中正确的个数是()A.4个B.3个C.2个D.1个【分析】根据等边三角形的性质和定义,可得:有一个角为60°的等腰三角形是等边三角形;三个内角都相等的三角形为等边三角形;再由中线的性质和三角形内角和的定义可解答本题.【解答】解:(1):因为外角和与其对应的内角的和是180°,已知有一个外角是120°,即是有一个内角是60°,有一个内角为60°的等腰三角形是等边三角形.该结论正确.(2):两个外角相等说明该三角形中两个内角相等,而等腰三角形的两个底角是相等的,故不能确定该三角形是等边三角形.该结论错误.(3):等腰三角形的底边上的高和中线本来就是重合的,“有一边”可能是底边,故不能保证该三角形是等边三角形.该结论错误.(4):三个外角都相等的三角形是等边三角形.正确;故选:C.【点评】本题考查等边三角形的判定,解题的关键是灵活运用的等边三角形的判定方法解决问题.5.(2022秋•邗江区月考)如图,直线m∥n,△ABC是等边三角形,顶点B在直线n上,直线m交AB 于点E,交AC于点F,若∠1=140°,则∠2的度数是()A.80°B.100°C.120°D.140°【分析】先根据等边三角形的性质可得∠A=∠B=∠C=60°,由三角形外角的性质可得∠AEF的度数,由平行线的性质可得同旁内角互补,可得结论.【解答】解:∵△ABC是等边三角形,∴∠A=60°.对于△AEF,∵∠1=∠A+∠AEF=140°,∴∠AEF=140°﹣60°=80°,∴∠DEB=∠AEF=80°,∵m∥n,∴∠2+∠DEB=180°,∴∠2=180°﹣80°=100°,故选:B.【点评】本题主要考查了等边三角形的性质,平行线的性质,三角形外角的性质,题目比较基础,熟练掌握性质是解题的关键.二.填空题(共13小题)6.(2022秋•江阴市期中)已知△ABC中,AB=AC=6,∠C=60°,则BC=6.【分析】先利用等腰三角形的性质得到∠B=∠C=60°,则可判断△ABC为等边三角形,然后根据等边三角形的性质得到BC=AB.【解答】解:∵AB=AC=6,∴∠B=∠C=60°,∴△ABC为等边三角形,∴BC=AB=6.故答案为:6.【点评】本题考查了等边三角形的性质:等边三角形的三条边都相等,三个内角都相等,且都等于60°.7.(2022秋•建邺区校级月考)如图,已知△ABC是等边三角形,AD是中线,E在AC上,AE=AD,则∠EDC=.【分析】由AD是等边△ABC的中线,根据等边三角形中:三线合一的性质,即可求得AD⊥BC,∠CAD =30°,又由AD=AE,根据等边对等角与三角形内角和定理,即可求得∠ADE的度数,继而求得答案.【解答】解:∵AD是等边△ABC的中线,∴AD⊥BC,∠BAD=∠CAD=∠BAC=×60°=30°,∴∠ADC=90°,∵AD=AE,∴∠ADE=∠AED=(180°﹣∠CAD)=75°,∴∠EDC=∠ADC﹣∠ADE=90°﹣75°=15°.故答案为:15°.【点评】此题考查了等边三角形的性质、等腰三角形的性质以及三角形内角和定理.此题难度不大,解题的关键是注意数形结合思想的应用.8.(2022秋•崇川区校级月考)如图,已知△ABC中,∠A=60°,D为AB上一点,且AC=2AD+BD,∠B=4∠ACD,则∠DCB的度数是.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
旋转的证明与计算
模块一:旋转应用之等边旋转
类型二:正方形中的旋转 例题1.正方形ABCD 内一点到三顶点距离分别是1,2,3,则正方形的面积等于
考点:旋转的性质;正方形的性质
分析:把△PAB 绕A 点逆时针旋转90°得△EAD ,把△CPB 绕C 点顺时针旋转90°得△CFD ,连PE ,PF ,则∠1=∠2,∠3=∠4,得到∠2+∠4=90°,∠EDF=180°,即E ,D ,F 共线,且ED=PB=2,DF=PB=2,△APE ,△CPF 均为等腰直角三角形,所以2
11121=⨯⨯=∆APE S ;2
93321=⨯⨯=∆CPF S ,再在△PEF 中,PE=2,PF=23,EF=4,利用勾股定理的逆定理得到△PEF 为直角三角形,∠PEF=90°,则22422
121=⨯⨯=⨯⨯=∆EF EP S PEF 最后利用S 正方形
A B C D =S 五边形A P C F E =S △P E F +S △A P E +S △C P F ,即可得到答案.
跟踪训练:
2,PC=4,则∠APC的大小是多1、如图点P是等边三角形ABC内部一点,且PA=2,PB=3
少度?
考点:旋转的性质;勾股定理的逆定理
分析:由于△ABC为等边三角形,所以将△ABP绕A点逆时针旋转
60°得△ACP′,根据旋转的性质得到AB与AC重合,∠PAP′=60°,
2
AP′=AP=2,P′C=PB=3
,则△APP′是等边三角形,得到PP′=2;在△PPC中,利用勾股定理的逆定理可得到∠PP′C=90°,同时得到∠P′CP=30°,因此∠P′PC=60°,即可得APC=∠APP′+∠P′PC.
2、把两块边长为4的等边三角板ABC和DEF先如图1放置,使三角板DEF的顶点D与三角板ABC的AC边的中点重合,DF经过点B,射线DE与射线AB相交于点M,接着把三角形板ABC 固定不动,将三角形板DEF由图11-1所示的位置绕点D按逆时针方向旋转,设旋转角为α.其中0°<α<90°,射线DF与线段BC相交于点N(如图2示).
(1)当0°<α<60°时,求AM•CN的值;
(2)当0°<α<60°时,设AM=x,两块三角形板重叠部分的面积为y,求y与x的函数解析式并求定义域;
(3)当BM=2时,求两块三角形板重叠部分的面积.
考点:相似三角形的判定与性质;三角形的面积;等边三角形的性质;旋转的性质
分析:(1)根据等边三角形的性质得到∠A=∠C=∠EDF=60°,则∠AMD+∠ADM=120°,∠ADM+∠NDC=120°,可得∠AMD=∠NDC ,根据相似三角形的判定定理得到△AMD ∽△CDN ,有相似的性质得到AM :DC=AD :CN ,即AM •CN=DC •AD ,然后把DC=AD=2代入计算即可;
(2)分别过D 点作DP ⊥AB 于P ,DQ ⊥BC 于Q ,连DB ,根据等边三角形的性质得∠A=∠C=60°,而DA=DC=2,根据含30°的直角三角形三边的关系得到AP=CQ=1,DP=DQ=3,由AM=x ,得CN=x 4,MB=4-x ,BN=x
44 ,两块三角形板重叠部分为四边形DMBN ,则y=S △D B M +S △D B N ,然后根据三角形的面积公式计算即可,易得到当0°<α<60°时,x 的取值范围为1<x <4;
(3)当M 在线段AB 上,BM=2时,x=4-2=2,把x=2代入(2)的关系式中计算即可.当M 点在线段AB 的延长线上,过D 作DH ∥BC 交AB 于H ,BP=2
1DH=1,由△AMD ∽△CDN ,则AM :DC=AD :CN ,即AM •CN=DC •AD ,可计算出CN ,然后根据三角形的面积公式可计算出S △D P N ,即两块三角形板重叠部分的面积.
3、如图,已知△ABC为等边三角形,M为三角形外任意一点.
(1)请你借助旋转知识说明AM≤BM+CM;
(2)线段AM是否存在最大值?若存在,请指出存在的条件;若不存
在,请说明理由.
考点:旋转的性质;三角形三边关系;等边三角形的性质.
分析:(1)应把AM和BM所在的三角形旋转,与AM组成三角形,将△
BMC绕B点逆时针方向旋转,使C点与A点重合,得△BM′A,易得△
BMM′为正三角形,根据三角形三边关系即可证明.
(2)由(1)得线段AM存在最大值,M′在AM上时
4、如图,P是正△ABC内一点,PA=3,PB=4,PC=5,将线段PA以点A为旋转中心逆时针旋转60°得到线段AP1,连结P1C.
(1)判断△APB与△AP1C是否全等,请说明理由;
(2)求∠APB的度数;
(3)求△APB 与△APC的面积之和;
(4)直接写出△BPC的面积,不需要说理.
考点:旋转的性质;全等三角形的判定与性质;等边三角形的性质;
勾股定理.
分析:(1)根据正三角形的性质求出AB=AC,∠BAC=60°,再根据旋
转的性质可得AP1=AP,然后求出∠CAP1=∠BAP,再利用“边角边”证
明△APB与△AP1C全等即可;
(2)连结PP1,求出△PAP1是等边三角形,根据等边三角形的性质可
得PP1=AP=3,∠AP1P=60°,再利用勾股定理逆定理求出∠CP1P=90°,
然后计算即可得解;
(3)根据全等三角形的面积相等求出△APB与△APC的面积之和等于四边形APCP1的面积,然后根据等边三角形的面积与直角三角形的面积列式计算即可得解;
(4)同理求出△ABP和△BPC的面积的和,△APC和△BPC的面积的和,从而求出△ABC的面积,然后根据△BPC的面积=△ABC的面积-△APB与△APC的面积的和计算即可得解.
参考答案:
1、
解:四边形ABCD为正方形,PA=1,PB=2,PC=3,
把△PAB绕A点逆时针旋转90°得△EAD,把△CPB绕C点顺时针旋转90°得△CFD,连PE,PF,如图,
∴∠1=∠2,∠3=∠4,
而∠1+∠3=90°,
∴∠2+∠4=90°,
而∠ADC=90°,
∴∠EDF=180°,即E,D,F共线;
由旋转的性质得到△APE,△CPF均为等腰直角三角形,并且ED=PB=2,DF=PB=2,
2、
3、
解答:(1)∵△ABC和△DEF都是边长为4的等边三角形,∴∠A=∠C=∠EDF=60°,
∴∠AMD+∠ADM=120°,∠ADM+∠NDC=120°,
∴∠AMD=∠NDC,
∴△AMD∽△CDN,
∴AM:DC=AD:CN,即AM•CN=DC•AD,
而D点为AC的中点,
∴DC=AD=2,
∴AM•CN=4;
(2)分别过D点作DP⊥AB于P,DQ⊥BC于Q,连DB,如图∵∠A=∠C=60°,DA=DC=2,∴AP=CQ=1,
∴DP=DQ=3,
∵BD为等边三角形的高,
∴点D到EF的距离为DB,
∴两块三角形板重叠部分为四边形DMBN,
在图(1)中,AM=1,
∴当0°<α<60°时,x的取值范围为1<x<4;
(3)当M 在线段AB 上,BM=2时,x=4-2=2,
当M 点在线段AB 的延长线上,如图(备用图),
过D 作DH ∥BC 交AB 于H ,
∴DH=2
1BC=2,BH=2, ∵BM=2,
∴BP=2
1DH=1,与①一样可证得△AMD ∽△CDN , ∴AM :DC=AD :CN ,即AM •CN=DC •AD ,
4、解答:(1)将△BMC 绕B 点逆时针方向旋转,使C 点与A 点重合,得△BM ′A , ∵∠MBM ′=60°,BM=BM ′,AM ′=MC .
∴△BMM ′为正三角形.
∴MM ′=BM .
①若M ′在AM 上,
则AM=AM ′+MM ′=BM+MC ,
②若M ′不在AM 上,连接AM ′、MM ′,
在△AMM ′中,根据三角形三边关系可知:
AM <AM ′+MM ′,
∴AM <BM+MC ,
综上所述:AM ≤BM+CM ;
(2)线段AM 有最大值.
当且仅当M ′在AM 上时,AM=BM+MC ;
存在的条件是:∠BMC=120°.
5、解答:解:(1)∵△ABC 是正三角形,
∴AB=AC ,∠BAC=60°,
∵线段AP 以点A 为旋转中心逆时针旋转60°得到线段AP 1,
∴AP=AP 1,∠PAP 1=60°,
∵∠BAP+∠PAC=∠BAC=60°,
∠CAP 1+∠PAC=∠PAP 1=60°,
∴∠BAP=∠CAP 1,
∵在△APB 与△AP 1C 中,
∴△APB≌△AP1C(SAS);
(2)连结PP1,
∴AP=AP1,∠PAP1=60°,
∴△PAP1是等边三角形,
∴PP1=AP=3,∠AP1P=60°,
∵△APB≌△AP1C,
∴CP1=BP=4,
∵CP=5,
∴PP12+CP12=CP2,
∴△CP1P是直角三角形,∠CP1P=90°,
∴∠APB=∠AP1P+∠CP1P=60°+90°=150°;。
