狼羊过河问题
人狼羊菜过河七种方法

人狼羊菜过河七种方法在生活中,我们经常会遇到一些有趣的问题,比如如何让人狼、羊和菜过河。
这个问题看似简单,但实际上需要我们动动脑筋,找到最合适的方法。
下面,我将为大家介绍七种不同的方法,希望能够帮助大家更好地理解和解决这个有趣的问题。
方法一,先让羊过河,再回来带狼过河,最后带菜过河。
这种方法在实际生活中比较常见,可以有效地解决问题,但需要注意控制好时间,避免狼和羊之间发生冲突。
方法二,先让狼过河,再回来带羊过河,最后带菜过河。
这种方法可以有效地避免狼和羊之间的冲突,但需要注意控制好时间,避免羊和菜之间发生冲突。
方法三,先让菜过河,再回来带羊过河,再带狼过河。
这种方法可以有效地避免狼和羊之间的冲突,但需要注意控制好时间,避免菜和羊之间发生冲突。
方法四,先让羊和菜一起过河,再回来带狼过河。
这种方法可以有效地减少来回的次数,但需要注意控制好时间,避免狼和羊之间发生冲突。
方法五,先让狼和菜一起过河,再回来带羊过河。
这种方法可以有效地减少来回的次数,但需要注意控制好时间,避免狼和羊之间发生冲突。
方法六,先让狼带着羊过河,然后狼回来,再让狼带着菜过河。
这种方法可以有效地减少来回的次数,但需要注意控制好狼的行为,避免狼和羊之间发生冲突。
方法七,先让狼过河,然后狼回来,再让菜过河,最后让狼带着羊过河。
这种方法可以有效地避免狼和羊之间的冲突,但需要注意控制好时间,避免狼和菜之间发生冲突。
通过以上七种方法的介绍,我们可以看到,在解决问题的过程中,我们需要充分发挥自己的智慧,灵活运用各种方法,找到最合适的解决方案。
希望大家在面对类似的问题时,能够灵活运用这些方法,找到最佳的解决方案。
同时,也希望大家在生活中能够多多思考,勇于创新,不断提升自己的解决问题的能力。
这样,我们才能更好地应对生活中的各种挑战,迎接更美好的未来。
人狼羊菜渡河问题

人、狼、羊、菜安全渡河问题安全渡河问题又称作“人狼羊菜”问题,其具体描述为:一个人带着一条狼、一只羊、一筐白菜过河但由于船太小,人一次只能带一样东西乘船过河。
狼和羊、羊和白菜不能单独留在同岸,否则羊或白菜会被吃掉。
该问题可使用图论中的最短路算法进行求解。
问题分析根据题意,人不在场时,狼要吃羊,羊要吃菜,因此,人不在场时,不能将狼与羊、羊与菜留在河的任一岸。
可用四维向量v=(m,n,p,q)来表示状态,m表示人,n代表狼,p代表羊,q代表白菜,且m,n,p,q ∈{0,1},0代表在对岸,1代表在此岸。
例如,状态(0,1,1,0)表示人和菜在对岸,而狼和羊在此岸,这时人不在场,狼要吃羊,因此,这个状态是不可行的。
通过穷举法将所有可行的状态列举出来,可行的状态有(1,1,1,1),(1,1,1,0),(1,1,0,1),(1,0,1,1),(1,0,1,0),(0,1,0,1),(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,0,0,0)。
可行状态共有十种。
每一次的渡河行为改变现有的状态。
现构造赋权图G=(V,E,W),其中顶点集V={v1,…, v10}中的顶点(按照上面的顺序编号)分别表示上述10个可行状态,当且仅当对应的两个可行状态之间存在一个可行转移时两顶点之间才有边连接,并且对应的权重取为1,当两个顶点之间不存在可行转移时,可以把相应的权重取为∞。
因此问题变为在图G中寻找一条由初始状态(1,1,1,1)出发,经最小次数转移到达最终状态(0,0,0,0)的转移过程,即求从状态(1,1,1,1)到状态(0,0,0,0)的最短路径。
该问题难点在于计算邻接矩阵,由于摆渡一次就改变现有状态,为此再引入一个四维状态转移向量,用它来反映摆渡情况。
用1表示过河,0表示未过河。
例如,(1,1,0,0)表示人带狼过河。
状态转移只有四种情况,用如下向量表示:(1,0,0,0),(1,1,0,0),(1,0,1,0),(1,0,0,1)现在规定状态向量与转移向量之间的运算为0+0=0,1+0=1,0+1=1,1+1=0通过上面的定义,如果某一个可行状态加上转移向量得到的新向量还属于可行状态,则这两个可行状态对应的顶点之间就存在一条边。
狼和小羊过河数学题

感谢百度文库让我们在这里与你相见,您的下载就是我们最大的动力。
狼和小羊过河数学题
1. 题目描述
有一只狼、一只小羊和一艘小船,船一次只能载一个动物,狼会吃小羊,在小羊不被狼吃掉的前提下,如何让狼和小羊都安全过河呢?
2. 解题思路
我们可以这样想,因为狼会吃小羊,所以不能让狼和小羊单独在一起,除非狼已经在对岸了。
首先让小羊划船到对岸,然后小羊把船划回来。
接着让狼划船到对岸,这时候狼在对岸,小羊在原岸。
然后让在对岸的狼把船划回来,最后小羊再划船到对岸,这样小羊和狼就都安全过河了。
3. 答案
先送小羊过河,小羊返回;送狼过河,狼返回;再送小羊过河。
4. 解析
这个答案的关键在于避免狼和小羊单独相处的情况。
第一步送小羊过河,因为狼在原岸不会吃到对岸的小羊;小羊返回是为了把船带回来以便送狼过河;狼过河后在对岸,但是不能让狼把船带回来,不然小羊就会被吃,所以让狼返回;最后再送小羊过河就都安全了。
第 1 页共 1 页。
渡河问题20160430
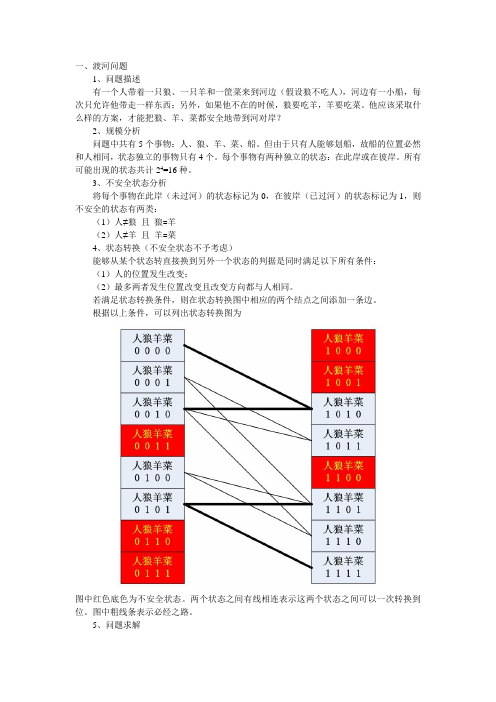
一、渡河问题1、问题描述有一个人带着一只狼、一只羊和一筐菜来到河边(假设狼不吃人),河边有一小船,每次只允许他带走一样东西;另外,如果他不在的时候,狼要吃羊,羊要吃菜。
他应该采取什么样的方案,才能把狼、羊、菜都安全地带到河对岸?2、规模分析问题中共有5个事物:人、狼、羊、菜、船。
但由于只有人能够划船,故船的位置必然和人相同,状态独立的事物只有4个。
每个事物有两种独立的状态:在此岸或在彼岸。
所有可能出现的状态共计24=16种。
3、不安全状态分析将每个事物在此岸(未过河)的状态标记为0,在彼岸(已过河)的状态标记为1,则不安全的状态有两类:(1)人≠狼且狼=羊(2)人≠羊且羊=菜4、状态转换(不安全状态不予考虑)能够从某个状态转直接换到另外一个状态的判据是同时满足以下所有条件:(1)人的位置发生改变;(2)最多两者发生位置改变且改变方向都与人相同。
若满足状态转换条件,则在状态转换图中相应的两个结点之间添加一条边。
根据以上条件,可以列出状态转换图为图中红色底色为不安全状态。
两个状态之间有线相连表示这两个状态之间可以一次转换到位。
图中粗线条表示必经之路。
5、问题求解渡河问题的求解即是在状态转换图中寻找从起始结点(0,0,0,0)到终止结点(1,1,1,1)之间的最短路径。
该最短路径可能不止一条,每条最短路径都是该问题的最佳可行解。
该问题的全部的两个最佳可行解为:人狼羊菜0 0 0 01 0 1 00 0 1 01 1 1 00 1 0 01 1 0 10 1 0 11 1 1 1人狼羊菜0 0 0 01 0 1 00 0 1 01 0 1 10 0 0 11 1 0 10 1 0 11 1 1 1整个过程至少需要7步(划船7次,3.5个来回)才能完成。
具体过程可以有两种:(1)将羊带过河,自己返回;将狼带过河,将羊带回;将菜带过河,自己返回;将羊带过河。
(2)将羊带过河,自己返回;将菜带过河,将羊带回;将狼带过河,自己返回;将羊带过河。
过河大师45关攻略

过河大师45关攻略
问题:船一次最多乘坐2只动物,岸上狼的数量大于羊,就会吃羊,空船不能开走。
步骤:
1、首先是先一只狼一只羊过河,然后一只羊回来;
2、接着就是两只狼过河,一只狼回来;
3、两只羊过河,一只羊一只狼回来;
4、两只羊过河,一只狼回来;
5、两只狼过河,一只狼回来;
6、最后就是两只狼过河,即可完成。
问题:船能一次上三个人,(僵尸也算),无论船上和岸上,只要僵尸的数量大于人就会被吃人,只要人能够开船
步骤:
1、首先是一人一僵尸过河,然后一人回来;
2、接着就是两个人只一个僵尸过河,两个人回来;
3、三人过河,一人回来;
4、一人一僵尸过河,即可。
问题:桥一次能承重两只羊,时间按走得慢的那只计算,只要在规定的时间内没有过河就会被狼吃掉,狼还有17分钟过来步骤:
1、首先是1分钟和2分钟过河,然后一分钟回来;
2、接着就是5分钟和10分钟过河,2分钟回来;
3、1分钟和2分钟过河,即可完成。
一年级数学巧妙渡河

一年级数学--巧妙渡河
猎人要把一只狼,一头羊和一篮白菜从河的左岸带到右岸,但他的渡船太小,一次只能带一样。
因为狼要吃羊,羊会吃白菜,所以狼和羊,羊和白菜不能在无人监视的情况下相处。
问猎人怎样才能达到目的?
解:稍加思考就可得到渡河的方法,如下:
第一次:猎人把羊带至右岸;
第二次:猎人单身回左岸,把白菜带至右岸,此时右岸有猎人,羊和白菜;
第三次:猎人再把羊带回左岸,放下羊把狼带至右岸,此时右岸有猎人,狼和白菜;
第四次:猎人单身回左岸,最后把羊带至右岸,便可完成渡河的任务。
(完)。
人狼羊菜安全渡河问题
人狼羊菜安全渡河问题摘要安全渡河问题又称作“人狼羊菜” 问题,其具体描述为:一个人带着一条狼、一只羊、一筐白菜过河但由于船太小,人一次只能带一样东西乘船过河。
狼和羊、羊和白菜不能单独留在同岸,否则羊或白菜会被吃掉。
本文尝试应用运筹学中的图理论中的树知识来解决该问题。
问题分析设图的顶点 v=(m, n, p, q), m 表示人, n 代表狼, p 代表羊, q 代表白菜,且m, n, p, q ∈{-1, 0, 1} , -1 代表此岸, 0 代表船上, 1 代表彼岸。
根据题意,问题变成了找出从顶点(-1, -1, -1, -1)到顶点(1, 1, 1, 1)路径(即是一棵以(-1, -1,-1, -1)为根结点,(1, 1, 1, 1, )为叶子结点的树)的问题。
通过分析问题知道:顶点 v 必须满足以下条件:1,当m≠0 时,n, p, q≠0 因为乘船时必须有人在上面;2,当m≠p 时,n≠p, q≠p 即当人与羊不在一起时,必羊和狼不在一起,羊和菜不在一起;3, 当 n、 p、 q 中有一个为 0 时其余两个都不能为 0.设相邻顶点 Vi=(m1, n1, p1, q1) , Vj=(m2, n2, p2, q2) . 设Tm=m2-m1, Tn=n2-n1, Tp=p2-p1, Tq=q2-q1, 易见T∈(-1, 0, 1) ,因为状态必须是渐变的,不能逾越中间一个状态。
路径应该满足以下条件:1,| Tm| ≠0,即人前后的状态必须改变;2, | Tn| +| Tp| +| Tq| =0 或=1,因为最多仅能有一个物品随人转移,可以为0 是因为允许人一个物品都不带;3,当| Tn| +| Tp| +| Tq| =1 时设状态改变的物品为 x,必有 Tx=Tm,因为物体状态的改变必是人状态改变的结果,且与人的改变方向一致。
根据上述规则建立符合条件的树:1,用穷举法产生 81 个顶点;2,由顶点法则排除不合理点,还剩 k 个可行点;3,用(-1, -1, -1, -1)和(1, 1, 1, 1)分别作为根结点和叶子结点;4,用路径法则选取正确点:从(-1, -1, -1, -1)为起点开始从剩下的k-1-1 个可行顶点中找到合理点,再以此点为新的起点从剩下的 k-1-1-1 个可行点中按路径法则找合理点. . . . . . 以此类推找到最后一个合理点为(1, 1, 1,1)。
狼羊过河
截图3
表中的处理函数非常简单,就是根据当前状态以及过河动作,得到一个新状态,如果过河动作与当前状态矛盾,
则返回失败,以FARMER_GO_TAKE_WOLF动作对应的处理函数ProcessFarmerGoTakeWolf()为例,看看ProcessFarmerGoTakeWolf()函数
本题算法的核心就是对这个状态树进行深度优先遍历,当某个状态满足结束状态时就输出一组结果。
需要注意的是,并不是每个动作都可以得到一个新状态,比如“农夫带狼过河”这个动作,
对于那些狼已经在河对岸的状态就是无效的,无法得到新状态,因此这个八叉树并不是满树。除此之外,
题目要求的合法性判断也可以砍掉很多无效的状态。最后一点需要注意的是,即使是有效的状态,也会有重复,
Farmer go back, item states is : 0 0 1 0
Farmer take vegetable go over river, item states is : 1 0 1 1
Farmer take sheep go back, item states is : 0 0 0 1
这个检查由IsProcessedState()函数完成,IsProcessedState()函数的实现也很简单,就是遍历states,
与新状态比较是否有相同状态,代码如下:
截图5
运行程序,最终得到的结果是:
Find Result 1:
Unknown action, item states is : 0 0 0 0
终状态,如果是则说明这个搜索路径可以得到一个解,于是调用PrintResult()函数打印结果,随后的return表示终止设个搜索路
一年级数学巧妙渡河
巧妙渡河
猎人要把一只狼,一头羊和一篮白菜从河的左岸带到右岸,但他的渡船太小,一次只能带一样。
因为狼要吃羊,羊会吃白菜,所以狼和羊,羊和白菜不能在无人监视的情况下相处。
问猎人怎样才能达到目的?
解:稍加思考就可得到渡河的方法,如下:
第一次:猎人把羊带至右岸;
第二次:猎人单身回左岸,把白菜带至右岸,此时右岸有猎人,羊和白菜;
第三次:猎人再把羊带回左岸,放下羊把狼带至右岸,此时右岸有猎人,狼和白菜;
第四次:猎人单身回左岸,最后把羊带至右岸,便可完成渡河的任务。
提供:农大子校廖爱华。
狼羊草过河-图论
狼羊草过河问题描述•一位农夫带了狼、羊、草,准备过河。
可是小船每次只能容下农夫和一件物品。
渔民不在时,狼会吃羊、羊会吃草。
而且,我们假设,狼或羊在农夫不在时不会自己跑掉或被人牵走且农夫会划船。
要求我们设计一个方案,使人、狼、羊、草都能安全过河。
问题分析及假设过河问题相当于状态的转移。
初状态是人,狼,羊,草均在此岸,目标终状态是人,狼,羊,草均在对岸。
定义以下两种向量表示状态的转移:•状态向量:用四维向量(人,狼,羊,草)表示人,狼,羊,草各自的状态,记“在此岸”时各分量为“1”,否则为“0”。
例如:(1,1,1,1)表示人,狼,羊,草均在此岸,(0,0,0,0)表示人,狼,羊,草均在对岸。
•运载向量:用四维向量(人,狼,羊,草)表示他们各自被运载的情况,记“被运载”时各分量为“1”,否则记为“0”。
例如:(1,1,0,0)表示被运载的是人和狼,又如(1,0,1,0)表示被运载的是人和羊。
模型定义根据题设要求,在满足系统限定条件下,可得以下状态向量和运载向量集合:•用S表示所有允许状态向量的集合,则S={(1,1,1,1),(1,1,1,0),(1,1,0,1),(1,0,1,1),(1,0,1,0),(0,1,0,1),(0,0,0,1),(0,0,1,0),(0,1,0,0),(0,0,0,0)}•用D表示所有允许运载向量的集合,则D={(1,0,0,0),(1,1,0,0),(1,0,1,0),(1,0,0,1)}状态转移方程:原状态⊕运载=现状态运算规则:1+1=0,1+0=1,0+1=1,0+0=0可取状态向量允许运载方式:可取状态向量+ 可取运载向量=模型求解(1,1,0,0)(1,0,1,0)(1,0,0,1)(1,0,0,0)1.(1,1,1,1) += (0,0,1,1)×= (0,1,0,1)√= (0,1,1,0)×= (0,1,1,1)×(1,1,0,0)(1,0,1,0)(1,0,0,1)(1,0,0,0)2.(0,1,0,1) += (1,0,0,1)×= (1,1,1,1) ×= (1,1,0,0)×= (1,1,0,1)√解法一:初始状态(1,1,1,1)经多次运载状态变化成最终状态(0,0,0,0)(1,1,0,0)(1,0,1,0)(1,0,0,1)(1,0,0,0)3.(1,1,0,1) += (0,0,0,1)√= (0,1,1,1) ×= (0,1,0,0)√= (0,1,0,1)√(1,1,0,0)(1,0,1,0)(1,0,0,1)(1,0,0,0)4.1. (0,0,0,1) += (1,1,0,1)√= (1,0,1,1) √= (1,0,0,0)×= (1,0,0,1)×(1,1,0,0)(1,0,1,0)(1,0,0,1)(1,0,0,0)4.2.(0,1,0,0) += (1,0,0,0)×= (1,1,1,0) √= (1,1,0,1)√= (1,1,0,0)×4.3. (0,1,0,1)与上述第二步重复,必定不是最优解,故不用进行下去。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
狼、羊、菜过河问题
1.模型建立
用0-1将人、狼、羊、菜河这边的所有状态表示出来(其中状态1代表在河这边,状态0代表在河对岸),共有16种状态。
由题设条件知,状态(0,1,1,0),(0,0,1,1)(0,1,1,1,)是不允许的,从而对应状态(1,0,0,1)(1,1,0,0)(1,0,0,0,)也是不允许的。
最后得到10种状态。
将它们分别标号如下:
1(1 1 1 1)2(1 0 1 1)3(0 0 0 1)4(1 1 0 1)5(1 1 1 0)6(1 0 1 0)7(0 1 0 1)8(0 1 0 0)9(0 0 1 0)10(0 0 0 0)然后将各状态能够相互转移的状态用1表示,不能相互转移的状态用无穷大inf表示,得到关于这10种状态的一个10*10的邻接矩阵。
利用Floyd算法,在matlab上运行,即可找出该过河问题的最佳答案。
所得的邻接矩阵如下:
[inf inf inf inf inf inf 1 inf inf inf
inf inf 1 inf inf inf inf inf 1 inf
inf 1 inf 1 inf inf inf inf inf inf
inf inf 1 inf inf inf 1 1 inf inf
inf inf inf inf inf inf inf 1 1 inf
inf inf inf inf inf inf inf inf 1 1
1 inf inf 1 inf inf inf inf inf inf
inf inf inf 1 1 inf inf inf inf inf
inf 1 inf inf 1 1 inf inf inf inf
inf inf inf inf inf 1 inf inf inf inf ]
利用Floyd算法:
function [D,path]=floyd(a)
n=size(a,1);
D=a;
path=zeros(n,n);
for i=1:n
for j=1:n
if D(i,j)~=inf
path(i,j)=j;
end
end
end
for k=1:n
for i=1:n
for j=1:n
if D(i,k)+D(k,j)<D(i,j)
D(i,j)=D(i,k)+D(k,j);
path(i,j)=path(i,k);
end
end
end
end
function [L,R]=router(D,path,1,10)
L=zeros(0,0);
R=s;
while 1
if s==t
L=fliplr(L);
L=[0,L];
return
end
L=[L,D(s,t)];
R=[R,path(s,t)];
s=path(s,t);
End
输入
a=[inf inf inf inf inf inf 1 inf inf inf
inf inf 1 inf inf inf inf inf 1 inf
inf 1 inf 1 inf inf inf inf inf inf
inf inf 1 inf inf inf 1 1 inf inf
inf inf inf inf inf inf inf 1 1 inf
inf inf inf inf inf inf inf inf 1 1
1 inf inf 1 inf inf inf inf inf inf
inf inf inf 1 1 inf inf inf inf inf
inf 1 inf inf 1 1 inf inf inf inf
inf inf inf inf inf 1 inf inf inf inf ]
得到:
D =
2 4
3 2
4 6 1 3
5 7
4 2 1 2 2 2 3 3 1 3
3 1 2 1 3 3 2 2 2 4
2 2 1 2 2 4 1 1
3 5
4 2 3 2 2 2 3 1 1 3
6 2 3 4 2 2 5 3 1 1
1 3
2 1
3 5 2 2
4 6
3 3 2 1 1 3 2 2 2 4
5 1 2 3 1 1 4 2 2 2
7 3 4 5 3 1 6 4 2 2
path =
7 7 7 7 7 7 7 7 7 7
3 3 3 3 9 9 3 3 9 9
4 2 2 4 4 2 4 4 2 2
7 3 3 3 8 3 7 8 3 3
8 9 8 8 8 9 8 8 9 9
9 9 9 9 9 9 9 9 9 10
1 4 4 4 4 4 1 4 4 4
4 4 4 4
5 5 4 4 5 5
2 2 2 2 5 6 2 5 2 6
6 6 6 6 6 6 6 6 6 6
L =
0 1 2 3 4 5 6 7
R =
1 7 4 3
2 9 6 10
可得到过河的状态转移为:
1---7---4---3---2---9---6---10
即人将羊送到河对岸,回来再将狼送到河对岸,在对岸将羊拉回来,再将菜送到河对岸,回来时再和羊一起到河对岸,人狼羊菜全部过河,问题得到解决。
