人狼羊菜渡河问题
渡河问题

一个人带了一只狼、一只山羊和一棵白菜想 要渡河。河上有一只独木船,每次除人外只 能带一样东西,另外如果人不在时狼就要吃 山羊,羊就要吃白菜。问应该怎样安排渡河, 才能做到既把所有东西都带过河,而且在河 上来回的次数又最少? 设M代表人,W代表狼,S代表山羊,V代表 白菜。
渡河问题
算法思想: 用集合表示在某岸上的所有情况(16种): [MWSV] [MWS] [MWV] [MSV] [WSV] [MW] [MS] [MV] [WS] [WV] [SV] [M] [S] [V] [空] 剩下的10种情况,按若甲经过一次渡河可变成乙, 那么就在甲与乙之间连一条边,由此得到如下图G: MWSV MWS MWV MSV 找一条连接顶点MWSV与空,并且包含边数最少的路.
实习六-农夫过河问题

农夫过河问题一、需求分析1.问题描述:一个农夫带着一只狼、一只羊和一棵白菜,身处河的南岸。
他要把这些东西全部运到北岸。
他面前只有一条小船,船只能容下他和一件物品,另外只有农夫才能撑船。
如果农夫在场,则狼不能吃羊,羊不能吃白菜,否则狼会吃羊,羊会吃白菜,所以农夫不能留下羊和白菜自己离开,也不能留下狼和羊自己离开,而狼不吃白菜。
2.基本要求:(1)利用图的存储结构(2)图的搜索算法(3)求出农夫将所有的东西运过河的所有方案二、设计1. 设计思想(1)存储结构以邻接矩阵存储合理状态,用一个一维数组保存所有的方案;(2)主要算法基本思想人,狼,羊和白菜共有2的四次方16种状态(河岸的状态可由人的状态确定),去掉不允许出现的6种状态,10个状态对应矩阵的10个结点值,然后根据状态的连续改变初始化矩阵,接着就用递归的深度优先法搜索所有的路径,即求出过河的方案。
main2. 设计表示(1)函数调用关系图main→Judge→Initiate→DFS→Push→StackPop→Top→GetTop→printfpath→Ch(2)函数接口规格说明int Judge(int a,int b) //将16种状态通过a,b输入,去掉不允许的6种int GetTop(Path *path,int *m) //出栈int Push(Path *path,int m) //入栈int Top(Path *path ,int *m) //读出栈顶值void Initiate(AdjMGraph *G,int n)//邻接矩阵顶点数为n的邻接矩阵G的建立int DFS(AdjMGraph *G,Path *path,int x,int t) 图G中搜索的起始点为X,从t点开始搜索与x关联的顶点,搜索过的点入栈path。
int printfpath(Path *path) //复制出出栈path中所有值,用FA【】保存void Printf(AdjMGraph *G)//辅助:邻接矩阵输出,用于观察搜索的过程。
3第三章最短路问题

现在我们就来构造一个图G,它的顶点就是这10 种情况,G中的边是按照下述原则来连的;如果情况 甲经过一次渡河可以变成情况乙,那么就在情况甲与 乙之间连一条边.
MWSV MWS MWV WSV MS
WV
W
S
V
Ø
例如,MWSV经过一次渡河可以变成WV(人带着羊 过河,左岸留下狼和白菜),又例如MWV经过一次渡河 可以变为W(人带着白菜过河,留下狼),或变为V.当 然反过来,W也可以变为MWV(人带着白菜从右岸返回 左岸).
§3.2 求最短有向路的标号法
这一节介绍一种求有向图上最短有向路的方法 ,叫做标号法。
所谓标号,我们是指与图的每一个顶点对应的一个 数(或几个数).例如设G=(V,A)的顶点集合是V={v1,v2, …,vn},如果我们能使v1对应一个数b(1),v2对应数 b(2),…,vn对应数b(n),那么,这些数b(i)就称为vi的 标号,当然,在不同的问题中,标号b(i)一般代表不同 的意义.
从上面的简单比较久可以看出,为什么说计算 次数是n的多项式的方法是有效的,而计算次数是 n的指数函数的方法是无效的.另外,也可以看出, 单靠提高计算机的速度还不够,还必须从数学上寻 求有效的计算方法.
现在再回过头来看看标号法好不好.回想一下标 号法的各轮计算,可以看出,它只包含两种运算: 加法与比较大小(比较大小也需要花费时间,所以 也要考虑).加法用于计算k(i,j),每计算一个k(i,j)进 行一次加法,而且每一条弧最多只计算一次.因此, 如果图中有m条弧,那么至多进行m次加法.对于一 个有n个顶点的简单有向图来说,最多有n(n-1)条 弧(假设从每一个顶点vi出发,都有n-1条弧指向其 他的n-1个顶点),因此,最多进行n(n-1)次加法, 放宽一点,也可以说,至多进行n2次加法.
人狼羊菜渡河问题(含Matlab程序)

人、狼、羊、菜安全渡河问题安全渡河问题又称作“人狼羊菜”问题,其具体描述为:一个人带着一条狼、一只羊、一筐白菜过河但由于船太小,人一次只能带一样东西乘船过河。
狼和羊、羊和白菜不能单独留在同岸,否则羊或白菜会被吃掉。
该问题可使用图论中的最短路算法进行求解。
问题分析根据题意,人不在场时,狼要吃羊,羊要吃菜,因此,人不在场时,不能将狼与羊、羊与菜留在河的任一岸。
可用四维向量v=(m,n,p,q)来表示状态,m表示人,n代表狼,p代表羊,q代表白菜,且m,n,p,q ∈{0,1},0代表在对岸,1代表在此岸。
例如,状态(0,1,1,0)表示人和菜在对岸,而狼和羊在此岸,这时人不在场,狼要吃羊,因此,这个状态是不可行的。
通过穷举法将所有可行的状态列举出来,可行的状态有(1,1,1,1),(1,1,1,0),(1,1,0,1),(1,0,1,1),(1,0,1,0),(0,1,0,1),(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,0,0,0)。
可行状态共有十种。
每一次的渡河行为改变现有的状态。
现构造赋权图G=(V,E,W),其中顶点集V={v1,…, v10}中的顶点(按照上面的顺序编号)分别表示上述10个可行状态,当且仅当对应的两个可行状态之间存在一个可行转移时两顶点之间才有边连接,并且对应的权重取为1,当两个顶点之间不存在可行转移时,可以把相应的权重取为∞。
因此问题变为在图G中寻找一条由初始状态(1,1,1,1)出发,经最小次数转移到达最终状态(0,0,0,0)的转移过程,即求从状态(1,1,1,1)到状态(0,0,0,0)的最短路径。
该问题难点在于计算邻接矩阵,由于摆渡一次就改变现有状态,为此再引入一个四维状态转移向量,用它来反映摆渡情况。
用1表示过河,0表示未过河。
例如,(1,1,0,0)表示人带狼过河。
状态转移只有四种情况,用如下向量表示:(1,0,0,0),(1,1,0,0),(1,0,1,0),(1,0,0,1)现在规定状态向量与转移向量之间的运算为0+0=0,1+0=1,0+1=1,1+1=0通过上面的定义,如果某一个可行状态加上转移向量得到的新向量还属于可行状态,则这两个可行状态对应的顶点之间就存在一条边。
渡河问题20160430
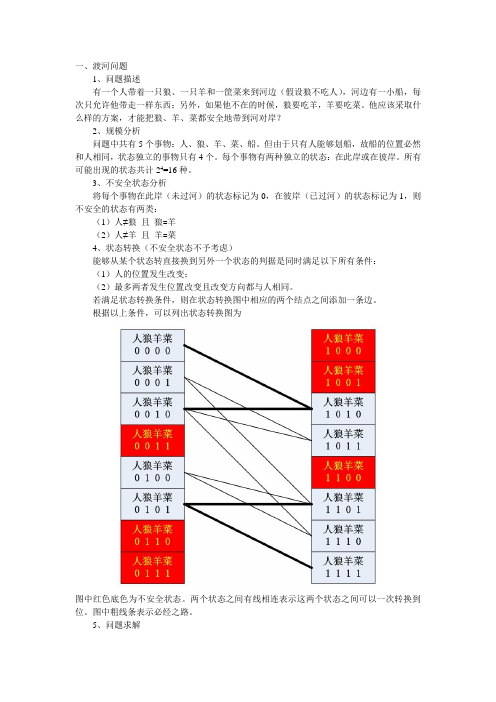
一、渡河问题1、问题描述有一个人带着一只狼、一只羊和一筐菜来到河边(假设狼不吃人),河边有一小船,每次只允许他带走一样东西;另外,如果他不在的时候,狼要吃羊,羊要吃菜。
他应该采取什么样的方案,才能把狼、羊、菜都安全地带到河对岸?2、规模分析问题中共有5个事物:人、狼、羊、菜、船。
但由于只有人能够划船,故船的位置必然和人相同,状态独立的事物只有4个。
每个事物有两种独立的状态:在此岸或在彼岸。
所有可能出现的状态共计24=16种。
3、不安全状态分析将每个事物在此岸(未过河)的状态标记为0,在彼岸(已过河)的状态标记为1,则不安全的状态有两类:(1)人≠狼且狼=羊(2)人≠羊且羊=菜4、状态转换(不安全状态不予考虑)能够从某个状态转直接换到另外一个状态的判据是同时满足以下所有条件:(1)人的位置发生改变;(2)最多两者发生位置改变且改变方向都与人相同。
若满足状态转换条件,则在状态转换图中相应的两个结点之间添加一条边。
根据以上条件,可以列出状态转换图为图中红色底色为不安全状态。
两个状态之间有线相连表示这两个状态之间可以一次转换到位。
图中粗线条表示必经之路。
5、问题求解渡河问题的求解即是在状态转换图中寻找从起始结点(0,0,0,0)到终止结点(1,1,1,1)之间的最短路径。
该最短路径可能不止一条,每条最短路径都是该问题的最佳可行解。
该问题的全部的两个最佳可行解为:人狼羊菜0 0 0 01 0 1 00 0 1 01 1 1 00 1 0 01 1 0 10 1 0 11 1 1 1人狼羊菜0 0 0 01 0 1 00 0 1 01 0 1 10 0 0 11 1 0 10 1 0 11 1 1 1整个过程至少需要7步(划船7次,3.5个来回)才能完成。
具体过程可以有两种:(1)将羊带过河,自己返回;将狼带过河,将羊带回;将菜带过河,自己返回;将羊带过河。
(2)将羊带过河,自己返回;将菜带过河,将羊带回;将狼带过河,自己返回;将羊带过河。
人狼羊菜过河七种方法

人狼羊菜过河七种方法在生活中,我们经常会遇到这样的问题,一个人狼、一只羊和一棵菜需要过河,但只有一条小船,且小船只能携带一个人或一只动物或一棵菜。
而且,如果人狼单独留在岸上,它会吃掉羊;羊单独留在岸上,它会吃掉菜。
那么,该如何设计过河方案,才能让人狼、羊和菜都能平安过河呢?下面就来介绍七种不同的方法,让我们一起来看看吧。
方法一,首先,将羊带到对岸,然后返回原岸,将狼带到对岸,再将羊带回原岸,最后将菜带到对岸。
这样,就能让人狼、羊和菜都安全过河。
方法二,首先,将狼带到对岸,然后返回原岸,将羊带到对岸,再将狼带回原岸,最后将菜带到对岸。
同样可以让人狼、羊和菜都安全过河。
方法三,首先,将菜带到对岸,然后返回原岸,将羊带到对岸,再将菜带回原岸,最后将狼带到对岸。
这样也可以让人狼、羊和菜都安全过河。
方法四,首先,将菜和狼带到对岸,然后返回原岸,将狼放下,再将羊带到对岸,再将菜带回原岸,最后将菜带到对岸。
同样可以让人狼、羊和菜都安全过河。
方法五,首先,将狼和菜带到对岸,然后返回原岸,将狼放下,再将羊带到对岸,再将狼带回原岸,最后将菜带到对岸。
这样也可以让人狼、羊和菜都安全过河。
方法六,首先,将狼带到对岸,然后返回原岸,将狼放下,再将菜带到对岸,再将狼带回原岸,最后将羊带到对岸。
同样可以让人狼、羊和菜都安全过河。
方法七,首先,将狼和羊带到对岸,然后返回原岸,将羊放下,再将狼带到对岸,再将羊带回原岸,最后将菜带到对岸。
这样也可以让人狼、羊和菜都安全过河。
通过以上七种方法,我们可以看到,只要合理安排顺序,就能够让人狼、羊和菜都安全过河。
这也启示我们在生活中,遇到问题时,只要有耐心、灵活思维,总能够找到解决的方法。
希望这些方法对你有所启发,谢谢阅读。
摆渡过河分析
摆渡过河
问题重述:
一只狼、一头山羊和一箩卷心菜在河的同侧。
一个摆渡人要将它们运过河去,但由于船小,他一次只能运三者之一过河。
显然,不管是狼和山羊,还
是山羊和卷心菜,都不能在无人监视的情况下留在一起。
问摆渡人应怎样把它们运过河去
问题分析:
由题意知人划船一次只能运三者之一或者自己独自划船,且无论在河的左岸还是右岸都要保证无人情况下狼和山羊,山羊和卷心菜不能单独在一起。
在这里,羊所受的限制条件是最多的,所以羊只能独处或在船上被带走,因此,
A:人首先只能把山羊带去河的对岸(右岸),将山羊放在右岸;
B:人自己回来,可以带狼过去也可以带卷心菜过去,若带卷心菜去对岸,因为卷心菜不能与山羊在一起,所以人回来时要将山羊再带回左岸;
C:人将山羊留在左岸,带狼去对岸,将狼放在右岸;
{
D:人自己回来再将山羊带去对岸。
用图论方法:对于人,狼,山羊,卷心菜的位置状态,可用1表示在左岸,用0表示不在左岸,则由无人情况下狼和山羊,山羊和卷心菜不能单独在一起,列出可以存在的状态如下表:
%
注释:
A表示人,狼,山羊,卷心菜都在河的左岸;
B表示狼和卷心菜在河的左岸,人和山羊在河的对岸(右岸)
将上表中各种状态作为顶点,将两个可以转变的状态点之间连一条有向边,可得到下图
摆渡人把他们运过河去,最优方案是从上面有向图中找到一条从A点到J点的最短路径。
即ABCIHFGJ或者ABCDEFGJ.!。
摆渡问题
摆渡问题让我们从最古老的趣味数学问题之一——摆渡问题开始说起。
中世纪,英国数学家阿尔昆(Alcuin,735~804)在其《益智集》(Problems for the Quickening of the Mind)中提出:有人携带一只狼、一只羊、一篮白菜渡河。
唯一的工具是一条小船。
小船一次只能载他自己和三样东西中的一样。
如果只留下羊和白菜在一起,羊就会吃掉白菜;如果留下羊和狼在一起,狼就会吃掉羊。
问这个人如何摆渡到对岸,使白菜、羊、和狼都安然无恙?16世纪,意大利数学家塔塔格里亚(N.Tartaglia)将其设计成一个新版本:三位美丽的新娘和她们的爱吃醋的先生一同旅行。
他们来到了一条河边,但只有一条小船,小船一次只能载二人。
为了避免有人吃醋,他们约定:除非自己的先生在身旁,否则任一女士不得和其他男人在一起。
问怎样安排渡河?答案是往返11次。
如果只有两对夫妇,则往返5次就够了;如果有四对及更多对夫妇,那么问题无解。
这个问题后来又被推广成:●对夫妻用一条船过河,该船至多可载n-1个人,条件仍是任一女士除非自己的丈夫在身旁不得和其他男人在一起。
问怎样安排渡河的步骤?(n=3时,y=11;n=4时y=9;n>4时y=7)●问一条船至少能载几个(x)人时,才能使n对夫妻可乘它渡河,而任一女士除非自己的丈夫在身边,否则不得和别的男人在一起;任何一个都会划船。
并求往返摆渡的最少次数(y)。
类似地还有火车转轨问题。
图中有一火车头L和2节货车车厢W1和W2,DA是W1和W2所在侧线的公共部分,长度足够停放W1或W2,但不能同时容下两节车厢,也容不下火车头L。
这样,停在DA上的车厢可以转轨到侧线上。
工程师的工作是转换W1和W2的位置。
问如何完成?这个问题并不难,但如果有更多的车厢(如在铁路货物分类站),要按车厢目的地先后顺序进行排列,那么工程师就需要有很高的数学水平才能完成职责了。
C语言-人狼羊菜问题-最容易看懂的解决方法及代码
C语⾔-⼈狼⽺菜问题-最容易看懂的解决⽅法及代码题⽬描述:农夫需要把狼、⽺、菜和⾃⼰运到河对岸去,只有农夫能够划船,⽽且船⽐较⼩,除农夫之外每次只能运⼀种东西,还有⼀个棘⼿问题,就是如果没有农夫看着,⽺会偷吃菜,狼会吃⽺。
请考虑⼀种⽅法,让农夫能够安全地安排这些东西和他⾃⼰过河。
想这个问题⼀连想了好⼏天,本⼈没有系统的学过算法,有些概念也不是很清楚,只因解决问题为⽬标。
尝试过图论解决,但⽤floyed算法只能算出最短路径值,如何输出过程,⼀直没想出好的解决⽅法。
然后看了下⾯这篇⽂章,尝试抛弃图论,⽤树的思想来解决这个问题。
建议阅读下⾯代码时,先看看这篇⽂章。
在写代码时,本⼈采⽤了上述⽂章中的思想,⼜借鉴了图论中存储结点的⼀些⽅法。
我觉得这样写应该⾮常容易看懂了。
具体思路见代码。
1 #include <stdio.h>2#define INF 99993//8个动作4char *action[8]={"农夫单独过河","农夫带狼过河","农夫带⽺过河","农夫带菜过河",5"农夫单独返回","农夫带狼返回","农夫带⽺返回","农夫带菜返回"};6//10种状态7char *state[10]={"⼈狼⽺菜","⼈狼⽺","⼈狼菜","⼈⽺菜","⼈⽺","狼菜","狼","⽺","菜","空"};89//状态转换规则:GA[i][j]=k 表⽰【状态i】可以通过【动作k】转换到【状态j】,GA[i][j]=INF表⽰不可直接转换10int GA[10][10]={INF,INF,INF,INF,INF, 2,INF,INF,INF,INF,11 INF,INF,INF,INF,INF,INF, 2, 1,INF,INF,12 INF,INF,INF,INF,INF, 0, 3,INF, 1,INF,13 INF,INF,INF,INF,INF,INF,INF, 3, 2,INF,14 INF,INF,INF,INF,INF,INF,INF, 0,INF, 2,156,INF, 4,INF,INF,INF,INF,INF,INF,INF,16 INF, 6, 7,INF,INF,INF,INF,INF,INF,INF,17 INF, 5,INF, 7, 4,INF,INF,INF,INF,INF,18 INF,INF, 5, 6,INF,INF,INF,INF,INF,INF,19 INF,INF,INF,INF, 6,INF,INF,INF,INF,INF};2021//记录每⼀步的动作22int record_action[20];23//记录每⼀步动作后的状态24int record_state[20];2526//搜索从第step步开始、第i个结点到第n个结点的过程(step从0算起)27void search(int i,int n,int step)28 {29int k;//动作30int j;//可能要转换到的状态31if(i==n)32 {33for(k=0;k<step;k++)34 printf("step %d: %s,左岸还剩 %s\n",k+1,action[record_action[k]],state[record_state[k]]);35 printf("step count:%d\n\n",step);36return;37 }38//查找在当前【状态i】下能转换到的【其它状态j】,并且【状态j】不能在之前出现过39//查找时可能会出现多个 j,所以这是⼀个多叉树40for(k=0;k<8;k++)41 {42for(j=0;j<10;j++)43if(GA[i][j]!=INF&&GA[i][j]==k)//判断状态i能否通过动作k转换到状态j44 {45int m;46//下⾯这个循环是判断状态j在之前是否出现过47for(m=0;m<step;m++)48if(j==record_state[m])break;49if(m<step)continue;50//如果j满⾜前⾯所有条件,则记录这⼀步51 record_action[step]=k; //第step步所使⽤的动作52 record_state[step]=j; //第step步所转换的状态53 search(j,n,step+1); //继续搜索下⼀步54 }55 }5657 }58int main()59 {60 search(0,9,0);61return0;62 }。
数学建模人狼羊菜问题
Байду номын сангаас第7次孃河:人,羊,从左岸到达右岸 濺河成功
第4次渡河:人,菜,从右岸回到左岸 此渡河方案不可行
第3次渡河:人,从左岸到达右岸 此渡河方秦不可行
将可取状态及可取运载分别编成矩阵。共分为五个m文件,一个
主文件xduhe.m数,分别为:
1、duhe(L,B,M,s)函数。
用来实现渡河总思路。 思路为:将起始矩阵A分别与可取运载相加(使 用二进制法则),判断相加后的矩阵C是否是【0,0,0,0】,如果是, 则渡河成功。否则,用fuhe(C,M)函数判断C是否是可取状态,如 果是,则打印并将C与初始矩阵合并成新矩阵,继续调用duhe.m函 数。
我们可以用四维向量来表示状态, 其中第一分量表示人, 第二分 量表示狼,第三分量表示羊,第四分量表示菜;当人或物在此岸时相 应分量取1,在对岸时则取0。
根据题意,人不在场时,狼要吃羊,羊要吃菜,因此,人不在场 时,不能将狼与羊,羊与菜留在河的任一岸。例如,状态(0,1,1,0)表示人和菜在对岸,而狼和羊在此岸,这时人不在场的情况下狼 要吃羊,因此,这个状态是不可行的。 我们通过穷举法将所有可行的状态列举出来,可行的状态有 (1,1,1,1),(1,1,1,0),(1,1,0,1),(1,0,1,1),(1,0,1,0) (0,1,0,1),(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,0,0,0) 可行状态共有十种。每一次的渡河行为改变现有的状态。 用1表示过河,0表示未过河。例如, (1,1,0,0)表示 人带狼过河。状态转移只有四种情况,用如下的向量表示。 (1,0,0,0),(1,1,0,0),(1,0,1,0),(1,0,0,1) 五,模型的建立、模型求解、模型的结果和检验
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人、狼、羊、菜安全渡河问题
安全渡河问题又称作“人狼羊菜”问题,其具体描述为:一个人带着一条狼、一只羊、一筐白菜过河但由于船太小,人一次只能带一样东西乘船过河。
狼和羊、羊和白菜不能单独留在同岸,否则羊或白菜会被吃掉。
该问题可使用图论中的最短路算法进行求解。
问题分析
根据题意,人不在场时,狼要吃羊,羊要吃菜,因此,人不在场时,不能将狼与羊、羊与菜留在河的任一岸。
可用四维向量v=(m,n,p,q)来表示状态,m表示人,n代表狼,p代表羊,q代表白菜,且m,n,p,q ∈{0,1},0代表在对岸,1代表在此岸。
例如,状态(0,1,1,0)表示人和菜在对岸,而狼和羊在此岸,这时人不在场,狼要吃羊,因此,这个状态是不可行的。
通过穷举法将所有可行的状态列举出来,可行的状态有
(1,1,1,1),(1,1,1,0),(1,1,0,1),(1,0,1,1),(1,0,1,0),(0,1,0,1),(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,0,0,0)。
可行状态共有十种。
每一次的渡河行为改变现有的状态。
现构造赋权图
G=(V,E,W),其中顶点集V={v
1,…, v
10
}中的顶点(按照上面的顺序编号)分别表
示上述10个可行状态,当且仅当对应的两个可行状态之间存在一个可行转移时两顶点之间才有边连接,并且对应的权重取为1,当两个顶点之间不存在可行转移时,可以把相应的权重取为∞。
因此问题变为在图G中寻找一条由初始状态(1,1,1,1)出发,经最小次数转移到达最终状态(0,0,0,0)的转移过程,即求从状态(1,1,1,1)到状态(0,0,0,0)的最短路径。
该问题难点在于计算邻接矩阵,由于摆渡一次就改变现有状态,为此再引入一个四维状态转移向量,用它来反映摆渡情况。
用1表示过河,0表示未过河。
例如,(1,1,0,0)表示人带狼过河。
状态转移只有四种情况,用如下向量表示:
(1,0,0,0),(1,1,0,0),(1,0,1,0),(1,0,0,1)现在规定状态向量与转移向量之间的运算为
0+0=0,1+0=1,0+1=1,1+1=0
通过上面的定义,如果某一个可行状态加上转移向量得到的新向量还属于可行状态,则这两个可行状态对应的顶点之间就存在一条边。
用计算机编程时,可以利用普通向量的异或运算实现,具体的Matlab程序如下:
clc,clear
a=[1 1 1 1;1 1 1 0;1 1 0 1;1 0 1 1;1 0 1 0;
0 1 0 1;0 1 0 0;0 0 1 0;0 0 0 1;0 0 0 0];%每一行是一个可行状态
b=[1 0 0 0;1 1 0 0;1 0 1 0;1 0 0 1];%每一行是一个转移状态
w=zeros(10);%邻接矩阵初始化
for i=1:9
for j=i+1:10
for k=1:4
if findstr(xor(a(i,:),b(k,:)),a(j,:))
w(i,j) = 1;
end
end
end
end
w = w,; %变成下三角矩阵
c = sparse(w); %构造稀疏矩阵
[x,y,z]= graphshortestpath(c,1,10,’Directed’,0) %该图是无向图,Directed属性值为0
h =
view(biograph(c,[],’ShowArrows’,’off’,’ShowWeights’,’off’));
%画出无向图
Edges = getedgesbynodeid(h);%提取句柄h中的边集
set(Edges,’LineColor’,[0 0 0];%为例将来打印清除,边画成黑色
set(Edges,’LineWidth’,;%线型宽度设置为
赋权图G之间的状态转移关系如下图所示:
图可行状态之间的转移
最终求得的状态转移顺序之一为:
1 6 3 7
2 8 5 10
对应方案为:经过7次渡河就可以把狼、羊、蔬菜运过河,第一次运羊过河,空船返回;第二次运菜过河,带羊返回;第三次运狼过河,空船返回;第四次运羊过河。
另一种方案同理可由图得,请读者自行写出。
参考文献
[1]司守奎,孙玺菁.数学建模算法与应用[M].北京:国防工业出版社,2015.
[2]郭强,孙浩.运筹学原理与算法[M].西安:西北工业大学出版社,2006.
[3]严蔚敏,吴伟民.数据结构[M].北京:清华大学出版社,2002.。
