人狼羊菜渡河问题(含Matlab程序)
算法谜题1,狼羊菜过河

算法谜题1,狼⽺菜过河问题描述农夫需要把狼、⽺、菜和⾃⼰运到河对岸去,只有农夫能够划船,⽽且船⽐较⼩,除农夫之外每次只能运⼀种东西,还有⼀个棘⼿问题,就是如果没有农夫看着,⽺会偷吃菜,狼会吃⽺。
请考虑⼀种⽅法,让农夫能够安全地安排这些东西和他⾃⼰过河。
分析问题很简单,但如何⽤计算机求解呢。
农夫渡河从本质上是⼀种状态的改变。
有农夫、狼、⽺、菜四个个体,任何时刻每个个体的状态只有⼀种,每个个体有两种状态(没有过河、已经过河)。
依次⽤4位分别代表农夫、狼、⽺、菜,0表⽰未过河,1表⽰已过河。
则起始状态为0000,⽬标状态为1111。
共有8种过河动作(状态转换运算)农夫单独过河农夫带狼过河农夫带⽺过河农夫带菜过河农夫单独返回农夫带狼返回农夫带⽺返回农夫带菜返回优先级:农夫过河时,优先带货物;回返时优先不带货物。
有限种状态:可能有16(2^4)种状态,但因为狼吃⽺,⽺吃菜的限制,部分状态是⽆法成⽴的。
实现状态空间树(回溯法)是以0000为根的⼀颗状态树,当某个叶⼦节点是状态1111,则表⽰从根到这个叶⼦节点之间的状态序列是本问题的⼀个解,需要避免出现重复状态导致死循环。
⽅法1:每个状态有8种可选动作,转换为8个新状态,但在特定状态下某些动作是⽆效的。
定义8种状态转换运算,对当前节点遍历执⾏这8种运算,找到所有⼦节点⽅法2:依据当前状态,判别它所有可选的动作(最多4种)。
class Program{static void Main(string[] args){var original = new State();var path = new List<State>();path.Add(original);int count = 0;Search(path, ref count);Console.ReadKey();}private static void Search(List<State> path, ref int count){var cur = path[path.Count - 1];if (cur.Man && cur.Wolf && cur.Vegetable && cur.Sheep){count++;Console.WriteLine($"解{count}:");path.ForEach((a) => { Console.WriteLine(a.Action); });return;}if (cur.Man){Switch(path, ref count, cur, "返回");}else{Switch(path, ref count, cur, "过河");}}private static void Switch(List<State> path, ref int count, State cur, string action){var newState = cur.Copy();newState.Man = !newState.Man;newState.Action = "独⾃" + action;Action(path, ref count, newState);if (cur.Sheep == cur.Man){newState.Sheep = !newState.Sheep;newState.Action = "带着⽺" + action;Action(path, ref count, newState);newState.Sheep = !newState.Sheep;}if (cur.Wolf == cur.Man){newState.Wolf = !newState.Wolf;newState.Action = "带着狼" + action;Action(path, ref count, newState);newState.Wolf = !newState.Wolf;}if (cur.Vegetable == cur.Man){newState.Vegetable = !newState.Vegetable;newState.Action = "带着菜" + action;Action(path, ref count, newState);newState.Vegetable = !newState.Vegetable;}}private static void Action(List<State> path, ref int count, State newState) {if (newState.IsOk){foreach (var item in path){if (item.Equals(newState)){return;}}path.Add(newState);Search(path, ref count);path.RemoveAt(path.Count - 1);}}//false 表⽰未过河, true表⽰已过河private class State{public bool Man { get; set; }public bool Wolf { get; set; }public bool Sheep { get; set; }public bool Vegetable { get; set; }public string Action { get; set; }public bool IsOk{get{if (Wolf == Sheep && Wolf != Man){return false;}if (Sheep == Vegetable && Sheep != Man){return false;}return true;}}public State Copy(){return new State{Man = this.Man,Wolf = this.Wolf,Sheep = this.Sheep,Vegetable = this.Vegetable};}public bool Equals(State newState){return (this.Man == newState.Man&& this.Wolf == newState.Wolf&& this.Sheep == newState.Sheep&& this.Vegetable == newState.Vegetable);}}}状态空间图所有状态作为图的节点遍历图,找出所有从0000到1111的路径连接状态的条件农夫的状态要不⼀样(只有农夫可以划船,每次过河,不能缺农夫)最多只有⼀个其他个体的状态不⼀样(⼀次只能带⼀个过河),且这个个体的状态要与农夫⼀致。
渡河问题20160430
一、渡河问题1、问题描述有一个人带着一只狼、一只羊和一筐菜来到河边(假设狼不吃人),河边有一小船,每次只允许他带走一样东西;另外,如果他不在的时候,狼要吃羊,羊要吃菜。
他应该采取什么样的方案,才能把狼、羊、菜都安全地带到河对岸?2、规模分析问题中共有5个事物:人、狼、羊、菜、船。
但由于只有人能够划船,故船的位置必然和人相同,状态独立的事物只有4个。
每个事物有两种独立的状态:在此岸或在彼岸。
所有可能出现的状态共计24=16种。
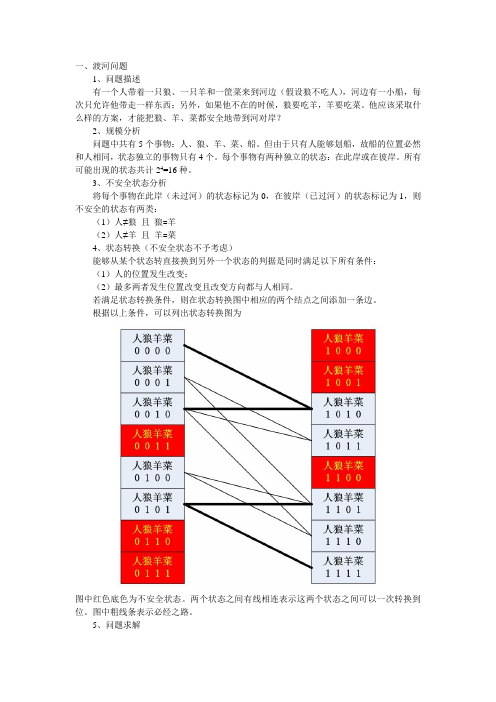
3、不安全状态分析将每个事物在此岸(未过河)的状态标记为0,在彼岸(已过河)的状态标记为1,则不安全的状态有两类:(1)人≠狼且狼=羊(2)人≠羊且羊=菜4、状态转换(不安全状态不予考虑)能够从某个状态转直接换到另外一个状态的判据是同时满足以下所有条件:(1)人的位置发生改变;(2)最多两者发生位置改变且改变方向都与人相同。
若满足状态转换条件,则在状态转换图中相应的两个结点之间添加一条边。
根据以上条件,可以列出状态转换图为图中红色底色为不安全状态。
两个状态之间有线相连表示这两个状态之间可以一次转换到位。
图中粗线条表示必经之路。
5、问题求解渡河问题的求解即是在状态转换图中寻找从起始结点(0,0,0,0)到终止结点(1,1,1,1)之间的最短路径。
该最短路径可能不止一条,每条最短路径都是该问题的最佳可行解。
该问题的全部的两个最佳可行解为:人狼羊菜0 0 0 01 0 1 00 0 1 01 1 1 00 1 0 01 1 0 10 1 0 11 1 1 1人狼羊菜0 0 0 01 0 1 00 0 1 01 0 1 10 0 0 11 1 0 10 1 0 11 1 1 1整个过程至少需要7步(划船7次,3.5个来回)才能完成。
具体过程可以有两种:(1)将羊带过河,自己返回;将狼带过河,将羊带回;将菜带过河,自己返回;将羊带过河。
(2)将羊带过河,自己返回;将菜带过河,将羊带回;将狼带过河,自己返回;将羊带过河。
人工智能复习资料1

人工智能复习题
唐 海
人、狼、羊、菜过河问题
问题:有一农夫带一条狼,一只羊和一框青菜与从河的左 岸乘船倒右岸,但受到下列条件的限制: (1) 船太小,农夫每次只能带一样东西过河; (2) 如果没有农夫看管,则狼要吃羊,羊要吃菜。 请设计一个过河方案,使得农夫、浪、羊都能不受损失的 过河,画出相应的状态空间图。 题示: (1) 用四元组(农夫,狼,羊,菜)表示状态,其中每个 元素都为0或1,用1表示在左岸,用0表示在右岸。 (2) 把每次过河的一种安排作为一种操作,每次过河都必 须有农夫,因为只有他可以划船。
人、狼、羊、菜过河问题
第三步,定义操作,即用于状态变换的算 符组F
由于每次过河船上都必须有农夫,且除农夫外船上只能载 狼,羊和菜中的一种,故算符定义如下: L(i)表示农夫从左岸将第i样东西送到右岸(i=1表示狼, i=2表示羊,i=3表示菜,i=0表示船上除农夫外不载任何 东西)。由于农夫必须在船上,故对农夫的表示省略。 R (i)表示农夫从右岸将第i样东西带到左岸(i=1表示狼, i=2表示羊,i=3表示菜,i=0表示船上除农夫外不载任何 东西)。同样,对农夫的表示省略。 这样,所定义的算符组F可以有以下8种算符: L(0),L(1),L(2),L(3) R(0),R(1),R(2),R(3)
平时成绩:遗传算法源程序。以“学号_姓名”作 为文件夹名。
1、人工智能有哪些研究领域?你能列举出一些与汽车相关的研究领 域吗? 2、对于农夫过河问题,分析其中的产生式规则,组成规则库,并给 出初始事实数据和目标条件,建立一个小型产生式系统并运行之。 3、用状态可见搜索法求解农夫、狗、鸡、米问题。(提示:用四元 组(农夫、狗、鸡、米)表示状态,其中每个元素都可为0或1,0表 示在左岸,1表示在右岸;把每次过河的一种安排作为一个算符,每 次过河都必修有农夫。) 4、请把下列命题用一个语义网络表示出来: (1)树和草都是植物。 (2)树和草都有叶和根。 (3)水草是草,且生长在水中。 (4)果树是树,且会结果。 (5)梨树是果树的一种,它会结梨。 5、遗传算法基本步骤。 6、给出多边形、凸多边形、三角形的语义框架体系。
人狼羊过河问题

}
}
//处理路径表:从路径表中反推(从最终步-->开始步)
i=15;//最后一步
if(route[i]==-1) { //若没有方法可以走到1111,则任务失败。
cout<<"过河失败!"<<endl;
return 0;
}
for(j=15;route[i]!=-1 && i>=0;j--){ //route[i]!=-1相当于那一步走不通,那就不用选取了
queue[rear]=Status; rear=(rear+1)%16;//入队
while(front!=rear){
Status=queue[front];front=(front+1)%16;//出队
visited[Status]=1; //访问
for(j=0;j<4;j++){
nextStatus=Status^choice[j]; //从curStatus状态到下一状态nextStatus
在河的一岸,人、狼、羊、草、均要过河,船需人划,而且最多载一物,当人不在时,狼会吃羊,羊会吃草;试安排人狼羊草安全渡河。
一、分析问题
人带着狼、羊和草,身处河的一岸。他要把这些东西全部运到彼岸。问题是他面前只有一条小船,船小到只能容下他和一件物品,另外船必须有人划。而且,因为狼能吃羊,而羊爱吃草,所以人不能留下羊和草或者狼和羊单独在河的一边。以下是解决方案:
现在的问题变成:
从初始状态二进制0000(全部在河的南岸)出发,寻找一种全部由安全状态构成的状态序列,它以二进制1111(全部到达河的北岸)为最终目标,并且在序列中的每一个状态都可以从前一状态通过人(可以带一样东西)划船过河的动作到达。
狼羊过河问题

狼、羊、菜过河问题1.模型建立用0-1将人、狼、羊、菜河这边的所有状态表示出来(其中状态1代表在河这边,状态0代表在河对岸),共有16种状态。
由题设条件知,状态(0,1,1,0),(0,0,1,1)(0,1,1,1,)是不允许的,从而对应状态(1,0,0,1)(1,1,0,0)(1,0,0,0,)也是不允许的。
最后得到10种状态。
将它们分别标号如下:1(1 1 1 1)2(1 0 1 1)3(0 0 0 1)4(1 1 0 1)5(1 1 1 0)6(1 0 1 0)7(0 1 0 1)8(0 1 0 0)9(0 0 1 0)10(0 0 0 0)然后将各状态能够相互转移的状态用1表示,不能相互转移的状态用无穷大inf表示,得到关于这10种状态的一个10*10的邻接矩阵。
利用Floyd算法,在matlab上运行,即可找出该过河问题的最佳答案。
所得的邻接矩阵如下:[inf inf inf inf inf inf 1 inf inf infinf inf 1 inf inf inf inf inf 1 infinf 1 inf 1 inf inf inf inf inf infinf inf 1 inf inf inf 1 1 inf infinf inf inf inf inf inf inf 1 1 infinf inf inf inf inf inf inf inf 1 11 inf inf 1 inf inf inf inf inf infinf inf inf 1 1 inf inf inf inf infinf 1 inf inf 1 1 inf inf inf infinf inf inf inf inf 1 inf inf inf inf ]利用Floyd算法:function [D,path]=floyd(a)n=size(a,1);D=a;path=zeros(n,n);for i=1:nfor j=1:nif D(i,j)~=infpath(i,j)=j;endendendfor k=1:nfor i=1:nfor j=1:nif D(i,k)+D(k,j)<D(i,j)D(i,j)=D(i,k)+D(k,j);path(i,j)=path(i,k);endendendendfunction [L,R]=router(D,path,1,10)L=zeros(0,0);R=s;while 1if s==tL=fliplr(L);L=[0,L];returnendL=[L,D(s,t)];R=[R,path(s,t)];s=path(s,t);End输入a=[inf inf inf inf inf inf 1 inf inf infinf inf 1 inf inf inf inf inf 1 infinf 1 inf 1 inf inf inf inf inf infinf inf 1 inf inf inf 1 1 inf infinf inf inf inf inf inf inf 1 1 infinf inf inf inf inf inf inf inf 1 11 inf inf 1 inf inf inf inf inf infinf inf inf 1 1 inf inf inf inf infinf 1 inf inf 1 1 inf inf inf infinf inf inf inf inf 1 inf inf inf inf ]得到:D =2 43 24 6 1 35 74 2 1 2 2 2 3 3 1 33 1 2 1 3 3 2 2 2 42 2 1 2 2 4 1 13 54 2 3 2 2 2 3 1 1 36 2 3 4 2 2 5 3 1 11 32 13 5 2 24 63 3 2 1 1 3 2 2 2 45 1 2 3 1 1 4 2 2 27 3 4 5 3 1 6 4 2 2path =7 7 7 7 7 7 7 7 7 73 3 3 3 9 9 3 3 9 94 2 2 4 4 2 4 4 2 27 3 3 3 8 3 7 8 3 38 9 8 8 8 9 8 8 9 99 9 9 9 9 9 9 9 9 101 4 4 4 4 4 1 4 4 44 4 4 45 5 4 4 5 52 2 2 2 5 6 2 5 2 66 6 6 6 6 6 6 6 6 6L =0 1 2 3 4 5 6 7R =1 7 4 32 9 6 10可得到过河的状态转移为:1---7---4---3---2---9---6---10即人将羊送到河对岸,回来再将狼送到河对岸,在对岸将羊拉回来,再将菜送到河对岸,回来时再和羊一起到河对岸,人狼羊菜全部过河,问题得到解决。
摆渡人过河问题

《数学建模与计算》问题摆渡人过河问题摘要:摆渡人过河问题属于状态转移问题。
所谓状态转移问题,是研究在一定条件下,系统由一个状态向另一个状态转移能否实现,如果可以转移的话,应如何具体实现?将人狼羊菜依次用一个四维向量表示,对每一分量按二进制法则进行运算,这种运算成为可取运算.将这种运算方法设计为Matlab语言,进行计算机的计算。
关键词:状态转移问题,思维向量一、问题的提出一摆渡人欲将一只狼,一头羊和一篮白菜渡过河,由于船小,摆渡人一次至多带一物过河,并且狼与羊,羊与白菜不能离开摆渡人时放在一起,请给摆渡人设计出度和方法模拟图。
二、问题的分析这个问题可以用递推方法解决,但我们可以将其转换成状态转移问题来解决。
可取状态A共有10个,即(1,1,1,1)、(0,0,0,0)、(1,1,1,0)、(0,0,0,1)、(1,1,0,1)、(0,0,1,0)、(1,0,1,1)、(0,1,0,0)、(1,0,1,0)、(0,1,0,1)。
可取运载B有4个(1,1,0,0)、(1,0,1,0)、(1,0,0,1)、(1,0,0,0)。
规定A和B的每一分量相加时按二进制进行,这样一次渡河就是一个可取状态和一个可取运载相加,在判断和向量是否属于可取状态即可。
三、定义符号说明Y:表示该状态是可取的;N:表示该状态不是可取的;V:表示该状态虽然可取但已重复。
四、模型的分析、建立将人、狼、羊、菜依次用一个四维向量表示,当一物在左岸时,记相应的分量为1,否则记为0,如表示人和羊在左岸,并称为一个状态,由问题中的限制条件,有些状态是允许的,有的是不允许的。
凡系统可以允许存在的状态称为可取状态,比如是一个可取状态,但是一个不可取状态,此外,把每运载一次也用一个四维向量来表示,如表示人和狼在船上,而羊和白菜不在船上,这自然是可取的运载,因为船可载两物,而出则是不可取运载,这样,利用穷举法可得到:(1)可取状态A共有10个上面5个正好是下面5个的相反状态。
人狼羊菜过河问题的解法及代码
⼈狼⽺菜过河问题的解法及代码⼈狼⽺菜问题是计算机领域中的经典问题。
之所以经典,⼀⽅⾯这是编译原理等课程中的⼀个建模及编码问题,另⼀⽅⾯也经常被作为智⼒题⽤在⾯试中。
本⽂讨论的是怎么建模、编码的问题。
问题描述:⼀个农夫有⼀条船,和狼、⽺、菜,农夫要把这3样东西运到河到另⼀边,农夫每次最多只能通过这个船运⼀样东西,要防⽌狼吃⽺、⽺吃⽩菜(即不能在没有农夫在的情况下同时在同⼀岸边),该怎么过?该问题的解决分为2个阶段,第⼀阶段是对状态建模,第⼆阶段是⽤⼴度遍历来找到问题的解。
其中⼴度遍历阶段和“量⽔问题”的⼴度遍历解法类似。
问题抽象:建⽴⼀个struct型的state,其中包括4个bool型的变量a1 a2 a3 a4分别对应⼈、狼、⽺、菜的状态,值为true代表在起始的河岸边,false代表在对岸,起始时4个分量都为true。
农夫每过⼀次河⽣成⼀个新的state。
根据题⽬可知,农夫过⼀次河a1取反,且a2 a3 a4值与a1相同的分量也可以分别取反分别⽣成⼀个新的state代表被农夫运到河的对岸的各种选择。
只有a1取反⽽a2 a3 a4都没取反⽣成的新状态代表农夫⾃⼰过河没有带东西。
每次⽣成⼀个新状态后,⾸先要检查是否达到了终⽌状态(a1 a2 a3 a4都为false),其次要检查是否是合法状态(要同时考虑⼀个state对应的河两岸是否有狼吃⽺、⽺吃⽩菜的情况出现),如果状态合法、没到终⽌状态且没有在⼴度遍历队列中出现过,则将状态插⼊⼴度遍历队列,否则将该状态丢弃。
在此过程中我们没有考虑正在渡河的情况,因为每次过河船上总是有⼈,不会出现冲突,视其为不稳定状态直接忽略。
代码如下:#include<iostream>using namespace std;#define MAX 500struct state{bool a1,a2,a3,a4;int parentId;//⽤于回溯输出解决步骤state(){a1 = a2 = a3 = a4 = true;//true表⽰在A地(起始岸边)parentId=-1;}};bool equal(state& astate,state& bstate){if(astate.a1==bstate.a1&&astate.a2==bstate.a2&&astate.a3==bstate.a3&&astate.a4==bstate.a4){return true;}return false;}void assign(state& astate,state& bstate){astate.a1=bstate.a1;astate.a2=bstate.a2;astate.a3=bstate.a3;astate.a4=bstate.a4;astate.parentId = bstate.parentId;}state currentState;state sQueue[MAX];int startPos = 0;int endPos = 1;bool isInQueue(state& newState){for(int i=0;i<endPos;i++){if(equal(newState,sQueue[i])){return true;}}return false;}bool isValidState(state& newState){//总共可能有16种状态。
编译原理过河问题的自动机
一个人带着狼、山羊和白菜在一条河的左岸。
有一条船,大小正好能装下这个人和其他三件东西中的一件。
人和他的随行物都要过到河的右岸。
人每次只能将一件东西摆渡过河。
但若人将狼和羊留在同一岸而无人照顾的话,狼将把羊吃掉。
类似地,若羊和白菜留下来无人照看,羊将会吃掉白菜。
请问是否有可能渡过河去,使得羊和白菜都不被吃掉?如果可能,请用有穷自动机写出渡河的方法。
【分析】这是一道经典的智力题,很显然是有办法渡河的,关键是如何用有穷自动机来求解渡河方案。
有穷自动机描述的是状态和状态之间的转换,对于本题,可以把人、狼、山羊和白菜都在左岸作为有穷自动机的初始状态,而把他们都在右岸作为终止状态,只要构造一个自动机使得存在一条从初始状态到终止状态的路径就可以了。
首先构造有穷自动机的状态集,可以用{{M,W,G,C},{}}表示人、狼、山羊和白菜都在左岸,用{{},{M,W,G,C}}表示人、狼、山羊和白菜都在右岸。
可能存在的状态共有1+4+4*3+4+1=22个,但其中有些状态是不安全的,如{{G,C},{M,W}}表示人和狼在右岸,山羊和白菜在左岸,山羊会吃了白菜。
去掉不安全的状态,剩下的状态就是要构造的有穷自动机的状态集,共10个状态:{{M,W,G,C},{}} {{},{M,W,G,C}} {{M,W,G},{C}} {{M,W,C},{G}} {{M,G,C},{W}} {{C},{M,W,G}} {{W},{M,G,C}} {{M,G},{W,C}} {{W,C},{M,G}}接下来为有穷自动机添加箭弧,用<M>表示人独自过河,用<MW>表示人和狼一起过河,用<MG>表示人和山羊一起过河,用<MC>表示人和白菜一起过河。
在状态之间只要可以使用箭弧连接的都加上箭弧,则得到一个状态转换图,如图3.7所示。
状态转换图观察所求得的有穷自动机的状态转换图,可以发现从初始状态到终止状态之间存在两条较短的路径,它们分别为{<MG> <M> <MW> <MG> <MC> <M> <MG>}和{<MG> <M> <MC> <MG> <MW> <M> <MG>}这两条路径就是两种正确的渡河方法。
C语言-人狼羊菜问题-最容易看懂的解决方法及代码
C语⾔-⼈狼⽺菜问题-最容易看懂的解决⽅法及代码题⽬描述:农夫需要把狼、⽺、菜和⾃⼰运到河对岸去,只有农夫能够划船,⽽且船⽐较⼩,除农夫之外每次只能运⼀种东西,还有⼀个棘⼿问题,就是如果没有农夫看着,⽺会偷吃菜,狼会吃⽺。
请考虑⼀种⽅法,让农夫能够安全地安排这些东西和他⾃⼰过河。
想这个问题⼀连想了好⼏天,本⼈没有系统的学过算法,有些概念也不是很清楚,只因解决问题为⽬标。
尝试过图论解决,但⽤floyed算法只能算出最短路径值,如何输出过程,⼀直没想出好的解决⽅法。
然后看了下⾯这篇⽂章,尝试抛弃图论,⽤树的思想来解决这个问题。
建议阅读下⾯代码时,先看看这篇⽂章。
在写代码时,本⼈采⽤了上述⽂章中的思想,⼜借鉴了图论中存储结点的⼀些⽅法。
我觉得这样写应该⾮常容易看懂了。
具体思路见代码。
1 #include <stdio.h>2#define INF 99993//8个动作4char *action[8]={"农夫单独过河","农夫带狼过河","农夫带⽺过河","农夫带菜过河",5"农夫单独返回","农夫带狼返回","农夫带⽺返回","农夫带菜返回"};6//10种状态7char *state[10]={"⼈狼⽺菜","⼈狼⽺","⼈狼菜","⼈⽺菜","⼈⽺","狼菜","狼","⽺","菜","空"};89//状态转换规则:GA[i][j]=k 表⽰【状态i】可以通过【动作k】转换到【状态j】,GA[i][j]=INF表⽰不可直接转换10int GA[10][10]={INF,INF,INF,INF,INF, 2,INF,INF,INF,INF,11 INF,INF,INF,INF,INF,INF, 2, 1,INF,INF,12 INF,INF,INF,INF,INF, 0, 3,INF, 1,INF,13 INF,INF,INF,INF,INF,INF,INF, 3, 2,INF,14 INF,INF,INF,INF,INF,INF,INF, 0,INF, 2,156,INF, 4,INF,INF,INF,INF,INF,INF,INF,16 INF, 6, 7,INF,INF,INF,INF,INF,INF,INF,17 INF, 5,INF, 7, 4,INF,INF,INF,INF,INF,18 INF,INF, 5, 6,INF,INF,INF,INF,INF,INF,19 INF,INF,INF,INF, 6,INF,INF,INF,INF,INF};2021//记录每⼀步的动作22int record_action[20];23//记录每⼀步动作后的状态24int record_state[20];2526//搜索从第step步开始、第i个结点到第n个结点的过程(step从0算起)27void search(int i,int n,int step)28 {29int k;//动作30int j;//可能要转换到的状态31if(i==n)32 {33for(k=0;k<step;k++)34 printf("step %d: %s,左岸还剩 %s\n",k+1,action[record_action[k]],state[record_state[k]]);35 printf("step count:%d\n\n",step);36return;37 }38//查找在当前【状态i】下能转换到的【其它状态j】,并且【状态j】不能在之前出现过39//查找时可能会出现多个 j,所以这是⼀个多叉树40for(k=0;k<8;k++)41 {42for(j=0;j<10;j++)43if(GA[i][j]!=INF&&GA[i][j]==k)//判断状态i能否通过动作k转换到状态j44 {45int m;46//下⾯这个循环是判断状态j在之前是否出现过47for(m=0;m<step;m++)48if(j==record_state[m])break;49if(m<step)continue;50//如果j满⾜前⾯所有条件,则记录这⼀步51 record_action[step]=k; //第step步所使⽤的动作52 record_state[step]=j; //第step步所转换的状态53 search(j,n,step+1); //继续搜索下⼀步54 }55 }5657 }58int main()59 {60 search(0,9,0);61return0;62 }。
人狼羊菜渡河问题(含MATLAB程序)
人狼羊菜渡河问题(含MATLAB程序)人、狼、羊、菜安全渡河问题安全过河问题也被称为“人狼羊菜”问题,具体描述为:一个人带着一只狼、一只羊和一篮白菜过河,但由于船太小,一个人一次只能带一件东西乘船过河。
狼和羊,羊和卷心菜不能单独呆在同一个河岸上,否则羊或卷心菜就会被吃掉。
这个问题可以用图论中的最短路径算法来解决。
问题分析根据题意,人不在场时,狼要吃羊,羊要吃菜,因此,人不在场时,不能将狼与羊、羊与菜留在河的任一岸。
可用四维向量v=(m,n,p,q)来表示状态,m表示人,n代表狼,p代表羊,q代表白菜,且m,n,p,q∈{0,1},0代表在对岸,1代表在此岸。
例如,状态(0,1,1,0)表示人和菜在对岸,而狼和羊在此岸,这时人不在场,狼要吃羊,因此,这个状态是不可行的。
通过穷举法列出所有可行状态。
可行状态是(1,1,1,1),(1,1,1,0),(1,1,0,1),(1,0,1,1),(1,0,1,0),(0,1,0,1),(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,0,0,0)。
有十种可行的状态。
每次过河行为都会改变现有状态。
构造了加权图G=(V,e,w),其中顶点集V={V1,?,V10}(按上述顺序编号)中的顶点分别代表上述10种可行状态。
当且仅当对应的两个可行状态之间存在可行转移时,两个顶点之间存在边连接,且对应的权重为1。
当两个顶点之间没有可行的过渡时,相应的权重可以取为∞.因此问题变为在图g中寻找一条由初始状态(1,1,1,1)出发,经最小次数转移到达最终状态(0,0,0,0)的转移过程,即求从状态(1,1,1,1)到状态(0,0,0,0)的最短路径。
这个问题的难点是计算邻接矩阵。
由于轮渡一次改变现有状态,因此引入了四维状态转移向量来反映轮渡情况。
1表示过河,0表示不过河。
例如,(1,1,0,0)表示人们和狼一起过河。
状态转换只有四种情况,它们由以下向量表示:(1,0,0,0),(1,1,0,0),(1,0,1,0),(1,0,0,1)现在指定状态向量和转换向量之间的运算为0+0=0,1+0=1,0+1=1,1+1=0根据上述定义,如果从可行状态获得的新向量加上转移向量仍然属于可行状态,则对应于两个可行状态的顶点之间存在边。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人、狼、羊、菜安全渡河问题
安全渡河问题又称作“人狼羊菜”问题,其具体描述为:一个人带着一条狼、一只羊、一筐白菜过河但由于船太小,人一次只能带一样东西乘船过河。
狼和羊、羊和白菜不能单独留在同岸,否则羊或白菜会被吃掉。
该问题可使用图论中的最短路算法进行求解。
问题分析
根据题意,人不在场时,狼要吃羊,羊要吃菜,因此,人不在场时,不能将狼与羊、羊与菜留在河的任一岸。
可用四维向量v=(m,n,p,q)来表示状态,m表示人,n代表狼,p代表羊,q代表白菜,且m,n,p,q ∈{0,1},0代表在对岸,1代表在此岸。
例如,状态(0,1,1,0)表示人和菜在对岸,而狼和羊在此岸,这时人不在场,狼要吃羊,因此,这个状态是不可行的。
通过穷举法将所有可行的状态列举出来,可行的状态有
(1,1,1,1),(1,1,1,0),(1,1,0,1),(1,0,1,1),(1,0,1,0),(0,1,0,1),
(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,0,0,0)。
可行状态共有十种。
每一次的渡河行为改变现有的状态。
现构造赋权图
G=(V,E,W),其中顶点集V={v1,…, v10}中的顶点(按照上面的顺序编号)分别表示上述10个可行状态,当且仅当对应的两个可行状态之间存在一个可行转移时两顶点之间才有边连接,并且对应的权重取为1,当两个顶点之间不存在可行转移时,可以把相应的权重取为∞。
因此问题变为在图G中寻找一条由初始状态(1,1,1,1)出发,经最小次数转移到达最终状态(0,0,0,0)的转移过程,即求从状态(1,1,1,1)到状态(0,0,0,0)的最短路径。
该问题难点在于计算邻接矩阵,由于摆渡一次就改变现有状态,为此再引入一个四维状态转移向量,用它来反映摆渡情况。
用1表示过河,0表示未过河。
例如,(1,1,0,0)表示人带狼过河。
状态转移只有四种情况,用如下向量表示:
(1,0,0,0),(1,1,0,0),(1,0,1,0),(1,0,0,1)
现在规定状态向量与转移向量之间的运算为
0+0=0,1+0=1,0+1=1,1+1=0
通过上面的定义,如果某一个可行状态加上转移向量得到的新向量还属于可行状态,则这两个可行状态对应的顶点之间就存在一条边。
用计算机编程时,可以利用普通向量的异或运算实现,具体的Matlab程序如下:
clc,clear
a=[1 1 1 1;1 1 1 0;1 1 0 1;1 0 1 1;1 0 1 0;
0 1 0 1;0 1 0 0;0 0 1 0;0 0 0 1;0 0 0 0];%每一行是一个可行状态
b=[1 0 0 0;1 1 0 0;1 0 1 0;1 0 0 1];%每一行是一个转移状态
w=zeros(10);%邻接矩阵初始化
for i=1:9
for j=i+1:10
for k=1:4
if findstr(xor(a(i,:),b(k,:)),a(j,:))
w(i,j) = 1;
end
end
end
end
w = w,;%变成下三角矩阵
c = sparse(w); %构造稀疏矩阵
[x,y,z]= graphshortestpath(c,1,10,’Directed’,0) %该图是无向图,Directed属性值为0
h = view(biograph(c,[],’ShowArrows’,’off’,’ShowWeights’,’off’));
%画出无向图
Edges = getedgesbynodeid(h);%提取句柄h中的边集
set(Edges,’LineColor’,[0 0 0];%为例将来打印清除,边画成黑
色
set(Edges,’LineWidth’,1.5);%线型宽度设置为1.5
赋权图G之间的状态转移关系如下图所示:
图可行状态之间的转移
最终求得的状态转移顺序之一为:
1 6 3 7
2 8 5 10
对应方案为:经过7次渡河就可以把狼、羊、蔬菜运过河,第一次运羊过河,空船返回;第二次运菜过河,带羊返回;第三次运狼过河,空船返回;第四次运羊过河。
另一种方案同理可由图得,请读者自行写出。
参考文献
[1]司守奎,孙玺菁.数学建模算法与应用[M].北京:国防工业出版社,2015.
[2]郭强,孙浩.运筹学原理与算法[M].西安:西北工业大学出版社,2006.
[3]严蔚敏,吴伟民.数据结构[M].北京:清华大学出版社,2002.。
